Next Article in Journal
Minimizing the Impact of Intermittent Wind Power on Multiperiod Power System Operation with Pumped Hydro Generation
Next Article in Special Issue
Trusted Simulation Using Proteus Model for a PV System: Test Case of an Improved HC MPPT Algorithm
Previous Article in Journal
Research on DFIG-ES System to Enhance the Fast-Frequency Response Capability of Wind Farms
Previous Article in Special Issue
Microcontroller-Based Strategies for the Incorporation of Solar to Domestic Electricity
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 12
Issue 18
10.3390/en12183582
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

A Review on Optimization and Control Methods Used to Provide Transient Stability in Microgrids

by
Seyfettin Vadi
1,
Sanjeevikumar Padmanaban
2,*,
Ramazan Bayindir
3,*,
Frede Blaabjerg
4 and
Lucian Mihet-Popa
5
1
Department of Electronics and Automation, Vocational School of Technical Sciences, Gazi University, 06500 Ankara, Turkey
2
Department of Energy Technology, Aalborg University, 6700 Esbjerg, Denmark
3
Department of Electrical and Electronics Engineering, Faculty of Technology, Gazi University, 06500 Ankara, Turkey
4
Center of Reliable Power Electronics (CORPE), Department of Energy Technology, Aalborg University, 9220 Aalborg, Denmark
5
Faculty of Engineering, Østfold University College, Kobberslagerstredet 5, 1671 Kråkeroy-Fredrikstad, Norway
*
Authors to whom correspondence should be addressed.
Energies 2019, 12(18), 3582; https://doi.org/10.3390/en12183582
Submission received: 26 July 2019 / Revised: 8 September 2019 / Accepted: 10 September 2019 / Published: 19 September 2019
(This article belongs to the Special Issue Power Converters, Electric Drives and Energy Storage Systems for Electrified Transportation and Smart Grid)
Browse Figures
Versions Notes

Abstract

:
Microgrids are distribution networks consisting of distributed energy sources such as photovoltaic and wind turbines, that have traditionally been one of the most popular sources of energy. Furthermore, microgrids consist of energy storage systems and loads (e.g., industrial and residential) that may operate in grid-connected mode or islanded mode. While microgrids are an efficient source in terms of inexpensive, clean and renewable energy for distributed renewable energy sources that are connected to the existing grid, these renewable energy sources also cause many difficulties to the microgrid due to their characteristics. These difficulties mainly include voltage collapses, voltage and frequency fluctuations and phase difference faults in both islanded mode and in the grid-connected mode operations. Stability of the microgrid structure is necessary for providing transient stability using intelligent optimization methods to eliminate the abovementioned difficulties that affect power quality. This paper presents optimization and control techniques that can be used to provide transient stability in the islanded or grid-connected mode operations of a microgrid comprising renewable energy sources. The results obtained from these techniques were compared, analyzing studies in the literature and finding the advantages and disadvantages of the various methods presented. Thus, a comprehensive review of research on microgrid stability is presented to identify and guide future studies.

1. Introduction

Power systems that generate electricity from renewable energy sources have in recent times increased their share in the total installed power capacity of electrical energy generation as a result of various advantages [1]. In addition, this increase in large-scale solar photovoltaic systems and wind power systems has resulted in problems affecting the quality of the electrical power produced [2]. These problems increase the sensitivity of the grid against harmonic distortions and fluctuations, and reduce frequency stability [3,4,5]. Increased use of renewable energy sources in recent years has enabled the supply of clean, cheap and low-cost energy, but has caused several problems in electricity transmission and distribution networks.
Since the 2010s, it has been observed in wind power and solar photovoltaic systems that a limited amount of total reserve capacity can provide energy to the system. At this point, microgrids are the most reliable solution for the integration of renewable energy sources within a wider electricity network. An example of a microgrid is presented in Figure 1 [6].
Microgrids provide a promising solution for today’s electrical energy problems based on the reliable, safe, environment-friendly and sustainable electric energy obtained from renewable energy sources [7]. By restructuring the microgrids, a contribution is made to the activities of energy planning and management, voltage stability and energy efficiency [8,9]. The use of renewable energy sources with an electricity network has negative effects on power quality [10], specifically connection and stability problems. Insufficiencies of active and reactive power capacity in the distribution transformers of different countries cause connection problems [11]. Stability problems are due to insufficiencies of a grid under normal operating conditions [12]. In order to solve these problems, electrical infrastructure needs to be renewed and expanded.
Another source affecting a power system’s stability is the structure of renewable energy sources that the grid connection conducts on power electronic topologies. This problem generally has two effects, the first one being harmonic problems, as inverters generate significant current and voltage harmonics. Additionally, as stated above, it is desirable that the installed power rate of such types of renewable energy source increase in the grid while the total system capacity decrease. The second problem, which is more important, is the stability of grid [13].
Stability of the microgrids is defined as the balanced operation of all elements constituting the grid under normal operation conditions and achieving a reasonable balance following any disturbing effect. Transient stability in a microgrid is defined as the feature of an energy system that enables it to remain in a stable equilibrium state under normal conditions, and that allows it to regain a desired equilibrium after being subjected to disturbances arising from very general situations such as the switching on and off of circuit elements, voltage collapse, voltage and frequency fluctuation, phase difference fault, error in the islanded mode operation and grid-connected operation and so on. In other words, the stability purpose the synchronous operation of alternative energy sources in the grid. [14].
Stability is analyzed under three headings in a framework of the power system analysis: voltage, frequency stability and rotor angle stability [15]. Voltage stability depends on the reactive power balance generated and consumed in the power system, while frequency stability depends on the balance of active powers generated and consumed in the power system. Rotor angle stability is defined as the ability of synchronous generators in the grid to remain synchronized with each other. To achieve constant sinusoidal system frequency, stator voltages of the synchronous generators should run together in the same frequency. Frequency is a result of the mechanical speed of the rotor. For example, if any change occurs in the load, the stator current oscillates at the mechanical speed of the rotor, and hence at the frequency and angle of the rotor of the synchronous generator [16,17].
Ensuring the stability of the microgrids, providing balanced operation, preventing any disturbing impact in the system while switching on and off energy sources and restructuring to introduce a dynamic structure to the present system is realized in [18]. This dynamic structure will reduce the losses by using load management and voltage profiling for the loads on the microgrid. In the event of a fault, the affected zone is isolated, and the restructuring process is carried out by supplying energy to the load by order of importance and increasing usage rates by the specific switching processes [19]. The works of optimum restructuring and transition stability provide some benefits such as efficient usage of energy sources, meeting the energy requirements with the lowest possible cost, minimizing active power losses and switching processes, increasing energy quality accordingly (which ensures voltage stability), increasing network reliability, providing a solution with minimum loss in the event of a fault, increasing the entire system’s efficiency, achieving optimum power quality and providing the necessary capacity [20].
A literature review reveals several studies on microgrids. The design, analysis and control of microgrids are current issues studied in the literature, and researchers have conducted studies on many subjects such as alternative current (AC) and direct current (DC) microgrid control and management, central control architecture, power quality and protection, multiple-agent systems, standards-based information and communication technologies, online optimization techniques and energy management systems [17].
Because of the variety of sources increases in the microgrids, restructuring becomes complicated and restricted. Furthermore, it causes to different combinations and objectivities of the multi-purpose optimization problems [21]. Classical optimization methods are applied to solve this problem; however, in some cases, these methods are an approach to the local minimum rather than the global minimum. Moreover, some classical methods cannot solve integer code problems. These deficiencies have been overcome by the use of evolutionary methods in the literature. The well-known methods used to solve restructuring problems are classified as follows:
  • Heuristic methods, branch changes, branches and limits, single-cycle optimization and loop breaking, etc.
  • Metaheuristic methods such as simulated annealing (SA), the genetic algorithm (GA), evolutionary programming (EP), ant colony optimization (ACO) and the harmony search algorithm (HSA).
  • Artificial neural networks (ANNs) such as machine-learning algorithms.
Each of these methods has advantages and disadvantages. When the studies carried out in the literature are analyzed, it is seen that the problems that arise in providing transient stability in microgrids are solved by these methods. The solution to the problem of providing transient stability includes the components of objective function and system operation constraints. The common objective of all problems of providing transient stability in a microgrid is to achieve power quality and minimize energy cost by connecting to the present network of energy sources at a steady state [22].
This review paper presents the studies in the literature in regards to their contributions to energy efficiency, prioritizing the use of energy regenerated by renewable energy sources, use of optimization and control methods and maintaining a continuity of the energy. To compare the capabilities of the control methods that used in island mode and grid-connected microgrids in terms of transient stability, optimization and control methods are examined. Besides the comparison, advantages, disadvantages and limitations of the control methods are discussed in detail. Another aim of this paper is to examine the research available on microgrid transient stability.

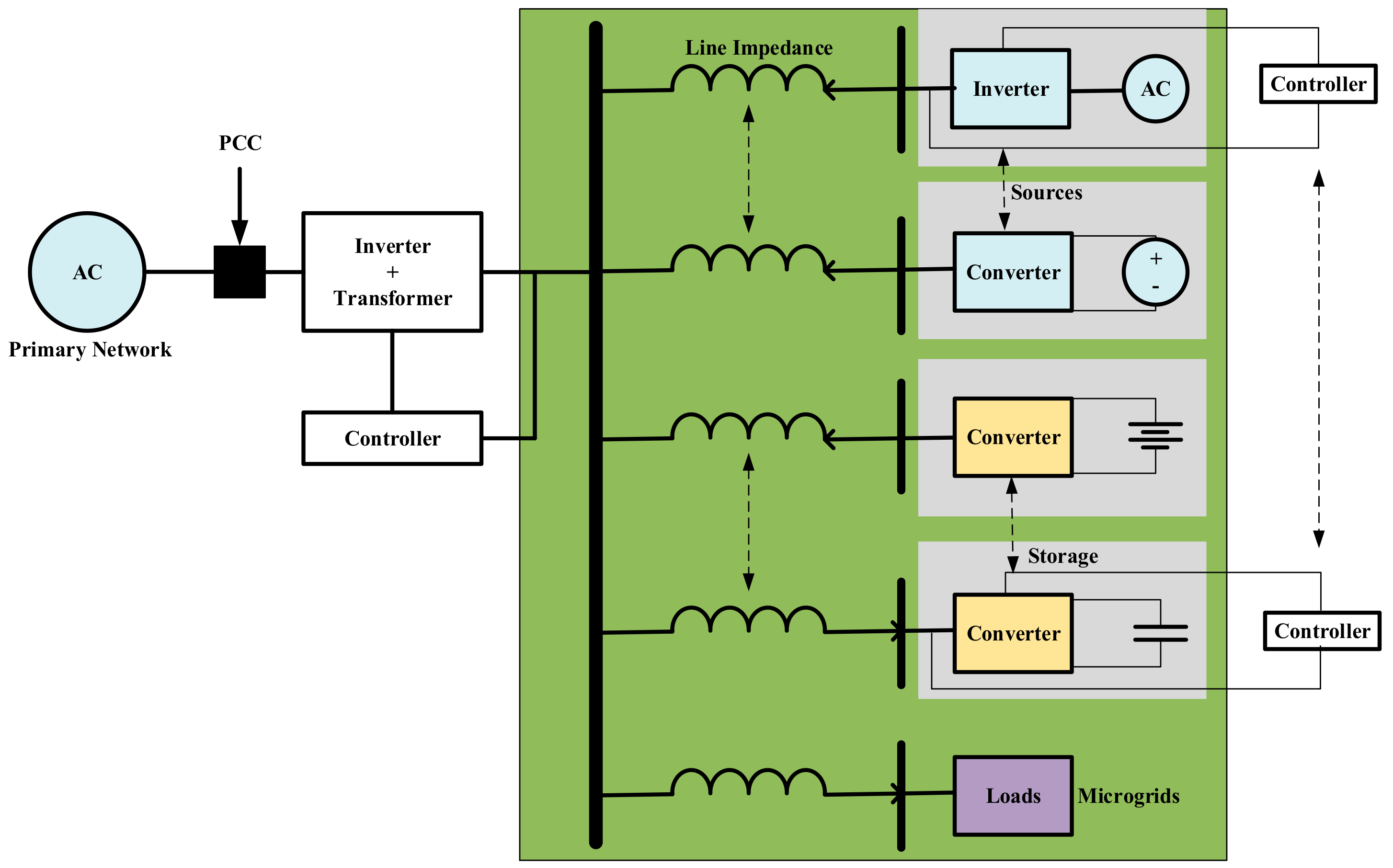
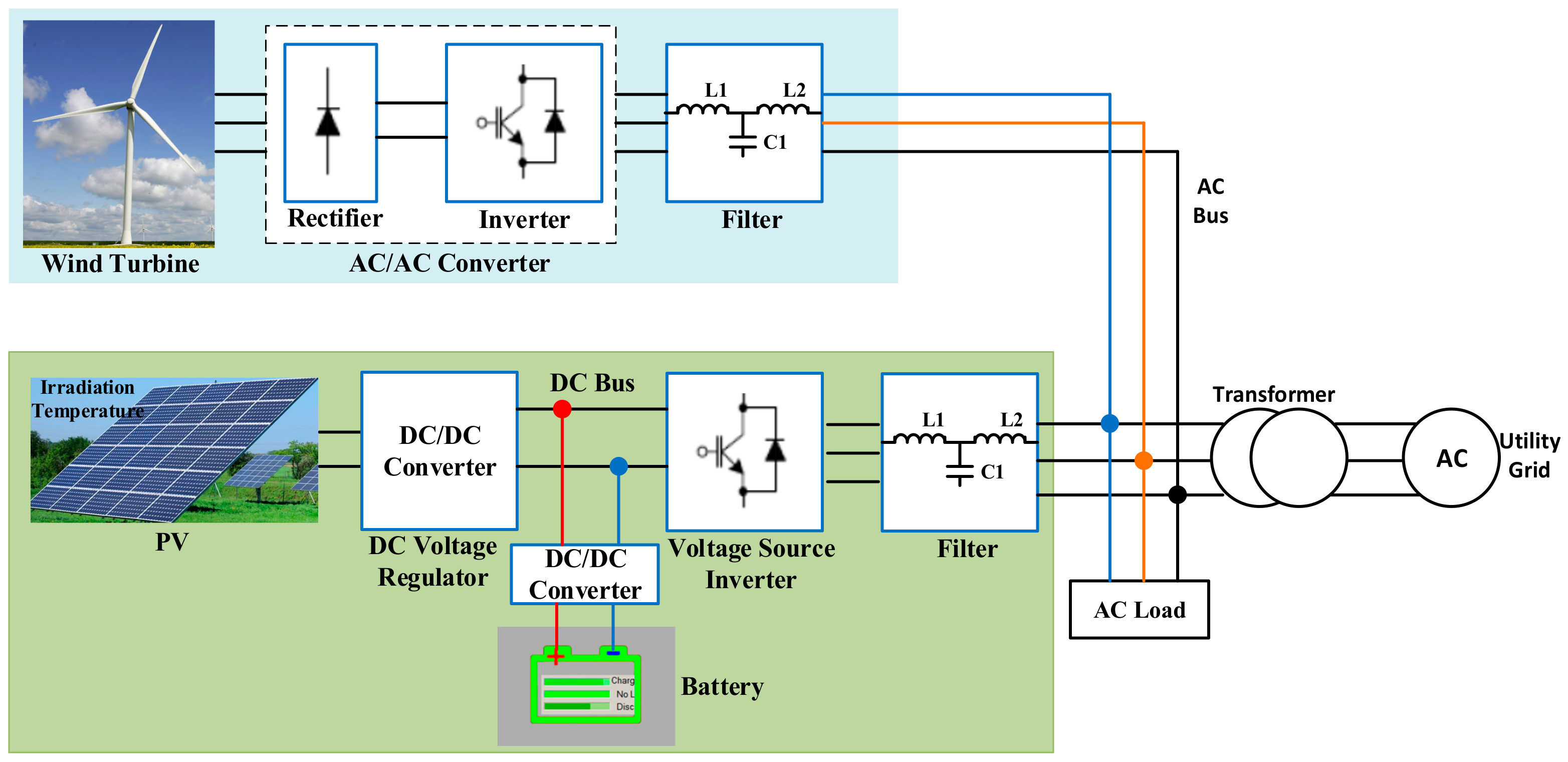
2. Control in Microgrids

There are two main energy source types in microgrids. One of them is a DC source comprising fuel cells, solar panels and batteries, whereas the other source is AC, comprising microturbines and wind turbines in which output voltage is rectified.
Both source types are generally DC sources created by use of an inverter [23]. The inverter structure for a DC source is shown in Figure 2a, and the inverter structure for an AC source is shown in Figure 2b.
Current, voltage and frequency parameters in the output of the inverter are determined by the control method of the inverter. The output voltage is directly related to the intensity of the capacitor voltage on the side of DC. Storage quantity in the capacitors is less than the storage quantity in the rotating field and, therefore, control methods are of great significance [24]. Different application strategies are used to manage the power flow control by depending on source number. It requires an energy management system to activate and deactivate of the sources. [25,26]. Moreover, power flow in the grid connected mode is provided by using sliding mode control (SMC), model predictive control (MPC), power-reactive (PQ) control and droop control—a robust, fuzzy logic control. [27]. A transient in an electrical system is defined by a sudden change in circuit conditions, such as when a system is switched on and off, or a fault occurs. These faults are small signal faults, unbalanced voltage or steady state faults. Firstly, small signal faults cause droop gains and load fluctuations to influence the voltage stability of a grid or microgrid. The small signal faults of grids are analyzed using a linearized model of the network, distributed generations (DGs), control units of DG, and loads. Secondly, voltage and frequency amplitude generated from energy sources cause unbalanced voltage and frequency. As such, voltage and frequency stability should be provided in power systems. Thirdly, steady state fault causes to the tracking error on control operations. [28].
Dynamic and transient analyses are important concepts in power systems. The infrastructure of the main electric grid evolves with the integration of hybrid energy systems that form renewable energy systems. The hybrid microgrid is a grid structure comprising both grid and renewable energy sources, or renewable energy sources only. As shown in Figure 3, hybrid microgrids can comprise more than one energy source in the same distribution grid [29,30]. In renewable energy sources or hybrid energy systems, this situation can be prevented using control algorithms that run independently of system parameters, such as the sliding mode control method, whereas unknown system parameters or changes in system control algorithm parameters that depend on model parameters, such as the model predictive control method, adversely affect control efficiency [31,32].
The stability conditions in microgrids used in the literature are presented in Figure 4 [33,34,35,36,37]. Stability methods have been applied in both grid-connected mode and islanded mode. These methods are used to provide small signal, voltage and frequency stability. The stability is implemented in the short term, ultra-short term and long term.

3. Transient Stability in Grid-Connected Microgrids

The dynamic response of grid-connected microgrids were examined using different control strategies based on an analysis of dynamic behavior of the system when exposed to the fault current and important distortions in the distributed energy systems [38]. Recent studies have focused on simulation studies of transient stability in grid-connected microgrids, and the studies analyzed in the literature have generally used MATLAB/SIMULINK platforms [39]. Methods employed in grid-connected microgrids are presented in Figure 5. These methods are use a single algorithm, hybrid algorithm or an algorithm created by the use of computer software tools [40]. These methods have advantages and disadvantages when compared with each other. Optimization algorithms, such as genetic, particle swarm and artificial bee colony algorithms (as well as others), are used in respect to frequency, voltage regulation and the reduction of current ripple for transient stability in AC or DC microgrids comprising wind turbines, photovoltaic energy, fuel cells, battery energy storage systems and flywheel energy storage while operating in islanded mode. Proportional and integral (PI), proportional and derivative (PD) or proportional, derivative and integral (PID) control methods are generally used in a feedback system. However, parameters of these methods are defined as constant while the algorithm designing, it negatively affect the system in cases of resource or load change. The automatic adjustment of parameters is required in order to eliminate negative statements [41]. The optimization algorithms used to automatically adjust parameters are given in Figure 5.
The genetic algorithm (GA) is effective and useful in areas where a search space is large and complex, and where a solution is very difficult to achieve in a limited search space. This algorithm is commonly used in situations that are not expressed in a particular mathematical model [42]. The particle swarm algorithm starts with a population containing random solutions and tries to provide an optimum response by updating each iteration. Iteration number, swarm quantity, correction factor and inertia moment are important for this algorithm [43]. In particle swarm optimization (PSO), particles change their position until the number of iterations is completed. Thus, each particle benefits from the experience of not only the best particle in the swarm, but also all other particles in the swarm.
The artificial bee colony (ABC) algorithm determines least amount of energy necessary for honeybees to travel the shortest path between their home and a food source according to environmental conditions in the natural environment. This system in bees is applied to power systems, and the optimum solution is searched. Since the control parameter is low, it has a simple structure that can be used for both numerical and discrete problems. Furthermore, the algorithm is used both alone and as a hybrid. When the algorithm is used as a hybrid in a power system, structures emerge that are more dynamic and possess greater stability [44].
The use of algorithms in microgrids is a very sensitive and important issue for a grid in terms of control and coordination of the distributed generation systems. It has been seen that the frequency and voltage values of a system are generally set by the grid according to the co-functioning of the microgrid with the distribution grid, and a cost analysis of grid-connected microgrids has been realized in the literature [45,46,47,48]. The maximum efficiency of renewable energy sources is achieved using optimization and control algorithms, as well as by utilizing the most efficient use of storage members and by supplying the minimum amount of energy from the grid to ensure stable operation of the system with minimum cost [49].
Microgrids are connected to the system with a power electronic converter and inverter (DC-DC, DC-AC, etc.). Since energy flows occur between parallel energy sources, the energy flows are controlled [46]. This control is generally carried out using the droop control method, a method that is used for sharing power between synchronous generators [50]. The most important characteristic of this method is that it allows power sharing between sources, and does not require communication infrastructure [51]. The relationship between active power-frequency and reactive power-voltage used for droop control is shown in Figure 6. Inverters are connected to the system in parallel according to the used method [52]. This control method is also used for sharing power between uninterrupted power sources (UPS) connected in parallel without a control cable.
Although a high level of reliability and flexibility is achieved by this technique, it also has some disadvantages. For instance, when the loads in the system are non-linear, and harmonic current is taken into consideration, this control method does not share power as a result of power sharing [53]. To solve this problem, harmonic current sharing methods are combined with virtual impedance adding methods, adaptive methods, droop control methods for the smoothest power share and frequency–voltage balance [54]. Another disadvantage of the droop control method is that frequency and voltage values are determined based on the load [55]. To solve this problem, central, non-central (distributed control) and hierarchical control structures are implemented. These are the methods used most commonly in the literature [56].
It has been demonstrated that non-central and hierarchical control methods can provide the production balance of plants with power electronic-based inverters [57]. The requirement of communication infrastructure for the central control method, and redesigning if a new grid is installed, restricts the area of use of this control method [58]. The non-central control method is more appropriate for microgrids—since communication infrastructure is not necessary, it distributes the power more adequately for non-linear loads and works based on local measurements [59,60,61]. In non-central control systems, active–reactive power values and voltage-frequency values are adjusted according to the voltage and current data sent by the distributed generation system.
Numerous droop control techniques have been employed in microgrid applications. For example, droop control methods providing the share of harmonic current [62], droop control methods sharing the power based on the power angle [59], adaptive droop control methods that can adapt to variables [63], droop control methods that can share power by use of virtual impedance [64] and so on have been used in microgrid applications. However, the important disadvantage of these systems is that the voltage and frequency values of microgrids in slanded mode vary by load variation [65]. To eliminate this disadvantage, the secondary control function is enabled. This function follows load and regeneration changes, determines frequency and voltage reference lines and sends a warning to all units. In this way, voltage and frequency fluctuation become a near-zero value [66,67].
The hierarchical control method is a frequently used method for controlling microgrids. It has a three-layer control structure and a method designed to manage power systems with large-scale synchronous machines. Use of this method with some variations for microgrids has been proposed. The first control layer is the primary control, which provides the control of the internal structure of the distributed generation network. The main purpose of this control layer is to control the active and reactive power balance, depending on the frequency and voltage, by imitating synchronous generator behavior. By these means, energy flows between parallel inverters are prevented and power is shared adequately [68].
The second control layer is referred to as the secondary control and is designed to minimize frequency and voltage fluctuations of the system. Due to load and process values of generators in the system, which may vary continuously, voltage and frequency values vary as well [69]. To prevent this fluctuation, the secondary control method is used. Frequency and voltage values of the system are compared to the reference values [70]. The fault statement is sent to all units to prevent disruption of the system balance, and is generally used to maintain the grid frequency fluctuation limit at ±0.2Hz [71]. Characteristics of primary and secondary control methods are presented in Figure 7.
The final control layer is the tertiary control. This control method is used to control the power flow between the microgrid and the main grid. While the microgrid and main grid run together, power flow is controlled by frequency and voltage values.
The frequency value of the main grid is constant. Therefore, power exchanges between the main grid and microgrid depend on the droop characteristic of the microgrid [72,73]. Power exchanges are controlled by changing reference frequency and voltage values of the microgrid [74]. The characteristics of the tertiary control method are shown in Figure 8. As seen in Figure 8, fmg is the frequency at maximum generated power, Emg is the voltage at maximum generated power, Pgmax is the maximum generated power, Qgmax is the maximum reactive power, fg is the frequency generated and Eg is the voltage generated for the tertiary control method. In addition, the tertiary control method shows the relation between f (frequency) and Pgmax (maximum generated active power), as well as between f (frequency) and Qgmax (maximum generated reactive power). These control methods are frequently used in the literature to control different types of microgrids [75], especially AC microgrids, although they have recently started to be applied to DC microgrids [76]. A number of grid elements, such as solar energy systems, storage elements and electric vehicle charging stations, are features of a DC microgrid [77].
Another control method, known as the robust droop control method, is commonly used in distributed loads where there are high-voltage multiple microgrids [78]. As seen in Figure 10, P1 and P2 are active power in the traditional droop control strategy, P1-2 and P2-2 are active power in the proposed control strategy, Q1 and Q2 are reactive power in the traditional droop control strategy and Q1-2 and Q2-2 are reactive power in the proposed control strategy. In Figure 9, the system achieves a stable state condition after a shorter time (around 2 s) compared to the traditional control method, and subsequently shares its power [79].
Moreover, the robust droop control method shares power at a higher voltage level than the traditional droop control method. Reactive power share is not achieved by the traditional droop control method and is equalized to an approximate reference value by the robust droop control method [80,81].

4. Transient Stability in Islanded Mode Microgrids

The transient stability of the islanded mode microgrid is affected by the type of load connected to the system and the responsiveness of the control strategy used for distributed generation (DG) interfaces. Different types of control strategy of the inverter affect all systems, so it is important to provide transient stability.
Frequency, voltage and transient time intervals according to their standards as well as simulated activities in islanded mode are presented in Table 1. A small variation signal in islanded mode causes important distortions in harmonics, active–reactive power balance, frequency and voltage according to this table, and the standards referred to as the optimal operation band are shown in Table 1.
International organizations such as the IEC (International Electrotechnical Commission) and IEEE (Institute of Electrical and Electronics Engineers have defined certain standards for interconnection, operation and control of microgrids in conjunction with the main grid. The standards offer operation ranges relevant to performance, testing, safety and maintenance of the integrated power system. Detection time is the transition time to operation in island mode. Quality factor is an important parameter used to determine the reliability and robustness of any islanding detection mode. Also, nominal voltage and frequency range are optimal operation standards of islanding detection time [82].

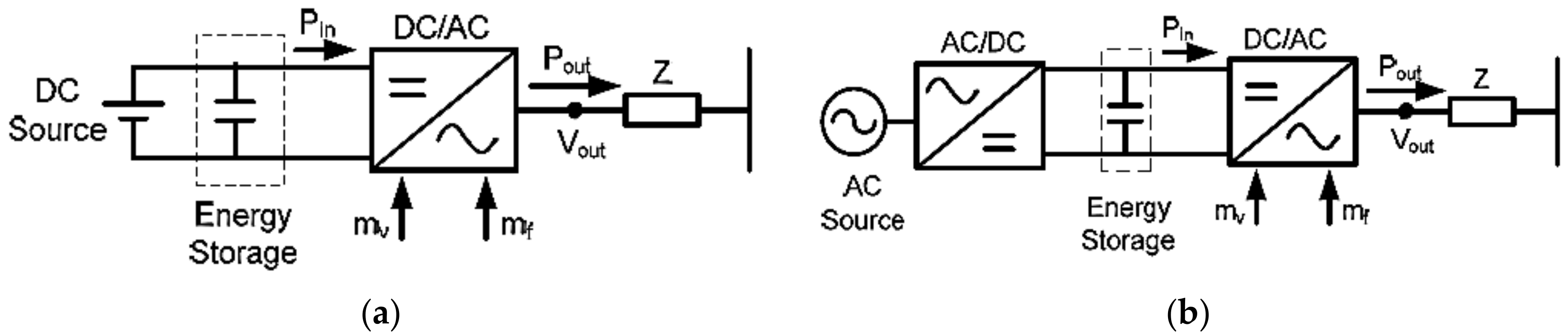
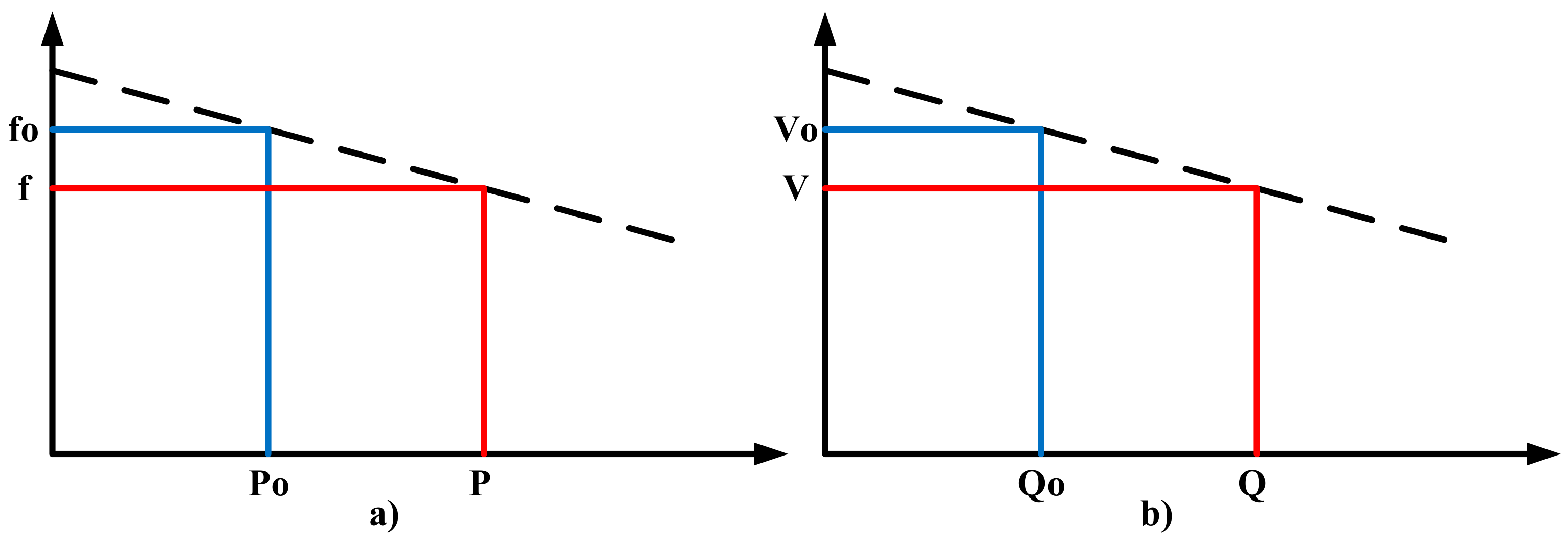
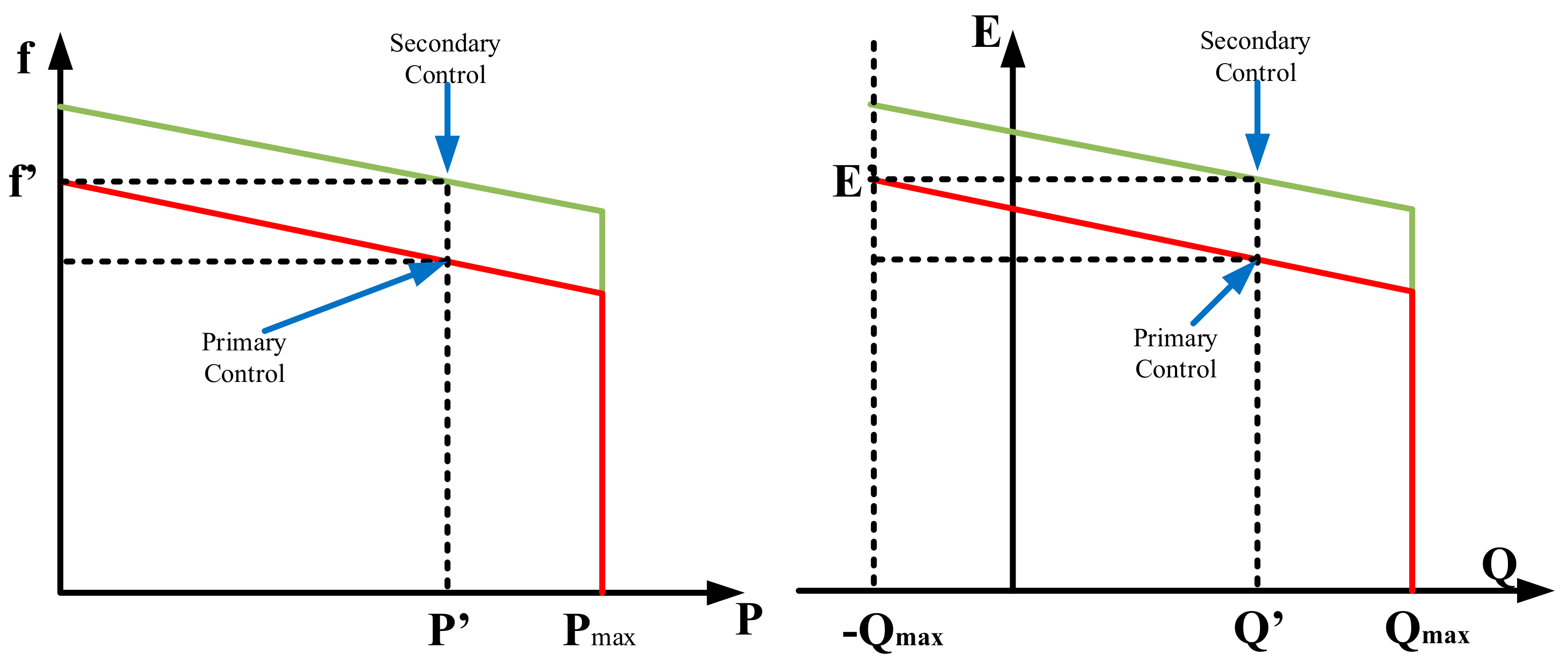
4.1. P-Q Control Methods

The purpose of the P-Q control is to ensure equally distributed generation between active power and reactive power. As seen in Figure 10 and Figure 11, the P-Q control is performed by controlling frequency and voltage control during load sharing. Frequency stability varies by the size of the load. Frequency stability for an overloaded system lasts longer than a less-loaded system. For this reason, the load is shared by the sources for frequency stability [83].

4.2. PI/PID Algorithms

The PI/PID algorithms consisting of a proportional, derivative and integral composition are used to maintain system performance in double-fed asynchronous generator wind turbines in the event of a fault [84]. This algorithm are used to reduce overvoltage and stability errors in a flexible AC transmission systems (FACTS) unit [85], which uses battery systems in the event of voltage and frequency fluctuations to increase energy flow. In the statement of fault in the system, the P-Q control is provided with PI for balanced compensation [86]. Unique PI design is not useful in reducing the harmonics at high frequencies.
The control structure is simple and provides the required performance. Also, it is commonly used in industry. Optimization of three parameters changes the operation points. Moreover, it is not stable enough to adapt itself to the load variations. Since PI/PID controllers are more stable in linear systems, the structure does not show stable behavior due to the dynamic behavior of non-linear systems [86].

4.3. Model Predictive Control Method

The facts that concepts in the MPC management are simple and the controller is heuristic are considered a significant advantage. MPC is a control strategy devised for both large, multiple input–output control problems, and for inequality constraints on the inputs or outputs. MPC design parameters should be chosen carefully. MPC is the preferred solution for difficult control problems [87,88].
The operating principle of an MPC controller is shown in Figure 12. This control method is an algorithm that is used to predict the future behavior of a system. Free and forced response are the prediction components of this method. The expected behavior of system output y (t+j) is shown by free response. In addition, it is accepted that the future values of the actuating variables will be equal to zero. The additional component of the system response is formed by forced response, which is based on the pre-calculated set of future-actuating values u (t+j).
The total response of system behavior is determined as the sum of free and forced responses for the entire future system’s behavior in linear systems. The sum process is calculated using the superposition principle. This sum is pre-calculated up to a prediction horizon, which is determined by a set of future reference values output by the system. The difference in future control error between the future reference and pre-calculated actual values is then obtained. This method takes system restrictions and the cost function into account, and a set of optimum future values u (t+j) from the expected error are determined by this method [88,89].
The MPC leads to a high calculation density because of the pre-calculation of the system’s behavior. The calculation density is significantly reduced at a control horizon. When the horizon is reached in a steady state, the controller output remains constant. This situation is shown Figure 13.
The MPC is used to eliminate the following errors in the grid-connected operation and excessive values using fuzzy logic to reduce fluctuations and eliminate the adverse effects of time delay and stability errors. The MPC estimates the critical parameters while evaluating them. It is also used to minimize harmonics in the network current via advanced estimation algorithm, which is used under the adaptive current control for three phases in normal operation mode [90].
Advantages of the MPC method can be listed as follows:
  • Concepts are very heuristic and easy to understand;
  • It is used in multi-variable systems;
  • It prevents idle time;
  • Addition of non-linear structures is easy;
  • Constraints are eliminated by simple solutions.
Extension to the controller is very easy in many application systems.
Disadvantages of the MPC method compared to the classical controllers can be listed as follows:
  • It has numerous mathematical operations;
  • Quality of the model created affects the controlling performance directly;
  • Addition or removal in the systems requires regulations in the controller.
The MPC controls the interaction and constraints between the variables and selects the optimal strategy. In this way, it completes the operation quickly and provides economic benefits. It predicts dynamic behavior in linear or non-linear systems, and is more proper for multi-variable systems. The model is defined correctly, and while unknown parameters are not dealt with, performance analysis is quite difficult [90].

4.4. Linear Quadratic Control Applications

The linear quadratic control (LQC) method is used to eliminate oscillation in three-phase inverters, harmonic distortion and voltage and frequency degradation in grid-connected photovoltaic systems. DC voltage in the inverter is used to compensate for the voltage in the line and optimize energy flow to the loads. Stable operation in different models of the algorithm is used to eliminate small-scale noise and regulate voltage and current. At a low-level DC voltage, a Kalman filter is used to reduce the oscillation in the output [91]. Linear quadratic control, which is one of the optimal control methods, has a more stable structure than the PI/PID control algorithm since matrix weights are adjusted simply. However, the analytical solution of the algorithm is quite difficult and does not work in the event of constraints [92].

4.5. Sliding Model Control Method

The SMC is a control method used in non-linear systems and discretely timed running systems. It carries out the control as a function of systems switching at high frequencies. The essential principle of the control is that a certain sliding manifold (surface) uses a reference path as an orbit, and the controlled system can be directed to the required balance point [93]. The main advantage of a system having SMC characteristics is that it guarantees stability and robustness against parameter uncertainties [94]. The SMC is used for providing feedback for variable-rate wind turbines and the continuity of wind turbines in the event of a fault with the present fixed-switching method. It is also used for the grid-connected three-phase inverter, to provide reliability and stability in distributed generation. By means of dynamic behavior against uncertainties and distortion, it is used more in non-linear systems. It is mathematically responsive due to a low computational process [95].

4.6. Robust Control Method

The robust control method (RCM) is the control approach designed to absorb faults in the event of uncertain parameters and degradation. It is commonly used in microgrid applications [96], especially for maintaining stability in the grid-connected mode and current control in three-phase inverters, as well as to rectify frequency fluctuations in grid-connected inverters [97]. Moreover, it is used to eliminate uncertainties in control systems generally, as well as cross-linking applications between communication paths. However, it may not be practical in large-scale applications since there is no constraint [98].

4.7. Particle Swarm Algorithm Applications

The PSO is an algorithm developed by observing social behaviors of bird and fish shoal, which is used to improve PI/PID parameters [99]. The algorithm begins with a population including random solutions and updates in every iteration, and tries to give the optimum response. The PSO automatically adjusts the gains of the PI/PID controller in the circuit to maintain the required performance [100]. It designates the most suitable position or value [101] and is used to improve the energy quality in designating the position and layout of distributed regeneration [102]. It is generally used for the optimization of non-linear, non-derivative and multi-mode functions. In addition to being simple and easy to implement, it also has an adjustable parameter structure. The disadvantage of the PSO algorithm is that while it is close to optimal levels, its calculation time depends on the adjustment time of the PSO parameters [103,104,105,106].

5. Discussion

In distributed generation, load sharing between production and distribution is performed by a primary control. This is the first and main step of microgrid transient control. The primary control provides the voltage and frequency stability between consumption and production in an on-gird microgrid. This paper aimed to introduce the control methods used in transient stability of microgrids and clearly explain its advantages and disadvantages.
For this purpose, the control methods used for transient stability have been given in Table 2. The control methods, including MPC, SMC, LQC and PSO, provide a reduced voltage and frequency ripple, transient stability among energy sources and prevention of voltage collapse. However, they also require well-known parameters belonging to the mathematical model of the system in order to use the control methods. Unlike these methods, the droop control method has worked to measure the system parameters belonging to the distributed operation of microgrids composed of renewable energy sources. In addition, the usage of this method is simple. The method provides steady and precise results on frequency stability of an overloaded system, and on power-share at high voltages, regardless of constraints or limitations. This paper presents droop control as the most highly preferred method for microgrid stability. The PSO algorithm starts with a population containing random solutions and tries to provide the optimum response by updating each iteration as the particles change their position until the number of iterations is completed. Thus, each particle benefits from the experience of not only the best particle in the swarm, but also all other particles in the swarm.
Since the ABC algorithm has very few control parameters, the system response is simple and faster when compared to other algorithms. It can be used for both numerical and discrete problems. GA is effective and useful in areas where the search space is large and complex, although it is very difficult to discover the solution with a limited search space. This algorithm is commonly used in situations that are not expressed in a particular mathematical model.

6. Conclusions and Evaluation

Modern society faces energy sustainability problems as energy demand increases and electricity transmission and distribution lines become old. Modernization of conventional grid architecture, innovative solutions and technologies and global warming are leading to limited investments, energy product systems and energy dependency. This study aims to raise awareness of the studies present in the literature in terms of contributing to energy efficiency, and to prioritize the use of energy regenerated by renewable energy sources through optimization and control methods in maintaining the continuation of energy.
Optimization and control methods were investigated to control the microgrid and provide transient stability in an islanded mode for grid-connected microgrids. In addition, this research paper is a preliminary examination of the frequency and voltage control strategy of islanded mode among grid-connected microgrids. The effect of optimization and control methods on reducing switching losses and pressure of the power electronic components of the inverter and converter are great. It is considered that developing the existing solutions as proposed in the literature and implementing them in the future will make significant technical contributions that could increase the total installed power rate of renewable energy plants for electric energy regeneration, and accordingly maintain the frequency stability of the grid.
The classification methods given in this review paper will help researchers select appropriate control methods that are used for microgrid transient stability, such as voltage collapse, voltage and frequency fluctuation, phase difference fault, error in the islanded mode operation and grid-connected operation. Therefore, the control method contributes to providing accurate microgrid transient stability. The fast dynamic response, stability, dynamic behavior, harmonic distortion, transient response, connection type, energy source type, voltage level, voltage–frequency control and behavior in the non-linear loads of each method are examined regularly. Therefore, it is helpful to conduct research on control methods used in microgrid transient stability. This study on the advantages and disadvantages of control and optimization algorithms, which are used for microgrid transient stability, could provide suggestions for further research and applications.

Author Contributions

All authors contributed equally for the research activities and for its final presentation as a full manuscript.

Funding

No source of funding for this research activity.

Acknowledgments

The authors would like to acknowledge the support and technical expertise received from the center for Bioenergy and Green Engineering, and Center of Reliable Power Electronics (CORPE) Department of Energy Technology, Aalborg University, Esbjerg, Denmark, which made this publication possible.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zhang, D.; Evangelisti, S.; Lettieri, P.; Papageorgiou, L.G. Economic and environmental scheduling of smart homes with microgrid: DER operation and electrical tasks. Energy Convers. Manag. 2016, 110, 113–124. [Google Scholar] [CrossRef] [Green Version]
  2. Camblong, H.; Baudoin, S.; Vechiu, I.; Etxeberria, A. Design of a SOFC/GT/SCs hybrid power system to supply a rural isolated microgrid. Energy Convers. Manag. 2016, 117, 12–20. [Google Scholar] [CrossRef]
  3. Siksnelyte, I.; Zavadskas, E.K.; Streimikiene, D.; Sharma, D. An overview of multi-criteria decision-making methods in dealing with sustainable energy development issues. Energies 2018, 11, 2754. [Google Scholar] [CrossRef]
  4. Blechinger, P.; Cader, C.; Bertheau, P.; Huyskens, H.; Seguin, R.; Breyer, C. Global analysis of the techno-economic potential of renewable energy hybrid systems on small islands. Energy Policy 2016, 98, 674–687. [Google Scholar] [CrossRef]
  5. Singh, S.; Singh, M.; Kaushik, S.C. Feasibility study of an islanded microgrid in rural area consisting of PV, wind, biomass and battery energy storage system. Energy Convers. Manag. 2016, 128, 178–190. [Google Scholar] [CrossRef]
  6. Rahbar, K.; Chai, C.C.; Zhang, R. Energy cooperation optimization in microgrids with renewable energy integration. IEEE Trans. Smart Grid 2018, 9, 1482–1493. [Google Scholar] [CrossRef]
  7. Carli, R.; Dotoli, M. Decentralized control for residential energy management of a smart users’ microgrid with renewable energy exchange. IEEE/CAA J. Automatica Sinica 2019, 6, 641–656. [Google Scholar] [CrossRef]
  8. Siddaiah, R.; Saini, R.P. A review on planning, configurations, modeling and optimization techniques of hybrid renewable energy systems for off grid applications. Renew. Sustain. Energy Rev. 2016, 58, 376–396. [Google Scholar] [CrossRef]
  9. Dragičević, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC microgrids—Part II: A review of power architectures, applications, and standardization issues. IEEE Trans. Power Electron. 2016, 31, 3528–3549. [Google Scholar] [CrossRef]
  10. Khatib, T.; Ibrahim, I.A.; Mohamed, A. A review on sizing methodologies of photovoltaic array and storage battery in a standalone photovoltaic system. Energy Convers. Manag. 2016, 120, 430–448. [Google Scholar] [CrossRef]
  11. Louie, H. Operational analysis of hybrid solar/wind microgrids using measured data. Energy Sustain. Dev. 2016, 31, 108–117. [Google Scholar] [CrossRef]
  12. An, L.N.; Tuan, T.Q. Dynamic programming for optimal energy management of hybrid wind–PV–diesel–battery. Energies 2018, 11, 3039. [Google Scholar] [CrossRef]
  13. Sinha, S.; Chandel, S.S. Prospects of solar photovoltaic–micro-wind based hybrid power systems in western Himalayan state of Himachal Pradesh in India. Energy Convers. Manag. 2015, 105, 1340–1351. [Google Scholar] [CrossRef]
  14. Kuang, Y.; Zhang, Y.; Zhou, B.; Li, C.; Cao, Y.; Li, L.; Zeng, L. A review of renewable energy utilization in islands. Renew. Sustain. Energy Rev. 2016, 59, 504–513. [Google Scholar] [CrossRef]
  15. Bingol, O.; Burcin Ozkaya, B. Analysis and comparison of different PV array configurations under partial shading conditions. Solar Energy 2018, 160, 336–343. [Google Scholar] [CrossRef]
  16. Sandhu, E.M.; Thakur, D.T. Issues, challenges, causes, impacts and utilization of renewable energy sources-grid integration. Int. J. Eng. Res. Appl. 2014, 4, 636–643. [Google Scholar]
  17. Amjad, A.M.; Salam, Z. A review of soft computing methods for harmonics elimination PWM for inverters in renewable energy conversion systems. Renew. Sustain. Energy Rev. 2014, 3, 141–153. [Google Scholar] [CrossRef]
  18. Dhakouani, A.; Znouda, E.; Bouden, C. Impacts of energy efficiency policies on the integration of renewable energy. Energy Policy 2019, 133, 1–10. [Google Scholar] [CrossRef]
  19. Dou, C.X.; Yang, J.; Li, X.; Gui, T.; Bi, Y. Decentralized coordinated control for large power system based on transient stability assessmen. Electr. Power Energy Syst. 2013, 46, 153–162. [Google Scholar] [CrossRef]
  20. Godpromesse, K.; Raphael, G. An improved direct feedback linearization technique for transient stability enhancement and voltage regulation of power generators. Electr. Power Energy Syst. 2010, 32, 809–816. [Google Scholar]
  21. Bakhshi, M.; Hosein, M.; Holakooie, H.; Rabiee, A. Fuzzy based damping controller for TCSC using local measurements to enhance transient stability of power systems. Electr. Power Energy Syst. 2017, 85, 12–21. [Google Scholar] [CrossRef]
  22. Huang, T.; Wang, J. A practical method of transient stability analysis of stochastic power systems based on EEAC. Electr. Power Energy Syst. 2019, 107, 167–176. [Google Scholar] [CrossRef]
  23. Andishgar, M.H.; Gholipour, E.; Hooshmand, R.A. An overview of control approaches of inverter-based microgrids in islanding mode of operation. Renew. Sustain. Energy Rev. 2017, 80, 1043–1060. [Google Scholar] [CrossRef]
  24. Roslan, M.F.; Hannan, M.A.; Ker, P.J.; Uddin, M.N. Microgrid control methods toward achieving sustainable energy management. Appl. Energy 2019, 240, 583–607. [Google Scholar] [CrossRef]
  25. Kamgarpour, M.; Beyss, C.; Fuchs, A. Reachability-based control synthesis for power system stability. IFAC-PapersOnLine 2016, 49, 238–243. [Google Scholar] [CrossRef]
  26. Urtasun, A.; Sanchis, P.; Luis Marroyo, L. State-of-charge-based droop control for stand-alone AC supply systems with distributed energy storage. Energy Convers. Manag. 2015, 106, 709–720. [Google Scholar] [CrossRef] [Green Version]
  27. Rokrok, E.; Shafie-Khah, M.; João, P.; Catalão, S. Review of primary voltage and frequency control methods for inverter-based islanded microgrids with distributed generation. Renew. Sustain. Energy Rev. 2018, 82, 3225–3235. [Google Scholar] [CrossRef]
  28. Subramanian, A.S.R.; Gundersen, T.; Adams, T.A. Modeling and simulation of energy systems: A review. Processes 2018, 6, 238. [Google Scholar] [CrossRef]
  29. Yazdanian, M.; Mehrizi-Sani, A. Distributed control techniques in microgrids. IEEE Trans. Smart Grid 2014, 5, 2901–2909. [Google Scholar] [CrossRef]
  30. Dragičević, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC microgrids—Part I: A review of control strategies and stabilization techniques. IEEE Trans. Power Electr. 2016, 31, 4876–4891. [Google Scholar]
  31. Irmak, E.; Güler, N. A model predictive control-based hybrid MPPT method for boost converters. Int. J. Electr. 2019, 1–16. [Google Scholar] [CrossRef]
  32. Hou, B.; Liu, J.; Dong, F.; Wang, M.; Anle Mu, A. Sliding mode control strategy of voltage source inverter based on load current sliding mode observer. In Proceedings of the IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 1–5. [Google Scholar]
  33. Zahraee, S.M.; Khalaji Assadi, M.; Saidur, R. Application of artificial intelligence methods for hybrid energy system optimization. Renew. Sustain. Energy Rev. 2016, 66, 617–630. [Google Scholar] [CrossRef]
  34. Guerrero, J.M.; Chandorkar, M.; Lee, T.L.; Loh, P.C. Advanced control architectures for intelligent microgrids—Part I: Decentralized and hierarchical control. IEEE Trans. Ind. Electr. 2013, 60, 1254–1262. [Google Scholar] [CrossRef]
  35. Zhaoxia, X.; Haodong, F.; Guerrero, J.M.; Hongwei, F. Hierarchical control of a photovoltaic/battery based DC microgrid including electric vehicle wireless charging station. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 5–8 November 2017; pp. 2522–2527. [Google Scholar]
  36. Mi, Y.; Zhang, H.; Fu, Y.; Wang, C.; Loh, P.C.; Wang, P. Intelligent power sharing of DC isolated microgrid based on fuzzy sliding mode droop control. IEEE Trans. Smart Grid 2018, 10, 2396–2406. [Google Scholar] [CrossRef]
  37. Dufo-López, R.; Cristóbal-Monreal, I.R.; Yusta, J.M. Optimisation of PV-winddiesel-battery stand-alone systems to minimise cost and maximise human development index and job creation. Renew. Energy 2016, 94, 280–293. [Google Scholar]
  38. Yan, J.; Liu, Y.; Han, S.; Wang, Y.; Feng, S. Reviews on uncertainty analysis of wind power forecasting. Renew. Sustain. Energy Rev. 2015, 52, 1322–1330. [Google Scholar] [CrossRef]
  39. Sinha, S.; Chandel, S.S. Review of recent trends in optimization techniques for solar photovoltaic–wind based hybrid energy systems. Renew. Sustain. Energy Rev. 2015, 50, 755–769. [Google Scholar] [CrossRef]
  40. Chauhan, A.; Saini, R.P. A review on integrated renewable energy system based power generation for stand-alone applications: Configurations, storage options, sizing methodologies and control. Renew. Sustain. Energy. Rev. 2014, 38, 99–120. [Google Scholar] [CrossRef]
  41. Kato, T.; Kimpara, Y.; Tamakoshi, T.; Kurimoto, M.; Funabashi, T.; Sugimoto, S. An experimental study on dual P-f droop control of photovoltaic power generation for supporting grid frequency regulation. IFAC PapersOnLine 2018, 51, 622–627. [Google Scholar] [CrossRef]
  42. Puri, V.; Jha, S.; Kumar, R.; Priyadarshini, I.; Son, L.H.; Abdel-Basset, M.; Elhoseny, M.; Long, H.V. A Hybrid Artificial Intelligence and Internet of Things Model for Generation of Renewable Resource of Energy. IEEE Access 2019, 7, 111181–111191. [Google Scholar] [CrossRef]
  43. Al Busaidi, A.S.; Kazem, H.A.; Al-Badi, A.H.; Farooq Khan, M. A review of optimum sizing of hybrid PV–Wind renewable energy systems in Oman. Renew. Sustain. Energy Rev. 2016, 53, 185–193. [Google Scholar] [CrossRef]
  44. Upadhyay, S.; Sharma, M.P. A review on configurations, control and sizing methodologies of hybrid energy systems. Renew. Sustain. Energy Rev. 2014, 38, 47–63. [Google Scholar] [CrossRef]
  45. Fathima, A.H.; Palanisamy, K. Optimization in microgrids with hybrid energy systems–A review. Renew. Sustain. Energy Rev. 2015, 45, 431–446. [Google Scholar] [CrossRef]
  46. Shivarama Krishna, K.; Sathish Kumar, K. A review on hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2015, 52, 907–916. [Google Scholar] [CrossRef]
  47. Askarzadeh, A. Optimisation of solar and wind energy systems: A survey. Int. J. Ambient Energy 2017, 38, 653–662. [Google Scholar] [CrossRef]
  48. Erdinc, O.; Uzunoglu, M. Optimum design of hybrid renewable energy systems: Overview of different approaches. Renew. Sustain. Energy Rev. 2012, 16, 1412–1425. [Google Scholar] [CrossRef]
  49. Fadaee, M.; Radzi, M.A.M. Multi-objective optimization of a stand-alone hybrid renewable energy system by using evolutionary algorithms: A review. Renew. Sustain. Energy Rev. 2012, 16, 3364–3369. [Google Scholar] [CrossRef]
  50. Luna-Rubio, R.; Trejo-Perea, M.; Vargas-Vázquez, D.; Ríos-Moreno, G.J. Optimal sizing of renewable hybrids energy systems: A review of methodologies. Sol. Energy 2012, 86, 1077–1088. [Google Scholar] [CrossRef]
  51. Bourennani, F.; Rahnamayan, S.; Naterer, G.F. Optimal design methods for hybrid renewable energy systems. Int. J. Green Energy 2014, 12, 148–159. [Google Scholar] [CrossRef]
  52. Bidram., A.; Davoudi., A. Hierarchical structure of microgrids control system. IEEE Trans. Smart Grid 2012, 3, 1963–1976. [Google Scholar] [CrossRef]
  53. Yang, X.; Su, J.; Lü, Z.; Liu, H.; Li, R. Overview on micro-grid technology. Proc. CSEE 2014, 34, 57–70. [Google Scholar]
  54. Naeem, A.; Hassan, N.U.; Yuen, C.; Muyeen, S.M. Maximizing the economic benefits of a grid-tied microgrid using solar-wind complementarity. Energies 2019, 12, 395. [Google Scholar] [CrossRef]
  55. Wang, Y.; Jiang, H.; Zhou, L.; Xing, P. An Improved Adaptive Droop Control Strategy for Power Sharing in Micro-Grid. In Proceedings of the 8th International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 27–28 August 2016. [Google Scholar]
  56. European-Commission. Renewable Energy Progress Report. Available online: europa.eu/rapid/press-release_IP-15-5180_en.pdf (accessed on 12 September 2015).
  57. Leisen, R.; Steffen, B.; Weber, C. Regulatory risk and the resilience of new sustainable business models in the energy sector. J. Cleaner Prod. 2019, 219, 865–878. [Google Scholar] [CrossRef]
  58. Khan, W.; Ahmad, F.; Alam, M.S. Fast EV charging station integration with grid ensuring optimal and quality power exchange. Eng. Sci. Technol. Int. J. 2019, 22, 143–152. [Google Scholar] [CrossRef]
  59. Mahmoud, M.S.; Alyazidi, N.M.; Abouheaf, M.I. Adaptive intelligent techniques for microgrid control systems: A survey. Int. J. Electr Power Energy Syst. 2017, 90, 292–305. [Google Scholar] [CrossRef]
  60. Xiangning, X.; Zheng, C.; Nian, L. Integrated mode and key issues of renewable energy sources and electric vehicles’ charging and discharging facilities in microgrid. Trans. China Electrotech. Soc. 2013, 28, 1–14. [Google Scholar]
  61. Monica, P.; Kowsalya, M. Control strategies of parallel operated inverters in renewable energy application: A review. Renew. Sustain. Energy Rev. 2016, 65, 885–901. [Google Scholar] [CrossRef]
  62. Bouzid, A.M.; Sicard, P.; Hicham Chaoui, H.; Cheriti, A.; Sechilariu, M.; Guerrero, M.J. A novel decoupled trigonometric saturated droop controller for power sharing in islanded low-voltage microgrids. Electr. Power Syst. Res. 2019, 168, 146–161. [Google Scholar] [CrossRef]
  63. Monica, P.; Kowsalya, M.; Tejaswi, P.C. Control of parallel-connected inverters to achieve proportional load sharing. Energy Procedis 2017, 117, 600–606. [Google Scholar] [CrossRef]
  64. Lu, X.; Guerrero, J.M.; Sun, K.; Vasquez, J.C. An improved droop control method for DC microgrids based on low bandwidth communication with DC bus voltage restoration and enhanced current sharing Accuracy. IEEE Trans. Power Electron. 2014, 29, 1800–1813. [Google Scholar] [CrossRef]
  65. Rodriguez-Diaz, E.; Vasquez, J.C.; Guerrero, J.M. Potential energy savings by using direct current for residential applications: A Danish household study case. In Proceedings of the 2017 IEEE Second International Conference on DC Microgrids (ICDCM), Bamberg, Germany, 27–29 June 2017; pp. 547–552. [Google Scholar]
  66. Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of power converters in AC microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
  67. Shariatzadeh, F.; Kumar, N.; Srivastava, A.K. Optimal control algorithms for reconfiguration of shipboard microgrid distribution system using intelligent techniques. IEEE Trans. Ind. Appl. 2017, 53, 474–482. [Google Scholar] [CrossRef]
  68. Guerrero, J.M.; Loh, P.C.; Lee, T.L.; Chandorkar, M. Advanced control architectures for intelligent microgrids—Part II: Power quality, energy storage, and AC/DC microgrids. IEEE Trans. Ind. Electr. 2013, 60, 1263–1270. [Google Scholar] [CrossRef]
  69. Sadeghkhani, I.; Golshan, M.E.H.; Mehrizi-Sani, A.; Guerrero, J. Low voltage ride-through of a droop-based three-phase four-wire grid-connected microgrid. IET Gener. Transm. Distrib. 2018, 12, 1906–1914. [Google Scholar] [CrossRef]
  70. Li, C.; Chaudhary, S.K.; Savaghebi, M.; Vasquez, J.C.; Guerrero, J.M. Power flow analysis for low-voltage AC and DC microgrids considering droop control and virtual impedance. IEEE Trans. Smart Grid 2017, 8, 2754–2764. [Google Scholar] [CrossRef]
  71. Mohammad, S.; Afsharnia, A.S. A robust nonlinear stabilizer as a controller for improving transient stability in micro-grids. ISA Trans. 2017, 66, 46–63. [Google Scholar]
  72. He, Y.; Kockelman, K.M.; Perrine, K.A. Optimal locations of U.S. fast charging stations for long-distance trip completion by battery electric vehicles. J. Cleaner Prod. 2019, 214, 452–461. [Google Scholar] [CrossRef]
  73. Qin, M.; Chan, K.W.; Chung, C.Y.; Luo, X.; Wu, T. Optimal planning and operation of energy storage systems in radial networks for wind power integration with reserve support. IET Gener. Transm. Distrib. 2016, 10, 2019–2025. [Google Scholar] [CrossRef]
  74. Li, C.; Coelho, E.A.A.; Dragicevic, T.; Guerrero, J.M.; Vasquez, J.C. Multiagent-based distributed state of charge balancing control for distributed energy storage units in AC microgrids. IEEE Trans. Ind. Appl. 2017, 53, 2369–2381. [Google Scholar] [CrossRef]
  75. Kaper, S.K.; Choudhary, N.K. A Review of power management and stability issues in microgrid. In Proceedings of the 1st IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; pp. 1–6. [Google Scholar]
  76. Arani, A.A.K.; Gharehpetian, G.B.; Abedi, M. Review on energy storage systems control methods in microgrids. Electr. Power Energy Syst. 2019, 107, 745–757. [Google Scholar] [CrossRef]
  77. Sbordone, D.; Bertini, I.; Di Pietra, B.; Falvo, M.C.; Genovese, A.; Martirano, L. EV fast charging stations and energy storage technologies: A real implementation in the smart microgrid paradigm. Electr. Power Syst. Res. 2015, 120, 96–108. [Google Scholar] [CrossRef]
  78. Abusara Mohammad, A.; Sharkh Suleiman, M.; Guerrero Josep, M. Improved droop control strategy for grid-connected inverters. Sustain Energy Grids Netw. 2015, 1, 10–19. [Google Scholar] [CrossRef] [Green Version]
  79. Li, H.; Wu, Z.; Zhang, J.; Li, H. Wind-solar-storage hybrid microgrid control strategy based on SVPWM converter. J. Netw. 2014, 9, 1596. [Google Scholar]
  80. Shuai, Z.; Shanglin, M.O.; Jun, W.A.N.G.; Shen, Z.J.; Wei, T.; Yan, F. Droop control method for load share and voltage regulation in high-voltage microgrids. J. Mod. Power Syst. Clean Energy 2016, 4, 76–86. [Google Scholar] [CrossRef] [Green Version]
  81. Singh, R.; Kirar, M. Transient Stability analysis and improvement in microgrid. In Proceedings of the International Conference on Electrical Power and Energy Systems (ICEPES), Bhopal, Madhya Pradesh, India, 14–16 May 2016; pp. 239–245. [Google Scholar]
  82. Liu, J.; Hossain, M.J.; Lu, J.; Rafi, F.H.M.; Li, H. A hybrid AC/DC microgrid control system based on a virtual synchronous generator for smooth transient performances. Electr. Power Syst. Res. 2018, 162, 169–182. [Google Scholar] [CrossRef]
  83. Sahoo, B.P.; Panda, S. Improved grey wolf optimization technique for fuzzy aided PID controller design for power system frequency control. Sustain. Energy Grids Netw. 2018, 16, 278–299. [Google Scholar] [CrossRef]
  84. Hameed, S.; Das, B.; Pant, V. A self-tuning fuzzy PI controller for TCSC to improve power system stability. Electr. Power Syst. Res. 2008, 78, 1726–1735. [Google Scholar] [CrossRef]
  85. Dash, P.; Saikia, L.C.; Sanha, N. Automatic generation control of multi area thermal system using Bat algorithm optimized PD–PID cascade controller. Int. J. Electric. Power Energy Syst. 2015, 68, 364–372. [Google Scholar] [CrossRef]
  86. Sahu, R.K.; Panda, S.; Chandra Sekhar, G.T. A novel hybrid PSO-PS optimized fuzzy PI controller for AGC in multi area interconnected power systems. Int. J. Electr. Power Energy Syst. 2015, 64, 880–893. [Google Scholar] [CrossRef]
  87. Mayne, D.Q. Model predictive control: Recent developments and future promise. Automatica 2014, 50, 2967–2986. [Google Scholar] [CrossRef]
  88. Incremona, G.P.; Ferrara, A.; Magni, L. MPC for robot manipulators with integral sliding modes generation. IEEE/ASME Trans. Mech. 2017, 22, 1299–1307. [Google Scholar] [CrossRef]
  89. Incremona, G.P.; Ferrara, A.; Magni, L. Asyn-chronous networked MPC with ISM for uncertain nonlinear systems. IEEE Trans. Automat. Control 2017, 62, 4305–4317. [Google Scholar] [CrossRef]
  90. Hosseini, S.M.; Carli, R.; Dotoli, M. Model predictive control for real-time residential energy scheduling under uncertainties. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics, Miyazaki, Japan, 7–10 October 2018. [Google Scholar]
  91. Fard, M.; Aldeen, M. Linear quadratic regulator design for a hybrid photovoltaicbattery system. In Proceedings of the 2016 Australian Control Conference (AuCC), Newcastle, Australia, 3–4 November 2016; pp. 347–352. [Google Scholar]
  92. Tang, C.Y.; Chen, Y.F.; Chen, Y.M.; Chang, Y.Y. DC-link voltage control strategy for three-phase back-to-back active power conditioners. IEEE Trans. Ind. Appl. 2015, 62, 6306–6316. [Google Scholar] [CrossRef]
  93. Trip, S.; Cucuzzella, M.; Ferrara, A.; DePersis, C. An energy function based design of second order sliding modes for automatic generation control. In Proceedings of the 20th IFAC World Congress, Toulouse, France, 9–14 July 2017. [Google Scholar]
  94. Cucuzzella, M.; Trip, S.; DePersis, C.; Ferrara, A. Distributed second order sliding modes for optimal load frequency control. In Proceedings of the American Control Conference, Seattle, WA, USA, 24–26 May 2017. [Google Scholar]
  95. Cucuzzella, M.; Incremona, G.P.; Ferrara, A. Third order sliding mode voltage control in microgrids. In Proceedings of the IEEE European Control Conference, Linz, Austria, 15–17 July 2015. [Google Scholar]
  96. Zhang, C.K.; Jiang, L.; Wu, Q.H.; He, Y.; Wu, M. Delay-dependent robust load frequency control for time delay power systems. IEEE Trans. Power Syst. 2013, 28, 2192–2201. [Google Scholar] [CrossRef]
  97. Ning, C. Robust H¥ load-frequency control in interconnected power systems. IET Control Theory Appl. 2016, 10, 67–75. [Google Scholar]
  98. Bevrani, H.; Feizi, M.R.; Ataee, S. Robust Frequency control in an islanded microgrid: H¥ and m-synthesis approaches. IEEE Trans. Smart Grid 2016, 7, 706–717. [Google Scholar] [CrossRef]
  99. Hasanien, H.M. Particle swarm design optimization of transverse flux linear motor for weight reduction and improvement of thrust force. IEEE Trans. Industr. Electron 2011, 58, 4048–4056. [Google Scholar] [CrossRef]
  100. Saad, N.H.; El-Sattar, A.A.; Mansour, A.E.A.M. A novel control strategy for grid connected hybrid renewable energy systems using improved particle swarm optimization. Ain Shams Eng. J. 2018, 9, 2195–2214. [Google Scholar] [CrossRef]
  101. Maleki, A.; Ameri, M.; Keynia, F. Scrutiny of multifarious particle swarm optimization for finding the optimal size of a PV/wind/battery hybrid system. Renew. Energy 2015, 80, 552–563. [Google Scholar] [CrossRef]
  102. Hassan, A.; Kandil, M.; Saadawi, M.; Saeed, M. Modified particle swarm optimisation technique for optimal design of small renewable energy system supplying a specific load at Mansoura University. IET Renew. Power Gener. 2015, 9, 474–483. [Google Scholar] [CrossRef]
  103. Sharafi, M.; Elmekkawy, T.Y. Multi-objective optimal design of hybrid renewable energy systems using PSO-simulation based approach. Renew. Energy 2014, 68, 67–79. [Google Scholar] [CrossRef]
  104. Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical control of droop-controlled AC and DC microgrids—A general approach toward standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
  105. Olivares, D.E.; Cañizares, C.A.; Kazerani, M.; Member, S. A centralized optimal energy management system for microgrids. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–6. [Google Scholar]
  106. Mojica-Nava, E.; Macana, C.A.; Quijano, N. Dynamic population games for optimal dispatch on hierarchical microgrid control. IEEE Trans. Syst. Man Cybern. Syst 2014, 44, 306–317. [Google Scholar] [CrossRef]
Energies 12 03582 g001 550
Figure 1. General structure of the microgrid.
Figure 1. General structure of the microgrid.
Energies 12 03582 g001
Energies 12 03582 g002 550
Figure 2. (a) Inverter for DC source. (b). Inverter for AC source.
Figure 2. (a) Inverter for DC source. (b). Inverter for AC source.
Energies 12 03582 g002
Energies 12 03582 g003 550
Figure 3. The general structure of a hybrid microgrid.
Figure 3. The general structure of a hybrid microgrid.
Energies 12 03582 g003
Energies 12 03582 g004 550
Figure 4. Methods for stability in microgrids.
Figure 4. Methods for stability in microgrids.
Energies 12 03582 g004
Energies 12 03582 g005 550
Figure 5. Methods employed in grid-connected microgrids.
Figure 5. Methods employed in grid-connected microgrids.
Energies 12 03582 g005
Energies 12 03582 g006 550
Figure 6. (a) Frequency reducing characteristic. (b) Voltage reducing characteristic.
Figure 6. (a) Frequency reducing characteristic. (b) Voltage reducing characteristic.
Energies 12 03582 g006
Energies 12 03582 g007 550
Figure 7. Characteristics of primary and secondary control methods [65].
Figure 7. Characteristics of primary and secondary control methods [65].
Energies 12 03582 g007
Energies 12 03582 g008 550
Figure 8. Characteristics of the tertiary control method.
Figure 8. Characteristics of the tertiary control method.
Energies 12 03582 g008
Energies 12 03582 g009 550
Figure 9. Comparison between the new robust droop control and the conventional droop control [80].
Figure 9. Comparison between the new robust droop control and the conventional droop control [80].
Energies 12 03582 g009
Energies 12 03582 g010 550
Figure 10. Voltage and frequency control block diagram [83].
Figure 10. Voltage and frequency control block diagram [83].
Energies 12 03582 g010
Energies 12 03582 g011 550
Figure 11. P-Q control structure [81].
Figure 11. P-Q control structure [81].
Energies 12 03582 g011
Energies 12 03582 g012 550
Figure 12. General structure of an MPC controller.
Figure 12. General structure of an MPC controller.
Energies 12 03582 g012
Energies 12 03582 g013 550
Figure 13. MPC operation model.
Figure 13. MPC operation model.
Energies 12 03582 g013
Table
Table 1. Optimal operation standard for the microgrid in islanded mode [82].
Table 1. Optimal operation standard for the microgrid in islanded mode [82].
StandardsQuality Factor (QF)Nominal Frequency RangeNominal Voltage RangeIslanding Detection Time
UL 17412.559.3 < f < 60.588% < V < 110%t < 2s
IEEE 929-20002.559.3 < f < 60.588% < V < 110%t < 2s
VDE 0126-1-1247.5 < f < 50.588% < V < 110%t < 0.2s
IEC 621161(f-1.5Hz) < f < (f+1.5Hz)85% < V < 115%t < 2s
IEEE1547159.3 < f < 60.588% < V < 110%t < 2s
Korean Standard159.3 < f < 60.588% < V < 110%t < 0.5s
Table
Table 2. Control methods used for transient stability in microgrids.
Table 2. Control methods used for transient stability in microgrids.
Control Method AdvantagesDisadvantagesType of ConnectionEnergy SourcesVoltage LevelRef. Number
Linear Quadratic Control (LQC)The method is used in three-phase inverters to eliminate oscillation and degradation. DC in the inverter is used to compensate for the voltage in the line and optimize the energy flow to the loads.Analytical solution of the algorithm is quite difficult and does not work with constraints.Grid-connected mode, islanded modeGrid and renewable energy sources Moderate–high[93]
Sliding Mode Control (SMC)The method provides high precision, fast dynamic response and high stability in the event of distortion in large-scale loads. By means of dynamic behavior against uncertainties and distortion, it is used more in non-linear systems. It also provides a fast reaction due to low mathematical calculation.Non-stability in linear systemsGrid-connected mode, islanded modeGrid and renewable energy sources Moderate–high[94]
PI/PID ControlPI control is not as stable in adapting itself to load variations. It is more stable in linear systems. Transient response is slow and control parameters are not controlled by the fluctuation of power. It does not show stable behavior with dynamic system responses in a non-linear system. It is very slow at reducing harmonics.Islanded modeGrid and renewable energy sources Moderate[85]
Droop ControlThe method provides frequency stability for overloaded systems. Permits power sharing in high-voltage multi-microgrids and at high-voltage levels.Fault rate in permanent voltage and power fluctuations.
Fluctuates the frequency and voltage values based on load and reactive power-share fails.		Grid-connected mode, islanded modeGrid and renewable energy sources, synchronous generator High[55]
Model Predictive Control (MPC)MPC settlement time is shorter. MPC is used to eliminate errors and excessive values in the grid-connected operation and minimize the harmonics in the network current.System model and initial parameters are required to achieve accuracy.Grid-connected mode, islanded modeGrid and renewable energy sources Moderate[89]
Particle Swarm Optimization (PSO) AlgorithmThe algorithm is used for the optimization of non-linear, non-derivative and multi-mode functions.Its disadvantages include being close to the optimal level and calculation time depends on the adjustment time of PSO parameters.Grid-connected mode, islanded modeGrid and renewable energy sources Moderate[102]

Share and Cite

MDPI and ACS Style

Vadi, S.; Padmanaban, S.; Bayindir, R.; Blaabjerg, F.; Mihet-Popa, L. A Review on Optimization and Control Methods Used to Provide Transient Stability in Microgrids. Energies 2019, 12, 3582. https://doi.org/10.3390/en12183582

AMA Style

Vadi S, Padmanaban S, Bayindir R, Blaabjerg F, Mihet-Popa L. A Review on Optimization and Control Methods Used to Provide Transient Stability in Microgrids. Energies. 2019; 12(18):3582. https://doi.org/10.3390/en12183582

Chicago/Turabian Style

Vadi, Seyfettin, Sanjeevikumar Padmanaban, Ramazan Bayindir, Frede Blaabjerg, and Lucian Mihet-Popa. 2019. "A Review on Optimization and Control Methods Used to Provide Transient Stability in Microgrids" Energies 12, no. 18: 3582. https://doi.org/10.3390/en12183582

APA Style

Vadi, S., Padmanaban, S., Bayindir, R., Blaabjerg, F., & Mihet-Popa, L. (2019). A Review on Optimization and Control Methods Used to Provide Transient Stability in Microgrids. Energies, 12(18), 3582. https://doi.org/10.3390/en12183582

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop