A Novel Temperature–Hysteresis Model for Power Battery of Electric Vehicles with an Adaptive Joint Estimator on State of Charge and Power
Abstract
:1. Introduction
2. Battery Model
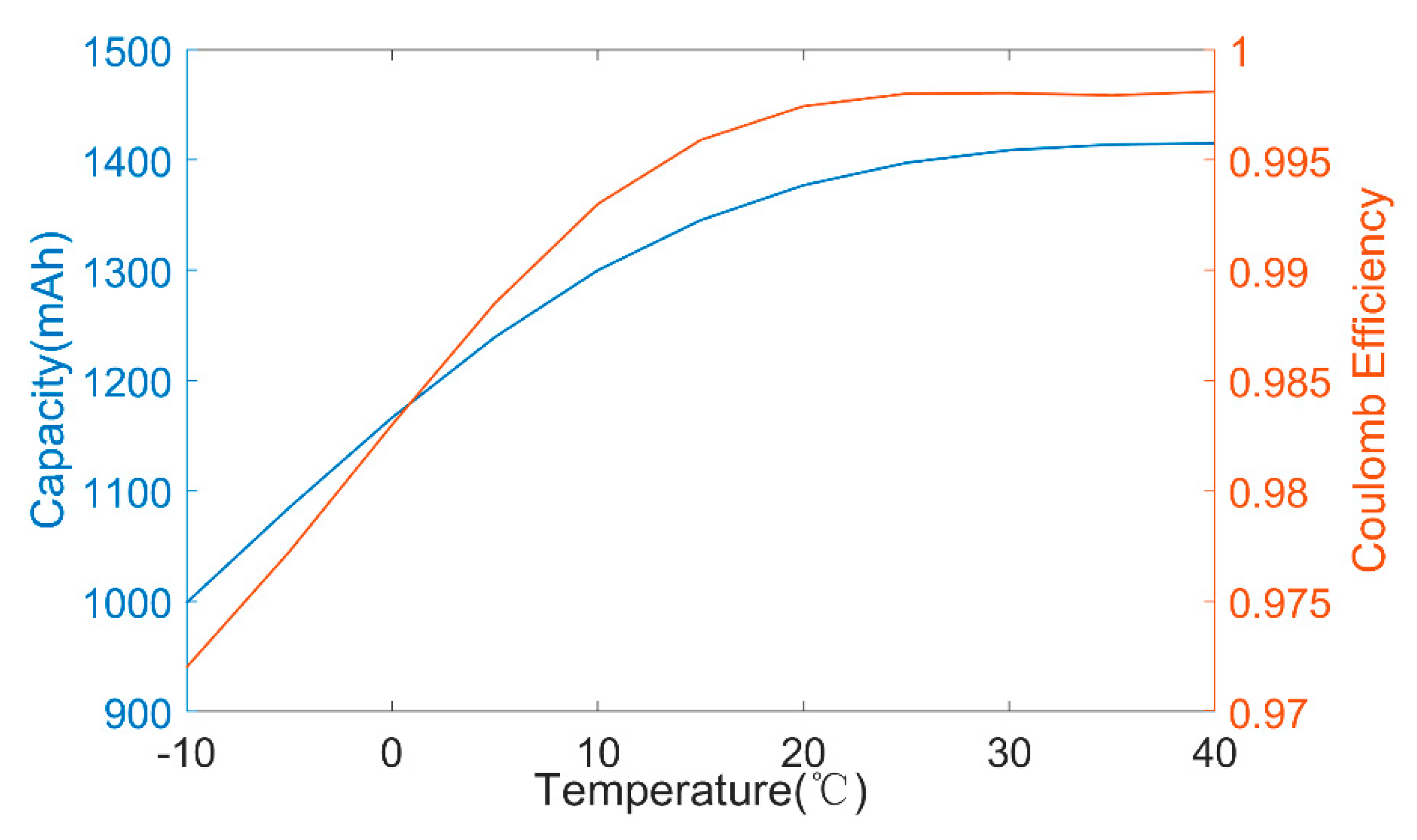
2.1. Temperature-Based Capacity Model
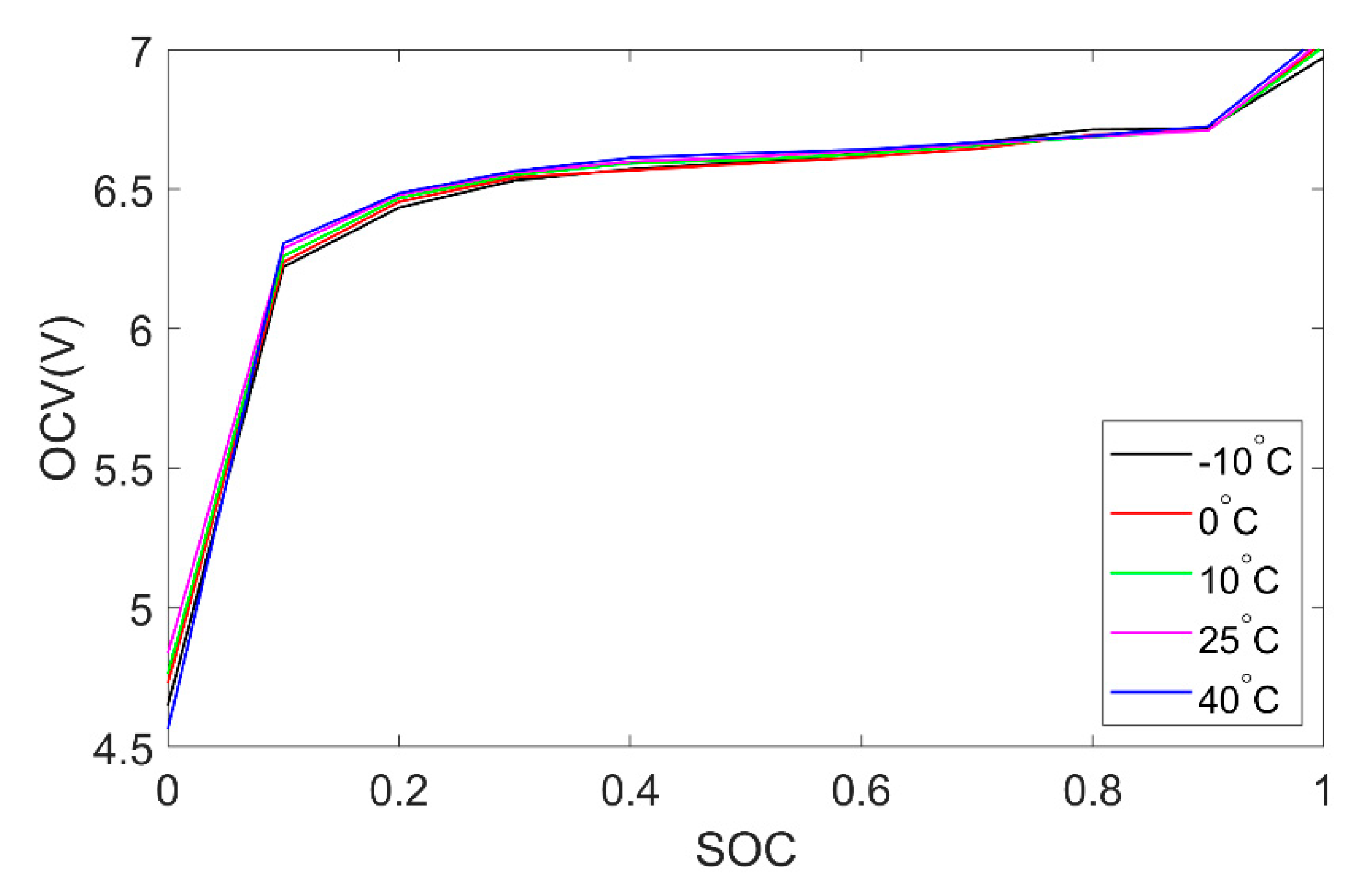
2.2. Temperature-Based Hysteresis Voltage Model
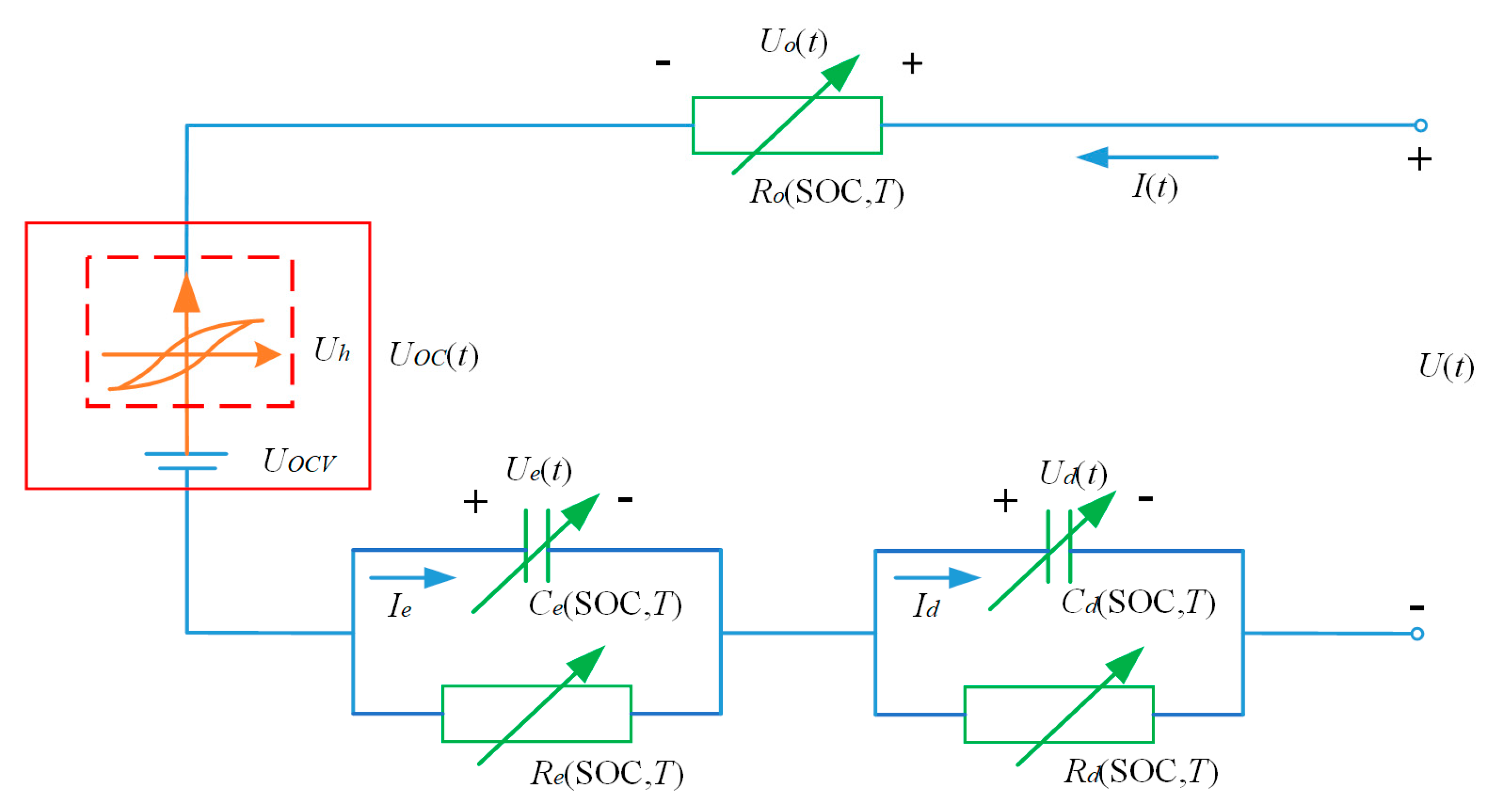
2.3. Temperature–Hysteresis Battery Model
3. Battery SOC and SOP Joint Estimator
3.1. SOC Estimation Based on the AUKF Method
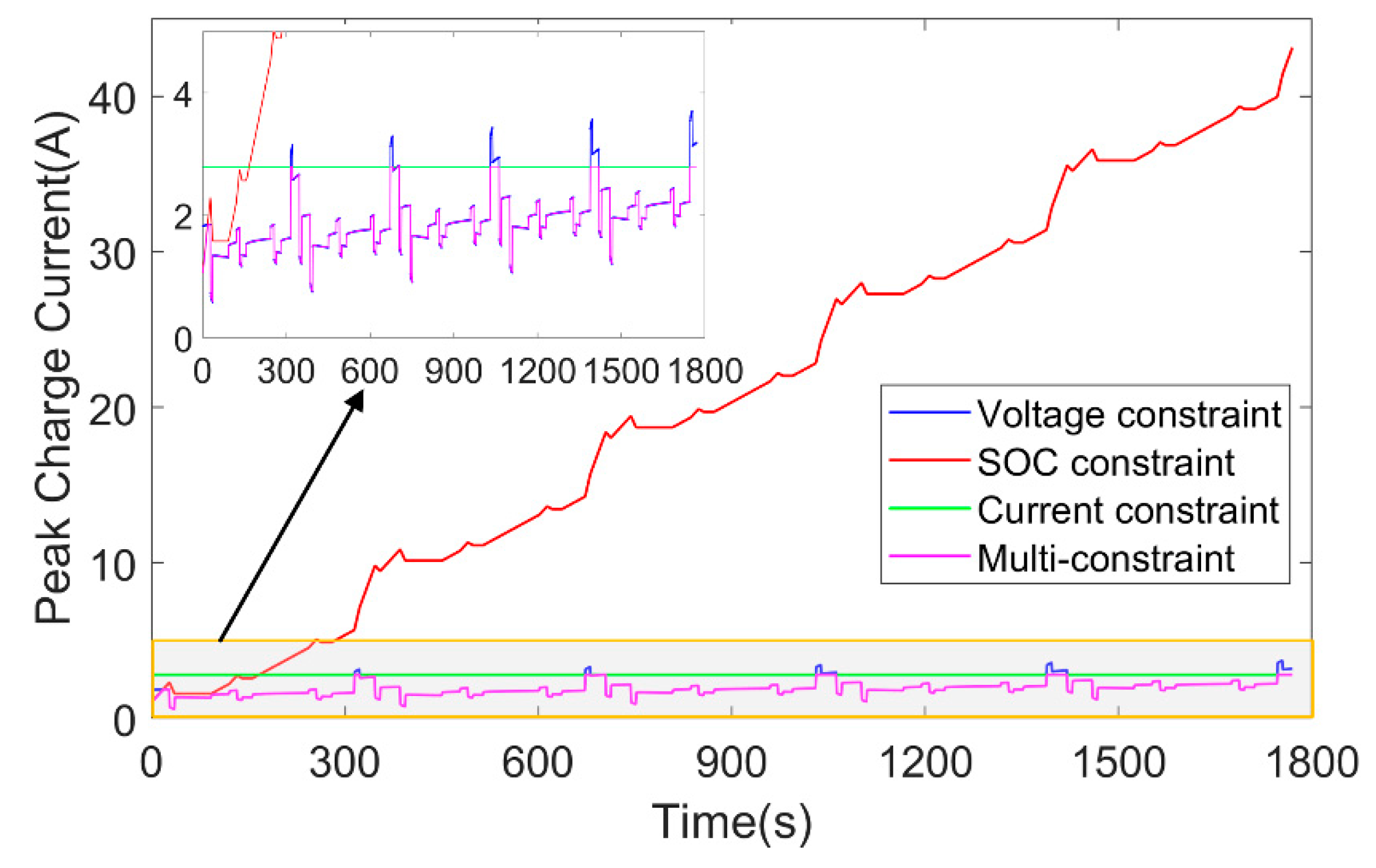
3.2. SOP Estimation Under Multiple Constraints
3.2.1. Current Constraint
3.2.2. Voltage Constraint
3.2.3. SOC Constraint
3.2.4. Multiple Constraints
3.3. Model-Based SOC and SOP Joint Estimator
4. Verification and Discussion
4.1. Model Identification and Verification
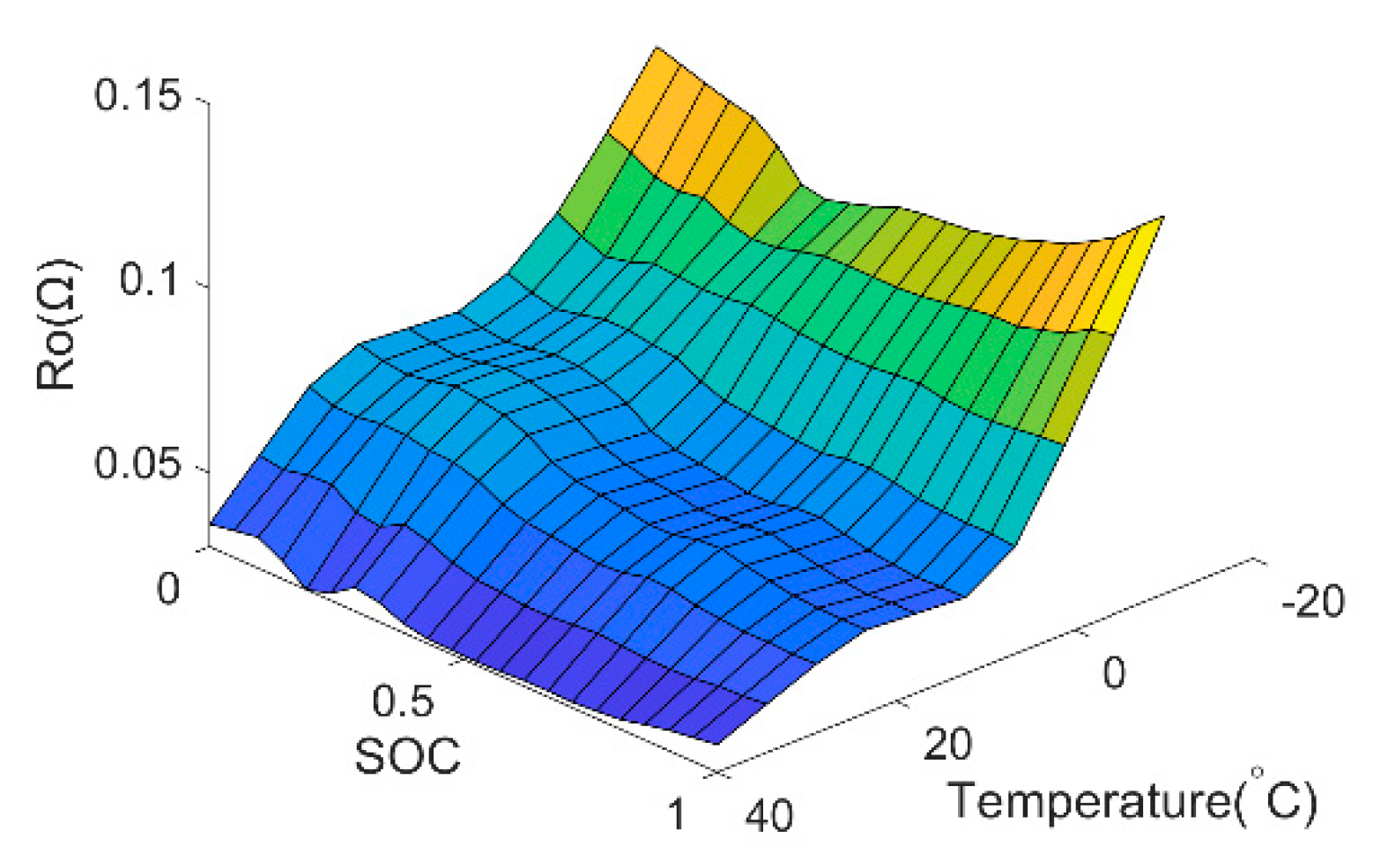
4.1.1. Model Parameters Identification
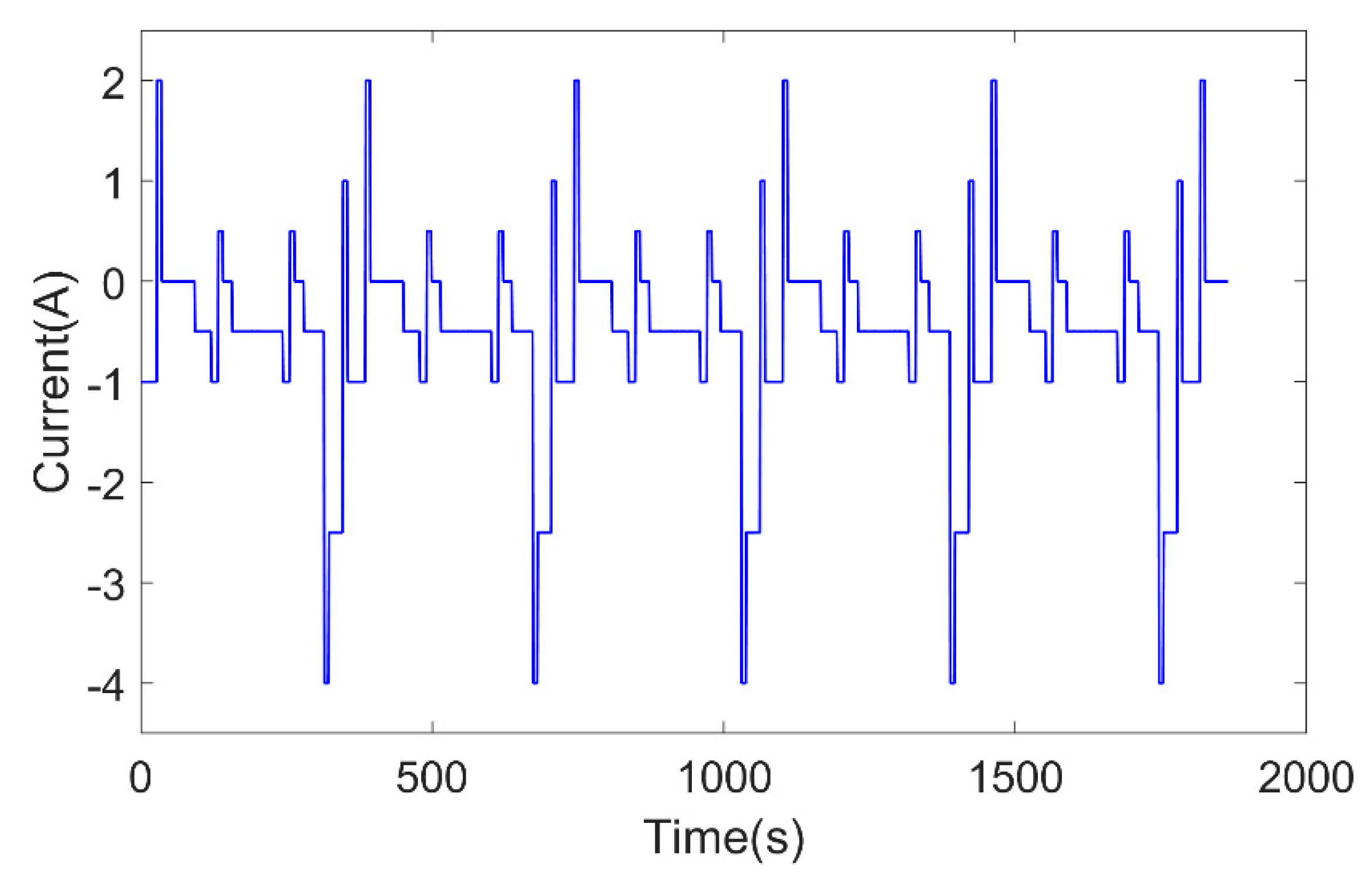
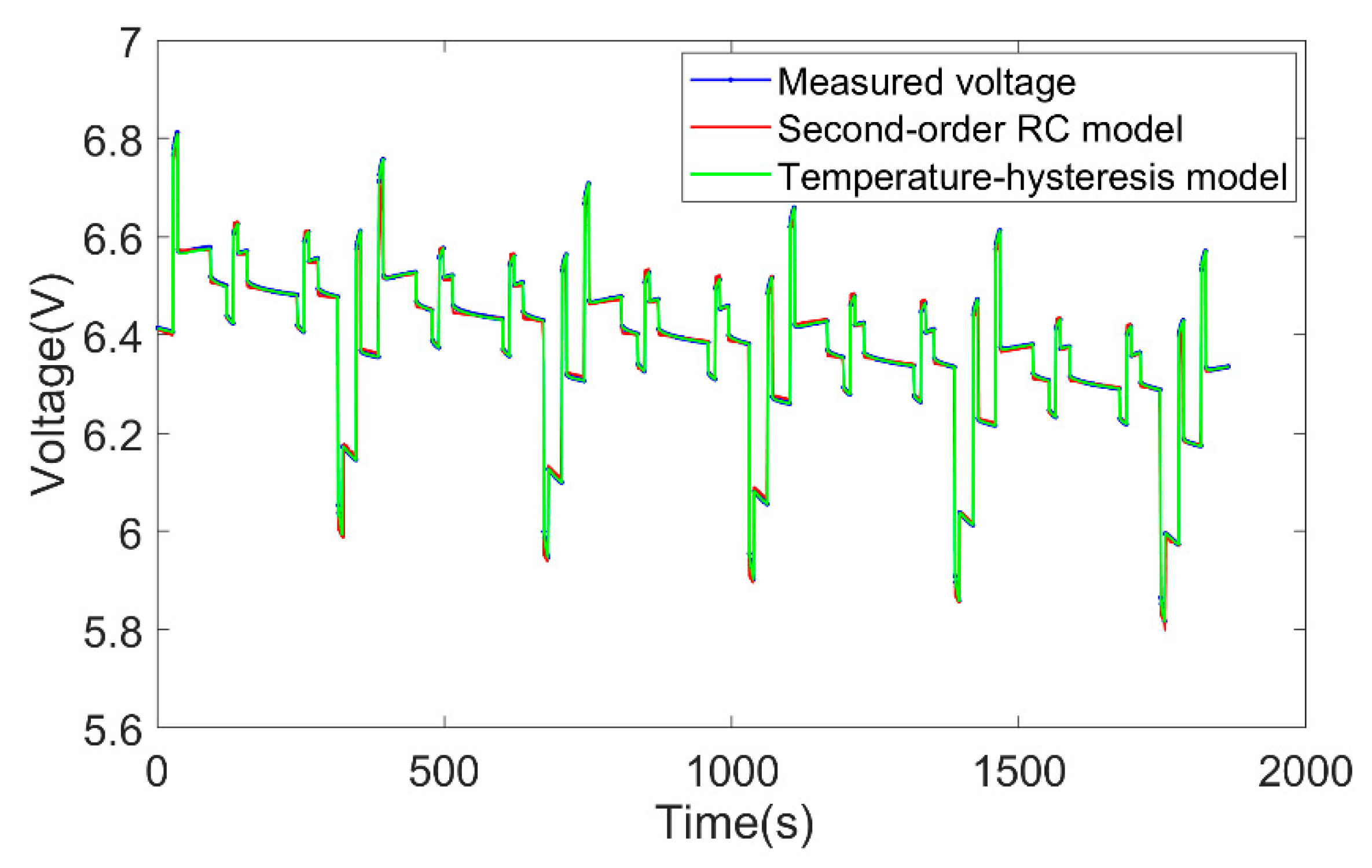
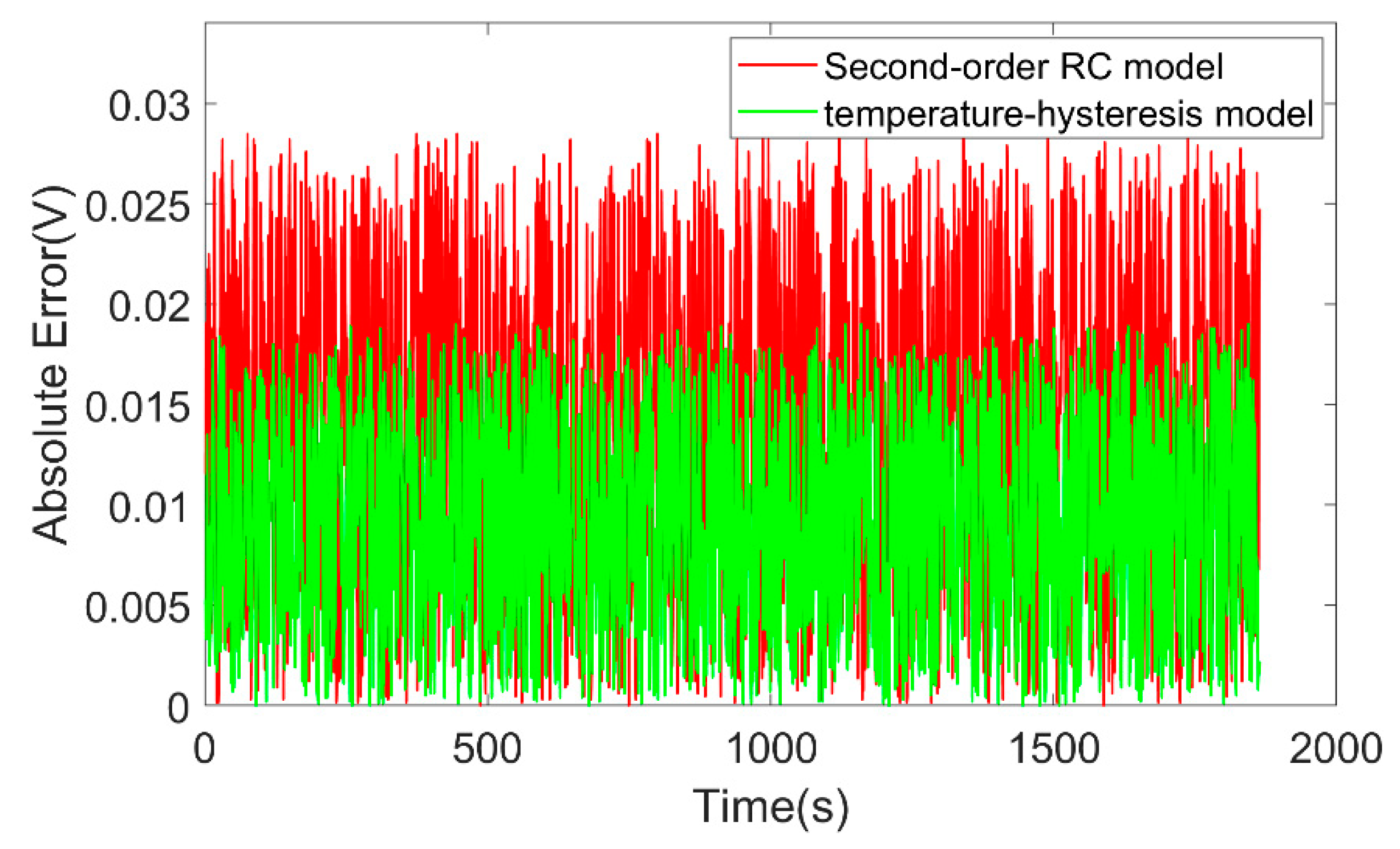
4.1.2. Model Verification Under Constant Temperature Condition
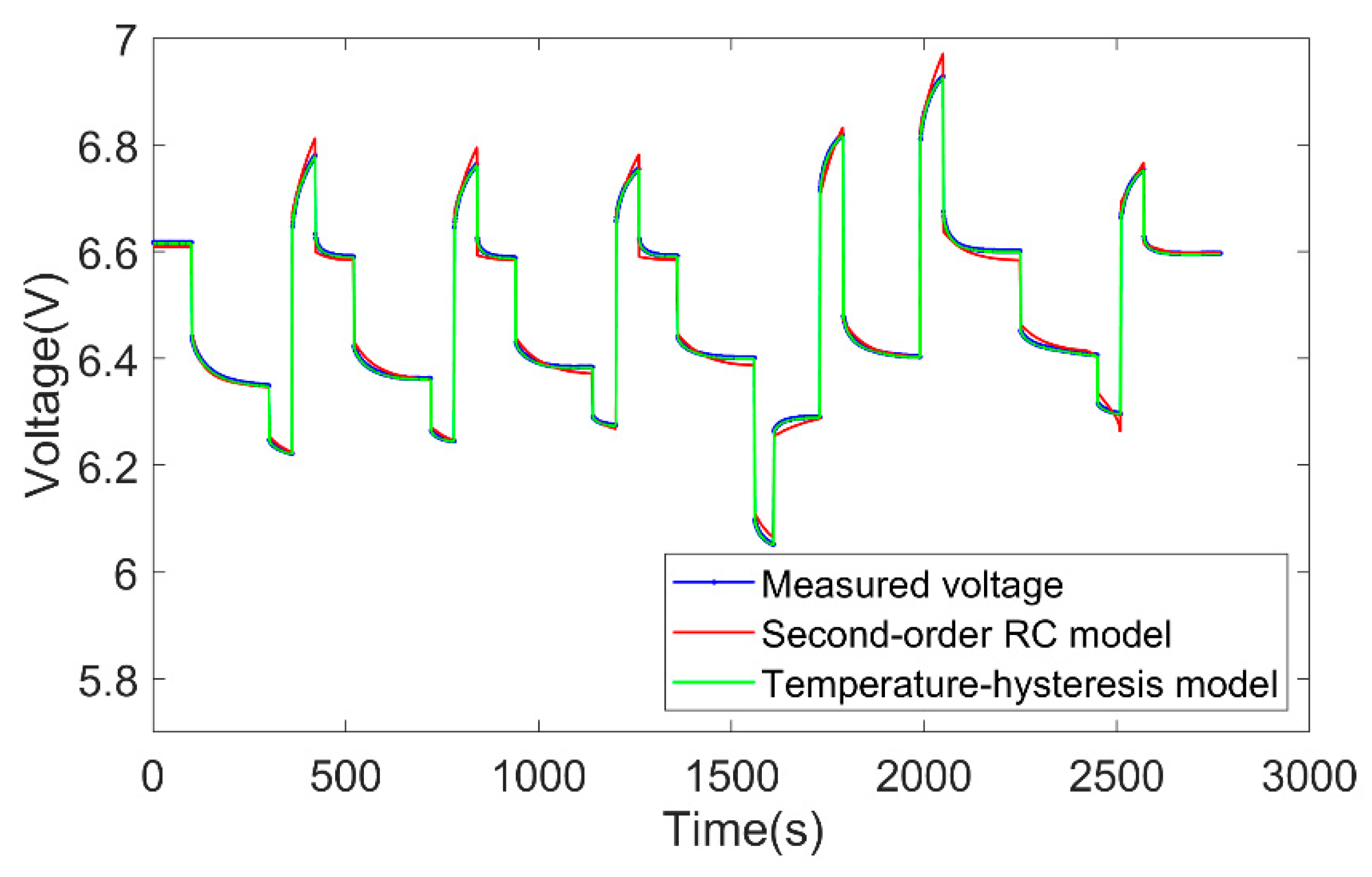
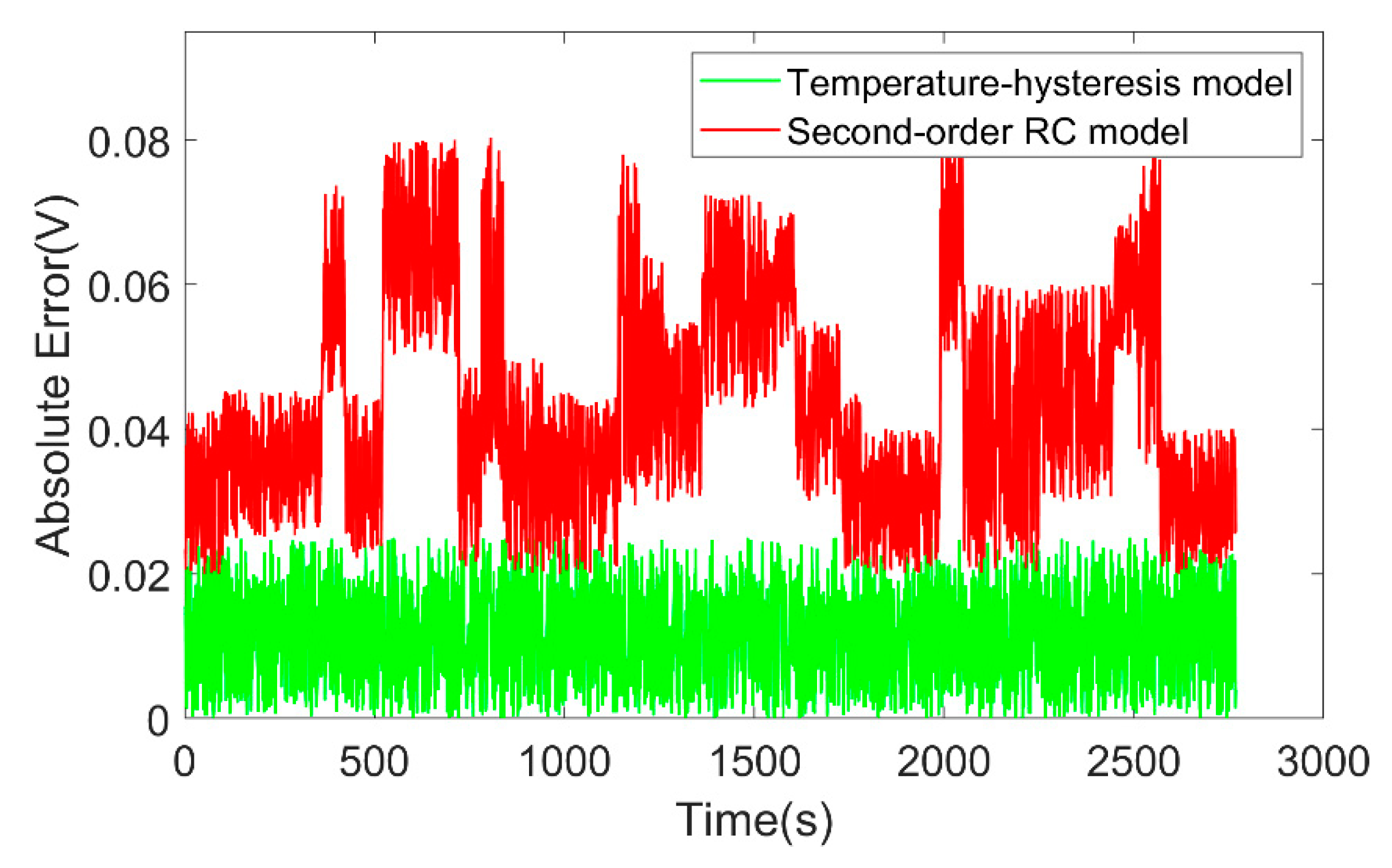
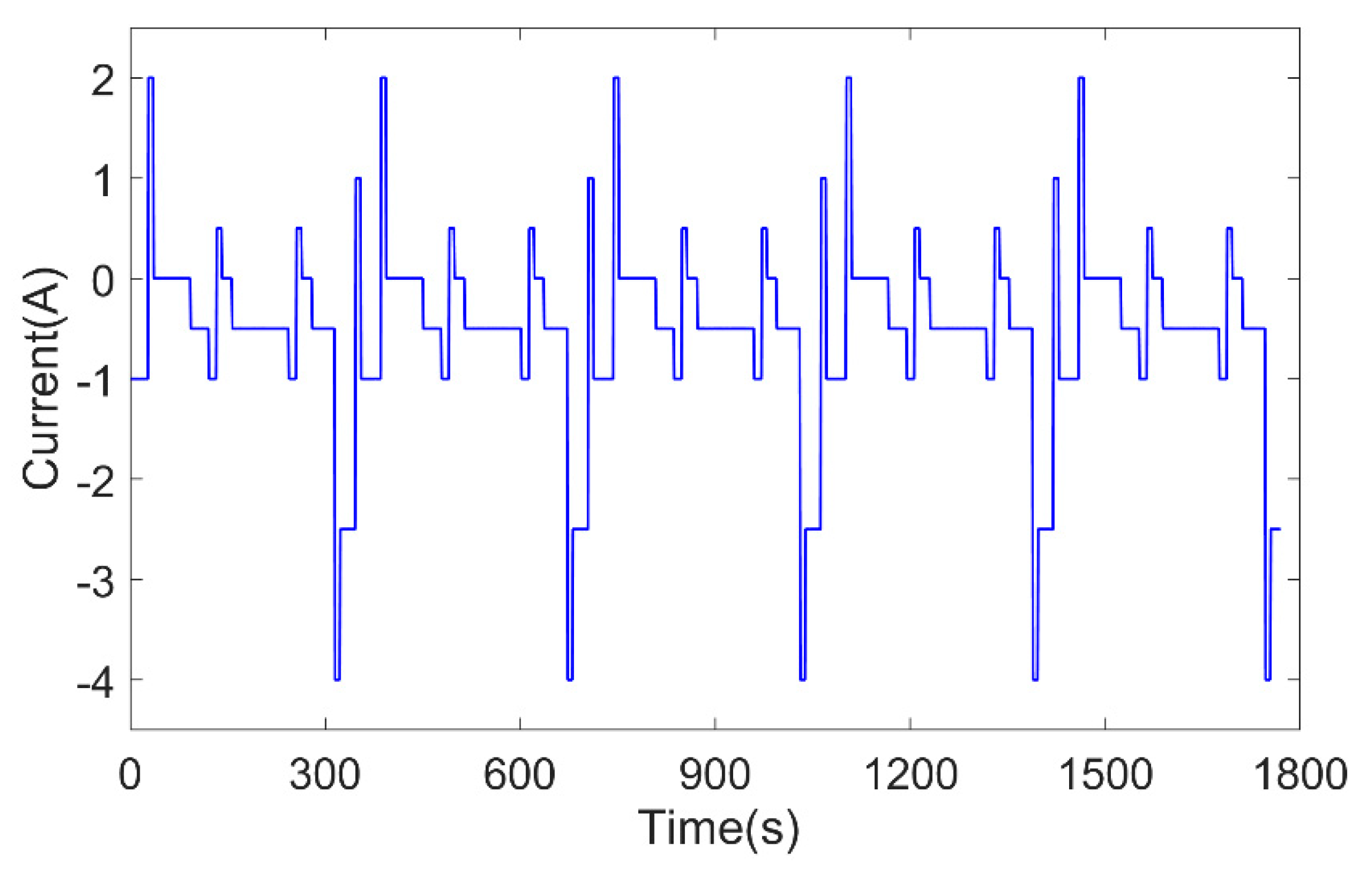
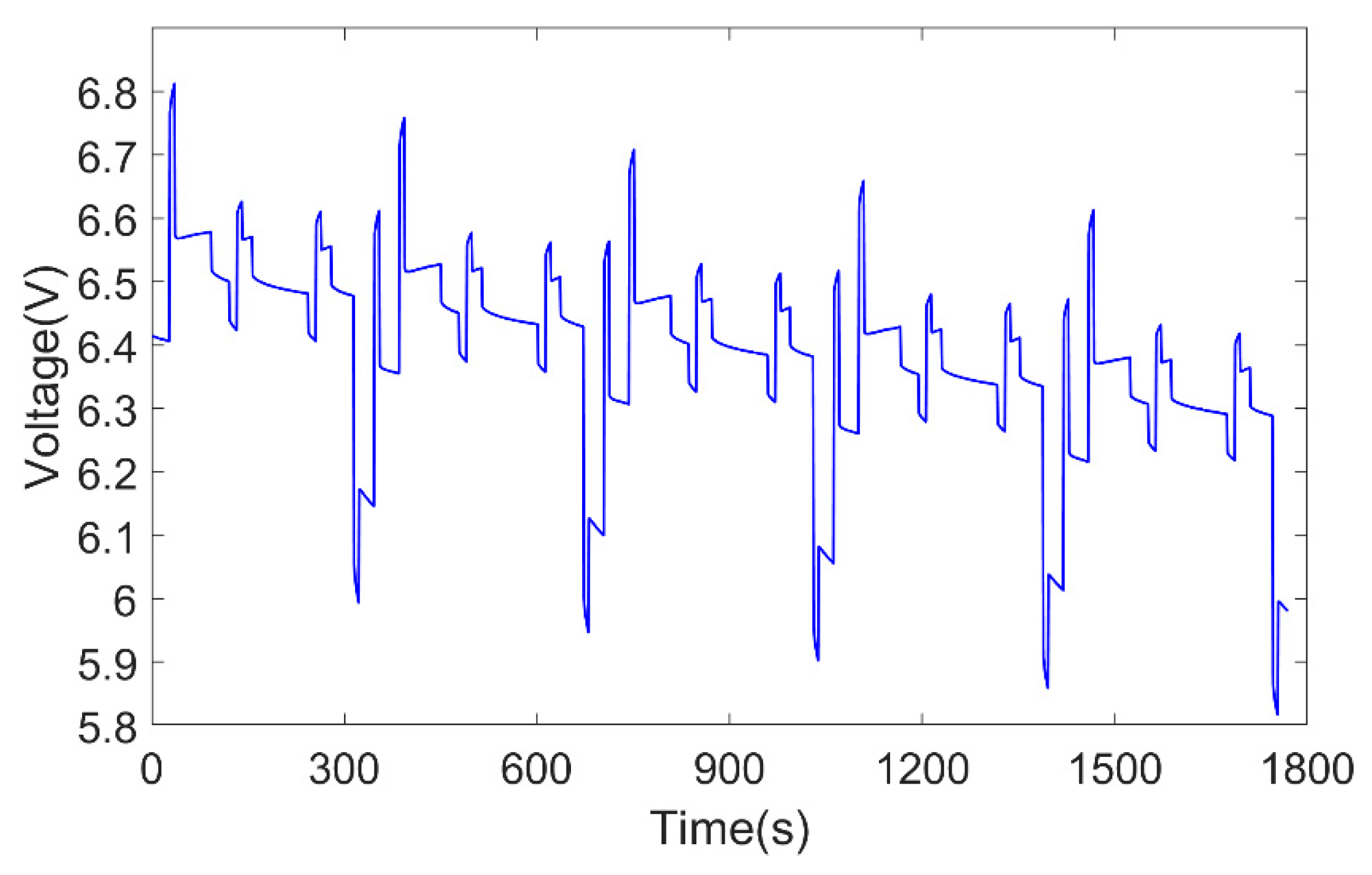
4.1.3. Model Verification Under Variable Temperature Conditions
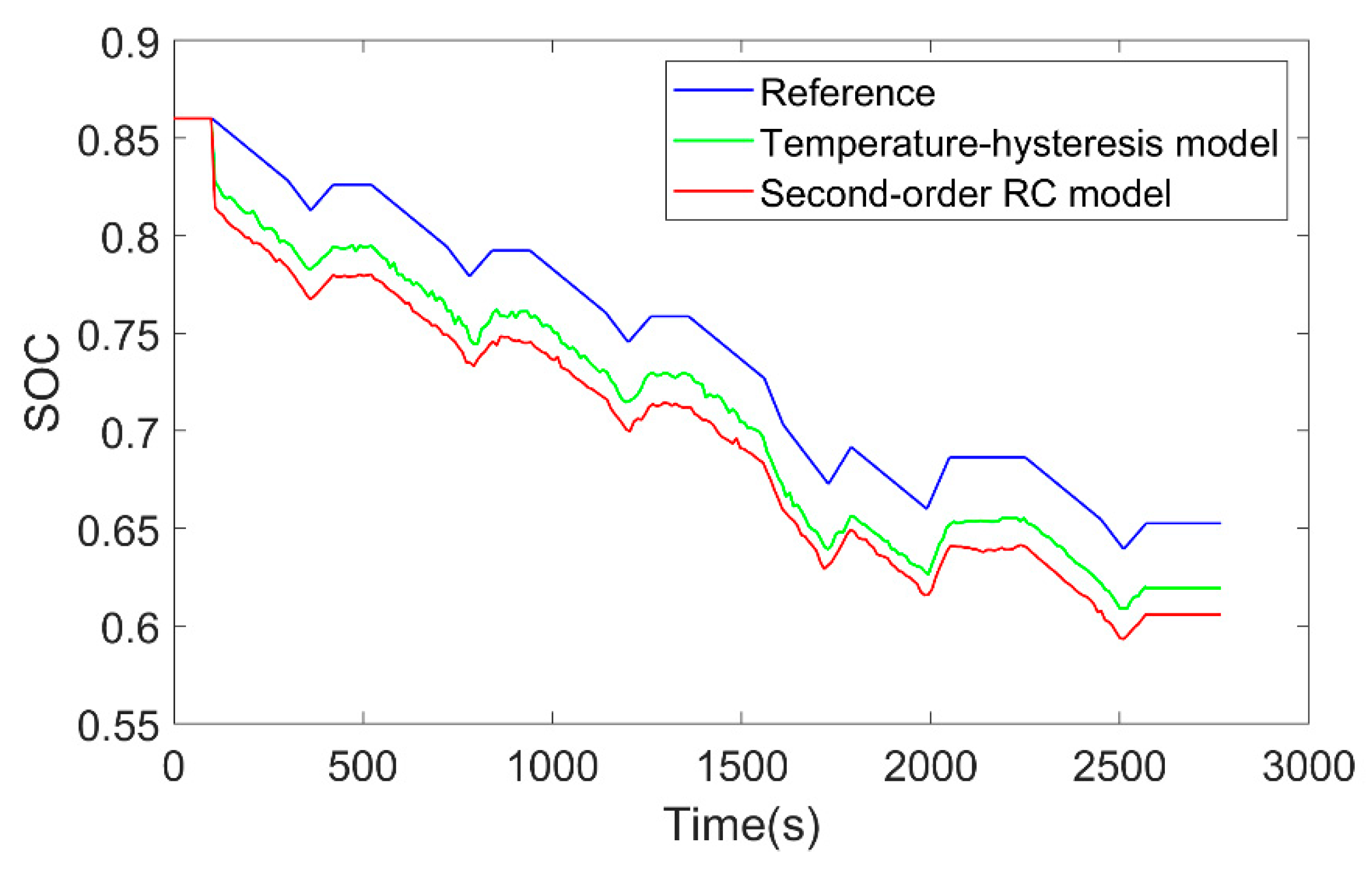
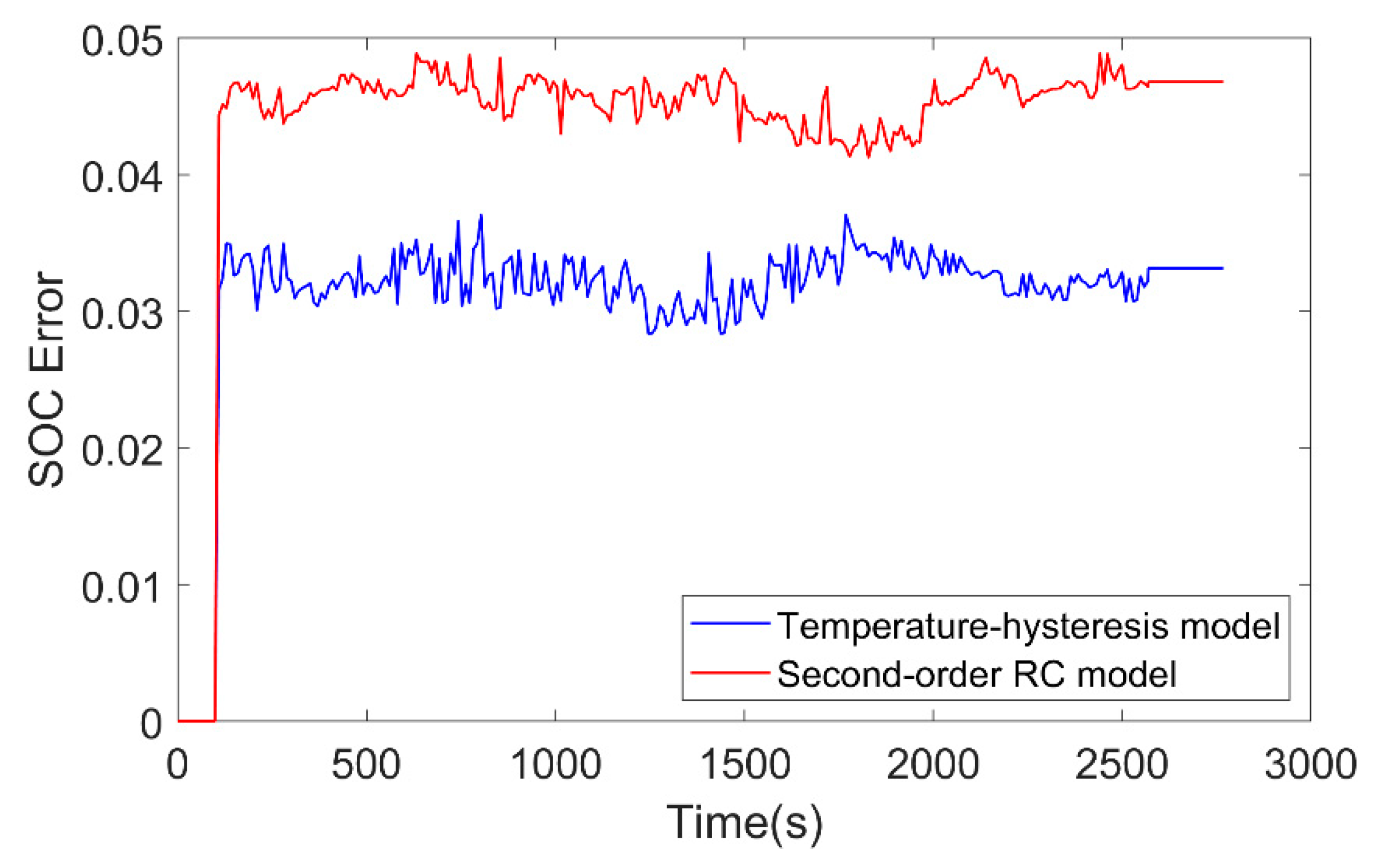
4.2. Verification of the SOC and SOP Joint Estimation
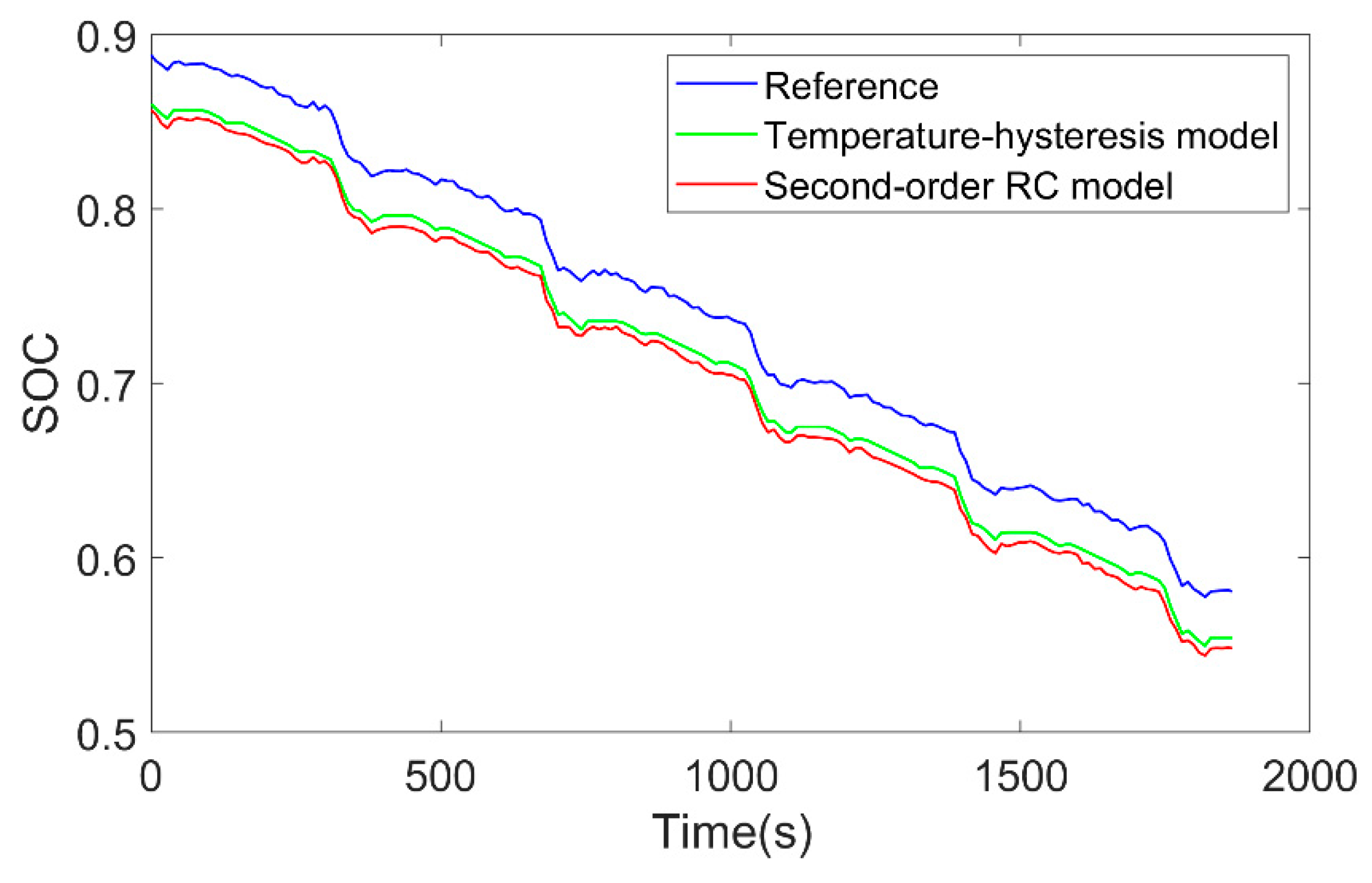
4.2.1. Verification of the SOC Estimation
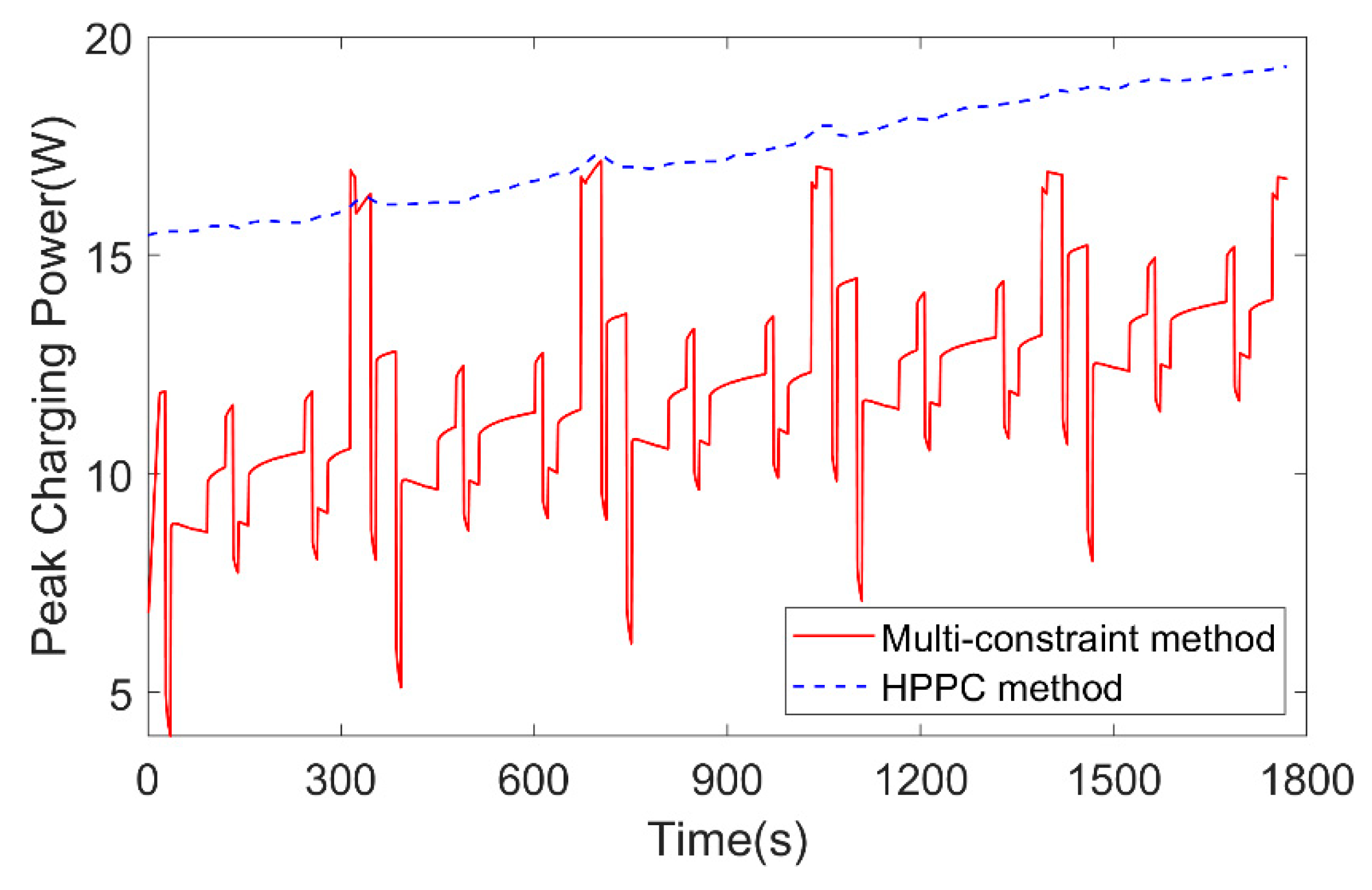
4.2.2. Verification of the SOP Estimation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbols | |
| Q | battery capacity: mAh |
| T | battery temperature, °C |
| η | coulombic efficiency |
| I | load current, A |
| maximum hysteresis voltage, V | |
| hysteresis voltage, V | |
| Sgn(·) | sign function |
| open-circuit voltage, V | |
| ohmic resistance, Ω | |
| electrochemical polarization resistance, Ω | |
| concentration polarization resistance, Ω | |
| electrochemical polarization capacitance, F | |
| concentration polarization capacitance, F | |
| τ | sampling period, s |
| system state vector | |
| system input vector | |
| system noise | |
| measurement noise | |
| Subscripts and Superscripts | |
| k | time step index |
| chg | charge |
| dis | discharge |
| max | maximum |
| min | minimum |
| ^ | estimation value |
| Abbreviations | |
| SOC | state of charge |
| SOP | state of power |
| EV | electric vehicle |
| AUKF | adaptive unscented Kalman filter |
| UKF | unscented Kalman filter |
| ECM | equivalent circuit model |
| OCV | open-circuit voltage |
| HPPC | hybrid pulse power characteristic |
| DST | dynamic stress test |
| RMSE | root mean square error |
| C | discharge rate |
References
- Un-Noor, F.; Padmanaban, S.; Mihet-Popa, L.; Mollah, M.N.; Hossain, E.; Sciubba, E. A Comprehensive Study of Key Electric Vehicle (EV) Components, Technologies, Challenges, Impacts, and Future Direction of Development. Energies 2017, 10, 1217. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Source 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Xiong, R.; Cao, J.; Yu, Q.; He, H.; Sun, F. Critical Review on the Battery State of Charge Estimation Methods for Electric Vehicles. IEEE Access 2018, 6, 1832–1843. [Google Scholar] [CrossRef]
- Sun, F.; Xiong, R.; He, H. Estimation of state-of-charge and state-of-power capability of lithium-ion battery considering varying health conditions. J. Power Sources 2014, 259, 166–176. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Chen, Z. A method for joint estimation of state-of-charge and available energy of LiFePO4 batteries. Appl. Energy 2014, 135, 81–87. [Google Scholar] [CrossRef]
- Plett, G.L. High-performance battery-pack power estimation using a dynamic cell model. IEEE Trans. Veh. Technol. 2004, 53, 1586–1593. [Google Scholar] [CrossRef]
- Lei, P.; Zhu, C.; Wang, T.; Lu, R.; Chan, C. Online peak power prediction based on a parameter and state estimator for lithium-ion batteries in electric vehicles. Energy 2014, 66, 766–778. [Google Scholar]
- Zhang, W.; Shi, W.; Ma, Z. Adaptive unscented kalman filter based state of energy and power capability estimation approach for lithium-ion battery. J. Power Sources 2015, 289, 50–62. [Google Scholar] [CrossRef]
- Nejad, S.; Gladwin, D.T.; Stone, D.A. A systematic review of lumped-parameter equivalent circuit models for real-time estimation of lithium-ion battery states. J. Power Sources 2016, 316, 183–196. [Google Scholar] [CrossRef] [Green Version]
- He, H.; Zhang, X.; Xiong, R.; Xu, Y.; Guo, H. Online model-based estimation of state-of-charge and open-circuit voltage of lithium-ion batteries in electric vehicles. Energy 2012, 66, 310–318. [Google Scholar] [CrossRef]
- Smith, K.A.; Rahn, C.D.; Wang, C.Y. Model-Based electrochemical estimation and constraint management for pulse operation of Lithium Ion batteries. IEEE Trans. Control Syst. Technol. 2010, 18, 654–663. [Google Scholar] [CrossRef]
- Chen, S.; Fu, Y.; Mi, C.C. State of Charge Estimation of Lithium Ion Batteries in Electric Drive Vehicles Using Extended Kalman Filtering. IEEE Trans. Veh. Technol. 2013, 62, 1020–1030. [Google Scholar] [CrossRef]
- Guo, M.; Kim, G.H.; White, R.E. A three-dimensional multi-physics model for a Li-ion battery. J. Power Sources 2013, 240, 80–94. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Wu, J.; Chen, Z. A novel method for lithium-ion battery state of energy and state of power estimation based on multi-time-scale filter. Appl. Energy 2018, 216, 442–451. [Google Scholar] [CrossRef]
- Tian, Y.; Xia, B.Z.; Wang, M.W.; Sun, W.; Xu, Z.H. Comparison study on two model-based adaptive algorithms for SOC estimation of lithium-ion batteries in electric vehicles. Energies 2014, 7, 8446–8464. [Google Scholar] [CrossRef]
- Zhu, L.; Sun, Z.; Dai, H.; Wei, X. A novel modeling methodology of open circuit voltage hysteresis for LiFePO4 batteries based on an adaptive discrete Preisach model. Appl. Energy 2015, 155, 91–109. [Google Scholar] [CrossRef]
- Hu, X.S.; Li, S.B.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Yoon, S.; Hwang, I.; Lee, C. Power capability analysis in lithium ion batteries using electrochemical impedance spectroscopy. J. Electroanal. Chem. 2011, 655, 32–38. [Google Scholar] [CrossRef]
- Feng, T.; Yang, L.; Zhao, X.; Zhang, H.; Qiang, J. Online identification of lithium-ion battery parameters based on an improved equivalent-circuit model and its implementation on battery state-of-power prediction. J. Power Sources 2015, 281, 192–203. [Google Scholar] [CrossRef]
- Idaho National Engineering & Environmental Laboratory. Battery Test Manual for Plug-in Hybrid Electric Vehicles; Assistant Secretary for Energy Efficiency and Renewable Energy (EE) Idaho Operations Office: Idaho Falls, ID, USA, 2010. [Google Scholar]
- Pesaran, A.A. Battery thermal models for hybrid vehicle simulations. J. Power Sources 2002, 110, 377–382. [Google Scholar] [CrossRef]
- Sun, F.; Xiong, R.; He, H.; Li, W.; Aussems, J.E.E. Model-based dynamic multi-parameter method for peak power estimation of lithium-ion batteries. Appl. Energy 2012, 96, 378–386. [Google Scholar] [CrossRef]
- Fleischer, C.; Waag, W.; Bai, Z.; Sauer, D.U. Self-learning state-of-available-power prediction for lithium-ion batteries in electrical vehicles. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference (VPPC), Seoul, Korea, 9–12 October 2012; pp. 370–375. [Google Scholar]
- Xiong, R.; Sun, F.; Gong, X.; He, H. Adaptive state of charge estimator for lithium-ion cells series battery pack in electric vehicles. J. Power Sources 2013, 242, 699–713. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Zheng, F.; Xing, Y.; Jiang, J.; Sun, B.; Kim, J.; Pecht, M. Influence of different open circuit voltage tests on state of charge online estimation for lithium-ion batteries. Appl. Energy 2016, 183, 513–525. [Google Scholar] [CrossRef]
- Zhang, C.; Li, K.; Deng, J.; Song, S. Improved Real-time State-of-Charge Estimation of LiFePO4 Battery Based on a Novel Thermoelectric Model. IEEE Trans. Ind. Electron. 2016, 64, 654–663. [Google Scholar] [CrossRef]
- Thele, M.; Bohlen, O.; Sauer, D.U.; Karden, E. Development of a voltage-behavior model for NiMH batteries using an impedance-based modeling concept. J. Power Sources 2018, 175, 635–643. [Google Scholar] [CrossRef]
- Xia, B.; Wang, H.; Tian, Y.; Wang, M.; Sun, W.; Xu, Z. State of Charge Estimation of Lithium-Ion Batteries Using an Adaptive Cubature Kalman Filter. Energies 2015, 8, 5916–5936. [Google Scholar] [CrossRef] [Green Version]
- Xiong, R.; Sun, F.; Gong, X.; Gao, C. A data-driven based adaptive state of charge estimator of lithium-ion polymer battery used in electric vehicles. Appl. Energy 2014, 113, 1421–1433. [Google Scholar] [CrossRef]
- Barai, A.; Widanage, W.D.; Marco, J.; McGordon, A.; Jennings, P. A study of the open circuit voltage characterization technique and hysteresis assessment of lithium-ion cells. J. Power Sources 2015, 295, 99–107. [Google Scholar] [CrossRef]
- Yu, Q.; Xiong, R.; Lin, C.; Shen, W.; Deng, J. Lithium-ion Battery Parameters and State-of-Charge Joint Estimation Based on H infinity and Unscented Kalman Filters. IEEE Trans. Veh. Technol. 2017, 66, 8693–8701. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Zhang, W.; Sharkh, S.M. Estimation of State of Charge of Lithium-Ion Batteries Usedin HEV Using Robust Extended Kalman Filtering. Energies 2012, 5, 1098–1115. [Google Scholar] [CrossRef]


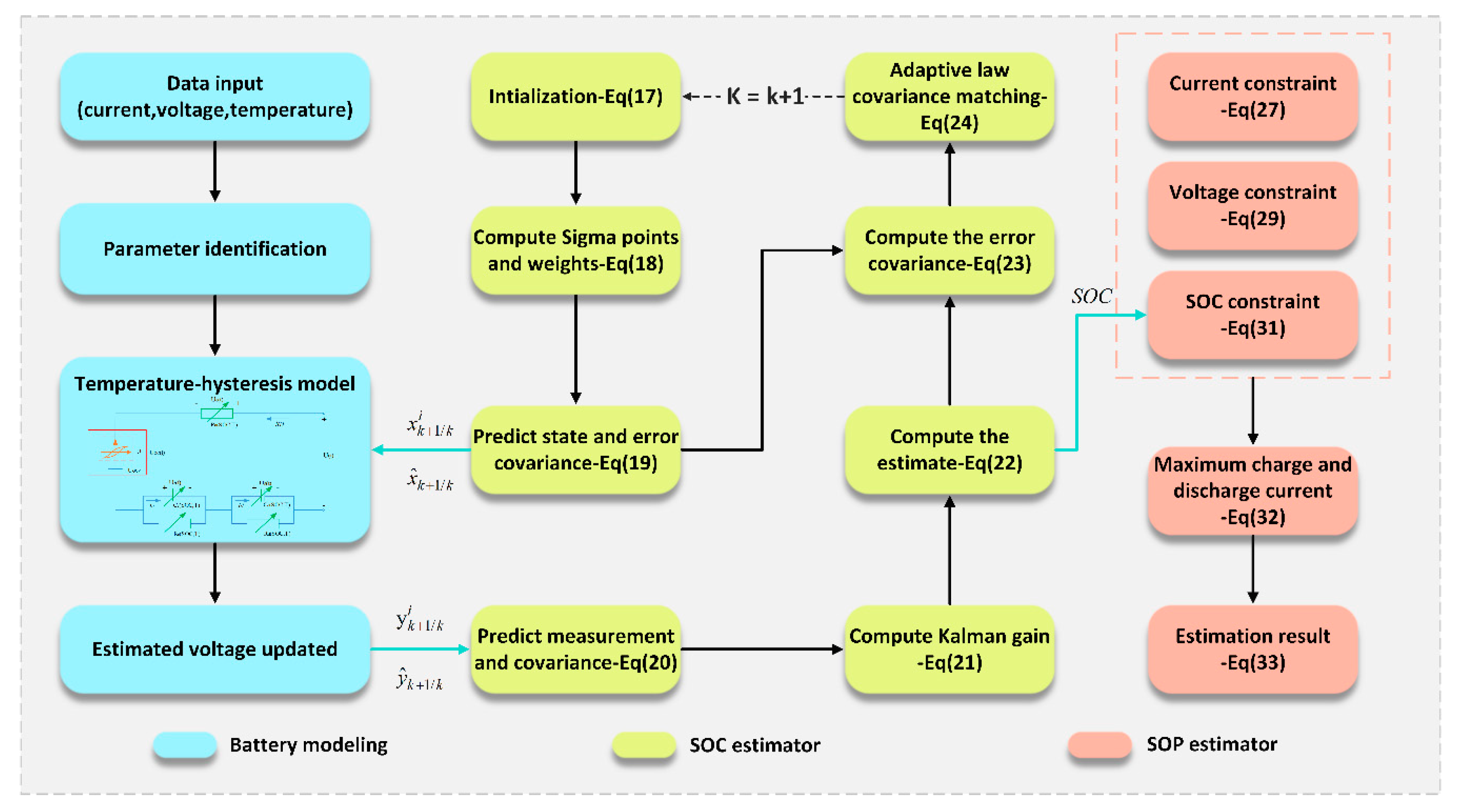







| Nonlinear state-space model | |
| (16) | |
| Step I: Initialization | |
| For k = 0, set: | (17) |
| Step II: Computation: For k = 1, 2, compute | |
| Compute Sigma points and weights: | |
| (18) | |
| Predict state and error covariance: | |
| (19) | |
| Predict measurement and covariance: | |
| (20) | |
| Compute Kalman gain: | (21) |
| Compute the estimate: | (22) |
| Compute the error covariance: | (23) |
| Adaptive law covariance matching: | |
| (24) |
| −281.5 | 1462 | −0.5098 | −0.0139 | −0.0659 | 0.9985 |
| Model Parameter | Fitting Equation |
|---|---|
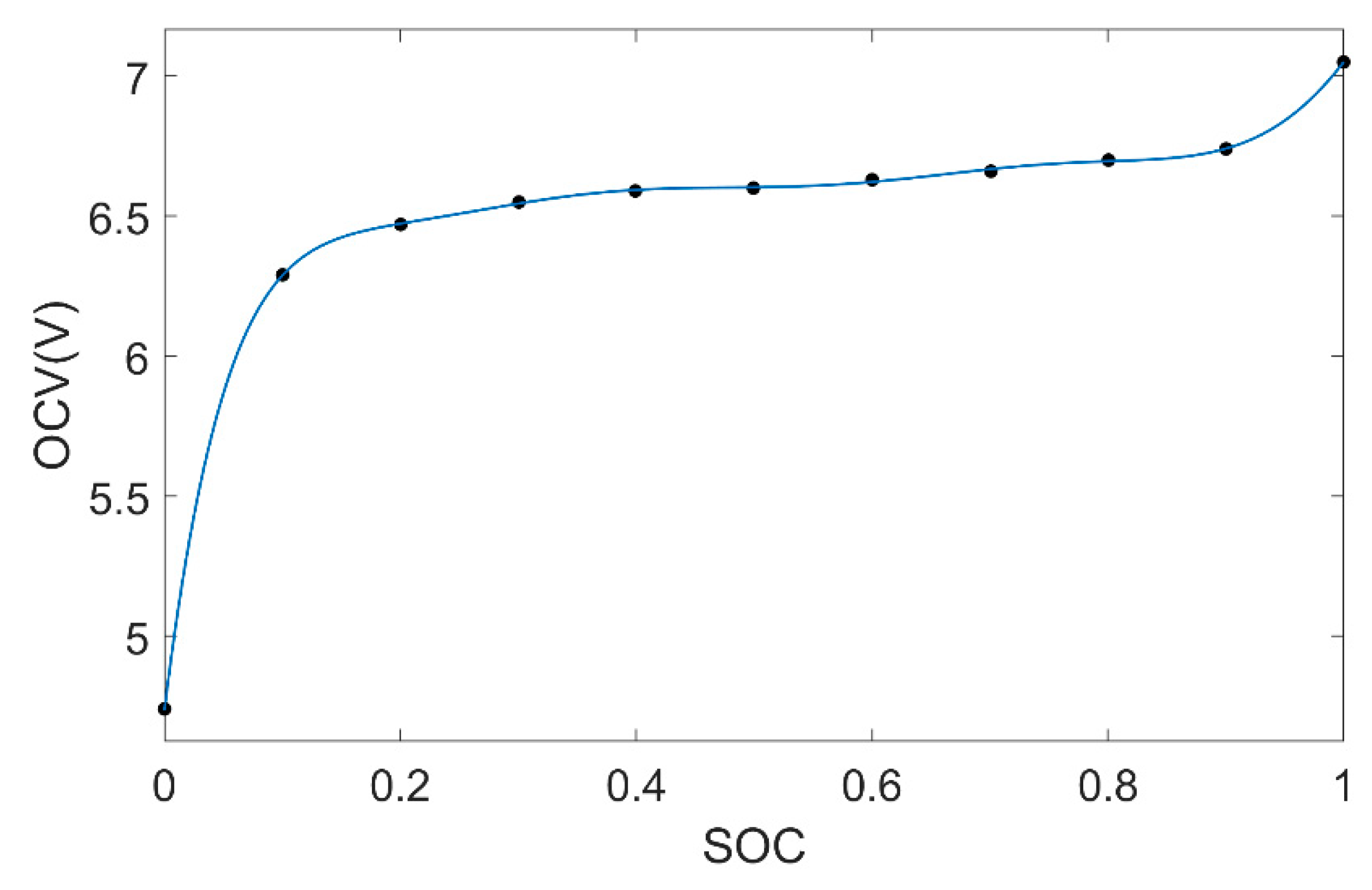
| SOC | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| OCV(V) | 4.736 | 6.285 | 6.469 | 6.549 | 6.588 | 6.607 | 6.629 | 6.598 | 6.701 | 6.744 | 7.051 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, X.; Zhao, X.; Wang, G.; Liu, W. A Novel Temperature–Hysteresis Model for Power Battery of Electric Vehicles with an Adaptive Joint Estimator on State of Charge and Power. Energies 2019, 12, 3621. https://doi.org/10.3390/en12193621
Lei X, Zhao X, Wang G, Liu W. A Novel Temperature–Hysteresis Model for Power Battery of Electric Vehicles with an Adaptive Joint Estimator on State of Charge and Power. Energies. 2019; 12(19):3621. https://doi.org/10.3390/en12193621
Chicago/Turabian StyleLei, Xu, Xi Zhao, Guiping Wang, and Weiyu Liu. 2019. "A Novel Temperature–Hysteresis Model for Power Battery of Electric Vehicles with an Adaptive Joint Estimator on State of Charge and Power" Energies 12, no. 19: 3621. https://doi.org/10.3390/en12193621





