Several Problems with Froude-Number Based Scale Modeling of Fires in Small Compartments
Abstract
1. Introduction
2. Froude-Number Based Fire Modeling
- The Froude-numbers of both of the fires are equal;
- All geometrical features related to the fire and the environment are scaled with the same scale;
- The fires are occurring at well-ventilated conditions, i.e. the combustion is not significantly influenced by the reduced-scale, and the combustion efficiency in full and reduced-scale is similar;
- The flow in the buoyant plume is turbulent.
- The heat release rate of the fire [kW]
- Time [s]
- Energy [kJ]
- Air velocity [m/s]
- Mass flow [kg/s]
- Temperature [K]
3. Materials and Methods
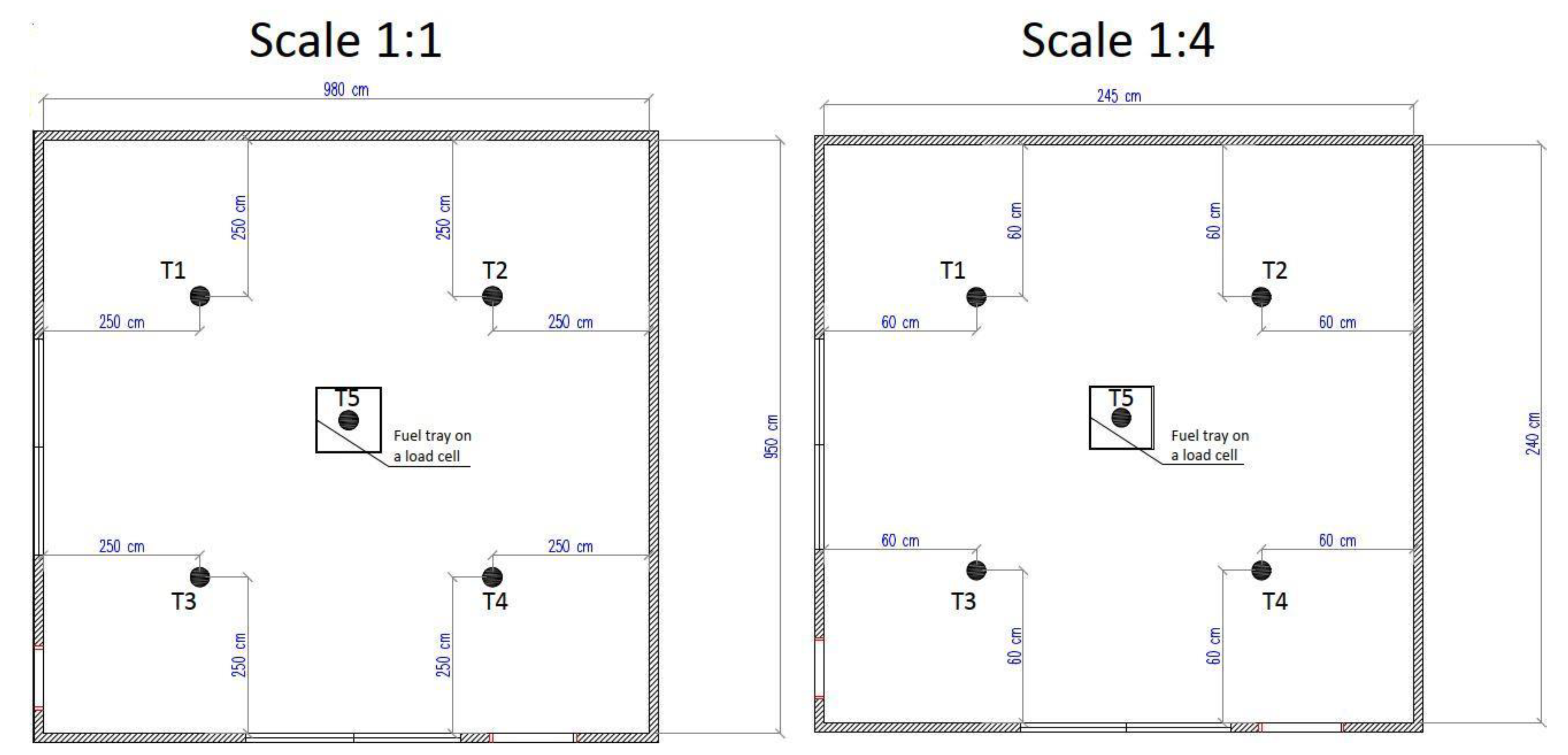
3.1. Experimental Setup
- -
- 4 type K 1mm Ni-Cr thermocouples (T1-T4) placed in the corners of the compartment, used to measure the average temperature of the smoke layer, extended uncertainty of the measurement was estimated at 0.3 °C;
- -
- 1 type K 1mm Ni-Cr thermocouple placed in the plume centerline, underneath the ceiling (T5), used to measure the peak temperature of the smoke upon entering the smoke layer, extended uncertainty of the measurement was estimated at 0.3 °C;
- -
- load cell with a resolution of 0.01 g was used to measure the mass-loss rate of fuel in the tray in both experiments, with extended uncertainty of 0.02 g;
3.2. Numerical Simulations
3.3. Mesh Sensitivity Analysis for CFD Simulations
4. Results
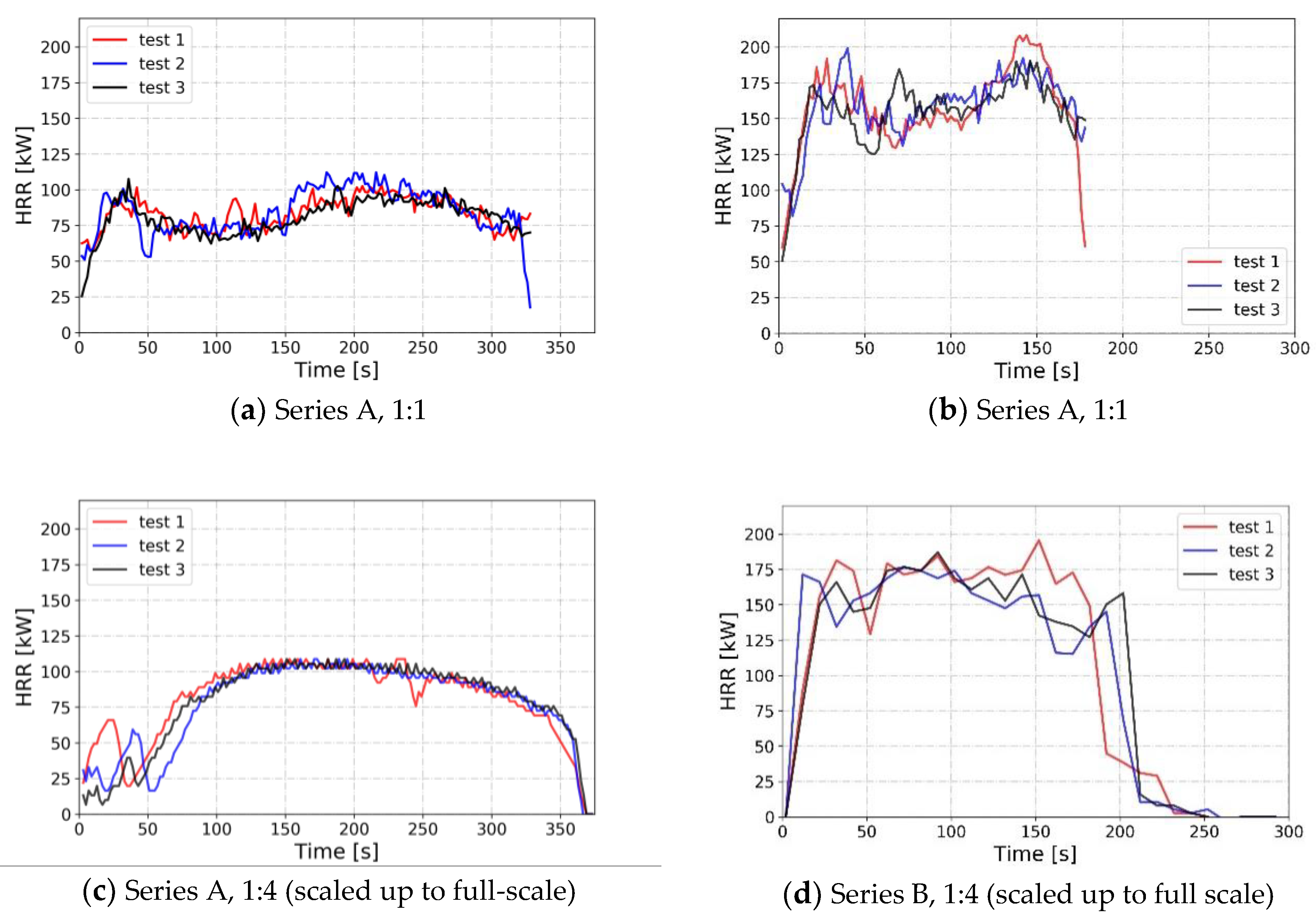
4.1. Experimental Research
4.2. Numerical Modeling
5. Discussion
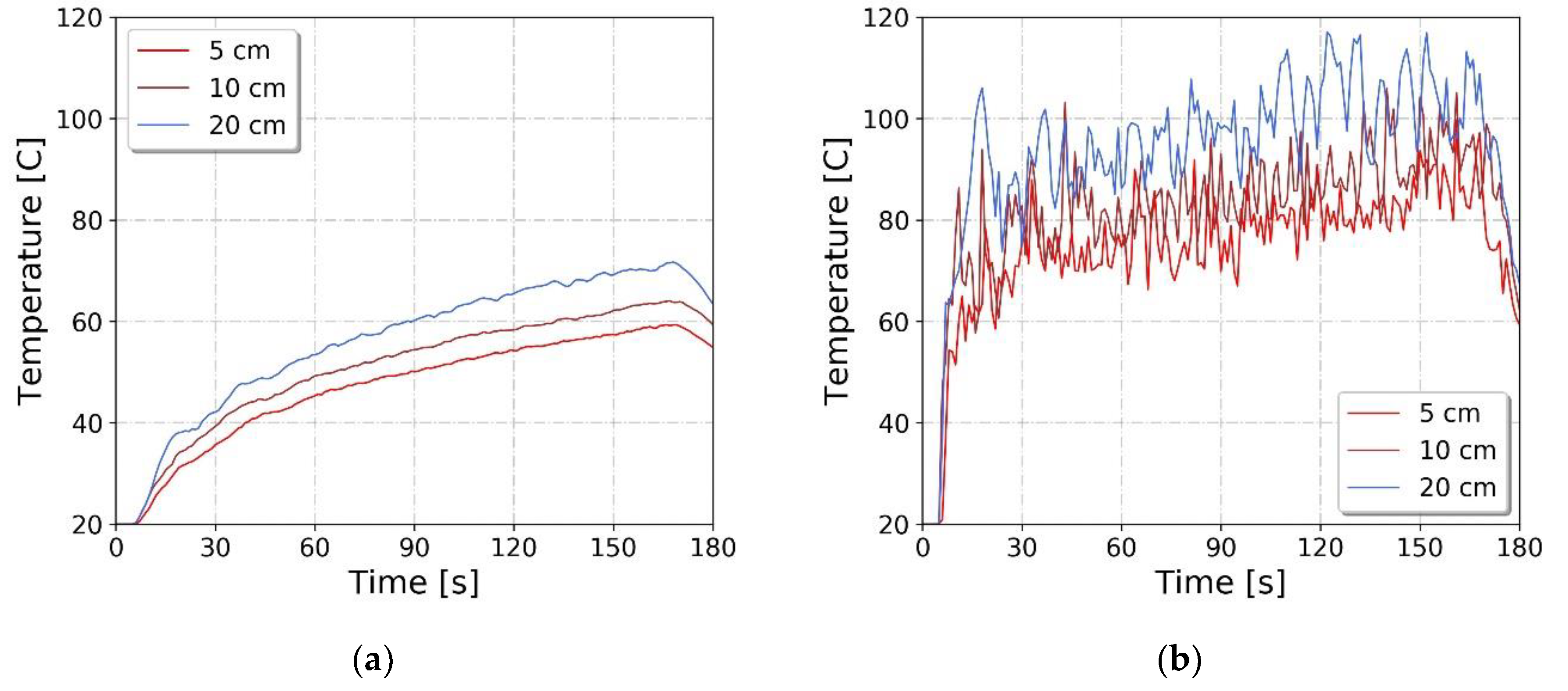
5.1. Modeling the Temperature of the Smoke
5.2. Problems with Maintaining the Reynolds Number and Laminar Flames
5.3. The Influence of the Thermal Inertia of the Boundaries
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
List of Symbols
| specific heat [J/kgK] | |
| D | diameter of the plume |
| E | energy [J] |
| Fr | Froude dimensionless number |
| g | gravitational pull of Earth [N/kg] |
| Hc | Heat of combustion [kJ/kg] |
| k | conductivity [W/m K] |
| Κ | Radiation absorption coefficient |
| l | characteristic length [m] |
| mass flow [kg/s] | |
| Nu | Nusselt number |
| Re | Reynolds dimensionless number |
| T | Temperature [K] |
| t | time [s] |
| µ | kinematic viscosity [m²/s] |
| u | air flow velocity [m/s] |
| Q | rate of heat release [kW] |
| x | characteristic dimension [m] |
| ρ | density [kg/m³] |
| Π | dimensionless group |
Subscripts
| f | full-scale model |
| m | reduced-scale model |
| o | ambient |
References
- McGrattan, K. Fire modeling: Where are we? Where are we going? Fire Saf. Sci. 2005, 8, 53–68. [Google Scholar] [CrossRef]
- McGrattan, K.; Miles, S. Modeling Fires Using Computational Fluid Dynamics (CFD). In SFPE Handbook of Fire Protection Engineering; Springer: New York, NY, USA, 2016; pp. 1034–1065. [Google Scholar]
- Thomas, P.H.; Hinkley, P.L.; Theobald, C.R.; Simms, D.L. Investigations into the Flow of Hot Gases in Roof Venting; Her Majesty’s Stationary Office: London, UK, 1963. [Google Scholar]
- Carey, A.C. Scale Modeling of Static Fires in a Complex Geometry for Forensic Fire Applications. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 2010. [Google Scholar]
- Quintiere, J.G.; Carey, A.C.; Reeves, L.; Mccarthy, L.K. 2008-DN-BX-K178: Scale Modeling in Fire Reconstruction; Natopnal Criminal Justice Reference Service: Rockville, MD, USA, 2017. [Google Scholar]
- Merci, B. Introduction to Fluid Mechanics. In SFPE Handbook of Fire Protection Engineering; Springer: New York, NY, USA, 2016; pp. 1–24. [Google Scholar]
- Thomas, P.H. Dimensional analysis: A magic art in fire research? Fire Saf. J. 2000, 34, 111–141. [Google Scholar] [CrossRef]
- Węgrzyński, W.; Antosiewicz, P.; Burdzy, T.; Zimny, M.; Krasuski, A. Smoke Obscuration Measurements in Reduced-Scale Fire Modeling Based on Froude Number Similarity. Sensors 2019, 19, 3628. [Google Scholar] [CrossRef] [PubMed]
- Williams, F.A. Scalling Mass Fires. In Fire Research Abstracts and Reviews, Volume 11; National Academies Press: Washington, DC, USA, 1969; pp. 1–22. ISBN 978-0-309-30950-9. [Google Scholar]
- Prahl, J.; Emmons, H.W. Fire induced flow through an opening. Combust. Flame 1975, 25, 369–385. [Google Scholar] [CrossRef]
- Harrison, R.; Spearpoint, M. The Balcony Spill Plume: Entrainment of Air into a Flow from a Compartment Opening to a Higher Projecting Balcony. Fire Technol. 2007, 43, 301–317. [Google Scholar] [CrossRef][Green Version]
- Węgrzyński, W.; Konecki, M. Influence of the fire location and the size of a compartment on the heat and smoke flow out of the compartment. AIP Conf. Proc. 2018, 1922, 110007. [Google Scholar]
- Quintiere, J.G. Scaling applications in fire research. Fire Saf. J. 1989, 15, 3–29. [Google Scholar] [CrossRef]
- Quintiere, J.G. Fundamentals of Fire Phenomena; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Zohuri, B. Dimensional Analysis and Self-Similarity Methods for Engineers and Scientists; Springer: New York, NY, USA, 2015; ISBN 9783319134765. [Google Scholar]
- Zimny, M. Physical modeling of a fire with the use of the Froude number. Bud. Archit. 2019, 18, 71–80. [Google Scholar]
- Brzezińska, D. Ventilation System Influence on Hydrogen Explosion Hazards in Industrial Lead-Acid Battery Rooms. Energies 2018, 11, 2086. [Google Scholar] [CrossRef]
- Li, Y.Z.; Ingason, H.; Lönnermark, A. Runehamar Tunnel Fire Tests; SP Technical Research Institute of Sweden: Borås, Sweden, 2011. [Google Scholar]
- Kim, D.H.; Park, W.H. Experiment by using reduced scale models for the fire safety of a rescue station in very long rail tunnel in Korea. Tunn. Undergr. Space Technol. 2006, 21, 303. [Google Scholar] [CrossRef]
- Lönnermark, A.; Lindström, J.; Li, Y.Z. Model-Scale Metro Car Fire Tests of Sweden; SP Technical Research Institute of Sweden: Borås, Sweden, 2011; ISBN 9789186622657. [Google Scholar]
- Heskestad, G. Modeling of enclosure fires. Symp. Combust. 1973, 14, 1021–1030. [Google Scholar] [CrossRef]
- Himoto, K.; Shinohara, M.; Sekizawa, A.; Takanashi, K.; Saiki, H. A field experiment on fire spread within a group of model houses. Fire Saf. J. 2018, 96, 105–114. [Google Scholar] [CrossRef]
- Croce, P.A.; Xin, Y. Scale modeling of quasi-steady wood crib fires in enclosures. Fire Saf. J. 2005, 40, 245–266. [Google Scholar] [CrossRef]
- Quintiere, J.; Mccaffrey, J.; Kashiwagi, T. A scaling study of a corridor subject to a room fire. Combust. Sci. Technol. 1978, 18, 1–19. [Google Scholar] [CrossRef]
- Arini, D.; Pancawardani, F.; Santoso, M.A.; Sugiarto, B.; Nugroho, Y.S. Froude Modeling of Fire Phenomena: Observation of Fire-induced Smoke Movement in Basement Structure for Firefighting Purpose. Procedia Eng. 2017, 170, 182–188. [Google Scholar] [CrossRef]
- Węgrzyński, W. Partitions and the flow of smoke in large volume buildings. Archit. Civ. Eng. Environ. 2018, 11, 155–164. [Google Scholar] [CrossRef]
- Tanaka, F.; Kawabata, N.; Ura, F. Smoke spreading characteristics during a fire in a shallow urban road tunnel with roof openings under a longitudinal external wind blowing. Fire Saf. J. 2017, 90, 156–168. [Google Scholar] [CrossRef]
- Kayili, S.; Yozgatligil, A.; Eralp, O.C. Effect of Ventilation and Geometrical Parameters of the Burning Object on the Heat Release Rate in Tunnel Fires. Combust. Sci. Technol. 2012, 184, 165–177. [Google Scholar] [CrossRef]
- Li, Y.Z.; Ingason, H. Model scale tunnel fire tests with automatic sprinkler. Fire Saf. J. 2013, 61, 298–313. [Google Scholar] [CrossRef]
- Li, Y.Z.; Lei, B.; Ingason, H. Scale modeling and numerical simulation of smoke control for rescue stations in long railway tunnels. J. Fire Prot. Eng. 2012, 22, 101–131. [Google Scholar] [CrossRef]
- Zhao, P.; Yuan, Z.; Yuan, Y.; Yu, N.; Yu, T. A Study on Ceiling Temperature Distribution and Critical Exhaust Volumetric Flow Rate in a Long-Distance Subway Tunnel Fire with a Two-Point Extraction Ventilation System. Energies 2019, 12, 1411. [Google Scholar] [CrossRef]
- Ingason, H.; Li, Y.Z. Model scale tunnel fire tests with longitudinal ventilation. Fire Saf. J. 2010, 45, 371–384. [Google Scholar] [CrossRef]
- Khattri, S.K.; Log, T.; Kraaijeveld, A. Tunnel Fire Dynamics as a Function of Longitudinal Ventilation Air Oxygen Content. Sustainability 2019, 11, 203. [Google Scholar] [CrossRef]
- McGrattan, K.; Hostikka, S.; McDermott, R.; Floyd, J.; Weinschenk, C.; Overholt, K. Fire Dynamics Simulator User’s Guide, 6th ed.; National Insitute of Standards and Technology: Gaithersburg, MD, USA, 2017.
- McGrattan, K.; Hostikka, S.; McDermott, R.; Floyd, J.; Weinschenk, C.; Overholt, K. Fire Dynamics Simulator Technical Reference Guide. Volume 3: Validation, 6th ed.; NIST Special Publication 1018-3; National Insitute of Standards and Technology: Gaithersburg, MD, USA, 2015; Volume 1.
- Thunderhead Engineering. PyroSim User Manual; Thunderhead Engineering: Manhattan, KS, USA, 2017; p. 167. [Google Scholar]
- Hill, K.; Dreisbach, J.; Joglar, F.; Najafi, B.; McGrattan, K.; Peacock, R.; Hamins, A. Verification and Validation of Selected Fire Models for Nuclear Power Plant Aplications, Volume 7; U.S. NRC: Washington, DC, USA, 2014.
- Hurley, M.J. SFPE Handbook of Fire Protection Engineering; Hurley, M.J., Gottuk, D., Hall, J.R., Jr., Harada, K., Kuligowski, E., Puchovsky, M., Torero, J., Watts, J.M., Jr., Wieczorek, C., Eds.; Springer: New York, NY, USA, 2016; ISBN 978-1-4939-2565-0. [Google Scholar]
- Barsim, M.M.; Bassily, M.A.; El-Batsh, H.M.; Rihan, Y.A.; Sherif, M.M. Froude scaling modeling in an Atrium Fire equipped with natural and transient forced ventilation. Int. J. Vent. 2019, 1–23. [Google Scholar] [CrossRef]
- Tanaka, F.; Fukaya, K.; Moinuddin, K.A.M. Development of a technique for establishing a pseudo tunnel length. Proc. Combust. Inst. 2019, 37, 3985–3992. [Google Scholar] [CrossRef]


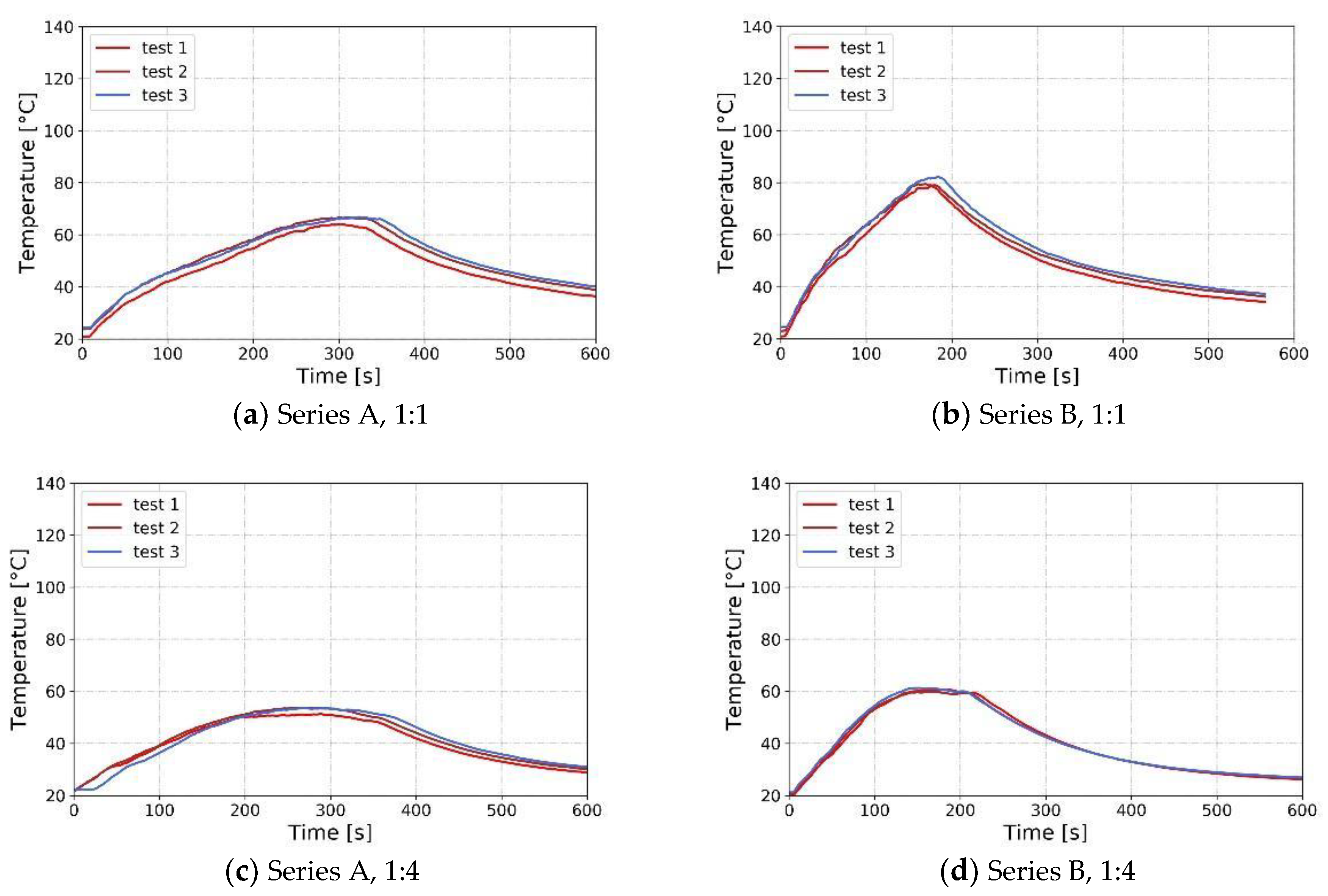

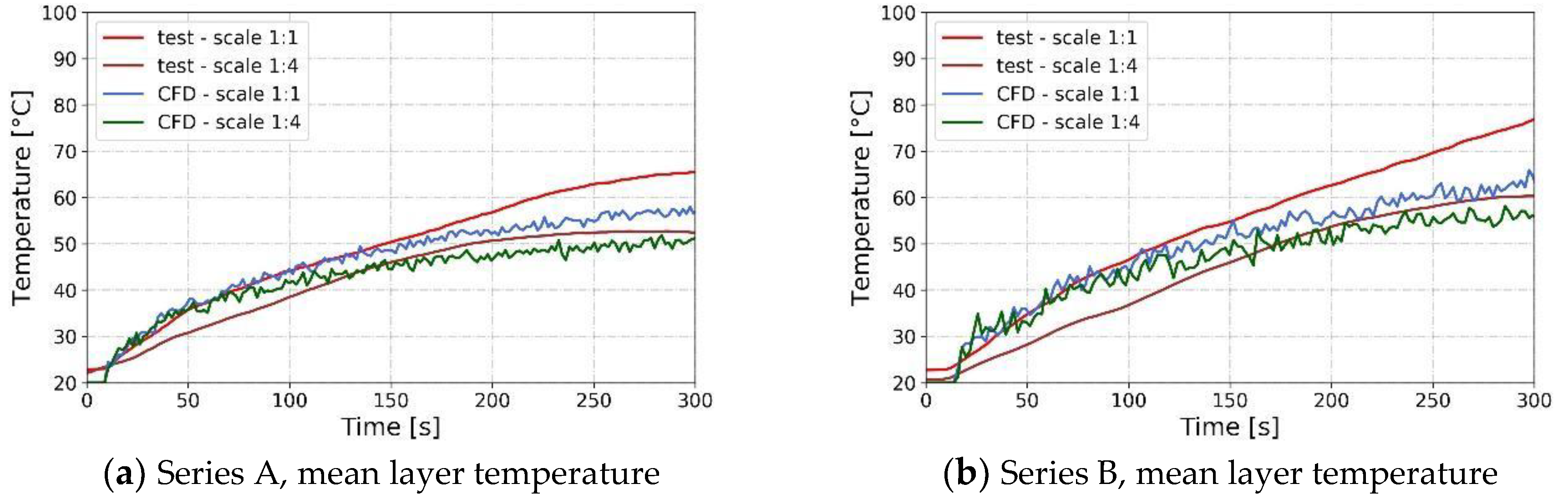
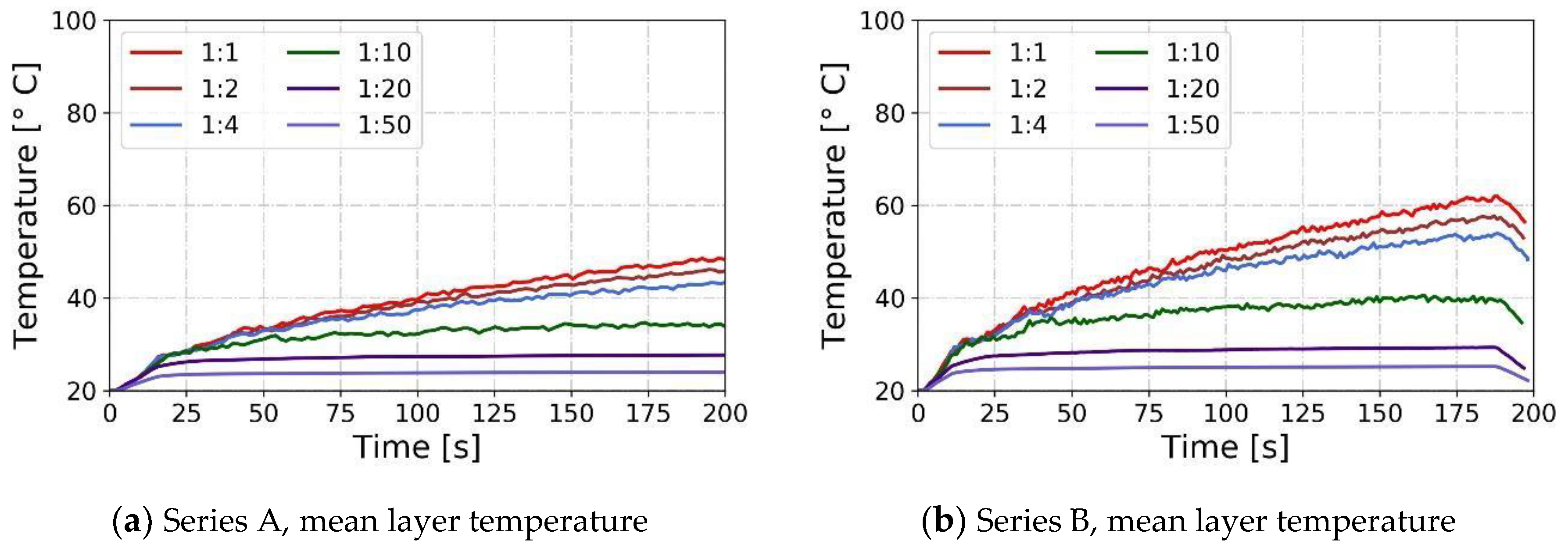
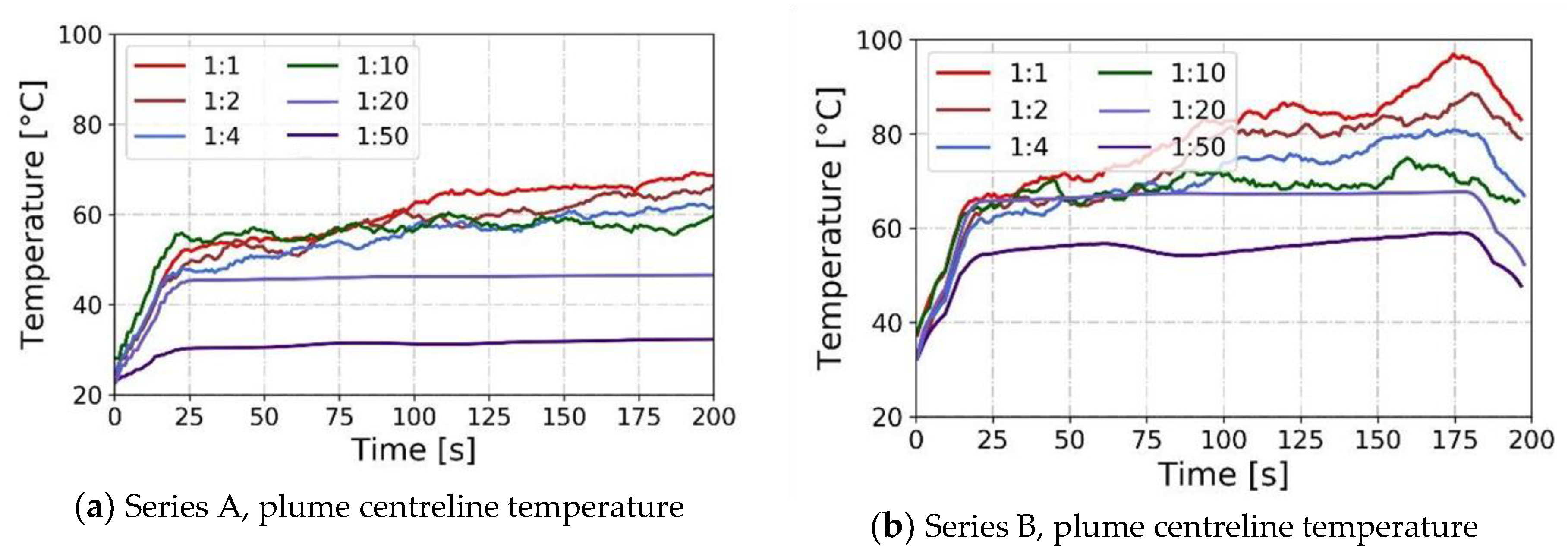
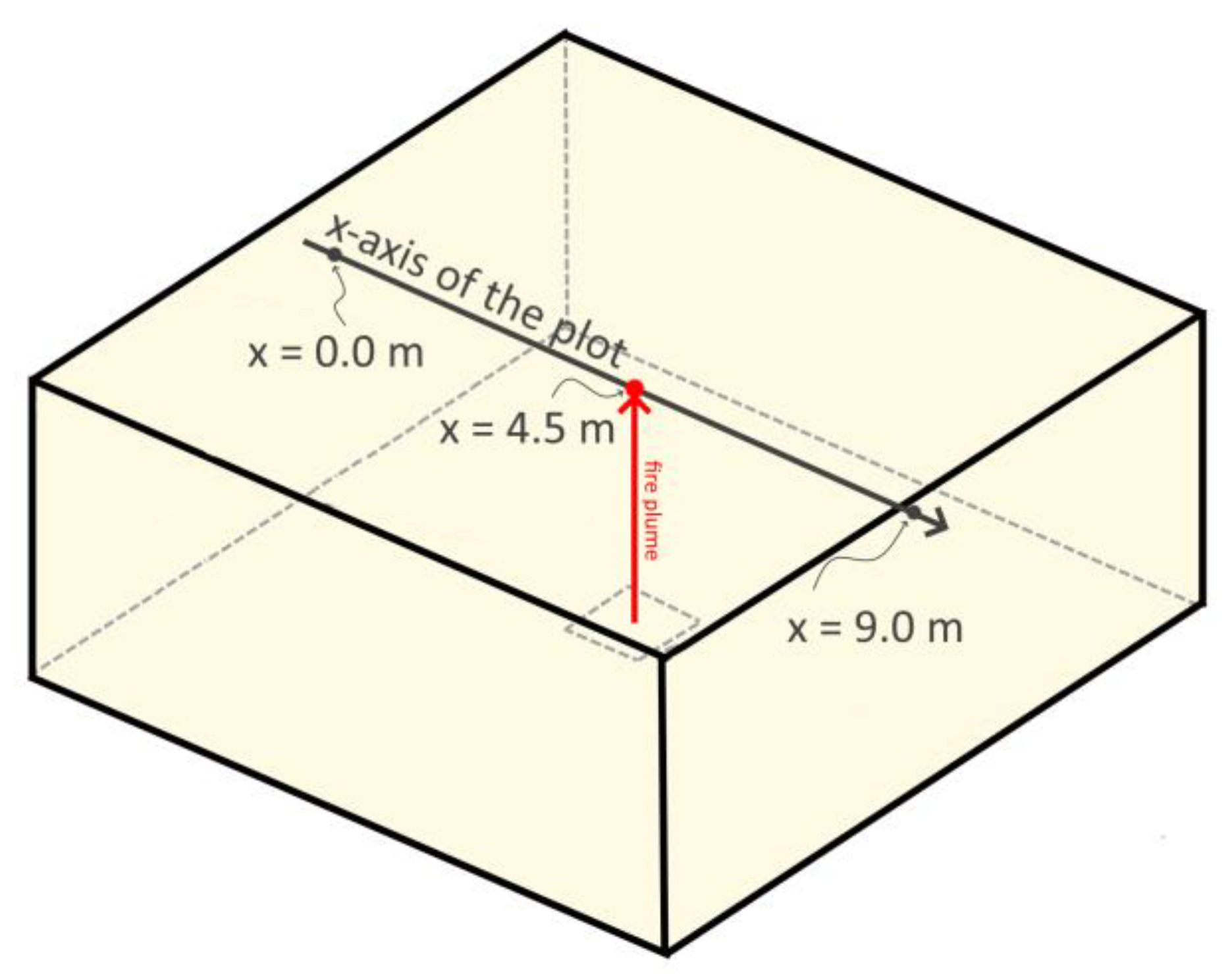
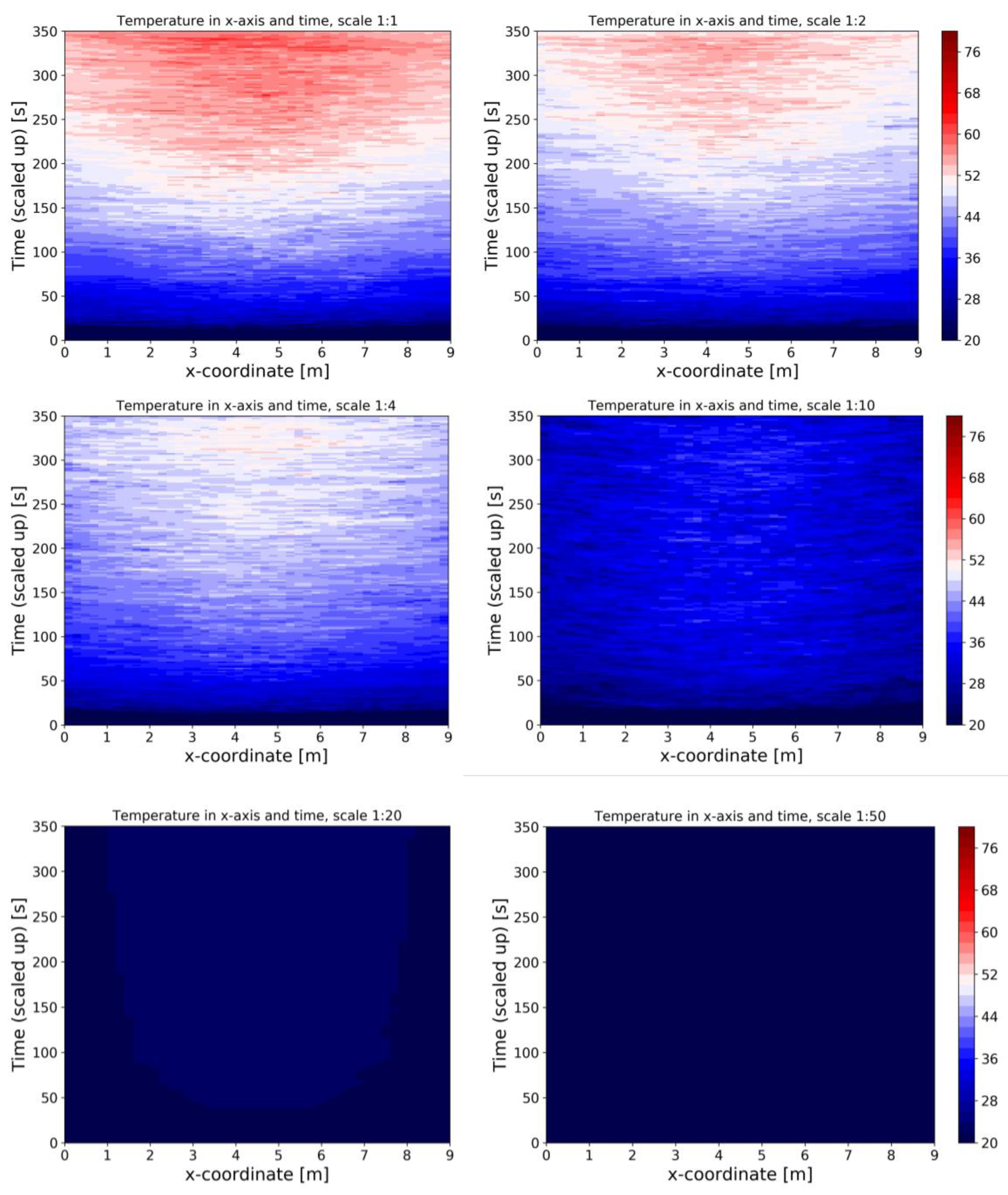
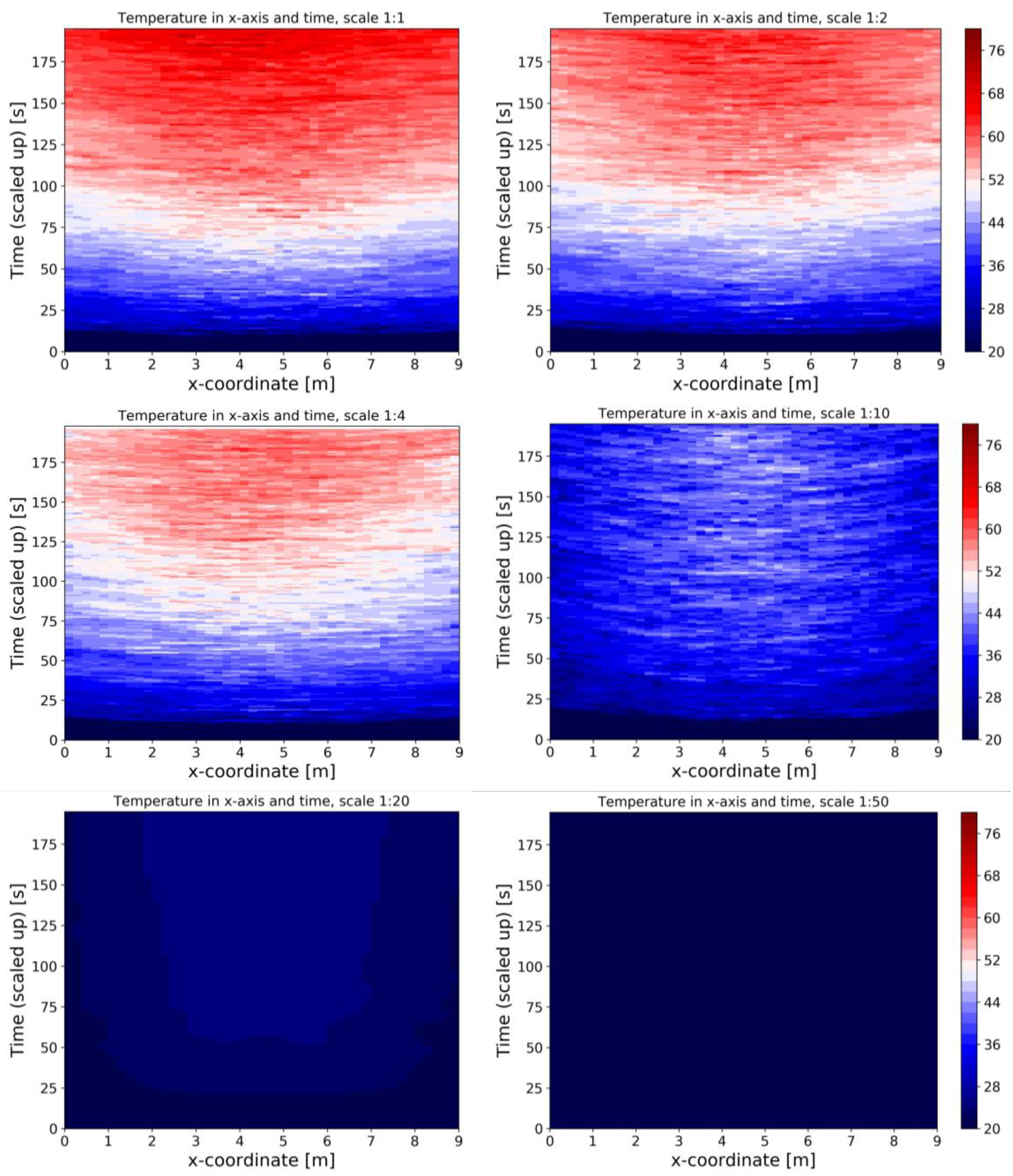
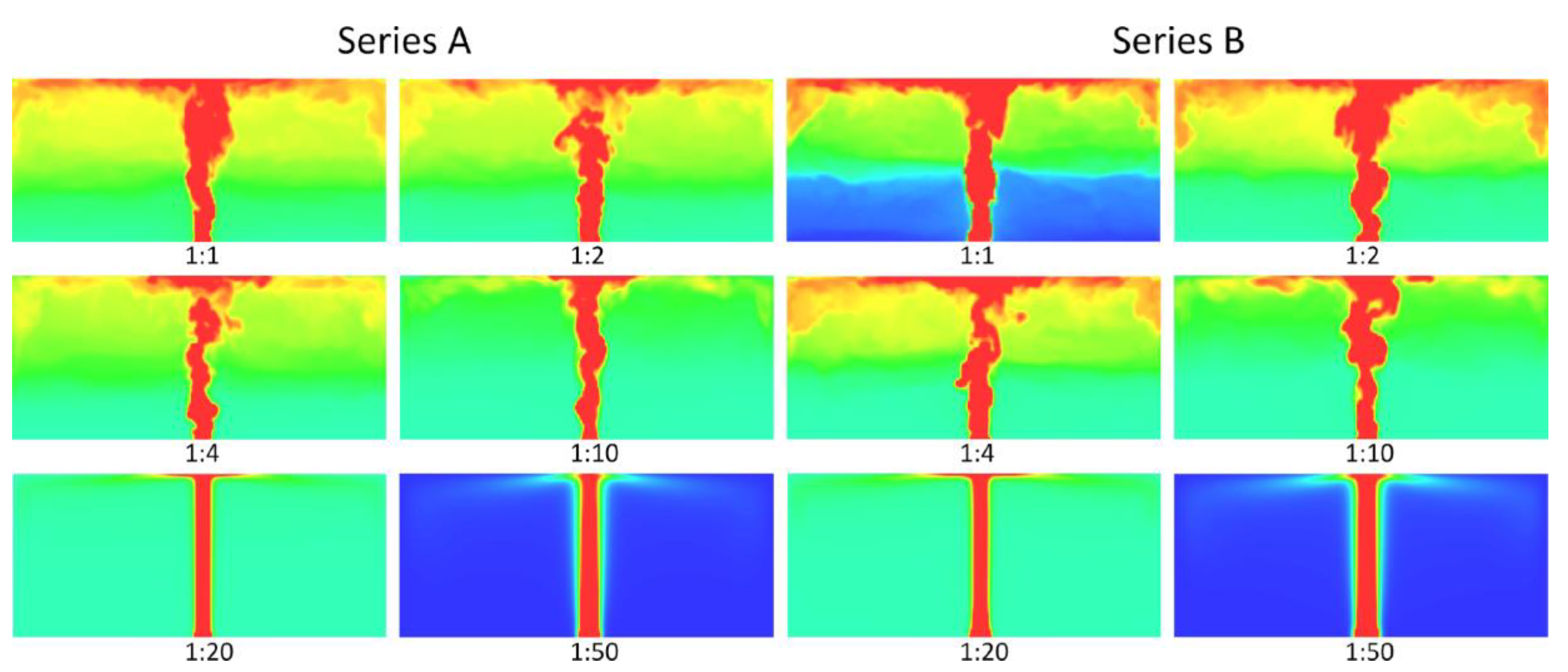
| Scale | Compartment of Interest | Number of Experiments | HRR (Reduced-Scale) | Reference |
|---|---|---|---|---|
| 1:1 | Road tunnel | 5 | 6000–202,000 kW | [18] |
| 1:2 | Railway car | 10 | 90–1247 kW | [20] |
| 1:2 | Compartment | n/a | n/a | [21] |
| 1:3.5 | Group of houses | 2 | up to 100,000 kW | [22] |
| 1:4 | Compartment | 165 | n/a | [23] |
| 1:7 | Room | 3 | 300–1500 kW | [24] |
| 1:8 | Cellar | 1 | 18.31 kW | [25] |
| 1:8 | Corridor | 5 | 50–300 kW | [4] |
| 1:10 | Shopping mall | 48 | 7.6 kW | [26] |
| 1:10 | Shopping mall | 25 | 6–10.3 kW | [11] |
| 1:12 | Road tunnel | 5 | 15.1–72.8 kW | [27] |
| 1:13 | Road tunnel | 61 | 7.81–215.1 kW | [28] |
| 1:15 | Road tunnel | 28 | 6.7–430.1 kW | [29] |
| 1:20 | Road tunnel | 54 | n/a (5–25 MW in full scale) | [30] |
| 1:20 | Subway tunnel | 116 | 1.48–3.52 kW | [31] |
| 1:23 | Road tunnel | 12 | 102.2–320.8 kW | [32] |
| 1:48 | Train tunnel | 1 | 0.31–1.88 kW | [19] |
| undefined | Small scale tunnel | 1 | 82 kW | [33] |
| Series | Series A | Series B | ||
|---|---|---|---|---|
| 1:1 | 1:4 | 1:1 | 1:4 | |
| HRR [kW] | 81.7 kW | 2.55 kW | 158 kW | 4.94 kW |
| volume of fuel [L] | 1.015 | 0.0158 L | 1.015 L | 0.0158 L |
| mass of fuel [g] | 0.6943 kg | 0.0108 kg | 0.6943 kg | 0.0108 kg |
| duration of the fire (real time) [s] | 350 s | 175 s | 181 s | 90.5 s |
| tray size [m] | 0.33 × 0.33 m | 0.075 × 0.075 m | 0.50 × 0.50 m | 0.125 × 0.125 m |
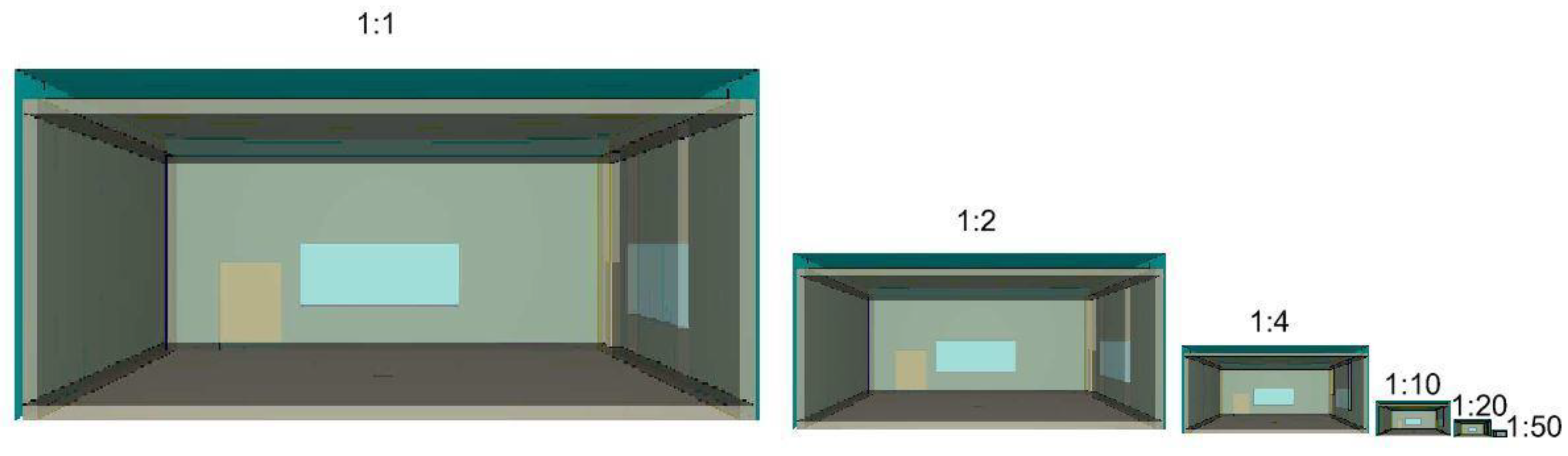
| Scenario | Scale | Model Dimensions [m] | Grid Size [m] | Number of Grid Cells |
|---|---|---|---|---|
| 1 A, B | 1:1 | 9.6 × 9.6 × 4.2 | 0.05 | 3,897,600 |
| 2 A, B | 1:2 | 4.8 × 4.8 × 2.1 | 0.025 | 3,897,600 |
| 3 A, B | 1:4 | 2.4 × 2.4 × 1.05 | 0.0125 | 3,897,600 |
| 4 A, B | 1:10 | 0.96 × 0.96 × 0.42 | 0.005 | 3,897,600 |
| 5 A, B | 1:20 | 0.48 × 0.48 0.21 | 0.0025 | 3,897,600 |
| 6 A, B | 1:50 | 0.192 × 0.192 × 0.084 | 0.001 | 3,897,600 |
| Scenario | Scale | Tray Size [m] | HRR Per Unit of Area [kW/] | Calculation Time [s] | Length of a Time Step for Results Analysis [s] |
|---|---|---|---|---|---|
| 1 A | 1:1 | 0.35 × 0.35 | 750 | 350 | 1.75 |
| 1 B | 1:1 | 0.5 × 0.5 | 584 | 197 | 0.975 |
| 2 A | 1:2 | 0.175 × 0.175 | 530 | 247 | 1.24 |
| 2 B | 1:2 | 0.25 × 0.25 | 414 | 139 | 0.7 |
| 3 A | 1:4 | 0.0875 × 0.0875 | 375 | 175 | 0.88 |
| 3 B | 1:4 | 0.125 × 0.125 | 293 | 99 | 0.49 |
| 4 A | 1:10 | 0.035 × 0.035 | 237 | 110 | 0.55 |
| 4 B | 1:10 | 0.05 × 0.05 | 185 | 62 | 0.31 |
| 5 A | 1:20 | 0.0175 × 0.0175 | 167 | 78 | 0.39 |
| 5 B | 1:20 | 0.025 × 0.025 | 131 | 44 | 0.22 |
| 6 A | 1:50 | 0.007 × 0.007 | 106 | 50 | 0.25 |
| 6 B | 1:50 | 0.01 × 0.01 | 83 | 28 | 0.14 |
| Scale | Velocity [m/s] (CFD) | Velocity [m/s] (Calculated with Equation (9)) | Reynolds Number (CFD) 1 | Reynolds Number (Calculated) 1 |
|---|---|---|---|---|
| Series A | ||||
| 1:1 | 1.50 | 1.50 | 27,531 | 27,531 |
| 1:2 | 0.95 | 1.06 | 8718 | 9734 |
| 1:4 | 0.65 | 0.75 | 2982 | 3441 |
| 1:10 | 0.40 | 0.47 | 734 | 871 |
| 1:20 | 0.05 | 0.34 | 46 | 308 |
| 1:50 | 0.08 | 0.21 | 29 | 78 |
| Series B | ||||
| 1:1 | 1.50 | 1.50 | 41,713 | 41,713 |
| 1:2 | 1.00 | 1.06 | 13,904 | 14,748 |
| 1:4 | 0.80 | 0.75 | 5562 | 5214 |
| 1:10 | 0,50 | 0.47 | 1390 | 1319 |
| 1:20 | 0.07 | 0.34 | 97 | 466 |
| 1:50 | 0.09 | 0.21 | 50 | 118 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zimny, M.; Antosiewicz, P.; Krajewski, G.; Burdzy, T.; Krasuski, A.; Węgrzyński, W. Several Problems with Froude-Number Based Scale Modeling of Fires in Small Compartments. Energies 2019, 12, 3625. https://doi.org/10.3390/en12193625
Zimny M, Antosiewicz P, Krajewski G, Burdzy T, Krasuski A, Węgrzyński W. Several Problems with Froude-Number Based Scale Modeling of Fires in Small Compartments. Energies. 2019; 12(19):3625. https://doi.org/10.3390/en12193625
Chicago/Turabian StyleZimny, Mateusz, Piotr Antosiewicz, Grzegorz Krajewski, Tomasz Burdzy, Adam Krasuski, and Wojciech Węgrzyński. 2019. "Several Problems with Froude-Number Based Scale Modeling of Fires in Small Compartments" Energies 12, no. 19: 3625. https://doi.org/10.3390/en12193625
APA StyleZimny, M., Antosiewicz, P., Krajewski, G., Burdzy, T., Krasuski, A., & Węgrzyński, W. (2019). Several Problems with Froude-Number Based Scale Modeling of Fires in Small Compartments. Energies, 12(19), 3625. https://doi.org/10.3390/en12193625





