1. Introduction
Solid oxide fuel cells (SOFCs) are one of the most efficient types of power generation fuel cells. The efficiency of SOFC-based electricity generators exceeds that of conventional thermal cycles. Higher electrical efficiencies are expected if waste heat or fuel from the high-temperature SOFC is further used in the thermal cycles. An efficiency in excess of 70% is, for example, projected for the SOFC-gas turbine combined cycle concepts [
1,
2,
3].
We analyzed a combined power generation cycle with low- and high-temperature SOFCs arranged in series (including a gas turbine) and revealed that the two-staged SOFC cycle has both higher SOFC power generation efficiency and higher combined cycle efficiency [
4,
5]. Some groups have also worked on the development of in-series interconnection SOFCs enabling a high-voltage and high-fuel-use compact unit [
6,
7].
A thermodynamic analysis of different SOFC combined cycles, including a novel reciprocating engine integrated scheme, have been discussed in recent years [
8]. These studies investigate system performance to analyze the constant efficiency, stack power density, and fraction of total power delivered in different SOFC combined cycles. Herein, a combined heat and power (CHP) or combined cool, heat, and power (CCHP) system using an SOFC was investigated. The influence of several effective parameters (cell temperatures, pressures, fuel use coefficients, and system air: fuel ratios) on SOFC-CHP were investigated. Pirkandi et al. [
9] developed a tubular single cell SOFC by using a self-established electrochemical model, including activation, ohmic, and concentrative losses. Increasing the working pressure and temperature of the cell causes the voltage to increase and enhances the cell’s performance.
Therefore, the system’s thermal and mass flow management directly affects the performance of the cell or system. An SOFC dynamic model based on electrochemical reactions and enthalpy balance equations was developed to solve thermal management issues [
10]. Furthermore, the interactions between components of the micro-CHP system and SOFCs were analyzed by off-design simulation [
11]. The electrical and overall efficiency maps can be used to establish an operating strategy for SOFC systems.
Moreover, we evaluated the potential of integrating a gasification-SOFC-CHP system in an existing manufacturing production process. The integrated SOFC/Gasifier can be considered a high-efficiency tri-generator capable of accomplishing energy valorization of high quality [
12,
13]. High-temperature fuel cells are appropriate energy converters for biogas. Different types of feeds as mixtures were considered. These mixtures differ from each other in the composition of their gaseous substances and their quantity of CO [
14]. Stack performances were mapped by varying some operating cell parameters: the operating temperature and the fuel use factor. In particular, different mixtures made up of 10%, 15%, and 20% CO were taken into account at different operating temperatures (923, 973, and 1003 K) [
15].
An optimized control system with a hybrid system transient model was implemented, validated, and tested. Compared to previous studies, we better performance in controlling fuel cell temperature, reducing the pressure gap between cathode and anode sides, and generating a higher safe margin for the steam-to-carbon ratio [
16]. Hence, optimized operating procedures and controlling strategies should be developed to implement a high-efficiency and reliable SOFC combined system.
For the long-term operation test of an SOFC system, a multi-supply–multi-demand-controlled strategy was provided, which was deemed to be effective for year-round operation of the SOFC combined cycle under changing climatic and loading conditions [
17]. This control strategy can be realized for an actual CCHP system linked up with a building and energy management system.
Moreover, not only energy and heat management but also component materials are considered for a developing a SOFC system. Due to thermal shock issues of the SOFC stack and system, both the large thermal gradients in the system and thermal expansion coefficient mismatches must be avoided [
18]. Therefore, the start-up and thermal aspects of SOFC stacks embedded in a whole system with additional components, such as reformers, heat exchangers, and catalytic burners, are key factors in the system’s demonstration.
In addition, anode off-gas recycling and fuel control are methods used to increase the system efficiency. Different operating conditions and system configurations can increase the stack net electrical efficiency to 57% by implementing an anode off-gas recycle rate of 65% and a fuel use for the stack of 55% [
19]. The estimation of balance of power (BOP) for the SOFC system and minimization of the system’s heat loss are key factors to establish a high performance SOFC system. If the external heat transfer coefficient related to the environments is decreased to 50%, the system’s heat loss is reduced significantly, and the reformer’s efficiency is enhanced [
20].
We used a previously developed dynamic SOFC model, which consists of mass and energy balances and an electrochemical model that relates the fuel and air gas compositions and temperature to voltage, current density, and other relevant fuel cell variables. Knowledge of the dynamic behavior of these variables is important when looking for suitable control strategies [
21,
22,
23]. Predictions of the model provide basic insight into the operation of power generation-based SOFC systems during various transients and support its further design modifications [
24].
To improve the performance and efficiency of the SOFC power generation system, and achieve thermal control of the whole SOFC system, we used a thermodynamic method and a dynamic analysis model to calculate the gas outlet temperature from the dual SOFC stack and hot box in several different operating conditions. The predictions that can be made using thermodynamic equations are essential for understanding and modeling SOFC performance, since SOFCs transform chemical energy into electrical energy.
This paper focuses on the numerical simulations of a 10 kW SOFC-CHP system with a two-stack module. The performance parameters of an SOFC system, fuel use rate, operating temperature, current, and mass flow rate are discussed. To optimize the system control strategy, the previous parameters are modulated to increase the electrical power and fuel use rate. The dynamic model is built to be multi-dimensional and time-dependent to simulate the status of each component in the SOFC system from start-up to power generation.
Finally, the simulation model for the SOFC-CHP with dual stacks is presented to evaluate different operating parameters, with a focus on achieving the maximum possible power efficiency. As a potential distributed power generator, the long-term effects of the studied SOFC-CHP systems are also investigated. The dynamic analysis of the long-term operating SOFC-CHP system shows that the total daily output power can be increased by using the optimal control strategy.
2. Method
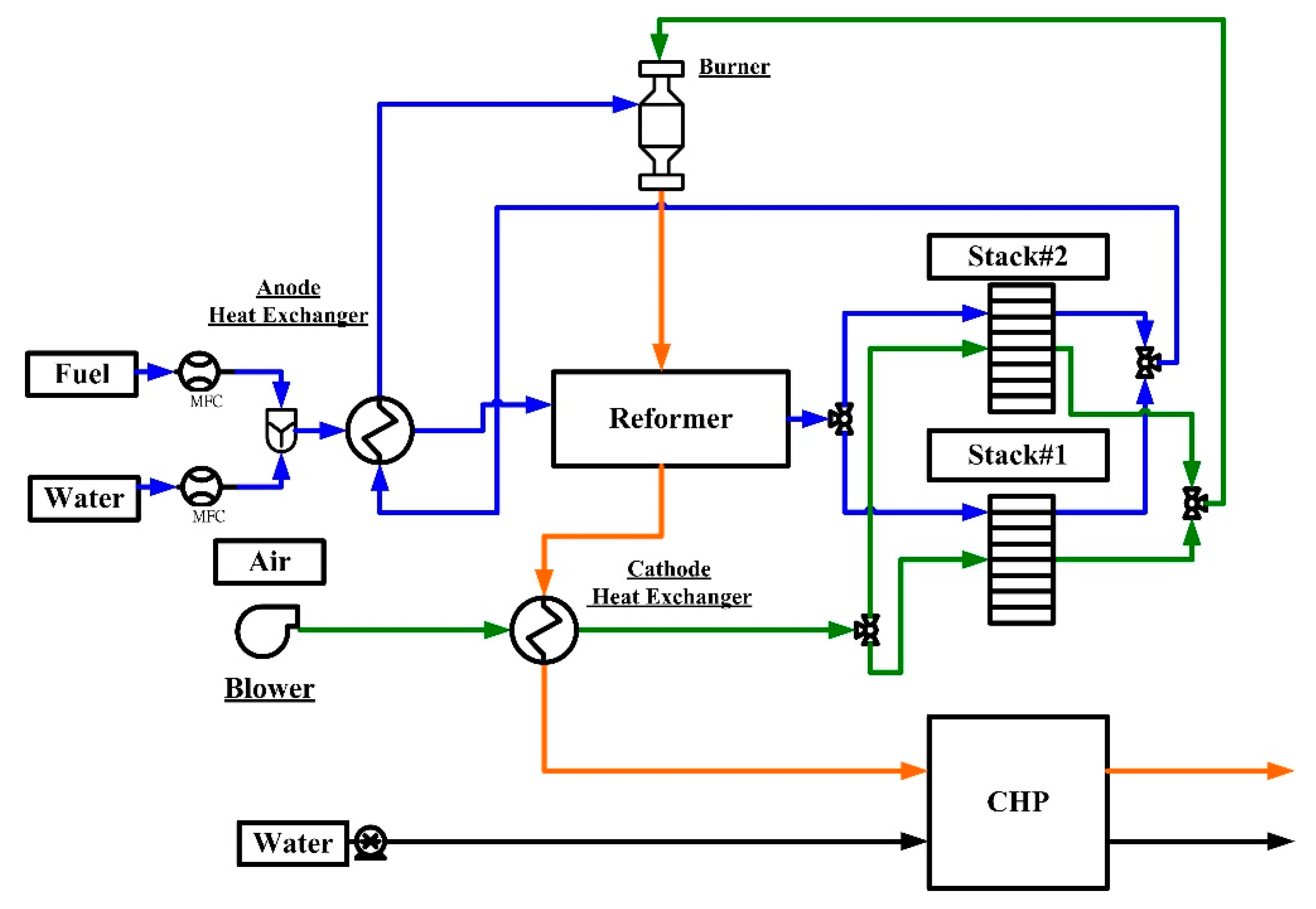
The SOFC power system can be divided into three main parts, the stack module, the hot box, and the cold box. The stack module integrates multi-stacks with series and parallel connections to convert the chemical energy of fuel gas to electrical power and heat. To make the system operate under efficient thermodynamic equilibrium, the components of the hot box, e.g., the heat exchanger, burner, and reformer, are used for the heat and mass transfer and recovery of the fluids in the system. The cold box includes balance of plant (BOP) components to control the fluid flow rates and power loading, and to ensure that the system is safely operating.
In this paper, a theoretical model for oxygen-ion conducting SOFC systems is simulated using the Thermolib, which is a toolbox based on MATLAB/Simulink for the design and development of thermodynamic systems. The simulation program of Thermolib has been used to simulate the system widely, including SOFC systems. For example, T. C. Cheng et al. [
25] used Thermolib to calculate the proton type of an SOFC system and analyze its efficiency for different flow rations. D. Y. Tanaka et al. [
26] used Thermolib to calculate SOFC efficiency and analyze the influence between fuel use and efficiency. In this paper, Thermolib is used to simulate the dynamic process of the whole SOFC system. Thermolib is a program that can be accurately fit to simulate heat components, such as a heat exchanger, reformer, and SOFC stack. By using Thermolib, the parameters of heat components can be selected by a researcher to fit the true experiments. The numerical models are described below:
2.1. Numerical Modeling of the SOFC Stack
The electrochemical reactions of the solid oxide fuel cell are
To calculate the performance of the SOFC, the cell voltage variation under different loads is evaluated by the Bulter–Volmer Equation:
where
is the open circuit voltage,
is the ohmic impedance,
is the anode activation impedance,
is the cathode activation impedance,
is the anode concentration polarization impedance, and
is the cathode concentration polarization impedance. The impedance is calculated by the Nernst equation, as follows:
The parameters used in the above equations are listed in
Table 1 with reference to the literature [
27,
28,
29].
2.2. Numerical Modeling of the Hot Box Components
In this study, the steam reformer is used to convert methane to hydrogen gases. The performance of a reformer is mainly dependent on the chemical catalysts. The reactions are described as
The reaction of Equation (11) is the endothermic process, , while an exothermic process occurs in Equation (12): .
In an SOFC power system, an afterburner is required to combust the remaining fuel gases that exit the anode of the SOFC stack with a high temperature. The required heat energy of the methane reformer can be provided by the heat recovery of the combustion exhaust gases. For the methane-based SOFC system, the chemical energy of the anode off-gases is changed to heat energy by the following reaction:
The heat energy of combustion exhaust is recovered to preheat the fuel gases and the air entering the stack via the anode and cathode heat exchangers.
The heat exchanger plays an important role in the SOFC system, since the fuel and air flows that pass through the stack must be pre-heated with a temperature high enough to keep the stack temperature. The system’s efficiency is also significantly dependent on the efficiency of the heat exchangers. The heat capacity of the cold and hot gas streams in a heat exchanger is calculated as [
30]
The low and high values of the heat capacities of the hot and cold streams are assigned as Cmin and Cmax, which refers to the ratio of heat capacity (Cr) given by
The effectiveness of the heat exchanger is defined as the ratio of the actual heat transfer rate between the hot and cold streams and the maximum possible heat transfer rate between these streams (q
max):
where the theoretical maximum heat transfer rate is
where T
h,1 and T
c,1 are the hot stream inlet temperature and the cold stream inlet temperature, respectively. The effectiveness of the heat exchanger can be calculated by
The temperature of the hot and cold gas streams exiting the heat exchanger is obtained by
2.3. MATLAB/Simulink/Thermolib Simulation Procedure
By modeling the reactions of the SOFC stack and the hot box components, the power generation and system performance can be evaluated by numerical simulation [
30,
31,
32]. The simulated parameters in the studied SOFC-CHP system of this work are listed in
Table 2. The simulation procedure of an SOFC system via the MATLAB/Simulink/Thermolib tool includes the following steps:
- (a)
Perform the system design and confirm that the types of components and paths of the fuel, air, and exhaust gas flows are appropriate for thermodynamic equilibrium.
- (b)
Carry out the modeling of each thermal component and perform simulation test with operating parameters for validation.
- (c)
Connect the components of the SOFC system to carry out system simulation.
- (d)
For the dynamic simulation of an SOFC system, the calculation is performed under finite time intervals with specified time steps.
4. Conclusions
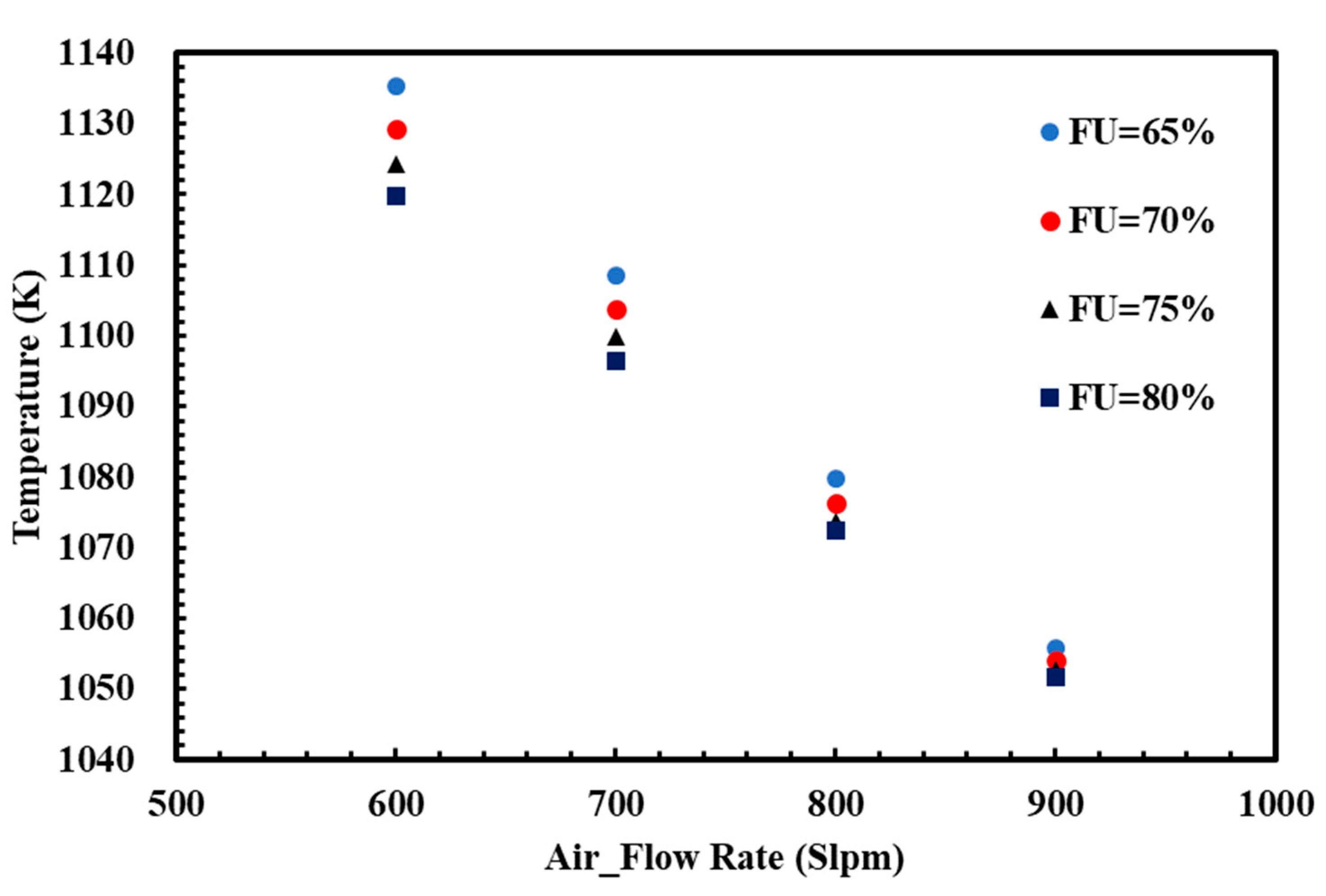
This paper performed the dynamic analysis of a 10 kW SOFC-CHP system with a two-stack module by numerical simulations. The performance of stacks, tail gas burners, heat exchangers and fuel reformers was modeled by the MATLAB/Simulink module. Since the performance of the SOFC stack is significantly affected by the operating temperature, the effects of the fuel use and air flow rates on the stack’s operating temperature and power generation are thoroughly discussed. The results indicate that the stack temperature raises as the FU decreases due to the increasing combustion heat from the burner to gas heat exchangers. The stack temperature can also be increased by reducing the air flow rate. Therefore, the air flow rate and operating current (which are related to the fuel use rate) of an SOFC system should be optimally regulated to achieve maximum power generation and efficiency.
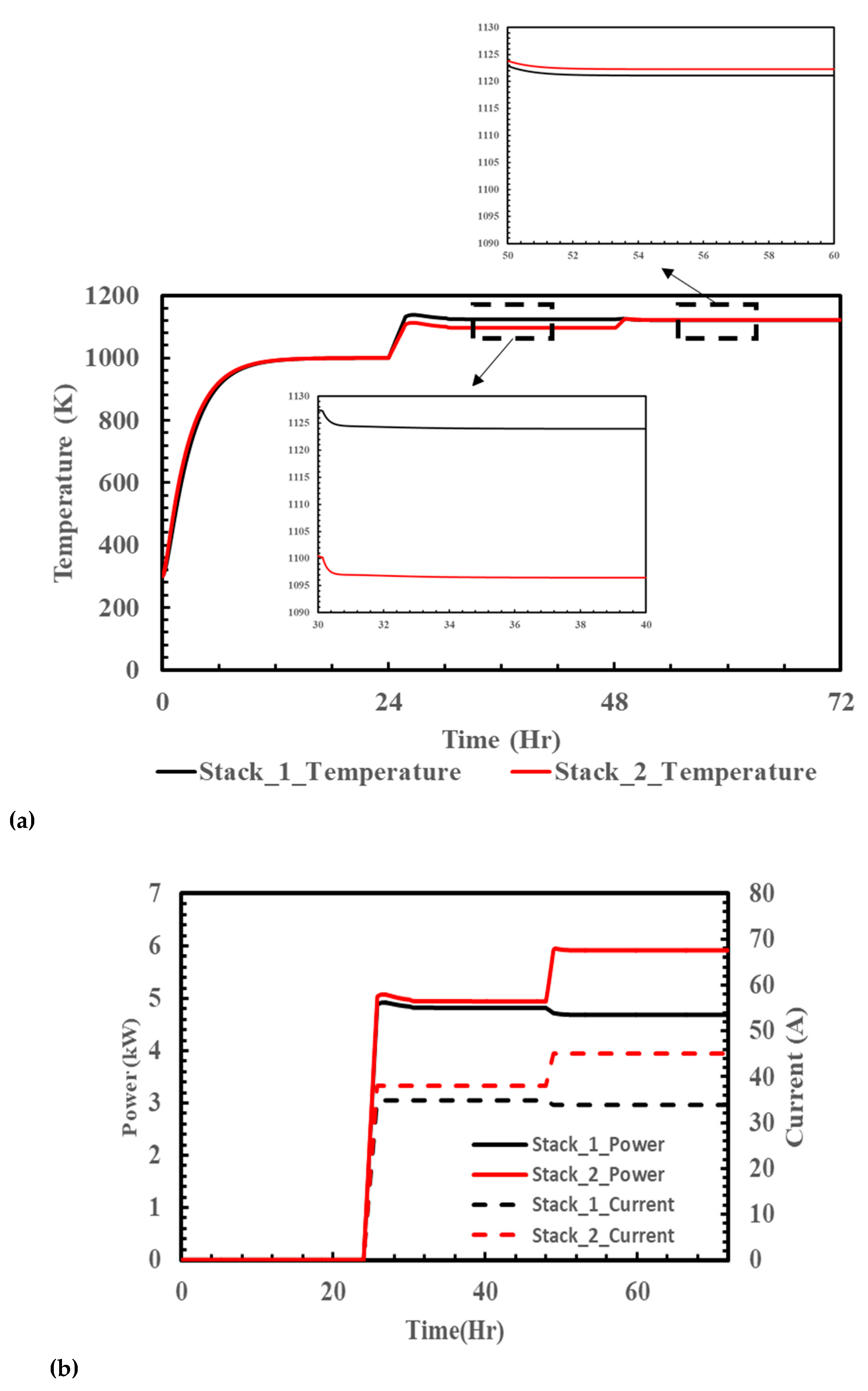
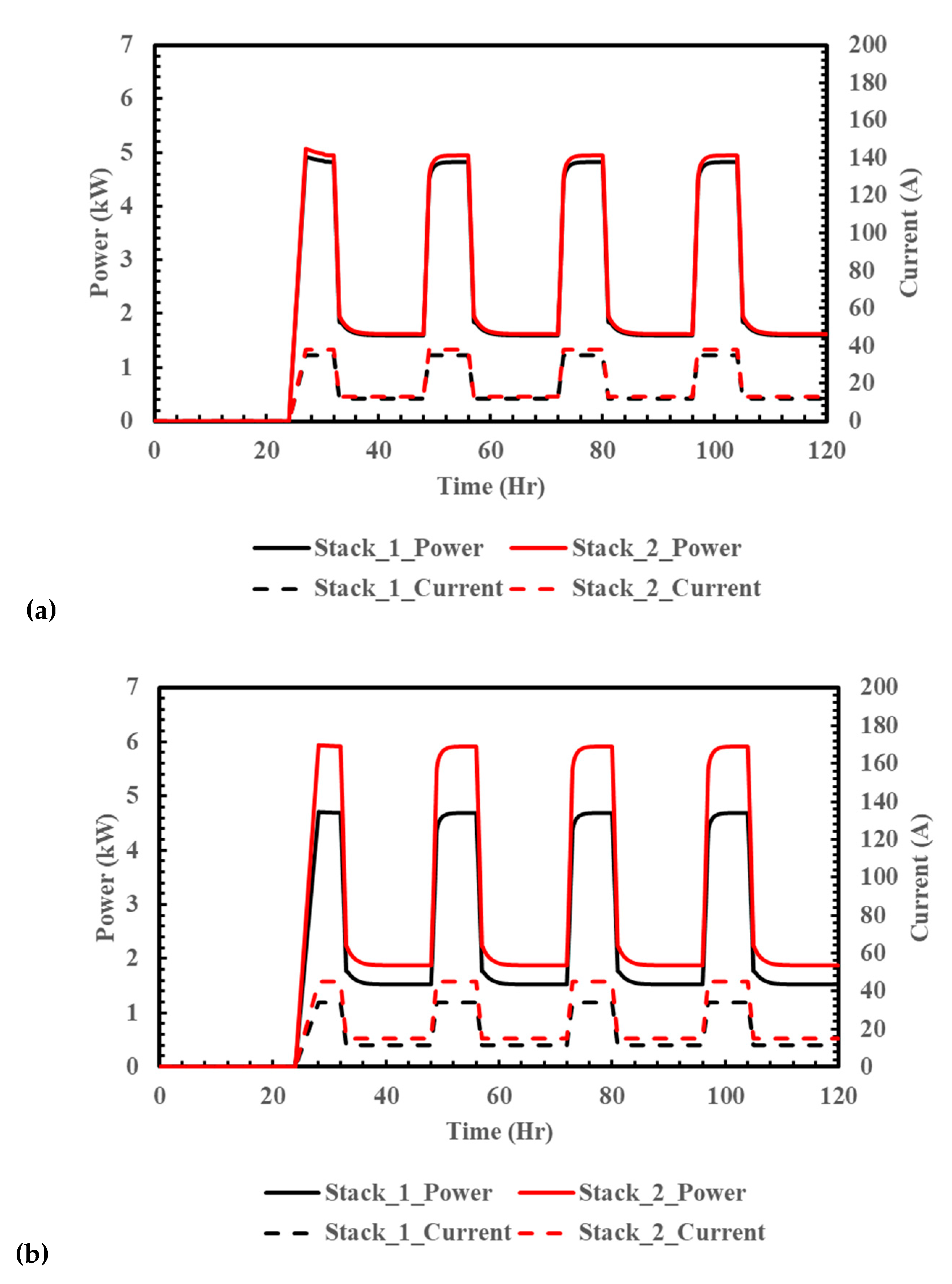
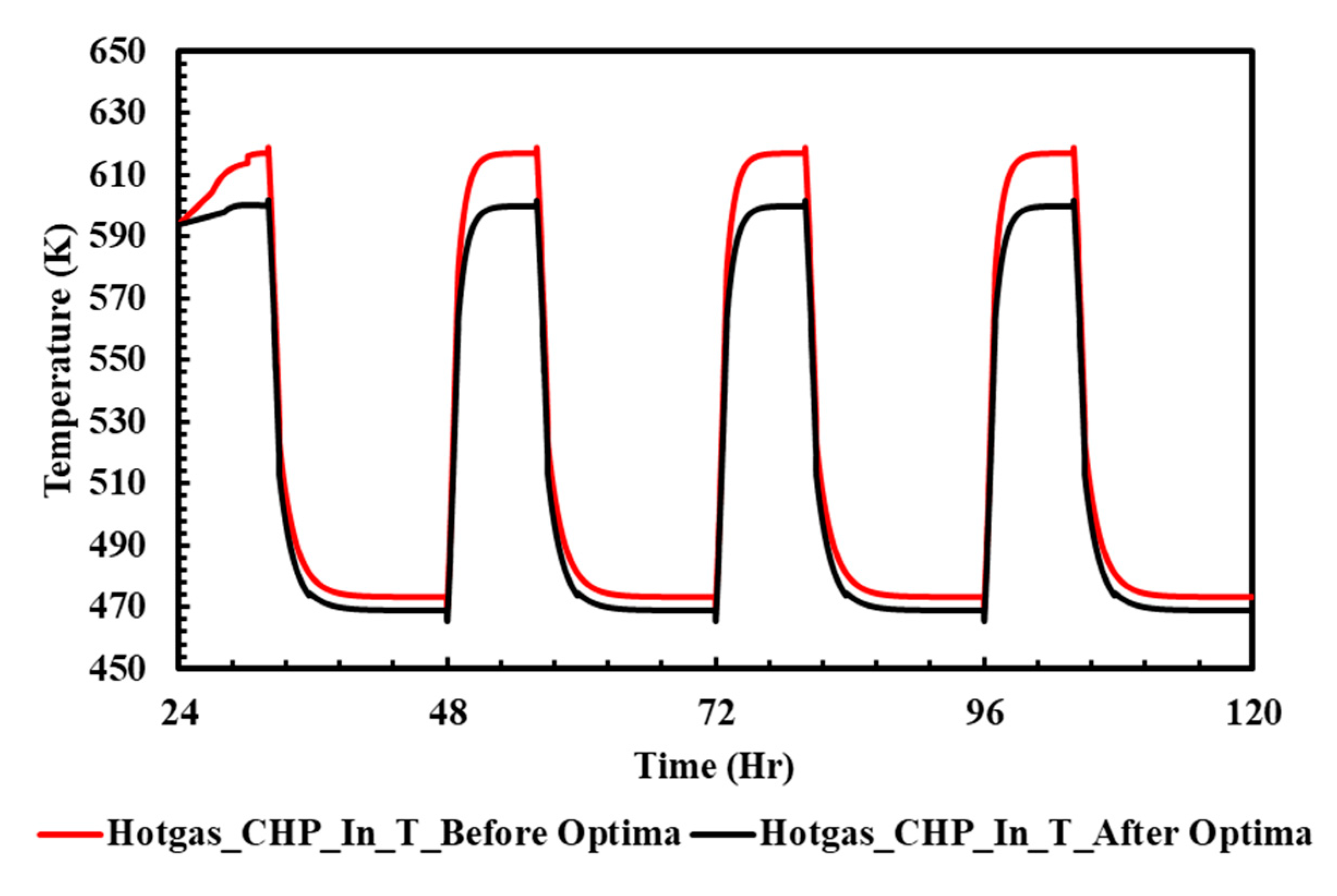
In the present study, the optimal control strategy for operating current and air flow rate was applied in an SOFC-CHP system, in which the gas flow rates into the two stacks were non-equal. The dynamic analysis shows that the operating temperatures of the two stacks have a difference of 33 K, which results in a reduced total power generation of 9.77 kW, with inconsistent FU rates of 78.3% and 56.8% for the two stacks. By using the optimal control strategy, the output power is increased to 10.6 kW, an increment of 8.5%. In this way, the FU rates of the two stacks are improved to 79% and 70%, respectively. As a potential distributed power generator, the long-term effects of the studied SOFC-CHP systems are also investigated. An operating period with 100%/30% input fuel flow rates is adopted to simulate the 8 h full/16 h standby loading mode of one day, which is applicable in, for example, residential or non-24 h working sites. Dynamic analysis of the long-term operating SOFC-CHP system shows that the total daily output power can be increased 7.34% by using the optimal control strategy developed in this study.
For a high-power SOFC module, the stacks are connected by series and parallel arrangements. Therefore, the manifold effect on the stack performance is an important issue. For SOFC-CHP system with maldistribution gas flows into each stack, the strategy of controlling both operating current and air flow rate is useful to eliminate the temperature difference between stacks caused by the manifold’s effects. Consequently, the power generation efficiency is increased.