Aerodynamic Performance and Wind-Induced Responses of Large Wind Turbine Systems with Meso-Scale Typhoon Effects
Abstract
:1. Introduction
2. Meso-Scale Typhoon Wind Field Simulation and Result Analysis
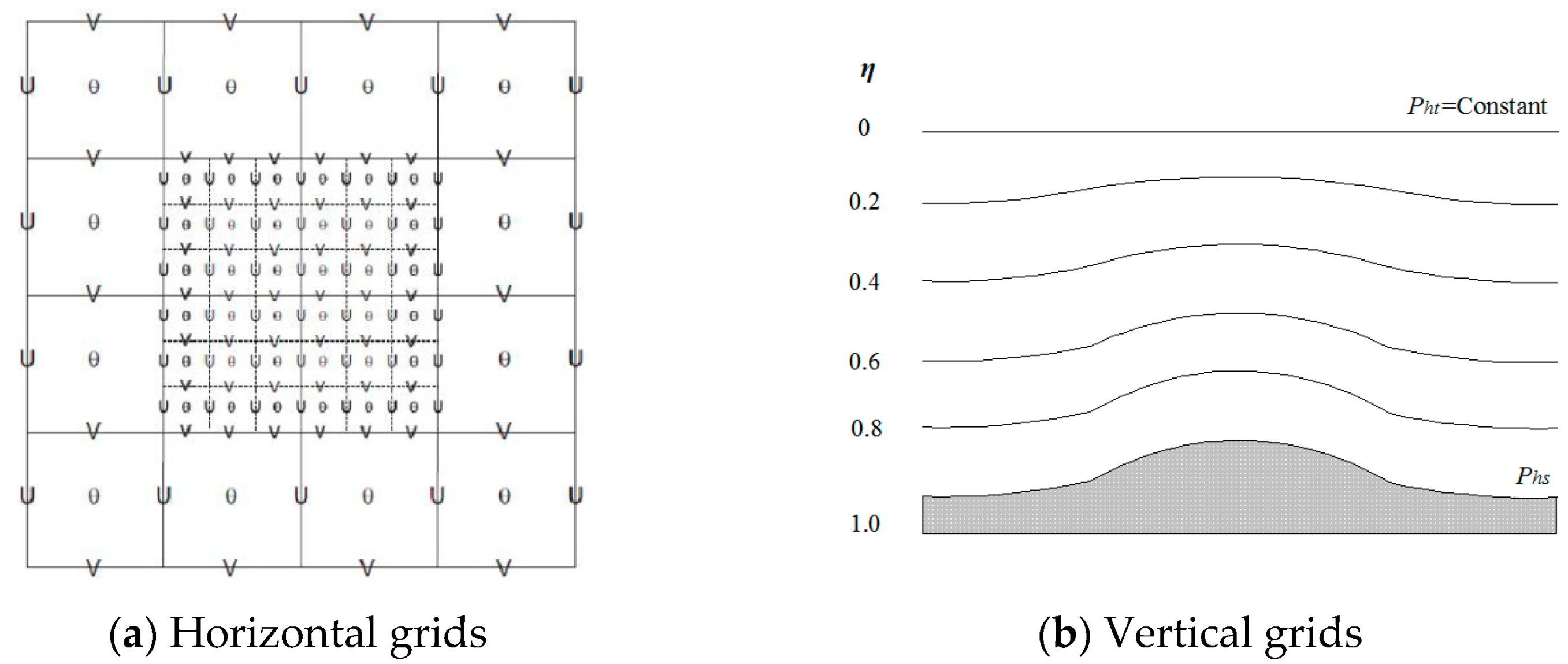
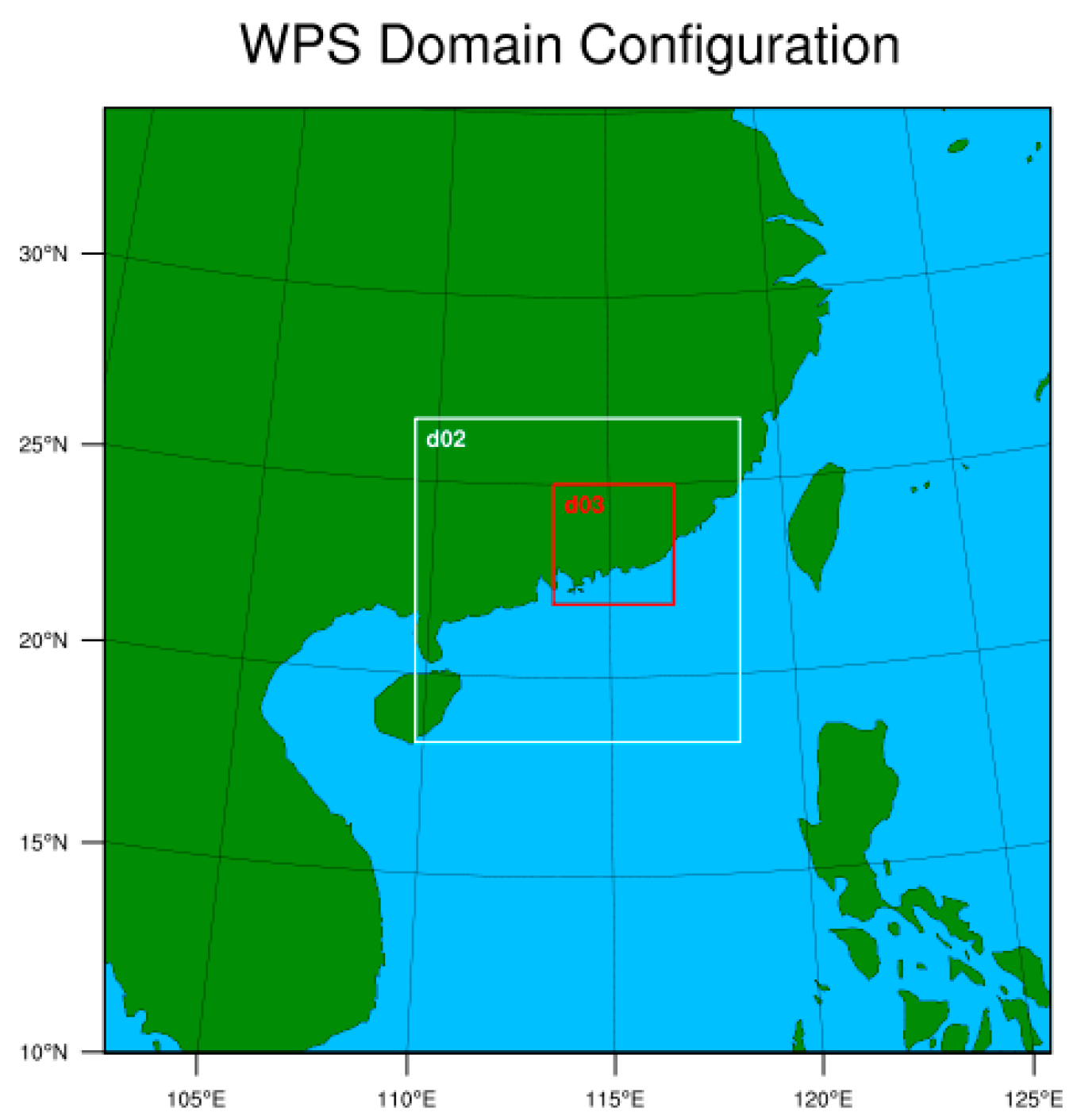
2.1. WRF Mode Meshing
2.2. Selection of the Parameterization Scheme
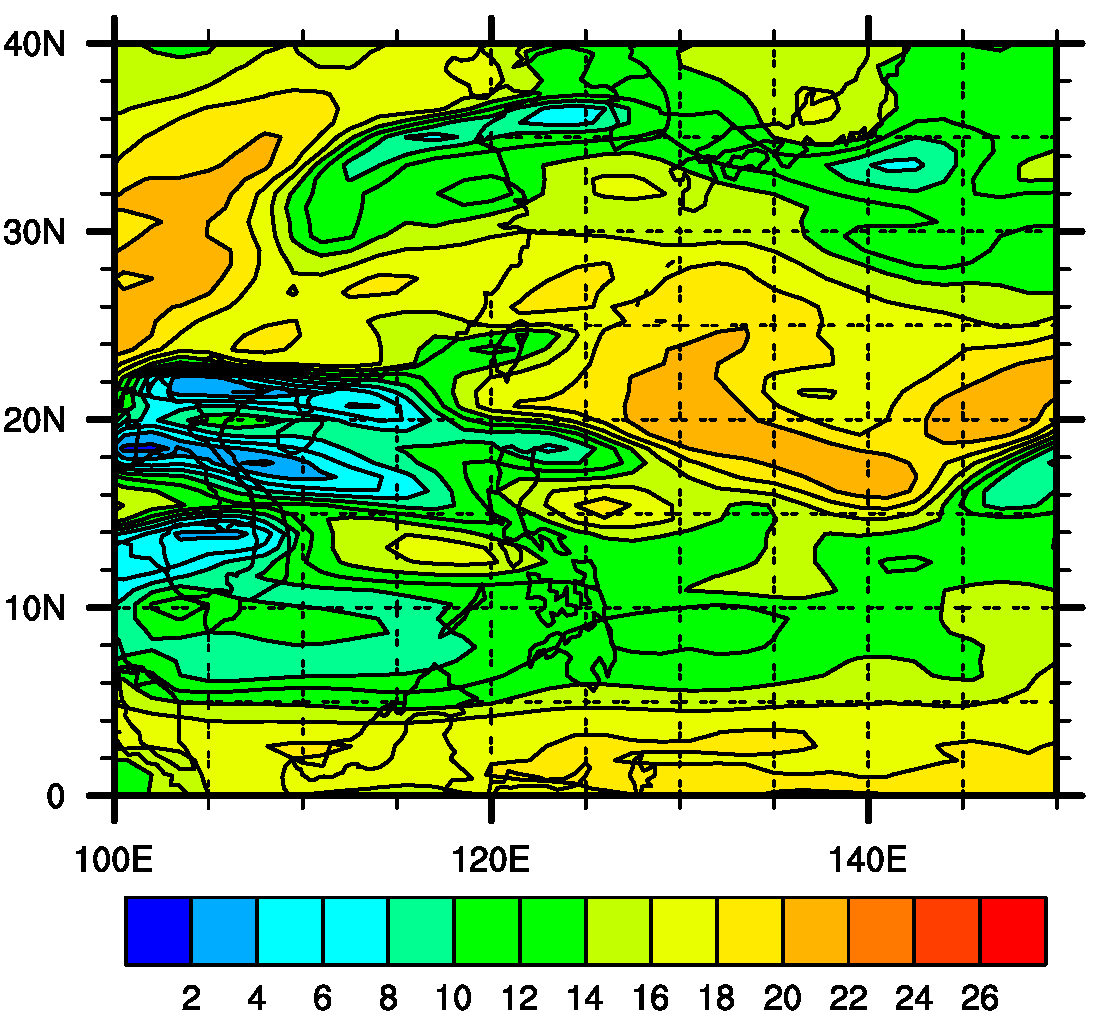
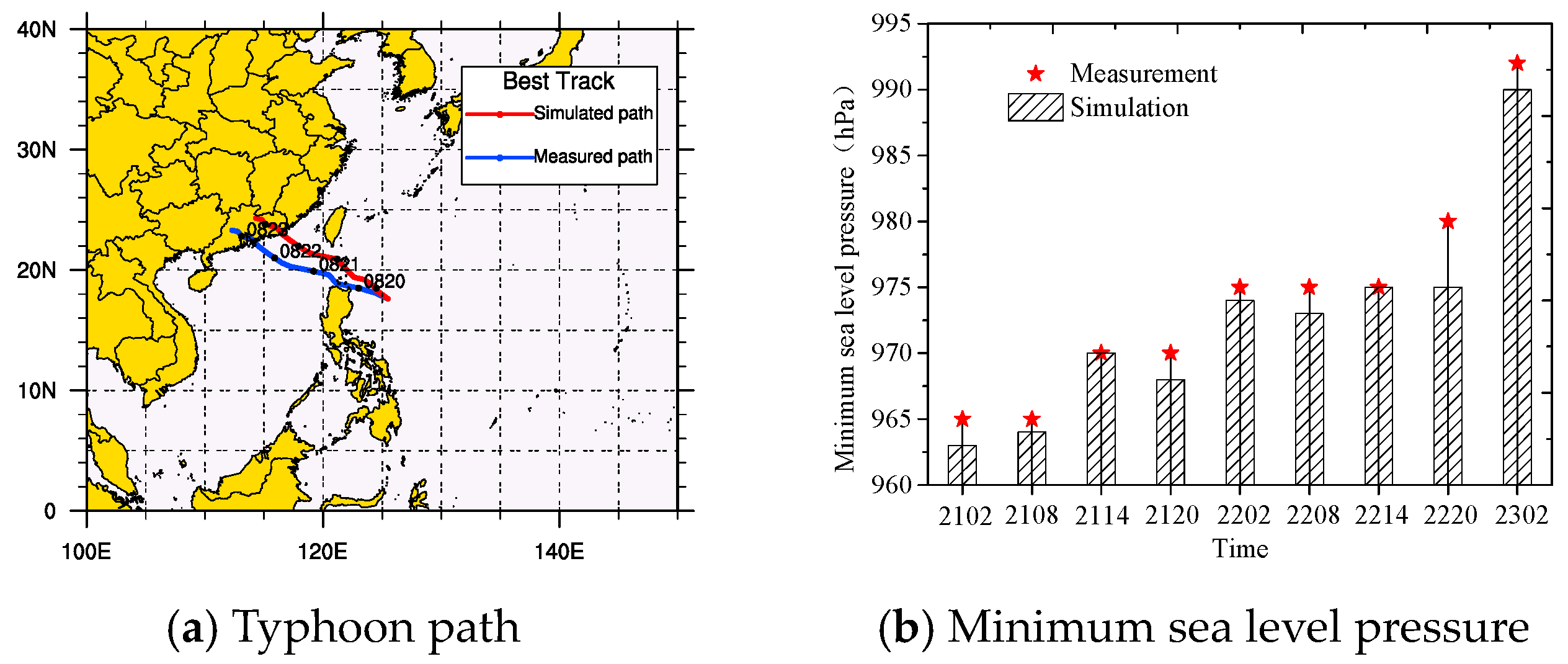
2.3. Validity Verification and Results Analysis
3. Micro-Scale CFD Numerical Simulation
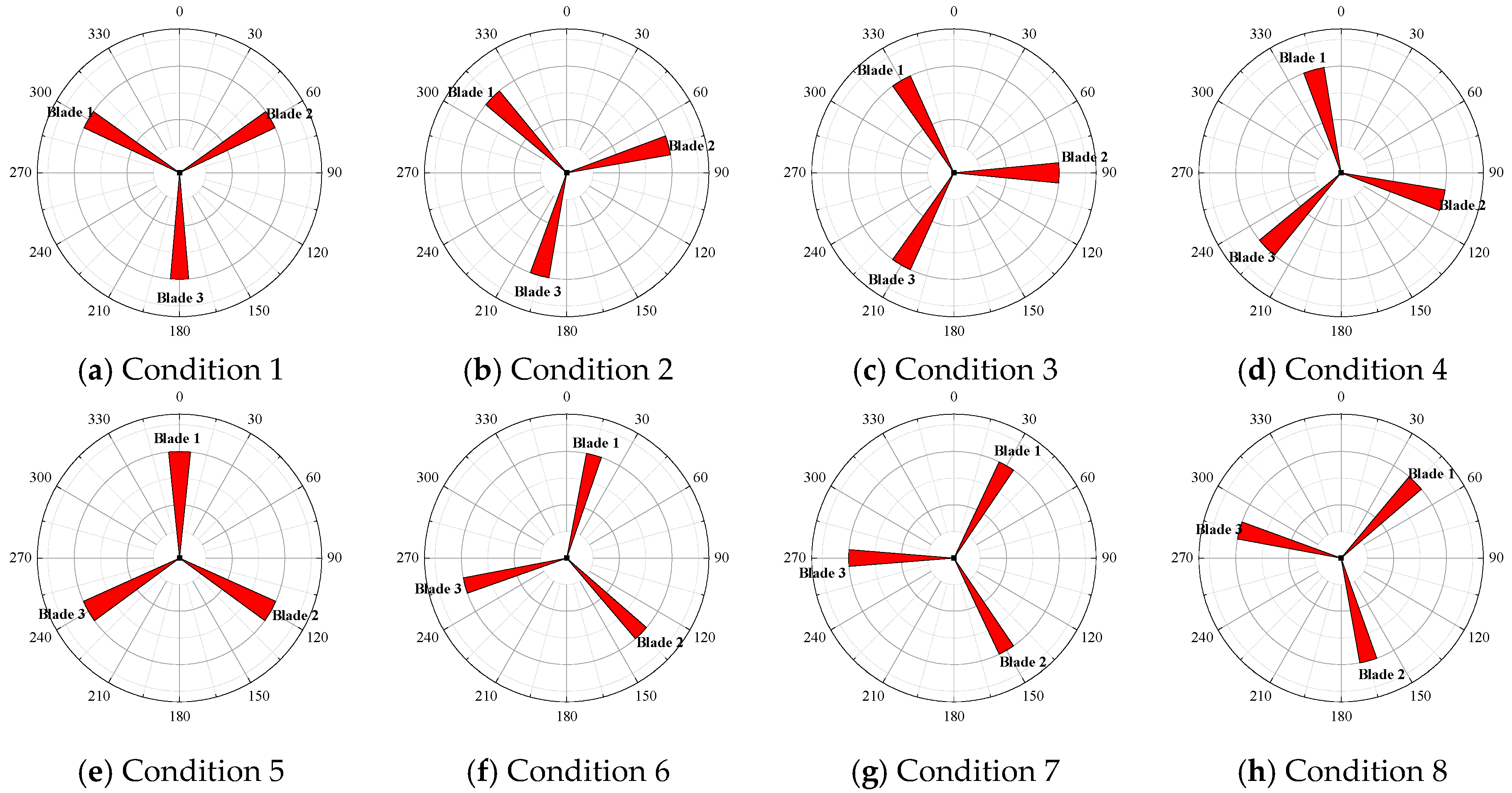
3.1. Brief Introduction to the Wind Turbine Model
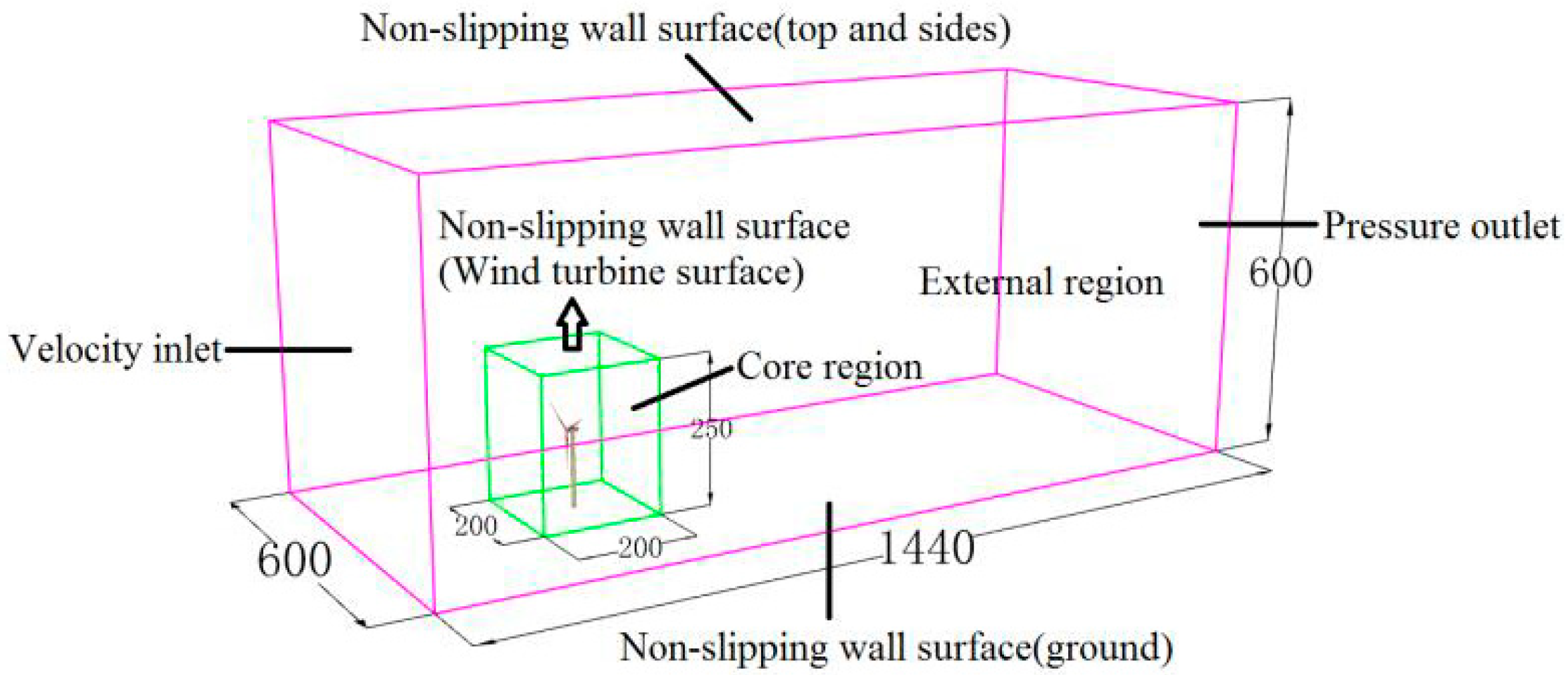
3.2. Computational Domain and Meshing
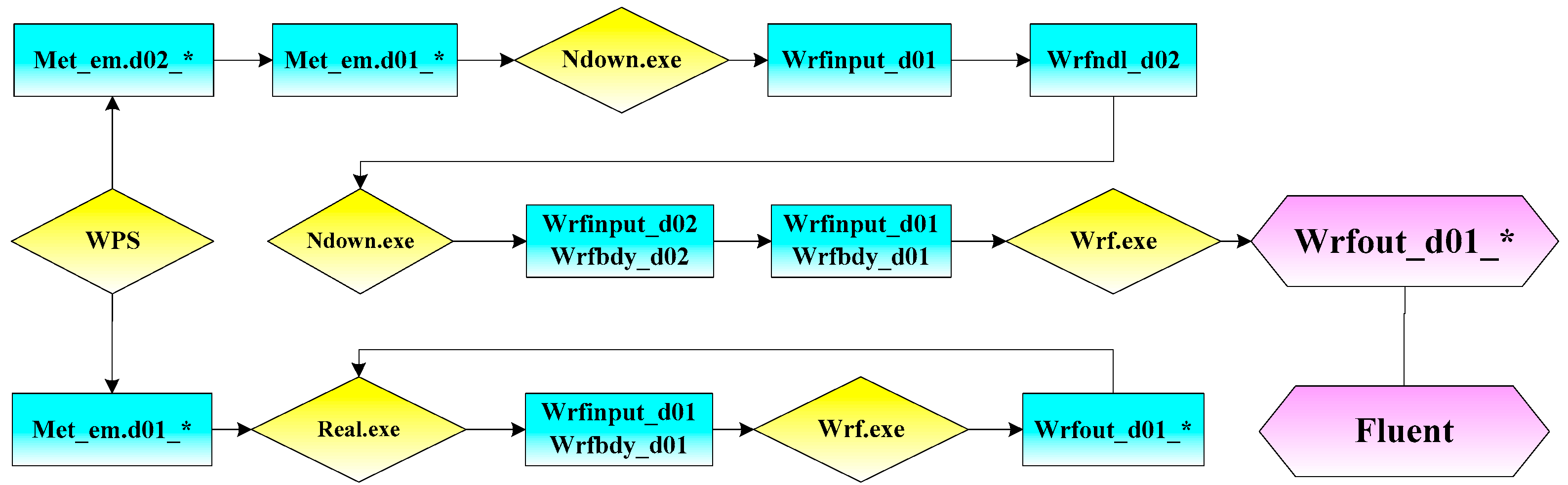
3.3. Micro-Scale Typhoon Simulation Technology
3.3.1. Micro-Scale Typhoon Simulation
3.3.2. Large Eddy Simulation (LES) Governing Equation
3.4. Boundary Conditions and Parameter Setting
4. Aerodynamic Performance Analysis
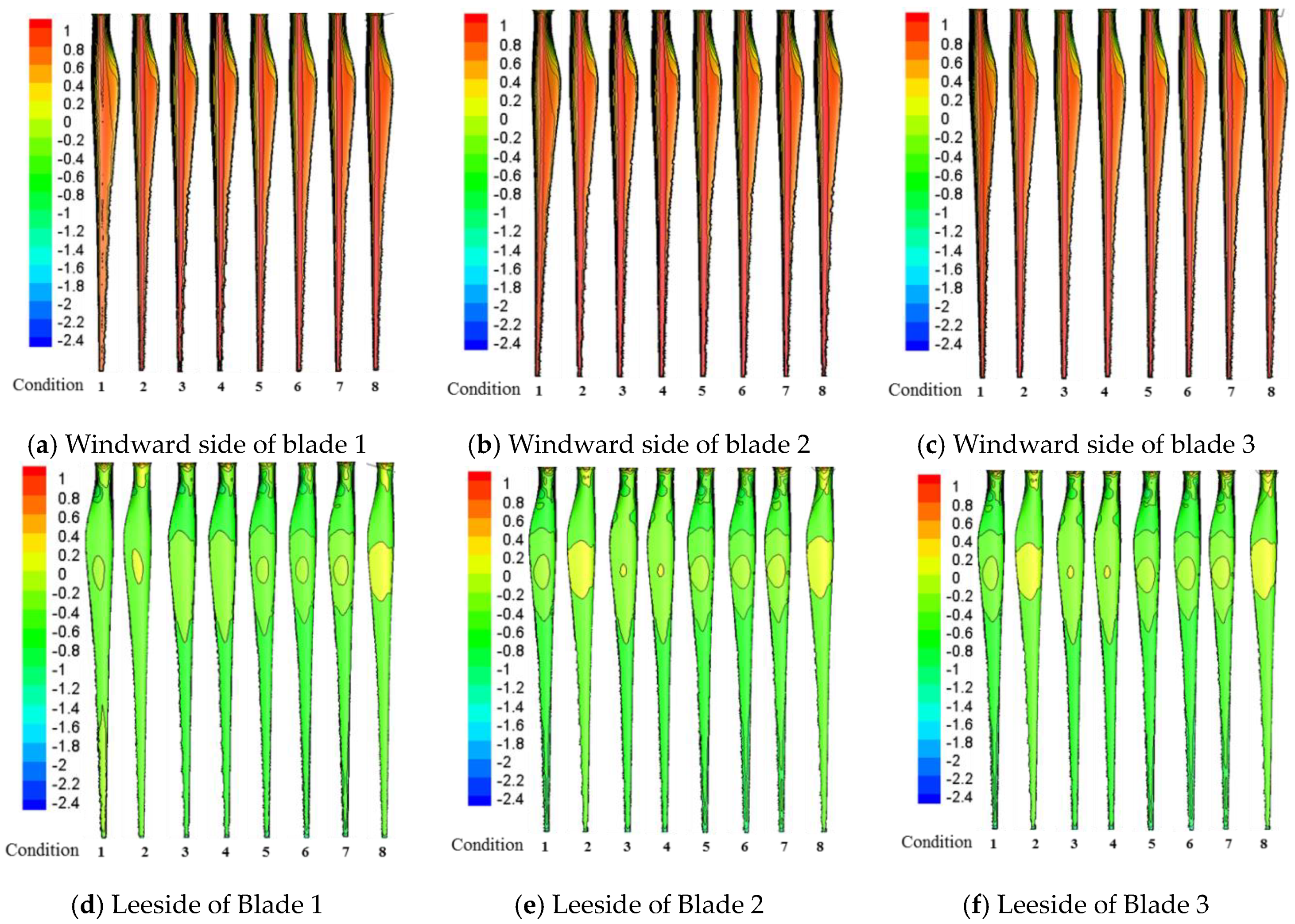
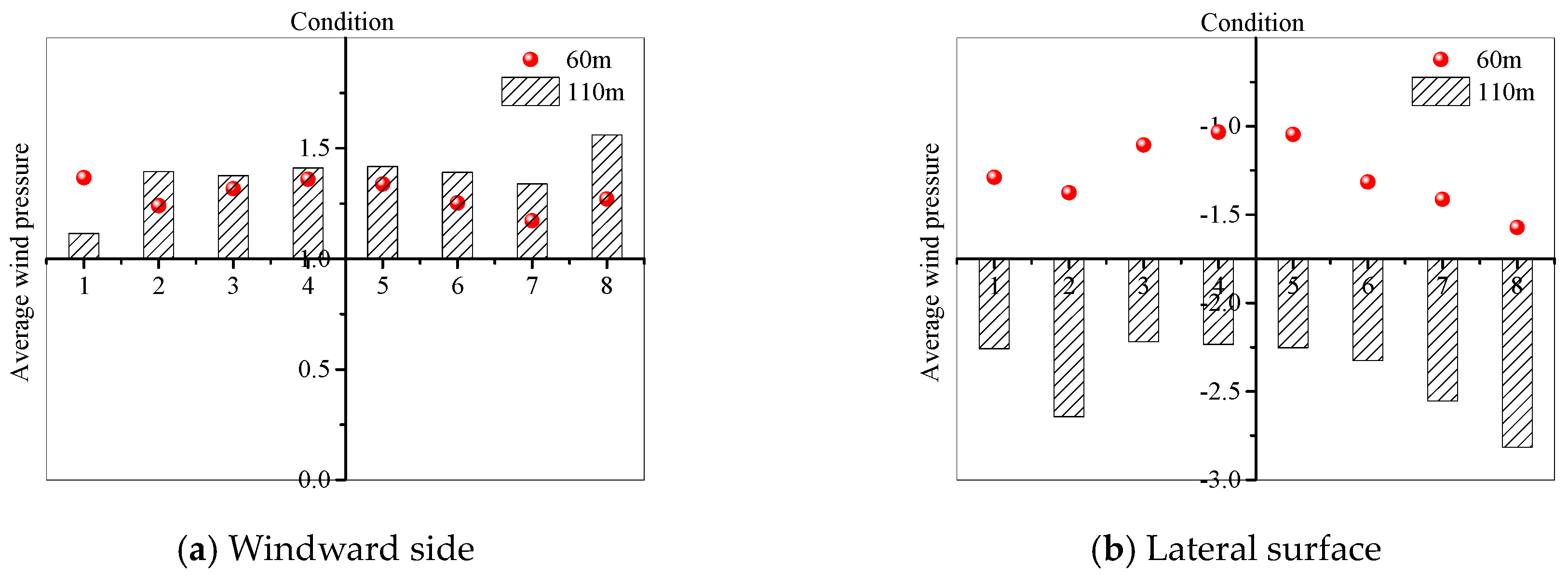
4.1. Average Wind Pressure Coefficient
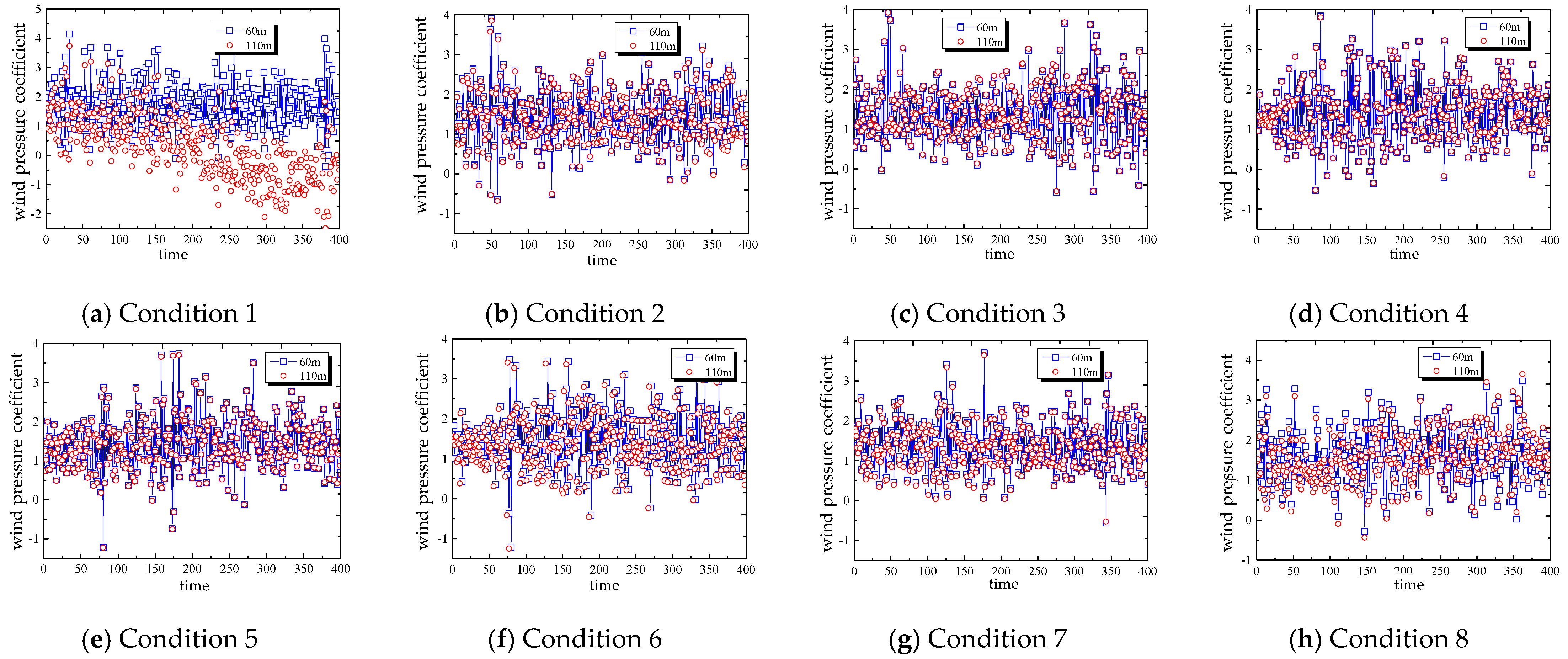
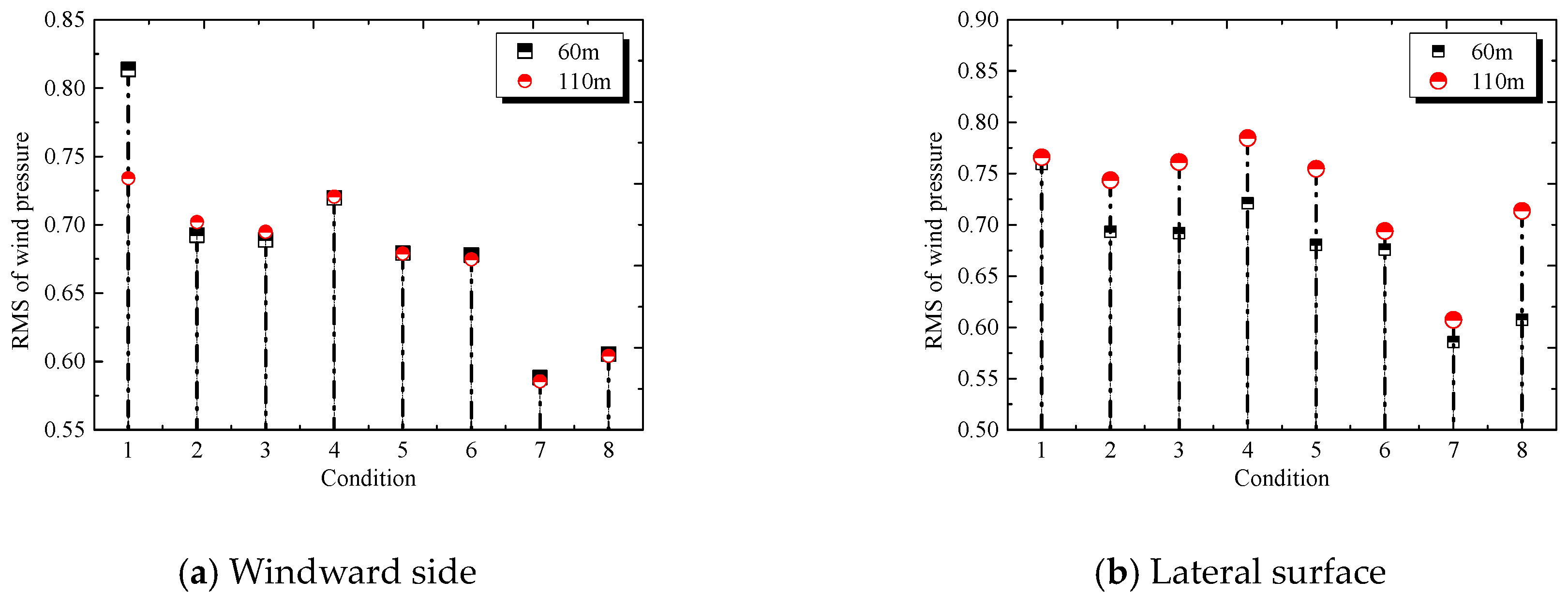
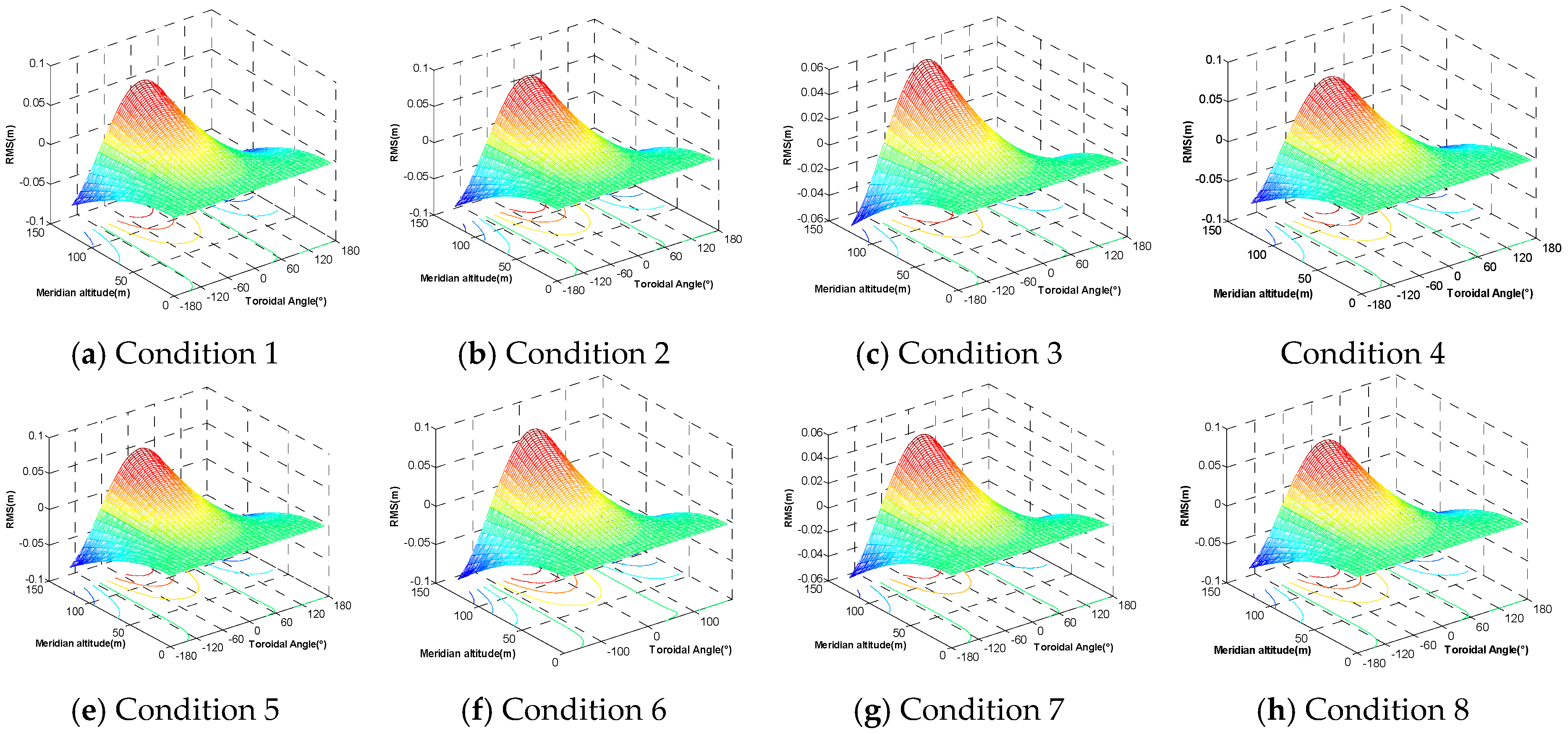
4.2. Coefficient of Fluctuating Wind Pressure
- (1)
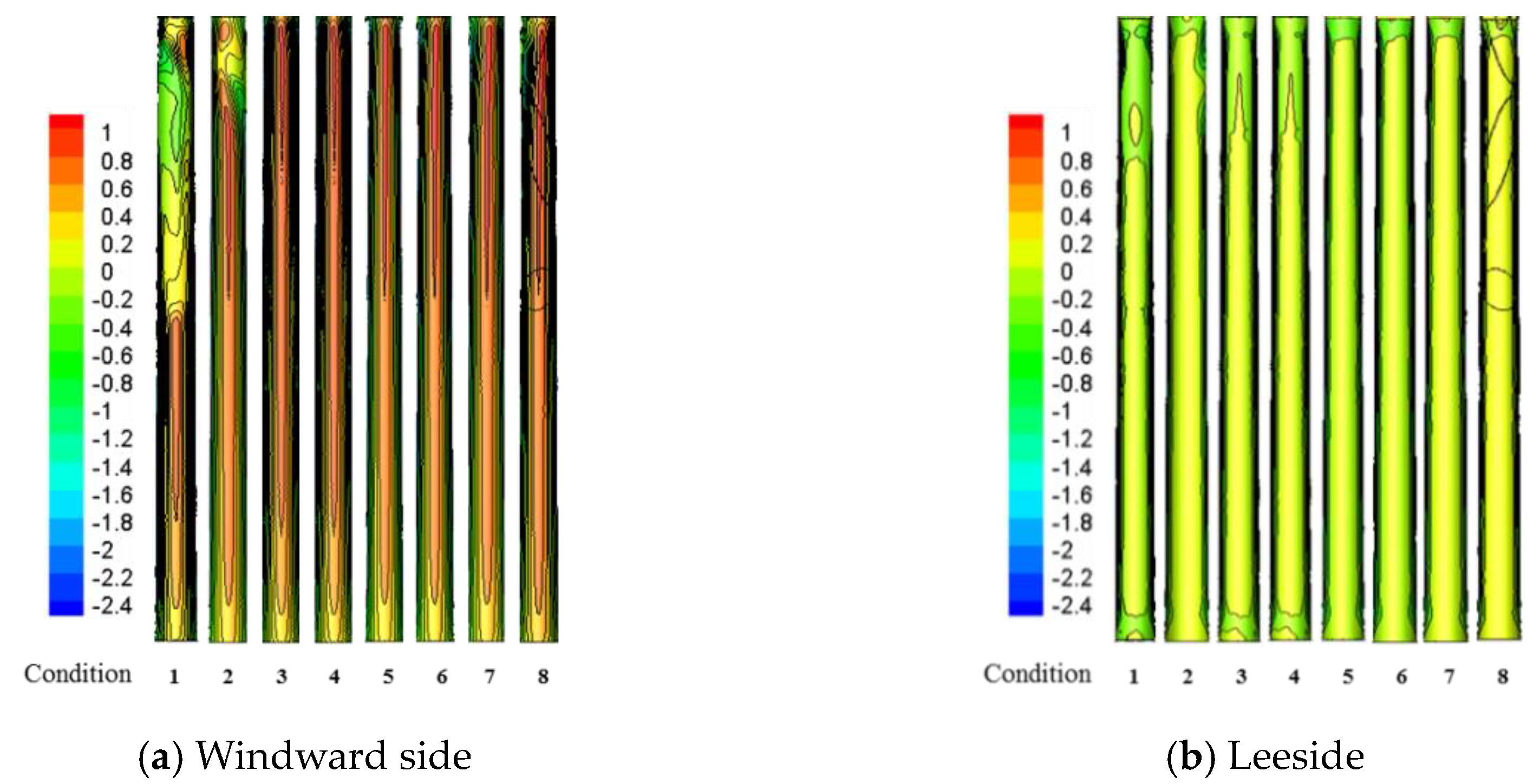
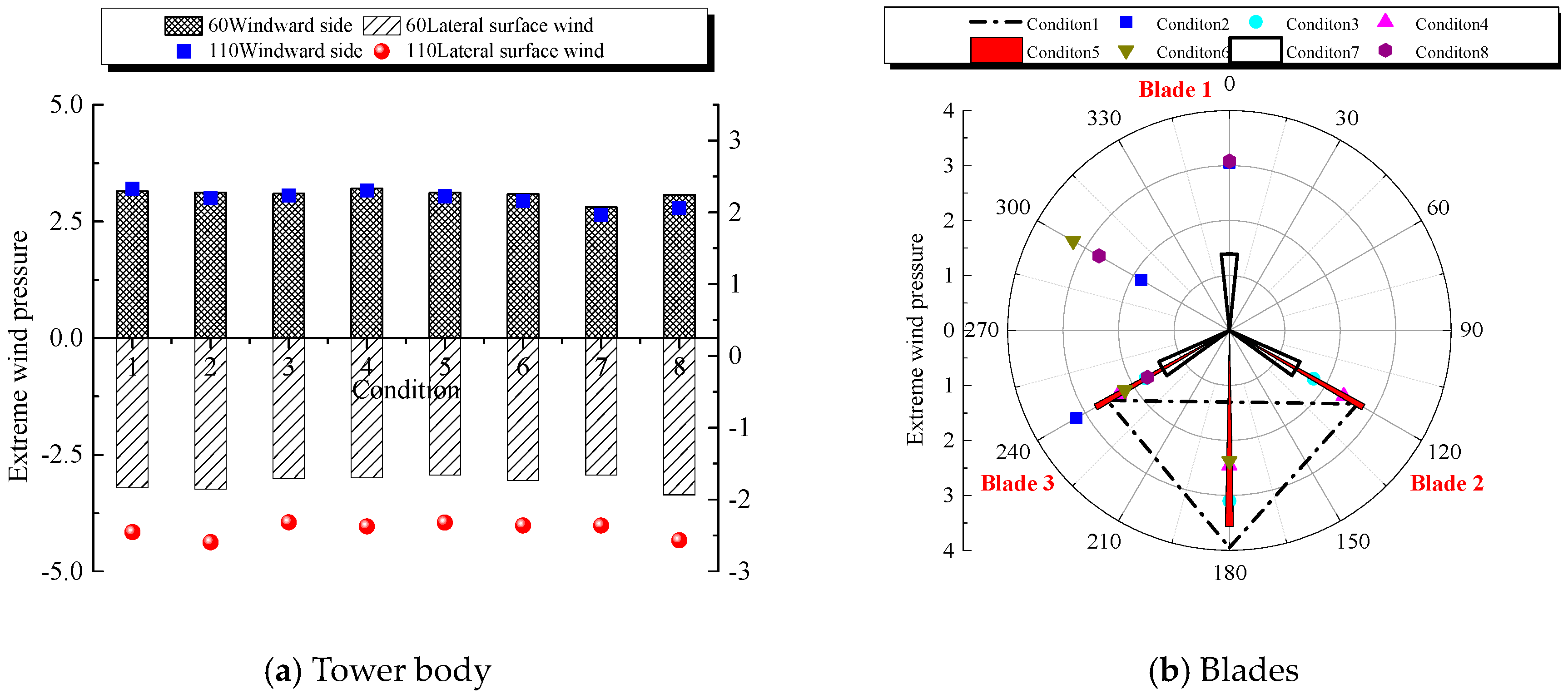
- The absolute value of the wind pressure coefficient in the disturbed zone of the windward side and lateral surface is significantly greater than the non-disturbed section. The mean wind pressure coefficient at 60 m height of the windward side in Condition 1 was higher than the numerical value at 110 m, indicating that blade shielding could influence the wind pressure coefficient of the tower body markedly. Additionally, the RMS of wind pressure on the windward side and lateral surface in the disturbed zone under no blade shielding effect was higher than that on the undisturbed zone.
- (2)
- The wind pressure coefficients on the windward side were similar at different zones of the tower body. However, there’s a great difference on the lateral surfaces. The difference when the lateral surface was not shielded by blades was significantly large than that under Condition 1. The average wind pressure coefficient and RMS of wind pressure under Condition 4 presented significant differences, with values of 1.20 and 0.06, respectively.
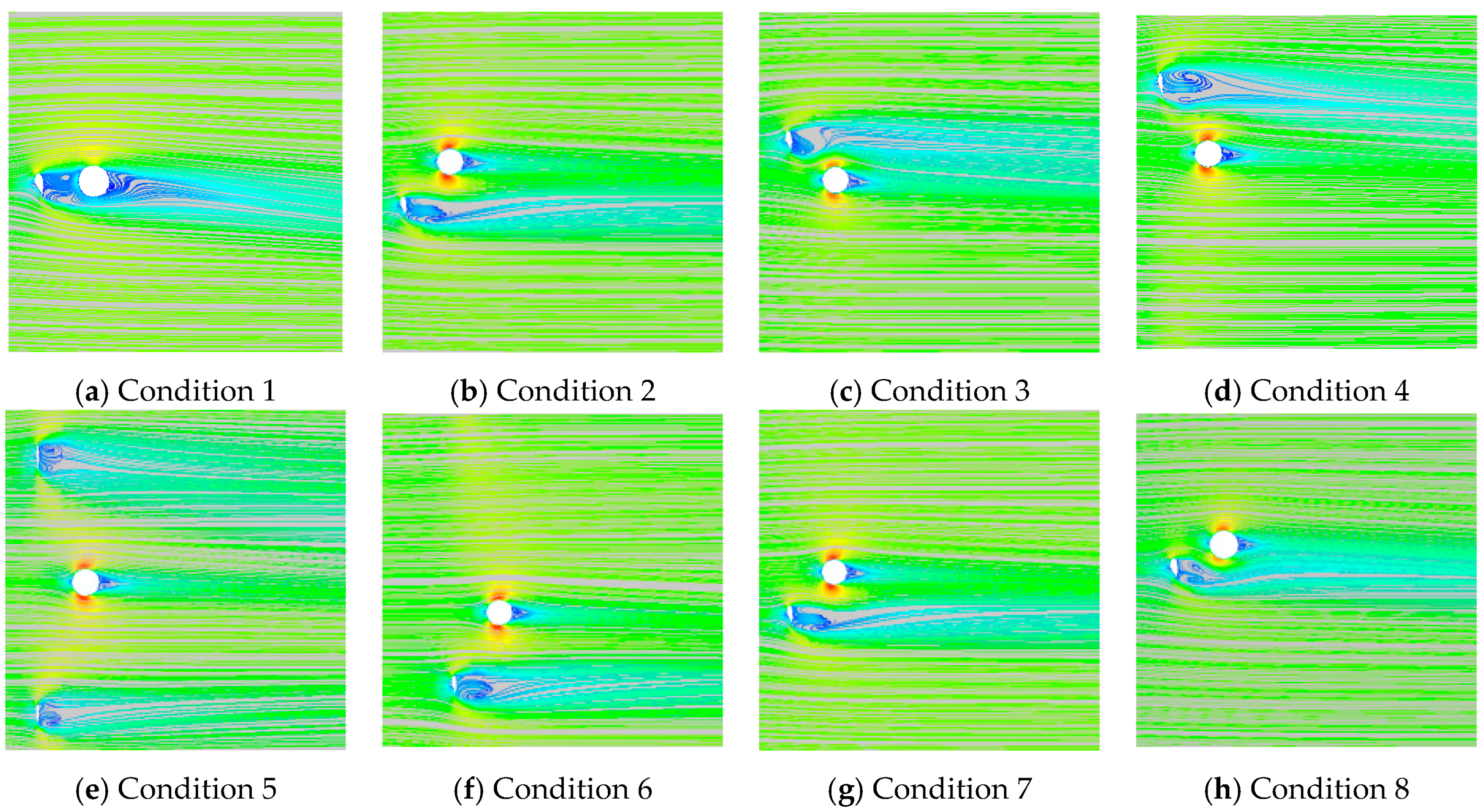
4.3. Characteristics of Airflow around the Tower Body
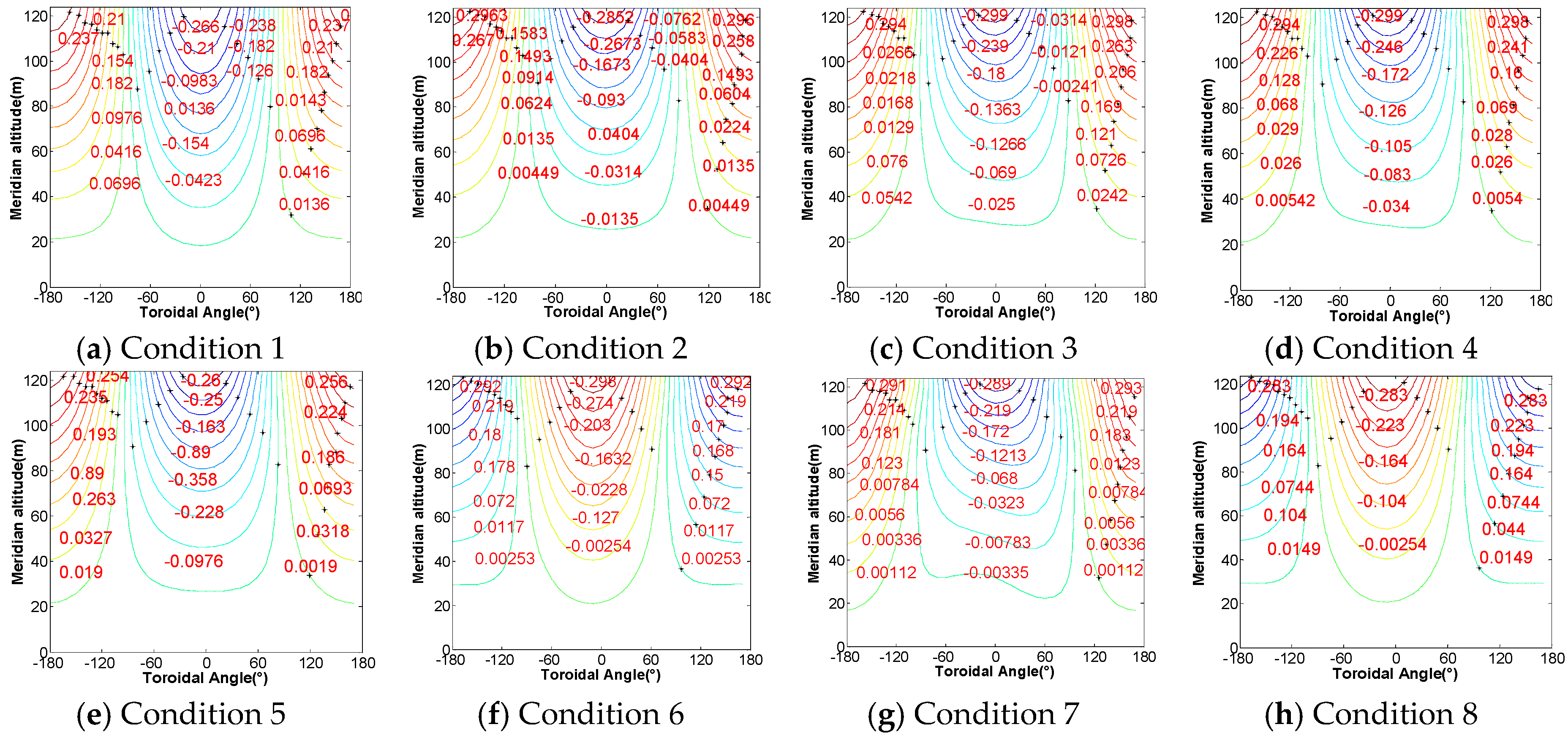
4.4. Vorticity Distribution
5. Wind-Induced Response Analysis
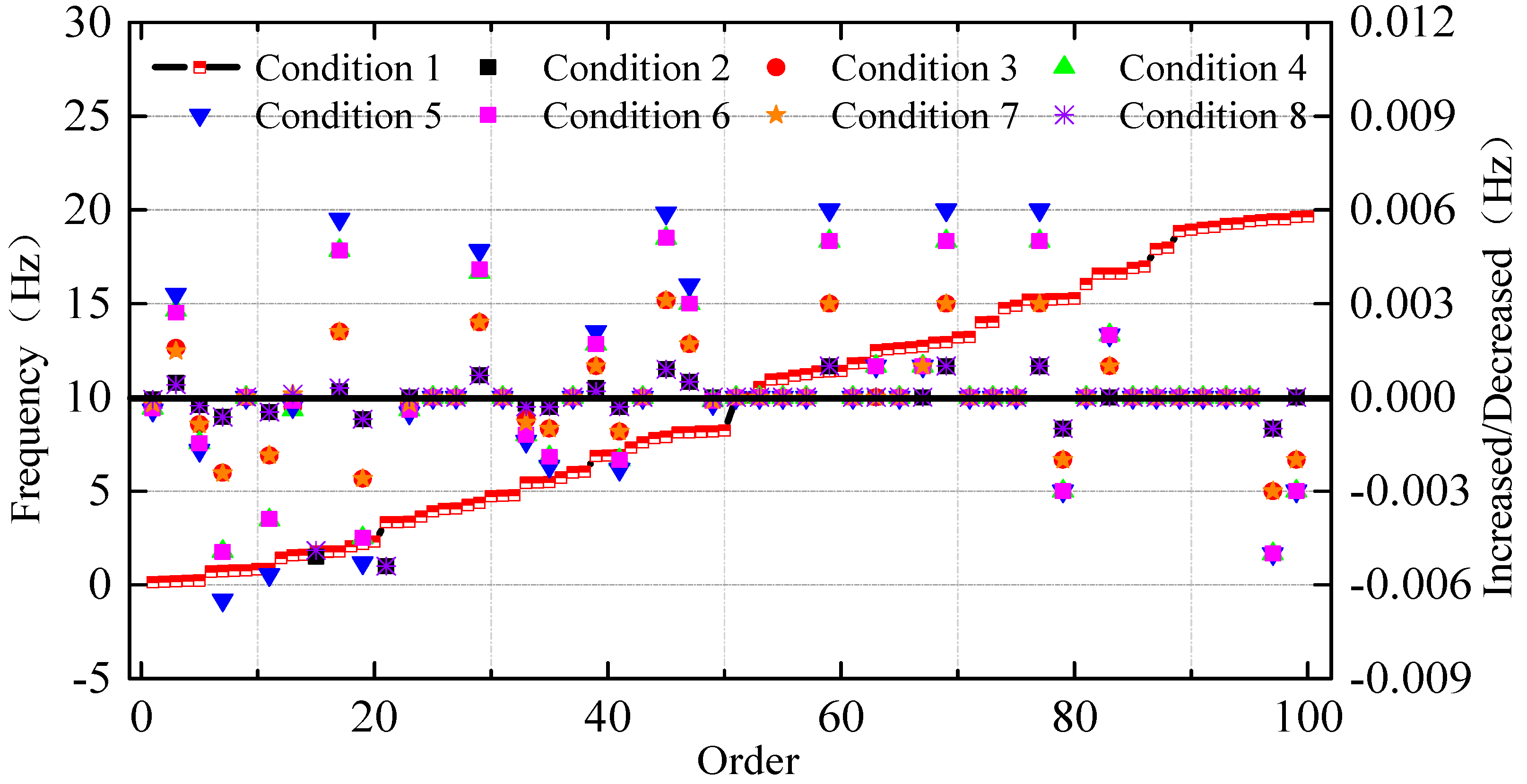
5.1. Finite Element Modeling and Dynamic Characteristics
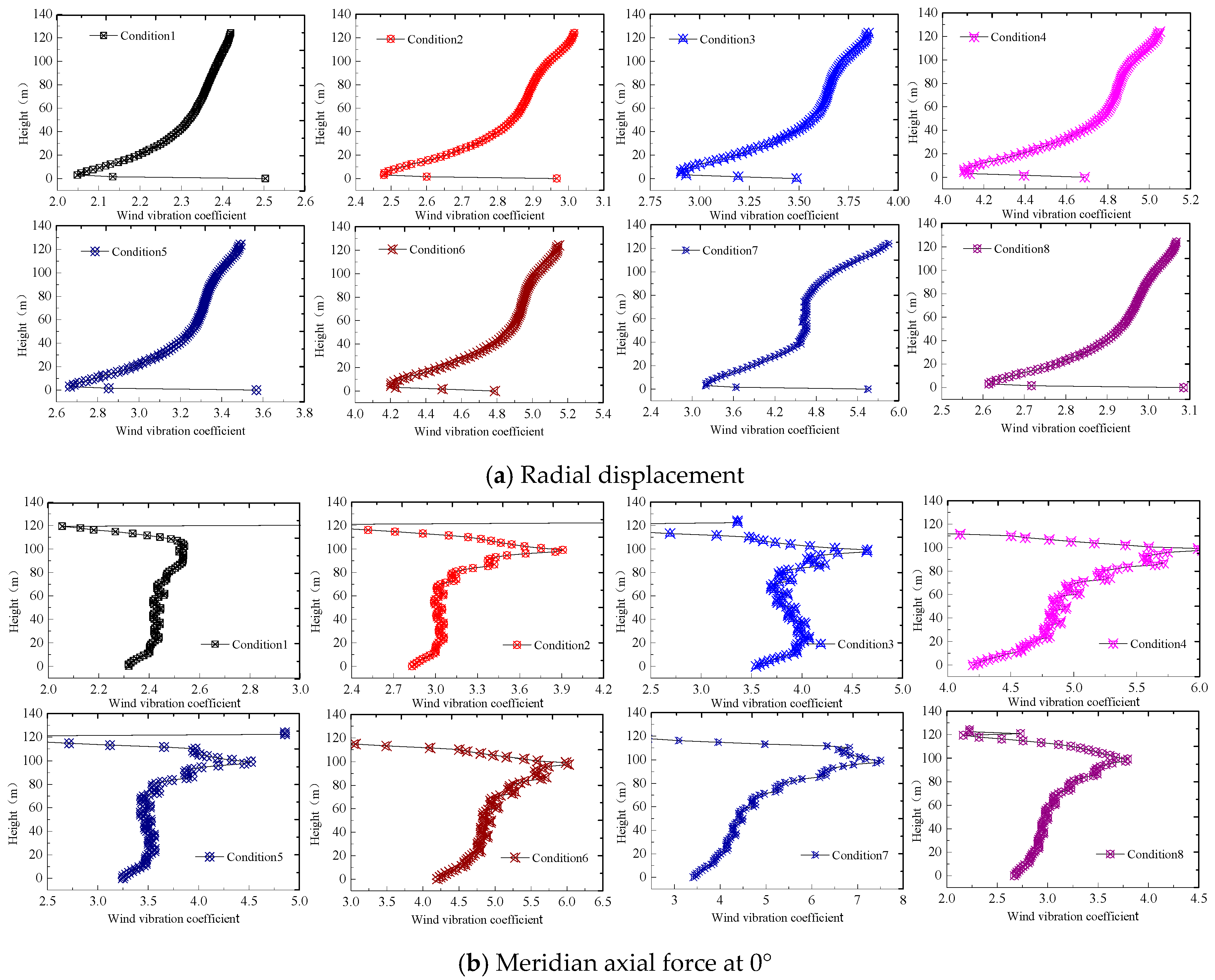
5.2. Wind-Induced Responses
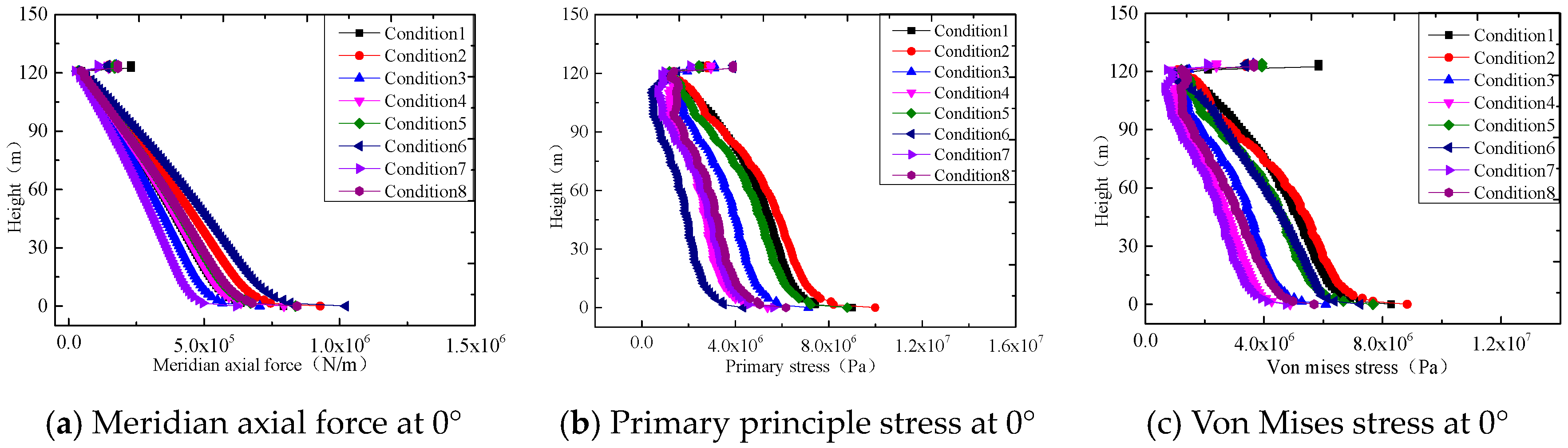
5.2.1. Responses of the Tower Body
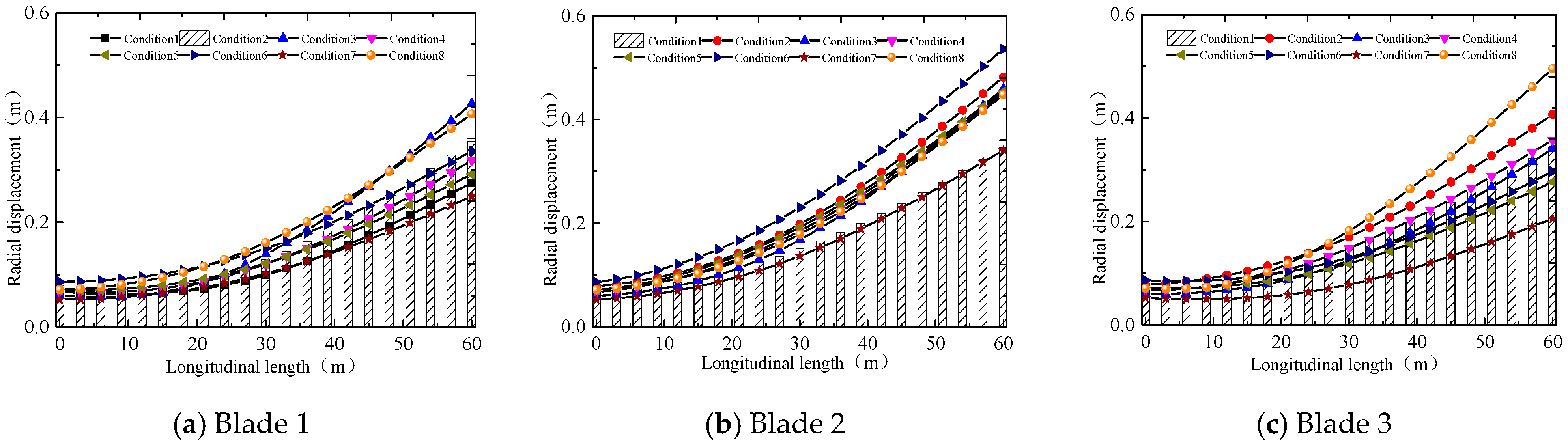
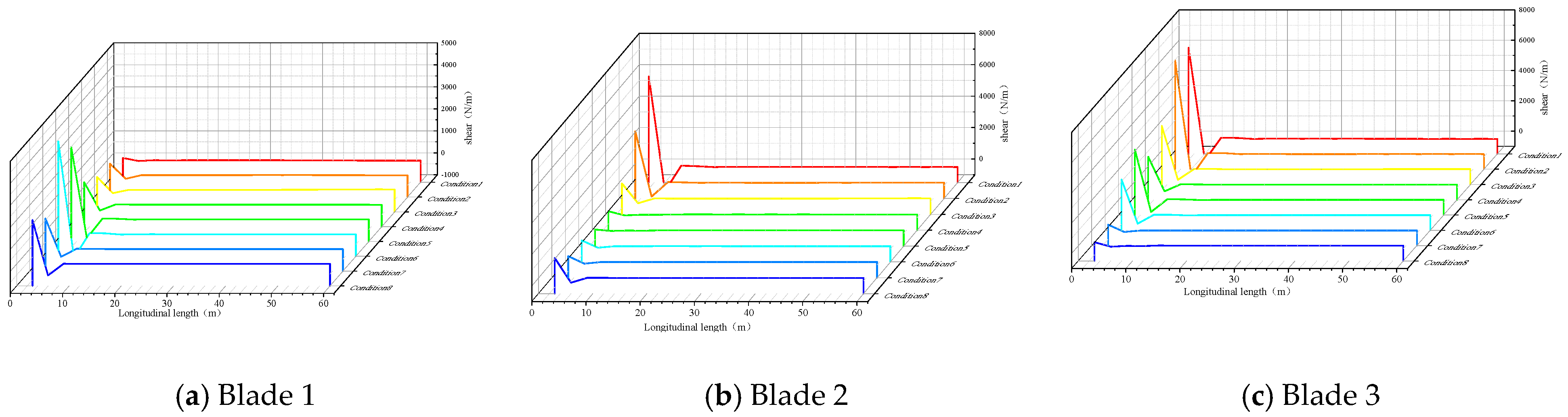
5.2.2. Responses of Blades
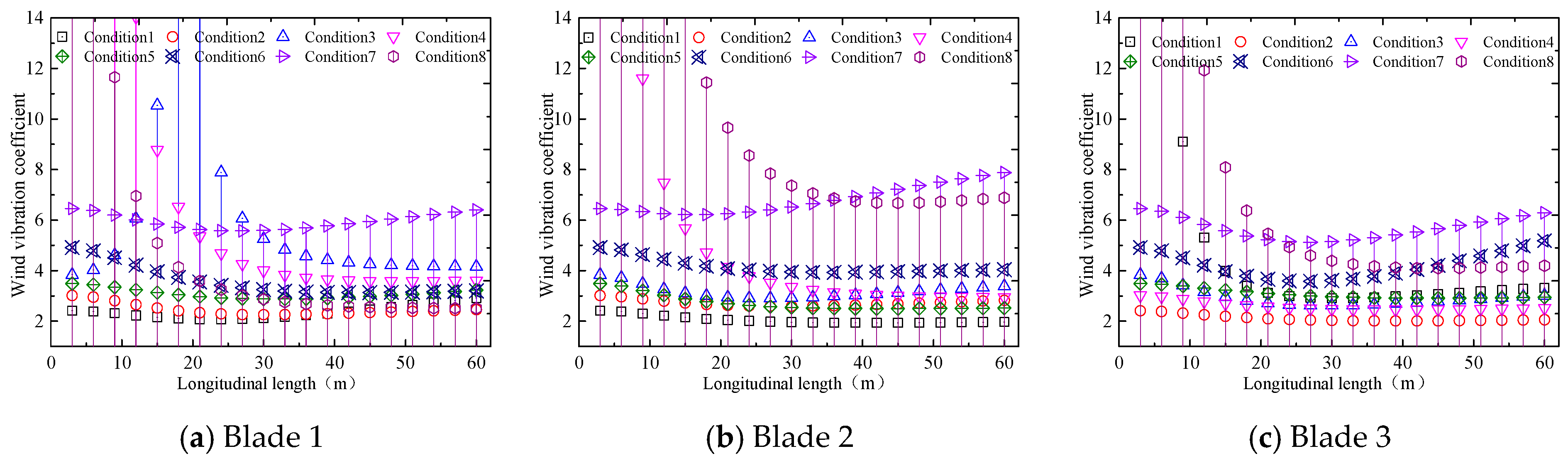
5.3. Wind Fluttering Factor
6. Conclusions
- (1)
- By comparing typhoon wind speed, wind intensity, wind direction and wind profile, it is concluded that the meso-scale WRF model can effectively simulate the near surface typhoon wind field. Based on the minimum least square method, the profile index of typhoon “Nuri” was fitted at 0.076. In this paper, the downscaling method can effectively simulate the 3D typhoon field of this kind of large-scale wind turbine system, which verifies the validity of the meso- and micro-scale nested simulation method, and provides the load input for the subsequent random wind pressure characteristics and wind vibration dynamic analysis.
- (2)
- The simulation results show that the wake zone is expanded gradually and the vorticity increment zone increases significantly under typhoon loads. Such a phenomenon is weakened with the reduction of the shielding area. The fluctuating and extreme wind pressures on blades and tower body are increase dramatically under typhoon loads. The maximum increase reaches 29%, which is appeared on the tower top of windward side. The fluctuating wind pressure is increased gradually as the blade shielding effect weakens.
- (3)
- Internal stresses and wind fluttering factor of blades and tower body are increased significantly under typhoon loads. When the tower body is not shielded by blades, the wind fluttering factor is decreased significantly. When the tower body is shielded by blades, the wind fluttering factor is increased significantly. The increase of radial displacement of the tower body is intensified as the shielding effect weakens. The maximum increase reaches 35%.
- (4)
- Based on our comprehensive analysis, when the large wind turbine is stopped under typhoon loads, the most unfavorable condition is when blade overlaps with the tower body completely (Condition 1). The safety redundancy reaches the maximum when the upper blade overlaps with the tower body completely (Condition 5).
Author Contributions
Funding
Conflicts of Interest
References
- Chen, B.; Wang, K.; Liu, J.; Gao, F. The impact of super typhoon Saomai(0608) on the offshore environment near the Yangtze estuary. Earth Sci. 2016, 41, 1402–1412. (In Chinese) [Google Scholar]
- Xiao, Y.F.; Duan, Z.D.; Xiao, Y.Q.; Ou, J.P.; Chang, L.; Li, Q.S. Typhoon wind hazard analysis for southeast China coastal regions. Struct. Saf. 2011, 33, 286–295. [Google Scholar] [CrossRef]
- GB/T 25383-2010. Wind Turbine Generator System-Rotor Blades; China Standards Press: Beijing, China, 2010. [Google Scholar]
- CCS-2008. China Classification Siciety-Specification for Wind Turbines; China Communication Press: Beijing, China, 2008. [Google Scholar]
- Carvalho, D.; Rocha, A.; Gómez-Gesteira, M.; Santos, C.S. WRF wind simulation and wind energy production estimates forced by different reanalyses: Comparison with observed data for Portugal. Appl. Energy 2014, 117, 116–126. [Google Scholar] [CrossRef]
- Maruyama, T.; Tomokiyo, E.; Maeda, J. Simulation ofstrong wind field by non-hydrostatic mesoscale modeland its applicability for wind hazard assessment ofbuildings and houses. Hydrol. Res. Lett. 2010, 4, 40–44. [Google Scholar] [CrossRef]
- Kim, S.Y.; Chun, H.Y. Stratospheric Gravity Waves Generated by Typhoon Saomai (2006): Numerical Modeling in a Moving Frame Following the Typhoon. J. Atmos. Sci. 2010, 67, 3617–3636. [Google Scholar] [CrossRef]
- Li, J.; Song, X.P.; Cheng, X.L.; Hu, F. Dynamical simulation of wind flow from synoptic scale to turbine scale. ACTA Energ. Sol. Sin. 2015, 36, 806–811. (In Chinese) [Google Scholar]
- Xu, Y.; He, H.; Song, J.; Hou, Y.; Li, F. Observations and Modeling of Typhoon Waves in the South China Sea. J. Phys. Oceanogr. 2017, 47, 1307–1324. [Google Scholar] [CrossRef]
- O’Brien, J.M.; Young, T.M.; O’Mahoney, D.C.; Griffin, P.C. Horizontal axis wind turbine research: A review of commercial CFD, FE codes and experimental practices. Prog. Aerosp. Sci. 2017, 92, 1–24. [Google Scholar] [CrossRef]
- Shen, L.; Han, Y.; Dong, G.C.; Cai, C.S. Numerical simulation of wind field on bridge site located in mountainous area and gorge based on WRF. China J. Highw. Transp. 2017, 30, 104–113. (In Chinese) [Google Scholar]
- Lundquist, J.K.; Mirocha, J.D.; Chow, F.K.; Kosovic, B.; Lundquist, K.A. Simulating atmosphere flow for wind energy applications with WRF-LES. Univ. North Tex. 2008, 7, 281–295. [Google Scholar]
- Dimitrov, N.; Natarajan, A.; Mann, J. Effects of normal and extreme turbulence spectral parameters on wind turbine loads. Renew. Energy 2017, 10, 1180–1193. [Google Scholar] [CrossRef]
- Li, Z.X.; Chan, T.H.T.; Ko, J.M. Evaluation of typhoon induced fatigue damage for Tsing Ma Bridge. Eng. Struct. 2002, 24, 1035–1047. [Google Scholar] [CrossRef]
- Papanastasiou, D.K.; Melas, D.; Lissaridis, I. Study of wind field under sea breeze conditions; an application of WRF model. Atmos. Res. 2010, 98, 102–117. [Google Scholar] [CrossRef]
- Lian, J.J.; Jia, Y.Y.; Wang, H.J. Numerical simulation for characteristics of wind loads of 2.5MW wind turbine under Typhoon. ACTA Energ. Sol. Sin. 2018, 39, 611–618. (In Chinese) [Google Scholar]
- Steele, C.J.; Dorling, S.R.; Glasow, R.V.; Bacon, J. Idealized WRF model sensitivity simulations of sea breeze types and their effects on offshore windfields. Atmos. Chem. Phys. 2013, 13, 443–461. [Google Scholar] [CrossRef] [Green Version]
- Marjanovic, N.; Mirocha, J.D.; Chow, F.K. Generalized Wind Turbine Actuator Disk Parameterization in the Weather Research and Forecasting (WRF) Model for Real-World Simulations. Am. Geophys. Union 2013, 12, 3–19. [Google Scholar]
- Wang, Z.Y.; Zhang, B.; Zhao, Y.; Liu, G. Dynamic response of wind turbine under Typhoon. ACTA Energ. Sol. Sin. 2013, 34, 1434–1442. (In Chinese) [Google Scholar]
- Ke, S.T.; Xu, L.; Ge, Y.J. The aerostatic response and stability performance of a wind turbine tower-blade coupled system considering blade shutdown position. Wind Struct. Int. J. 2017, 25, 507–535. [Google Scholar]
- Ke, S.T.; Wang, T.G.; Ge, Y.J.; Wang, H. Wind-induced fatigue of large HAWT coupled tower-blade structures considering aeroelastic and yaw effects. Struct. Des. Tall Spec. Build. 2017, 11, e1467. [Google Scholar] [CrossRef]
- Ke, S.T.; Yu, W.; Wang, T.G.; Zhao, L.; Ge, Y.J. Wind loads and load-effects of large scale wind turbine tower with different halt positions of blade. Wind Struct. Int. J. 2016, 23, 559–575. [Google Scholar] [CrossRef]
- Ke, S.T.; Yu, W.; Wang, T.G.; Ge, Y.J.; Tamura, Y. The effect of blade positions on the aerodynamic performances of wind turbine system. Wind Struct. Int. J. 2016, 24, 205–221. [Google Scholar] [CrossRef]
- Ke, S.T.; Wang, T.G.; Ge, Y.J.; Wang, H.; Tamura, Y. Aerodynamic loads and aeroelastic responses of WT tower-blade system in yaw condition. Struct. Eng. Mech. Int. J. 2015, 56, 1021–1040. [Google Scholar] [CrossRef]
- Basso, J.L.M.; Macedo, L.R.; Yamasaki, Y. Evaluation of time range forecasting of surface wind of WRF. Ciênc. E Nat. 2014, 36, 491–496. [Google Scholar]
- Miglietta, M.M.; Zecchetto, S.; Biasio, F.D. A comparison of WRF model simulations with SAR wind data in two case studies of orographic lee waves over the Eastern Mediterranean Sea. Atmos. Res. 2013, 120, 127–146. [Google Scholar] [CrossRef]
- Takeyama, Y.; Ohsawa, T.; Kozai, K.; Hasager, C.B.; Badger, M. Effectiveness of WRF wind direction for retrieving coastal sea surface wind from synthetic aperture radar. Wind Energy 2013, 16, 865–878. [Google Scholar] [CrossRef]
- GB50009-2012. Load Code for the Design of Building Structures; China Building Industry Press: Beijing, China, 2012. [Google Scholar]
- Vreman, B.; Geurts, B.; Kuerten, H. Large-eddy simulation of the turbulent mixing layer. J. Fluid Mech. 2017, 339, 357–390. [Google Scholar] [CrossRef]
- Shamsoddin, S.; Porté-Agel, F. Large-Eddy Simulation of Atmospheric Boundary-Layer Flow through a Wind Farm Sited on Topography. Bound.-Layer Meteorol. 2016, 163, 1–17. [Google Scholar] [CrossRef]
- Lu, C.; Li, Q.; Huang, S.; Chen, F.; Fu, X.; Guo, M. Simulation of large eddy of wind load on a long-span complex roof structure. China Civ. Eng. J. 2011, 44, 1–9. (In Chinese) [Google Scholar]










| WRF Parameters | Main Zone (D01) | Nesting Zone (D02) | Nesting Zone (D03) |
|---|---|---|---|
| Horizontal resolution | 13.5 km | 4.5 km | 1.5 km |
| Integral time step | 180 s | 180 s | 180 s |
| Microphysical process scheme | Lin | Lin | Lin |
| Long-wave radiation | RRTM | RRTM | RRTM |
| Short-wave radiation | Dudhai | Dudhai | Dudhai |
| Near-ground layer scheme | Monin-Obukhov | Monin-Obukhov | Monin-Obukhov |
| Land surface process scheme | Noah | Noah | Noah |
| Boundary layer scheme | MYJ | MYJ | MYJ |
| Cumulus convection parameter scheme | Kain-Fritsch | Kain-Fritsch | Kain-Fritsch |
| Position P/% | Blade Span R/m | Chord Length C/m | Inflow Angle φ/(º) | Blade Pitch Angle β/(º) | Position P/% | Blade Span R/m | Chord Length C/m | Inflow Angle φ/(º) | Blade Pitch Angle β/(º) |
|---|---|---|---|---|---|---|---|---|---|
| 5 | 3 | 2.9 | 0.823 | 37.14 | 55 | 33 | 1.95 | 0.169 | −0.293 |
| 10 | 6 | 3.66 | 0.64 | 26.672 | 60 | 36 | 1.75 | 0.156 | −1.072 |
| 15 | 9 | 4.41 | 0.507 | 19.069 | 65 | 39 | 1.58 | 0.144 | −1.736 |
| 20 | 12 | 4.56 | 0.414 | 13.692 | 70 | 42 | 1.42 | 0.134 | −2.310 |
| 25 | 15 | 4.25 | 0.346 | 9.83 | 75 | 45 | 1.27 | 0.125 | −2.810 |
| 30 | 18 | 3.91 | 0.296 | 6.976 | 80 | 48 | 1.12 | 0.118 | −3.250 |
| 35 | 21 | 3.59 | 0.258 | 4.802 | 85 | 51 | 0.98 | 0.111 | −3.640 |
| 40 | 24 | 3.05 | 0.229 | 3.103 | 90 | 54 | 0.83 | 0.105 | −3.987 |
| 45 | 27 | 2.63 | 0.205 | 1.742 | 95 | 57 | 0.69 | 0.099 | −4.299 |
| 50 | 30 | 2.29 | 0.186 | 0.63 | 100 | 60 | 0.54 | 0.095 | −4.580 |
| Orders | 1 | 25 | 53 | 85 | 93 |
|---|---|---|---|---|---|
| Inherent frequency | 0.14 Hz | 3.91 Hz | 10.53 Hz | 16.90 Hz | 19.25 Hz |
| Mode of vibration | 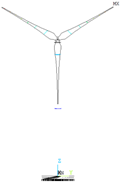 | 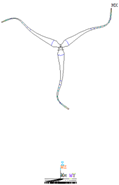 | 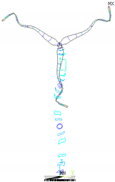 | 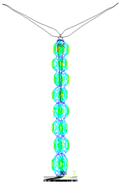 |  |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ke, S.; Xu, L.; Wang, T. Aerodynamic Performance and Wind-Induced Responses of Large Wind Turbine Systems with Meso-Scale Typhoon Effects. Energies 2019, 12, 3696. https://doi.org/10.3390/en12193696
Ke S, Xu L, Wang T. Aerodynamic Performance and Wind-Induced Responses of Large Wind Turbine Systems with Meso-Scale Typhoon Effects. Energies. 2019; 12(19):3696. https://doi.org/10.3390/en12193696
Chicago/Turabian StyleKe, Shitang, Lu Xu, and Tongguang Wang. 2019. "Aerodynamic Performance and Wind-Induced Responses of Large Wind Turbine Systems with Meso-Scale Typhoon Effects" Energies 12, no. 19: 3696. https://doi.org/10.3390/en12193696
APA StyleKe, S., Xu, L., & Wang, T. (2019). Aerodynamic Performance and Wind-Induced Responses of Large Wind Turbine Systems with Meso-Scale Typhoon Effects. Energies, 12(19), 3696. https://doi.org/10.3390/en12193696





