A Novel Machine Learning-Based Short-Circuit Current Prediction Method for Active Distribution Networks
Abstract
:1. Introduction
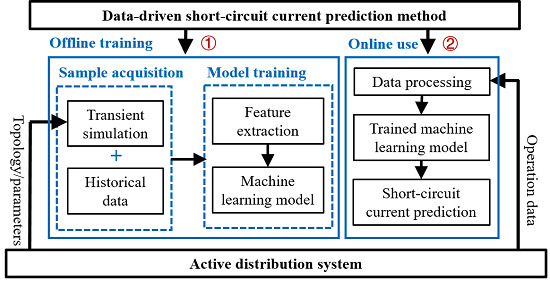
2. Overview and Consideration of the Proposed Methodology
3. Research Object and Sample Composition
3.1. Research Object
3.2. Sample Composition
4. XGBoost Method for Short-Circuit Current Prediction
4.1. XGBoost Algorithm
4.2. Performance Indicator
5. Data-Driven Short-Circuit Current Prediction Method
5.1. Sample Set Establishment
5.2. Short-Circuit Current Prediction Process
6. Case Study
6.1. Case and Sample Generation
6.2. Tests and Results
6.2.1. Hyperparameter Selection
6.2.2. Prediction Results
6.2.3. Comparison of the Different Machine Learning Methods
6.3. Requirement of Sample Set Size for Networks with Different Scales
6.4. The Applicable Scenarios of the Proposed Method
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Girgis, A.; Brahma, S. Effect of distributed generation on protective device coordination in distribution system. In Proceedings of the 2001 Large Engineering Systems Conference on Power Engineering, Halifax, NS, Canada, 11–13 July 2001; pp. 115–119. [Google Scholar]
- Wang, C.; Sun, X. An Improved Short Circuit Calculation Method for Distribution Network with Distributed Generations. Autom. Electr. Power Syst. 2012, 36, 54–58. [Google Scholar]
- Hooshyar, H.; Baran, M.E. Fault analysis on distribution feeders with high penetration of PV systems. IEEE Trans. Power Syst. 2012, 28, 2890–2896. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, N.; Ye, L. Fault analysis for distribution networks with current-controlled three-phase inverter-interfaced distributed generators. IEEE Trans. Power Del. 2015, 30, 1532–1542. [Google Scholar] [CrossRef]
- Yang, S.; Tong, X. Short-circuit Current Calculation of Distribution Network Containing Distributed Generators with Capability of Low Voltage Ride Through. Autom. Electr. Power Syst. 2016, 40, 93–99. [Google Scholar]
- Zhao, J.; Dong, Z.; Wen, F.; Xue, Y. Data Science for Energy Systems: Theory, Techniques and Prospect. Autom. Electr. Power Syst. 2017, 41, 1–11. [Google Scholar]
- Ramchurn, S.; Vytelingum, P.; Rogers, A.; Jennings, N.R. Putting the “smarts” into the smart grid: A grand challenge for artificial intelligence. Commun. ACM 2012, 55, 86–97. [Google Scholar] [CrossRef]
- Bose, B.K. Artificial intelligence techniques in smart grid and renewable energy systems—Some example applications. Proc. IEEE 2017, 105, 2262–2273. [Google Scholar] [CrossRef]
- Yang, T.; Zhao, L.; Wang, C. Review on Application of Artificial Intelligence in Power System and Integrated Energy System. Autom. Electr. Power Syst. 2019, 43, 8–20. [Google Scholar]
- Xu, Y.; Dong, Z.Y.; Zhao, J.H.; Zhang, P.; Wong, K.P. A reliable intelligent system for real-time dynamic security assessment of power systems. IEEE Trans. Power Syst. 2012, 27, 1253–1263. [Google Scholar] [CrossRef]
- Ding, N.; Benoit, C.; Foggia, G.; Bésanger, Y.; Wurtz, F. Neural network-based model design for short-term load forecast in distribution systems. IEEE Trans. Power Syst. 2015, 31, 72–81. [Google Scholar] [CrossRef]
- Zheng, H.; Yuan, J.; Chen, L. Short-term load forecasting using EMD-LSTM neural networks with a Xgboost algorithm for feature importance evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Fink, O.; Sansavini, G. Combined fault location and classification for power transmission lines fault diagnosis with integrated feature extraction. IEEE Trans. Ind. Electron. 2018, 65, 561–569. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Statist. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Bauer, E.; Kohavi, R. An Empirical Comparison of Voting Classification Algorithms: Bagging, Boosting, and Variants. Mach. Learn. 1999, 36, 105–139. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, C.; Lin, D.; He, B. An artificial intelligence based method for evaluating power grid node importance using network embedding and support vector regression. Front. Inform. Technol. Electron. Eng. 2019, 20, 816–828. [Google Scholar] [CrossRef]
- PES Test Feeder. IEEE PES AMPS DSAS Test Feeder Working Group. Available online: http://sites.ieee.org/pes-testfeeders/ (accessed on 28 August 2019).
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the Fourteenth International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; pp. 1137–1143. [Google Scholar]
- Wang, S.; Wang, C. Modern Distribution System Analysis, 2nd ed.; Higher Education Press: Beijing, China, 2014; pp. 248–251. [Google Scholar]







| Composition of the Sample | Symbol | Description |
|---|---|---|
| Sample type | f_type | The fault type |
| Feature | If | Short-circuit current when IIDGs are disconnected from the system |
| αj | Grid connection status of the IIDG | |
| SDGj | IIDG capacity | |
| line_cut | Cut-off line | |
| f_line | Fault line | |
| f_pos | Fault position | |
| Label | If_DG | Short-circuit current when IIDGs are connected to the system |
| No. | Sample Value (A) | Prediction Value (A) | APE (%) |
|---|---|---|---|
| 1 | 351.476 | 350.193 | 0.365 |
| 2 | 67.772 | 66.706 | 1.573 |
| 3 | 25.682 | 25.906 | 0.876 |
| 4 | 48.369 | 47.879 | 1.013 |
| 5 | 322.865 | 322.978 | 0.035 |
| Range of APE (%) | Number |
|---|---|
| 0–1 | 175 (76.1%) |
| 1–2 | 36 (15.6%) |
| 2–3 | 19 (8.3%) |
| Method | MAPE (%) | |
|---|---|---|
| Training | Testing | |
| SVR | 2.078 | 2.570 |
| RF | 1.074 | 1.298 |
| GBDT | 0.312 | 0.902 |
| XGBoost | 0.040 | 0.846 |
| Sample Set Size | IEEE 13-Node System | IEEE 34-Node System | IEEE 69-Node System | |||
|---|---|---|---|---|---|---|
| MAPE (%) | Prediction Time (ms) | MAPE (%) | Prediction Time (ms) | MAPE (%) | Prediction Time (ms) | |
| 15,000 | 0.670 | 0.089 | 1.439 | 0.151 | 1.406 | 0.144 |
| 20,000 | 0.624 | 0.090 | 1.354 | 0.177 | 1.396 | 0.141 |
| 25,000 | 0.615 | 0.111 | 1.163 | 0.180 | 1.262 | 0.174 |
| 30,000 | 0.602 | 0.101 | 1.042 | 0.177 | 1.257 | 0.165 |
| 35,000 | 0.591 | 0.097 | 0.847 | 0.184 | 1.149 | 0.177 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Wang, H.; Jiang, K.; He, B. A Novel Machine Learning-Based Short-Circuit Current Prediction Method for Active Distribution Networks. Energies 2019, 12, 3793. https://doi.org/10.3390/en12193793
Zheng X, Wang H, Jiang K, He B. A Novel Machine Learning-Based Short-Circuit Current Prediction Method for Active Distribution Networks. Energies. 2019; 12(19):3793. https://doi.org/10.3390/en12193793
Chicago/Turabian StyleZheng, Xiang, Huifang Wang, Kuan Jiang, and Benteng He. 2019. "A Novel Machine Learning-Based Short-Circuit Current Prediction Method for Active Distribution Networks" Energies 12, no. 19: 3793. https://doi.org/10.3390/en12193793
APA StyleZheng, X., Wang, H., Jiang, K., & He, B. (2019). A Novel Machine Learning-Based Short-Circuit Current Prediction Method for Active Distribution Networks. Energies, 12(19), 3793. https://doi.org/10.3390/en12193793