Voltage-Balancing Strategy for Three-Level Neutral Point Clamped Cascade Converter under Sequence Pulse Modulation
Abstract
:1. Introduction
2. The Basic Structure and Control Strategy of 3LNPC-CC
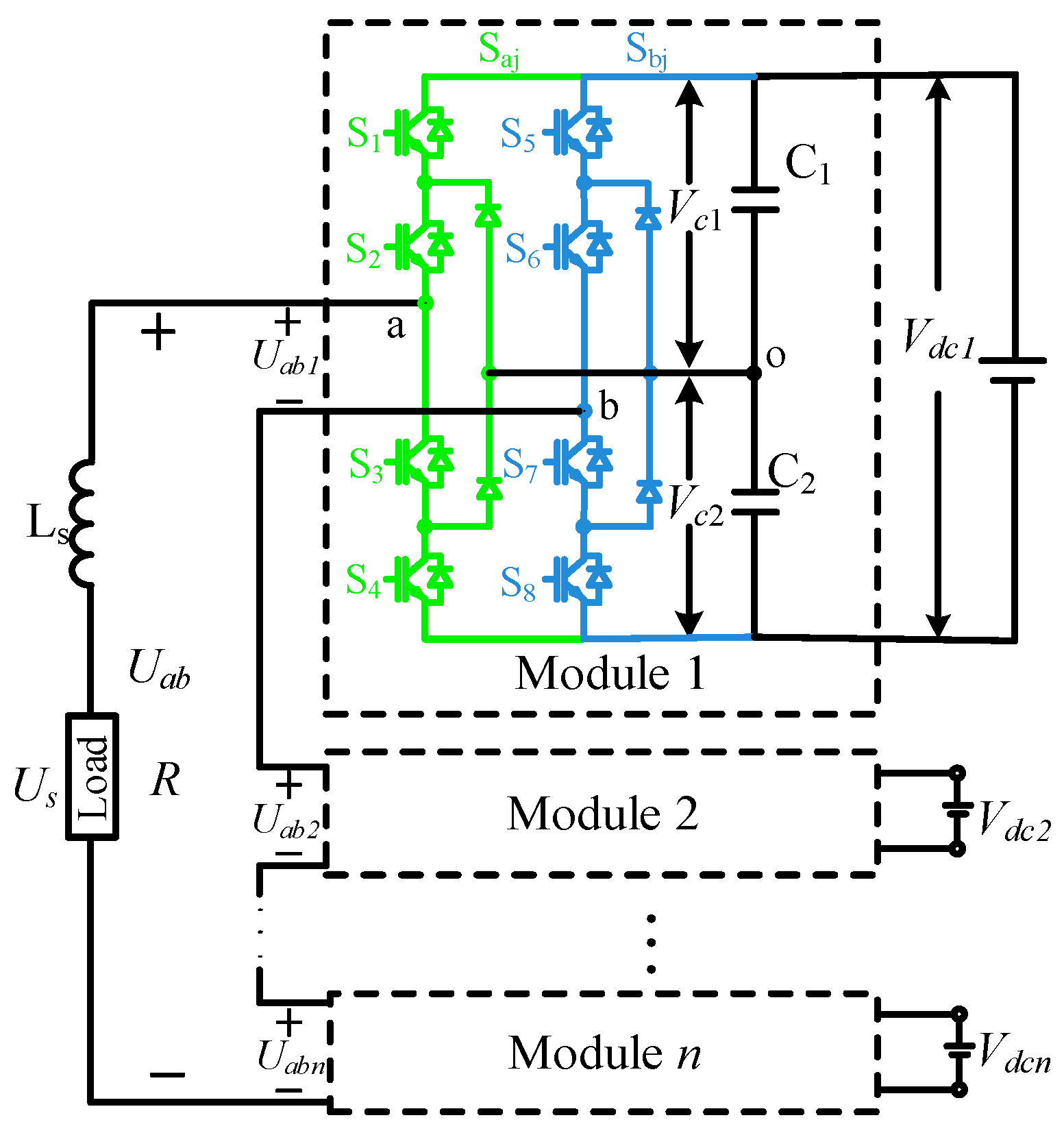
2.1. The Basic Structure of the Multi-Module 3LNPC-CC
2.2. Control Strategy of 3LNPC-CC
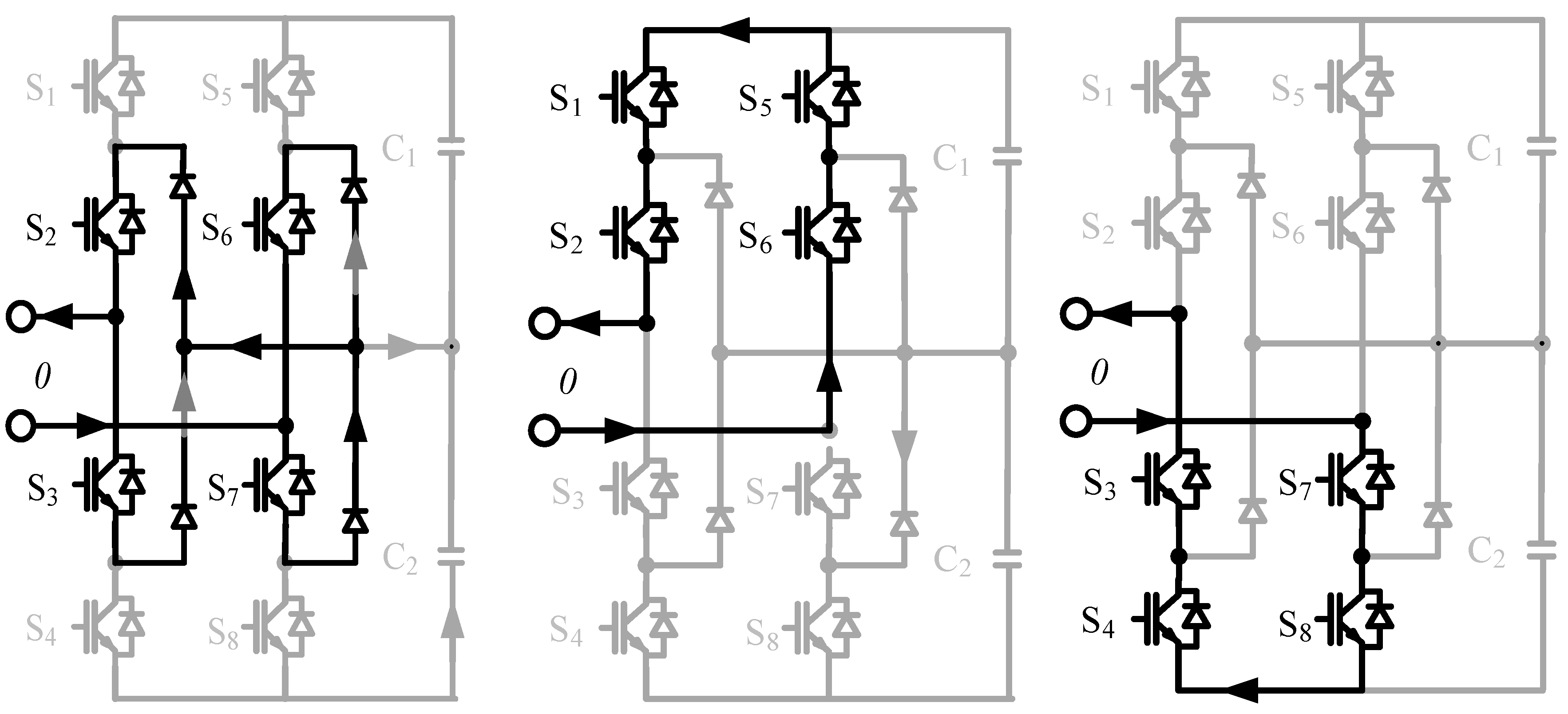
2.3. Module-Level Analyses of 3LNPC-CC
3. Sequence Pulse Modulation Strategy
- (1)
- The unbalanced capacitor voltage of inner-module;
- (2)
- The unbalanced capacitor voltage among sub-modules.
3.1. Carrier Cascaded Calculation
3.2. Sequence Pulse Generator
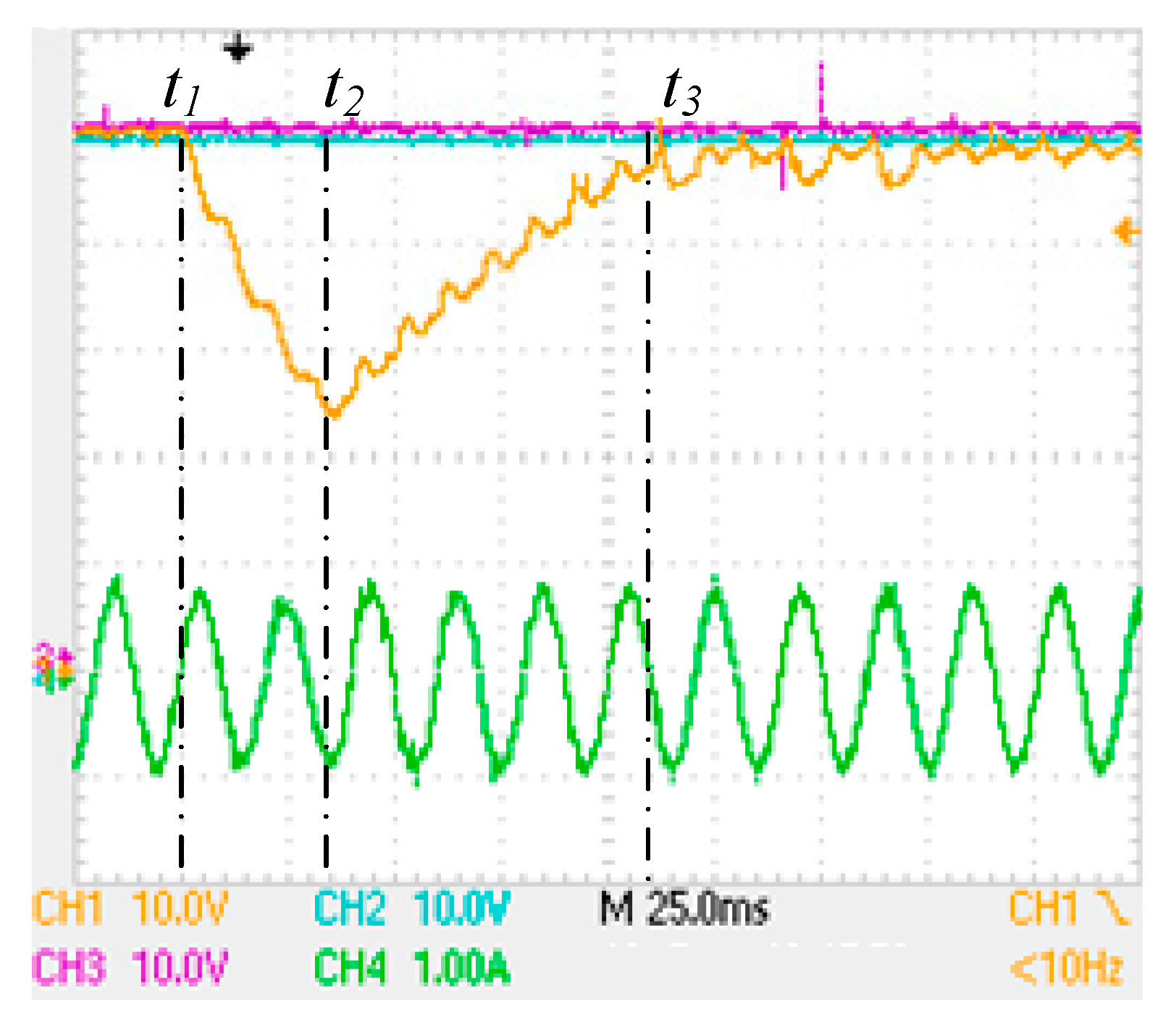
4. Limitation
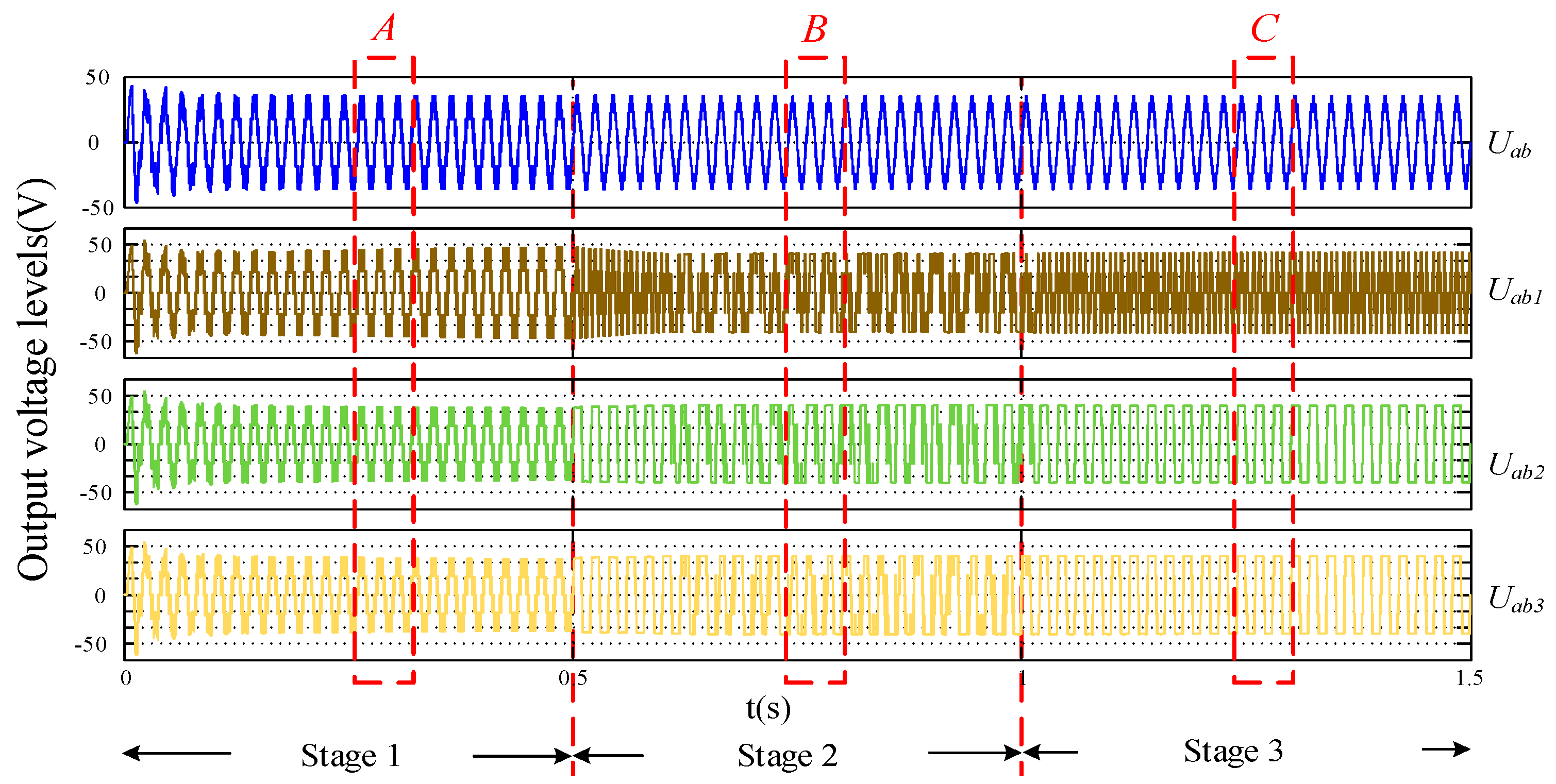
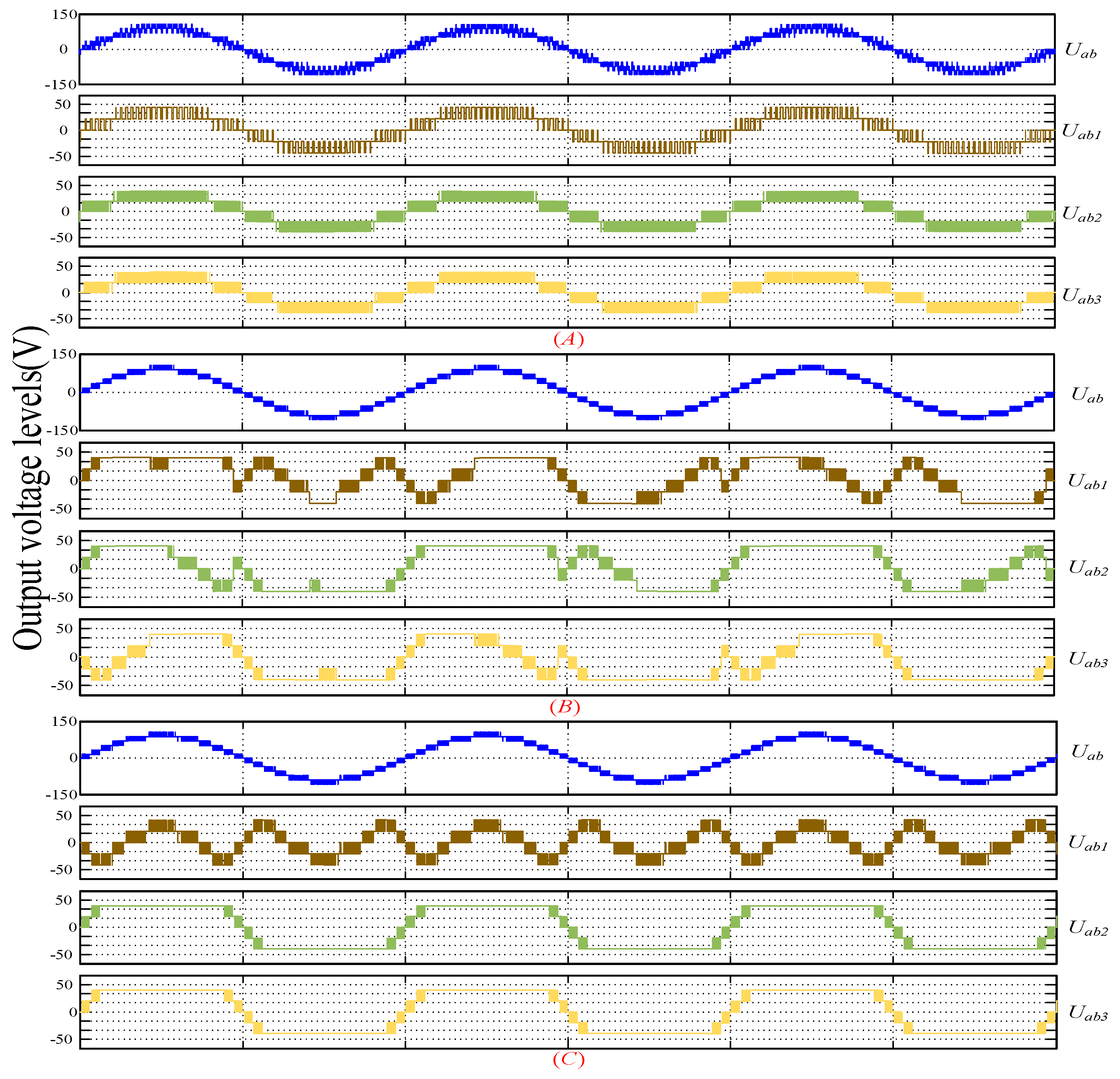
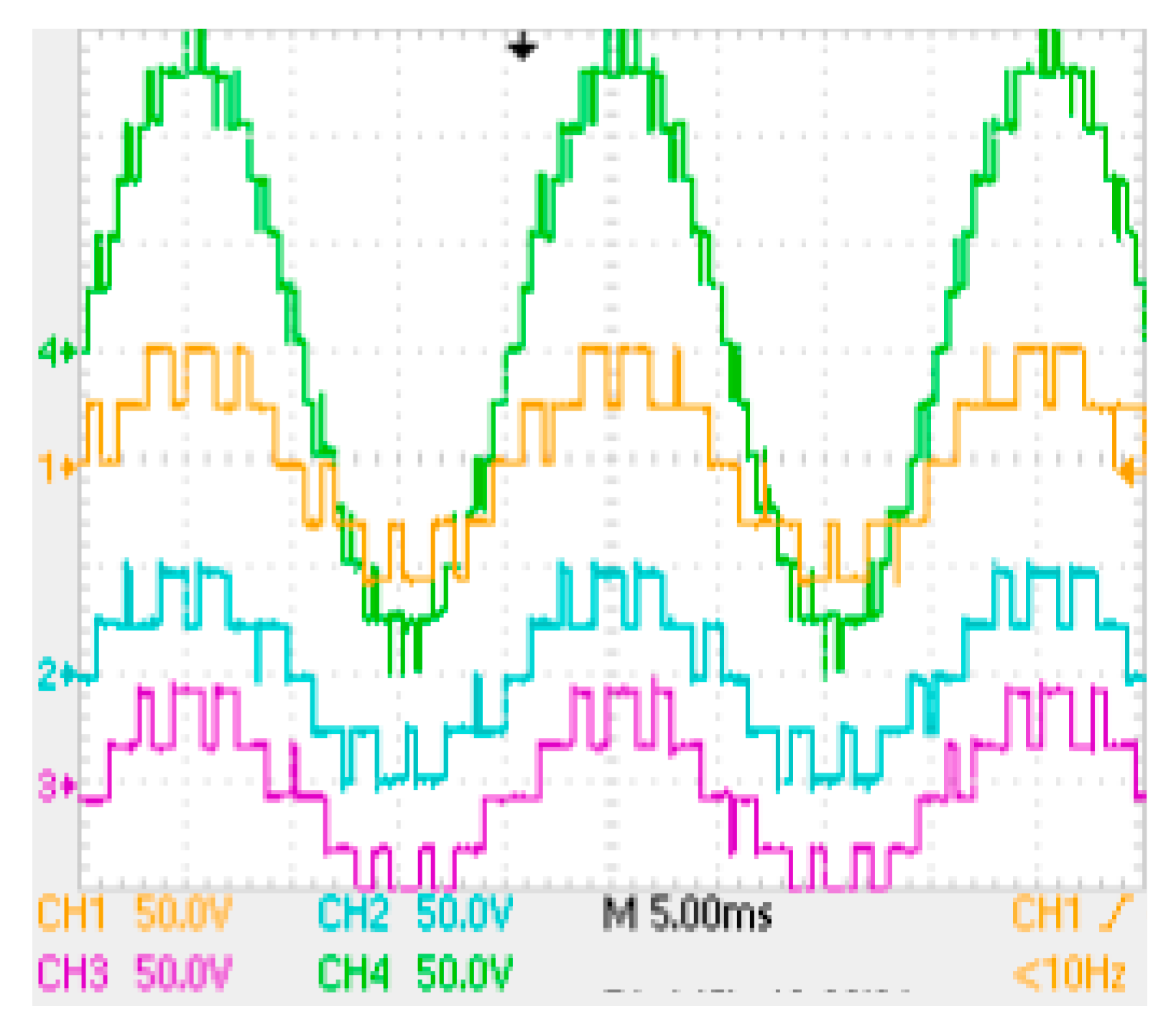
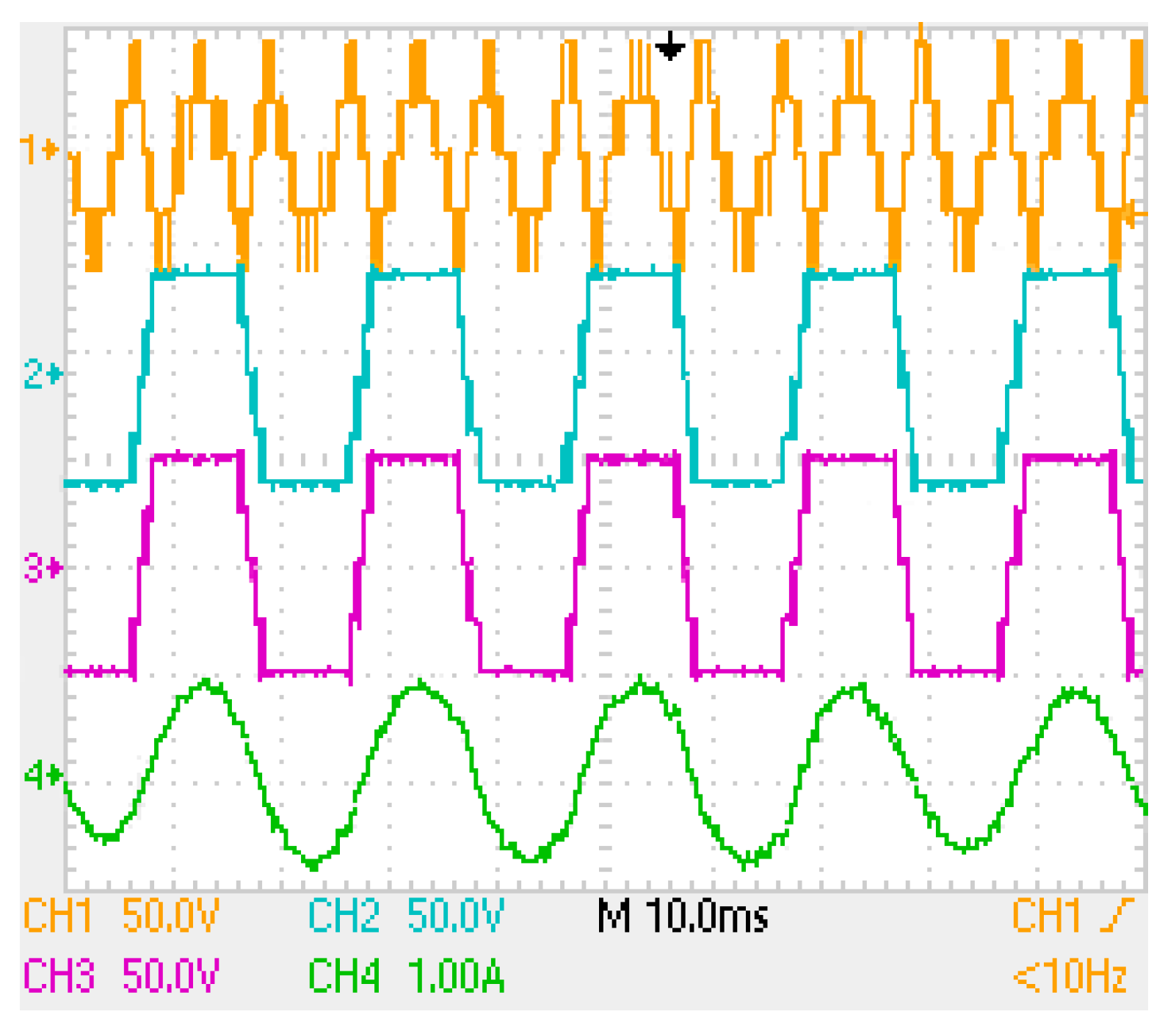
5. Simulation
6. Experimental Section
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, S.Y.; Bryant, A.; Mawby, P.; Xiang, D.W.; Ran, L.; Tavner, P. An industry-based survey of reliability in power electronic converters. In Proceedings of the IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009. [Google Scholar]
- Peng, T.; Dan, H.B.; Yang, J.; Deng, H.; Zhu, Q.; Wang, C.S.; Gui, W.H.; Guerrero, J.M. Open-Switch Fault Diagnosis and Fault Tolerant for Matrix Converter with Finite Control Set-Model Predictive Control. IEEE Trans. Ind. Electron. 2016, 63, 5953–5963. [Google Scholar] [CrossRef]
- Choi, J.H.; Kim, S.; Yoo, D.S.; Kim, K.H. A Diagnostic Method of Simultaneous Open-Switch Faults in Inverter-Fed Linear Induction Motor Drive for Reliability Enhancement. IEEE Trans. Ind. Electron. 2014, 62, 4065–4077. [Google Scholar] [CrossRef]
- Ge, X.L.; Pu, J.K.; Gou, B.; Liu, Y.C. An Open-Circuit Fault Diagnosis Approach for Single-Phase Three-Level Neutral-Point-Clamped Converters. IEEE Trans. Power Electron. 2017, 33, 2559–2570. [Google Scholar] [CrossRef]
- Lamb, J.; Mirafzal, B. Open-Circuit IGBT Fault Detection and Location Isolation for Cascaded Multilevel Converters. IEEE Trans. Ind. Electron. 2017, 64, 4846–4856. [Google Scholar] [CrossRef]
- Gautam, S.P.; Kumar, L.; Gupta, S.; Agrawal, N. A Single-Phase Five-Level Inverter Topology with Switch Fault-Tolerance Capabilities. IEEE Trans. Ind. Electron. 2016, 64, 2004–2014. [Google Scholar] [CrossRef]
- Choi, U.M.; Lee, K.B.; Blaabjerg, F. Diagnosis and Tolerant Strategy of an Open-Switch Fault for T-Type Three-Level Inverter Systems. IEEE Trans. Ind. Appl. 2013, 50, 495–508. [Google Scholar] [CrossRef]
- Gou, B.; Ge, X.; Wang, S.; Feng, X.; Kuo, J.B.; Habetler, T.G. An open-switch fault diagnosis method for single-phase PWM rectifier using a model-based approach in high-speed railway electrical traction drive system. IEEE Trans. Power Electron. 2016, 31, 3816–3826. [Google Scholar] [CrossRef]
- Dujic, D.; Zhao, C.H.; Mester, A.; Steinke, J.K.; Weiss, M.; Lewdeni-Schmid, S.; Chaudhuri, T.; Stefanutti, P. Power Electronic Traction Transformer-Low Voltage Prototype. IEEE Trans. Power Electron. 2013, 28, 5522–5534. [Google Scholar] [CrossRef]
- Peng, X.; He, X.; Han, P.; Lin, H.; Gao, S.; Shu, Z. Opposite Vector Based Phase Shift Carrier Space Vector Pulse Width Modulation for Extending the Voltage Balance Region in Single-Phase 3LNPC Cascaded Rectifier. IEEE Trans. Power Electron. 2017, 32, 7381–7393. [Google Scholar] [CrossRef]
- She, X.; Huang, A.Q. Current Sensorless Power Balance Strategy for DC/DC Converters in a Cascaded Multilevel Converter Based Solid State Transformer. IEEE Trans. Power Electron. 2013, 29, 17–22. [Google Scholar] [CrossRef]
- Sim, H.W.; Lee, J.S.; Lee, K.B. Detecting open-switch faults: Using asymmetric zero-voltage switching states. IEEE Ind. Appl. Mag. 2016, 22, 27–37. [Google Scholar] [CrossRef]
- Peng, X.; He, X.; Han, P.; Guo, A.; Shu, Z.; Gao, S. Smooth Switching Technique for Voltage Balance Management Based on Three-Level Neutral Point Clamped Cascaded Rectifier. Energies 2016, 9, 803. [Google Scholar] [CrossRef]
- Yang, S.Y.; Xiang, D.W.; Bryant, A.; Mawby, P.; Ran, L.; Tavner, P. Condition monitoring for device reliability in power electronic converters: A review. IEEE Trans. Power Electron. 2010, 25, 2734–2752. [Google Scholar] [CrossRef]
- Nicolas-Apruzzese, J.; Busquets-Monge, S.; Bordonau, J.; Alepuz, S.; Calle-Prado, A. Analysis of the Fault-Tolerance Capacity of the Multilevel Active-Clamped Converter. IEEE Trans. Ind. Electron. 2012, 60, 4773–4783. [Google Scholar] [CrossRef]
- Chen, A.; Hu, L.; Chen, L.; Deng, Y.; Yao, G.; He, X.N. A Multilevel Converter Topology with Fault-Tolerant Ability. In Proceedings of the Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 27 September 2004. [Google Scholar]
- Shu, Z.L.; He, X.Q.; Wang, Z.Y.; Qiu, D.Q.; Jing, Y.Z. Voltage Balancing Approaches for Diode-Clamped Multilevel Converters Using Auxiliary Capacitor-Based Circuits. IEEE Trans. Power Electron. 2012, 28, 2111–2124. [Google Scholar] [CrossRef]
- Shu, Z.L.; Zhu, H.F.; He, X.Q.; Ding, N.; Jing, Y.Z. One-inductor-based auxiliary circuit for dc-link capacitor voltage equalisation of diode-clamped multilevel converter. IET Power Electron. 2013, 6, 1339–1349. [Google Scholar] [CrossRef]
- Zhu, H.F.; Shu, Z.L.; Gao, F.H.; Qin, B.; Gao, S.B. Five-level diode-clamped active power filter using voltage space vector-based indirect current and predictive harmonic control. IET Power Electron. 2014, 7, 713–723. [Google Scholar] [CrossRef]
- Antonio, D.; Marco, L.; Vito Giuseppe, M.; Paola, R. Overview of PI-Based Solutions for the Control of DC Buses of a Single-Phase H-Bridge Multilevel Active Rectifier. IEEE Ind. Appl. Mag. 2008, 44, 857–866. [Google Scholar] [CrossRef]
- Morteza, M.; Ghias, F.; Hossein, I.; Seyed Mohammad, S. A Voltage Balancing Strategy with Extended Operating Region for Cascaded H-Bridge Converters. IEEE Trans. Power Electron. 2014, 29, 5044–5053. [Google Scholar] [CrossRef]
- She, X.; Huang, A.Q.; Wang, G. 3-D Space Modulation with Voltage Balancing Capability for a Cascaded Seven-Level Converter in a Solid-State Transformer. IEEE Trans. Power Electron. 2011, 26, 3778–3789. [Google Scholar] [CrossRef]
- Peng, X.; He, X.; Han, P.; Lin, X.; Shu, Z.; Gao, S. Sequence Pulse Modulation for Voltage Balance in a Cascaded H-Bridge Rectifier. J. Power Electron. 2017, 17, 664–673. [Google Scholar] [CrossRef]
- Lin, H.; Shu, Z.; He, X.; Liu, M. N-D SVPWM with DC Voltage Balancing and Vector Smooth transition Algorithm for Cascaded Multilevel Converter. IEEE Trans. Ind. Electron. 2018, 65, 3837–3847. [Google Scholar] [CrossRef]
- Han, P.; He, X.; Zhao, Z.; Yu, H.; Wang, Y.; Peng, X.; Shu, Z. DC-Link Capacitor Voltage Balanced Modulation Strategy Based on Three Level Neutral Point Clamped Cascaded Rectifier. J. Power Electron. 2019, 19, 99–107. [Google Scholar] [CrossRef]
- Yu, Y.; Konstantinou, G.; Hredzak, B.; Agelidis, V.G. Power Balance of Cascaded H-Bridge Multilevel Converters for Large-Scale Photovoltaic Integration. IEEE Trans. Power Electron. 2016, 31, 292–303. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Li, B.Q. Generalized Theory of Phase-Shifted Carrier PWM for Cascaded H-Bridge Converters and Modular Multilevel Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 589–605. [Google Scholar] [CrossRef]
- Sergio, B.M.; Griñó, R.; Nicolas-Apruzzese, J.; Bordonau, J. Decoupled DC-Link Capacitor Voltage Control of DC–AC Multilevel Multileg Converters. IEEE Trans. Ind Electron. 2016, 63, 1344–1349. [Google Scholar] [CrossRef]
- Li, J.; Georgios, K.; Harith, R.W.; Christopher, D.T.; Josep, P. Capacitor Voltage Reduction in Modular Multilevel Converters under Grid Voltages Unbalances. IEEE Trans. Power Deliv. 2019. [Google Scholar] [CrossRef]
- Jean-Michel, D.P.; Caio, R.D.; Humberto, P.; Fernanda, D.M. Phase Disposition Modulation with Sorting Algorithm for Symmetrical Cascaded Multilevel Converters. IEEE Trans. Ind Appl. 2019. [Google Scholar] [CrossRef]
- Han, P.; He, X.; Ren, H.; Wang, Y.; Peng, X.; Shu, Z.; Gao, S.; Wang, Y.B.; Chen, Z. Fault Diagnosis and System Reconfiguration Strategy of a Single-Phase Three-Level Neutral-Point-Clamped Cascaded Inverter. IEEE Trans. Ind. Appl. 2019, 55, 3863–3876. [Google Scholar] [CrossRef]













| PWMi | Sai | Sbi | C1i | C2i | DC-link |
|---|---|---|---|---|---|
| 2 | 1 | −1 | discharge | discharge | discharge |
| 1 | 1 | 0 | discharge | ||
| 0 | −1 | discharge | |||
| 0 | 1 | 1 | |||
| 0 | 0 | ||||
| −1 | −1 | ||||
| −1 | −1 | 0 | charge | ||
| 0 | 1 | charge | |||
| −2 | −1 | 0 | charge | charge | charge |
| m | SS1st | SS2nd | SS3th |
|---|---|---|---|
| 6 | 2 | 2 | 2 |
| 5 | 2 | 2 | 1 |
| 4 | 2 | 2 | 0 |
| 3 | 2 | 2 | −1 |
| 2 | 2 | 2 | −2 |
| 1 | 2 | 1 | −2 |
| 0 | 2 | 0 | −2 |
| −1 | 2 | −1 | −2 |
| −2 | 2 | −2 | −2 |
| −3 | 1 | −2 | −2 |
| −4 | 0 | −2 | −2 |
| −5 | −1 | −2 | −2 |
| −6 | −2 | −2 | −2 |
| m | SS1st | SS2nd | SS3th |
|---|---|---|---|
| 6 | 2 | 2 | 2 |
| 5 | 2 | 2 | 1 |
| 4 | 2 | 2 | 0 |
| 3 | 2 | 2 | −1 |
| 2 | 2 | 2 | −2 |
| 1 | 1 | 1 | −1 |
| 0 | 0 | 0 | 0 |
| −1 | −1 | −1 | 1 |
| −2 | −2 | −2 | 2 |
| −3 | −2 | −2 | 1 |
| −4 | −2 | −2 | 0 |
| −5 | −2 | −2 | −1 |
| −6 | −2 | −2 | −2 |
| M | Ta | Tb |
|---|---|---|
| I | (1–6Msin(ωt))Ts | (6Msin(ωt))Ts |
| II | (2–6Msin(ωt)) Ts | (6Msin(ωt)−1)Ts |
| III | (3–6Msin(ωt))Ts | (6Msin(ωt)−2)Ts |
| IV | (4–6Msin(ωt))Ts | (6Msin(ωt)−3)Ts |
| V | (5–6Msin(ωt))Ts | (6Msin(ωt)−4)Ts |
| VI | (6–6Msin(ωt))Ts | (6Msin(ωt)−5)Ts |
| Parameter Name | Parameter Value | Numbers |
|---|---|---|
| Filter capacitor | 10 μF | 1 |
| Filter inductance | 5 mL | 1 |
| DC-link voltage (Vdc) | 50 V | 3 |
| DC-link capacitor | 470 μF | 3 |
| Carrier wave frequency | 750 Hz | - |
| Modulation depth | 0.83 | - |
| Number of modules | 3 | - |
| Load of 3LNPC-CC | 50 Ω | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, L.; Peng, X.; Gao, S. Voltage-Balancing Strategy for Three-Level Neutral Point Clamped Cascade Converter under Sequence Pulse Modulation. Energies 2019, 12, 3829. https://doi.org/10.3390/en12203829
Yu L, Peng X, Gao S. Voltage-Balancing Strategy for Three-Level Neutral Point Clamped Cascade Converter under Sequence Pulse Modulation. Energies. 2019; 12(20):3829. https://doi.org/10.3390/en12203829
Chicago/Turabian StyleYu, Le, Xu Peng, and Shibin Gao. 2019. "Voltage-Balancing Strategy for Three-Level Neutral Point Clamped Cascade Converter under Sequence Pulse Modulation" Energies 12, no. 20: 3829. https://doi.org/10.3390/en12203829
APA StyleYu, L., Peng, X., & Gao, S. (2019). Voltage-Balancing Strategy for Three-Level Neutral Point Clamped Cascade Converter under Sequence Pulse Modulation. Energies, 12(20), 3829. https://doi.org/10.3390/en12203829




