A Formulation of the Thrust Coefficient for Representing Finite-Sized Farms of Tidal Energy Converters
Abstract
1. Introduction
2. Methods
2.1. Numerical Simulations
Model Validation
2.2. Parameterization of Farms of TEC Devices
2.2.1. Resultant Force for a Turbine Farm
2.2.2. Thrust Coefficient for a Turbine Farm
2.2.3. Setup for Numerical Simulations
3. Results and Discussion
3.1. Formulation of the Thrust Coefficient for Farms of Turbines
- (I)
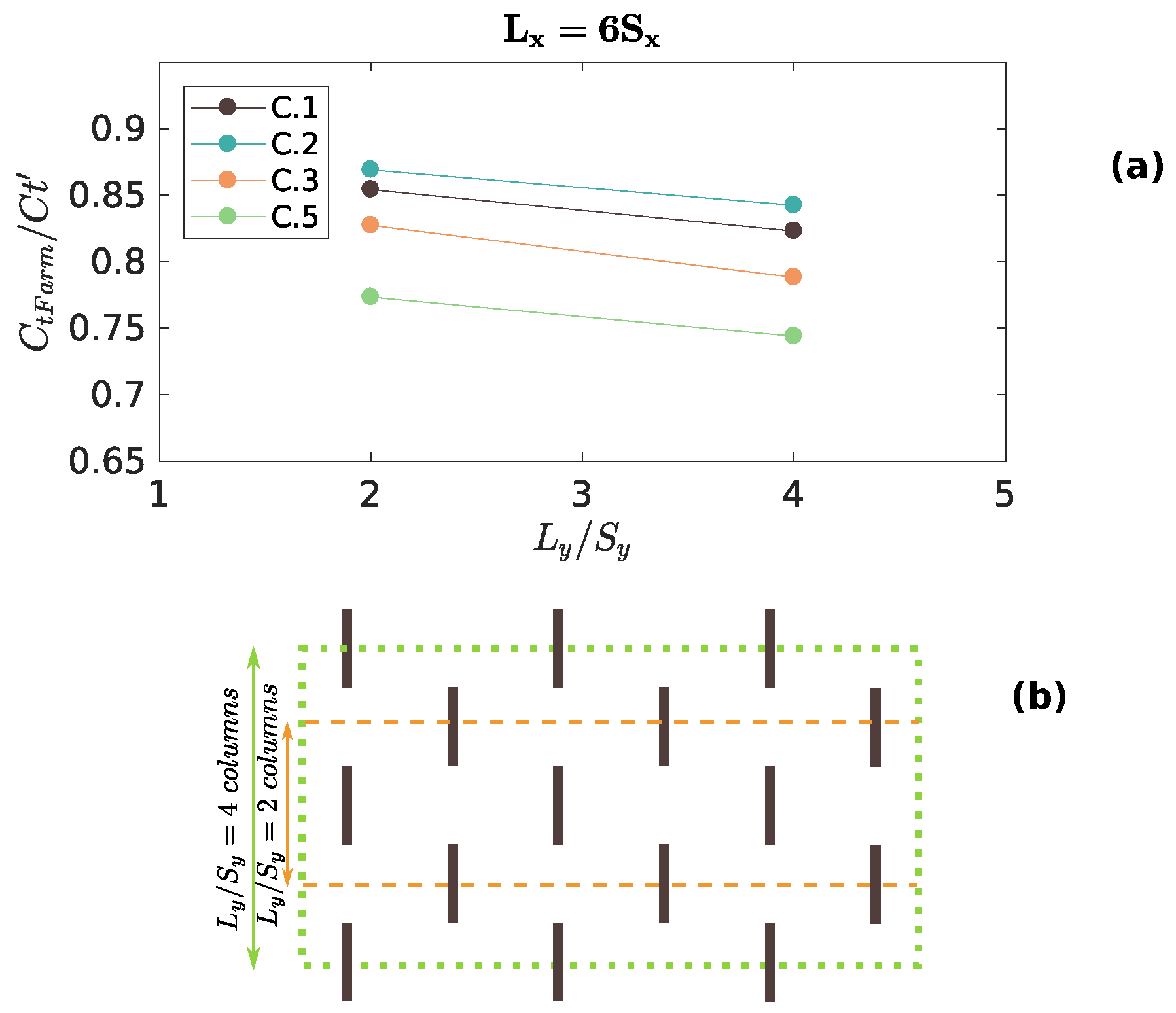
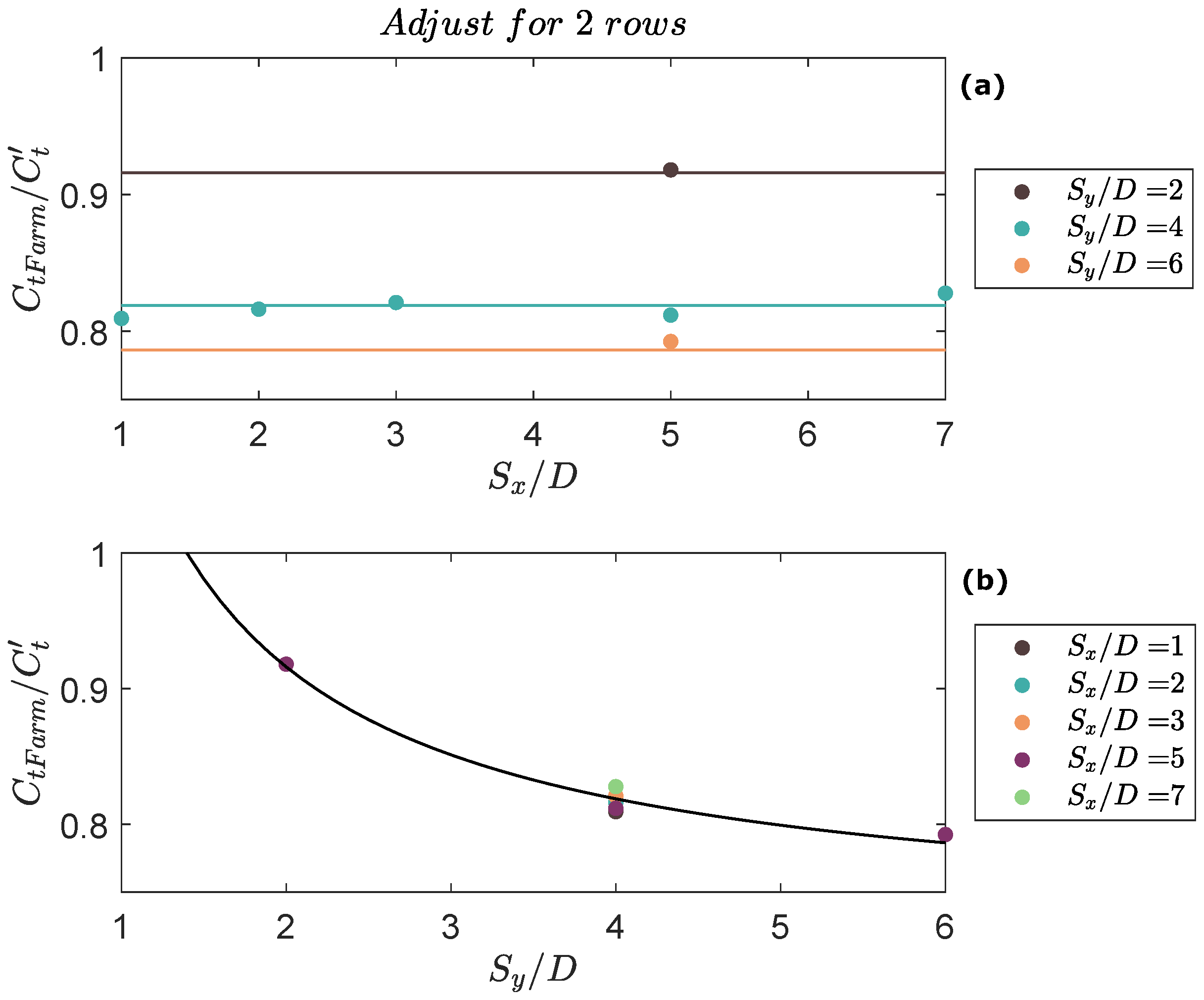
- For farms with two rows, the expression for is inversely proportional to the lateral distance between devices, . This value can go from , when the turbines are adjacent to each other, to for very laterally spaced farms, where one would expect the drag force to be additive since the wakes do not interact.
- (II)
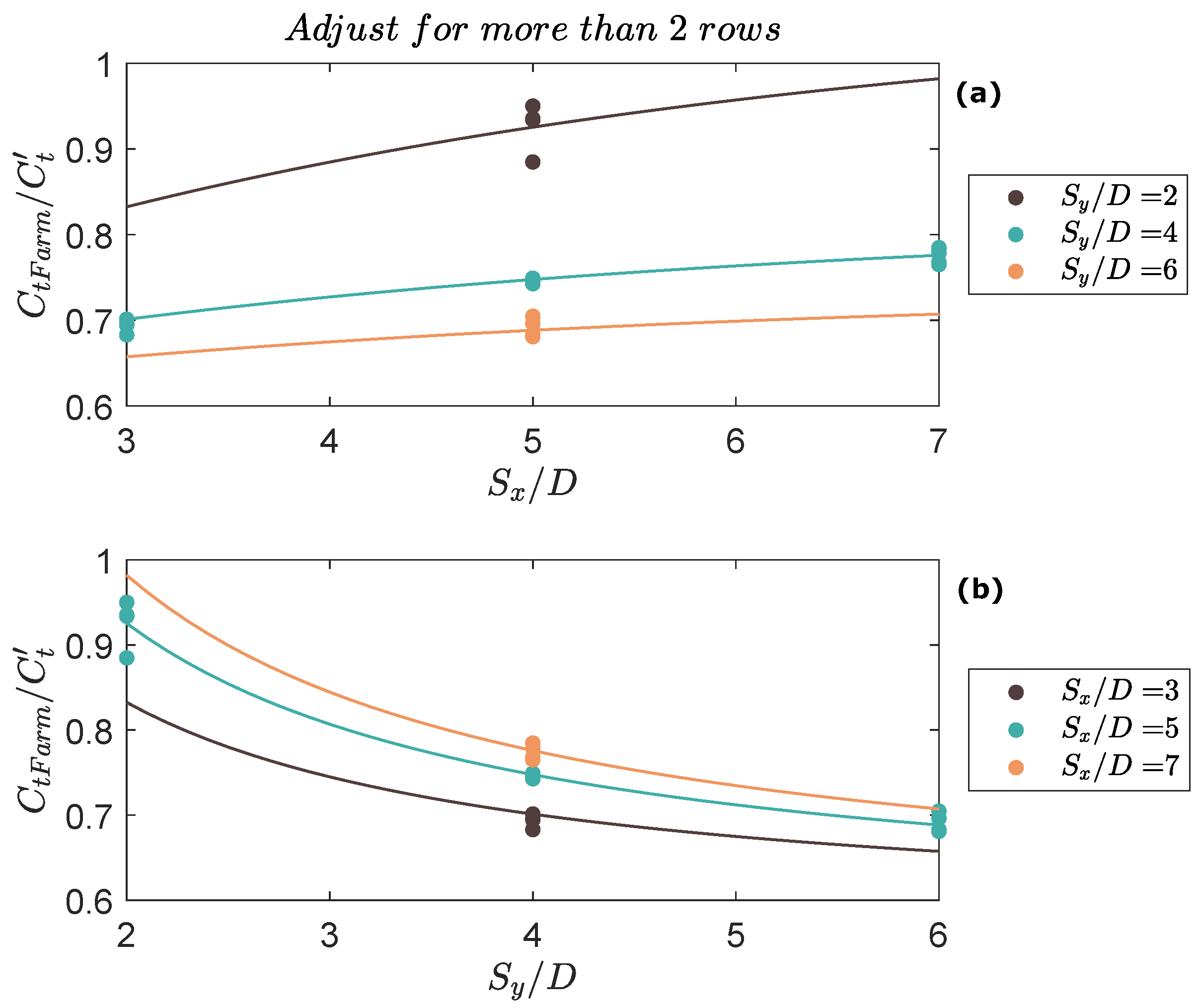
- For farms with more than two rows, the dependence of is still inversely proportional to , but also decays exponentially with the distance between the devices in the stream-wise direction . An exponential decay is proposed because it tends to zero as (i.e., the devices get closer), which captures the fact that the flow cannot penetrate the farm. On the other hand, when the stream-wise distance between the devices increases, the exponential term tends towards unity, which is equivalent to saying that becomes independent of . This expression is similar to the one proposed by Simón-Moral et al. [37] for parameterizing canopies of vegetation.
3.2. Comparison of Parameterization with Previous Work
4. Conclusions
- It is designed for staggered farms, where all the turbines occupy the same ground area.
- It does not consider a significant misalignment between the mean flow direction and the turbine axes.
- It is designed for devices that are installed at the bottom of the sea, and which do not interact with the free-surface.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DES | Detached-Eddy Simulations |
| LES | Large-Eddy Simulations |
| TEC | Tidal Energy Converter |
| RANS | Reynolds-Averaged Navier–Stokes |
| RMSE | Root Mean Square Error |
| RSR | Root mean square error-observations Standard deviation Ratio |
References
- IEA and World Bank. Sustainable Energy For All. Available online: https://datacatalog.worldbank.org/dataset/sustainable-energy-all (accessed on 18 March 2019).
- Hagerman, G.; Polagye, B.; Bedard, R.; Previsic, M. EPRI Guideline Methodology for Estimating Tidal Current Energy Resources and Power Production by Tidal In-Stream Energy Conversion (TISEC) Devices; Technical Report; Electric Power Research Institute: Palo alto, CA, USA, 2006. [Google Scholar]
- Tarbotton, M.; Larson, M. Canada Ocean Energy Atlas Phase 1: Potential Tidal Current Energy Resources Analysis Background; Canadian Hydraulics Centre: Ottawa, ON, Canada, 2006. [Google Scholar]
- Robins, P.E.; Neill, S.P.; Lewis, M.J.; Ward, S.L. Characterising the spatial and temporal variability of the tidal-stream energy resource over the northwest European shelf seas. Appl. Energy 2015, 147, 510–522. [Google Scholar] [CrossRef]
- Li, D.; Yao, Y.; Chen, Q.; Ye, Z. Numerical simulation of tidal current energy in Yangtze Estuary-Hangzhou Bay, China. In Proceedings of the OCEANS 2015, Genova, Italy, 18–21 May 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, T.; Copping, A.; Geerlofs, S. Modeling of in-stream tidal energy development and its potential effects in Tacoma Narrows, Washington, USA. Ocean Coast. Manag. 2014, 99, 52–62. [Google Scholar] [CrossRef]
- Nash, S.; O’Brien, N.; Olbert, A.; Hartnett, M. Modelling the far field hydro-environmental impacts of tidal farms—A focus on tidal regime, inter-tidal zones and flushing. Comput. Geosci. 2014, 71, 20–27. [Google Scholar] [CrossRef]
- Wang, T.; Yang, Z. A modeling study of tidal energy extraction and the associated impact on tidal circulation in a multi-inlet bay system of Puget Sound. Renew. Energy 2017, 114, 204–214. [Google Scholar] [CrossRef]
- Piano, M.; Robins, P.E.; Davies, A.G.; Neill, S.P. The Influence of Intra-Array Wake Dynamics on Depth-Averaged Kinetic Tidal Turbine Energy Extraction Simulations. Energies 2018, 11, 2852. [Google Scholar] [CrossRef]
- Myers, L.; Bahaj, A. An experimental investigation simulating flow effects in first generation marine current energy converter arrays. Renew. Energy 2012, 37, 28–36. [Google Scholar] [CrossRef]
- Nishino, T.; Willden, R.H.J. The efficiency of an array of tidal turbines partially blocking a wide channel. J. Fluid Mech. 2012, 708, 596–606. [Google Scholar] [CrossRef]
- Stansby, P.; Stallard, T. Fast optimisation of tidal stream turbine positions for power generation in small arrays with low blockage based on superposition of self-similar far-wake velocity deficit profiles. Renew. Energy 2016, 92, 366–375. [Google Scholar] [CrossRef]
- Fitch, A.C.; Olson, J.B.; Lundquist, J.K.; Dudhia, J.; Gupta, A.K.; Michalakes, J.; Barstad, I. Local and Mesoscale Impacts of Wind Farms as Parameterized in a Mesoscale NWP Model. Mon. Weather Rev. 2012, 140, 3017–3038. [Google Scholar] [CrossRef]
- Abkar, M.; Porté-Agel, F. A new wind-farm parameterization for large-scale atmospheric models. J. Renew. Sustain. Energy 2015, 7, 013121. [Google Scholar] [CrossRef]
- Calaf, M.; Meneveau, C.; Meyers, J. Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. Fluids 2010, 22, 015110. [Google Scholar] [CrossRef]
- Calaf, M.; Parlange, M.B.; Meneveau, C. Large eddy simulation study of scalar transport in fully developed wind-turbine array boundary layers. Phys. Fluids 2011, 23, 126603. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Lu, H.; Wu, Y.T. Interaction between Large Wind Farms and the Atmospheric Boundary Layer. Procedia IUTAM 2014, 10, 307–318. [Google Scholar] [CrossRef]
- Aghsaee, P.; Markfort, C.D. Effects of flow depth variations on the wake recovery behind a horizontal-axis hydrokinetic in-stream turbine. Renew. Energy 2018, 125, 620–629. [Google Scholar] [CrossRef]
- Kolekar, N.; Banerjee, A. Performance characterization and placement of a marine hydrokinetic turbine in a tidal channel under boundary proximity and blockage effects. Appl. Energy 2015, 148, 121–133. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. Rech. Aerosp. 1994, 1, 5–21. [Google Scholar]
- Escauriaza, C.; Sotiropoulos, F. Reynolds Number Effects on the Coherent Dynamics of the Turbulent Horseshoe Vortex System. Flow Turbul. Combust. 2011, 86, 231–262. [Google Scholar] [CrossRef]
- Escauriaza, C.; Sotiropoulos, F. Initial stages of erosion and bed form development in a turbulent flow around a cylindrical pier. J. Geophys. Res.-Earth 2011, 116. [Google Scholar] [CrossRef]
- Escauriaza, C.; Sotiropoulos, F. Lagrangian model of bed-load transport in turbulent junction flows. J. Fluid Mech. 2011, 666, 36–76. [Google Scholar] [CrossRef]
- Gajardo, D.; Escauriaza, C.; Ingram, D.M. Capturing the development and interactions of wakes in tidal turbine arrays using a coupled BEM-DES model. Ocean Eng. 2019, 181, 71–88. [Google Scholar] [CrossRef]
- Burton, T.; Sharpe, D.; Jenkins, N.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons, Ltd.: Chichester West Sussex, UK, 2011; ISBN 0-471-48997-2. [Google Scholar]
- Blackmore, T.; Batten, W.M.J.; Bahaj, A.S. Influence of turbulence on the wake of a marine current turbine simulator. Proc. R. Soc. A-Math. Phys. 2014, 470, 20140331. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, T.P.; Turnock, S.R.; Humphrey, V.F. Assessing the influence of inflow turbulence on noise and performance of a tidal turbine using large eddy simulations. Renew. Energy 2014, 71, 742–754. [Google Scholar] [CrossRef]
- Smirnov, A.; Shi, S.; Celic, I. Random flow generation technique for Large eddy simulations and particle-dynamics modeling. J. Fluids Eng. 2001, 123, 359–371. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Porté-Agel, F. Turbulent Flow Inside and Above a Wind Farm: A Wind-Tunnel Study. Energies 2011, 4, 1916–1936. [Google Scholar] [CrossRef]
- Markfort, C.D.; Zhang, W.; Porté-Agel, F. Turbulent flow and scalar transport through and over aligned and staggered wind farms. J. Turbul. 2012, 13. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porté-Agel, F. Simulation of Turbulent Flow Inside and Above Wind Farms: Model Validation and Layout Effects. Bound.-Layer Meteorol. 2013, 146, 181–205. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Stallard, T.; Collings, R.; Feng, T.; Whelan, J. Interactions between tidal turbine wakes: Experimental study of a group of three-bladed rotors. Philos. Trans. R. Soc. A 2013, 371, 20120159. [Google Scholar] [CrossRef]
- Frost, C.H.; Evans, P.S.; Harrold, M.J.; Mason-Jones, A.; O’Doherty, T.; O’Doherty, D.M. The impact of axial flow misalignment on a tidal turbine. Renew. Energy 2017, 113, 1333–1344. [Google Scholar] [CrossRef]
- Hill, C.; Musa, M.; Guala, M. Interaction between instream axial flow hydrokinetic turbines and uni-directional flow bedforms. Renew. Energy 2016, 86, 409–421. [Google Scholar] [CrossRef]
- Musa, M.; Hill, C.; Sotiropoulos, F.; Guala, M. Performance and resilience of hydrokinetic turbine arrays under large migrating fluvial bedforms. Nat. Energy 2018, 3, 839–846. [Google Scholar] [CrossRef]
- Simón-Moral, A.; Santiago, J.L.; Krayenhoff, E.S.; Martilli, A. Streamwise Versus Spanwise Spacing of Obstacle Arrays: Parametrization of the Effects on Drag and Turbulence. Bound.-Layer Meteorol. 2014, 151, 579–596. [Google Scholar] [CrossRef]
- Sørensen, J.N.; Shen, W.Z.; Munduate, X. Analysis of wake states by a full-field actuator disc model. Wind Energy 1998, 1, 73–88. [Google Scholar] [CrossRef]
- Mikkelsen, R.F. Actuator Disc Methods Applied to Wind Turbines. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 2004. [Google Scholar]
- Chen, Y.; Lin, B.; Lin, J.; Wang, S. Experimental study of wake structure behind a horizontal axis tidal stream turbine. Appl. Energy 2017, 196, 82–96. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H.; Beardsley, R.C. An Unstructured Grid, Finite-Volume, Three-Dimensional, Primitive Equations Ocean Model: Application to Coastal Ocean and Estuaries. J. Atmos. Ocean. Technol. 2003, 20, 159–186. [Google Scholar] [CrossRef]



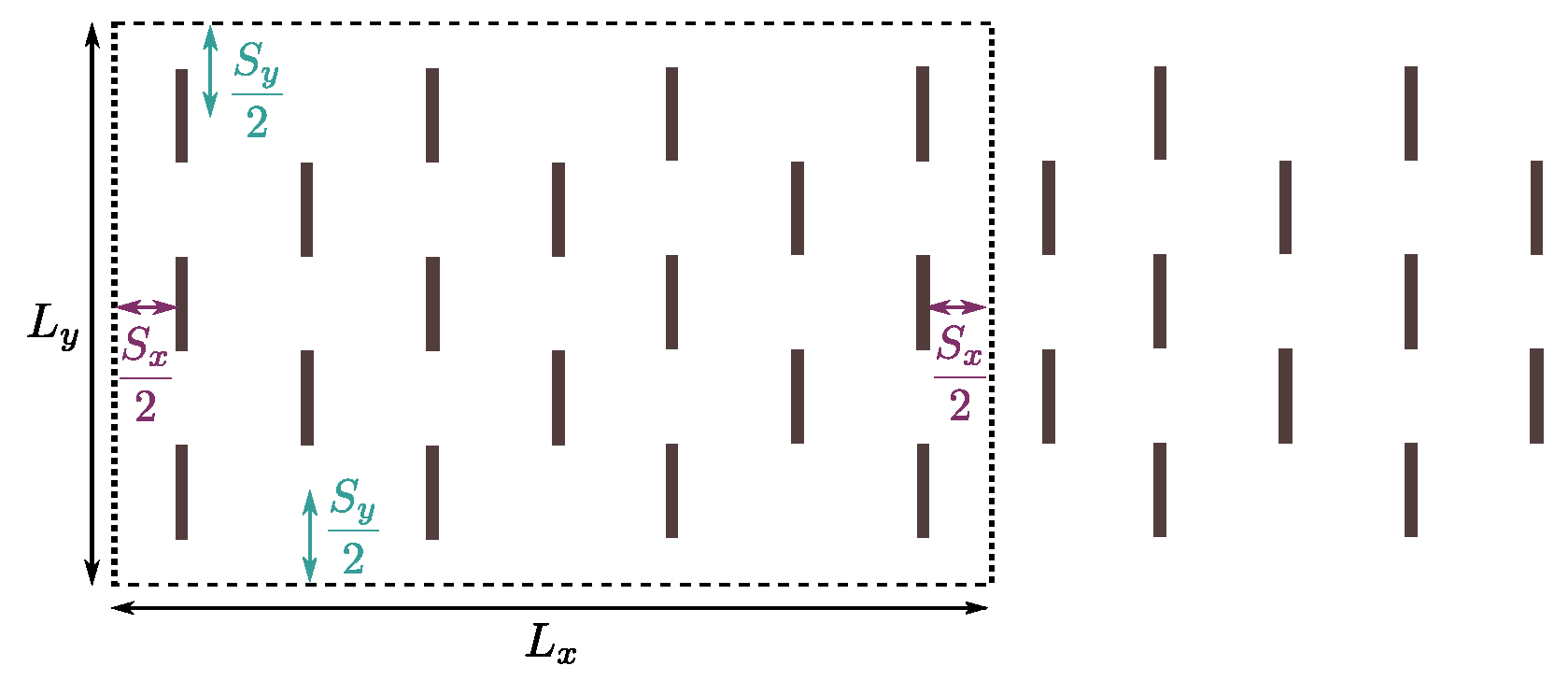



| Case | |||
|---|---|---|---|
| C.1 | 5 | 4 | 4.2 |
| C.2 | 7 | 4 | 4.2 |
| C.3 | 3 | 4 | 4.2 |
| C.4 | 5 | 2 | 4.2 |
| C.5 | 5 | 6 | 4.2 |
| C.6 | 5 | 4 | 3.3 |
| C.7 | 5 | 4 | 5.0 |
| Parameter | Value |
|---|---|
| Turbines diameter (D) | 10 m |
| Hub height () | 12 m |
| Thrust coefficient | 0.85 |
| Channel length () | 350 m |
| Channel width () | 240 m |
| Grid resolution () | 268 × 192 × 128 |
| Reynolds number based on the velocity at the hub () | |
| Lateral boundary conditions | Symmetric |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soto-Rivas, K.; Richter, D.; Escauriaza, C. A Formulation of the Thrust Coefficient for Representing Finite-Sized Farms of Tidal Energy Converters. Energies 2019, 12, 3861. https://doi.org/10.3390/en12203861
Soto-Rivas K, Richter D, Escauriaza C. A Formulation of the Thrust Coefficient for Representing Finite-Sized Farms of Tidal Energy Converters. Energies. 2019; 12(20):3861. https://doi.org/10.3390/en12203861
Chicago/Turabian StyleSoto-Rivas, Karina, David Richter, and Cristian Escauriaza. 2019. "A Formulation of the Thrust Coefficient for Representing Finite-Sized Farms of Tidal Energy Converters" Energies 12, no. 20: 3861. https://doi.org/10.3390/en12203861
APA StyleSoto-Rivas, K., Richter, D., & Escauriaza, C. (2019). A Formulation of the Thrust Coefficient for Representing Finite-Sized Farms of Tidal Energy Converters. Energies, 12(20), 3861. https://doi.org/10.3390/en12203861





