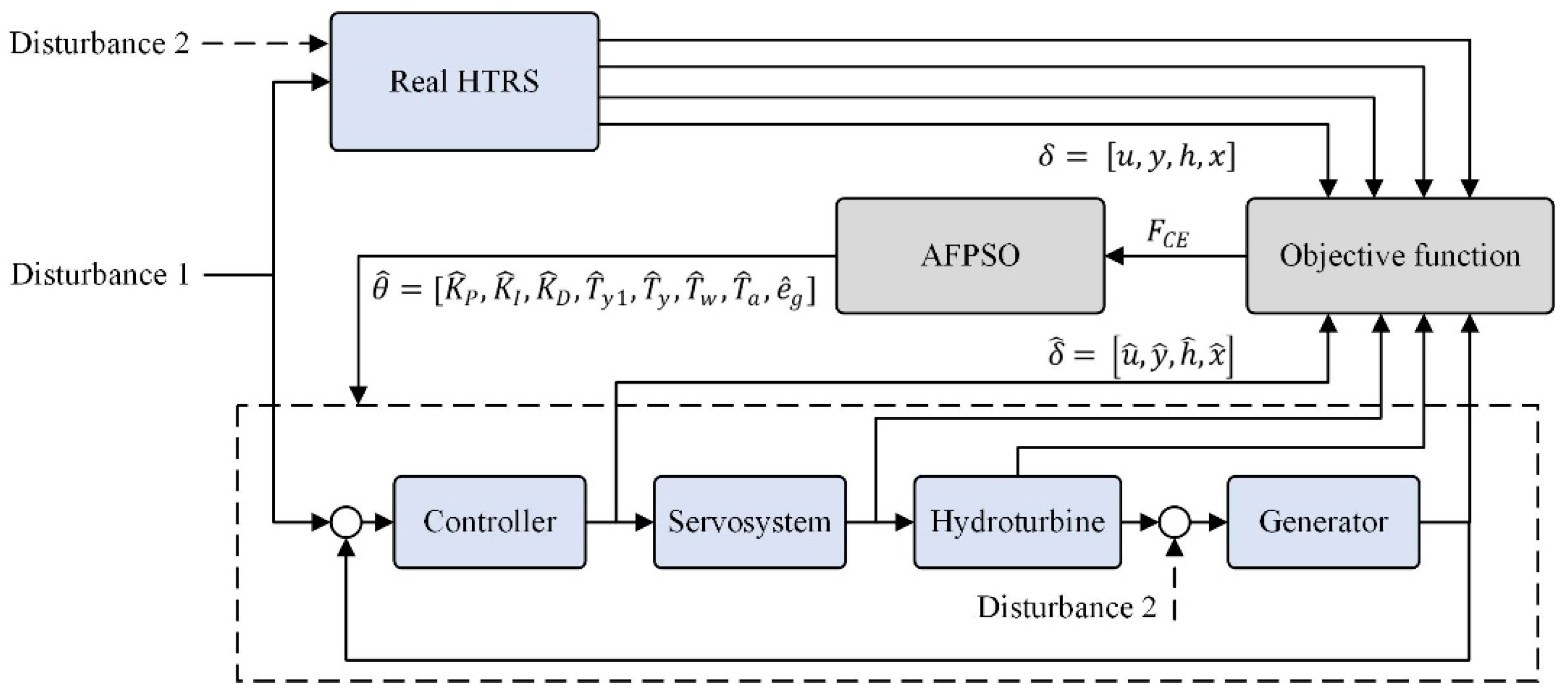
5.1. Test Conditions and Algorithm Parameters
The main research content in this paper is the parameter estimation of the HTRS in frequency control mode. The measured data comes from the step disturbance response of the unit under no-load conditions and load conditions, and the corresponding water head is 195 m. The known parameters are as follows. The differential time constant of the controller is 0.1175 (i.e.,
). The servo system has a delay of 0.1 s (i.e.,
), and the allowable range of the GVO is [0, 100%] (i.e.,
). The opening speed and closing speed of the guide vane are set as below: (1) the opening speed limit
; (2) the first-stage closing speed limit
if
; (3) the second-stage closing speed limit
sc2 = 26.5392 if
; (4) the third-stage closing speed limit
if
. For no-load and load conditions, the parameters of the controller and the hydro-turbine are different and determined by the GVO and the water head. The maximum output of the controller is 0.25 (i.e.,
) under the no-load condition, while it is not limited under the load condition. Detailed parameters of the HTRS under the two operating conditions are given in
Table 1.
The evolutionary computation methods used for the comparative experiments include standard genetic algorithm (SGA) [
49], gravitational search algorithm (GSA) [
50], biogeography-based optimization (BBO) [
51], and particle swarm optimization (PSO) [
52]. The parameter settings of each algorithm for solving the parameter estimation issue are shown in
Table 2 [
18,
53]. No parameter setting is required for AFPSO, and the size of the neighborhood increases linearly from 2 to the allowable maximum value. To ensure fairness, the population size is 30 and the iterations are 200.
5.2. Parameter Estimation under No-Load Condition
The actual values and initial range of the parameters to be identified under the no-load condition are listed in
Table 3. The step disturbance of frequency, used as the excitation of the real HTRS, is applied to the nonlinear simulation model (see disturbance 1 in
Figure 7). The disturbance quantity is set as −4 Hz (that is, the frequency suddenly decreases by 8% based on the rated value of 50 Hz). The parameter settings of the algorithms are the same as those of
Table 2. For each algorithm, 30 repeated tests are performed. The statistical results, including the average estimated value and the corresponding PE, the optimal fitness, as well as the average fitness change, are shown in
Table 4 and
Table 5, and
Figure 8, respectively.
It can be seen from
Table 4 that the estimated value of each parameter obtained by AFPSO is closest to the actual value, and the corresponding PE is also the smallest. AFPSO has a high identification accuracy that reaches to the level of 10
−5 for the parameters
and
, indicating that the two parameters are easy to be identified under the no-load condition. Analysis of the optimization results of the other algorithms can also lead to the same conclusion. Comparing the results of all the algorithms, it can be seen that the identification accuracy of the parameters
and
is relatively low, indicating that the state of the system is not sensitive enough to the changes of the two parameters.
It can be seen from
Table 5 that the maximum, average and minimum values of the optimal fitness (or objective function value) obtained by AFPSO are both better than with the other algorithms. Under the no-load condition, the average and maximum optimal fitness of GSA is the worst performing, while SGA and BBO have similar optimal fitness statistics (or solving ability). In the repeated tests, the minimum optimal fitness of AFPSO reaches 4.98 × 10
−9, that is, far smaller than the other algorithms, which illustrates AFPSO having a powerful local search ability and fast convergence to realize an accurate identification for HTRS under the no-load condition. It is seen from
Figure 8 that AFPSO keeps fast convergence after around 20 iterations and successfully jumps out of the local optimum. On the contrary, GSA has the slowest convergence and falls into the local optimum for a long time. Although PSO shows a rapid convergence in early iterations, it suffers from the same problem of premature convergence as GSA.
Under the no-load condition, comparison of the simulated output obtained by different algorithms with that of the real system is plotted in
Figure 9. There is an obvious two-stage closing law for the GVO during the change in the first 5 s, reflecting the nonlinear characteristic of the servo-system. From the overall trend of the curves, the simulated outputs obtained by GSA and PSO are quite different from that of the real system. Locally amplifying the transient process of each state variable (12–13 s), it can be clearly seen that the simulated output obtained by AFPSO can optimally approximate the dynamic characteristics of the real system. The parameter estimation effect of the algorithms can be sorted based on the observation of the local variation of the water head. The sorting results from good to bad according to performance is AFPSO, SGA, BBO, PSO and GSA, which is consistent with the results in
Figure 8.
5.3. Parameter Estimation under Load Condition
The actual value and initial range of the parameters to be identified under the load condition are shown in
Table 6 in which the control parameters are different from that of the no-load condition. The step disturbance of load, used as the excitation of the real HTRS, is applied to the established nonlinear simulation model (see disturbance 2 of
Figure 7). The disturbance quantity is set as −0.1 (that is, the load suddenly decreases by 10% based on the initial value of 600 MW). All parameter settings and test methods are the same as that of the no-load condition. The statistical results, including the average estimated value and the corresponding PE, the optimal fitness, as well as the average fitness change, are shown in
Table 7 and
Table 8, and
Figure 10, respectively.
As can be seen from
Table 7, the estimated value of each parameter calculated by AFPSO is closest to the actual value, and the corresponding PE is also the smallest. AFPSO has a high identification accuracy of 10
−5 for the parameters
and
, indicating they are easy to accurately estimate under the no-load condition. Comparing all the optimization results, the same conclusion as under the no-load condition can be drawn that the identification accuracy of the parameter
is always the lowest, revealing that the state of the system is not sensitive to the changes of the parameter
under both no-load and load conditions.
The results from
Table 8 show that the maximum, average and minimum values of the optimal fitness obtained by AFPSO are superior to the other algorithms. Under the load condition, the average optimal fitness of SGA is the worst performing, while that of GSA and PSO are similar to each other. In the repeated experiments, the minimum optimal fitness of AFPSO reaches 4.59 × 10
−9, that is, far smaller than the other algorithms, which indicates that the algorithm is indeed a promising tool for accurate parameter estimation of HTRS. The curves in
Figure 10 explain that AFPSO continuously maintains a fast convergence throughout iteration and effectively avoids the danger of falling into a local optimum. As the iteration increases, the convergence of SGA, BBO and PSO gradually becomes slow, affecting the final identification accuracy. Although the GSA converges faster in the late iteration, it wastes a large amount of computation time in the early stage, which means it is difficult to meet the requirements of the actual optimization problem.
Under the load condition, comparison of the simulated output obtained by different algorithms with that of the real system is plotted in
Figure 11. In the transition process, the movement law of the GVO is not restricted by the nonlinear factors. From the overall trend of the curves, the simulated output obtained by SGA and BBO is quite different from the real system. By locally amplifying the transient process of each state variable (12–12.01 s), it can be clearly seen that the simulated system obtained by AFPSO is the closest to the real system, indicating that it can completely replace the real system to conduct various experiments. It should be pointed out that the simulation models obtained by the other algorithms have the distinguishing approximation degree for different state variables. For example, the model determined by BBO simulates the change of the GVO better than that of PSO, while the model obtained by PSO can simulate the change of controller output (i.e.,
) better than that of BBO.
Comparing the results in
Figure 8 and
Figure 10, it can be found that the convergence of AFPSO in both load and no-load conditions manifests an algebraic decay (more or less), but the PSO in the no-load condition decays to an almost flat trend while it is not so in the load condition. This interesting phenomenon could be explained from the perspective of servo-system. It can be seen from the results of parameter estimation in
Table 4 and
Table 7 that the estimation accuracy of
is the worst in the two operating conditions. However, comparatively speaking, the estimation accuracy of
under the load operating condition is better than that of the no-load operating condition. On the one hand, the dynamic behavior of the HTRS is less affected by
compared with other parameters. So the algorithms used are not sensitive to the change near the actual value of
, which is the main reason why
is difficult to identify. On the other hand, the speed limit nonlinearity plays an important role in the transition process under the no-load operating condition, which can be obviously observed in
Figure 9. The nonlinearity further increases the difficulty for the estimation of
. In this situation, the change of
cannot determine the output of the servo-system. For the proposed AFPSO, the convergence can always keep an algebraic decay because of its global and local search ability throughout the iteration, while for PSO it is greatly affected by the complexity of a problem. Therefore, based on the above analysis, it can be concluded that in order to accurately identify the parameters of a system, one should make the best use of the experimental data that do not or less trigger the dynamic characteristics of nonlinear links.
Finally, the computational expense of different algorithms under the two operating conditions is compared and the results are listed in
Table 9. It can be seen from the table that SGA has the least computational expense while PSO has the most computational expense under both no-load and load operating conditions. Meanwhile, it is noticed that the mean time consumption of 30 repeated parameter estimation tests under the no-load operating condition is less than that under the load operating condition. This indicates that the former situation requires more computation than the latter in model simulation. Although the proposed AFPSO is not the best one in computational expense under the two operating conditions, it is superior to the PSO, GSA and BBO in both efficiency and accuracy, which indicates that the design of the algorithm is not at the cost of computational efficiency, but an overall improvement for the algorithm.