Mechanistic Characteristics of Double Dominant Frequencies of Acoustic Emission Signals in the Entire Fracture Process of Fine Sandstone
Abstract
:1. Introduction
2. Test and Data Processing
2.1. Outline of the Test
2.2. Basic Characteristic Mechanical Parameters of Specimens
2.3. Data Processing
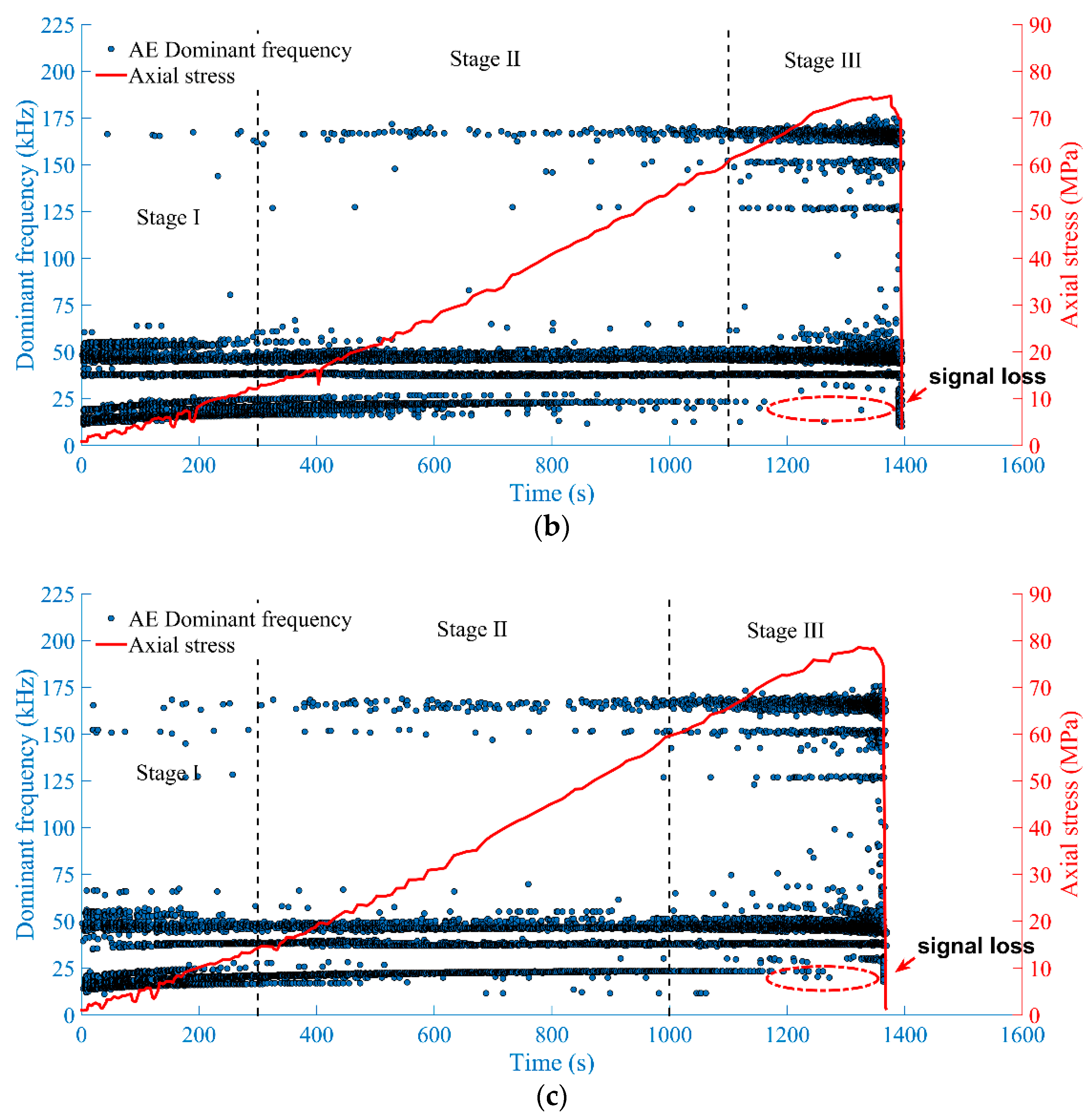
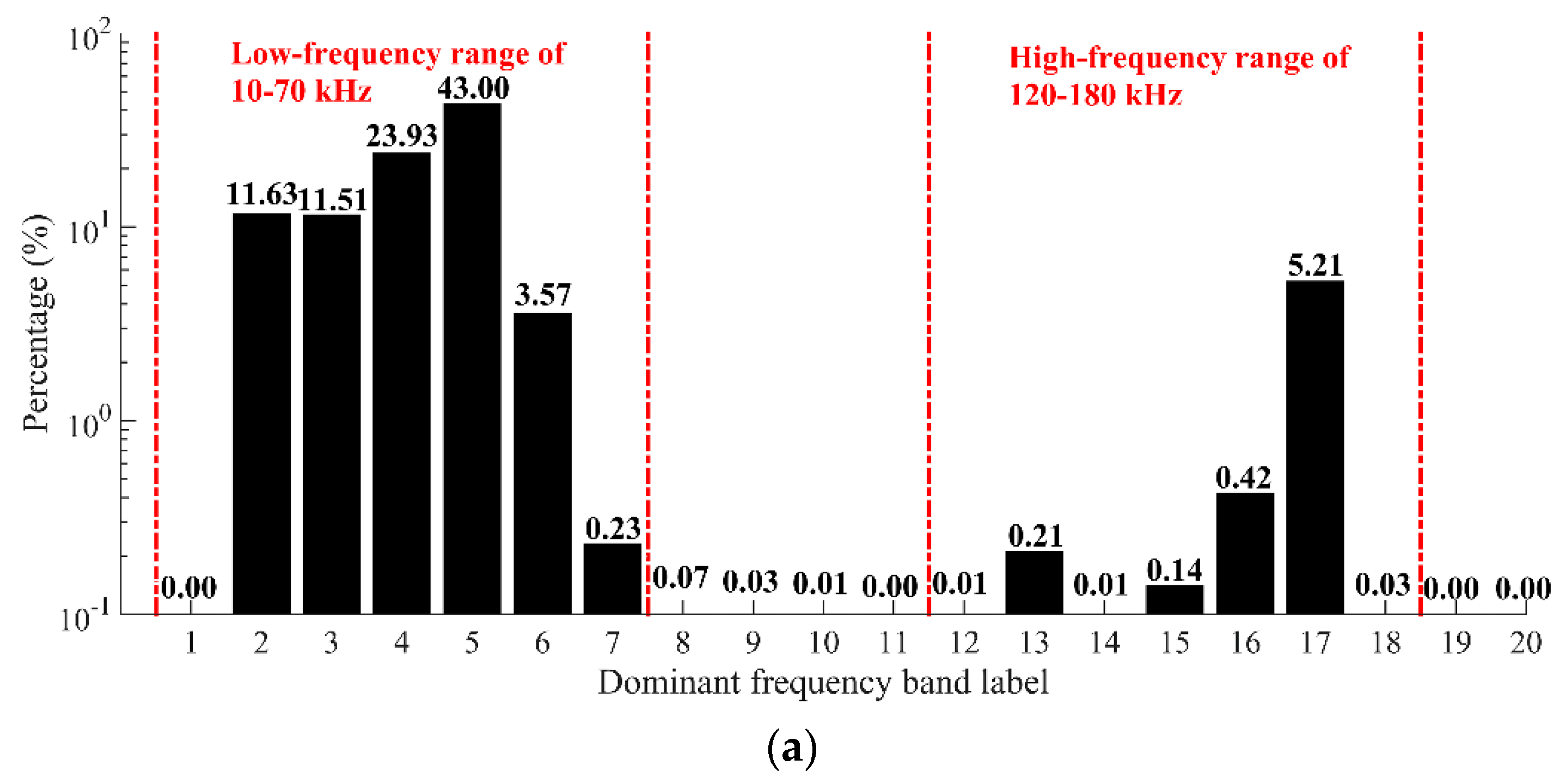
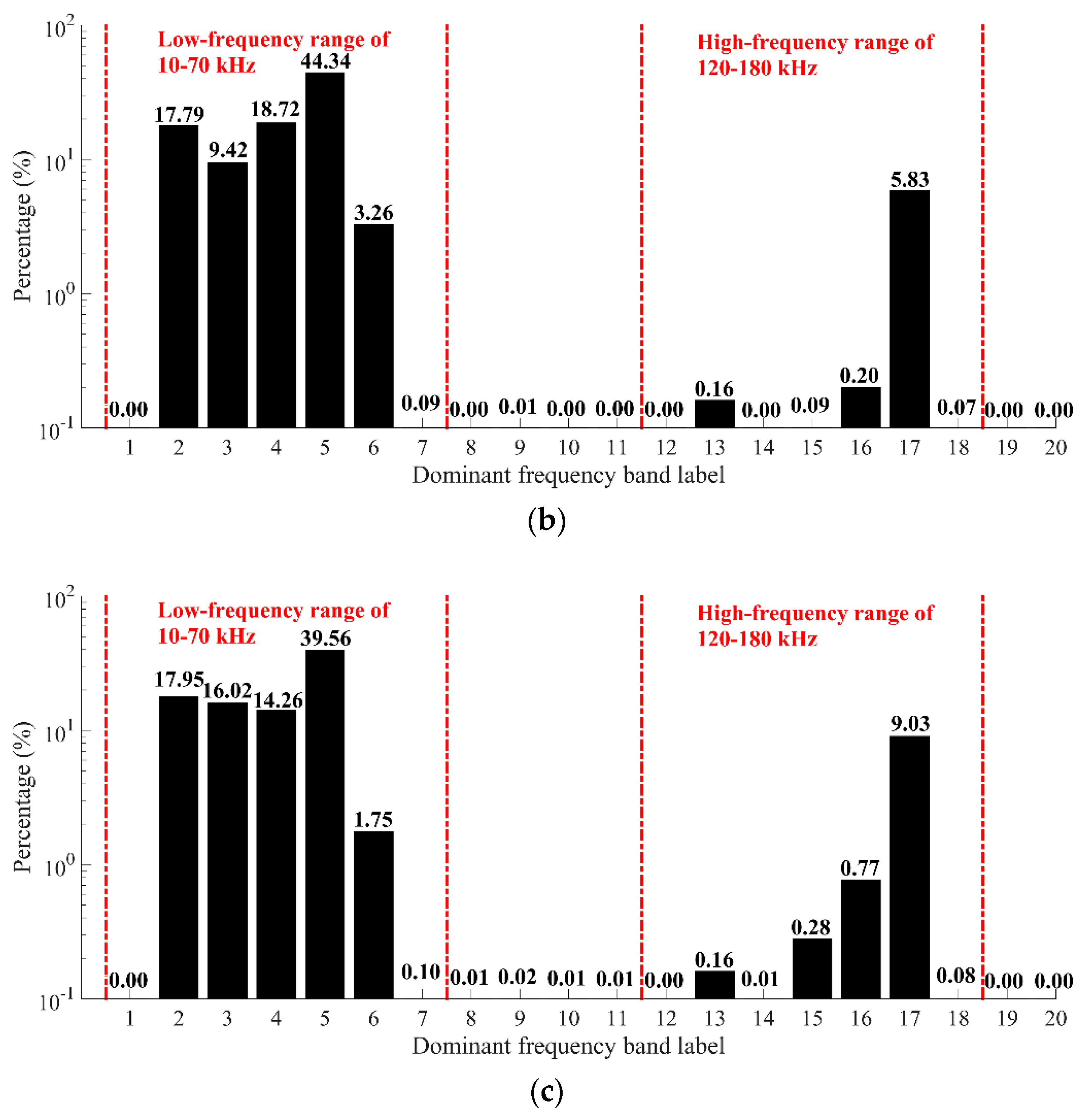
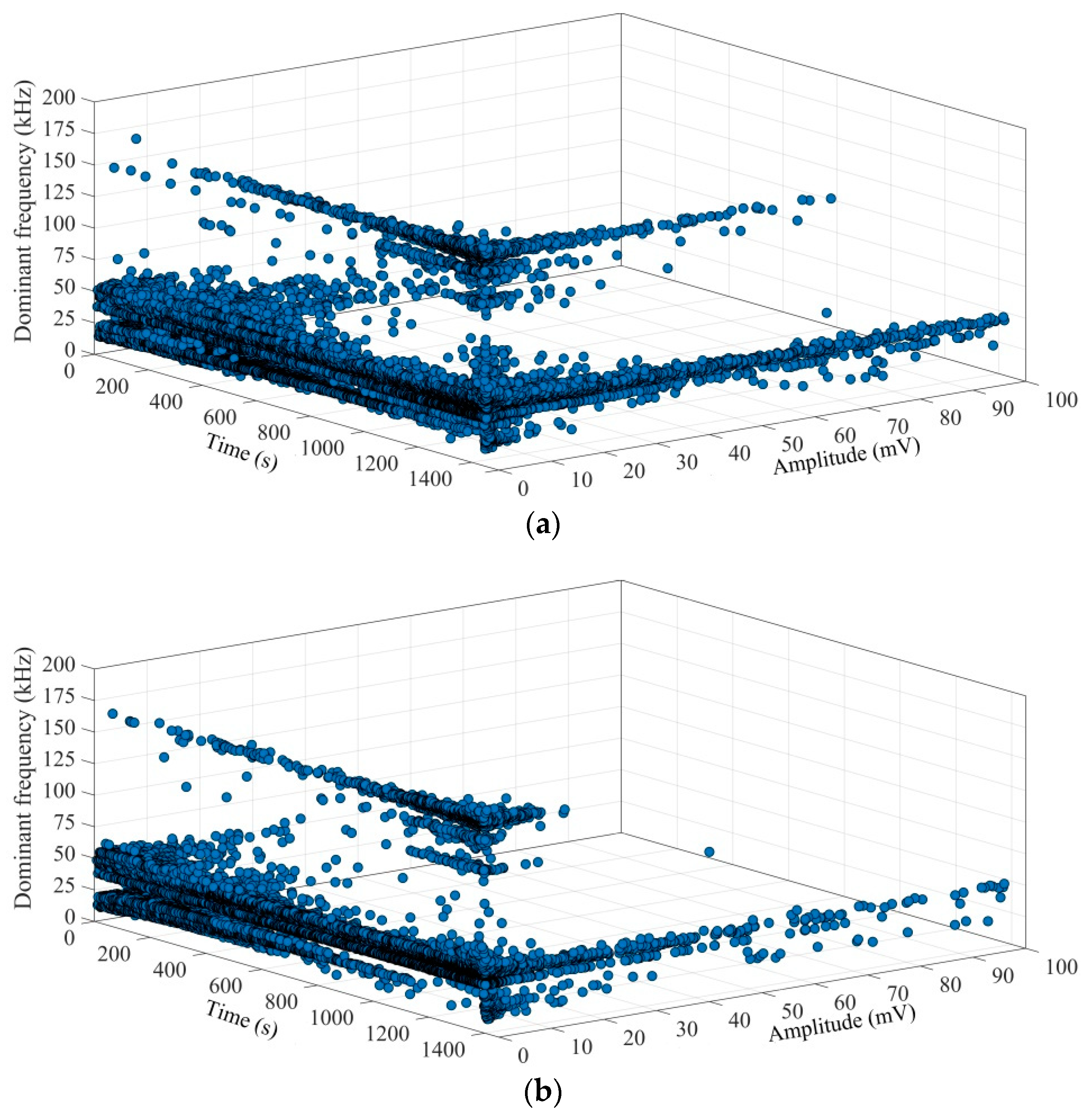
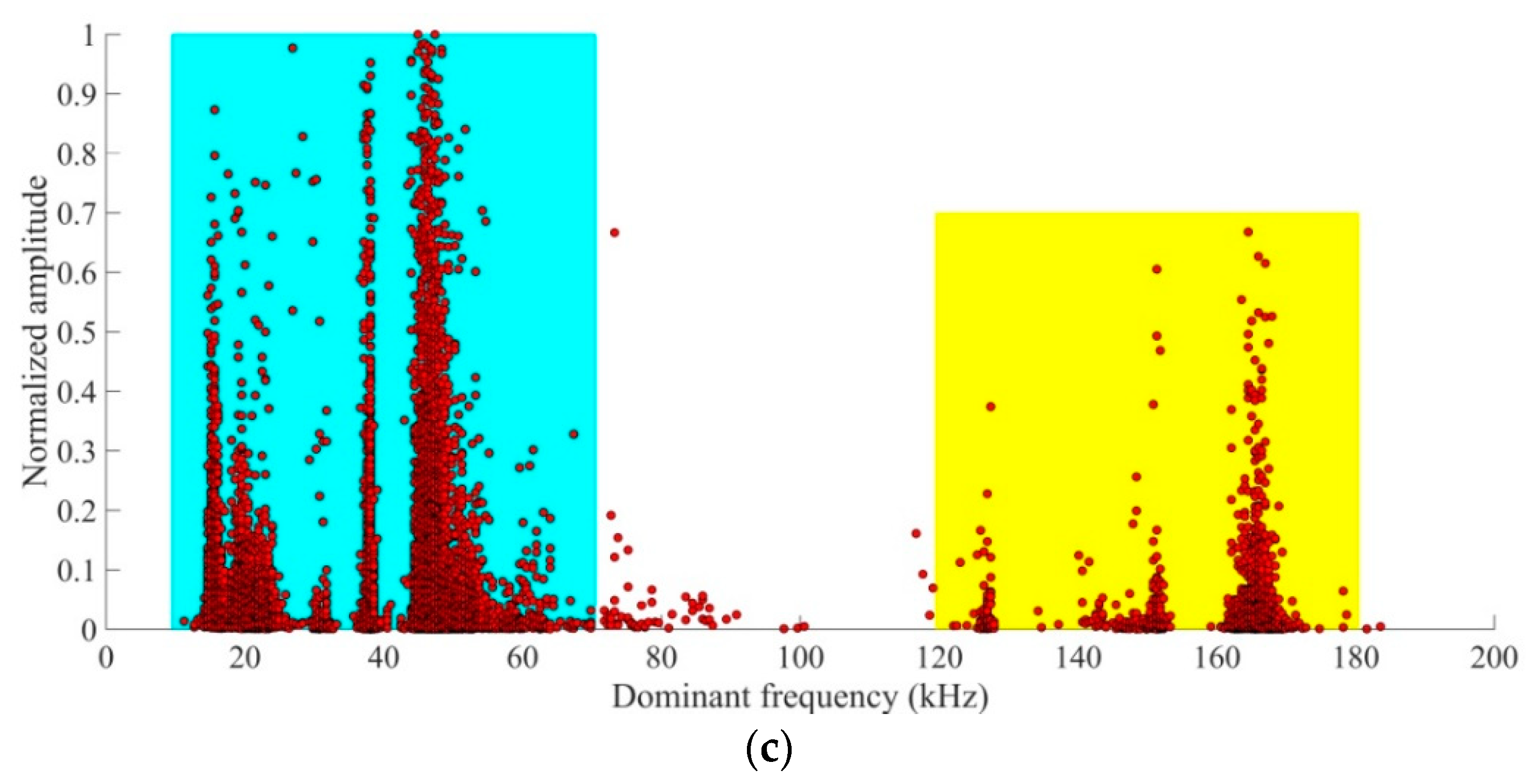
3. Analysis of the Dominant Frequency Characteristics of AE Signals
4. Analysis of AE Signal Amplitude and Fractal Characteristics
4.1. Characteristics of AE Signal Amplitude
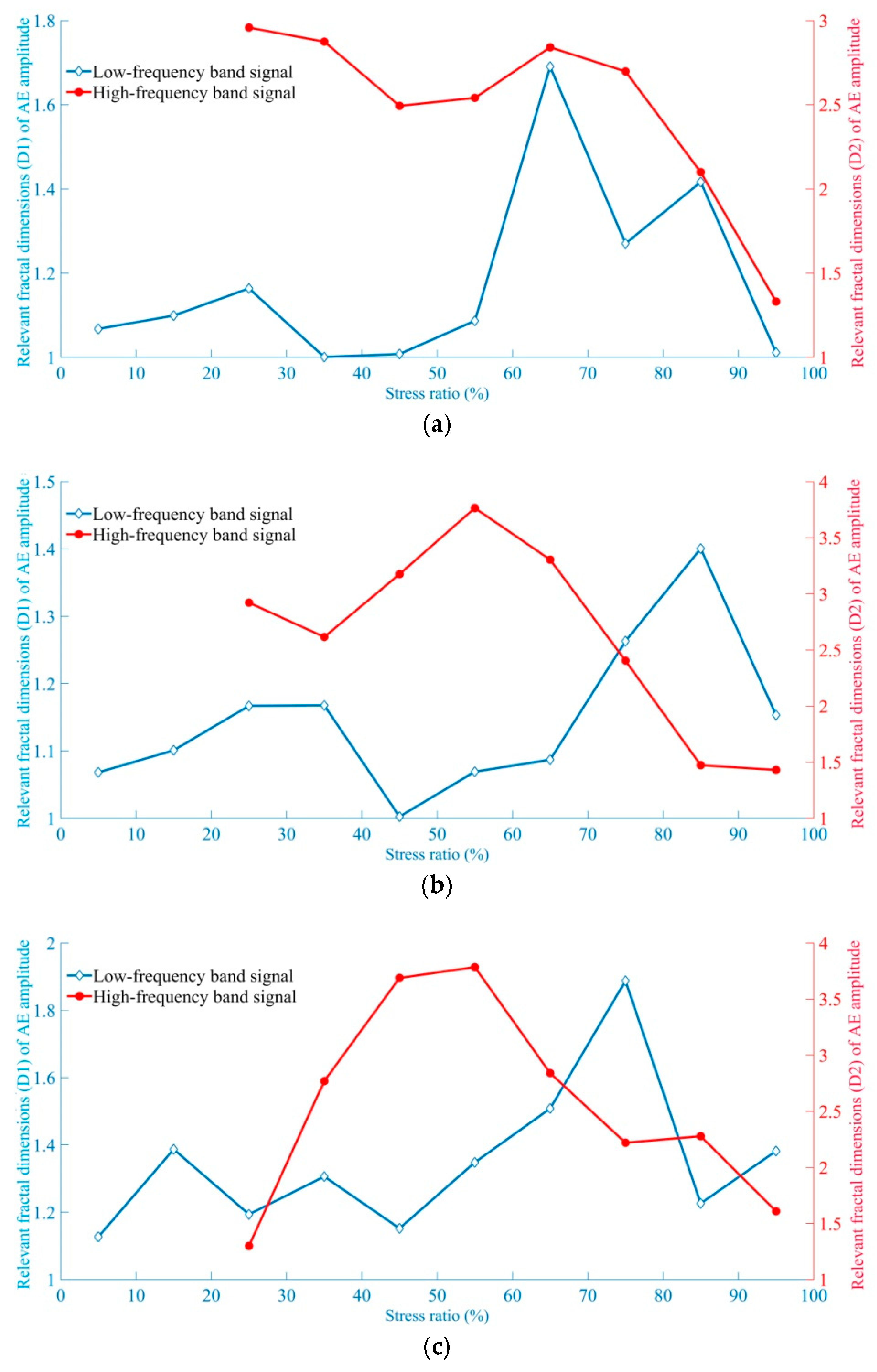
4.2. Fractal Characteristics of AE Signal Amplitude
5. Analysis of the Energy Ratio of Each AE Signal
5.1. Full Time-Domain Analysis
5.2. Wavelet Packet Band Decomposition
5.3. Method to Calculate Wavelength Packet Reconstruction Signal Band Energy
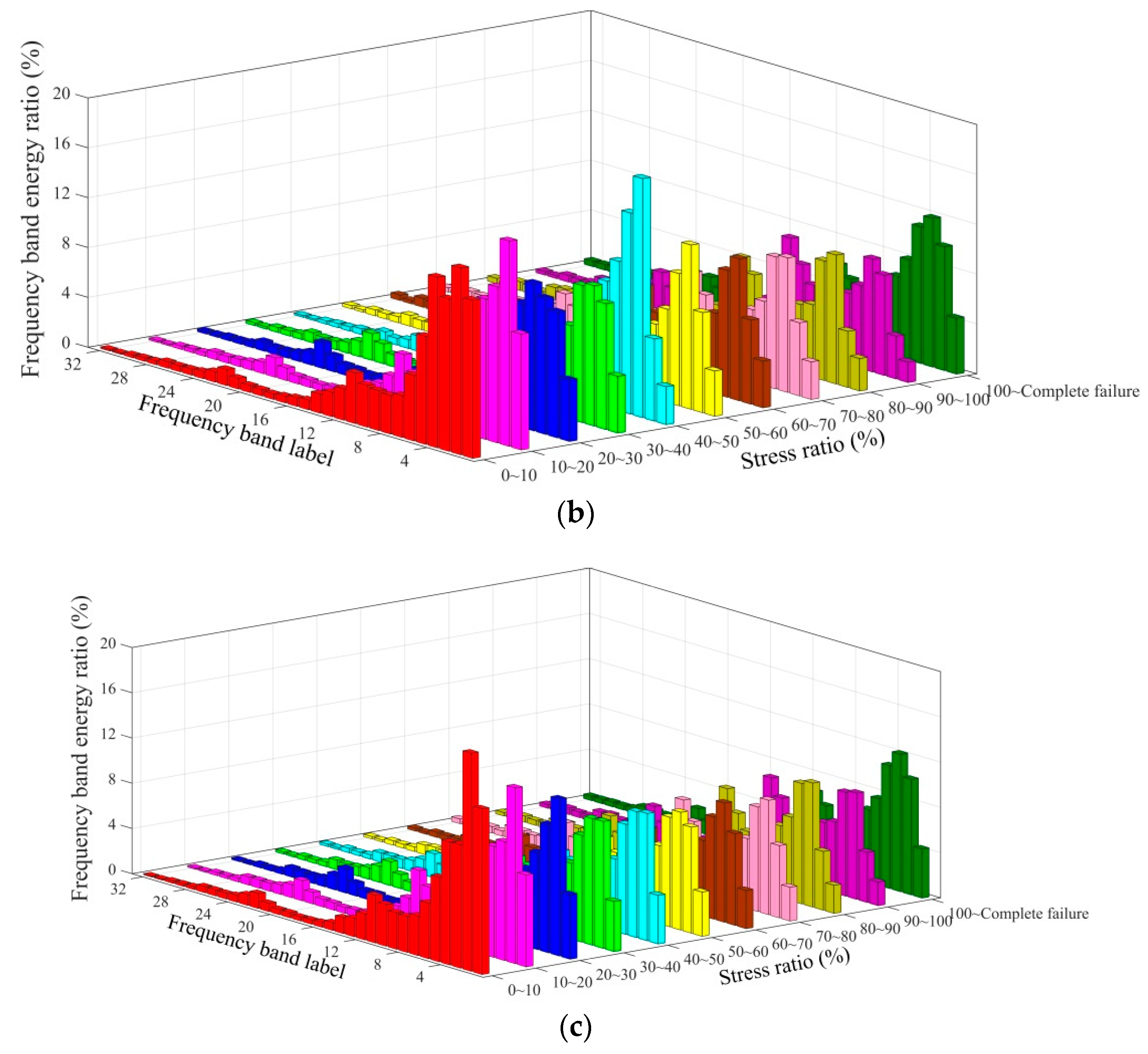
5.4. Energy Variation Pattern for AE Signal Bands
6. Conclusions
- (1)
- The AE signal during the entire fracture process of fine sandstone exhibited double dominant frequency bands. The low-frequency bands were concentrated at 10–70 kHz, the high-frequency bands were concentrated at 120–180 kHz, and the number of AE signals in the low-frequency bands was significantly higher than that in the high-frequency bands.
- (2)
- Combining the AE signal amplitude, the AE signals can be further subdivided into four types: low-frequency low-amplitude, low-frequency high-amplitude, high-frequency low-amplitude, and high-frequency high-amplitude signals. Different types of AE signals correspond to different types of fractures in rock.
- (3)
- For AE signal amplitude, the relevant fractal dimension D1 of the low-frequency band was generally lower than the relevant fractal dimension D2 of the high frequency band. Both D1 and D2 had a significant turning point involving a decrease in magnitude. Before the stress ratio reached 50%, D1 fluctuated considerably; however, the trend can still be seen as one involving, first, an increase in the fractal dimension, and then a subsequent decrease. D2 increased in the early stage, and after the stress ratio reached 50%, D2 continued to decrease.
- (4)
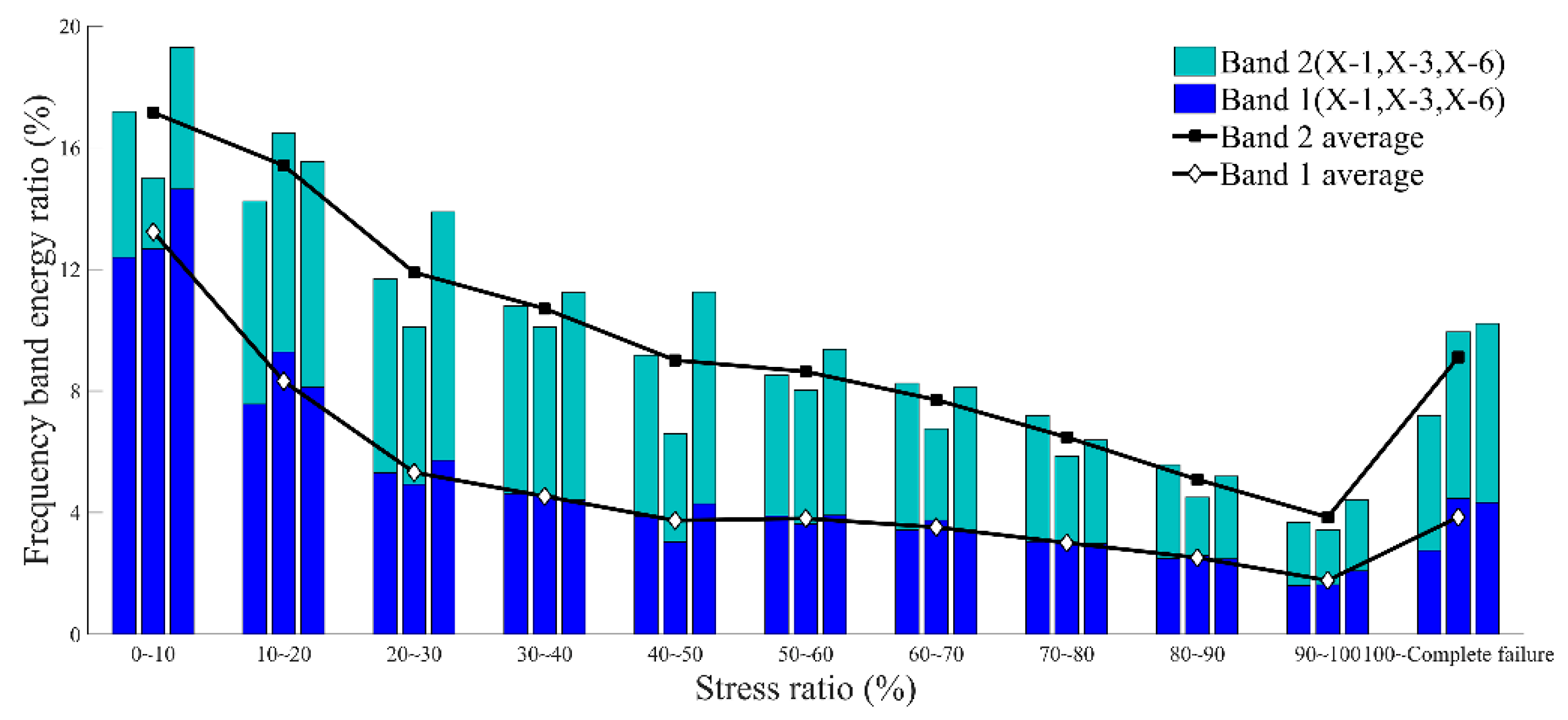
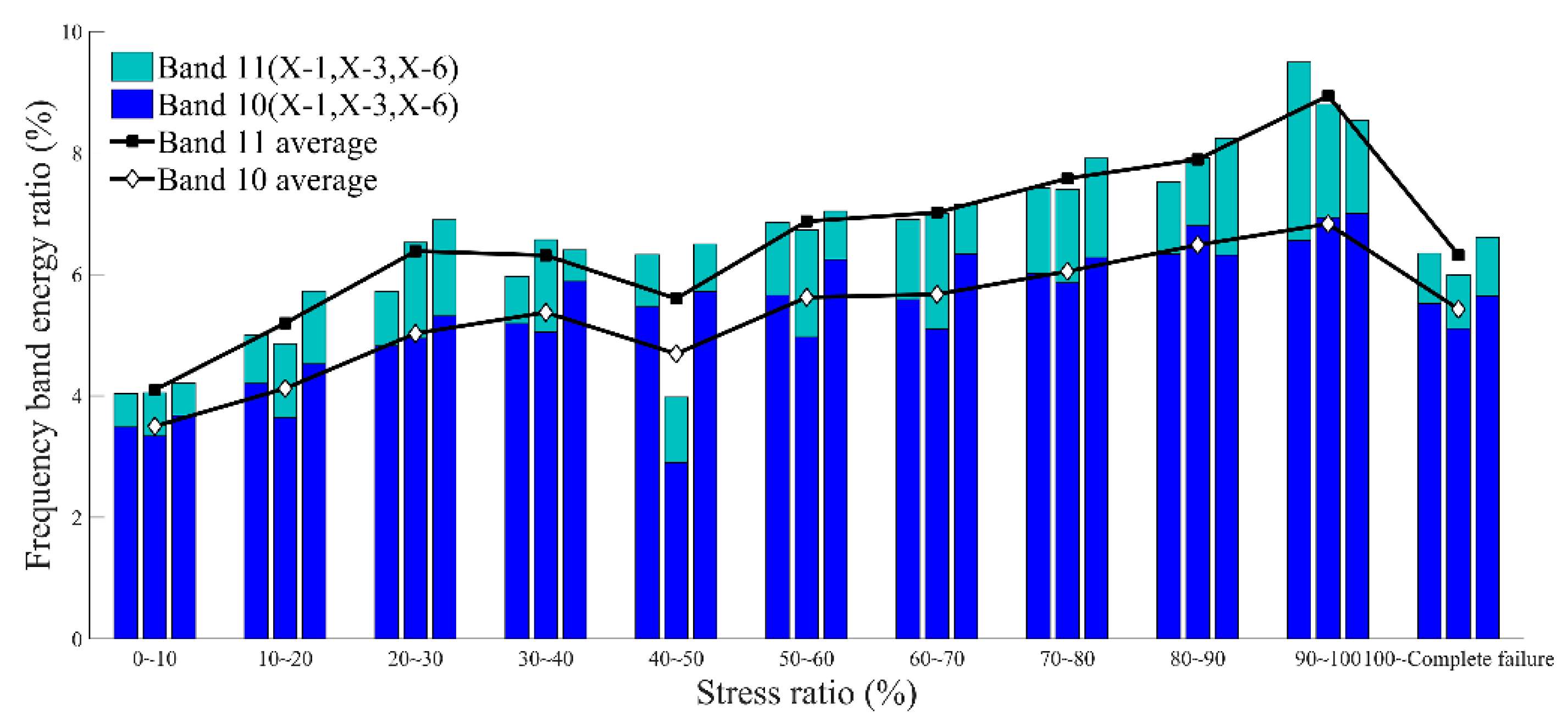
- The band energy of the AE signal in the fine sandstone was concentrated mainly in the range of 0–187.5 kHz (bands 1–12) in different failure stages, and the sum of average energy ratios was up to 79%. However, even in different stress ratio intervals, the energy ratio of each band did not exceed 20%. The energy ratios of bands 1 and 2 in the low-frequency band as well as those of bands 10 and 11 in the high-frequency band varied significantly with the stress ratio. Bands 1 and 2 exhibited the trend of first decreasing and later increasing, exhibiting the minimum value at a stress ratio of 90–100%; bands 10 and 11 exhibited the trend of first increasing and later decreasing, exhibiting the maximum value at a stress ratio of 90–100%.
Author Contributions
Funding
Conflicts of Interest
References
- Scruby, B.C. An introduction to acoustic emission. J. Phys. E. 1987, 20, 946–953. [Google Scholar] [CrossRef]
- Ji, H.G. Research and Application on Acoustic Emission Performance of Concrete Material; China Coal Industry Publishing House: Beijing, China, 2004; pp. 1–2. [Google Scholar]
- Lavrov, A. The Kaiser effect in rocks: Principles and stress estimation techniques. Int. J. Rock Mech. Min. 2003, 40, 151–171. [Google Scholar] [CrossRef]
- Liu, J.P.; Li, Y.H.; Xu, S.D.; Xu, S.; Jin, C.Y.; Liu, Z.S. Moment tensor analysis of acoustic emission for cracking mechanisms in rock with a pre-cut circular hole under uniaxial compression. Eng. Fract. Mech. 2015, 135, 206–218. [Google Scholar] [CrossRef]
- Li, L.R.; Deng, J.H.; Zheng, L.; Liu, J.F. Dominant frequency characteristics of acoustic emissions in white marble during direct tensile tests. Rock Mech. Rock Eng. 2017, 50, 1337–1346. [Google Scholar] [CrossRef]
- Sondergeld, C.H.; Estey, L.H. Acoustic emission study of microfracturing during the cyclic loading of Westerly granite. J. Geophys. Res. 1981, 86, 2915–2924. [Google Scholar] [CrossRef]
- Cai, M.; Morioka, H.; Kaiser, P.K.; Tasaka, Y.; Kurose, H.; Minami, M.; Maejima, T. Back-analysis of rock mass strength parameters using AE monitoring data. Int. J. Rock Mech. Min. 2007, 44, 538–549. [Google Scholar] [CrossRef]
- Du, F.; Wang, K.; Wang, G.D.; Jiang, Y.F.; Xin, C.P.; Zhang, X. Investigation on acoustic emission characteristics during deformation and failure of gas-bearing coal-rock combined bodies. J. Loss Prev. Process Ind. 2018, 55, 253–266. [Google Scholar] [CrossRef]
- Farahat, A.M.; Ohtsu, M. Evaluation of plastic damage in concrete by acoustic emission. J. Mater. Civ. Eng. 1995, 7, 148–153. [Google Scholar] [CrossRef]
- Bagde, M.N.; Petros, V. Fatigue and dynamic energy behaviour of rock subjected to cyclical loading. Int. J. Rock Mech. Min. 2009, 46, 200–209. [Google Scholar] [CrossRef]
- Moradian, Z.; Einstein, H.H.; Ballivy, G. Detection of cracking levels in brittle rocks by parametric analysis of the acoustic emission signals. Rock Mech. Rock Eng. 2016, 49, 785–800. [Google Scholar] [CrossRef]
- Shiotani, T.; Ohtsu, M.; Ikeda, K. Detection and evaluation of AE waves due to rock deformation. Constr. Build. Mater. 2001, 15, 235–246. [Google Scholar] [CrossRef]
- Stefano, D.S.; Adrienn, K.T. Laboratory and field studies on the use of acoustic emission for masonry bridges. NDT E Int. 2013, 55, 64–74. [Google Scholar]
- Aker, E.; Kuhn, D.; Vavrycuk, V.; Soldal, M.; Oye, V. Experimental investigation of acoustic emissions and their moment tensors in rock during failure. Int. J. Rock Mech. Min. 2014, 70, 286–295. [Google Scholar] [CrossRef]
- He, M.C.; Zhao, F.; Zhang, Y.; Du, S.; Guan, L. Feature evolution of dominant frequency components in acoustic emissions of instantaneous strain-type granitic rockburst simulation tests. Rock Soil Mech. 2015, 36, 1–8. [Google Scholar]
- Ji, H.G.; Wang, H.W.; Cao, S.Z.; Hou, Z.F.; Jin, Y. Experimental research on frequency characteristics of acoustic emission signals under uniaxial compression of granite. Chin. J. Rock Mech. Eng. 2012, 31, 2900–2905. [Google Scholar]
- Morgan, S.P.; Johnson, C.A.; Einstein, H.H. Cracking processes in Barre granite: Fracture process zones and crack coalescence. Int. J. Fract. 2013, 180, 177–204. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, G.F.; Wang, X.J.; Jin, J.F.; Deng, F. Research on energy distributions and fractal characteristics of Kaiser signal of acoustic emission in rock. Rock Soil Mech. 2008, 29, 3082–3088. [Google Scholar]
- Lai, Y.S.; Xiong, Y.; Cheng, L.F. Frequency band energy characteristics of acoustic emission signals in damage process of concrete under uniaxial compression. J. Vib. Shock 2014, 11, 177–182. [Google Scholar]
- Chen, S.W.; Yang, C.H.; Wang, G.B.; Liu, W. Similarity assessment of acoustic emission signals and its application in source localization. Ultrasonics 2017, 75, 36–45. [Google Scholar] [CrossRef]
- Cong, Y.; Feng, X.T.; Zheng, Y.R.; Wang, Z.Q.; Zhang, L.M. Experimental study on acoustic emission failure precursors of marble under different stress paths. Chin. J. Geotech. Eng. 2016, 38, 1193–1201. [Google Scholar]
- Deng, J.H.; Li, L.R.; Chen, F.; Liu, J.F.; Yu, J. Twin-peak Frequencies of Acoustic Emission Due to the Fracture of Marble and Their Possible Mechanism. Adv. Eng. Sci. 2018, 50, 12–17. [Google Scholar]
- Cai, M.; Kaiser, P.K.; Morioka, H.; Minami, M.; Maejima, T.; Tasaka, Y.; Kurose, H. FLAC/PFC coupled numerical simulation of AE in large-scale underground excavations. Int. J. Rock Mech. Min. 2007, 44, 550–564. [Google Scholar] [CrossRef]
- Zhu, Z.F.; Chen, G.Q.; Xiao, H.Y.; Liu, H.; Zhao, C. Study on crack propagation of rock bridge based on multi parameters analysis of acoustic emission. Chin. J. Rock Mech. Eng. 2018, 37, 909–918. [Google Scholar]
- Shen, B.T.; Stephansson, O.; Rinne, M. Modelling of Rock Fracturing Processes; CSIRO Earth Science and Resource Engineering: Brisbane, QLD, Australia, 2014; pp. 5–18. [Google Scholar]
- Zeng, P.; Liu, Y.J.; Ji, H.G.; Li, C.J. Coupling criteria and precursor identification characteristics of multi-band acoustic emission of gritstone fracture under uniaxial compression. Chin. J. Geotech. Eng. 2017, 39, 509–517. [Google Scholar]
- Chen, M.; Yang, S.Q.; Pathegama, G.R.; Yang, W.D.; Yin, P.F.; Zhang, Y.C.; Zhang, Q.Y. Fracture processes of rock-Like specimens containing nonpersistent fissures under uniaxial compression. Energies 2019, 12, 79. [Google Scholar] [CrossRef]
- Zhang, Z.B.; Wang, E.Y.; Li, N. Fractal characteristics of acoustic emission events based on single-link cluster method during uniaxial loading of rock. Chaos Solitons Fract. 2017, 104, 298–306. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Characterization of strange attractors. Phys. Rev. Lett. 1983, 50, 346–349. [Google Scholar] [CrossRef]
- Wu, X.Z.; Liu, X.X.; Liang, Z.Z.; Liu, X.; Yu, M. Experimental study of fractal dimension of acoustic emission serials different of different rocks under uniaxial compression. Rock Soil Mech. 2012, 33, 3561–3569. [Google Scholar]
- Ling, T.H.; Liao, Y.C.; Zhang, S. Application of wavelet packet method in frequency band energy distribution of rock acoustic emission signals under impact loading. J. Vib. Shock 2010, 10, 127–130. [Google Scholar]
- Chaparro, L. Signals and Systems Using MATLAB, 2nd ed.; Academic Press: Pittsburgh, PA, USA, 2015; pp. 333–396. [Google Scholar]
- Stormy, A. MATLAB: A Practical Introduction to Programming and Problem Solving, 4th ed.; Butterworth-Heinemann Elsevier Ltd.: Oxford, UK, 2017; pp. 443–501. [Google Scholar]

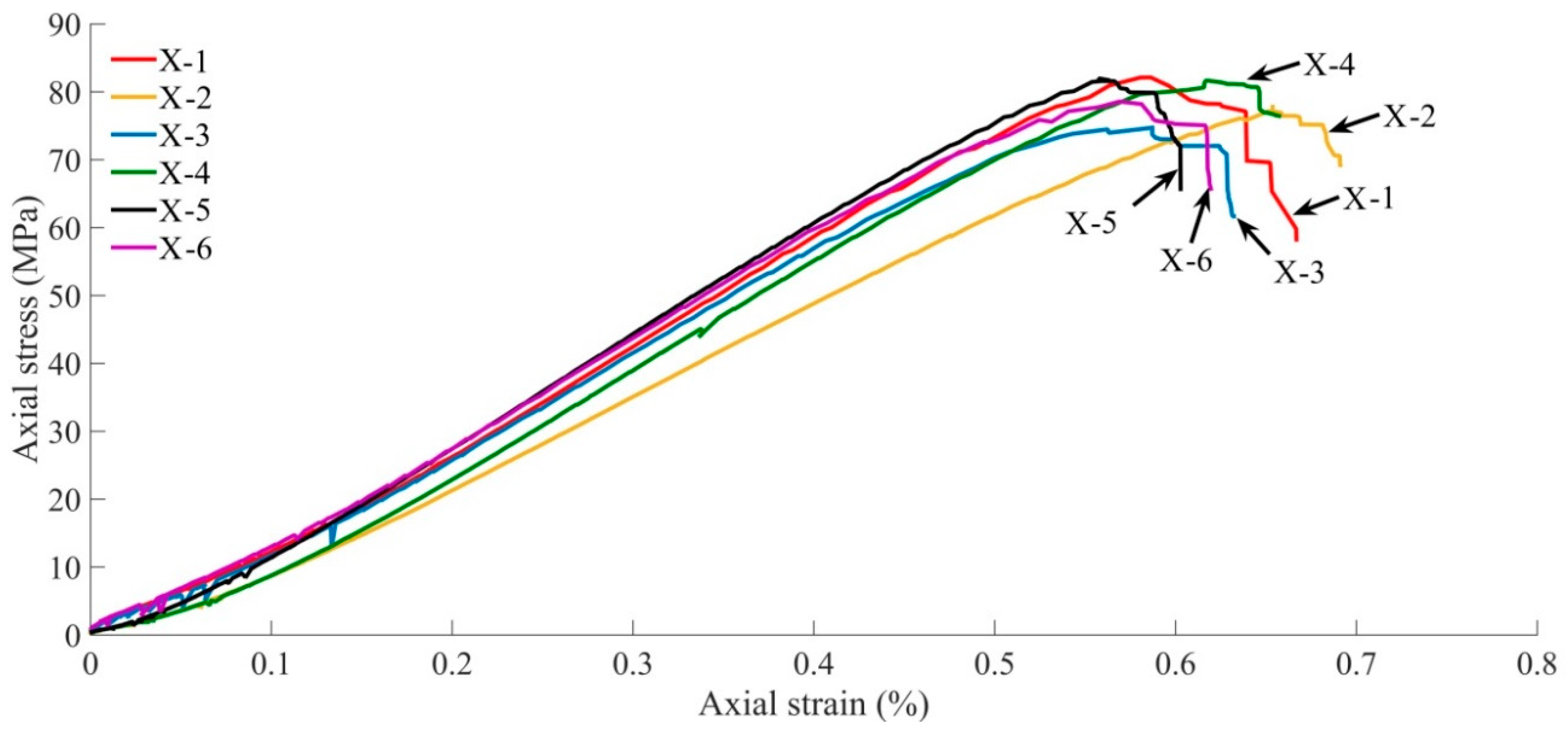






| Specimen Number | Diameter (mm) | Height (mm) | Loading Time (s) | Uniaxial Compressive Strength (MPa) | AE Waveform Quantity (pcs) |
|---|---|---|---|---|---|
| X-1 | 48.86 | 100.16 | 442.6 | 82.12 | 54,817 |
| X-2 | 48.78 | 100.18 | 443.2 | 78.09 | 40,755 |
| X-3 | 48.90 | 100.26 | 448.3 | 74.72 | 46,387 |
| X-4 | 48.74 | 100.20 | 446.6 | 81.68 | 45,560 |
| X-5 | 48.82 | 100.22 | 447.6 | 81.98 | 49,612 |
| X-6 | 48.80 | 100.18 | 447.4 | 78.57 | 38,250 |
| X-1 | X-3 | X-6 | ||||||
|---|---|---|---|---|---|---|---|---|
| Stress Ratio (%) | Corresponding Time Period (s) | Waveform Proportion (%) | Stress Ratio (%) | Corresponding Time Period (s) | Waveform Proportion (%) | Stress Ration (%) | Corresponding Time Period (s) | Waveform Proportion (%) |
| [0, 10] | 1~186 | 21.79 | [0, 10] | 1~177 | 19.86 | [0, 10] | 1~164 | 22.00 |
| [10, 20] | 187~394 | 15.53 | [10, 20] | 178~376 | 14.58 | [10, 20] | 165~350 | 12.15 |
| [20, 30] | 395~534 | 6.64 | [20, 30] | 377~513 | 6.74 | [20, 30] | 351~491 | 5.91 |
| [30, 40] | 535~667 | 5.03 | [30, 40] | 514~655 | 4.99 | [30, 40] | 492~630 | 4.41 |
| [40, 50] | 668~787 | 3.59 | [40, 50] | 656~754 | 3.14 | [40, 50] | 631~721 | 2.61 |
| [50, 60] | 788~906 | 2.78 | [50, 60] | 755~874 | 3.07 | [50, 60] | 722~830 | 2.49 |
| [60, 70] | 907~1030 | 2.79 | [60, 70] | 875~983 | 2.29 | [60, 70] | 831~953 | 2.51 |
| [70, 80] | 1031~1142 | 2.88 | [70, 80] | 984~1095 | 2.60 | [70, 80] | 954~1062 | 2.75 |
| [80, 90] | 1143~1260 | 5.28 | [80, 90] | 1096~1204 | 4.71 | [80, 90] | 1063~1158 | 4.28 |
| [90, 100] | 1261~1398 | 13.70 | [90, 100] | 1205~1377 | 29.24 | [90, 100] | 1159~1322 | 19.21 |
| [100, Complete failure] | 1399~1449 | 20.00 | [100, Complete failure] | 1378~1395 | 8.77 | [100, Complete failure] | 1323~1369 | 21.69 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Chang, X.; Liu, Y.; Chen, S. Mechanistic Characteristics of Double Dominant Frequencies of Acoustic Emission Signals in the Entire Fracture Process of Fine Sandstone. Energies 2019, 12, 3959. https://doi.org/10.3390/en12203959
Wang C, Chang X, Liu Y, Chen S. Mechanistic Characteristics of Double Dominant Frequencies of Acoustic Emission Signals in the Entire Fracture Process of Fine Sandstone. Energies. 2019; 12(20):3959. https://doi.org/10.3390/en12203959
Chicago/Turabian StyleWang, Chuangye, Xinke Chang, Yilin Liu, and Shijiang Chen. 2019. "Mechanistic Characteristics of Double Dominant Frequencies of Acoustic Emission Signals in the Entire Fracture Process of Fine Sandstone" Energies 12, no. 20: 3959. https://doi.org/10.3390/en12203959
APA StyleWang, C., Chang, X., Liu, Y., & Chen, S. (2019). Mechanistic Characteristics of Double Dominant Frequencies of Acoustic Emission Signals in the Entire Fracture Process of Fine Sandstone. Energies, 12(20), 3959. https://doi.org/10.3390/en12203959






