An Electro-Pneumatic Force Tracking System using Fuzzy Logic Based Volume Flow Control
Abstract
:1. Introduction
2. Volume Flow Feature of the Solenoid On-Off Valve
2.1. Testing Method
2.2. Experimental Setup of Measuring the Volume Flow
2.3. Testing Results
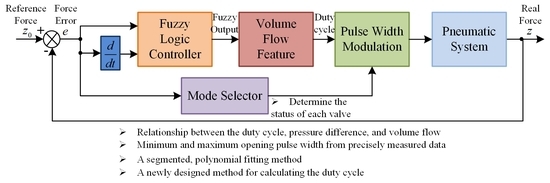
3. Controller Design for the Force Tracking System
3.1. Improved Volume Flow Control Method
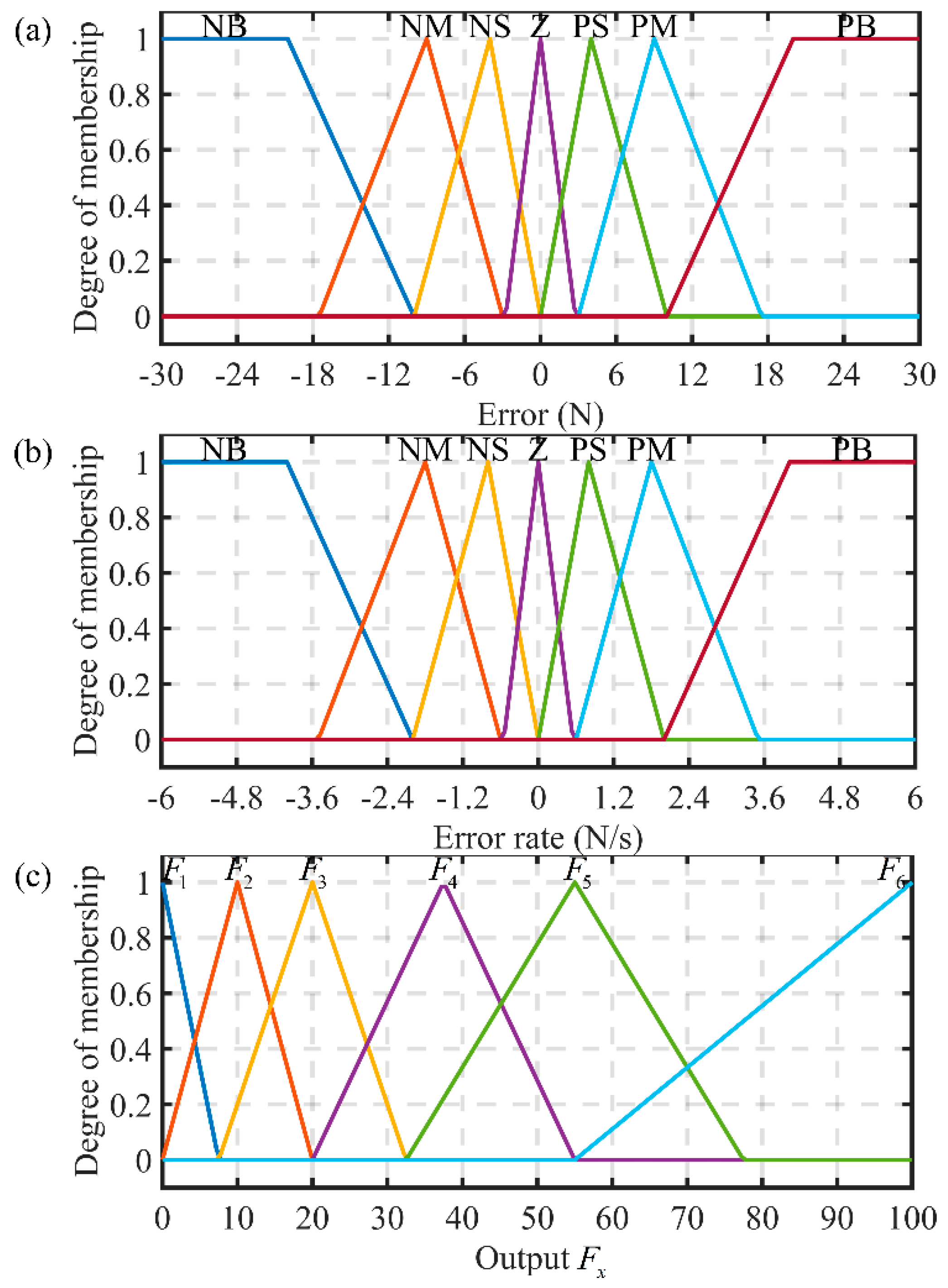
3.2. Fuzzy Logic Controller
3.3. Mode Selector
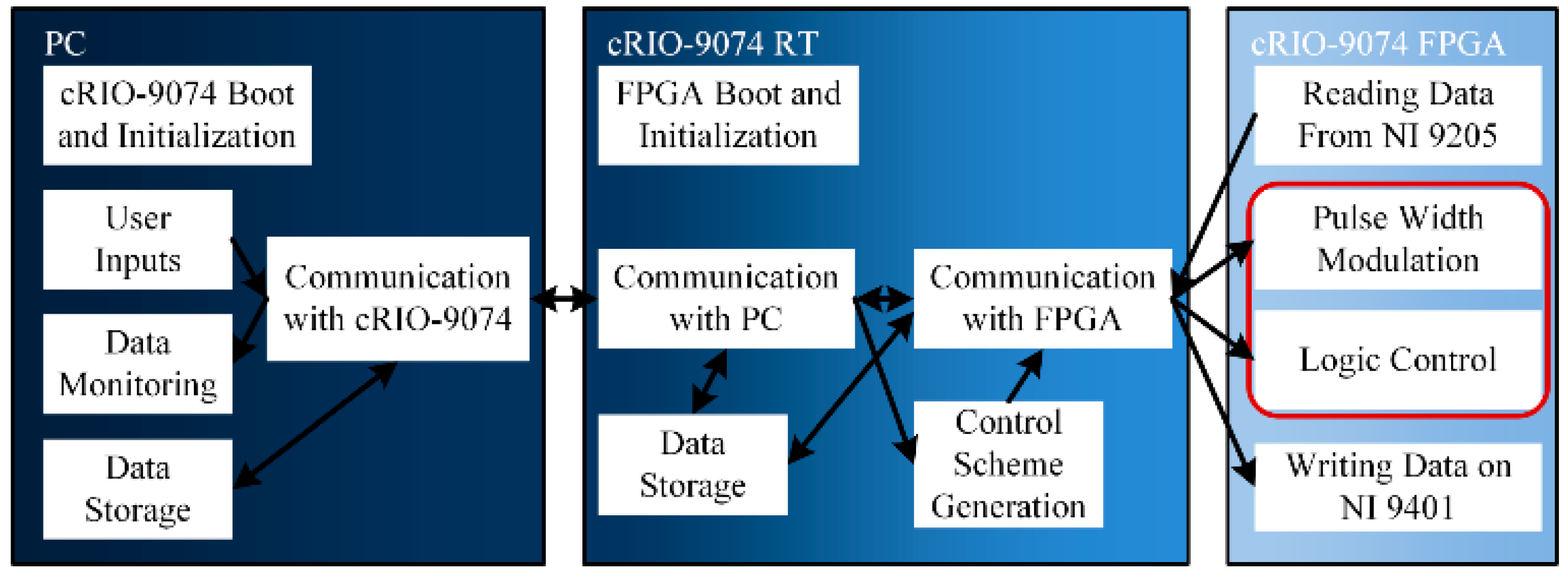
4. Experimental Setup
5. Experimental Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| volume flow [L/s] | |
| absolute input pressure of the valve [Pa] | |
| absolute output pressure of the valve [Pa] | |
| valve discharge coefficient [m3/(s·Pa)] | |
| stagnation temperature [K] | |
| inlet air temperature of the valve [K] | |
| specific pressure ratio | |
| critical pressure ratio | |
| PWM control period [s] | |
| PWM frequency [Hz] | |
| PWM pulse width [s] | |
| PWM duty cycle [%] | |
| pressure difference [Pa] | |
| pressure of the atmosphere [Pa] | |
| PWM minimum duty cycle [%] | |
| PWM maximum duty cycle [%] | |
| force of the rod [N] | |
| force of the spring [N] | |
| force caused by the atmosphere acting on the rod [N] | |
| total payloads [kg] | |
| acceleration of the rod [m/s2] | |
| normalized volume flow [%] | |
| coefficient of determination | |
| , , , and | pressure difference of the valves [Pa] |
| pressure of the air supply [Pa] | |
| pressure of the left chamber [Pa] | |
| pressure of the right chamber [Pa] | |
| and | pressure differences [Pa] |
| and | duty cycles [%] |
| force error [N] | |
| force error rate [N/s] | |
| output variable of the fuzzy logic controller | |
| force reference [N] | |
| IF-THEN rules | |
| , , and | linguistic variables |
| and | mode selector parameters |
| rod length [m] | |
| D | rod diameter [m] |
| Ls | spring length [m] |
| number of spring coils | |
| , ki, and kd | PID controller parameters |
References
- Zhang, Y.; Li, K.; Wang, G.; Liu, J.; Cai, M. Nonlinear Model Establishment and Experimental Verification of a Pneumatic Rotary Actuator Position Servo System. Energies 2019, 12, 1096. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, T.; Xie, Q. Intelligent real-time pressure tracking system using a novel hybrid control scheme. Trans. Inst. Meas. Control 2018, 40, 3744–3759. [Google Scholar] [CrossRef]
- Ahn, K.; Yokota, S. Intelligent switching control of pneumatic actuator using on/off solenoid valves. Mechatronics 2005, 15, 683–702. [Google Scholar] [CrossRef]
- Nguyen, T.; Leavitt, J.; Jabbari, F.; Bobrow, J. Accurate Sliding-Mode Control of Pneumatic Systems Using Low-Cost Solenoid Valves. IEEE/ASME Trans. Mechatron. 2007, 12, 216–219. [Google Scholar] [CrossRef]
- Taghizadeh, M.; Ghaffari, A.; Najafi, F. Modeling and identification of a solenoid valve for PWM control applications. Comptes Rendus Mécanique 2009, 337, 131–140. [Google Scholar] [CrossRef]
- Najjari, B.; Barakati, S.; Mohammadi, A.; Futohi, M.; Bostanian, M. Position control of an electro-pneumatic system based on PWM technique and FLC. ISA Trans. 2014, 53, 647–657. [Google Scholar] [CrossRef] [PubMed]
- Noritsugu, T. Development of PWM mode electro-pneumatic servomechanism. II: Position control of a pneumatic cylinder. J. Fluid Control. 1989, 17, 7–31. [Google Scholar]
- Jeong, H.S.; Kim, H.E. Experimental based analysis of the pressure control characteristics of an oil hydraulic three-way on/off solenoid valve controlled by PWM signal. J. Dyn. Syst. Meas. Control 2002, 124, 196–205. [Google Scholar] [CrossRef]
- Messina, A.; Giannoccaro, N.I.; Gentile, A. Experimenting and modelling the dynamics of pneumatic actuators controlled by the pulse width modulation (PWM) technique. Mechatronics 2005, 15, 859–881. [Google Scholar] [CrossRef]
- Zhang, J.; Lv, C.; Yue, X.; Li, Y.; Yuan, Y. Study on a linear relationship between limited pressure difference and coil current of on/off valve and its influential factors. ISA Trans. 2014, 53, 150–161. [Google Scholar] [CrossRef]
- Ahn, K.; Lee, B. Intelligent switching control of pneumatic cylinders by learning vector quantization neural network. J. Mech. Sci. Technol. 2005, 19, 529–539. [Google Scholar] [CrossRef]
- Bangaru, M.; Devaraj, S. Energy efficiency analysis of interconnected pneumatic cylinders servo positioning system. In Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 13–19 November 2015; p. V04AT04A034. [Google Scholar]
- Shih, M.C.; Ma, M.A. Position control of a pneumatic rodless cylinder using sliding mode MD-PWM control the high speed solenoid valves. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 1998, 41, 236–241. [Google Scholar]
- Hodgson, S.; Le, M.; Tavakoli, M.; Pham, M. Improved tracking and switching performance of an electro-pneumatic positioning system. Mechatronics 2012, 22, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Lin, Z.; Zhang, T.; Xie, Q.; Wei, Q. Electro-pneumatic position tracking control system based on an intelligent phase-change PWM strategy. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 512. [Google Scholar] [CrossRef]
- Kunt, C.; Singh, R.A. linear time varying model for on–off valve controlled pneumatic actuators. J. Dyn. Syst. Meas. Control 1990, 112, 740–747. [Google Scholar] [CrossRef]
- Barth, E.J.; Zhang, J.; Goldfarb, M. Control design for relative stability in a PWM-controlled pneumatic system. Trans. Am. Soc. Mech. Eng. J. Dyn. Syst. Meas. Control 2003, 125, 504–508. [Google Scholar] [CrossRef]
- Pohl, J.; Sethson, M.; Krus, P.; Palmberg, J.O. Modelling and validation of a fast switching valve intended for combustion engine valve trains. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2002, 216, 105–116. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, T.; Xie, Q.; Wei, Q. Intelligent electro-pneumatic position tracking system using improved mode-switching sliding control with fuzzy nonlinear gain. IEEE Access 2018, 6, 34462–34476. [Google Scholar] [CrossRef]
- Hodgson, S.; Tavakoli, M.; Pham, M.; Leleve, A. Nonlinear Discontinuous Dynamics Averaging and PWM-Based Sliding Control of Solenoid-Valve Pneumatic Actuators. IEEE/ASME Trans. Mechatron. 2015, 20, 876–888. [Google Scholar] [CrossRef]
- Pipan, M.; Herakovič, N. Volume flow characterization of PWM-controlled fast-switching pneumatic valves. Stroj. Vestn. J. Mech. Eng. 2016, 62, 543–550. [Google Scholar] [CrossRef]
- Pipan, M.; Herakovič, N. Closed-loop volume flow control algorithm for fast switching pneumatic valves with PWM signal. Control Eng. Pract. 2018, 70, 114–120. [Google Scholar] [CrossRef]
- Fu, H.; Jiang, T.; Cui, Y.; Li, B. Adaptive hydraulic potential energy transfer technology and its application to compressed air energy storage. Energies 2018, 11, 1845. [Google Scholar] [CrossRef]
- Li, Y.; Xiong, B.; Su, Y.; Tang, J.; Leng, Z. Particle Swarm Optimization-Based Power and Temperature Control Scheme for Grid-Connected DFIG-Based Dish-Stirling Solar-Thermal System. Energies 2019, 12, 1300. [Google Scholar] [CrossRef]
- Ma, Y.; Tao, L.; Zhou, X.; Li, W.; Shi, X. Analysis and Control of Wind Power Grid Integration Based on a Permanent Magnet Synchronous Generator Using a Fuzzy Logic System with Linear Extended State Observer. Energies 2019, 12, 2862. [Google Scholar] [CrossRef]
- Rahmat, M.F. Identification and non-linear control strategy for industrial pneumatic actuator. Int. J. Phys. Sci. 2012, 7, 2565–2579. [Google Scholar] [CrossRef]
- Salim, S.; Rahmat, M.; Faudzi, A.; Ismail, Z. Position control of pneumatic actuator using an enhancement of NPID controller based on the characteristic of rate variation nonlinear gain. Int. J. Adv. Manuf. Technol. 2014, 75, 181–195. [Google Scholar] [CrossRef]
- Shih, M.C.; Hwang, C.G. Fuzzy PWM control of the positions of a pneumatic robot cylinder using high speed solenoid valve. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 1997, 40, 469–476. [Google Scholar] [CrossRef]
- Pneumatic Fluid Power—Determination of Flow-Rate Characteristics of Components Using Compressible Fluids—Part 1: General Rules and Test Methods for Steady-State Flow, ISO 6358-1:2013. 2013. Available online: https://www.iso.org/standard/56612.html (accessed on 22 October 2019).
- McCloy, D.; Martin, H.R. Static characteristics of valves. In Control of Fluid Power: Analysis and Design, 2nd ed.; Halsted Press: New York, NY, USA, 1980; pp. 159–180. [Google Scholar]
- Wang, L. A Course in Fuzzy Systems and Control, 1st ed.; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1997; pp. 55–65. [Google Scholar]
- Mendes, J.; Araújo, R.; Sousa, P.; Apóstolo, F.; Alves, L. An architecture for adaptive fuzzy control in industrial environments. Comput. Ind. 2011, 62, 364–373. [Google Scholar] [CrossRef]
- Mendes, J.; Araújo, R.; Matias, T.; Seco, R.; Belchior, C. Automatic extraction of the fuzzy control system by a hierarchical genetic algorithm. Eng. Appl. Artif. Intell. 2014, 29, 70–78. [Google Scholar] [CrossRef]
- Ziegler, J.G.; Nichols, N.B. Optimum settings for automatic controllers. J. Dyn. Syst. Meas. Control 1993, 115, 220–222. [Google Scholar] [CrossRef]

















| 0.01 | 0.8063 | 1.788 | 0.9997 | 0.5943 |
| 0.03 | 0.9606 | 0.7687 | 0.9993 | 0.9722 |
| 0.05 | 0.9981 | 0.1662 | 0.9924 | 3.255 |
| 0.07 | 0.9739 | 0.618 | 0.9982 | 1.585 |
| 0.1 | 0.9819 | 0.504 | 0.9788 | 5.562 |
| 0.15 | 0.9798 | 0.5301 | 0.993 | 3.227 |
| 0.2 | 0.9887 | 0.4264 | 0.9871 | 4.395 |
| 0.3 | 0.9966 | 0.2136 | 0.9972 | 2.067 |
| Variable | Definition |
|---|---|
| NB | negative big |
| NM | negative medium |
| NS | negative small |
| Z | zero |
| PS | positive small |
| PM | positive medium |
| PB | positive big |
| Error | Error Rate | ||||||
|---|---|---|---|---|---|---|---|
| NB | NM | NS | Z | PS | PM | PB | |
| NB | |||||||
| NM | |||||||
| NS | |||||||
| Z | |||||||
| PS | |||||||
| PM | |||||||
| PB | |||||||
| Mode (State) | ||||
|---|---|---|---|---|
| V1 1 | PWM | PWM | closed | closed |
| V2 2 | closed | closed | closed | closed |
| V3 3 | closed | closed | closed | PWM |
| V4 4 | PWM | closed | closed | closed |
| Symbol | System Parameters | Value |
|---|---|---|
| valve discharge coefficient | 4 × 10−9 m3/(s·Pa) | |
| stagnation temperature | 293.15 K | |
| critical pressure ratio | 0.38 | |
| pressure of the air supply | 4 × 105 Pa | |
| pressure of the atmosphere | 1 × 105 Pa | |
| rod length | 0.1 m | |
| rod diameter | 0.024 m | |
| spring length | 0.15 m | |
| number of spring coils | 33 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Z.; Wei, Q.; Ji, R.; Huang, X.; Yuan, Y.; Zhao, Z. An Electro-Pneumatic Force Tracking System using Fuzzy Logic Based Volume Flow Control. Energies 2019, 12, 4011. https://doi.org/10.3390/en12204011
Lin Z, Wei Q, Ji R, Huang X, Yuan Y, Zhao Z. An Electro-Pneumatic Force Tracking System using Fuzzy Logic Based Volume Flow Control. Energies. 2019; 12(20):4011. https://doi.org/10.3390/en12204011
Chicago/Turabian StyleLin, Zhonglin, Qingyan Wei, Runmin Ji, Xianghua Huang, Yuan Yuan, and Zhiwen Zhao. 2019. "An Electro-Pneumatic Force Tracking System using Fuzzy Logic Based Volume Flow Control" Energies 12, no. 20: 4011. https://doi.org/10.3390/en12204011
APA StyleLin, Z., Wei, Q., Ji, R., Huang, X., Yuan, Y., & Zhao, Z. (2019). An Electro-Pneumatic Force Tracking System using Fuzzy Logic Based Volume Flow Control. Energies, 12(20), 4011. https://doi.org/10.3390/en12204011