Air-Floating Characteristics of Large-Diameter Multi-Bucket Foundation for Offshore Wind Turbines
Abstract
:1. Introduction
2. Theoretical Formulation
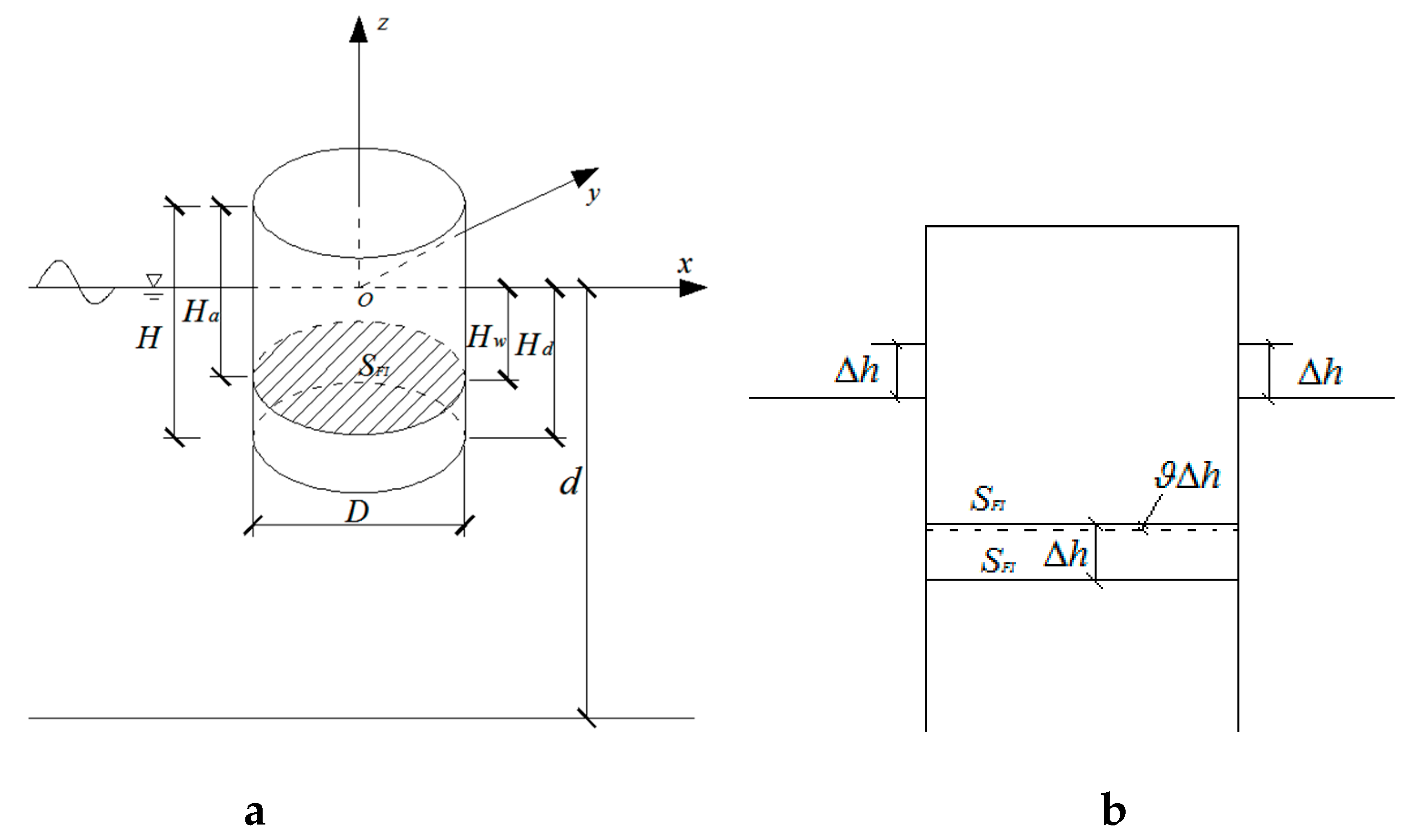
2.1. Theory of Air-Floating Mechanism for Single-Bucket Foundation
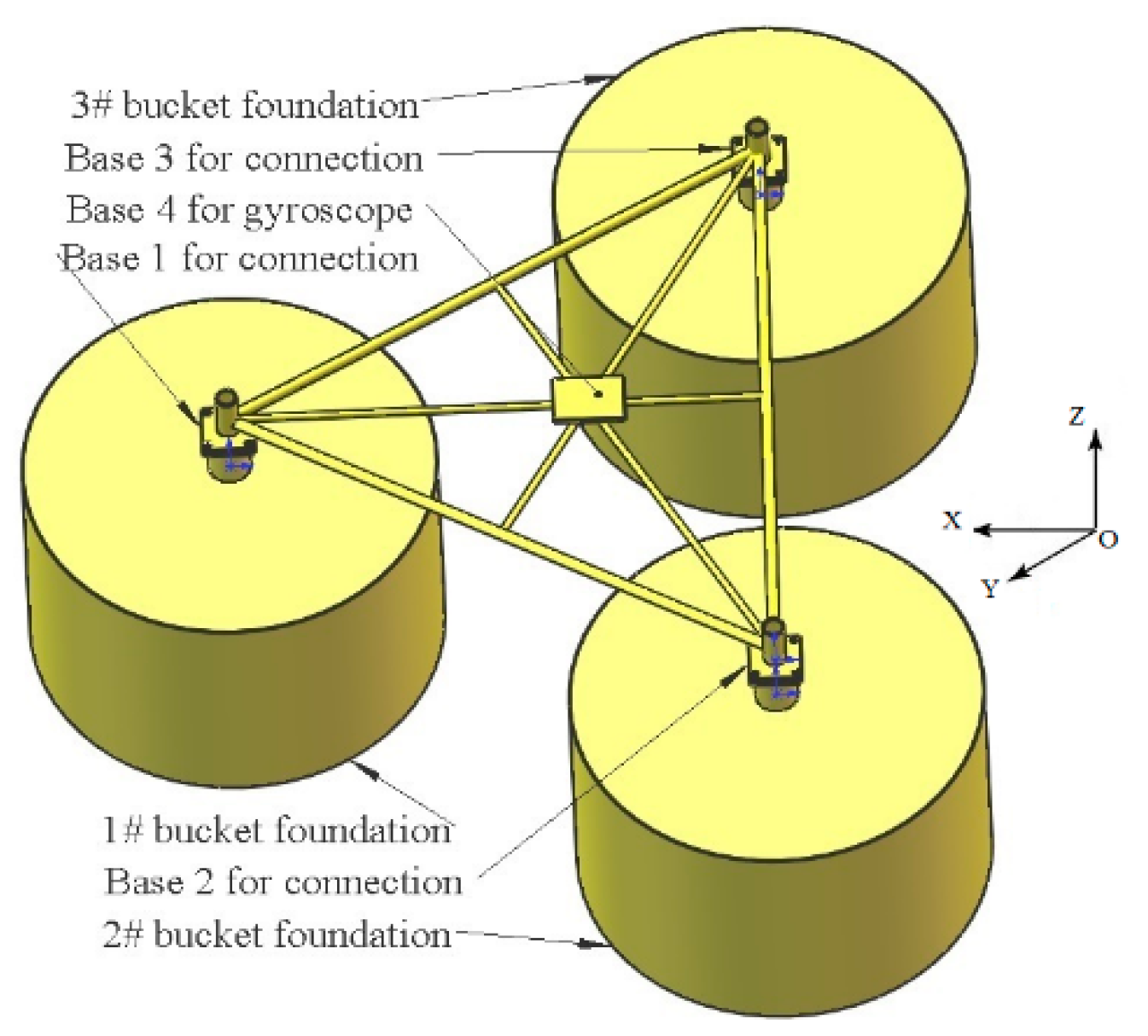
2.2. Equations of Oscillating Motion for Multi-Bucket Foundation
2.2.1. Equation of Heaving Motion
2.2.2. Equation of Rocking Motion
2.3. Method of Determining the Added Mass Coefficient and Damping Ratio for Oscillating Motion in Still Water
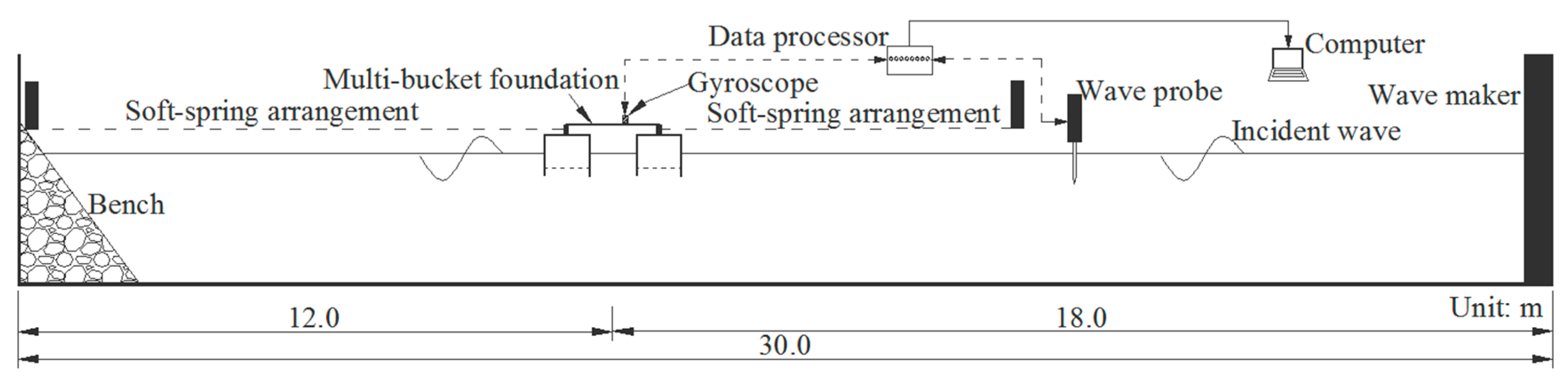
3. Experimental Designs and MOSES Simulations
3.1. Physical and Experiment Models
3.2. Experimental Setup
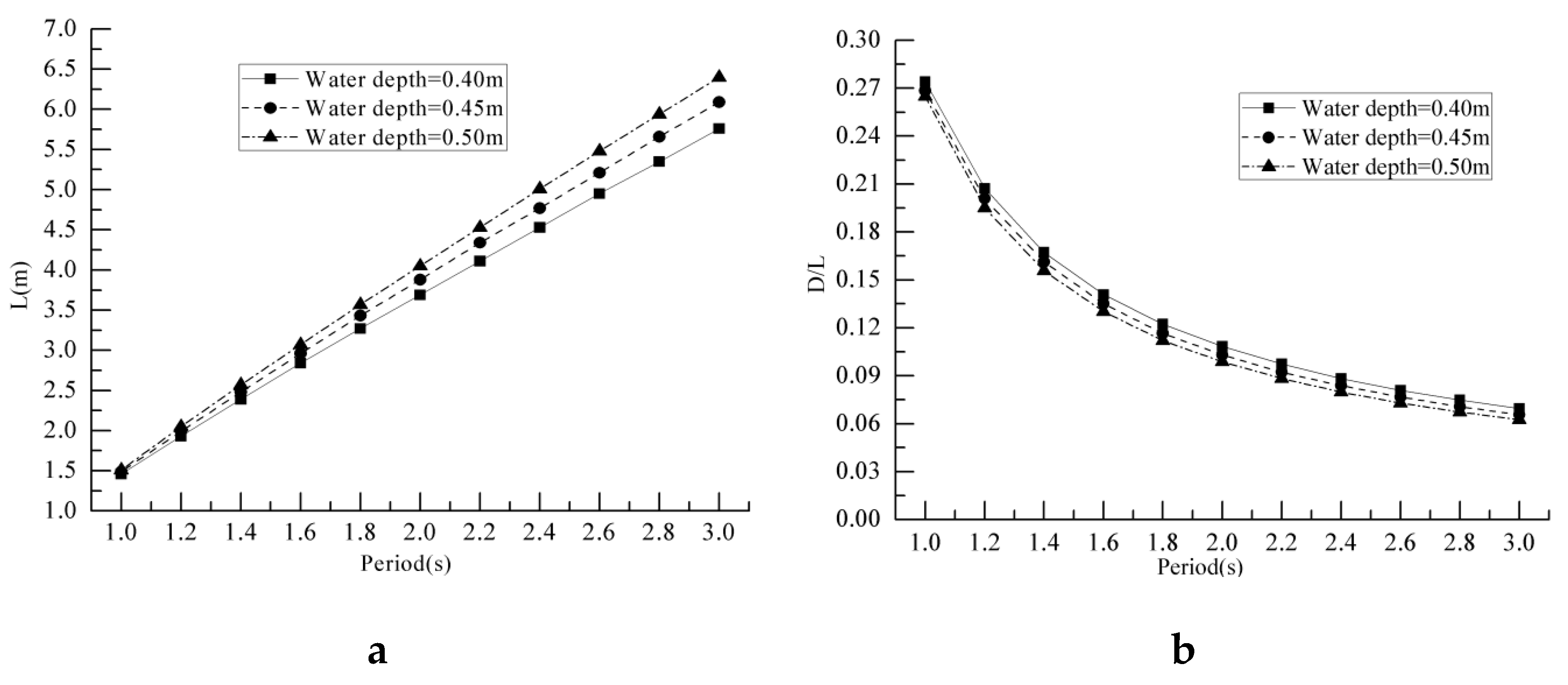
3.3. Tests in Regular Waves
3.4. MOSES Numerical Simulation
4. Results and Discussion
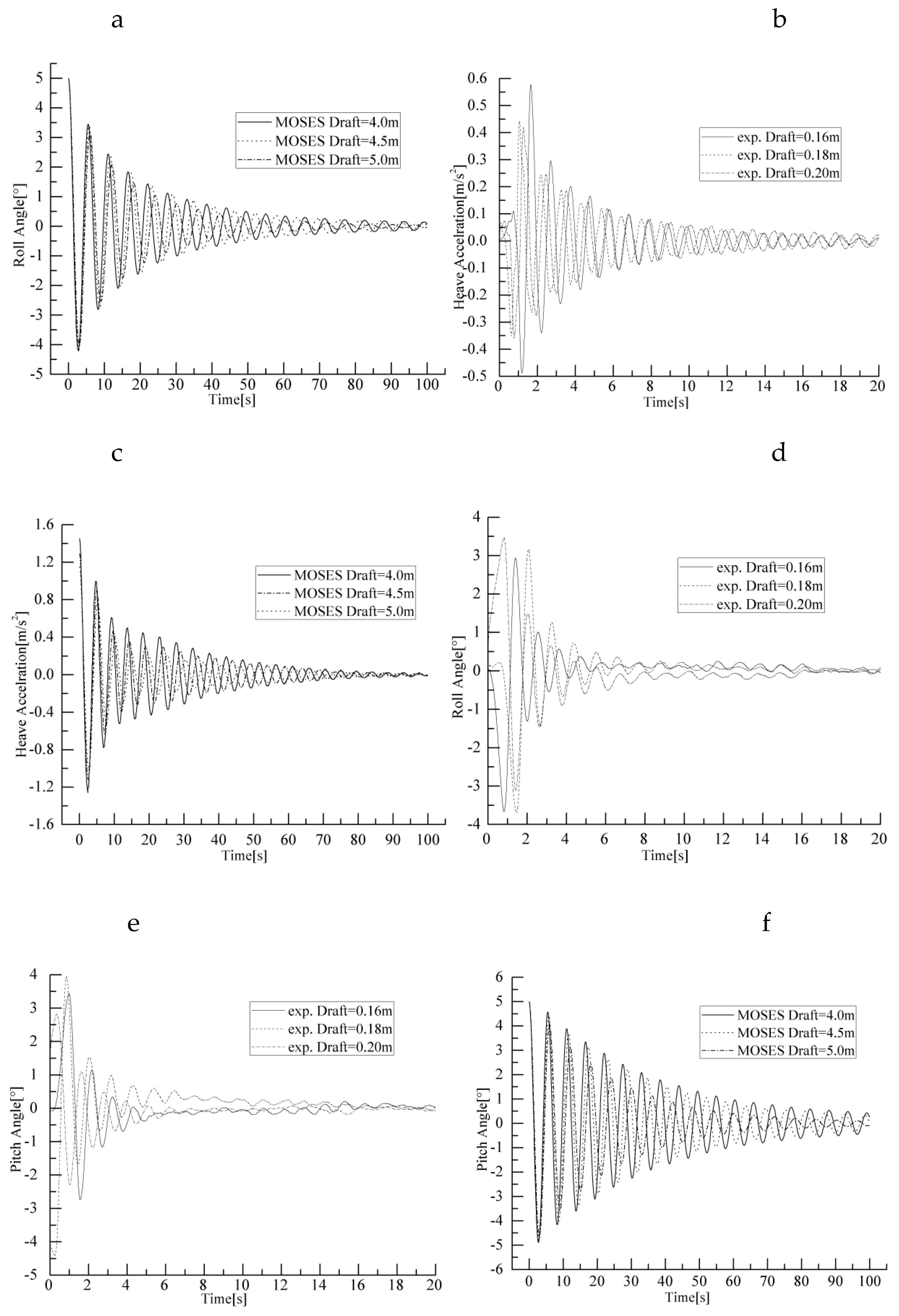
4.1. Free-Decay Tests
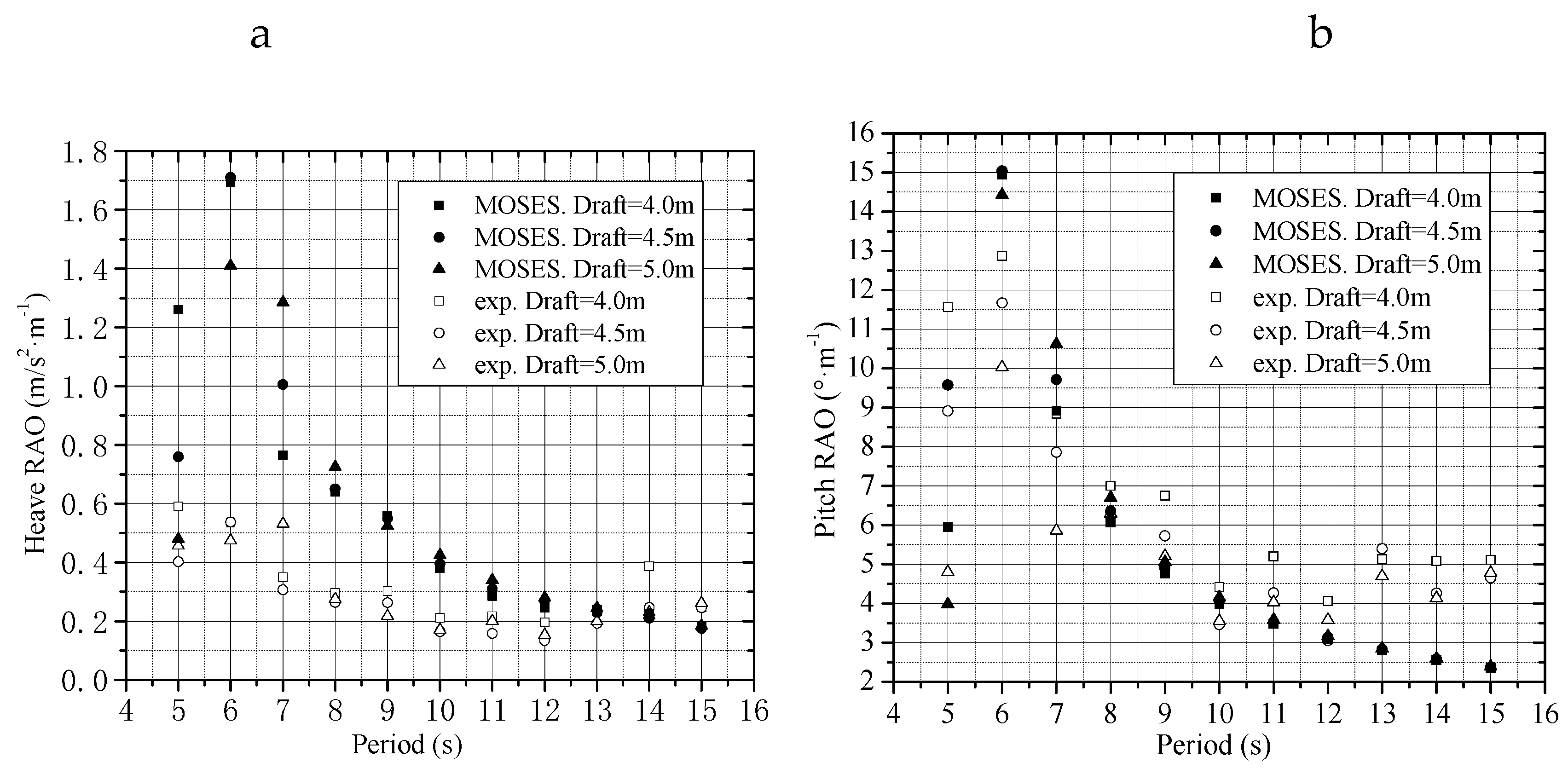
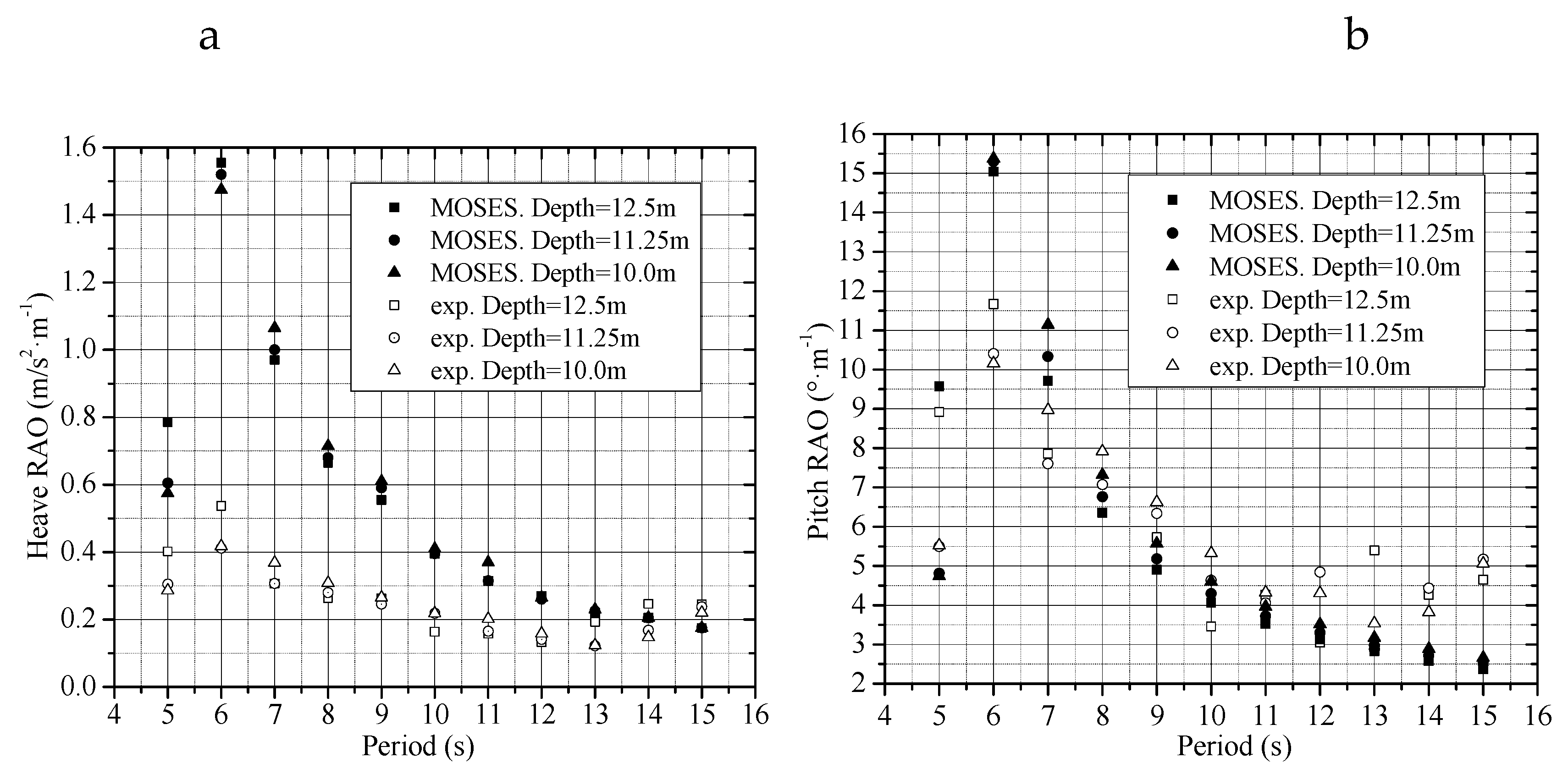
4.2. Motion Responses in Waves
4.2.1. Effects of Draft Heights
4.2.2. Effects of Water Depth
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| DOF | degree of freedom |
| LDMBF | large-diameter multi-bucket foundation |
| RAO | response amplitude operator |
| OWT | offshore wind turbine |
| SBJ | suction-bucket jacket |
| CBF | composite-bucket foundation |
| CGS | concrete gravity structure |
| LPCBF | large prestressed concrete bucket foundation |
| D | diameter of the bucket |
| A | cross-sectional area of the bucket |
| H | height of the i-th bucket foundation |
| Hd | draft of the i-th bucket foundation |
| Hf | freeboard of the i-th bucket foundation |
| Hw | difference of water head between the external and interior water surface |
| Pa | atmospheric pressure |
| Pb | pressure in the bucket |
| Gs | weight of the bucket |
| ms | mass of the i-th bucket |
| mw | mass of the water column inside the i-th bucket |
| Ms | total mass of the structure |
| Mw | total mass of the water column inside the structure |
| MbZ | total mass for the heaving motion |
| x, y, z | local cartesian coordinate system |
| X, Y, Z | global cartesian coordinate system |
| velocity for the heaving motion | |
| acceleration for the heaving motion | |
| Nz | damping coefficient for the heaving motion |
| Ca | stiffness of the air cushion in i-th bucket |
| Cw | stiffness of the water column in i-th bucket |
| CZ | total series stiffness of structure |
| FZ | force in the heaving direction |
| dimensionless parameter related to air compressibility | |
| movement distance in the heaving direction | |
| volume variation of the air cushion | |
| P0 | initial air pressure in the bucket |
| V0 | initial air volume in the bucket |
| P1 | air pressure after the movement |
| V1 | air volume after the movement |
| IbmX | total rolling inertia moment |
| IbmY | total pitching inertia moment |
| Ismx | rolling inertia moment of the structure |
| Ismy | pitching inertia moment of the structure |
| IwmX | total rolling inertia moment of the water plug in the bucket |
| IwmY | total pitching inertia moment of the water plug in the bucket |
| NmX | total damping coefficient of the rolling motion |
| NmY | total damping coefficient of the pitching motion |
| rolling angle | |
| rolling angular velocity | |
| rolling angular acceleration | |
| Fb | buoyancy |
| Fmx | moment in the rolling motion |
| Fbmx | rolling moment of buoyancy |
| Cmx | rolling restoring coefficient |
| FmX | total moment in the rolling motion |
| FbmX | total rolling moment of buoyancy |
| CmX | total rolling restoring coefficient |
| yc | y coordinate of rocking center of the structure |
| yb | y coordinate of floating center of the structure |
| heaving added mass coefficient of the structure | |
| rolling added mass coefficient of the structure | |
| pitch added mass coefficient of the structure | |
| g | gravitational acceleration |
| nZ | damping ratio of heaving motion |
| nmX | damping ratio of rolling motion |
| nmY | damping ratio of pitching motion |
References
- Snyder, B.; Kaiser, M.J. Ecological and economic cost-benefit analysis of offshore wind energy. Renew. Energy 2009, 34, 1567–1578. [Google Scholar] [CrossRef]
- Blanco, M.I. The economics of wind energy. Renew. Sustain. Energy Rev. 2009, 13, 1372–1382. [Google Scholar] [CrossRef]
- Wang, T. Global Offshore Wind Power Market-Statistics & Facts. 2019. Available online: https://www.statista.com/topics/2764/offshore-wind-energy/ (accessed on 15 July 2019).
- Byrne, B.W.; Houlsby, G.T.; Martin, C.; Fish, P. Suction caisson foundations for offshore wind turbines. Wind Eng. 2002, 26, 145–155. [Google Scholar] [CrossRef]
- Ding, H.; Liu, Y.; Zhang, P.; Le, C. Model tests on the bearing capacity of wide-shallow composite bucket foundations for offshore wind turbines in clay. Ocean Eng. 2015, 103, 114–122. [Google Scholar] [CrossRef]
- Houlsby, G.T.; Ibsen, L.B.; Byrne, B.W. Suction caissons for wind turbines. In Proceedings of the First International Symposium on Frontiers in Offshore Geotechnics, University of Western Australia, Perth, WA, Australia, 19–21 September 2005; pp. 75–93. [Google Scholar]
- Lars, B.I. The bucket foundation and its competitiveness versus monopiles and jacket structures. In Proceedings of the International Conference in Research at Alpha Ventus, Bremerhaven, Germany, 9–10 May 2012. [Google Scholar]
- Zhang, P.Y.; Han, Y.Q.; Ding, H.Y.; Zhang, S.Y. Field experiments on wet tows of an integrated transportation and installation vessel with two bucket foundations for offshore wind turbines. Ocean Eng. 2015, 108, 769–777. [Google Scholar] [CrossRef]
- Fu, D.F.; Bienen, B.; Gaudin, C.; Cassidy, M. Undrained capacity of a hybrid subsea skirted mat with caissons under combined loading. Canadian Geotech. J. 2014, 51, 934–949. [Google Scholar]
- Bie, S.A.; Ji, C.N.; Ren, Z.J.; Li, Z.Z. Study on floating properties and stability of air floated structures. China Ocean Eng. 2002, 16, 263–272. [Google Scholar]
- Ding, H.; Hu, R.; Le, C.; Zhang, P. Towing Operation Methods of Offshore Integrated Meteorological Mast for Offshore Wind Farms. J. Mar. Sci. Eng. 2019, 7, 100. [Google Scholar] [CrossRef]
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: London, UK, 1990. [Google Scholar]
- Qi, X.Y. Experimental Study on Behaviour of an Open Bottom Floating Platform in Wave, Wind and Current. In Proceedings of the International Offshore and Polar Engineering Conference, Osaka, Japan, 10–15 April 1994. [Google Scholar]
- Thiagarajan, K.P.; Morison-Thomas, M.T. Wave-induced motions of an air cushion structure in shallow water. Ocean Eng. 2006, 33, 1143–1160. [Google Scholar] [CrossRef]
- Thiagarajan, K.P.; Morris-Thomas, M.T.; Spargo, A. Heave and pitch response of an offshore platform with air cushion support in shallow water. In Proceedings of the 23rd International Conference Offshore Mechanic and Arctic Engineering, Vancouver, BC, Canada, 20–25 June 2004; pp. 1–7. [Google Scholar]
- Zhang, P.Y.; Ding, H.Y.; Le, C.H.; Huang, X. Motion analysis on integrated transportation technique for offshore wind turbines. J. Renew. Sustain. Energy 2013, 5, 053117. [Google Scholar] [CrossRef]
- Seidl, L.H. Development of an Air Stabilized Platform; University of Hawaii, Department of Ocean Engineering technical report submitted to US Department of Commerce, Maritime Administration; University of Hawaii: Honolulu, HI, USA, 1988. [Google Scholar]
- Bhattacharyya, R. Dynamics of Marine Vehicles; China Ocean Press: Beijing, China, 1982. [Google Scholar]
- James, F.J.; Wilson, J.F. Dynamics of Offshore Structures; A Wiley-Inter Science Publication: New York, NY, USA, 1984. [Google Scholar]
- Chenu, B.; Morris-Thomas, M.T.; Thiagarajan, K.P. Some hydrodynamic characteristics of an air-cushion supported concrete gravity structure. In Proceedings of the 15th Australasian Fluid Mechanics Conference, Sydney, Australia, 13–17 December 2004. [Google Scholar]
- Thiagarajan, K.P. Hydrostatic stability of compartmented structures supported by air cushions. J. Ship Res. 2009, 53, 151–158. [Google Scholar]
- Van Kessel, J.L.F. Aircushion Supported Mega-Floaters. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2010. [Google Scholar]
- Pinkster, J.A.; Fauzi, A. Motions and drift forces of air-supported structures in waves. In Proceedings of the Fifth Workshop on Nonlinear Wave Action on Structures and Ships, La Garde, France, 4 September 1998. [Google Scholar]
- Pinkster, J.A.; Fauzi, A.; Inoue, Y.; Tabeta, S. The behavior of large air cushion supported structures in waves. In Proceedings of the second International Conference on Hydroelasticity in Marine Technology, Fukuoka, Japan, 1–3 December 1998; pp. 497–506. [Google Scholar]
- Pinkster, J.A.; Meevers Scholte, E.J.A. The behavior of a large air-supported MOB at sea. Mar. Struct. 2001, 14, 163–179. [Google Scholar] [CrossRef]
- Tabeta, S. Model Experiments on Barge Type Floating Structures Supported by Air Cushions; Ship Hydromechanics Laboratory Report; Delft University of Technology: Delft, The Netherlands, 1998; p. 1125. [Google Scholar]
- Malenica, S.; Zalar, M. An alternative method for linear hydrodynamics of air cushion supported floating bodies. In Proceedings of the Fifth International Workshop on Water Waves and Floating Bodies, Caesarea, Israel, 17 February–1 March 2000; pp. 1–4. [Google Scholar]
- Guéret, R.; Hermans, A.J. Air cushion under floating offshore structure. In Proceedings of the Sixth International Workshop on Water Waves and Floating Bodies, Hiroshima, Japan, 22–25 April 2001; pp. 45–49. [Google Scholar]
- Kessel Van, J.L.F.; Pinkster, J.A. The effect of aircushion division on the structural loads of large floating offshore structures. In Proceedings of the ASME 2007 26th International Conference on Offshore Mechanics and Arctic Engineering, San Diego, CA, USA, 10–15 June 2007; American Society of Mechanical Engineers: New York, NY, USA, 2007. [Google Scholar]
- Van Kessel, J.L.F.; Pinkster, J.A. Wave-induced structural loads on different types of aircushion supported structures. In Proceedings of the Seventeenth International Offshore and Polar Engineering Conference, Lisbon, Portugal, 1–6 July 2007. [Google Scholar]
- Le, C.H.; Ding, H.Y.; Zhang, P.Y. Air-floating towing behaviors of multi-bucket foundation platform. China Ocean Eng. 2013, 27, 645–658. [Google Scholar] [CrossRef]
- Achmus, M.; Kuo, Y.S.; Abdel-Rahman, K. Behavior of monopile foundations under cyclic lateral load. Comput. Geotech. 2009, 36, 725–735. [Google Scholar] [CrossRef]
- Banerjee, A.; Chakraborty, T.; Matsagar, V. Evaluation of possibilities in geothermal energy extraction from oceanic crust using offshore wind turbine monopiles. Renew. Sustain. Energy Rev. 2018, 92, 685–700. [Google Scholar] [CrossRef]
- Banerjee, A.; Chakraborty, T.; Matsagar, V. Stochastic Dynamic Analysis of an Offshore Wind Turbine Considering Frequency-Dependent Soil–Structure Interaction Parameters. Int. J. Struct. Stab. Dyn. 2018, 18, 1850086. [Google Scholar] [CrossRef]
- Banerjee, A.; Chakraborty, T.; Matsagar, V.; Achmus, M. Dynamic analysis of an offshore wind turbine under random wind and wave excitation with soil-structure interaction and blade tower coupling. Soil Dyn. Earthq. Eng. 2019, 125, 105699. [Google Scholar] [CrossRef]
- Banerjee, A.; Chakraborty, T.; Matsagar, V. Dynamic analysis of an offshore monopile foundation used as heat exchanger for energy extraction. Renew. Energy 2019, 131, 518–548. [Google Scholar] [CrossRef]
- Le, C.H.; Kim, S.R. Evaluation of combined horizontal moment bearing capacities of tripod bucket foundations in undrained clay. Ocean Eng. 2014, 85, 100–109. [Google Scholar]
- Kinsman, B. Wind Waves: Their Generation and Propagation of the Ocean Surface; Dover Publications: New York, NY, USA, 1965. [Google Scholar]
- Andersen, L.V. Dynamic soil–structure interaction of polypod foundations. J. Comp. Struc. 2018, 7, 007. [Google Scholar] [CrossRef]
- Andersen, L.; Andersen, T.; Manuel, L. Model uncertainties for soil-structure interaction in Offshore Wind Turbine monopile foundations. J. Mar. Sci. Eng. 2018, 6, 87. [Google Scholar] [CrossRef]
- Peplow, A.T.; Andersen, L.V.; Bucinskas, P. Environmental vibration reduction utilizing an array of mass scatterers. Procedia Eng. 2017, 199, 1368–1373. [Google Scholar] [CrossRef]
- Bayat, M.; Andersen, L.V.; Ibsen, L.B. P-y-ẏ curves for dynamic analysis of offshore wind turbine monopile foundations. Soil Dyn. Earthq. Eng. 2016, 90, 38–51. [Google Scholar] [CrossRef]
- Bayat, M.; Andersen, L.V.; Ibsen, L.B.; Clausen, J. Influence of pore water in the seabed on dynamic response of offshore wind turbines on monopiles. Soil Dyn. Earthq. Eng. 2017, 100, 233–248. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V.; Datta, T.K. Distributed multiple tuned mass dampers for wind response control of chimney with flexible foundation. Procedia Eng. 2017, 199, 1641–1646. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V.; Datta, T.K. Along-wind response control of chimneys with distributed multiple tuned mass dampers. Struct. Control HLTH 2018, 2275. [Google Scholar] [CrossRef]
- Wu, X.H.; Zhang, L.W.; Wang, R.K. Ship Manoeuvring and Seakeaping; China Communication Press: Beijing, China, 1988. [Google Scholar]
- Yang, J.M.; Xiao, L.F., Sheng. Experimental study on hydrodynamics of Offshore Engineering; Shanghai Jiaotong University Press: Shanghai, China, 2008. [Google Scholar]
- MOSES. Reference Manual for Moses; Ultramarine Inc.: Houston, TX, USA, 2009. [Google Scholar]
- Andersen, P. Ship motion and sea loads in restricted water depth. Ocean Eng. 1979, 6, 557–569. [Google Scholar] [CrossRef]






| D (m) | H (m) | Hd (m) | Distance Between Bucket (m) | MS (kg) | MS + MW (kg) | Moment of Inertia (kg·m4) | Gravity Center of Structure above O (m) | |
|---|---|---|---|---|---|---|---|---|
| IbmX | IbmY | |||||||
| 0.4 | 0.25 | 0.16 | 0.6 | 18.75 | 61.83 | 4.691 | 4.697 | (0,0,0.156) |
| 0.4 | 0.25 | 0.18 | 0.6 | 18.75 | 69.56 | 5.311 | 5.317 | (0,0,0.156) |
| 0.4 | 0.25 | 0.20 | 0.6 | 18.75 | 77.28 | 5.967 | 5.972 | (0,0,0.156) |
| D (m) | H (m) | Hd (m) | Distance Between Bucket (m) | MS (kg) | MS + MW (kg) | Moment of Inertia (kg·m4) | Gravity Center of Structure Above O (m) | |
|---|---|---|---|---|---|---|---|---|
| IbmX | IbmY | |||||||
| 10.0 | 6.75 | 4.0 | 15.0 | 292.97 | 966.1 | 45.81 × 106 | 45.87 × 106 | (0,0,3.89) |
| 10.0 | 6.75 | 4.5 | 15.0 | 292.97 | 1086.9 | 51.87 × 106 | 51.92 × 106 | (0,0,3.89) |
| 10.0 | 6.75 | 5.0 | 15.0 | 292.97 | 1207.6 | 58.27 × 106 | 58.32 × 106 | (0,0,3.89) |
| Items | Hw (m) | MS (kg) | MS + MW (kg) | CZ (kN/m) | Td (s) | n | |||
|---|---|---|---|---|---|---|---|---|---|
| Test | MOSES | Error (%) | |||||||
| Heave | 0.16 | 18.75 | 61.83 | 3757.8 | 0.937 | 0.952 | 1.60 | 1.35 | 0.051 |
| 0.18 | 18.75 | 69.55 | 3763.1 | 0.967 | 0.976 | 0.93 | 1.28 | 0.055 | |
| 0.20 | 18.75 | 77.28 | 3768.4 | 0.991 | 1.000 | 0.91 | 1.21 | 0.064 | |
| Items | Hw (m) | Ms (kg) | IbmX(IbmY) (kg·m4) | CmX(CmY) (kN·m/rad) | Td (s) | n | |||
|---|---|---|---|---|---|---|---|---|---|
| Test | MOSES | Error (%) | |||||||
| Roll | 0.16 | 18.75 | 4.691 | 224.6 | 1.115 | 1.111 | 0.36 | 1.53 | 0.081 |
| 0.18 | 18.75 | 5.311 | 225.0 | 1.146 | 1.143 | 0.26 | 1.40 | 0.075 | |
| 0.20 | 18.75 | 5.967 | 226.6 | 1.177 | 1.176 | 0.08 | 1.32 | 0.066 | |
| Pitch | 0.16 | 18.75 | 4.69 | 224.6 | 1.112 | 1.111 | 0.09 | 1.49 | 0.095 |
| 0.18 | 18.75 | 5.31 | 225.0 | 1.144 | 1.143 | 0.09 | 1.39 | 0.088 | |
| 0.20 | 18.75 | 5.97 | 226.6 | 1.173 | 1.176 | 0.25 | 1.32 | 0.074 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhang, P.; Zhao, M.; Ding, H.; Le, C. Air-Floating Characteristics of Large-Diameter Multi-Bucket Foundation for Offshore Wind Turbines. Energies 2019, 12, 4108. https://doi.org/10.3390/en12214108
Liu X, Zhang P, Zhao M, Ding H, Le C. Air-Floating Characteristics of Large-Diameter Multi-Bucket Foundation for Offshore Wind Turbines. Energies. 2019; 12(21):4108. https://doi.org/10.3390/en12214108
Chicago/Turabian StyleLiu, Xianqing, Puyang Zhang, Mingjie Zhao, Hongyan Ding, and Conghuan Le. 2019. "Air-Floating Characteristics of Large-Diameter Multi-Bucket Foundation for Offshore Wind Turbines" Energies 12, no. 21: 4108. https://doi.org/10.3390/en12214108
APA StyleLiu, X., Zhang, P., Zhao, M., Ding, H., & Le, C. (2019). Air-Floating Characteristics of Large-Diameter Multi-Bucket Foundation for Offshore Wind Turbines. Energies, 12(21), 4108. https://doi.org/10.3390/en12214108






