Optimal Coordination of DOC Relays Incorporated into a Distributed Generation-Based Micro-Grid Using a Meta-Heuristic MVO Algorithm

Abstract

Distributed, generation-based micro-grids are increasingly being used in the build-up of the modern power system. However, the protection of these micro-grids has many challenges. One of the important challenges is the coordination of directional overcurrent (DOC) relays. The optimization of the coordination of DOC relays is considered a nonlinear programming problem with pre-defined constrains. In this paper, the problem of the optimal coordination of DOC relays is solved using a multi-verse optimization (MVO) algorithm which is inspired from cosmology science. The proposed algorithm is tested by applying it to Institute of Electrical and Electronics Engineers (IEEE) 3 bus and IEEE 9 bus networks. The performance of the proposed algorithm is compared with the particle swarm optimization (PSO) algorithm when applied to both networks. All results show that the performance of the MVO algorithm is better than PSO in terms of its reduction of both the overall operating time (OT) of DOC relays and the computational burden of the computer solving the optimization problem.

1. Introduction

The power system protection of micro-grids must have one main feature, which is the selectivity. For this purpose, the DOC relays are intensively incorporated in the protection of micro-grids since they measure both the magnitude and direction of the phase current to reassure that the fault is occurring within the intended protection zone [1,2]. However, the selectivity is guaranteed only if there is a total coordination between the main and back-up relays, as shown in Figure 1 [3]. This coordination becomes more complex in the presence of distributed generation because of the bidirectionality of the phase currents [4,5]. The coordination between primary and back-up relays is achieved by selecting suitable current tap setting (CTS) and time dial setting (TDS) to guarantee a coordination time interval (CTI) [3,6,7,8,9,10].

In the field of power systems protection, fast response of relays (and breakers) is very beneficial, as it assures the maximum safety of the equipment and personnel. In addition, reducing the tripping times in a given system increases its reliability and security, where a given system with faster tripping times will assure that bus bars, transmission lines, cables and all equipment will not be subjected to heavy current stresses which may damage the equipment and reduce its life time.

Also, reducing tripping time will ensure adequate time space for both main and backup protection systems, and this assures that in cases where main protection equipment fails to respond in case of a fault, the backup breaker will interrupt the fault as fast as possible.

If the overall tripping times increase, both main and backup protective devices will consequently take a longer time to interrupt the circuit in case of a fault, which may lead to extreme damage to equipment and risks to human safety.

Many researchers have been attracted to propose algorithms that solve the problem of the coordination of DOC relays. This problem was firstly solved by a trial and error approach; this is done by trying different settings randomly till achieving the proper coordination [11,12]. Although this method is very simple, it suffers from two drawbacks: The first is that it takes A very long time to reach the convergence, and the second is that this method may increase the overall operating time (OT) of the tripping [13]. This has directed the researchers to use the linear programming in solving the coordination problem by selecting the TDS only [14]. This method is very efficient in achieving the optimal coordination. However, this method depends mainly on the accurate selection of the initial condition of CTS, since if the selection is not accurate then the program will not converge [15].

Nonlinear programming has also been incorporated into the optimization of the coordination of DOC relays, which give better results when compared to linear programming. However, this method also depends on the proper selection of CTS which is also considered a drawback. Moreover, the computational burden of this method is very high [16].

In the recent years and after the advancement of metaheuristic optimization algorithms, these algorithms have attracted many researchers to solve the DOC relays coordination problem. One of the most popular bio-inspired optimization algorithms is the Particle Swarm Optimization (PSO) which is inspired from the biological behavior in the navigation of search space looking for food [17,18,19,20,21]. This method has been proposed by many research papers to solve the DOC relays coordination problem due to its robustness and familiarity [22].

However, this algorithm has a clear disadvantage, which is the dependability on the constructive cooperation rather than keeping track on each search member separately to find the fittest one [12]. Another important algorithm is the Genetic Algorithm which is inspired from the Darwinian evolution resembling the behavior of chromosomes till reaching a huge population [23,24,25,26,27]. Through this journey the variables of the objective function are updated, and the whole process is repeated till it reaches convergence. This method has the ability of supervising the position of each member to find the fittest one [28]. However, and unlike the PSO, it does not pay much attention to the cooperative behavior of all groups. Many other algorithms have also been incorporated in solving the DOC relays coordination problem, such as the Gravitational Search Algorithm [29], Biogeography-based optimization [8], Electromagnetic Field Optimization [30], Firefly algorithm [31] and the Whale Optimization Algorithm [32].

The Multi-Verse Optimization (MVO) has been recently proposed in [33]. The algorithm is based on the multi-verse theory, which proposes that there is more than one universe. It also describes the formation of these universes and how they are formed and allocated.

In this paper, the MVO is proposed for solving the DOC relay optimization problem through the selection of optimum CTS and TDS, so that the minimum OT is achieved. To test the performance of the proposed algorithm, it is applied to the IEEE 3 bus and IEEE 9 bus systems to show its advantages in terms of accuracy and efficiency. The obtained results from the MVO is compared with the PSO, which is very popular in solving the same problem.

The rest of this paper is organized as follows: Section 2 shows the definition of the DOC relay coordination problem including the mathematical representation of the OF. Section 3 introduces the MVO algorithm and how it is utilized to solve the DOC relay coordination problem. Section 4 shows the simulation results of different case studies.

2. Problem Definition

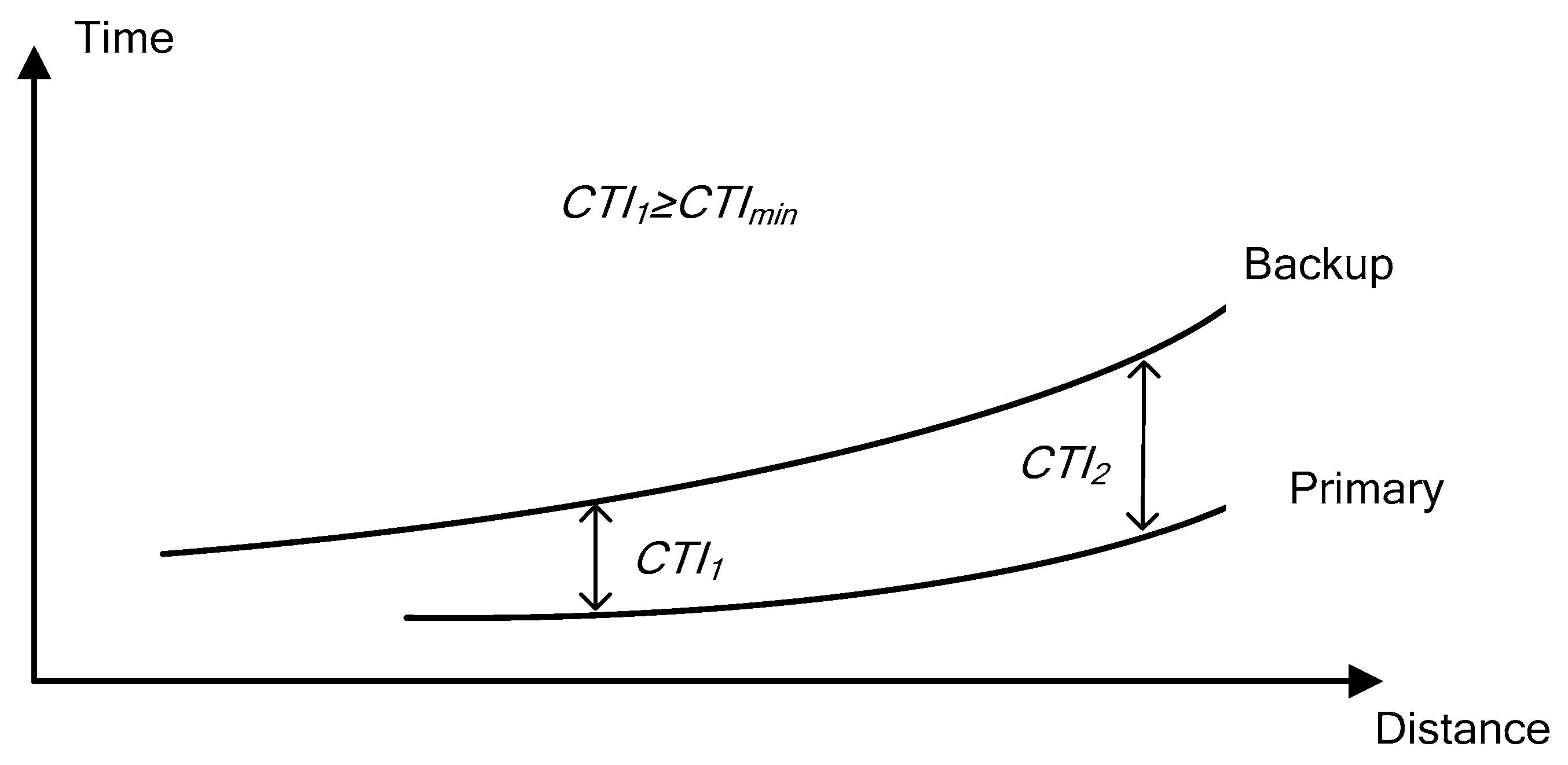
2.1. Formulation of the Objective Function

Each DOC relay has a dedicated Current Transformer (CT), so that the current passing through the relay, $I_{ik}$ is a fraction from the primary fault current, $I_{f, ik}$ as shown in (1):

$$I_{ik}=\frac{I_{f, ik}}{C{T}_{ratio}},$$

(1)

where $i$ is number of the relay, $k$ is the index of the fault location and $C{T}_{ratio}$ is the ratio between the primary current and secondary current. The OT of each relay can be calculated from (2):

$$T_{ik}=\frac{\alpha .TD{S}_i}{{\left(\frac{I_{ik}}{CT{S}_i}\right)}^n-1},$$

(2)

where $\alpha$ and $n$ are constant numbers are selected based on the required characteristics.

The optimization of the DOC relays aims to minimize the OT of all relays. So, the OF that needs to be minimized is expressed as per (3):

$$\min OF={\sum }_{i=1}^m\left({\sum }_{k=1}^n{T}_{ik}\right),$$

(3)

where $m$ is the number of the relays and $n$ is the number of possible fault locations.

2.2. Constraints of the Optimization Problem

The DOC relay coordination OF is considered a highly constrained function, as there are many factors, boundaries and constraints that must be employed before starting the optimization process. Firstly, there are certain limits for the CTS and TDS of each relay as per (4) and (5):

$$CT{S}_i^{\min }\le CT{S}_i\le CT{S}_i^{\max },$$

(4)

$$TD{S}_i^{\min }\le TD{S}_i\le TD{S}_i^{\max },$$

(5)

where $CT{S}_i^{min}$ and $CT{S}_i^{max}$ are the minimum and maximum values for the CTS of relay i according to the relay manufacturer.

Also, there are boundaries for the OT of each relay according to (6):

$$T_{ik}^{\min }\le T_{ik}\le T_{ik}^{\max },$$

(6)

where $T_{ik}^{min}$ is the minimum OT of relay i at fault k and this value is decided by the relay manufacturer. $T_{ik}^{max}$ is the maximum OT of relay i at fault k and this value is selected based on two main factors: The first factor is the thermal damage curve of the protected equipment, while the second is the stability margin of the zone related to the relay [12]. $T_{ik}^{max}$ must be lower than the time required to damage the protected equipment and at the same time it should guarantee the stability of the protected power system [12].

The last important constraint is the Coordination Time Interval (CTI), which is the time required to discriminate between primary and back-up relays to guarantee the system selectivity as shown in Figure 2 [16]. According to (7), the CTI is the OT difference between the back-relay j and the primary relay i.

$$CT{I}_k=T_{jk}-T_{ik},$$

(7)

It is important to be mentioned that the CTI must be higher than $CT{I}_{min}$, which is the minimum coordination time interval.

3. Multi-Verse Optimization

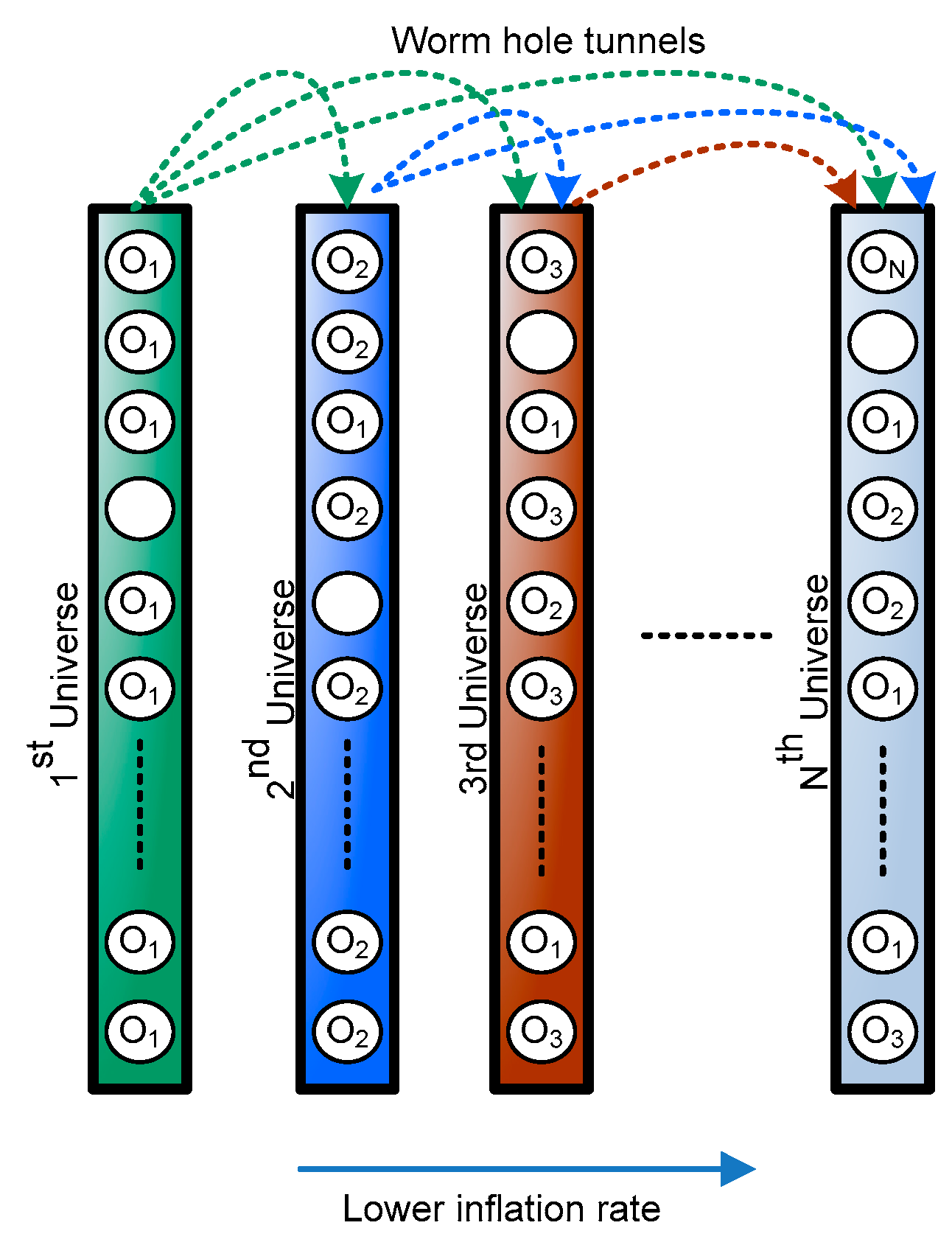
3.1. Basic Idea and Inspiration of MVO

The multi-verse theory which forms the basic idea of the MVO depends on three fundamental elements. The first is the white hole which has never been observed, as it occurs only either when a universe is created, or two adjacent universes are collapsed with each other. The second element is the black hole, which has a total opposite behavior to that of the white hole. Black holes are frequently observed, also they have massive gravitational forces that make them able to attract all ambient objects. The third element is the wormhole, which is responsible for exchanging objects between different universes or even between different parts at the same universe [33].

Also, the multi-verse theory describes the process of universe expansion which depends mainly on the inflation rate of it. The rate controls the formation of universe elements. The MVO search process resembles the process of reaching a stable situation of two parallel universes through the interaction between black, white and wormholes.

This method has been utilized in important applications related to optimization and the management of processes related to renewable energy and power systems [34].

The philosophy of the MVO is illustrated in Figure 3, where $n$ universes are present and each of them is considered a solution. A universe with high inflation rate will tend to send objects to other universes with a lower inflation rate through wormholes. The best universe/solution is the one having the lowest inflation rate to be able to receive objects from all other universes.

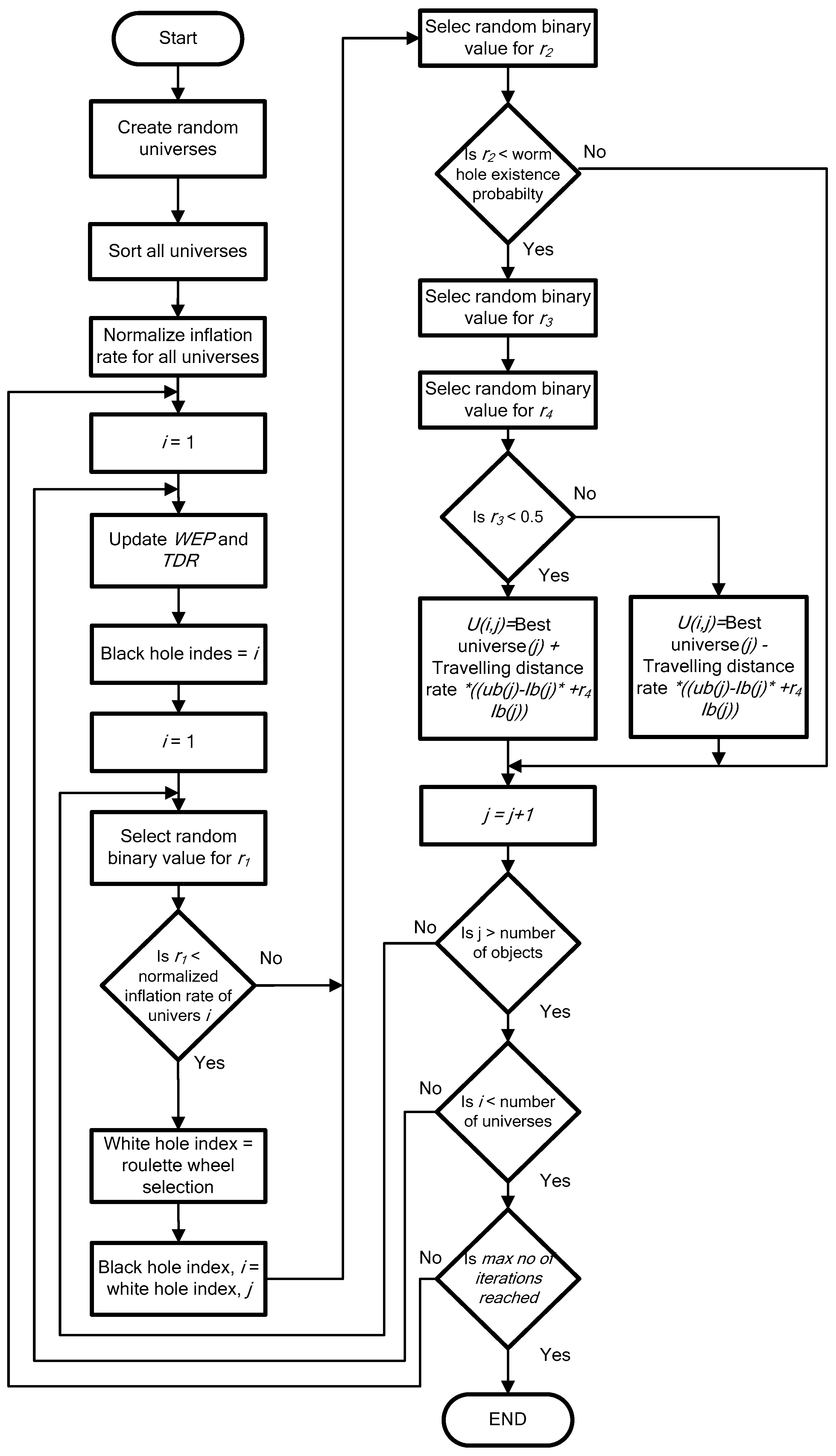
3.2. Mathematical Model of MVO Algorithm

Assume that d is the number of variables and n is the number of candidate solutions. All universes can be tabulated randomly using the roulette wheel mechanisms shown in (8) [34]:

$$U=\left[\begin{array}{c}\begin{array}{ccc}{x}_1^1& x_1^2& \dots \\ x_2^1& x_2^2& \dots \\ ⋮& ⋮& ⋮\end{array} \begin{array}{c}{x}_1^d\\ x_2^d\\ ⋮\end{array}\\ \begin{array}{cc}{x}_n^1& x_n^2\end{array} \begin{array}{cc}\dots & x_n^d\end{array}\end{array}\right]$$

(8)

where $x_i^j$ is the j^th parameter of the i^th universe. Each parameter can be calculated from (9):

$$x_i^j=\{\begin{array}{ll}{x}_k^j,& r_1<NI\left(U_i\right)\\ x_i^j,& r_1\ge NI\left(U_i\right)\end{array}$$

(9)

where $x_k^j$ is the j^th parameter of the k^th universe, $r_1$ is a random binary number which can be either 0 or 1, and $NI\left(U_i\right)$ is the inflation rate of the i^th universe. As shown in (9), the roulette wheel mechanism forms white holes based on different inflation rates. Universes with lower inflation have a high probability of receiving objects through white/black holes. However, each universe intends to make local changes using wormholes to improve its inflation rate. This mechanism can be described as per (10):

$$x_i^j=\{\begin{array}{cc}\begin{array}{c}\{\begin{array}{ll}{X}_j+TDR x (\left(u{b}_j-l{b}_j\right).r_4+l{b}_j,& r_3<0.5\\ X_j-TDR x (\left(u{b}_j-l{b}_j\right).r_4+l{b}_j,& r_3\ge 0.5 \end{array}\\ \end{array}& r_2<WEP\hfill \\ x_i^j& r_2\ge WEP\hfill \end{array}$$

(10)

where $X_j$ is the j^th element of the best solution (best universe created). $l{b}_j$ and $u{b}_j$ are the lower and upper bounds of this element. $r_2$, $r_3$ and $r_4$ are binary numbers. WEP is the wormhole existence probability while the TDR is traveling wave distance. The WEP is increased linearly against iterations to reassure the progress of the optimization algorithm and how it is far from finding the best solution. The WEP is updated based on adaptive equation as illustrated in (11):

$$WEP=\min +l x \left(\frac{\max -\min }{L}\right)$$

(11)

where min and max are the boundaries for the WEP coefficient. l is the order of the iteration while L is the maximum number of iterations.

TDR is also increased as the number of iterations increases to assure more accurate local search around the best solution. It is also updated according to adaptive formula as per (12):

$$TDR=1-\frac{l^{\frac{1}{p}}}{L^{\frac{1}{p}}}$$

(12)

where p is coefficient that controls the accuracy and speed of algorithm convergence. Figure 4 shows the flow chart of the MVO algorithm.

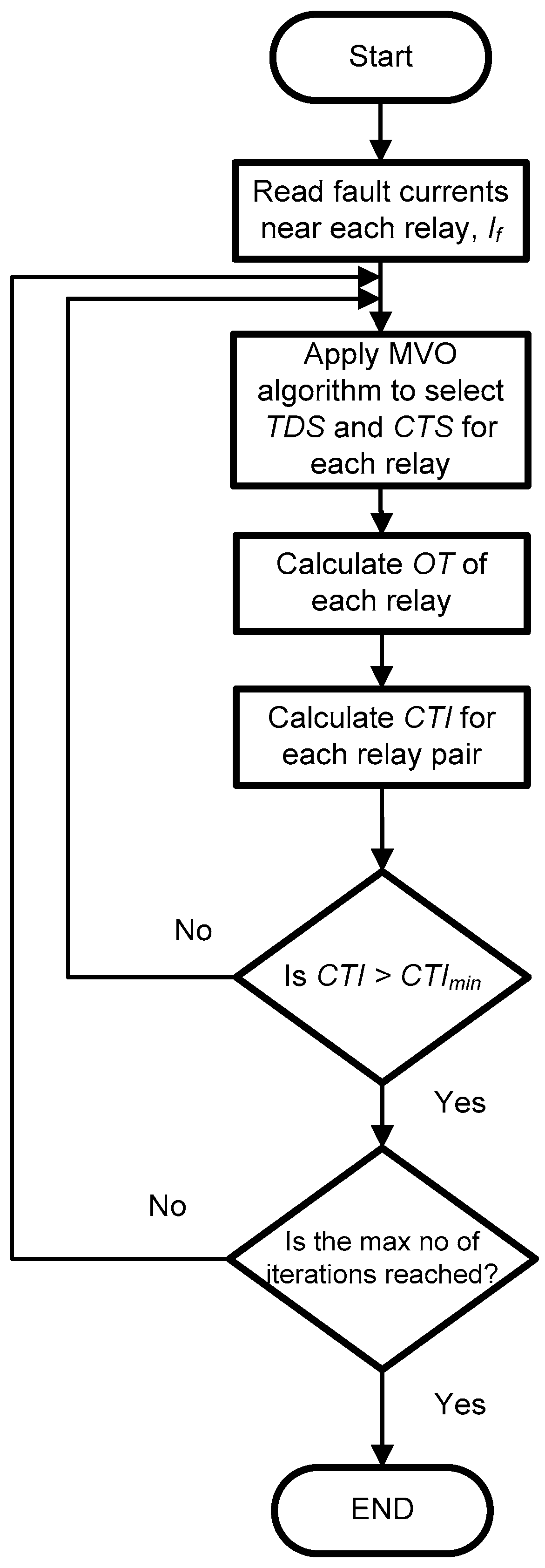
4. The Proposed Optimal Coordination Algorithm of DOC Relays

The proposed optimization algorithm utilizes the MVO algorithm in optimizing the DOC relays and minimizing the overall tripping time without violating the constrains of the OF. Firstly, the algorithm starts with reading the short circuit currents near the relays, then it applies the proposed MVO algorithm to choose TDS and Ip for each relay. The operating time of each relay is calculated based on the short circuit current and the selected TDS and Ip settings for each relay. After this step, the CTI for all relay pairs to ensure that it does not exceed the $CT{I}_{\min }$. Figure 5 shows a flow chart for the general steps followed to reach the optimum settings of DOC relays.

In the proposed algorithm, the universes represent the different solutions to the optimization problem which here will refer to the summation of the OT of all relays as per (3). The position of each parameter in any universe reflects the value of time dial setting and pick-up current that must be set to achieve the desired OT.

5. Simulation Results

In this section, the proposed MVO algorithm is tested on two different standard power systems layouts to evaluate its effectiveness. The simulation is carried out on both MATLAB (MathWorks Natick, MA, USA) and ETAP (Operation Technology, Inc., Irvine, CA, USA). power stations software packages. The simulation is repeated using a PSO algorithm which is considered a very popular optimization algorithm to evaluate the performance of the proposed algorithm in terms of convergence speed, accuracy of solutions and computational burden.

5.1. Case Study 1: The IEEE 3-Bus System

Single line diagram of the IEEE 3-bus system under investigation is shown in Figure 6. First, a short circuit analysis for all branch currents is conducted to find out primary and secondary fault currents. Results of the short circuit analysis for the system is illustrated in

Table 1. Fault currents of primary and backup relays for IEEE 3-bus system understudy [13,35].

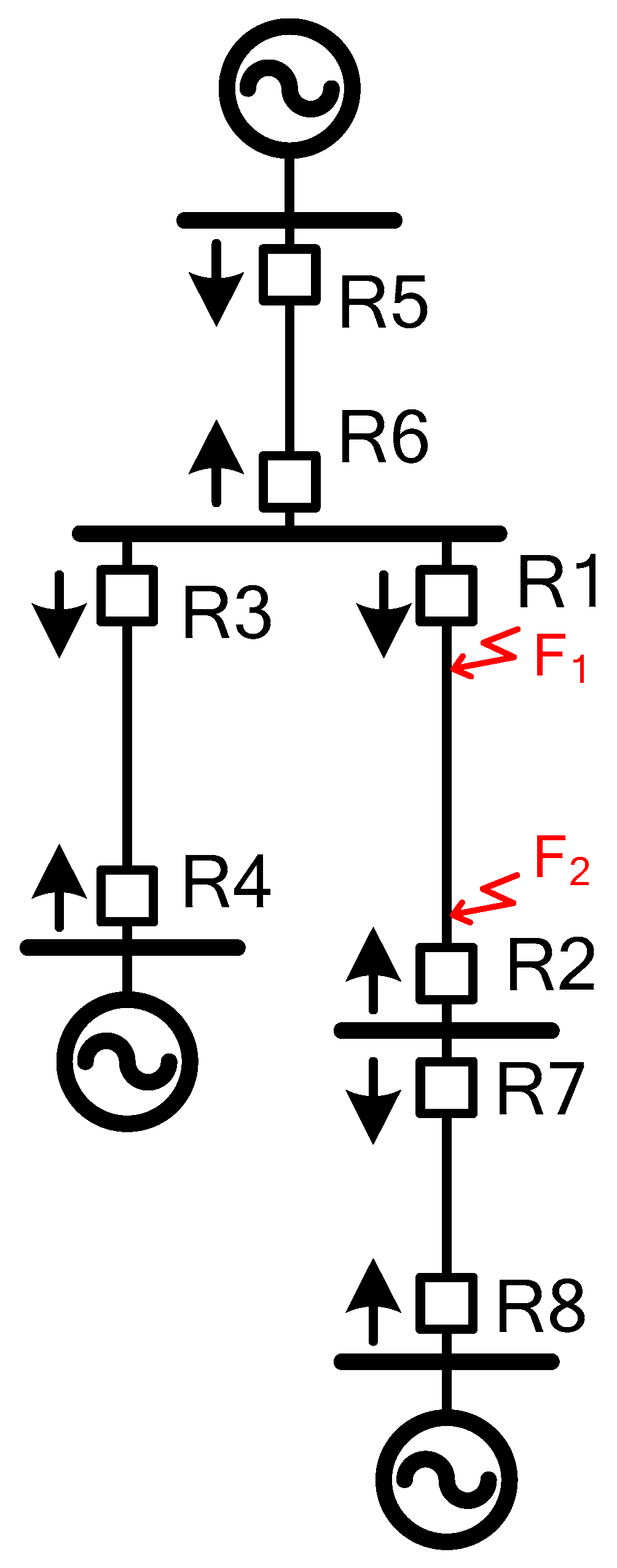
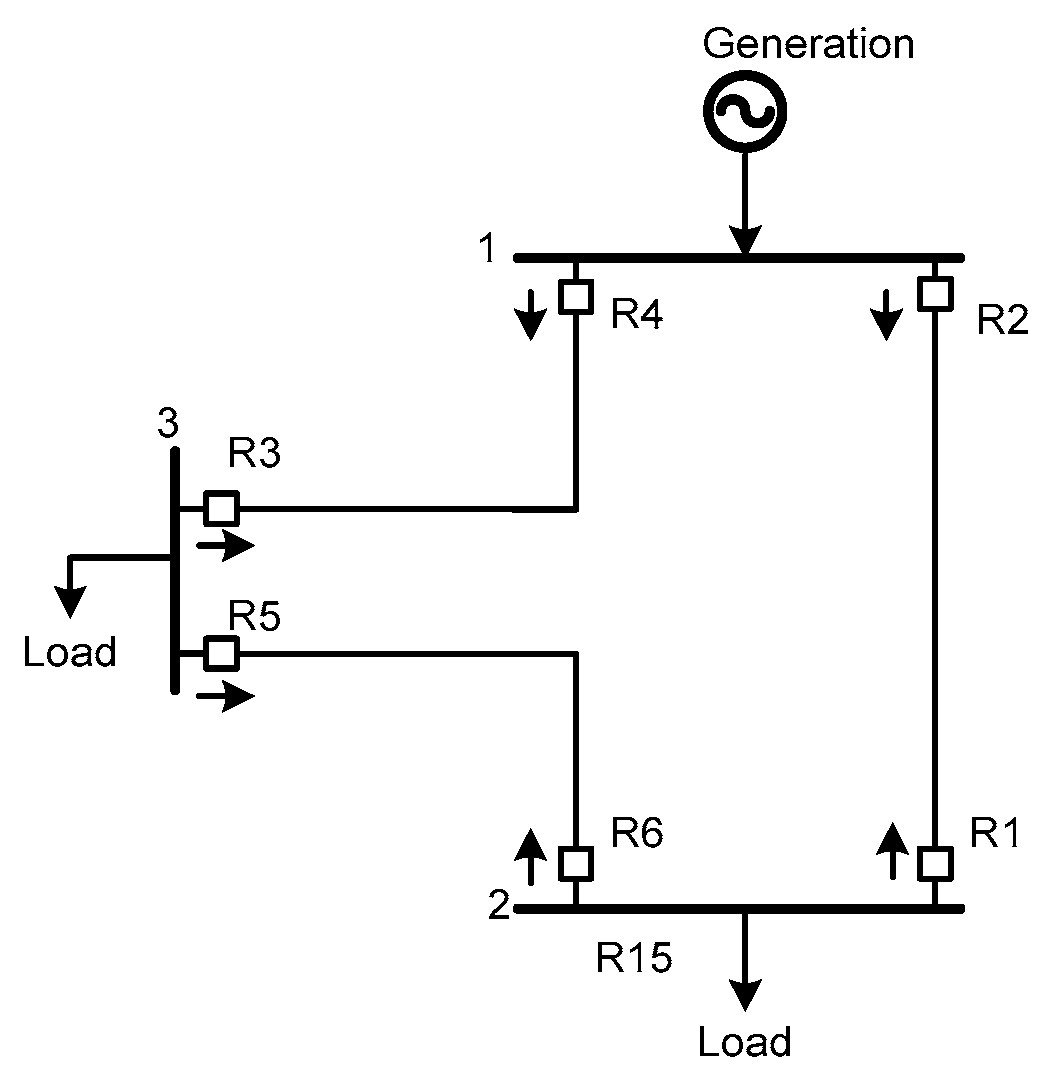
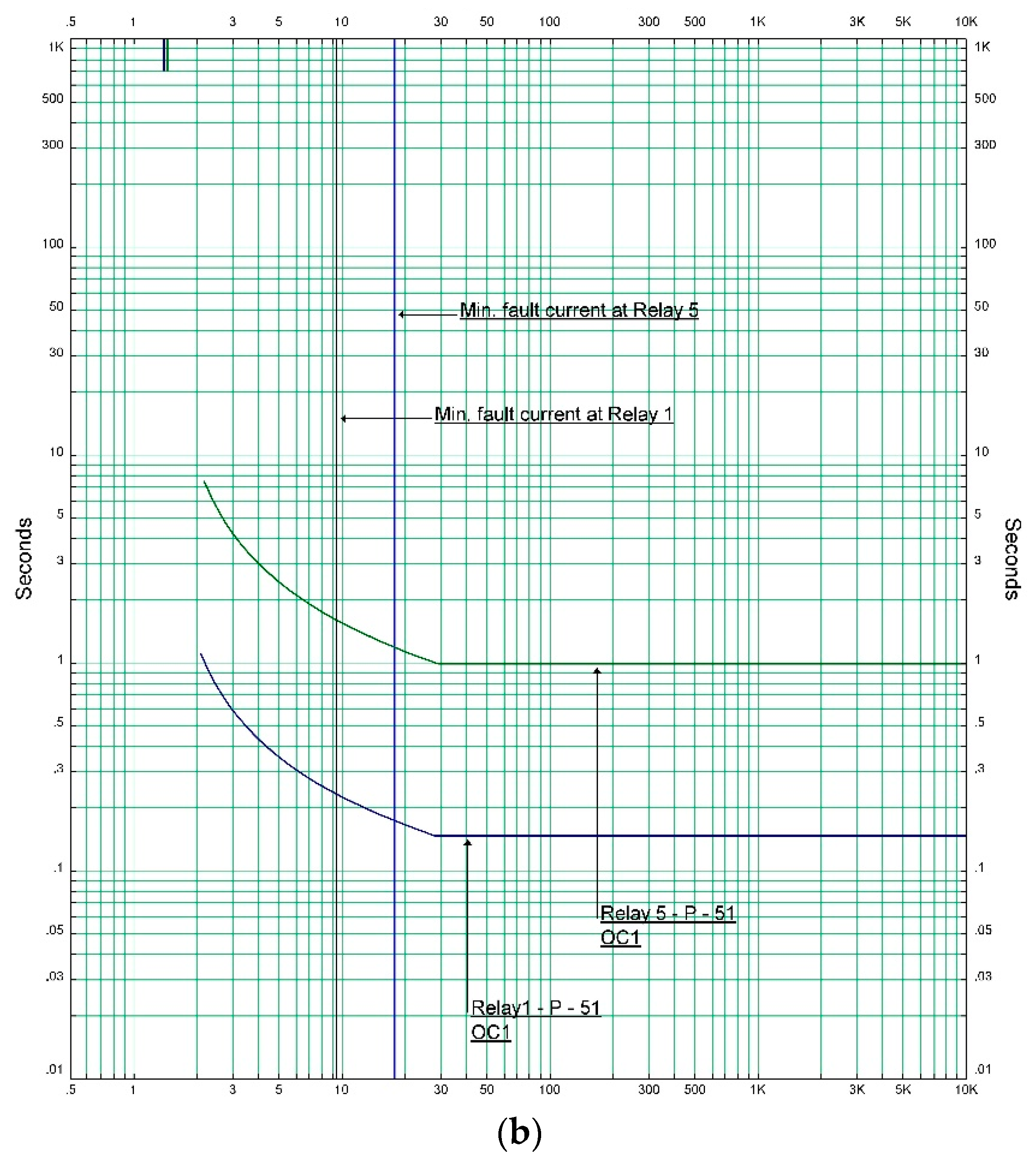
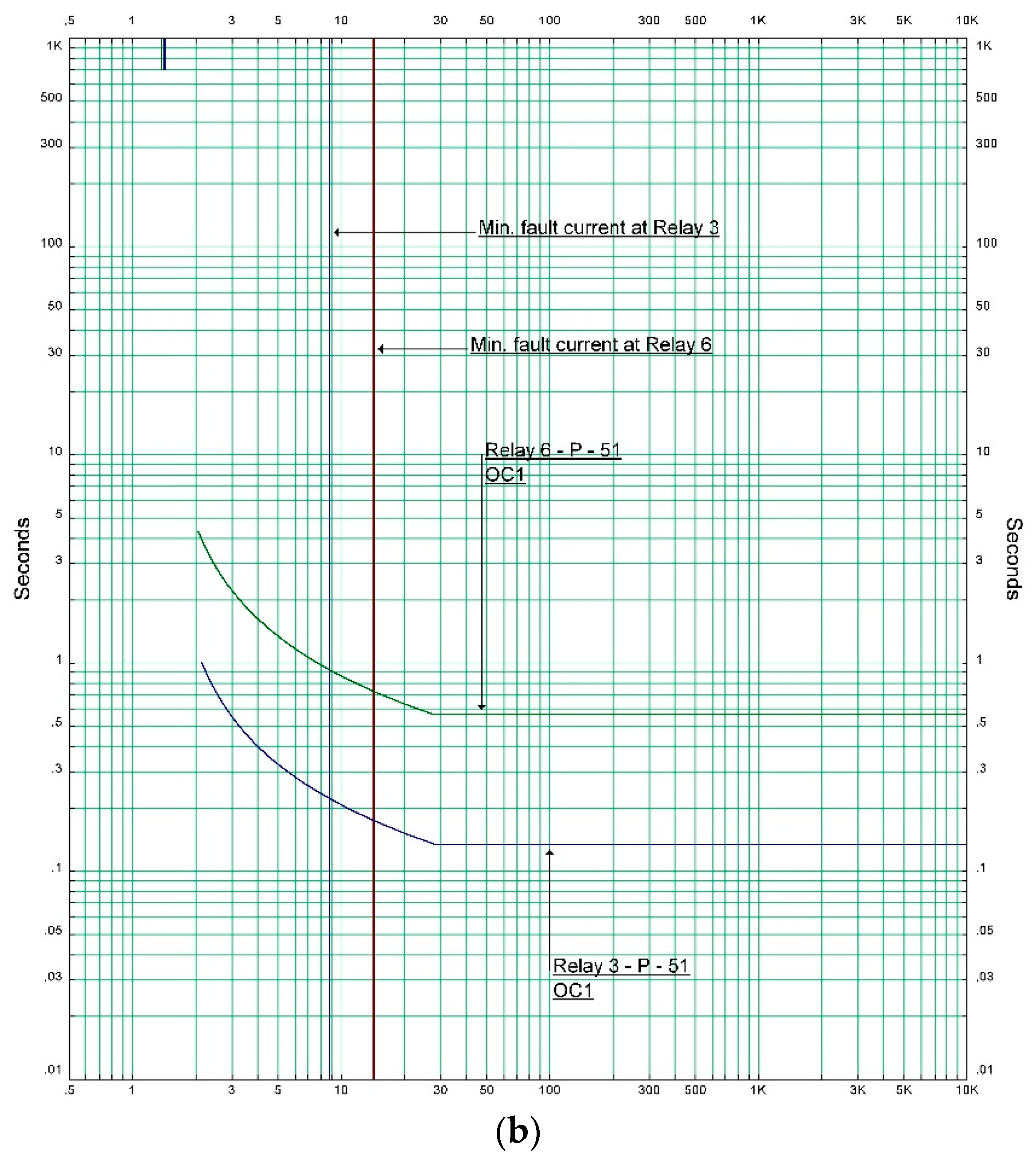
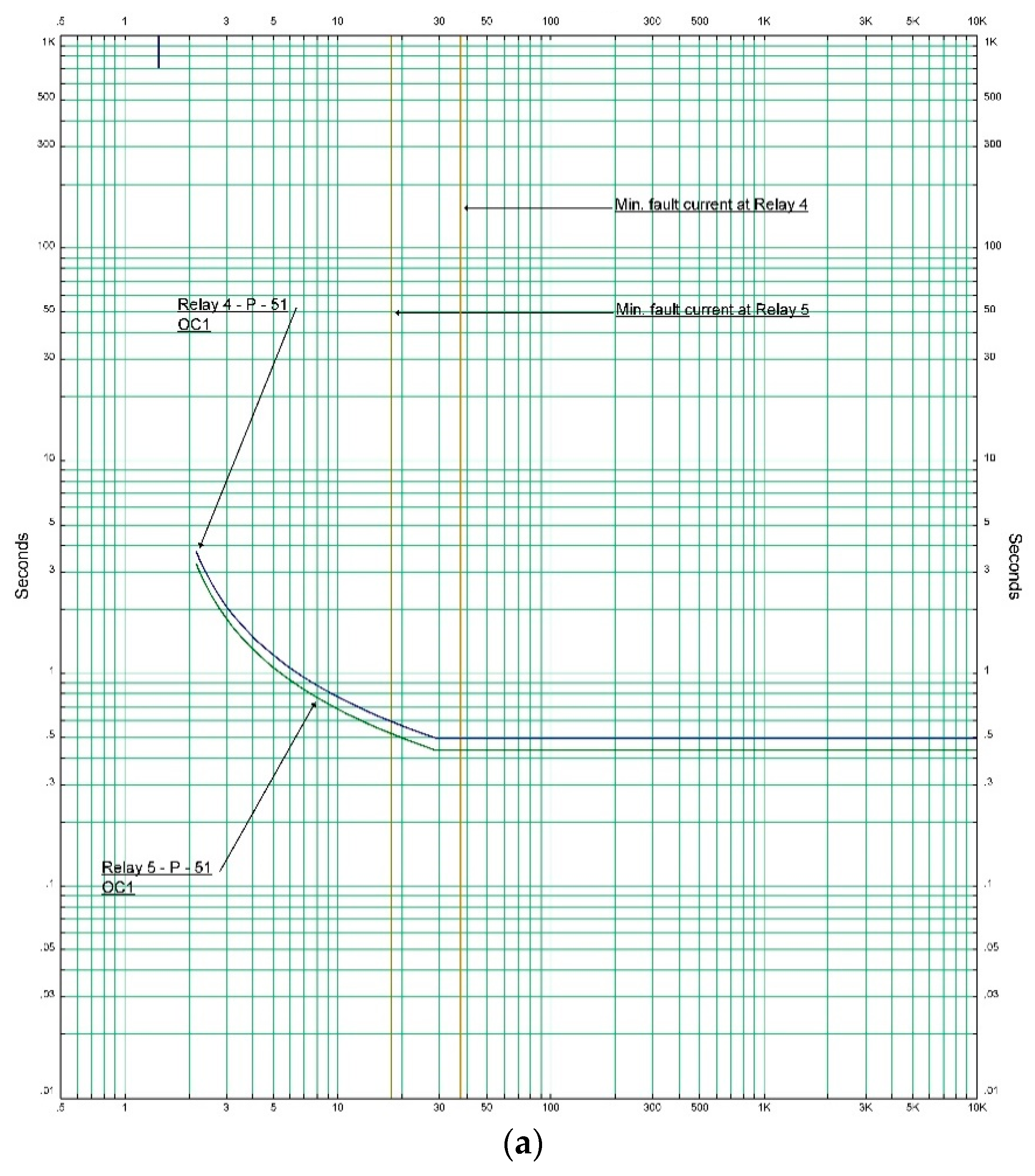
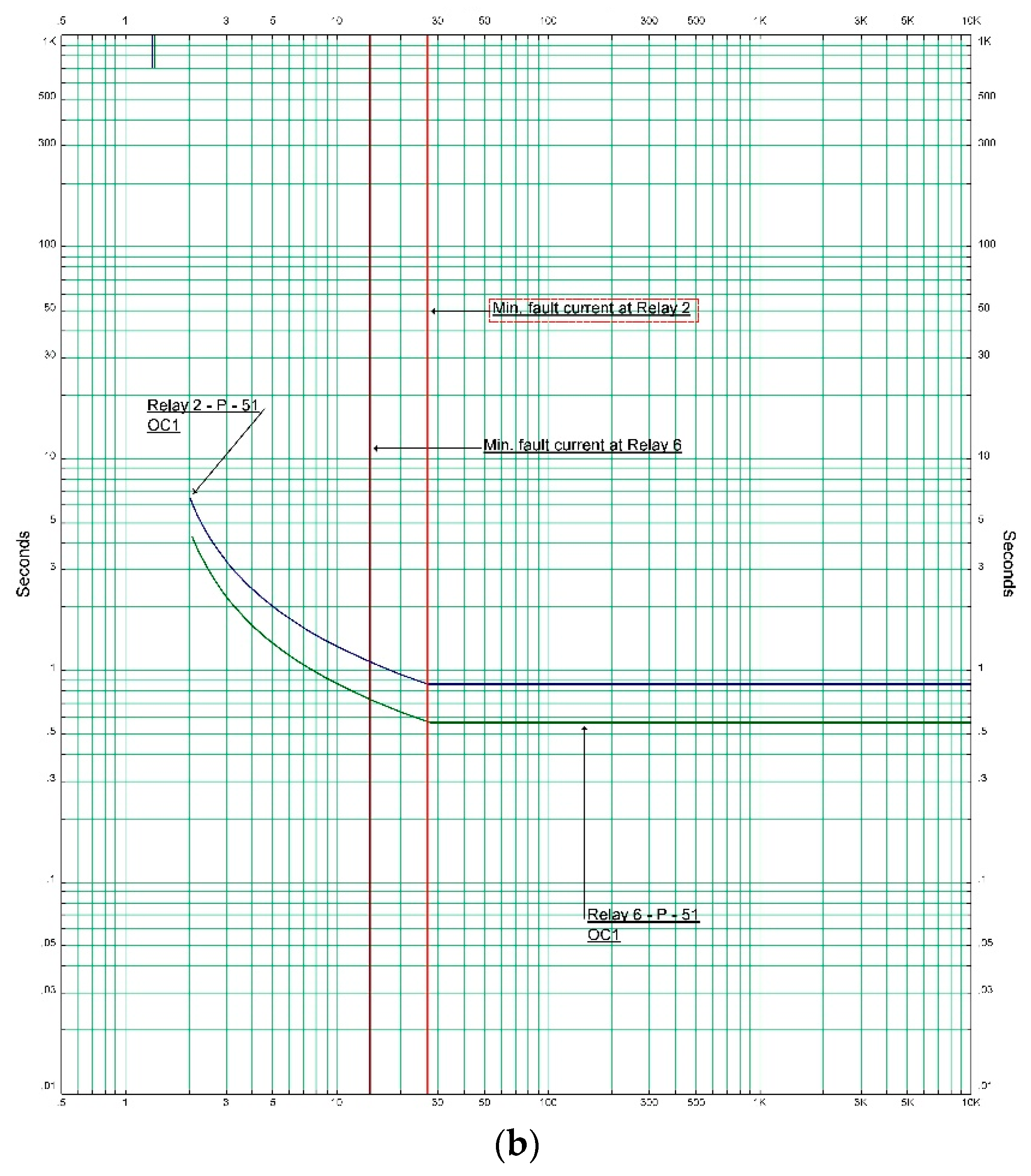
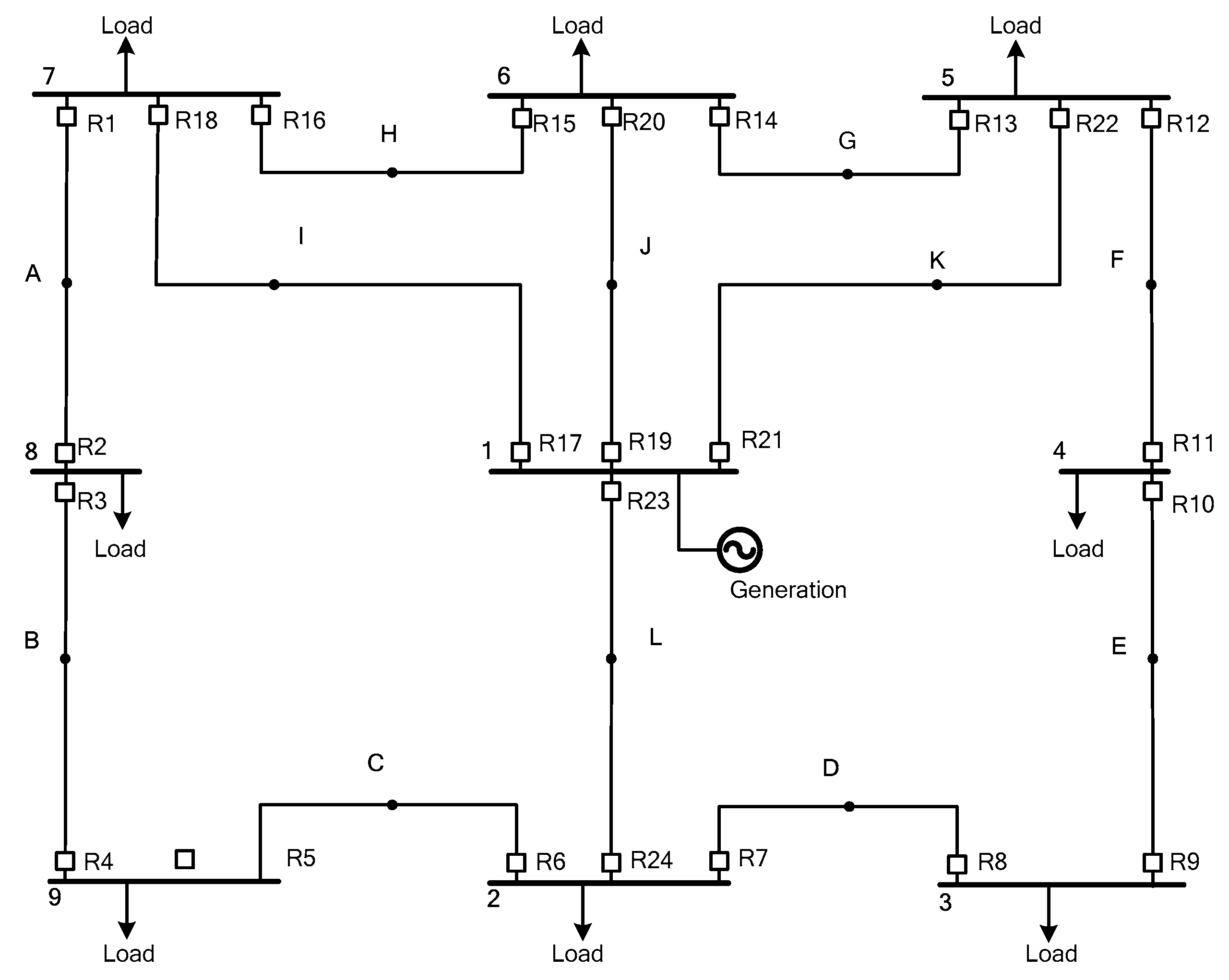
Primary Relay	Backup Relay	Primary Fault Current (A)	Secondary Fault Current (A)
R1	R5	9.46	14.08
R3	R6	8.81	12.07
R5	R4	17.93	25.9
R6	R2	14.35	19.2

.

Using MATLAB software, the system is simulated, and the coordination of the DOC relays is achieved using both the proposed MVO algorithm and the PSO algorithm. As shown in

Table 2. Simulation results for IEEE 3 bus system where the overall operating time (OT) is optimized using particle swarm optimization (PSO) and MVO algorithms.

Relay Number	Pick Up Current (PSO)	Time Dial Setting (PSO)	Pick Up Current (MVO)	Time Dial Setting (MVO)
1	1.4	0.065	1.4284	0.05
2	1.345	0.38	1.4969	0.2013
3	1.431	0.0591	1.336	0.05
4	1.365	0.6074	1.4433	0.2183
5	1.455	0.4367	1.4418	0.1912
6	1.38	0.2501	1.447	0.1876
Overall Tripping Time	9.209 s		4.964 s

, the OT of all relays is considerably reduced by using the proposed algorithm as it has been decreased from 9.209 s to 4.964 s. Also, in terms of the convergence speed, the proposed algorithm has higher convergence speed when compared to the PSO algorithm as shown in Figure 7.

Moreover, to verify the results obtained in Table 2, results are used to set the six relays, and the newly coordinated system is simulated using ETAP power stations simulation software. It can be observed that the proposed algorithm has more accurate results as it reduces the OT of each relay pair without violating the $CT{I}_{\min }$ or exceeding the boundaries of the CTS and TDS. This is clearly illustrated as shown in Figure 8, Figure 9, Figure 10 and Figure 11, where a comparison exists between results obtained from the proposed MVO algorithm and the PSO algorithm by showing the time-current curves for each relay pairs.

5.2. Case Study 2: The IEEE 9-Bus System

In this case, the IEEE 9 bus system is used for further verification of the proposed MVO algorithm where the single line diagram of the system in that case is shown in Figure 12. Similar to the previous case study, a short circuit analysis is carried out to obtain primary and back up fault currents and results are listed in

Table 3. Fault currents of primary an backup relays for the IEEE 9 bus system understudy [36].

Location	Primary Relay	Backup Relay	Primary Fault Current (kA)	Secondary Fault Current (kA)	Location	Primary Relay	Backup Relay	Primary Fault Current (kA)	Secondary Fault Current (kA)
A	R1	R15	24,779	9.150	G	R13	R11	16,087	3.088
	R1	R17	24,779	15.632		R13	R21	16,087	13
	R2	R4	8.327	8.327		R14	R16	18,213	6.285
B	R3	R1	16,390	16,930		R14	R19	18,213	11,934
	R4	R6	14,671	14,671	H	R15	R13	18,218	6.285
C	R5	R3	9.454	9.454		R15	R19	18,218	11,935
	R6	R8	23,280	4.777		R16	R2	16,087	3.088
	R6	R23	23,280	18,507		R16	R17	16,087	13
D	R7	R5	23,280	4.777	I	R18	R2	8.161	2.426
	R7	R23	23,280	18,507		R18	R15	8.161	5.736
	R8	R10	9.454	9.454	J	R20	R13	9.286	4.644
E	R9	R7	15,304	15,304		R20	R16	9.286	4.644
	R10	R12	16,490	16,490	K	R22	R11	8.161	2.426
F	R11	R9	8.326	8.327		R22	R14	8.161	5.736
	R12	R14	24,779	9.150	L	R24	R5	6.149	3.075
	R12	R21	24,779	15,631		R24	R8	6.149	3.075

. The coordination of the DOC relays is achieved using the proposed algorithm and the PSO algorithm.

Simulation results in this case are presented in

Table 4. Simulation results for IEEE 9 bus system where OT is optimized using PSO and MVO algorithms.

Relay Number	Pick Up Current (PSO)	Time Dial Setting (PSO)	Pick Up Current (MVO)	Time Dial Setting (MVO)
1	1.624	0.5702	0.50014	0.89758
2	1.321	0.4080	1.0332	0.37397
3	2.181	0.4131	1.5055	0.52843
4	1.138	0.6361	1.6936	0.37582
5	1.194	0.4456	1.3227	0.47198
6	1.957	0.6661	1.1088	0.65426
7	1.324	0.6667	2.143	0.59678
8	1.987	0.4053	1.2832	0.43074
9	1.469	0.5547	0.52688	0.77392
10	1.345	0.5632	1.6283	0.47139
11	0.941	0.4641	1.1773	0.29103
12	1.37	0.7049	1.047	0.79271
13	1.623	0.6047	1.0435	0.5042
14	1.114	0.6607	0.73153	0.77677
15	1.662	0.5650	1.7964	0.51331
16	1.518	0.6180	0.5	0.7673
17	1.392	0.7944	1.9575	0.84834
18	1.53	0.3172	2.0172	0.085839
19	1.621	0.6589	1.9127	0.74232
20	1.332	0.6028	0.58571	0.0178
21	1.684	0.8715	1.9693	0.85226
22	1.937	0.4269	2.2307	0.30646
23	1.678	0.9313	2.2652	0.81034
24	0.621	0.3483	0.50413	0.57707
Overall Tripping Time	24,381 s		20,887 s

. It can be observed that the OT of all relays is considerably reduced by using the proposed MVO algorithm in comparison with PSO algorithm, as it has been decreased from 24,381 s to 20,887 s. It is worth mentioning that the previous results are obtained by setting the MVO algorithm to run 400 iterations while the PSO algorithm is set to run 500 iterations. Proposed MVO converged faster in less iterations which means better performance and less computation burden.

6. Conclusions

In any given power system network at the occurrence of faults, it is required to isolate the fault as fast as possible to protect both the equipment from stress and the human from any risks. In this paper, a heuristic MVO optimization algorithm is presented as a solution to the directional over current relay coordination problem in micro-grids due to the bidirectional capabilities of system buses. The MVO algorithm is explained in detail, and the mathematical objective function is modeled with the aim of minimizing the overall tripping time of available protective relays in the system. The proposed MVO algorithm is tested on IEEE 3 bus and IEEE 9 bus systems, and results are compared with those obtained by the well-established PSO optimization algorithm. In both case studies the proposed MVO algorithm outperformed the PSO algorithm in all aspects. It can be concluded that OT, results convergence time and computation burden, have all been decreased significantly, which contributes to equipment and human safety, and increases overall system security.