Optimization of Feedforward Neural Networks Using an Improved Flower Pollination Algorithm for Short-Term Wind Speed Prediction
Abstract
:1. Introduction
2. Establishment of Forecasting Model
2.1. The Fundamentals of the FF Model
- (1)
- Initialize all connection weight v and threshold b using small random numbers.
- (2)
- Determine the structure of the FF model, input training samples and predictive output samples.
- (3)
- Calculate the outputs of the hidden layer under Equation (1) and the output layer under Equation (2) based on the forward propagation process.where is the output of the hidden layer; is the transfer function of the hidden layer; is the connection weight; is the node of the input layer; is the threshold of the hidden layer; is the number of hidden layers; is the output layer; is the transfer function of the output layer; is the connection weight; is the node of the hidden layer; is the threshold of the output layer; and is the number of output layers.
- (4)
- Update weights and thresholds using the back–propagation process, as shown in Equation (3):where and are the weights and thresholds at the and iteration, respectively; is a learning rate, and is the negative gradient of the output error at the iteration, that is, the fastest direction in gradient.
- (5)
- Repeat Steps (3) and (4) until the mean square error (E) reaches the predefined value:where S2 is the number of output layers; tk is the target value; and is the output value.
2.2. The Principle of IFPA
- (1)
- Initializing the parameters, such as the number of flower population N, the transformation probability parameters P and a random number rand ∈ (0,1) in FPA.
- (2)
- Finding the global optimal solution by comparing the values of the fitness of each solution.
- (3)
- If the conversion rate is p > rand (a predefined value), the solution is updated, and the transboundary process is implemented in the light of Equation (5):where and represent the solutions of the and generation, separately; is the global optimum solution; is the step length produced by pollen propagator Levyflying; and obeys the Levy distribution, and its value is substituted into Equation (6):where , is the step dimension, and is the minimum step dimension; is the standard Gamma function, and select ; and the Leavy flight step is generated under Mantegna’s algorithm [26].
- (4)
- If the conversion rate is , the solution is updated, and the transboundary process is implemented according to Equation (7):where is a random number on [0,1]; and and are pollen of flowers of the same plant species.
- (5)
- Compute Steps (3) and (4) to get the fitness of the data processing. Judge whether the fitness of the new solution reaches the optimal position. If yes, the fitness and solution is updated. Otherwise, the current fitness and solution remains unchanged.
- (6)
- If the fitness value of the global optimal is larger than the fitness value of the new solution value, then set a new solution as the global optimal solution.
- (7)
- Judge whether the end qualification is satisfied. If the conditions are met, the output is certified as the optimal value. Otherwise, return to Step (3).
2.3. Convergence of IFPA
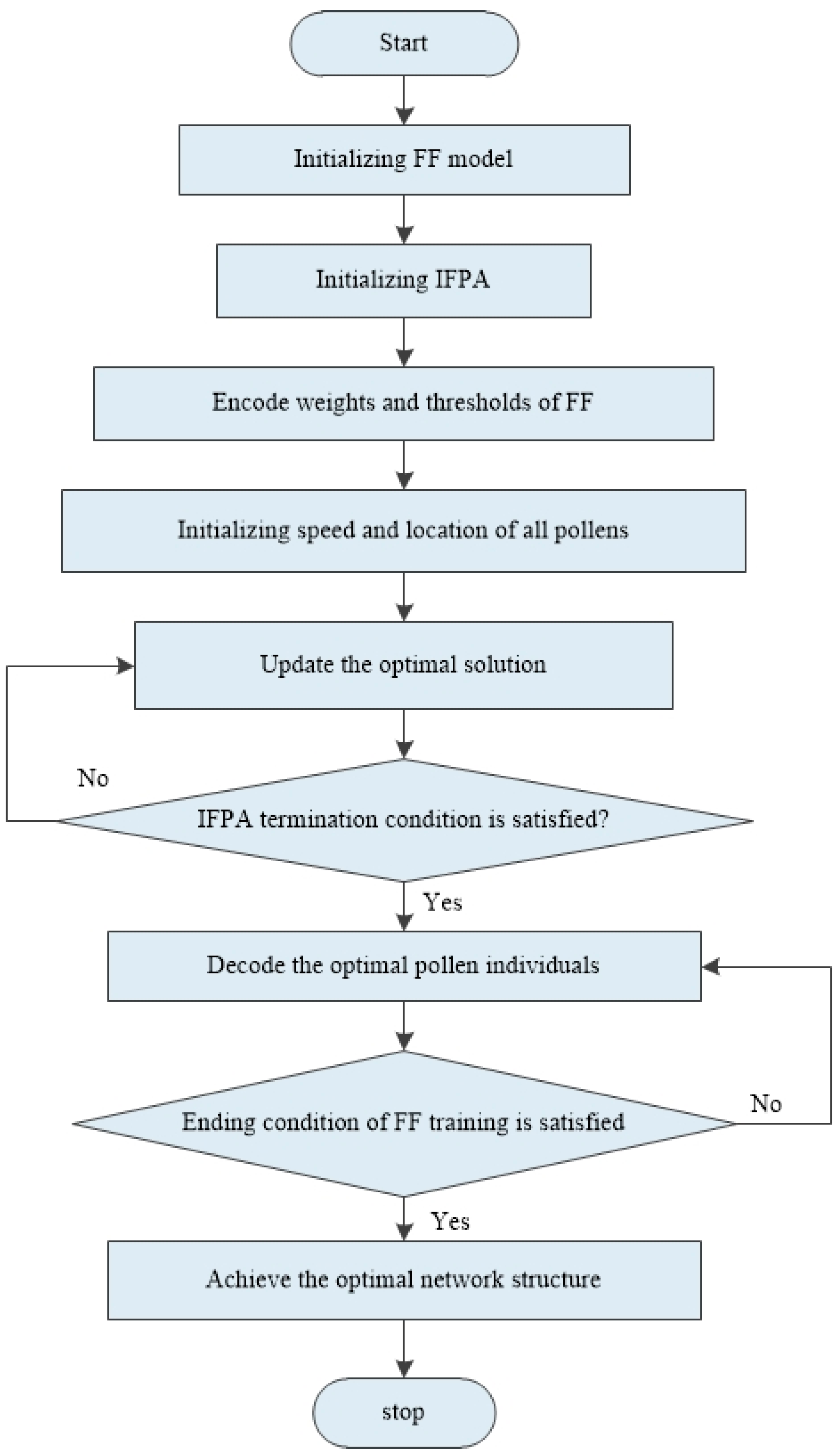
2.4. Optimization of the FF Model Based on IFPA
- (1)
- Initialize FF. Set input layer, hidden layer and output layer, initial network weight v and initial thresholds b.
- (2)
- Set the population number, the initial value of variation factor and network learning parameters, the maximum number of iterations and training end condition in IFPA algorithm.
- (3)
- The initial weight v and initial threshold b in FF neural network are encoded into individual pollens u, where each pollen represents the FF neural network structure.
- (4)
- The speed and position of all pollens are initialized, and the objective function of each pollen is kept computing until the minimum fitness value is reached.
- (5)
- A random value of rand is generated and compared with the conversion probability p. According to Equations (5) and (7) in FPA, the solution is kept being updated until the global optimal solution is reached.
- (6)
- If the termination condition of IFPA is met, proceed to the next step. Otherwise, return to Step (5).
- (7)
- The optimal pollen individual ui is decoded, and the decoded weights vi and bi are used as connection weight v and threshold b for FF.
- (8)
- If the ending condition of FF training is satisfied, the optimal network structure is thus obtained for further prediction. Otherwise, go back to Step (7).
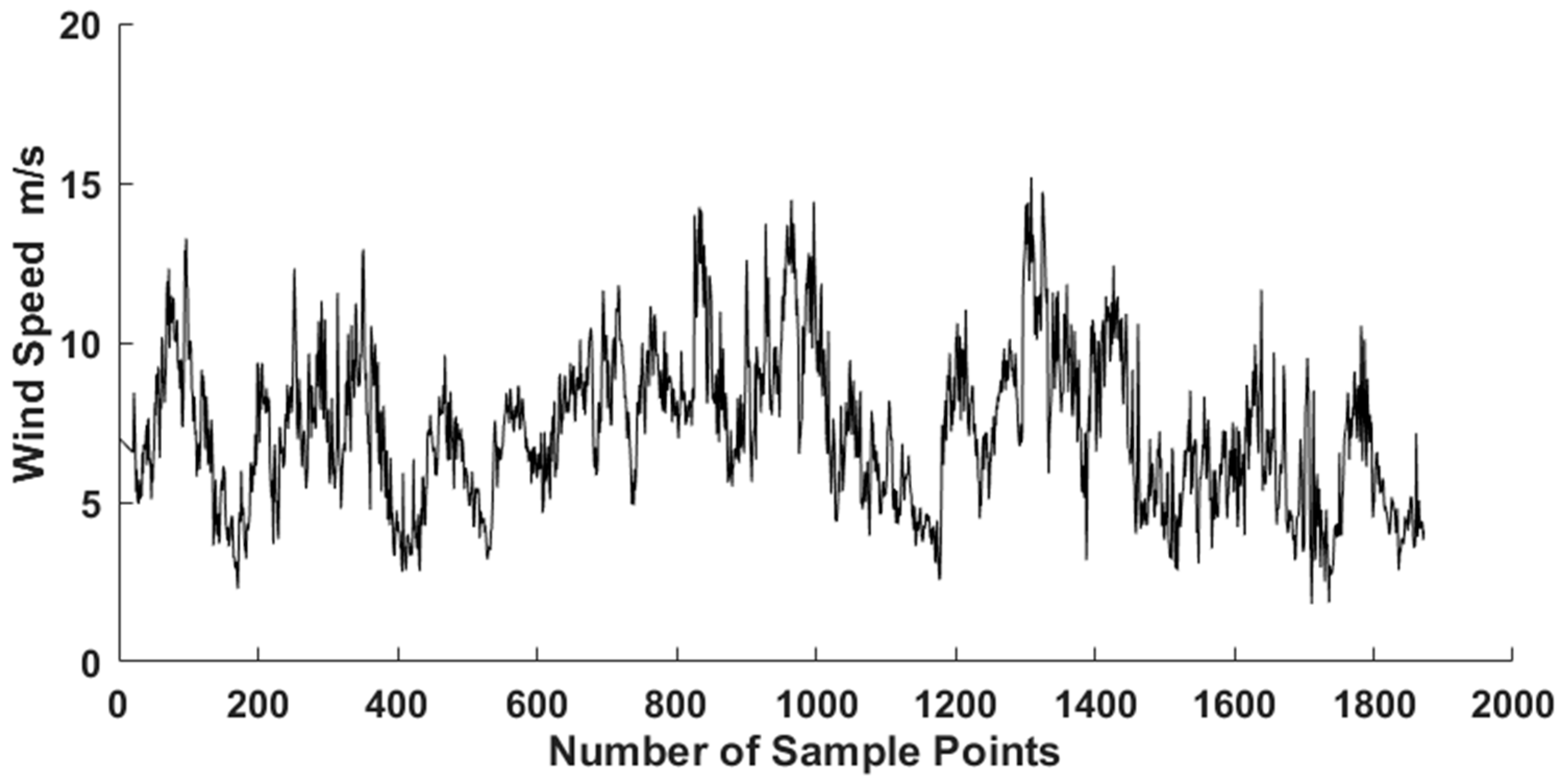
3. Analysis of Wind Speed Forecasting
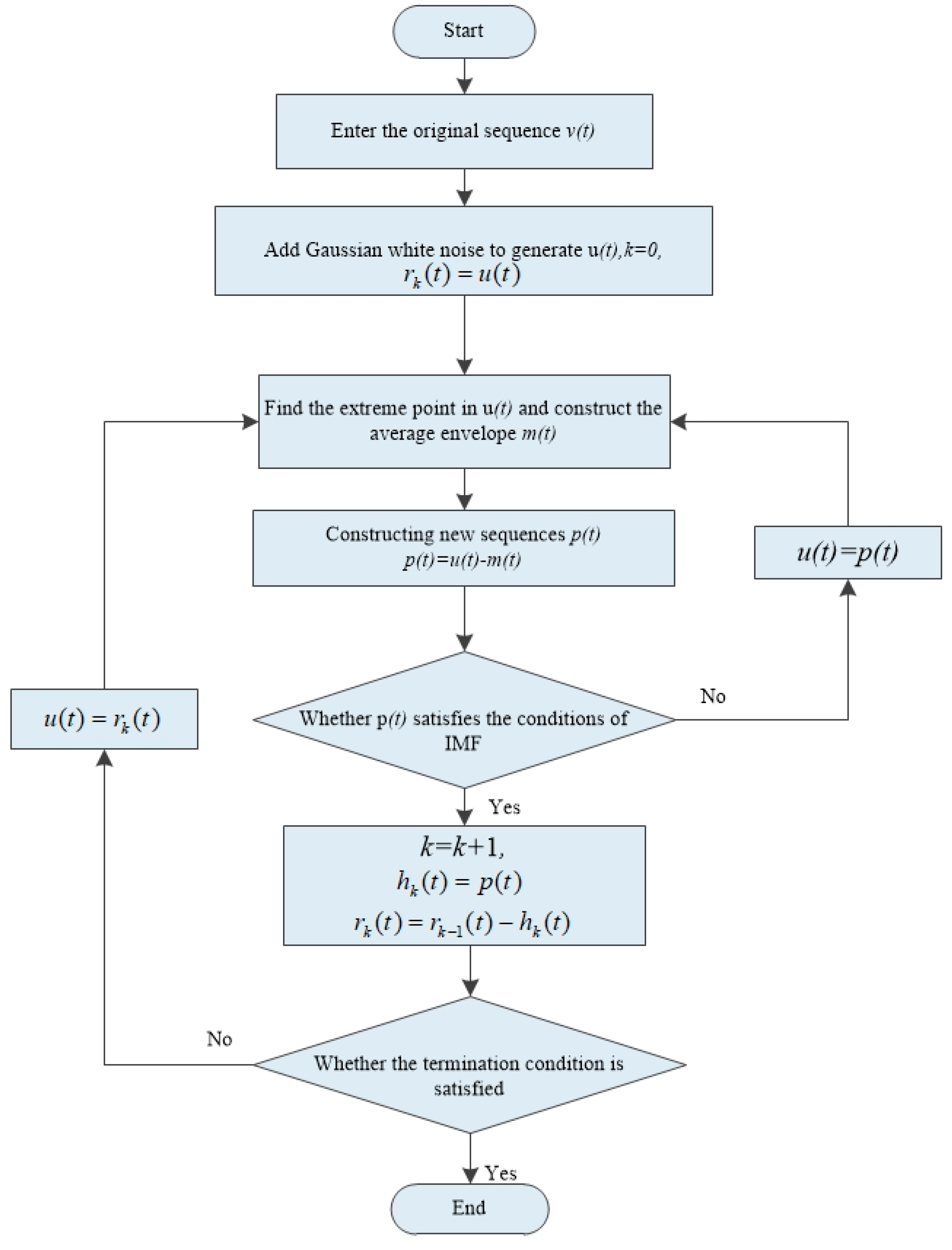
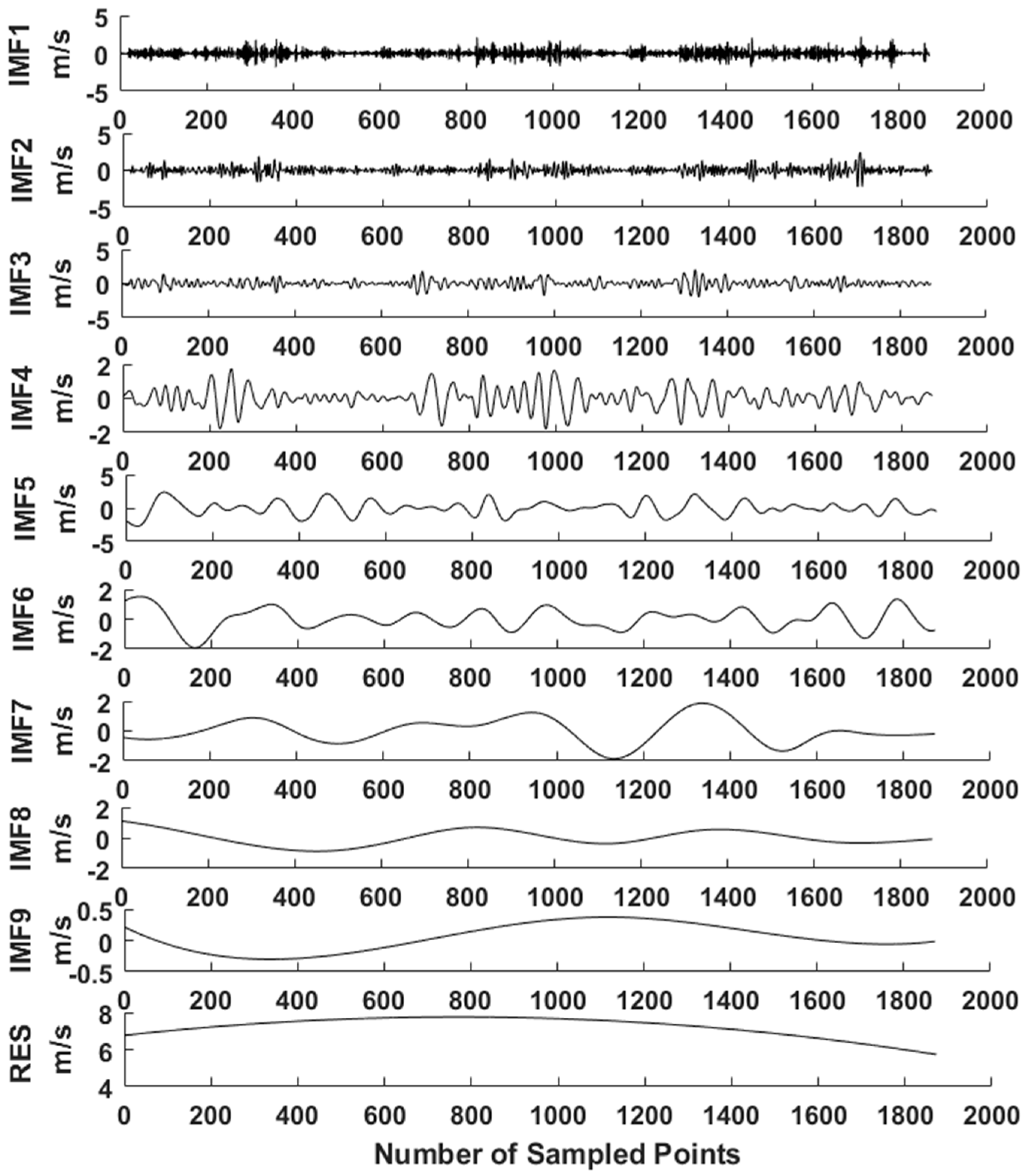
3.1. Preprocessing of Wind Speed Data
- (1)
- A normal white Gaussian noise sequence was added to the original sequence to generate a new sequence .
- (2)
- Find the maximum and minimum values in and fit the upper envelope and the lower envelope of .
- (3)
- Calculate the average envelope , and subtract it from the noise sequence to form a new sequence .
- (4)
- Justify if satisfies the IMF. If yes, the IMF, denoted as , is confirmed. Otherwise, repeat Steps (1) and (2) until it is satisfied.
- (5)
- The is subtracted from the original sequence , and the residual component is obtained.
- (6)
- Repeat the same process from the first step until , as shown in Equation (13), becomes a monotone function.
- (7)
- Finally, is decomposed into k IMFs with different oscillation modes, as shown in Equation (14).
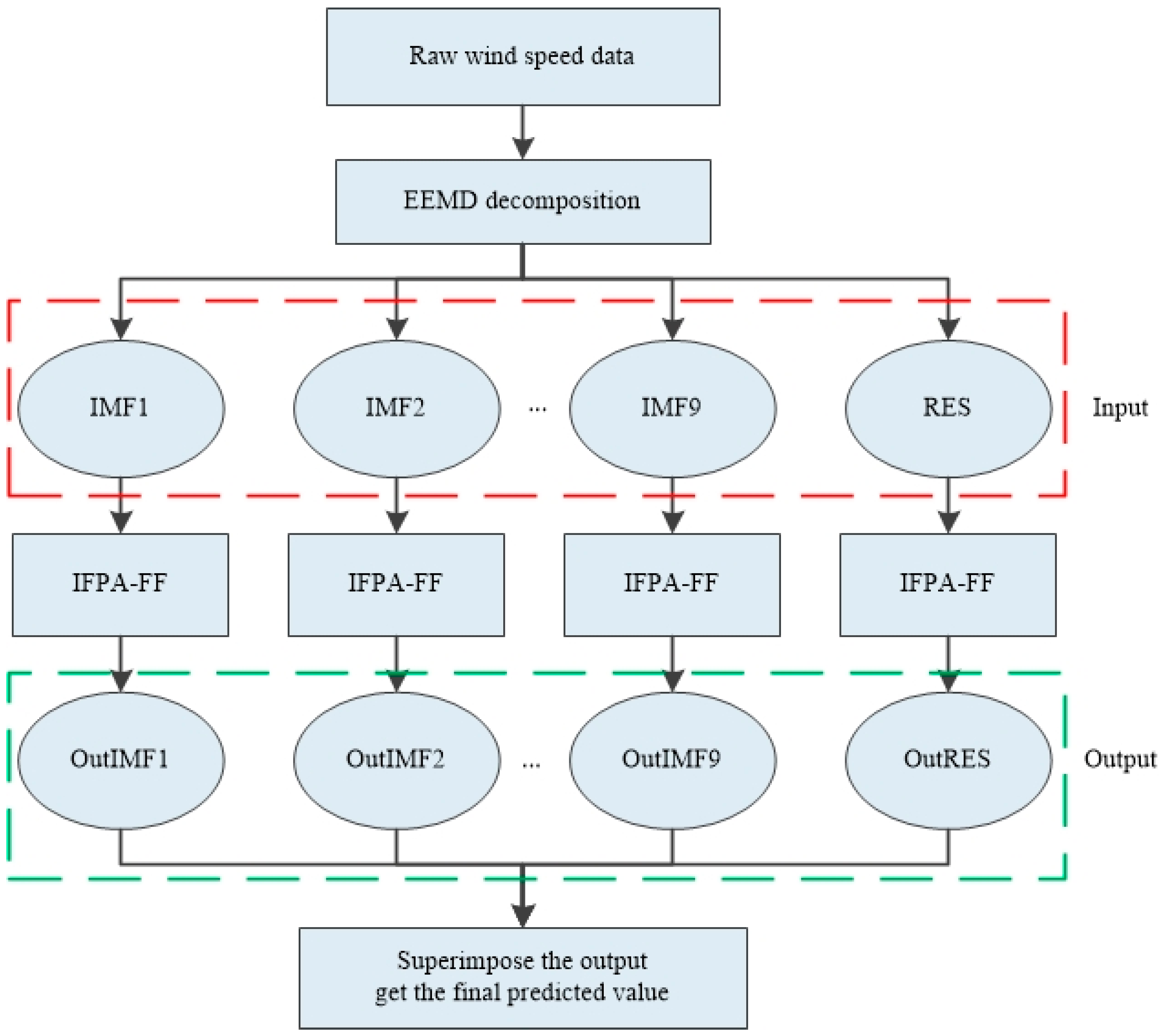
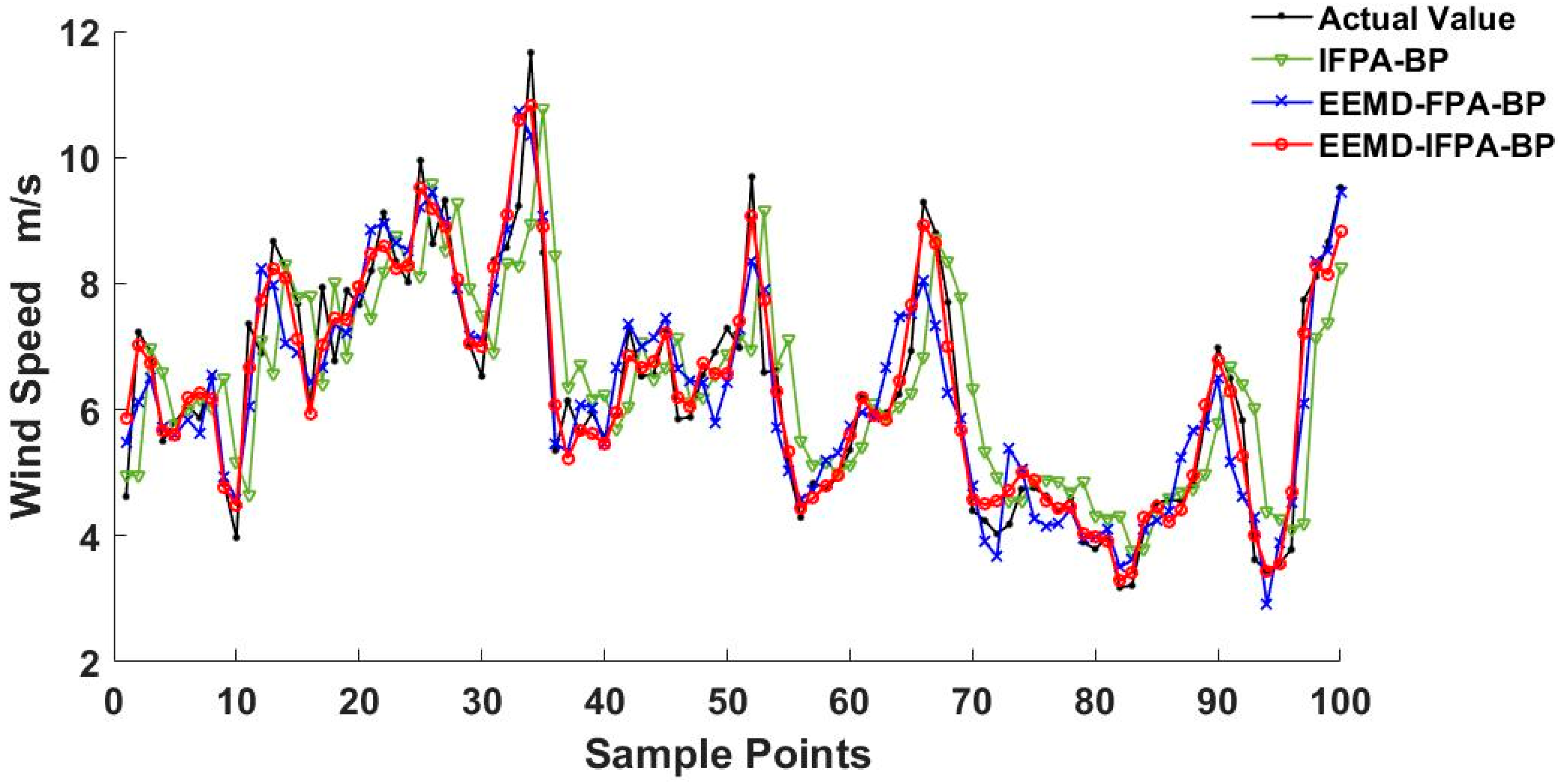
3.2. Wind Speed Forecasting Employed EEMD–IFPA–FF Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- William, P.M.; Keith, P.; Gerry, W.; Liu, Y.B.; William, L.M.; Sun, J.Z.; Luca, D.M.; Thomas, H.; David, J.; Sue, E.H. A wind power forecasting system to optimize grid integration. IEEE Trans. Sustain. Energy 2012, 3, 670–682. [Google Scholar]
- Wang, J.; Song, Y.; Liu, F.; Hou, R. Analysis and application of forecasting models in wind power integration: A review of multi-step-ahead wind speed forecasting models. Renew. Sustain. Energy Rev. 2016, 60, 960–981. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Khosravi, A.; Nahavandi, S. A New Fuzzy-Based Combined Prediction Interval for Wind Power Forecasting. IEEE Transa. Power Syst. 2015, 31, 1–9. [Google Scholar] [CrossRef]
- Madhiarasan, M.; Deepa, S.N. Comparative analysis on hidden neurons estimation in multi layer perceptron neural networks for wind speed forecasting. Artif. Intell. Rev. 2017, 48, 449–471. [Google Scholar] [CrossRef]
- Garcia-Ruiz, R.A.; Blanco-Claraco, J.L.; Lopez-Martinez, J.; Callejon-Ferre, A.J. Uncertainty-Aware Calibration of a Hot-Wire Anemometer With Gaussian Process Regression. IEEE Sens. J. 2019, 19, 7515–7524. [Google Scholar] [CrossRef]
- Sial, A.; Singh, A.; Mahanti, A.; Gong, M. Heuristics-Based Detection of Abnormal Energy Consumption. Smart Grid Innov. Front. Telecommun. 2018, 245, 21–31. [Google Scholar]
- Sial, A.; Singh, A.; Mahanti, A. Detecting anomalous energy consumption using contextual analysis of smart meter data. Wirel. Netw. J. 2019, 245, 1–18. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, H.; Wang, D.; Wang, G.; WU, J.; Bian, J.; Liu, J. A new method for wind speed forecasting based on copula theory. Environ. Res. 2018, 160, 365–371. [Google Scholar] [CrossRef]
- Li, L.L.; Sun, J.; Wang, C.H.; Zhou, Y.T.; Lin, K.P. Enhanced Gaussian Process Mixture Model for Short-Term Electric Load Forecasting. Inf. Sci. 2019, 477, 386–398. [Google Scholar] [CrossRef]
- Piotrowski, P.; Baczynski, D.; Kopyt, M.; Szafranek, K.; Helt, P.; Gulczynskl, T. Analysis of forecasted meteorological data (NWP) for efficient spatial forecasting of wind power generation. Electr. Power Syst. Res. 2019, 175, 105891. [Google Scholar] [CrossRef]
- Wang, J.Z.; Wang, S.Q.; Yang, W.D. A novel non-linear combination system for short-term wind speed forecast. Renew. Energy 2019, 143, 1172–1192. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.W.; Li, Y.F.; Duan, Z.; Xu, Y. Smart wind speed deep learning based multi-step forecasting model using singular spectrum analysis, convolutional Gated Recurrent Unit network and Support Vector Regression. Renew. Energy 2019, 143, 842–854. [Google Scholar] [CrossRef]
- Zhao, J.; Guo, Z.; Su, Z.; Zhao, Z.; Xiao, X.; Liu, F. An improved multi-step forecasting model based on WRF ensembles and creative fuzzy systems for wind speed. Appl. Energy 2016, 162, 808–826. [Google Scholar] [CrossRef]
- Nalcaci, G.; Ozmen, A.; Weber, G.W. Long-term load forecasting: Models based on MARS, ANN and LR methods. Cent. Eur. J. Oper. Res. 2019, 27, 1033–1049. [Google Scholar] [CrossRef]
- Madhiarasan, M.; Deepa, S.N. A novel criterion to select hidden neuron numbers in improved back propagation networks for wind speed forecasting. Appl. Intell. 2016, 44, 878–893. [Google Scholar] [CrossRef]
- Wang, J.Z.; Wang, Y.; Jiang, P. The study and application of a novel hybrid forecasting model—A case study of wind speed forecasting in China. Appl. Energy 2015, 143, 472–488. [Google Scholar] [CrossRef]
- Tascikaraoglu, A.; Sanandaji, B.M.; Poolla, K.; Varaiya, P. Exploiting sparsity of interconnections in spatio-temporal wind speed forecasting using Wavelet Transform. Appl. Energy 2016, 165, 735–747. [Google Scholar] [CrossRef] [Green Version]
- Alhussein, M.; Harider, S.L.; Aurangzeb, K. Microgrid-Level Energy Management Approach Based on Short-Term Forecasting of Wind Speed and Solar Irradiance. Energies 2019, 12, 1482. [Google Scholar] [CrossRef]
- Liu, Z.F.; Li, L.L.; Tseng, M.L.; Raymond, R.T.; Kathleen, B.A. Improving the reliability of photovoltaic and wind power storage systems using least squares support vector machine optimized by improved chicken swarm algorithm. Appl. Sci. 2019, 9, 3788. [Google Scholar] [CrossRef]
- Ding, M.; Zhou, H.; Xie, H. A gated recurrent unit neural networks based wind speed error correction model for short-term wind power forecasting. Neurocomputing 2019, 365, 54–61. [Google Scholar] [CrossRef]
- Zhao, W.; Wei, Y.M.; Su, Z. One day ahead wind speed forecasting: A resampling-based approach. Appl. Energy 2016, 178, 886–901. [Google Scholar] [CrossRef]
- Wang, H.Z.; Li, G.Q.; Wang, G.B.; Peng, J.; Jiang, H.; Liu, Y. Deep learning based ensemble approach for probabilistic wind power forecasting. Appl. Energy 2017, 188, 56–70. [Google Scholar] [CrossRef]
- Ding, Y. A novel decompose-ensemble methodology with AIC-ANN approach for crude oil forecasting. Energy 2018, 154, 328–336. [Google Scholar] [CrossRef]
- Mohammed, A.; Tomás, M. A review of modularization techniques in artificial neural networks. Artif. Intell. Rev. 2019, 52, 527–561. [Google Scholar] [Green Version]
- Abdel-Basset, M.; Shawky, L.A. Flower pollination algorithm: A comprehensive review. Artif. Intell. Rev. 2018, 52, 1–25. [Google Scholar] [CrossRef]
- Li, L.L.; Liu, Z.F.; Tseng, M.L. Enhancing the Lithium-ion battery life predictability using a hybrid method. Appl. Soft Comput. J. 2019, 74, 110–121. [Google Scholar] [CrossRef]
- Lei, X.; Fang, M.; Wu, F.X.; Chen, L. Improved flower pollination algorithm for identifying essential proteins. BMC Syst. Biol. 2018, 12, 46. [Google Scholar] [CrossRef]
- Li, L.L.; Zhang, X.B.; Tseng, M.L.; Lim, M.; Han, Y. Sustainable energy saving: A junction temperature numerical calculation method for power insulated gate bipolar transistor module. J. Clean. Prod. 2018, 185, 198–210. [Google Scholar] [CrossRef]
- Sabeti, M.; Boostani, R.; Davoodi, B. Improved particle swarm optimization to estimate bone age. IET Image Process. 2018, 12, 179–187. [Google Scholar] [CrossRef]
- Yuan, C.; Wang, J.; Yi, G. Estimation of key parameters in adaptive neuron model according to firing patterns based on improved particle swarm optimization algorithm. Mod. Phys. Lett. B 2017, 31, 1750060. [Google Scholar] [CrossRef]
- Yang, Y.K.; Jiao, S.J.; Wang, W.F. Cooperative media control parameter optimization of the integrated mixing and paving machine based on the fuzzy cuckoo search algorithm. J. Vis. Commun. Image Represent. 2019, 63, 102591. [Google Scholar] [CrossRef]
- Li, L.L.; Lv, C.M.; Tseng, M.L.; Song, M.L. Renewable energy utilization method: A novel Insulated Gate Bipolar Transistor switching losses prediction model. J. Clean. Prod. 2018, 176, 852–863. [Google Scholar] [CrossRef]
- Hu, J.; Wang, J. Wind and solar power probability density prediction via fuzzy information granulation and support vector quantile regression. Int. J. Electr. Power Energy Syst. 2019, 113, 515–527. [Google Scholar]
- Li, J.H.; Dai, Q. A new dual weights optimization incremental learning algorithm for time series forecasting. Appl. Intell. 2019, 49, 3668–3693. [Google Scholar] [CrossRef]
- Li, B.; Zhang, L.; Zhang, Q.; Yang, S.M. An EEMD-Based Denoising Method for Seismic Signal of High Arch Dam Combining Wavelet with Singular Spectrum Analysis. Shock Vib. 2019, 2019, 1–9. [Google Scholar] [CrossRef]
- Tan, Q.F.; Lei, X.H.; Wang, X.; Wang, H.; Wen, X.; Ji, Y.; Kang, A.Q. An adaptive middle and long-term runoff forecast model using EEMD-ANN hybrid approach. J. Hydrol. 2018, 567, 767–780. [Google Scholar] [CrossRef]
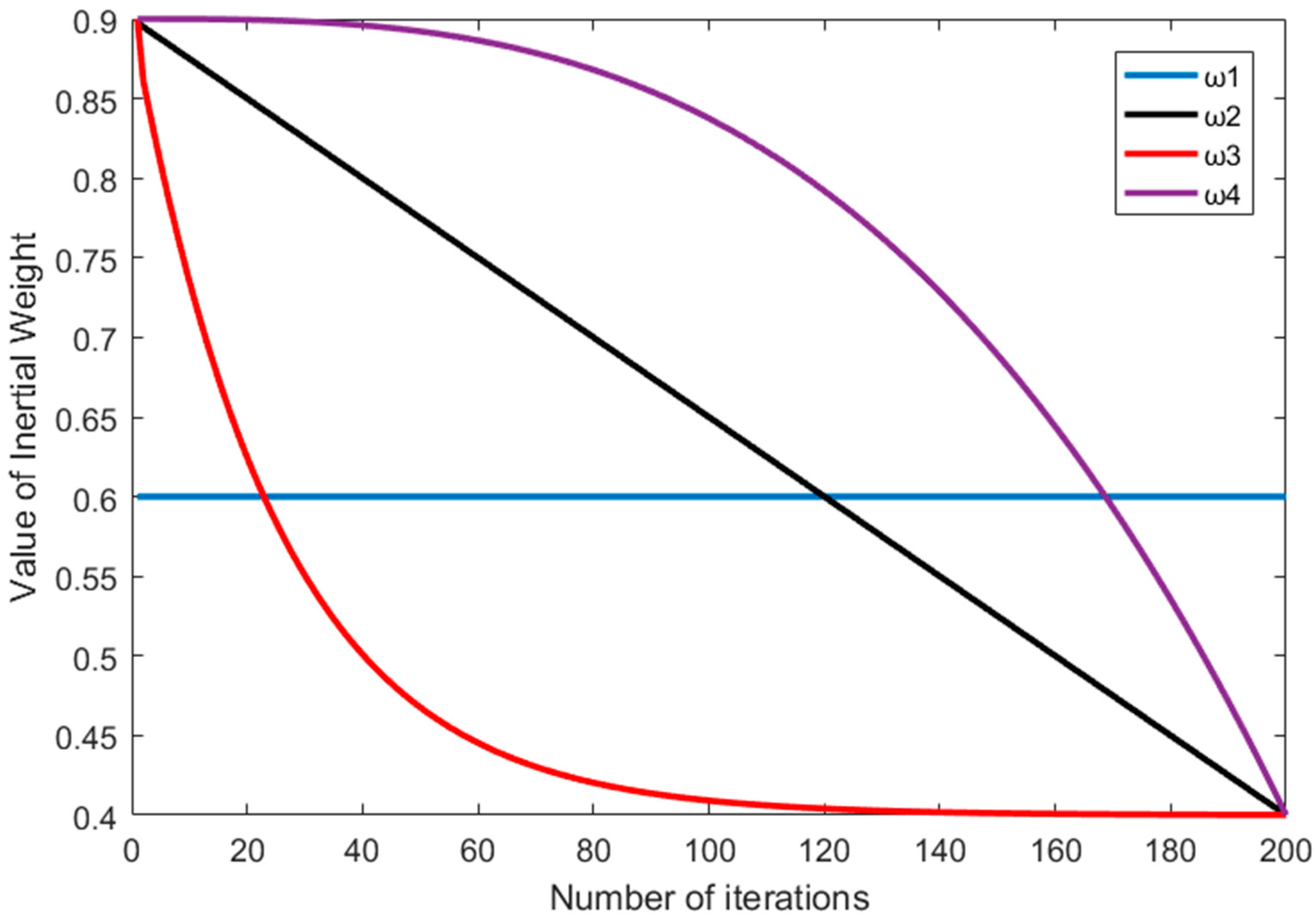
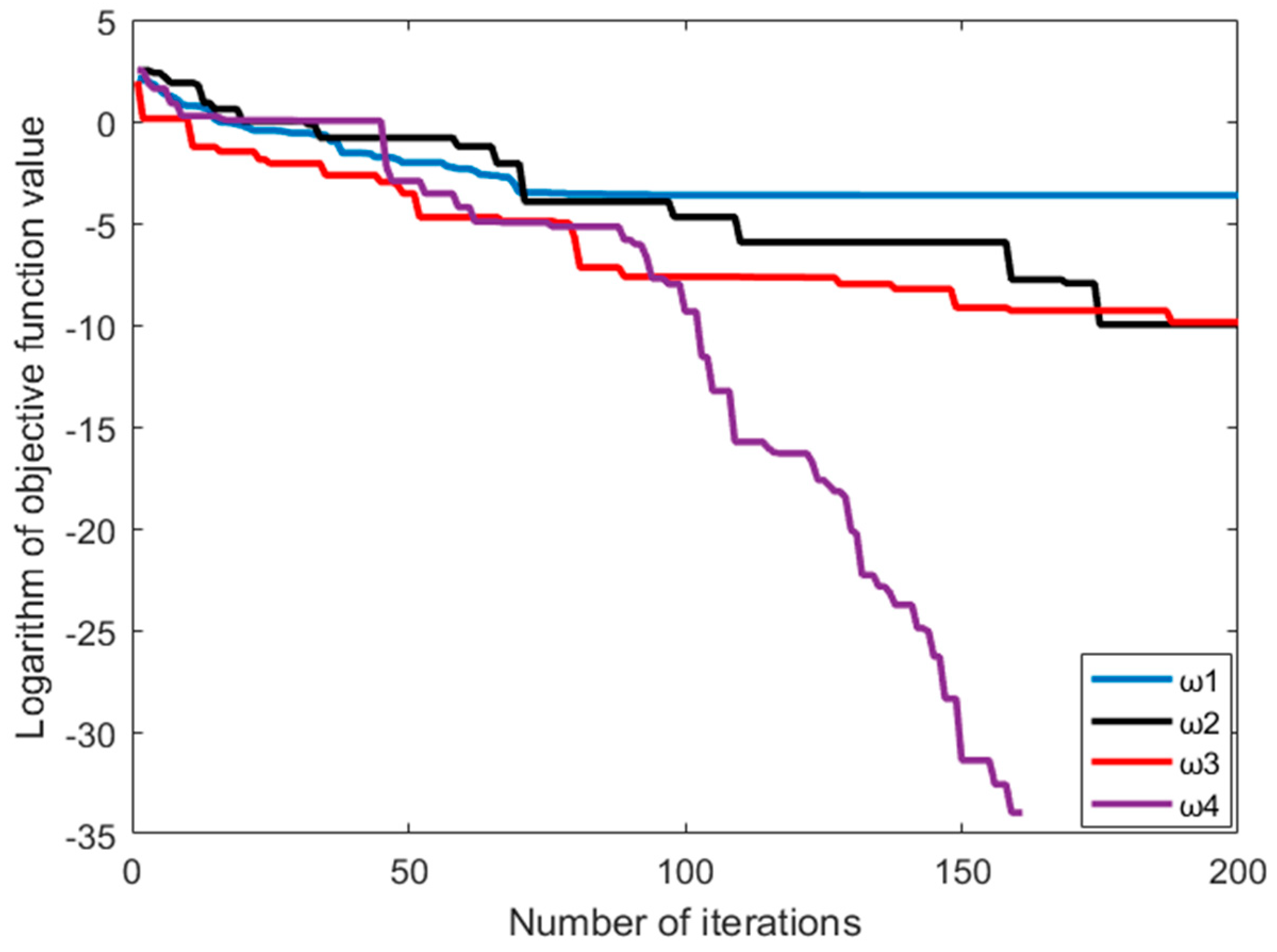
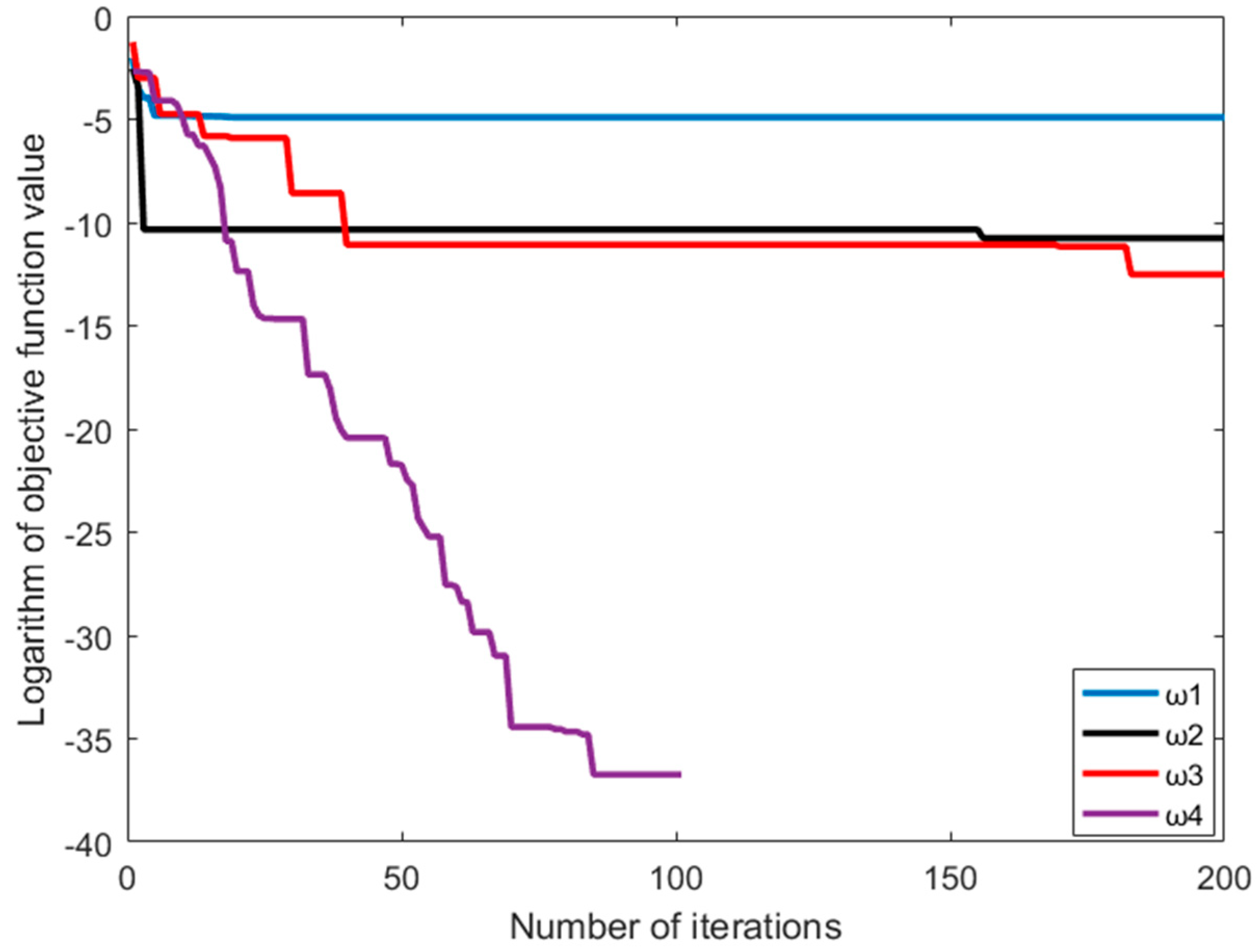
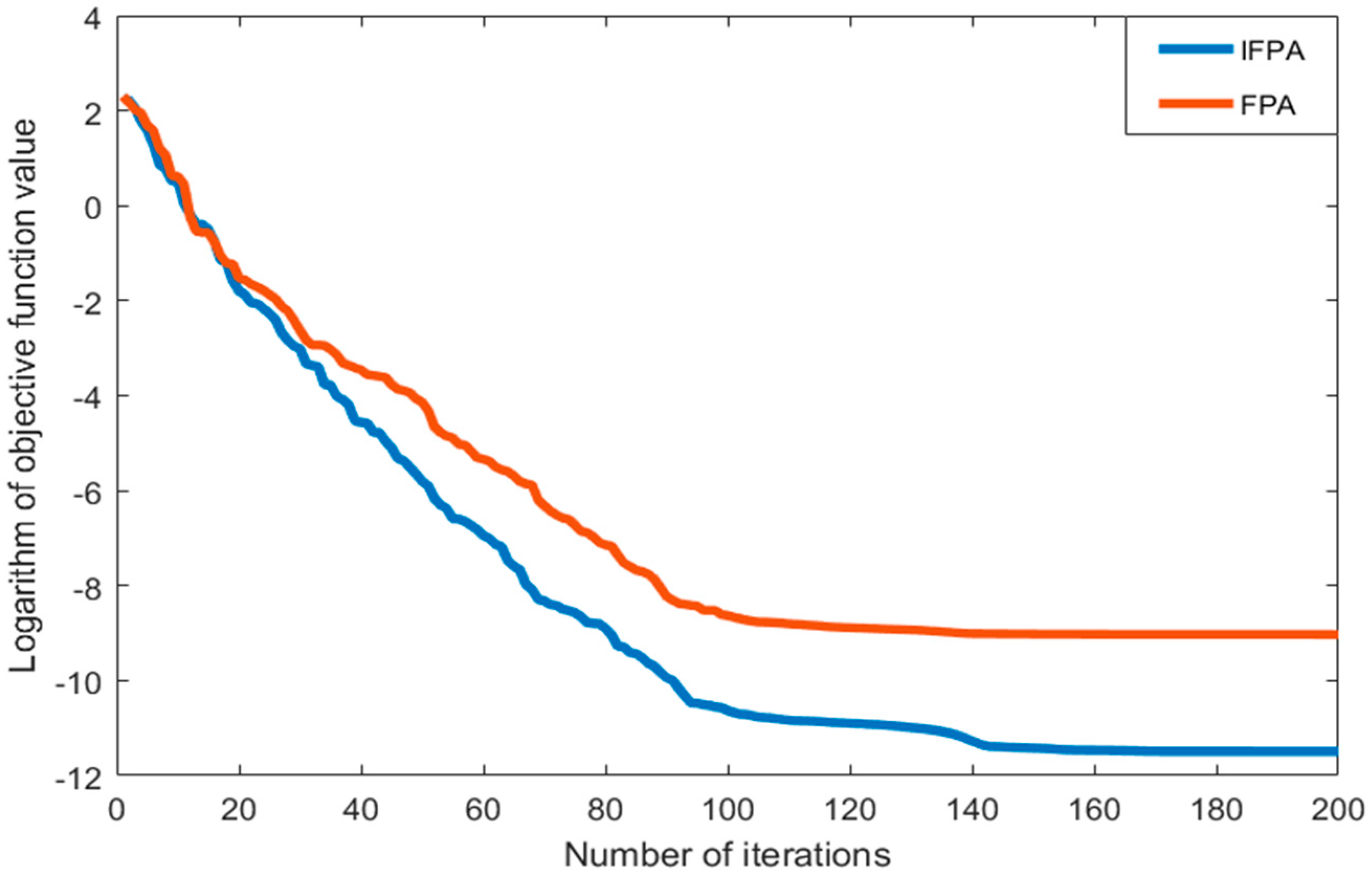
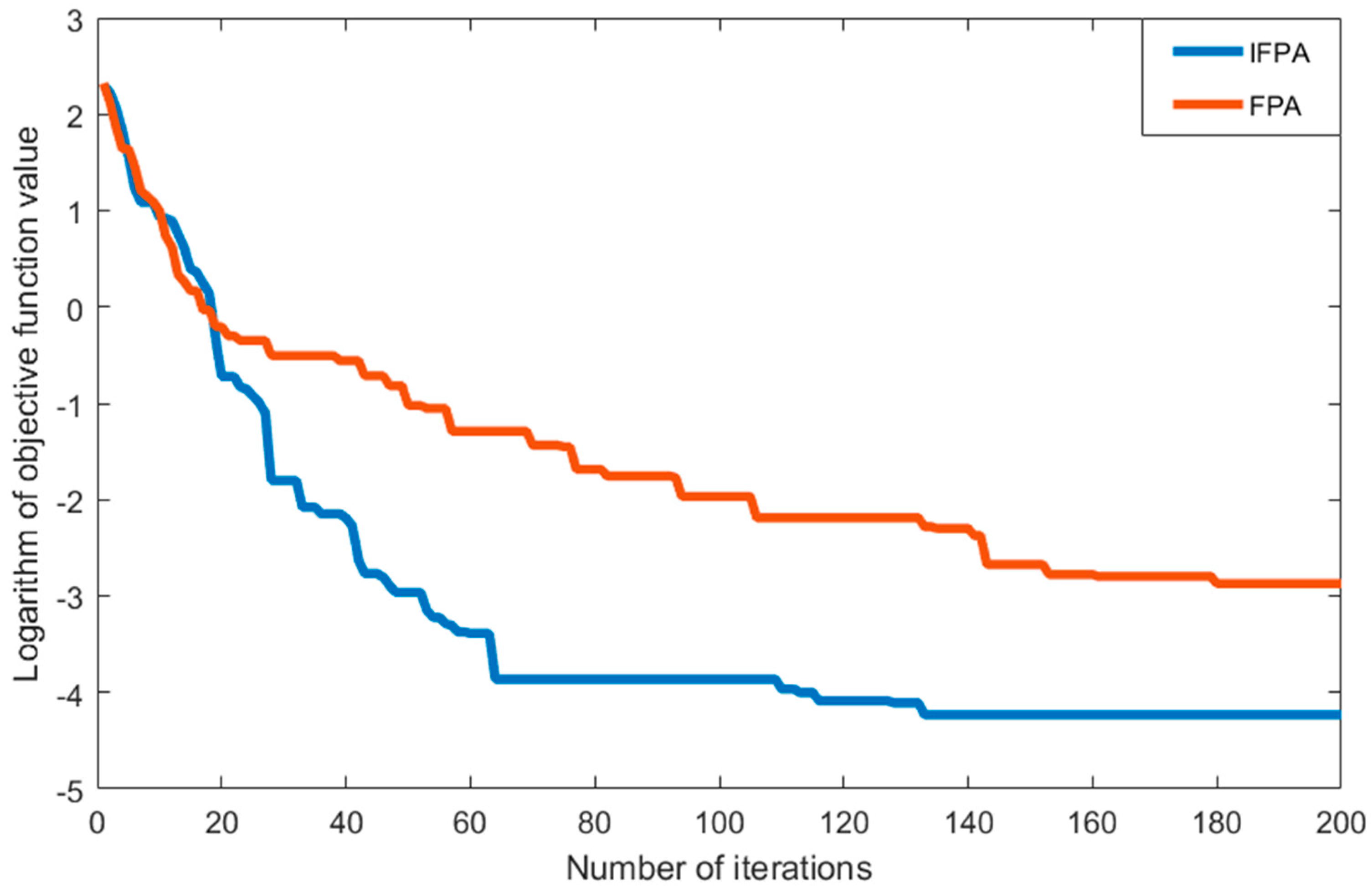
| Objective Function | Range | Optimal Value |
|---|---|---|
| Rastrigin | x ∈ [−5,5] | 0 |
| Griewank | x ∈ [−8,8] | 0 |
| Objective Function | Inertial Weight | Optimal Convergence Value | Worst Convergence Value | Average Convergence Value |
|---|---|---|---|---|
| Rastrigin | 0.0001 | 0.0265 | 0.0265 | |
| 0.0219 | 0.0313 | 0.0271 | ||
| 2.6130 × 10−10 | 0.0003 | 2.6236 × 10−08 | ||
| 0 | 0 | 0 | ||
| Griewank | 0.0742 | 0.7001 | 0.0826 | |
| 0.0213 | 0.1301 | 0.0213 | ||
| 3.6665 × 10−10 | 0.2881 | 2.42 × 10−10 | ||
| 0 | 0 | 0 |
| Objective Function | Range | Optimal Value |
|---|---|---|
| Schaffer | x ∈ [−5,5] | 0 |
| Ackley | x ∈ [−8,8] | 0 |
| Objective Function | Model | Optimal Convergence Value | Worst Convergence Value | Average Convergence Value |
|---|---|---|---|---|
| Schaffer | IFPA | 3.3621 × 10−79 | 0.0119 | 1.0221 × 10−65 |
| FPA | 1.1867 × 10−15 | 0.0661 | 0.0001 | |
| Ackley | IFPA | 2.5426 × 10−74 | 0.0379 | 3.7926 × 10−59 |
| FPA | 2.1884 × 10−05 | 0.0661 | 0.0661 |
| Maximum (m/s) | Minimum (m/s) | Mean (m/s) | Mode (m/s) | Mid-Value (m/s) | Standard Deviation (m/s) |
|---|---|---|---|---|---|
| 15.18 | 2.28 | 7.47 | 8.82 | 7.51 | 2.59 |
| FF | |||||||
| Input Layer Neurons | Hidden Layer Neurons | Output Layer Neurons | Iterations | Target Error | Learning Rate | ||
| 5 | 10–5 | 1 | 200 | 0.001 | 0.01 | ||
| FPA | |||||||
| Population Number | Dimension | Iterations | Transition Probability | ||||
| 20 | 10 | 200 | 0.8 | ||||
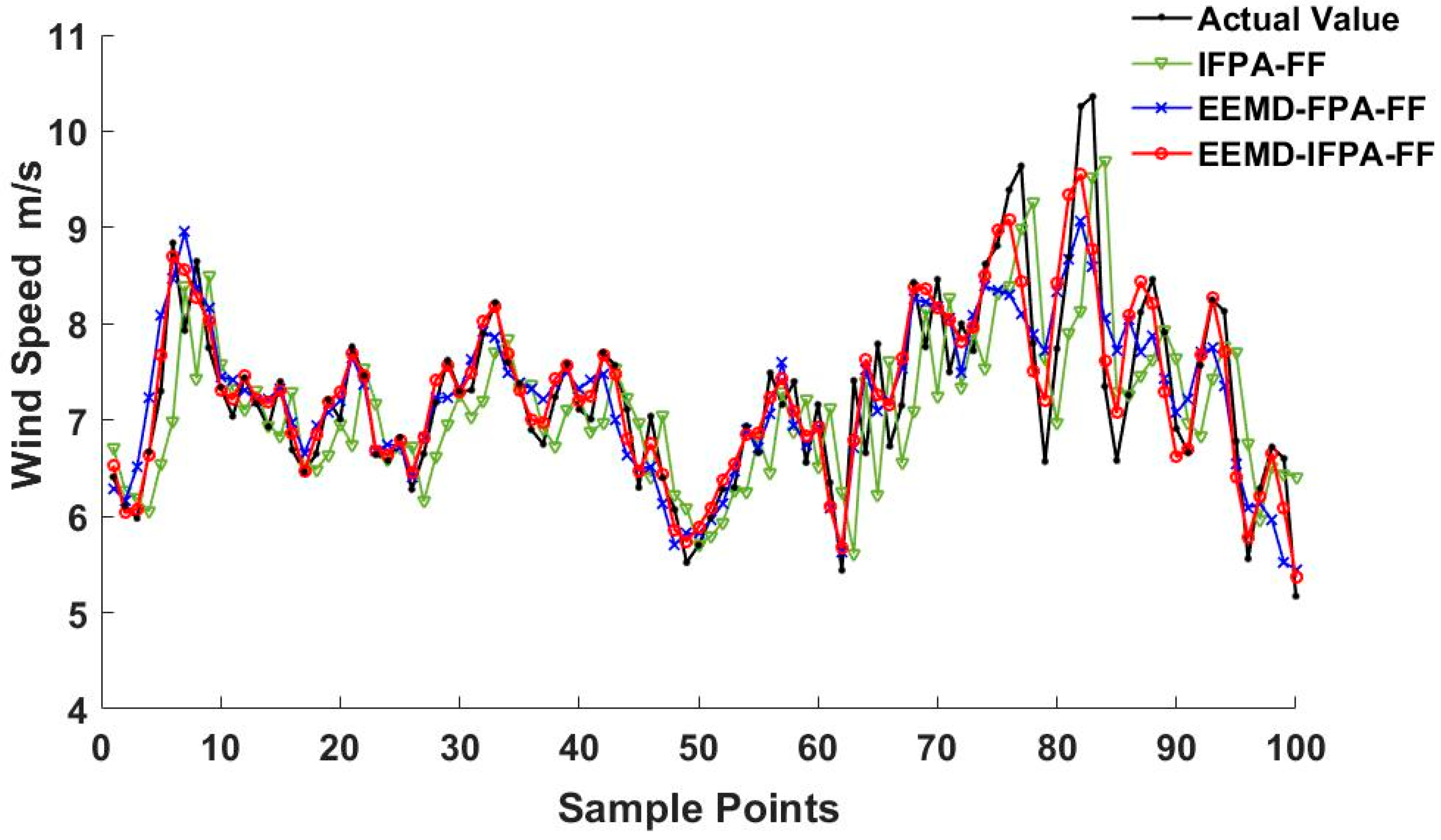
| Time | Model | MAE (m/s) | RMSE (m/s) | MAPE | R-Squared |
|---|---|---|---|---|---|
| EEMD–IFPA–FF | 0.1988 | 0.2097 | 6.0071% | 0.8772 | |
| 13 February | EEMD–FPA–FF | 0.3067 | 0.4077 | 7.1021% | 0.6912 |
| IFPA–FF | 0.3982 | 0.5131 | 9.0831% | 0.3144 | |
| EEMD–IFPA–FF | 0.2119 | 0.3019 | 6.7411% | 0.8038 | |
| 13 March | EEMD–FPA–FF | 0.4028 | 0.5257 | 9.2269% | 0.5981 |
| IFPA–FF | 0.5229 | 0.6941 | 11.8581% | 0.4719 | |
| EEMD–IFPA–FF | 0.3102 | 0.3931 | 7.7103% | 0.7963 | |
| 13 April | EEMD–FPA–FF | 0.4262 | 0.5733 | 9.7835% | 0.5492 |
| IFPA–FF | 0.7038 | 0.8291 | 13.2210% | 0.4045 |
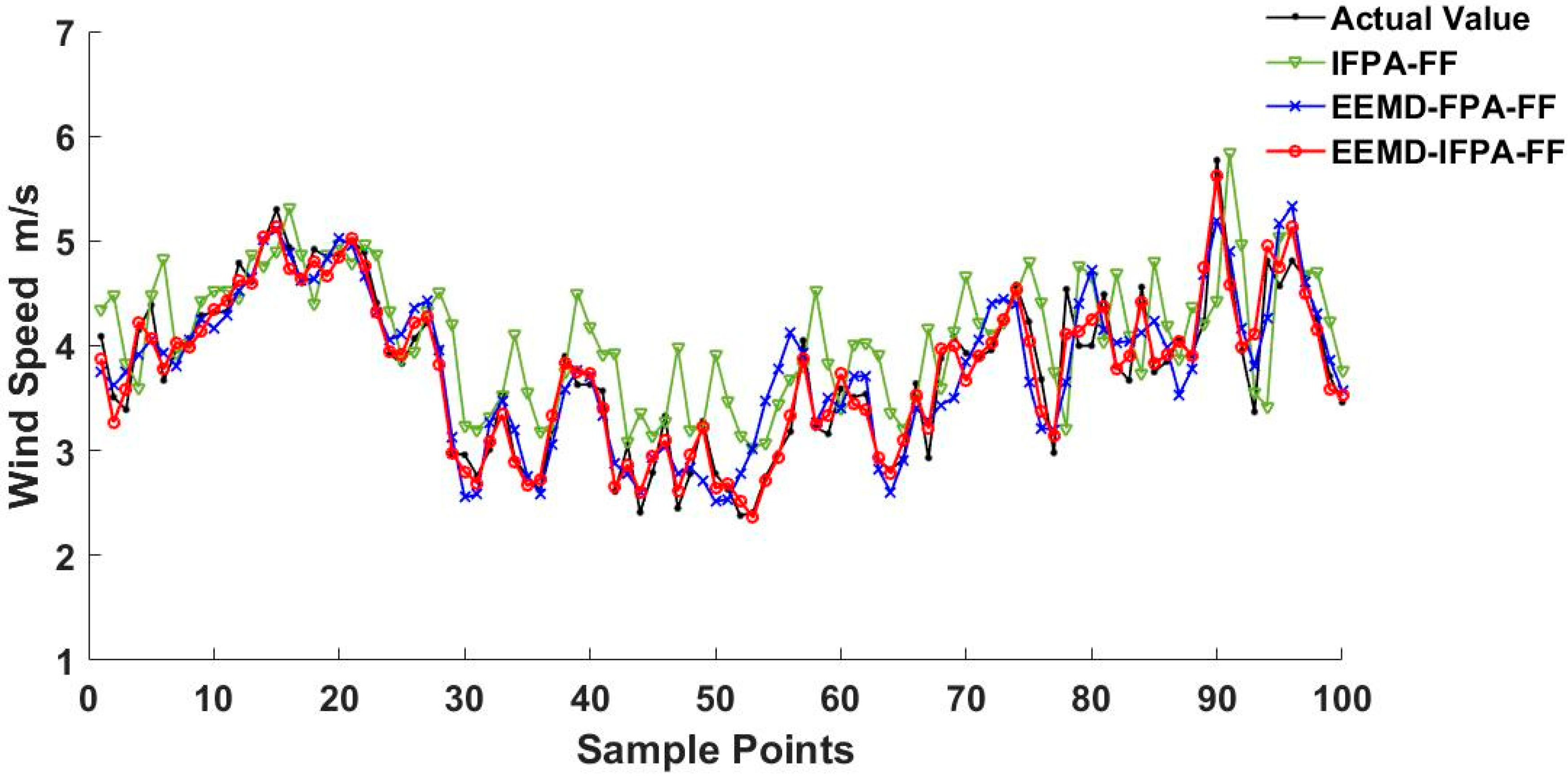
| Time | Model | MAE (m/s) | RMSE (m/s) | MAPE | R-Squared |
|---|---|---|---|---|---|
| EEMD–IFPA–FF | 0.2287 | 0.2584 | 6.2094% | 0.8594 | |
| 13 February | EEMD–FPA–FF | 0.3871 | 0.4440 | 7.4302% | 0.6246 |
| IFPA–FF | 0.4199 | 0.5670 | 9.9741% | 0.2049 | |
| EEMD–IFPA–FF | 0.3079 | 0.3695 | 7.2433% | 0.7789 | |
| 13 March | EEMD–FPA–FF | 0.4590 | 0.5728 | 9.8365% | 0.5479 |
| IFPA–FF | 0.5926 | 0.7802 | 12.9114% | 0.3942 | |
| EEMD–IFPA–FF | 0.3699 | 0.4303 | 8.3257% | 0.7436 | |
| 13 April | EEMD–FPA–FF | 0.5128 | 0.6817 | 10.7430% | 0.5017 |
| IFPA–FF | 0.7519 | 0.8924 | 14.6718% | 0.3370 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Y.; Li, H.; Lin, H.-C. Optimization of Feedforward Neural Networks Using an Improved Flower Pollination Algorithm for Short-Term Wind Speed Prediction. Energies 2019, 12, 4126. https://doi.org/10.3390/en12214126
Ren Y, Li H, Lin H-C. Optimization of Feedforward Neural Networks Using an Improved Flower Pollination Algorithm for Short-Term Wind Speed Prediction. Energies. 2019; 12(21):4126. https://doi.org/10.3390/en12214126
Chicago/Turabian StyleRen, Yidi, Hua Li, and Hsiung-Cheng Lin. 2019. "Optimization of Feedforward Neural Networks Using an Improved Flower Pollination Algorithm for Short-Term Wind Speed Prediction" Energies 12, no. 21: 4126. https://doi.org/10.3390/en12214126
APA StyleRen, Y., Li, H., & Lin, H.-C. (2019). Optimization of Feedforward Neural Networks Using an Improved Flower Pollination Algorithm for Short-Term Wind Speed Prediction. Energies, 12(21), 4126. https://doi.org/10.3390/en12214126





