Numerical Investigation and Optimization on Shell Side Performance of A Shell and Tube Heat Exchanger with Inclined Trefoil-Hole Baffles

Abstract

In this work, a shell and tube heat exchanger with inclined trefoil-hole baffles (STHX-IT) is proposed, and the numerical simulation is conducted to investigate the flow and heat transfer characteristics. A shell and tube heat exchanger with segmental baffles (STHX-SG) is also studied for the performance comparison. The results show that the heat transfer coefficient and pressure drop of the STHX-IT is averagely lower by 23.89% and 44.19% than those of the STHX-SG, but the heat transfer coefficient per pressure drop is higher by 36.38% on average. Further, the parametric studies of the inclination angle θ, trefoil-hole number n, and baffle cut δ are carried out for the STHX-IT. According to the numerical results, n and δ have more notable influence on shell side performance than θ. In detail, the heat transfer coefficient and pressure drop decrease slightly with θ increasing, and the overall performance is approximately equal; both the heat transfer coefficient and pressure drop decrease with the respective rising of n and δ, but the comprehensive performance shows a growing trend. Considering the synthetic effects of structural parameters, the multi-objective structure optimization using the genetic algorithm combined with the artificial neural networks is fulfilled. As a result, the Pareto front is obtained to characterize the behaviors of the maximum heat transfer rate and minimum pressure drop. The STHX-IT with the θ = 5.38°, n = 6, and δ = 43% is decided as the optimal solution by the TOPSIS method, whose Q/Δp is 2.34 times as much as that of the original STHX-SG.

1. Introduction

As one of the most widely utilized devices for heat transfer in industry, heat exchangers play a significant role in many fields, including chemical engineering, petroleum processing, power systems, and waste heat recovery. The shell and tube heat exchangers (STHXs) occupy more than 35% to 40% among various types owing to its simple manufacturing, high pressure-resistant ability, and low cost [1,2]. Baffles within the shell side are employed to support tubes, prevent vibration, guide flow direction, and increase fluid velocity. Thus, the structures of baffles exert an important influence on the thermal-hydraulic performance of the STHXs. The conventional shell and tube heat exchanger with segmental baffles (STHX-SG) provides a zigzag flow in the shell side, which have many advantages, such as high heat transfer performance, versatile adaptability, and simple maintenance. However, there still exist some drawbacks with the STHX-SG, for instance, high pressure loss, large flow dead zones, easy fouling, and flow-induced vibration. Therefore, numerous studies are focused on improving the comprehensive performance of the STHXs by overcoming the weaknesses above.

Various measures have been successfully applied to augment the heat transfer on the tube side, including shaped tubes, tube inserts, and turbulators [3,4,5,6,7,8,9,10]. While for the shell side, shaped tubes are also adopted to produce secondary flow and vortices with the fluid around tubes. Shirvan et al. [11] proposed the cosine wave tube to enhance the shell side performance in the STHX-SG, and optimized the tube geometry to maximize the thermal performance factor. Liu et al. [12] investigated numerically the shell side performance of the rod baffle heat exchangers with spirally corrugated tubes (RBHXsSCT). It was found that the tubes can augment the comprehensive performance of the RBHXsSCT when compared to the rod baffle heat exchangers with plain tubes (RBHXs). He et al. [13] carried out numerical simulations on the RBHXs with elliptic tubes and circular tubes, respectively. Results showed that the former one is an effective structure to improve the heat transfer rate of the non-Newtonian fluid. Yang et al. [14] reported a novel RBHX with eccentric spiral tubes, and analyzed the thermal-hydraulic characteristics both in shell side and tube side. It was concluded that the new structure has better performance on the tube side and slightly worse one on the shell side than the RBHX with plain tubes.

On the other hand, extensive attention is focused on modifying the baffle configurations to change the flow manner of shell-side fluid. The STHXs with helical baffles, first introduced by Lutcha and Nemcansky [15] and industrialized by ABB Lummus [16], are one of the popular research objects. Wang et al. [17,18,19] designed the STHX with continuous helical baffles, and it can generate ideal helical flow to enhance the shell side performance. However, due to the manufacture difficulties and high cost brought by the complex structures, their industrial applications are still restricted. Therefore, discontinuous helical baffles are developed gradually [20,21,22]. The longitudinal flow pattern on the shell side is also investigated by many researchers. Wang et al. [23,24] designed a new structure named double shell-pass RBHX (DS-RBHX), and the shell side is divided into two parts with a sleeve. Both the numerical and experimental studies revealed that the DS-RBHX performs better in flow and heat transfer than the single shell-pass RBHX. The STHXs with two different clamping type anti-vibration baffles were proposed by Yu et al. [25], and it is concluded that the new types of baffles are effective against the flow-induced vibration at the expense of lower comprehensive performance. Lei et al. [26] designed the novel STHXs with two types of louver baffles, which can produce oblique flow to reduce dead regions and increase local heat transfer. The round orifice plate baffle is a special type of supporting structure to generate longitudinal flow, among which the trefoil-hole baffles and quatrefoil-hole baffles are mostly used because of the high reliability in anti-vibration and anti-fouling. You et al. [27] reported a research on the shell side performance of the STHX with trefoil-hole baffles. They found that this kind of baffles can produce high-speed flush against tube walls, which intensively strengthens the flow resistance and the heat transfer coefficient. Maakoul et al. [28] numerically compared shell side performance among STHXs with trefoil-hole, helical, and segmental baffles, respectively. The results indicated that the trefoil-hole baffles augment the heat transfer with large pressure loss, and using helical baffles can achieve the highest comprehensive performance. Ma et al. [29] found that the shell side performance of the STHXs with trefoil-hole baffles is superior to that with quatrefoil-hole baffles. Meanwhile, the larger opening height can reduce the flow resistance, and thus display higher comprehensive performance for both STHXs.

The inclined baffles are commonly used to enhance heat transfer in tubes or channels, and their utilization in heat exchangers is proposed and studied recently [30,31,32]. Raj et al. [33] preliminarily investigated the impact of inclination angle on the thermal-hydraulic characteristics of the STHXs with inclined baffles. They concluded that the heat transfer performance changes slightly with the increasing inclination angle while the pressure drop decreases obviously, and 20° baffle inclination angle is the optimal parameter within their research ranges. Kumaresan et al. [34] found that the combination structure of 30% baffle cut and 35° baffle inclination angle has the higher heat transfer rate with minimum pressure drop.

The CFD method, which can provide detailed flow and temperature distributions along with accurate results, has become a prevailing strategy to predict the behaviors of STHXs. There are four main models, i.e., the unit model, the periodic model, the porous model, and the whole model, to investigate the shell side performance of STHXs. Yang et al. [35] compared these models on different aspects, and summarized a method to select the most proper model in practical applications. At the meantime, the optimization algorithms with the surrogate modeling technique have shown the effectiveness to determine the optimum structures in many applications. Wang et al. [36] achieved the best solutions for the STHX with staggered baffles by adopting the artificial neural network (ANN) and multi-objective genetic algorithm (MOGA). Wen et al. [37] optimized the structure of the STHXs with helical baffles by adopting the response surface methodology and MOGA. Zheng et al. [38] achieved the optimal Pareto front for the tube fitted vortex rod inserts by implementing ANN with MOGA.

However, few studies on shell side performance of the STHXs with inclined baffles have been reported. Further, the overall investigation and structure optimization on the STHXs combined with inclined baffles and trefoil-hole baffles has not been carried out. Therefore, considering the effects on decreasing pressure drop of inclined baffles and diminishing dead regions of trefoil-hole baffles, the novel structure, namely the STHX with inclined trefoil-hole baffles (STHX-IT), is proposed in this work. Numerical simulations are performed to investigate the flow and heat transfer characteristics of the STHX-IT, and the STHX-SG is selected as a reference. Meanwhile, the parametric analysis is carried out to discuss the effects of inclination angle θ, trefoil-hole number n, and baffle cut δ on the shell side performance. Finally, the combination of CFD, ANN, and MOGA are used to explore the optimal configurations for the STHX-IT.

2. Physical Models

In this study, the numerical simulations on the shell side of heat exchangers are conducted. According to our previous work by Yang et al. [35], the whole model can provide the most accurate results for the shell-side simulations, so it is adopted in this work. Figure 1 presents the geometric structures of the STHX-SG and STHX-IT. These heat exchangers have the same dimension for the shell, inlet, outlet, and tubes. Thirty-seven heat transfer tubes with the triangle arrangement are deployed in these models. Meanwhile, both STHX-SG and STHX-IT have seven baffles with the same baffle cut and baffle spacing. The detailed parameters of the STHX-IT model are listed in

Table 1. Geometric parameters of the STHX-IT model.

Item	Value
Shell parameters
Inner diameter of shell/mm	143
Shell length/mm	840
Baffle parameters
Baffle spacing/mm	100
Baffle inclination angle/°	0, 5, 10, 15, 20
Baffle cut/%	25, 30, 35, 40, 45
Trefoil-hole number	3, 4, 5, 6, 7
Trefoil opening height/mm	2.6
Tube parameters
Outer diameter of tube/mm	16
Tube pitch/mm	20.5

. The main difference between these two models lies in the baffles. The baffles of the STHX-SG are placed perpendicular to the central axis of the cylindrical shell and have no trefoil-holes, while it is quite distinct for the STHX-IT. There are three key configuration parameters for the STHX-IT, which are inclination angle θ, trefoil-hole number n, and baffle cut δ, respectively. As illustrated in Figure 2, θ is defined as the angle between the direction of baffle plane and the vertical plane of the shell central axis, and δ is defined as the ratio of the baffle cut height to the inner diameter of the shell, while h_t denotes the trefoil opening height. Figure 3 depicts the diverse trefoil-hole locations of baffles with different values of n. The STHX-SG model with the baffle cut δ of 25% and the STHX-IT model with inclination angle θ of 10°, trefoil-hole number n of 5, baffle cut δ of 25% are investigated and compared initially.

3. Numerical Simulation

3.1. Governing Equations

The numerical investigations can be simplified with the following assumptions:

(1)

The working fluid is incompressible and the influence of gravity is neglected;

(2)

The fluid flow is turbulent and the heat transfer is steady;

(3)

The thickness of baffles is assumed as zero;

(4)

The leakage flows around the baffles are ignored;

(5)

The outer shells of heat exchangers are considered to be well-insulated.

Based on the assumptions above, the governing equations for continuity, momentum, and energy in the computational domain are expressed as follows:

Continuity equation:

$$\frac{\partial \left(\rho u_j\right)}{x_j}=0$$

(1)

Momentum equation:

$$\frac{\partial (\rho u_i{u}_j)}{\partial x_j}=-\frac{\partial p}{\partial x_i}+\frac{\partial }{\partial x_j}\left(\mu \frac{\partial u_i}{\partial x_j}-\rho \overline{u_i^{\prime }{u}_j^{\prime }}\right)$$

(2)

Energy equation:

$$\frac{\partial \left(u_{j}T\right)}{\partial x_j}=\frac{\partial }{\partial x_j}\left(\frac{\lambda }{\rho c_p}\frac{\partial T}{\partial x_j}\right)$$

(3)

Compared with other k-ε models, the realizable k-ε turbulence model has excellent performance when dealing with flows of rotation, boundary layer with directional pressure gradients, separation, and secondary flow [39,40]. Therefore, the realizable k-ε turbulence model is employed to simulate the turbulent behaviors of the STHXs accurately. The model is expressed as follows [41]:

Turbulent kinetic energy equation:

$$\frac{\partial \left(\rho k\right)}{\partial t}+\frac{\partial \left(\rho k{u}_j\right)}{\partial x_j}=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right]+G_k-\rho \epsilon$$

(4)

Turbulent energy dissipation equation:

$$\frac{\partial \left(\rho \epsilon \right)}{\partial t}+\frac{\partial \left(\rho \epsilon u_j\right)}{\partial x_j}=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\epsilon }}\right)\frac{\partial \epsilon }{\partial x_j}\right]+\rho C_{1}E\epsilon -\rho C_2\frac{{\epsilon }^2}{k+\sqrt{\nu \epsilon }}$$

(5)

where k and ε are the turbulent kinetic energy and turbulent energy dissipation rate, respectively; σ_k and σ_ε are the Prandtl numbers corresponding to k and ε, respectively; G_k is the generation of k due to the average velocity gradient; C₁ and C₂ are empirical coefficients.

3.2. Boundary Conditions and Numerical Methods

The three-dimension, double-precision, and pressure-based solver is employed to conduct numerical simulations on the shell side of heat exchangers with the commercial software Fluent. The no-slip boundary condition is adopted on all solid surfaces, and the standard wall functions are used for the near wall region. The SIMPLE pressure–velocity coupling algorithm is adopted to discretize the governing equations. The second order upwind scheme is applied for the momentum, energy, turbulent kinetic energy, and turbulent dissipation rate, while the pressure term is treated with the standard scheme. The working fluid of the shell side is water, whose thermo–physical properties depending on temperature are shown in

Table 2. Thermo–physical properties of water.

Item	Unit	Value (293 K ≤ T ≤ 353 K)
ρ	kg/m3	$-0.003369T^2+1.733T+779.7$
cp	J/ (kg·K)	$0.01131T^2-7.095T+5290$
λ	W/(m·K)	$-1.298\times {10}^{-5}{T}^2+0.009629T-1.108$
μ	kg/(m·s)	$1.462\times {10}^{-7}{T}^2-0.0001049T+0.01917$

.

The inlet and outlet are set as the velocity inlet and pressure outlet, respectively. The shell-side inlet velocity is between 0.957 m/s and 2.073 m/s while the mass flow rate varies from 1.2 kg/s to 2.6 kg/s, and the temperature is 293 K. The baffle walls are set as adiabatic, and the tube walls are set as a constant temperature of 353 K. The turbulence intensity I and turbulence length scale l of the inlet, used as the turbulent specification method, are calculated as follows:

$$I=0.16R{e}_{in}^{-0.125}$$

(6)

$$l=0.07D_{in}$$

(7)

where $R{e}_{in}$ represent the Reynolds number, and $D_{in}$ is the inner diameter of the inlet.

3.3. Data Reduction

The shell-side heat transfer rate Q is expressed as:

$$Q=m\cdot c_p\cdot \left(T_{in}-T_{out}\right)$$

(8)

where m is the water mass flow rate, c_p is the specific heat of the fluid.

The heat transfer coefficient h is defined as:

$$h=\frac{Q}{A\cdot \Delta T_m}$$

(9)

where A is the heat transfer surface area, ΔT_m is the logarithmic mean temperature difference between the fluid and tube walls. They are calculated as follows:

$$A=N_t\cdot \pi \cdot d\cdot L$$

(10)

$$\Delta T_m=\frac{\Delta T_{max}-\Delta T_{min}}{ln\left(\frac{T_{max}}{\Delta T_{min}}\right)}$$

(11)

where N_t and d are the number and the outer diameter of tubes, respectively, L is the effective length of tube bundles. ΔT_max and ΔT_min are the maximum and minimum temperature difference between the fluid and tube walls, respectively.

ΔT_max and ΔT_min are calculated as:

$$\Delta T_{max}=T_w-T_{in}$$

(12)

$$\Delta T_{min}=T_w-T_{out}$$

(13)

where T_w is the temperature of tube walls, T_in and T_out are the fluid temperatures of inlet and outlet, respectively.

The pressure of outlet p_out is set as zero, and the pressure of inlet p_in can be obtained from numerical results. Thus the shell side pressure drop Δp is presented as follows:

$$\Delta p=p_{in}-p_{out}=p_{in}$$

(14)

3.4. Grid Generation and Independence Tests

The three-dimensional grid systems are generated by using Gambit software. In consideration of the complexity of shell-side flow, unstructured tetrahedral elements are adopted to discretize the computational domain. Generally, the model with larger mesh number can obtain more precise results at the expense of more computational workload. So it is necessary to select an appropriate mesh system in consideration of the balance. To guarantee the accuracy of numerical results, three grid systems are generated for each heat exchanger to carry out independence tests, and the results are presented in

Table 3. Results of different grid systems.

Grid Number	h/W·m−2·K−1	Error	Δp/Pa	Error
The STHX-SG model
4,178,785	6861.45	4.66%	16,759.73	2.74%
6,916,196	7096.37	1.40%	17,109.11	0.71%
9,522,788	7197.01	—	17,232.03	—
The STHX-IT model
4,409,629	5186.40	5.84%	9444.85	2.66%
7,171,143	5409.99	1.78%	9607.71	0.98%
9,791,198	5507.83	—	9702.84	—

. The heat transfer coefficient h and pressure drop Δp of each mesh model are calculated, and the results of the finest mesh model are selected as the comparison criterion. For the STHX-SG model, the heat transfer coefficient and pressure drop increase by 1.40% and 0.71% respectively when the cell number increases from 6,916,196 to 9,522,788. Likewise, it is found in the STHX-IT model that the relative deviations between the second grid (7,171,143 elements) and the third one (9,791,198 elements) are 1.78% for heat transfer coefficient and 0.98% for pressure drop, respectively. Therefore, grid systems with 6,916,196 elements and 7,171,143 elements are selected to perform the following simulations for the STHX-SG and the STHX-IT, respectively.

3.5. Model Validation

In order to validate the reliability of numerical models and solution methods, the numerical results of the STHX-SG are compared with the calculation values using Bell-Delaware method [42]. This method is developed with lots of experimental data, and has become the most accurate method to validate the STHX-SG in the open literature [43]. As shown in Figure 4, when the mass flow rate grows from 1.2 kg/s to 2.6 kg/s, the derivations of heat transfer coefficient are –9.19%–14.13% with an average value of 7.13%, and those of pressure drop are 3.34%–9.15% with the average error of 6.49%. The reasonable derivations are ascribed to the simplification of numerical models. Therefore, the agreement between the results obtained from numerical simulations and Bell-Delaware method checks the accuracy of the modeling approach mentioned above. Moreover, the previous work of our group also validated the precision of the modeling method to predict the shell-side performance in different kinds of STHXs, including the double shell-pass rod baffle heat exchanger [23,24] and the STHX with staggered baffles [36]. In addition, the numerical simulations are carried out for the STHX-SG that has the same geometric parameters and operating conditions as those described in literature [44], and the results are compared with the experimental data [44]. As shown in Figure 5, the deviations of the heat transfer coefficient are –4.47% – 6.58%, and those of the pressure drop is –15.73% – 5.41%, which also confirms the reliability of the numerical modelling method. Meanwhile, the same grid generation method, numerical method, and solution method are used for all geometrical models in this work. Hence the numerical models are precise enough to be adopted to analyze the thermo-hydraulic performance of STHXs in the current study.

4. Results and Discussion

4.1. Flow Fields and Temperature Distributions

Figure 6 illustrates the streamlines of the STHX-SG and STHX-IT for the whole shell side when the mass flow rate is 2 kg/s. The more specific velocity vectors of the central symmetry plane are depicted in Figure 7. We can notice the zigzag flow of the STHX-SG, which results in the triangle dead zones behind the baffles. In these dead zones, the velocity is slow compared with the mainstream, and heat transfer deterioration and fouling are consequently serious. The huge velocity difference between both sides of baffles also causes severe damage to them, and higher material strength should be put forward for baffles to guarantee the safety and running time. The enormous momentum losses due to abrupt flow direction changes contribute to great pressure drop, which implies more power consumption. As for the STHX-IT, it is observed that the inclined trefoil-hole baffles provide the oblique flow along the flow direction, and some fluid flows through the trefoil-holes instead of the mainstream between the baffles. The velocity distribution of the shell side becomes more uniform and well-developed. In particular, the flow structure of dead regions is smoother, thus the fouling problem would be alleviated, and the pressure drop is deduced to decrease sharply compared to the STHX-SG. However, the velocity in the mainstream region decreases due to the leakage flow through the holes of baffles, which leads to the lower intensity of the scouring effect between fluid and tube bundles. Consequently, poorer heat transfer performance is showed for the STHX-IT. The detailed thermo-hydraulic performance of the two models, caused by different flow structures, will be discussed in the following sections.

The temperature distributions of the STHX-SG and STHX-IT are presented in Figure 8. As depicted in Figure 8a for the STHX-SG, the fluid of the flow dead regions has difficulty in sufficiently mixing with the continuous cold liquid, and it keeps being heated by the tube walls. As a result, the local higher temperature zones are generated, and the heat transfer performance there is weakened. While the STHX-IT, shown in Figure 8b, has more evenly distributed temperature zones owing to the uniform velocity filed, which improves the poor heat transfer performance in the dead regions effectively. Nevertheless, the declining velocity in the mainstream brings about descending thermal performance and lower temperature for the whole shell side.

4.2. Flow and Heat Transfer Performance

The relationships of the heat transfer coefficient and pressure drop versus the mass flow rate are given in Figure 9. It is found that the heat transfer coefficient of the STHX-SG and STHX-IT both increase with the mass flow rate rising. The heat transfer coefficient of the STHX-IT is lower than that of the STHX-SG by an average percentage of 23.89% when the mass flow rate grows from 1.2 kg/s to 2.6 kg/s. It can be attributed to the leakage flow through the trefoil-holes and the decreased velocity in the mainstream of the STHX-IT mentioned above. Similarly, the pressure drop of the two STHXs both rises with the increase of mass flow rate. The pressure drop of the STHX-IT decreases by 44.19% on average compared with that of the STHX-SG. As analyzed in the previous section, there are two main reasons for the decreasing pressure drop. On the one hand, the inclination angle is designed to follow the flow direction and consequently ameliorate the dramatic change of the fluid movement. On the other hand, allowing fluid to leak from the holes efficiently eliminate the dead spaces behind the baffles, which smooths velocity distribution and accordingly reduces the pressure drop of the whole shell side.

4.3. Comprehensive Performance

Considering that the heat transfer coefficient and pressure drop of the STHX-IT simultaneously decrease as opposed to the STHX-SG, it is essential to analyze and compare the comprehensive performance of these two models. The heat transfer coefficient per pressure drop h/Δp is a frequently-used index to evaluate the overall performance of different heat exchangers. The higher value represents that more heat transfer coefficient can be achieved under the same pressure drop, which indicates better comprehensive performance. As shown in Figure 10, the h/Δp of the STHX-IT and STHX-SG both decrease with the growing of the mass flow rate. When the mass flow rate remains constant, the h/Δp of the STHX-IT is higher than that of the STHX-SG by an average percentage of 36.38%, which reveals the superior comprehensive performance of the STHX-IT. A sharper declining trend is found for the h/Δp when the mass flow rate is lower, and the gaps between them is gradually narrowing when the mass flow rate is higher.

4.4. Configuration Parameters Analysis

4.4.1. Effects of Inclination Angle θ

The effects of inclination angle θ on the heat transfer coefficient and pressure drop are shown in Figure 11 and Figure 12 when the trefoil-hole number is 5 and the baffle cut is 25% for the STHX-IT. It is noticed that the heat transfer coefficient and pressure drop both increase proportionally with the mass flow rate. Figure 11 shows that the heat transfer coefficient decreases with the rise of the inclination angle, indicating that the larger inclination angle results in poorer heat transfer performance. However, the influence of the inclination angle is not as significant for the pressure drop, especially in the situations of lower velocity. When the inclination angle changes from 0° to 20°, the oblique flow becomes more uniform, hence the flush effect of fluid to tube outer walls weakens, leading to the simultaneous decreasing of the flow and heat transfer performance. But the design of inclined baffles does not alter the zigzag flow pattern in the mainstream, and therefore the inclination angle has no significant impact on the shell side performance.

The comprehensive performance of the STHX-IT with different inclination angles is also investigated. Figure 13 shows the varying trends of the h/Δp with mass flow rate. As depicted, the h/Δp declines when the mass flow rate increases for all cases, which represents better overall performance for lower fluid velocity. When the mass flow rate remains constant, the h/Δp with different inclination angles are almost equal. It is mainly due to the little distinctions of the heat transfer coefficient and pressure drop. The relationship between the h/Δp and the inclination angle is not obvious, and we can notice that the maximum comprehensive performance reaches at θ = 0° and θ = 5°, indicating that these two values are the optimal choices among the given five when the trefoil-hole number is 5 and the baffle cut is 25%.

4.4.2. Effects of Trefoil-Hole Number n

Figure 14 and Figure 15 illustrate the effects of trefoil-hole number n on the heat transfer coefficient and pressure drop when the inclination angle is 10° and the baffle cut is 25% for the STHX-IT. Both the heat transfer coefficient and pressure drop rises with the growing mass flow rate under the same trefoil-hole number. Meanwhile, as the trefoil-hole number increasing, the heat transfer coefficient gradually decreases as well as the pressure drop. It can be ascribed to the larger amount of leakage flow through more trefoil-holes, which results in the decreasing flow velocity of the mainstream region and lower turbulence intensity. In brief, the situation of more trefoil-holes is disadvantageous to the heat transfer while beneficial to flow performance.

The comprehensive performance of different trefoil-hole number can be depicted through the relationship between the h/Δp and the mass flow rate, as expressed in Figure 16. It is found that the h/Δp is rising with the enlargement of the trefoil-hole number. When keeping the mass flow rate at 2 kg/s, the h/Δp at the STHX-IT with the trefoil-hole number changing from 4 to 7 grows by 5.35% to 21.39% than that with the trefoil-hole number of 3. Therefore, n = 7 is the best trefoil-hole number among the given five from the perspective of comprehensive performance.

4.4.3. Effects of Baffle Cut δ

Figure 17 and Figure 18 display the heat transfer coefficient and pressure drop at different baffle cut δ when the inclination angle is 10° and the trefoil-hole number is 5 for the STHX-IT. We can observe that with the expanding of the baffle cut, the heat transfer coefficient and pressure drop both declines under the same mass flow rate. The changing tendency is attributed to the increment of flow area at baffles when the baffle cut increases gradually, which leads to the reduction of flow velocity. Compared to the STHX-IT with the baffle cut of 25% when the mass flow rate is 2 kg/s, the heat transfer coefficient of that with the baffle cut of 45% decreases by 24.26%, and the pressure drop also declines by 44.17%. Consequently, the larger baffle cut generates more notable reduction for the pressure drop than the decline with the heat transfer coefficient, and improves the comprehensive performance consequently.

Figure 19 reveals that the h/Δp increases with the baffle cut rising from 25% to 45% when the mass flow rate keeps constant. Quantitively, the h/Δp at the baffle cut of 45% rises by 36.88% to 32.88% compared to that with the baffle cut of 25% when the mass flow rate changes from 1.2 kg/s to 2.6 kg/s. Thus, it can be deduced that the larger baffle cut demonstrates superior overall performance when the baffle cut is within the range of 25% and 45%.

4.5. Optimization Study

4.5.1. Optimization Procedure

The above sections discuss the effects of three primary parameters for the STHX-IT, respectively. The results illustrate that they have different influences on the thermal-hydraulic performance. However, it is difficult to figure out the optimal structures merely based on parametric studies, thus the synthetic effect of these parameters should be taken into consideration. As a result, it is necessary to carry out the multi-objective optimization to acquire favorable design schemes with maximum heat transfer rate and minimum pressure drop. Nevertheless, the workload is too heavy to simulate enough data for optimization procedure, so the ANN is used to explore the relationships between the input variables and output objectives. The sample data acquired from CFD simulations are employed to train the networks of ANN, then these networks are provided as objective functions for optimization using MOGA. Figure 20 displays the flow chart of detailed procedures.

4.5.2. Artificial Neural Networks Results

A three-layer back propagation ANN which has sigmoid hidden neurons and linear output neurons are displayed in Figure 21. Three geometric parameters, i.e., inclination angle θ, trefoil-hole number n, and baffle cut δ, are set as inputs, and the heat transfer rate Q or pressure drop Δp as output. It corresponds to three neurons in the input layer and one neuron in the output layer. In detail, random 80% and 20% data are used for training and testing, respectively. The accuracy of these surrogate models is evaluated using the performance functions of the relative error, Mean Square Error (MSE), and Coefficient of Determination (R²), which can be expressed as follows:

$$error=\frac{1}{N}{\displaystyle \sum _{i=1}^N\frac{\left|X_{i,ANN}-X_i\right|}{X_i}}$$

(15)

$$MSE=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left(X_{i,ANN}-X_i\right)}$$

(16)

$$R^2=1-{\displaystyle \sum _{i=1}^N\frac{{\left(X_{i,ANN}-X_i\right)}^2}{X_i^2}}$$

(17)

The number of neurons in the hidden layer significantly affects the training precision of ANNs, thus a neuron independence test is implemented to determine appropriate number of neurons for each network.

Table 4. Performance of artificial neural network (ANNs) with different neuron number in the hidden layer (%).

Number of Neurons	$\mathbf{Error}\mathbf{of} \mathit{Q}$		$\mathbf{Error}\mathbf{of} \mathbf{\Delta }\mathit{p}$
	Training	Validation	Training	Validation
1	0.96	1.03	2.50	2.77
2	0.71	0.82	2.46	2.77
3	0.43	0.52	1.76	2.09
4	0.28	0.35	1.17	1.53
5	0.18	0.23	0.66	0.82
6	0.14	0.21	0.62	0.82
7	0.18	0.29	0.43	0.58
8	0.14	0.24	0.43	0.72
9	0.15	0.26	0.81	1.26
10	0.12	0.26	0.41	0.76
11	0.14	0.29	0.40	0.71
12	0.12	0.28	0.52	1.06
13	0.20	0.47	0.60	1.11
14	0.16	0.31	0.84	1.59
15	0.13	0.38	0.51	1.35

shows the performance of two networks while varying the number of neurons. In order to avoid under-fitting or over-fitting, networks with six and seven neurons in the hidden layers are chosen for Q and Δp respectively, which illustrates the minimum errors both for training and validation. Figure 22 illustrates the deviations between predicted results by ANN and numerical results by CFD. The maximum values for Q are 0.58% and –0.72%, and those for Δp are 1.22% and –1.36%. Moreover, the MSE and R² are close to 0 and 1, respectively. Therefore, these two networks are sufficiently precise to predict the relationships between parameters and objectives.

4.5.3. Multi-Objective Optimization Results

The multi-objective optimization is used to optimize conflicting object functions, and the non-dominated sorting genetic algorithm (NSGA-II) is a widely-used method to execute the procedure because of the high efficiency and applicability. The result is a set of non-dominating solutions, i.e., Pareto front, instead of only one specific solution. In this study, the problem can be expressed as follows:

Minimization

$$J_1=-Q,J_2=\Delta p$$

Subject

$$\begin{gathered} 0\le \theta \le 20 \\ 3\le n\le 7 \\ 25\le \delta \le 45 \end{gathered}$$

Considering that the trefoil-hole number is an integer in practical applications, n should be rounded after completing the optimization procedure. The gamultiobj toolbox in Matlab is utilized for conducting NSGA-II, and the setting parameters are presented in

Table 5. Parameter settings for NSGA-II.

Parameter	Value
Population size	400
Pareto fraction	0.3
Crossover fraction	0.8
Generation	500
Functional tolerance	10−4

.

The Pareto front solved by NSGA-II is depicted in Figure 23. All points are the trade-off solutions with conflicting objective functions, and they provide a variety of schemes under distinct operating conditions. In order to decide the optimal structure among these points, the decision-making approach named the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) is applied. The purpose of this method is to find a relatively satisfactory solution between the positive ideal solution and the negative ideal one, and the criterion is set as the relative closeness to the ideal solution. Figure 23 shows that the summit of the relative closeness is reached at 0.787 while θ, n, and δ are equal to 5.38°, 6, and 43%, respectively. The objectives of the best solution, i.e., Q and Δp, and their comparisons with the STHX-SG are shown in

Table 6. Comparisons between the optimized structure of the STHX-IT and the STHX-SG.

Model Type	Structural Parameters			Objectives		Q/Δp
	θ/°	n	δ/%	Q/W	Δp/Pa
The optimized STHX-IT	5.38	6	43	275,447.66	5484.33	50.22
The STHX-SG	0	0	25	366,452.48	17,109.11	21.42

. When comparing with the STHX-SG, the heat transfer rate of the optimal geometrical model merely decreases by 24.83% with the remarkable reduction of the pressure drop by 67.95%. The heat transfer rate per pressure drop Q/Δp of the optimized STHX-IT is 2.34 times the value of the STHX-SG, which indicates that the STHX-IT can obtain more heat transfer rate under the same pressure drop. Therefore, the optimal structure of STHX-IT has superior thermo-hydraulic performance.

5. Conclusions

In this work, a novel shell and tube heat exchanger with inclined trefoil-hole baffles (STHX-IT) is proposed and numerically investigated to examine the heat transfer performance and pressure drop. The comparison studies between the STHX-IT and STHX-SG are also conducted. The parametric analysis of the inclination angle θ, the trefoil-hole number n, and the baffle cut δ, is carried out for the STHX-IT. The multi-objective optimization of the design variables is implemented by adopting the combination of CFD, ANN, and MOGA, whose aim is to obtain the maximum heat transfer rate with the minimum pressure drop. The major conclusions are outlined as follows:

(1) The inclined trefoil-hole baffles of the STHX-IT can generate oblique flow in the shell side, and uniform flow patterns and temperature distributions are observed through the numerical results.

(2) Compared with the conventional STHX-SG, the STHX-IT has lower heat transfer rate with more significant reduction in the pressure drop, thus possessing superior comprehensive performance characterized by the heat transfer coefficient per pressure drop.

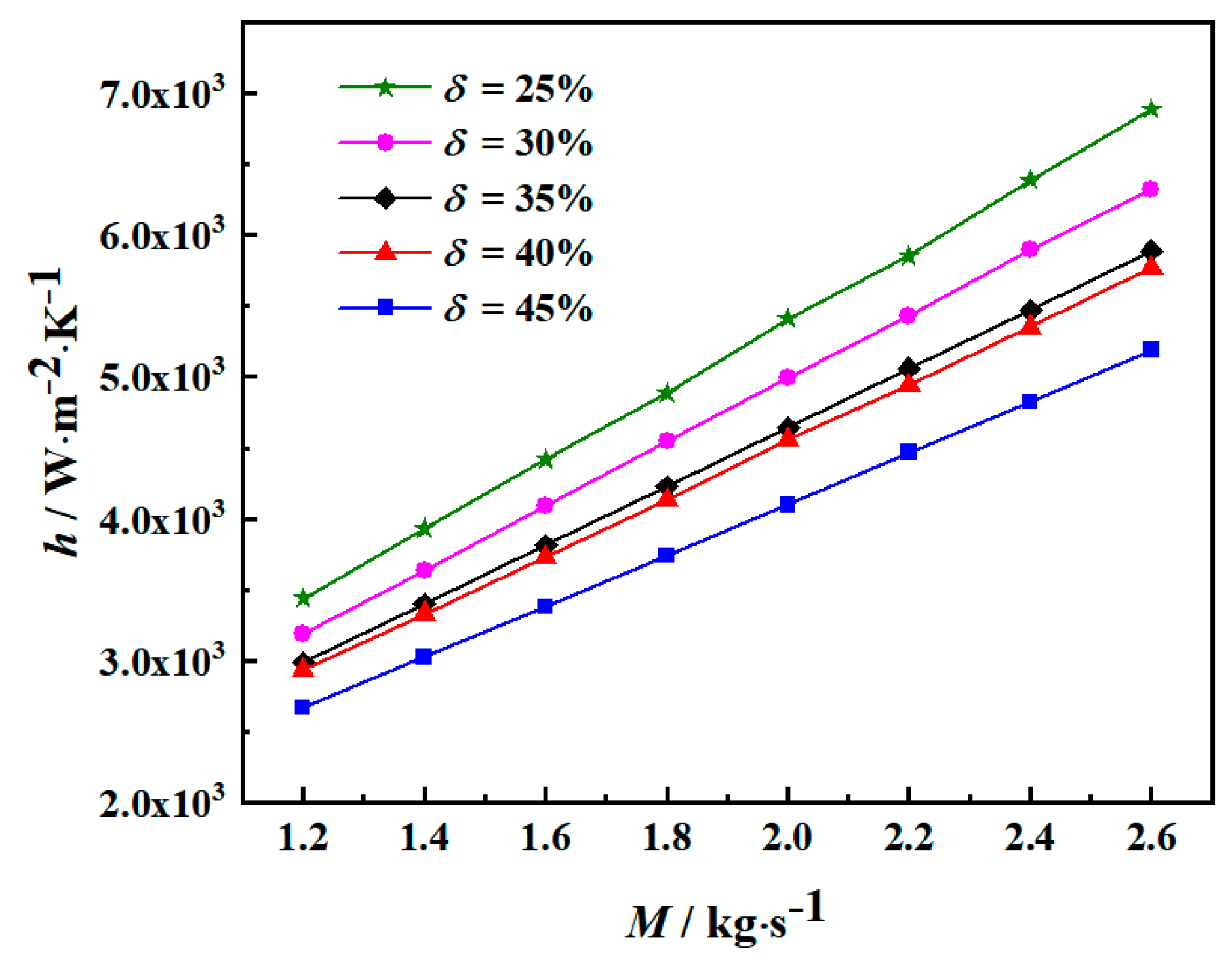
(3) According to the parametric studies, the heat transfer coefficient and pressure drop simultaneously decrease slightly with the inclination angle θ growing, and the comprehensive performance is approximately equal. The trefoil-hole number n and the baffle cut δ have more notable influence on the shell side performance. In detail, the larger trefoil-hole number and larger baffle cut both reduce the heat transfer rate and pressure drop, and bring in better comprehensive performance.

(4) The Pareto front corresponding to the best thermal-hydraulic performance is obtained by multi-objective optimization for the STHX-IT. The design parameters of θ = 5.38°, n = 6, and δ = 43% is chosen as the optimal structure by using the TOPSIS, whose Q/Δp can achieve 2.34 times as much as that of the STHX-SG.

As a final, the new STHX-IT proposed in this work is effective to enhance the comprehensive performance of shell side, which provides a meaningful solution to replace the STHX-SG in some industrial applications. In addition, the suitable combination of structural parameters can achieve optimum performance. According to the above results, small inclination angle, a certain number of trefoil-holes, and reasonable baffle cut should be considered.