Optical Performance Analysis of Single Flow Through and Concentric Tube Receiver Coupled with a Modified CPC Collector Under Different Configurations

Abstract

Compound parabolic concentrating (CPC) collectors have great potential to provide sustainable solar thermal energy for many applications operating in the medium temperature range. This paper presents the design, development and performance evaluation of a modified CPC collector integrated with an evacuated tube receiver. The optical performance of the designed CPC paired with concentric tube receiver is compared with that of a CPC coupled with single flow through evacuated tube receiver for stationary installation in the East-West and North-South directions. Ray tracing simulations of different configurations demonstrate that CPC coupled with single flow through receivers suffer high gap losses, especially at smaller incidence angles which are considerably alleviated by a concentric tube receiver arrangement. East-West installation of CPC paired with concentric tube receiver exhibited superior optical performance than all other configurations. The yearly average optical efficiency of CPC with concentric tube receiver was 5% higher than that of a single flow through receiver within the acceptance angle. A 60% truncated CPC coupled with concentric tube receiver emerged as the most effective design, which was fabricated for experimental testing. The tests conducted under actual outdoor tropical environmental conditions demonstrated that the experimental optical efficiency reached to about 69% in the case of N-S installation and 66.5% in an E-W arrangement. The experimental results closely match the simulation outcomes, which indicate the proposed performance prediction technique as instrumental for selecting the most effective configuration of CPC collectors for medium temperature heat supply.

1. Introduction

Compound parabolic concentrating collectors are non-imaging devices which have great potential to supply sustainable solar thermal energy in the medium (90–300 °C) temperature range [1,2]. CPC collectors, generally, don’t need continuous tracking mechanisms for lower concentration range (below 3×) and only seasonal or intermittent adjustments are required for medium concentration range (3–10×) [3,4]. The ability of CPC collectors to collect diffuse radiation [5] provides an additional advantage, especially in tropical regions where the percentage of diffuse radiation is relatively higher [6]. Owing to the promising benefits of these collectors, many researchers have designed and evaluated CPC collectors for various low-to-medium temperature applications, including industrial process heat [7], solar heating and cooling [8], water treatment and purification [9], methanol reforming and hydrogen production [10], building-integrated water heating systems [11] and photovoltaic/thermal (PV/T) hybrid systems [12].

After the introduction of CPC as a potential candidate for solar energy collection [13], many research studies have been conducted in this field [3,14,15]. Gallagher and Winston [16] reviewed basic principles of the non-imaging optical design of CPCs for some selected arrangements of evacuated and non-evacuated solar collectors. Derrick et al. [17] analyzed different concentrators with non-evacuated tubular absorbers and compared annual energy collection for East-West (E-W) and North-South (N-S) orientations. Aguilar-Jiménez et al. [18] also developed and experimentally tested a CPC collector integrated with a non-evacuated concentric tube receiver. Stationary installation of the collector in an E-W direction exhibited almost 6% better thermal performance than the N-S orientation. The coefficient of heat losses was also 10% higher in the case of E-W arrangement, probably due to the elevated temperature of the bared absorber. It is worth noting that thermal losses from the non-evacuated receivers of concentrating collectors are increased due to higher surface temperatures resulting from solar radiation concentrated on the smaller area of the absorbers. Thus, the benefit of radiation concentration is compromised by increased thermal losses. However, conduction and convection losses can be minimized by employing evacuated tube receiver (ETR) while radiation losses can be suppressed by applying selective coatings at the absorber surface which can also increase energy absorption [19]. An external CPC coupled with counterflow absorber with cylindrical fin enclosed in an evacuated glass tube was designed, developed, modeled and tested by Kim et al. [20]. Acceptance half angles of 34° and 60° were selected for stationary installation in E-W and N-S directions, respectively. The experimental results revealed that N-S arrangement showed better performance at relatively lower temperatures (<165 °C) while E-W installation was best for higher temperatures (with 40% efficiency at 200 °C), probably due to higher concentration ratio for this arrangement. Earlier, Balkoski [21] also analyzed three different evacuated tube receivers coupled with external CPC. Acceptance half angles of 34° and 60° were selected for E-W and N-S installations respectively. During the clear sky conditions, E-W arrangement of all collectors demonstrated superior performance at higher temperatures (>140 °C) as compared to N-S alignment which relatively performed better at lower temperatures. Thermal performance of N-S oriented collectors was slightly better than E-W installation during cloudy or hazy conditions. Nkwetta et al. [22] modified a heat pipe array by integrating it with an internal CPC and compared the thermal performance with another array comprising of an internal CPC coupled with direct flow absorber for both evacuated and non-evacuated options. Evacuated receivers paired with CPC demonstrated better performance than other arrangements. In another study [23], an internal CPC coupled with direct flow absorbers was integrated with heat pipe array as outlet manifold and was experimentally tested in both N-S and E-W configurations. The experimental results of N-S arrangement exhibited better performance than E-W installation. However, the optical performance was only evaluated for transverse angles of incident radiations [24] and the results for longitudinal direction were not available for comparative optical analysis.

Energy collection in a CPC collector greatly depends on the absorption of concentrated radiations at the absorber surface which is affected by configuration, material and surface properties of collector components as well as manufacturing and alignment accuracy [19]. Ray tracing is a very useful tool to precisely estimate the flux distribution and amount of solar energy available at the receiver. Many research studies [25,26,27,28] have successfully applied this method to evaluate the effect of different parameters on the optical performance of solar collectors. Chen et al. [29] used ray-tracing method to analyze the optical performance of an E-W oriented CPC collector coupled with tubular receiver for different truncation heights of reflectors and tilt angles. Terron-Hernandez et al. [30] also applied the ray-tracing technique to investigate the energy availability at the receiver surface for static and multi-position setups in E-W installations. A past literature review illustrates that stationary installation of a CPC collector is one of the main features to eliminate the need for complex and costly tracking mechanisms. In addition, the orientation also predominantly affects its optical performance which in turn influence the thermal behavior. Therefore, detailed optical performance evaluation under different configurations is imperative for precise performance prediction, selection, and installation to achieve the optimum yield throughout the year.

The previous research studies mainly focused on performance analysis of CPC collectors under specific conditions. Some research studies compared the performance of external CPC collectors but used different geometric characteristics for E-W and N-S installations. This paper presents the design, development and comparative performance analysis of modified CPCs coupled with SFT and CT receivers under different configurations. The same geometric characteristics are used for stationary installations of the collectors in N-S and E-W directions. The original height of the CPCs is truncated to save material and manufacturing cost with minor decrease in concentration ratio. The Monte Carlo ray-tracing method is used to determine the optical power at the absorber surface and results are presented to compare the daily energy collection during the effective operating time span. Moreover, four representative days (spring and autumn equinoxes as well as summer and winter solstices) are chosen for the yearly performance evaluation in both arrangements. CT receiver paired with 60% truncated reflectors (ensuing highest daily energy collection) is fabricated to experimentally test in both N-S and E-W installations. The results are presented to evaluate thermal performance under actual environmental conditions and validate the simulation data. The important outcome of this study is the determination of the optimum configuration of the modified CPC collector for stationary installation.

2. Materials and Methods

2.1. Evacuated Tube Receivers

The CPCs are designed based on two commercially available evacuated tube receivers. The single flow through evacuated tube (model JJR-T-2140 manufactured by Zhejiang Jiajiare New Energy Co., Ltd. China) is comprised of a stainless steel (SS 304/316) absorber tube enclosed in a high-quality borosilicate glass envelope with antireflective coating as shown in Figure 1a. The annular space between the metal and glass tube is evacuated (3 x 10⁻⁴ Pa at 200 °C) to suppress convection losses while outer surface of the metallic tube is coated with aluminum nitride to increase energy absorption and minimize radiation losses. Expansion bellows are provided at both ends to accommodate the uneven thermal expansion of metal and glass tube while metal to glass seals are also provided at both ends to secure the vacuum at higher temperatures.

The second evacuated tube receiver considered in this study is comprised of two concentric copper tubes enclosed in a high strength borosilicate glass envelope as shown in Figure 1b. Flat metallic fins attached to the outer metallic tube increase the surface area of the absorber to intercept the maximum amount of radiation and reduce gap losses. The space between the outer absorber tube and glass envelope is evacuated (<10⁻⁵ mbar) to suppress convection losses. Aluminum nitride coating applied at the external surface of the outer metallic tube as well as extended fins enhances the absorption of incident energy and minimizes radiation losses. The heat transfer fluid enters the inner tube, flows to the end from where it returns into the annulus space between the two metallic tubes and gets heated by incident solar energy. The detailed specifications of both SFT and CT receiver components are given in

Table 1. Parameters of the single flow through (SFT) and concentric tube (CT) evacuated receivers.

Parameter.	Design Value
	SFT Receiver	CT Receiver
Absorber Tube
Length (m)	L = 2.00	L = 2.00
Outer diameter (m)	do = 0.040	do = 0.053 (virtual)
Thickness (m)	t = 0.002	t = 0.001
Surface area (m2)	0.251	0.173
Material	Stainless steel	Copper (with Al fin)
Glass Tube
Length (m)	L = 2.00	L = 2.00
Outer diameter (m)	Dgo = 0.100	Dgo = 0.100
Thickness (m)	tg = 0.0025	tg = 0.0025
Material	Borosilicate glass	Borosilicate glass

.

Ideally, all solar radiation falling on the inlet aperture of a CPC at incidence angles within the limits of acceptance angle (±θ_a in Figure 1) are directed to the receiver placed at the exit aperture either directly or after reflecting from the concentrators. In the case of ETR, some radiation pass through the gap between the absorber and cusp after reflecting from concentrators and escape to the environment. The lost radiation result in optical losses which need a proper investigation to precisely predict the power available at the absorber surface and determine the net benefit of using ETR in all configurations.

2.2. CPC Geometric Design

The sun angle varies between −19.60° (north) and 27.84° (south) from vertical-axis at solar noon at the selected location (4.385 N and 100.979 E). Considering the maximum movement of the sun in celestial vault during the year and stationary installation of the proposed CPCs in N-S and E-W directions with aperture plane facing vertically upward, the acceptance half angle was selected to be 30°. The reflector profile with a tubular absorber of radius ‘r’ enclosed in a glass tube of radius ‘R’ was generated in MATLAB using Equation (1) [20]:

$$\{\begin{array}{l}x=r\mathit{sin}\varphi -k\left(\varphi \right)\mathit{cos}\varphi \\ y=-r\mathit{cos}\varphi -k\left(\varphi \right)\mathit{sin}\varphi \end{array}$$

(1)

where distance k(φ) is determined by the string method using Equation (2) [31]:

$$k\left(\varphi \right)=r\{\begin{array}{ll}\varphi +\gamma & for\phi \le \varphi \le \raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.+{\theta }_a\\ \frac{\frac{\pi }{2}+{\theta }_a+\varphi +2\gamma -cos(\varphi -{\theta }_a)}{1+sin(\varphi -{\theta }_a)}& for\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.+{\theta }_a\le \varphi \le \raisebox{1ex}{$3\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.-{\theta }_a\end{array}$$

(2)

where γ = [(R+g)² − r ²]^1/2 /r] − ϕ and ϕ = cos⁻¹[r/(R+g)], g is gap between absorber and reflector cusp.

Any point C on the reflector is defined by the angle φ (between line OD from the origin O to D and line CE between point C and tangent on the periphery of absorber at point E) and distance k(φ) as shown in Figure 2. The non-evacuated tubular receiver is normally in contact with the concentrator at the cusp in an ideal CPC. For ETR some gap (g) between the absorber and reflector is provided to accommodate the glass tube. Some additional gap (I_g) is also provided to ensure that the glass tube does not touch the cusp of the reflectors. The cross-section of the full height CPC coupled with ETR is shown in Figure 2.

The reflector profile for the concentric tube receiver with extended flat fins was constructed on the basis of a virtual tube whose radius was equal to the perimeter of virtual absorber shown with dotted lines in Figure 3a. Details of the virtual absorber tube calculations are given in Appendix A. Like the SFT receiver, a small gap between the tip of the lower fin of the CT absorber and cusp of the reflectors was provided to accommodate the glass envelope tube. Likewise, some additional space between the glass tube and cusp of the reflectors was also provided to avoid direct contact with the concentrator, as shown in Figure 3b.

2.3. CPC Reflector Truncation

The reflector height of a CPC is very large, especially with small acceptance angles which leads to high material and manufacturing cost. However, upper portions of reflectors become almost parallel to the axis of CPC and contribute very little in the enhancement of radiation concentration. Therefore, the top portions of the reflector were truncated to save a significant amount of material and manufacturing cost with a small decrease in the aperture width and concentration ratio (CR), as shown in Figure 4.

The effect of reflector truncation on the geometric parameters such as aperture width, reflector height, concentration ratio and acceptance angle for beam radiation for both receiver types is shown in Figure 5.

Reflector height decreased linearly while aperture width and CR decreased slowly for low truncation level and then sharply after about 60% truncation for both CPCs. This brings about the economic opportunity of significant savings in terms of reflector material and corresponding manufacturing cost. For example, more than half of the reflector material and manufacturing cost can be saved by reducing the reflector height to half of the full size with only a 7.3% corresponding decrease in aperture width and CR. The ratio of aperture width/reflector height also decreased slowly in the beginning and then steeply as the truncation level increased (especially after 70% truncation) which indicates that comparative reduction in aperture width was more for higher truncation levels of the reflectors. The final height of reflectors was selected to be 40% of the full size (60% truncation) for both CPCs. For this truncation level, the aperture width only decreased about 11% (from 0.360 m to 0.320 m) with 60% corresponding decrease in reflector height (from 0.340 m to 0.136 m) in case of SFT receiver. Similarly, aperture width decreased from 0.412 m to 0.367 m (11% decrease) while reflector height reduced from 0.406 m to 0.162 m (60% reduction) in case of CT receiver as shown in Figure 5a. The effect of reflector truncation on CR and effective acceptance angle for direct radiation can be seen in Figure 5b which shows that CR decreased from 2.87 to 2.55 and 2.50 to 2.23 for SFT and CT receivers respectively for the selected truncation level.

As a result of reflector truncation, field of view of the absorber is also increased, which enables direct and diffuse radiation to reach the receiver beyond ±θ_a. The effective acceptance angle for direct radiation (θ_t) increased from 30° to about 55° for a 60% truncated reflector in both CPCs. In this way, effective operating time was also increased from 4 h to 7 h for N-S installation. The average number of reflections within the CPC also decreases by reducing the height of concentrators as demonstrated in [32]. Construction details of the modified CPC troughs with full and truncated heights are presented in

Table 2. Construction parameters of CPC collectors.

Parameter	Unit	Design Value of CPC for
		SFT Receiver		CT Receiver
		Original	Modified	Original	Modified
Reflector height Reflector width	m	0.341 0.360	0.136 0.320	0.404 0.410	0.150 0.357
Aperture area	m2	0.720	0.640	0.820	0.714
Gap between absorber/fin and reflector	m	0.035	0.035	0.014	0.014
Gap between glass tube and reflector cusp	m	0.005	0.005	0.005	0.005
Concentration ratio (CR)	-	2.87	2.55	2.50	2.23
Acceptance half angle	degree	30	30 + 25	30	30 + 25
Concentrated radiation receiving time	hr	4	4	4	4
Direct radiation receiving time	hr	4	7	4	7

.

2.4. Energy Modeling

The total incident solar energy consists of both beam and diffuse irradiance. The conventional concentrating collectors can only collect direct or beam component of solar radiations while CPC collectors have the advantage of being able to intercept a fraction of the diffuse radiation as well, which make up a considerable proportion of the total irradiance, especially during rainy seasons and in tropical environments. Therefore, diffuse radiation should also be considered to determine the overall energy performance of CPC collectors. Total solar energy incident on the aperture plane of a CPC at any time is defined by the following equation:

$$G=G_b+G_d$$

(3)

Direct or beam radiation G_b is determined by the following equation:

$$G_b=G_{b,n}\mathit{cos}{\theta }_i$$

(4)

where G_b,n is direct normal irradiance and θ_i is the incidence angle of beam irradiance which varies with the movement of the Sun in the celestial vault and can be determined by using Equation (5) as mentioned in [33]:

$$\mathit{cos}{\theta }_i=\mathit{cos}{\theta }_z\mathit{cos}\beta +\mathit{sin}{\theta }_z\mathit{sin}\beta \mathit{sin}\left({\gamma }_s-\gamma \right)$$

(5)

where θ_z is zenith angle and β is tilt angle of the collector while γ_s and γ are the azimuth angles of the Sun and collector, respectively.

Equation (6) gives the power available at the outer surface of the absorber tube at any time:

$$S=G_{b}p{\tau }_e{\tau }_{CPC}{\alpha }_r+G_d{\overline{\tau }}_e{\overline{\tau }}_{CPC}{\overline{\alpha }}_r/C_g$$

(6)

where p is the gap loss factor which accounts for optical power lost due to the gap between absorber tube and cusp of reflectors, τ_CPC is the transmittance of the CPC which depends upon the reflectance of the concentrator and the average number of reflections before reaching the absorber. The terms with bars over them represent the average values used for calculating diffuse radiations, while C_g is the concentration ratio of the CPC.

Optical efficiency, defined as the ratio of power received at the absorber tube of ETR to that incident on the entry aperture of CPC is given by the following equation:

$${\eta }_o={\tau }_e{\tau }_{CPC}{\alpha }_r\left(1-L\right)$$

(7)

where 1 − L = gap efficiency and L is the average value of gap loss factor which is determined by following equation [31]:

$$L=\frac{\tan \varphi -\varphi }{\tan \varphi +\pi -\varphi }$$

(8)

Optical efficiency depends on the angular distribution of solar rays over the acceptance angle. Average optical efficiency, defined by the ratio of the radiation received by the inner tube of the ETR from all directions over the acceptance angle to that incident on the aperture of CPC during the operating time period, is calculated taking a lead from the concept presented by [34]. For isotropic radiations, average optical efficiency is expressed as:

$${\overline{\eta }}_o=\frac{{{\displaystyle \int }}_{-{\theta }_a}^{{\theta }_a}G\mathit{cos}\theta \eta \left(\theta \right)d\theta }{{{\displaystyle \int }}_{-{\theta }_a}^{{\theta }_a}G\mathit{cos}\theta d\theta }$$

(9)

The useful heat collected by the absorber tube (Q_r) is determined using the following equation:

$$Q_r={\eta }_o{G}_c{A}_a-U_c\left(T_r-T_{amb}\right)A_r$$

(10)

where U_c is heat loss coefficient of the collector, without considering the heat carried by the circulating fluid inside the absorber tube, which is determined by considering all thermal losses from the collector components as explained in [34]. Useful heat gained by the circulating fluid is determined considering the mean fluid temperature and losses from the absorber by using the following equation:

$$Q_u=F^{\prime }\left[S{A}_a-U_L\left(T_{fm}-T_{amb}\right)A_r\right]$$

(11)

where F´ is the efficiency factor which is determined as explained in [35,36], U_L is the overall heat loss coefficient, and T_fm is the mean fluid temperature. An alternative way of calculating the useful heat gain by circulating fluid is presented in Equation (12):

$$Q_u=F_R\left[S{A}_a-U_L\left(T_{fi}-T_{amb}\right)A_r\right]$$

(12)

where F_R is the collector heat removal factor defined by the ratio of actual heat transfer to the maximum possible heat transfer and is determined according to the procedure explained in [33]. For this study, useful heat carried by heat transfer fluid circulating through the absorber tube is determined by using the following equation:

$${\dot{Q}}_u=\dot{m}{C}_f\left(T_{fo}-T_{fi}\right)$$

(13)

where C_f is the heat capacity of the circulating fluid at mean fluid temperature. The overall efficiency of the collector, defined by the ratio of useful heat gain to the energy incident at the aperture plane, can be determined using the following equation:

$$\eta =\frac{Q_{net}}{Q_{in}}=\frac{{\dot{Q}}_u}{G{A}_a}=\frac{\dot{m}{C}_f\left(T_{fo}-T_{fi}\right)}{G{A}_a}$$

(14)

where G is the total solar irradiance incident on the aperture and A_a is the total aperture area of the collector.

2.5. Ray Tracing Simulation

A detailed optical analysis is imperative to assess the energy interaction with collector components and find out the power available at the absorber surface. The energy received at the absorber surface can be determined if the angle of incidence and energy content of solar radiation along with optical properties of the interacting surfaces are known. However, it becomes very cumbersome to precisely follow every ray and its energy interaction with all the surfaces it comes across in a complex optical system using conventional numerical methods. Ray tracing has emerged as a promising tool to estimate the amount and distribution of optical power in solar systems [29]. In this study, the Monte Carlo ray tracing method was used to simulate ray paths from source to the receiver (target) and evaluate the optical performance of the modified CPC collectors for different incidence angles. The virtual models developed in Solidworks were imported into the ray tracing software TracePro 7.8.1 (developed by Lambda Research Corporation Littleton, MA, USA). Material and surface properties for the collector components as given in

Table 3. Properties of CPC components for ray tracing simulations.

Component	Material	Reflectivity	Absorptivity	Transmissivity	Emissivity
Reflector	Aluminium (Alanod)	0.92	0.08	-	0.05
Glass Tube	Borosilicate glass (with anti-reflective coating)	-	0.002	0.98	0.91
Absorbers (both SFT and CT)	Copper (with AlN coating)	-	0.94	-	<0.06

were assumed to be independent of temperature for comparative analysis of the collectors under different configurations.

Since the radiation source was considered at sufficiently long-distance, parallel radiations were assumed for the ray tracing analysis. 100,000 rays were used, which are adequate to obtain the precise amount of power at the outer surface of the absorber [37]. Environmental conditions were specified after setting-up the system parameters and ray tracing simulations were performed for 7 h of effective operating time (from 10:00 am to 5:00 pm local time) for all arrangements. Clear sky conditions (with 1000 W/m² as hemispherical irradiance) were used in this study to simplify the analysis and focused on the comparative performance evaluation under different scenarios of both configurations. Optical energy intercepted by both collectors oriented in N-S and E-W directions was determined for stationary installation at the selected location (latitude 4.385 °N, longitude 100.979 °E). Four representative cases (spring and autumn equinoxes as well as summer and winter solstices) were considered for the comparison of daily energy collection and annual optical performance evaluation in order to choose the best configuration prior to actual implementation.

2.6. Experimental System

The 60% truncated CPC paired with CT receiver, which emerged as the best choice among all configurations, was selected for experimental testing. CPC troughs were fabricated using highly reflecting Alanod sheets as the concentrators and assembled with CT receivers. The whole CPC module was installed on the base frame along with all measuring instruments as per the schematic diagram shown in Figure 6. The location of measuring instruments is also illustrated in the schematic diagram. PT-100 was used to measure the temperature at designated places. The flow rate of the HTF (Therminol-55 oil) was measured by Oval Flowpet-5G flowmeter. A first-class pyranometer (EKO MS-402) mounted on the main frame of the collector was used to measure the global solar radiations in the plane of the collector’s aperture while pyrheliometer (EKO MS-56) installed on sun-tracking platform (STR-21G), was used to measure the direct solar radiations. The wind velocity was measured by using an anemometer (Adafruit, New York, NY, USA).

The experimental test rig was installed at the test site of the Solar Thermal Advanced Research Center (STARC), Universiti Teknologi PETRONAS, Malaysia (latitude 4.385 °N, longitude 100.979 °E). The test rig was flexible enough to be oriented in any direction and tilting of troughs along their longitudinal axes. The whole system shown in Figure 7 was tested under actual outdoor environmental conditions for both N-S and E-W arrangements following the guidelines provided in ISO9806-2017 standard for testing solar thermal collectors.

The measuring instruments were connected with a datalogger (Graphtec GL-820 Totsuka-ku, Yokohama 244-8503, Japan) for continuous monitoring and recording of the parameters at 60 s intervals. A separate cooling system was designed and integrated with the heat exchanger/storage tank of the collector to achieve steady-state conditions at different inlet temperatures of the circulating fluid. The data were recorded at different inlet temperatures while keeping the flow rate at 156 kg/h which is equivalent to 0.02 kg/s.m² recommended by ISO9806 standard for testing solar thermal collectors. The recorded data were analyzed by considering the circulating oil properties at mean temperature.

2.7. Uncertainty Analysis

The uncertainty of the measuring parameters was estimated to determine accuracy of the experimental results. The main sources of errors were associated with the measurements of temperatures, flow rate and solar irradiance. The uncertainty analysis was done by following the method of Kline and McClintock (1953) using the following equation:

$$U_{\eta }=\sqrt{{\left(\frac{\partial \eta }{\partial \dot{m}}{u}_{\dot{m}}\right)}^2+{\left(\frac{\partial \eta }{\partial △T}{u}_{△T}\right)}^2+{\left(\frac{\partial \eta }{\partial G}{u}_G\right)}^2}$$

(15)

where u_ṁ, u_ΔT and u_G are the errors associated with the measurement of flow rate, temperature and solar irradiance, respectively. The errors in collector area and specific heat capacity are assumed to be negligible for the determination of total uncertainty calculation. The errors in the measurement of flow rate, temperature and solar irradiance were 0.5%, 1.2% and 1.0%, respectively. The maximum relative uncertainty of the experimental thermal efficiency was found to be 1.64%.

3. Results and Discussion

3.1. Ray Path Diagrams

The energy received at the absorber surface mainly depends on the shape, alignment, and manufacturing of the collector components as well as the material and surface properties. Trajectories of the incident and reflected radiations for different configurations were obtained using Monte Carlo ray tracing technique which works on the principle of geometric optics as well as statistical methods to simulate the behavior of optical systems to trace the transmission path of all individual rays originating from the source to the receiver. Figure 8 shows the ray paths of radiations intercepted by the absorber of SFT receiver coupled with truncated CPC placed in N-S orientation at different incidence angles. The incident radiations approach the absorber either directly or after reflecting from concentrators. Both direct and reflected radiations are intercepted by the absorber as long as θ_i ≤ ±θ_a as shown in Figure 8a–c, while only direct radiations can reach the absorber beyond the acceptance angle (±θ_a ≤θ_i ≤ ±θ_t) in case of truncated CPCs as shown in Figure 8d–f. The reflected radiations concentrate on a certain region of the absorber tube which gradually shifts upward with increasing incidence angle of incoming radiations. Large gaps in ray paths especially visible in Figure 8a indicate the radiations that pass-through the space between the absorber tube and reflector cusp after reflecting from concentrators and escape to the environment. These escaping radiations result in optical losses called gap losses which are significant in case of SFT receivers, especially at smaller incidence angles. The gap losses gradually reduce as θ_i approach the maximum limit of θ_a (herein called limiting acceptance angle, θ_a-max). Incoming radiations falling outside ±θ_a-max (not shown in these figures) escape to the environment after reflecting from the mirrors and do not concentrate at the absorber surface.

In case of the CT receiver, extended flat fins reduce the gap between absorber and reflector cusp which enables the absorber to intercept more radiations especially mirrored from the reflectors. Small gaps in the ray paths of incident radiations are still visible in Figure 9a–c, which indicate a trivial amount of radiations reflected from the mirror surfaces and escaped to the environment either directly or after passing through the small opening between the absorber fin and reflector cusp. Similar to the CPC coupled with SFT receiver, incoming radiations are concentrated on the absorber of CT receiver as long as θ_i ≤ ±θ_a while only direct radiations can reach the absorber beyond ±θ_a-max, depending on the truncation level of the reflectors.

A comparative analysis of Figure 8a and Figure 9a shows that the amount of lost radiations in case of CT receiver is much less than the SFT receiver for the same incidence angles. Moreover, extended flat fins also enable the CT receiver to intercept direct radiations for a comparatively longer period for the same truncation level, which in turn increases the overall effective operating time of the collector.

3.2. Optical Power Collection

Optical power available at the outer surface of the absorbers averaged on a half-hourly basis was determined for comparative analysis under different configurations. Four representative cases (spring and autumn equinoxes as well as summer and winter solstices) were considered to evaluate the yearly optical performance. The power intercepted by both collectors was high in the concentrated zone (for θ_i ≤ ±θ_a) while some additional power was also collected beyond the acceptance angle (±θ_a ≤ θ_i ≤ ±θ_t) due to truncation of reflectors which lead to increase in overall effective operating time of the collectors (for direct radiations). The maximum energy collection rate was achieved at about 11:30 h and 15:30 h which corresponds to incidence angles close to the edge ray angles (extreme limits of ±θ_a) in all cases of N-S oriented collectors. These observations are analogous to the ray path diagrams shown in Figure 8 and Figure 9. Daily average energy collection and optical efficiencies were also evaluated and compared for stationary installation of both collectors in N-S and E-W orientations.

3.2.1. Optical Power in North-South Installations

The stationary installation of truncated CPC coupled with SFT receiver in N-S direction achieved the maximum power density at spring and autumn equinoxes (about 600 W/m²) which reduced to 550 W/m² and 510 W/m² at the summer and winter solstice, respectively, as shown in Figure 10a–d.

The power density was reduced by approximately 40% of the maximum value at noontime which can be attributed to high gap losses resulting from the large opening between the absorber tube and the cusp of the reflectors (about 0.035 m). The gap losses showed an increasing trend with decreasing incidence angle and became maximum at the middle of the day where solar radiations fall normal to the CPC aperture. The power density in case of a CT receiver integrated with a truncated CPC placed in the N-S direction also followed similar trends. The power density at the outer surface of the absorber was comparatively much higher in the concentrated zone while some additional power was also collected beyond ±θ_a in case of CT receiver paired with truncated CPC. The maximum power density (about 675 W/m²) was found near ±θ_a-max at the spring and autumn equinoxes as well as at the summer solstice which dropped to about 607 W/m² (11% less than the maximum value) at noontime as shown in Figure 10a–c. The maximum energy flux at the winter solstice was found a little lower (about 580 W/m²) which further reduced to 515 W/m² (11% less than the maximum value) at midday for stationary installation in N-S direction as shown in Figure 10d.

Comparative analysis of the truncated CPCs coupled with SFT and CT receivers installed in N-S direction demonstrates that reduction in optical power density at mid-day in case of SFT receiver was significantly ameliorated by employing a CT receiver. The reason could be attributed to the reduced gap losses with extended flat fins in the CT receiver which intercept most of the radiations which were lost in the case of the SFT receiver. Since the direction of the flat fins was kept vertical to minimize gap losses, the absorber of the CT receiver captured the maximum amount of radiations reflected from the concentrators. Energy collection beyond the acceptance angle was also higher in the case of the CT receiver due to the interception of beam radiations by the extended flat fins for a longer period. The optical power density was improved by approximately 70% at midday and 10–20% near ±θ_a-max at spring and autumn equinoxes, respectively, by employing a CT receiver with 60% truncated CPCs. The corresponding improvement at the summer solstice was 80% at noontime and 20–30% near ±θ_a-max. The energy flux rate at the winter solstice was slightly lower and an improvement of 60% at noontime and 20–30% near ±θ_a-max was observed by using a CT receiver. The overall optical power density was increased on average by 70% at midday and 15–20% near ±θ_a-max angle by using a CT receiver paired with 60% truncated CPC installed in N-S direction.

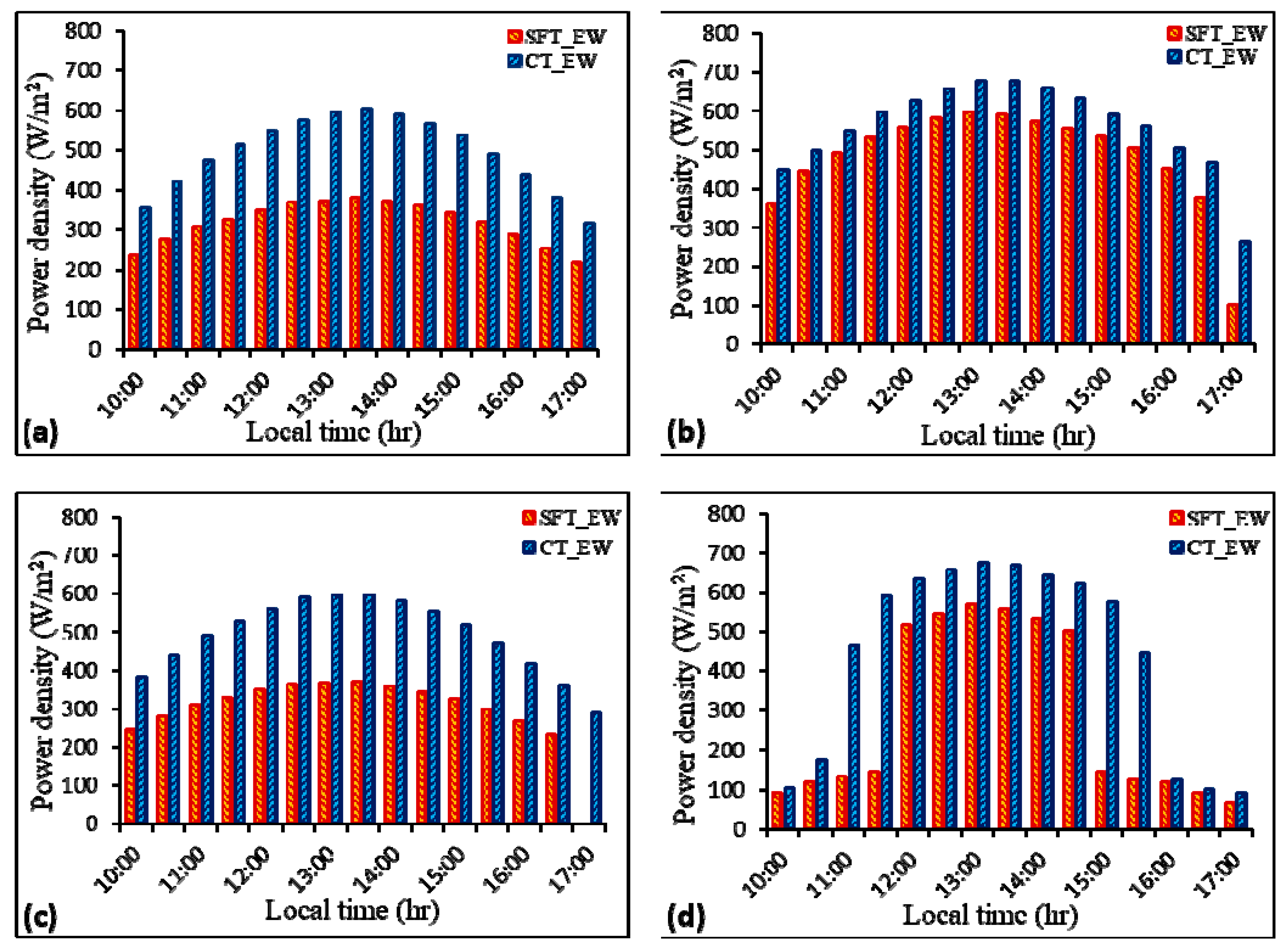
3.2.2. Optical Power in East-West Installations

The optical flux intercepted by the absorbers of both SFT and CT receivers integrated with CPCs placed in the E-W direction was also determined for the same time span (10:00 h to 17:00 h). The SFT receiver coupled with CPC achieved its maximum power density (over 590 W/m²) at noontime at the summer solstice which was almost double the corresponding value for N-S orientation. The possible reason for the higher power density in the SFT receiver for this arrangement can be attributed to the fact that incidence angle remained close to ±θ_a-max where gap losses were minimum which in turn increased the energy capture as shown in Figure 11b. At the spring and autumn equinoxes, the incidence angle of solar radiations remained close to the normal to aperture plane along the longitudinal axis of the E-W-oriented CPC which resulted in higher gap losses and reduced optical power density. However, the optical power density increased smoothly from the morning and reached the maximum value of about 380 W/m² at noontime as shown in Figure 11a,c. These flux values were higher than the corresponding values in N-S-oriented SFT collectors. At the winter solstice, effective power collection was only established from 12:00 h to 15:00 h as shown in Figure 11d. This interesting observation can be attributed to the possible reason that the sun movement in the celestial vault for this configuration is such that solar radiations fall within the acceptance angle of the CPC only in this time span. However, overall daily energy collection was still 4% higher than the corresponding value in N-S orientation. For E-W installation, optical power collection was improved in all seasons by employing the CT receiver. The rate of energy density at midday of spring and autumn equinoxes was around 600 W/m² which was almost 40% higher than the corresponding values of SFT receiver installed in the same direction. Similarly, maximum power density at summer solstice was 680 W/m² at noontime as shown in Figure 11b, which was 12% higher than the corresponding values of an E-W-oriented SFT receiver. At the winter solstice, the CT receiver integrated with CPC achieved a maximum value of power density (about 675 W/m²) at noontime, as shown in Figure 11d, which was almost 17% higher than the corresponding value for SFT receiver placed in the same direction.

Comparative analysis of both CPCs for the two orientations revealed that optical power density at the absorber of an E-W-oriented CT receiver at midday was almost equal to the corresponding value of a CT receiver and 40% higher than that of SFT receiver placed in N-S direction at the spring and autumn equinoxes. Similarly, the maximum power density at a CT receiver placed in the E-W direction was more than double the corresponding value of a N-S-oriented SFT receiver and 20% higher than a CT receiver at the summer solstice. At the winter solstice, a CT receiver integrated with CPC installed in the E-W direction achieved the maximum power density at noontime, which was 60% and 40% higher than the SFT and CT receivers, respectively, placed in the N-S direction. Overall, the CPC collector with CT receiver placed in the E-W direction demonstrated the highest power collection amongst all the configurations.

3.3. Comparison of Daily Average Energy Collection

Daily optical energy intercepted by both collectors placed in the N-S and E-W directions was also determined for the four representative cases.

Table 4. Daily optical energy collection (in MJ) by truncated CPC coupled with SFT and CT receivers under different configurations.

Month	CPC_SFT Receiver		CPC_CT Receiver
	E-W Installation	N-S Installation	E-W Installation	N-S Installation
Spring	5.483	5.281	9.498	7.978
Summer	8.365	5.004	10.813	7.978
Autumn	5.318	5.267	9.470	7.927
Winter	4.899	4.620	8.444	6.488
Annual average	6.016	5.043	9.556	7.593

gives the comparative analysis of daily energy collection during the selected operating time span (10:00 to 17:00 h) and under different configurations. Daily energy collection for the E-W installation was higher than the corresponding arrangement in the N-S direction for all seasons. SFT receiver coupled with CPC collected the maximum daily energy at the summer solstice and minimum at the winter solstice for both N-S and E-W installations. A similar pattern was followed by a CT receiver paired with CPC in all seasons for both orientations. CPC coupled with CT receiver installed in the E-W direction achieved the maximum optical energy collection (over 10 MJ) during the selected time span at the summer solstice, which was almost double than the amount intercepted by N-S installation of CPC with SFT receiver (about 5 MJ) during the same time span. The minimum energy was collected by SFT receiver (about 4.6 MJ) during the winter solstice.

3.4. Instantaneous Optical Efficiency

Optical simulations were run for both CPC collectors to evaluate the performance under different arrangements. Optical efficiency defined by the ratio of the power available at the outer surface of the absorber to that incident at the inlet aperture of the collector was determined for the concentration-time period (4 h) as well as for the overall effective operating time period (7 h). The optical efficiencies showed similar trends to power collection under different configurations. A significant reduction in the optical efficiency of CPC paired with SFT receiver was observed for incidence angles approaching the minimum value (at midday), predominantly due to higher gap losses as shown in Figure 12a–d. The reduction in optical efficiency at noontime was avoided by employing a CT receiver, especially in the N-S orientation.

The optical efficiency of a truncated CPC coupled with SFT receiver placed in the N-S direction was over 70% near ±θ_a-max, which dropped to about 40% at noontime (43% less than the maximum efficiency) at the spring and autumn equinoxes as well as the summer and winter solstice. Similarly, a truncated CPC with CT receiver achieved about 70% efficiency near ±θ_a-max, which reduced to about 55% (21.5% less than maximum) at noontime for the same orientation as shown in Figure 12a–d. Thus over 30% improvement in optical efficiency at midday was observed by using a CT receiver instead of the SFT receiver in the N-S direction. For an E-W arrangement of a truncated CPC with CT receiver, the maximum optical efficiency was 54% at noontime during the spring and autumn equinoxes. Peak efficiency of the CT receiver joined with a truncated CPC in the E-W arrangement was over 64% at midday of the summer solstice. The CPC together with CT receiver placed in the E-W direction achieved 69% at noontime of the winter solstice.

Comparative analysis of the different configurations illustrates that a CPC with CT receiver in an E-W arrangement was almost 20% more efficient than the SFT receiver in the N-S as well as the E-S direction and equal to that of a CT receiver in a N-S orientation at noontime of the spring and autumn solstices. At the summer solstice, a CPC with CT receiver in the E-W direction showed 15% higher efficiency than SFT and CT receivers placed in a N-S orientation while 10% less than the corresponding efficiency with the SFT receiver. Approximately 40% and 25% improvement in midday optical efficiency was observed by using a CT receiver with truncated CPC in the E-W direction as compared to a N-S oriented SFT and CT receivers, respectively, at the winter solstice. Overall, the optical efficiency in case of a CPC coupled with CT receiver was higher in all configurations except at summer solstice where an SFT receiver placed in the E-W direction surpassed the other configurations.

3.5. Daily Average Optical Efficiency

Average optical efficiency was also determined for the concentration-time period as well as for overall effective operating time period using Equation (9) to compare the performance of both collector types under different arrangements. Figure 13a and Figure 13b show the average values of optical efficiencies for the concentration-time period (4 h) and for the overall effective operating time period (7 h), respectively.

CPC coupled with SFT receiver placed in E-W direction exhibited the highest average optical efficiency (about 70% for concentrated time and 65% for overall operating time) at summer and winter solstices which are attributed to the incidence angle approaching the limiting acceptance angle. For the same arrangement, minimum average optical efficiencies were observed during the spring and autumn equinoxes. For N-S installation, average optical efficiency achieved by CPC with SFT receiver was almost uniform (about 54%) for all seasons. Comparative analysis shows that a CPC paired with a CT receiver is slightly more efficient than the SFT receiver for all arrangements except E-W installation at the summer and winter solstices where the SFT receiver was a little more efficient. Annual average optical efficiency during the concentrated time period was also slightly higher in case of a CPC with CT receiver as compared to a CPC with SFT receiver.

3.6. Validation of the Optical Simulation Results

The simulation results were compared and validated by experimental testing of a module consisting of CT receiver coupled with truncated CPC installed in both N-S and E-W arrangements under actual outdoor tropical weather conditions. The solar irradiance, ambient temperature, wind velocity, flow rate, inlet, outlet and storage temperatures of the HTF were recorded at intervals of 60 s. The half-hourly averaged values of logged parameters are shown in Figure 14 and Figure 15 for E-W installation (on 12th Apr 2019) and for N-S arrangement (on 26th Apr 2019), respectively. The solar irradiance exhibited large variations during both selected days, especially in the afternoon which is typical behavior of solar irradiance in tropical regions. In E-W installation, the outlet temperature of HTF reached about 92 °C at noontime while ambient temperature only slightly varied during the test period. The maximum outlet temperature on 26th Apr (for N-S arrangement) was about 112 °C at 11:30 h, which was higher than 12th Apr (E-W installation) due to relatively higher solar irradiance.

The outlet temperature of HTF dropped after about 13:30 h in case of N-S installation due to fast decrease in solar irradiance as can be seen in Figure 15a. The heat gained by the circulating fluid was also determined at average mass flow rate of 156 kg/h which is equivalent to 0.02 kg/s-m² as per ISO9806 standard of testing solar collectors. The heat gain followed trends almost similar to the incident solar irradiance.

Comparison of the E-W and N-S configurations illustrates that the outlet temperature of the HTF started increasing earlier (at about 9:00 am) for the E-W installation while in case of a N-S arrangement, the outlet temperature increased slowly in the beginning and then rapidly after about 10:30 h. The useful heat gained by the circulating fluid averaged on a half-hourly basis was also determined for both orientations. Thermal energy capture in case of N-S installation was more than that of E-W installation before noon due to the higher solar irradiance and incidence angle of sunrays reaching the limiting acceptance angle where gap losses were minimum. Similar behavior was also predicted by our ray tracing simulation study. The net heat gain dropped after 12:00 h due to a sudden decrease in the incident solar irradiance.

A series of experiments were carried out around noontime to compare the overall performance of the CPC collector paired with CT receiver placed in the E-W and N-S directions. An additional secondary cooling circuit was incorporated in the system, and chilled water was circulated to control the inlet temperature of the primary HTF at different levels. The characteristic curves were obtained by changing the inlet temperatures while keeping the solar irradiance, ambient temperature and flow rate within the limits defined by ISO9806 standard for testing solar collectors. Figure 16 demonstrates the characteristic curve of overall efficiency of the CPC paired with CT receiver placed in E-W and N-S directions against reduced inlet temperature which is defined by the following equation:

$$T_i^{*}=\frac{T_{fi}-T_{amb}}{G{A}_a}$$

(16)

Experimental results demonstrate that the maximum optical efficiency of the CPC paired with CT receiver reached to about 70% in the case of N-S installation while 66.5% in the E-W arrangement which closely match the simulation data.

Comparative analysis of the two arrangements shows that N-S installation yield better performance at lower inlet temperatures while E-W arrangement exhibit better efficiency at a relatively higher outlet temperature of the HTF. Since the CPC collector is meant to supply thermal energy in the medium temperature range, therefore E-W configuration of the proposed system is preferred over N-S installation without any tracking requirements. Moreover, the experimental performance closely matches the simulation outcome under clear sky weather conditions. Thus, simulation outcome is validated by reaching similar conclusions in terms of collector configurations and the overall thermal performance of the system which entails the presented performance prediction method as instrumental in deciding the best configuration and arrangement.

4. Conclusions

Design, development and comparative optical performance of modified CPCs integrated with SFT and CT receivers is presented in this paper. Ray tracing simulations were performed to evaluate the optical performance of both collectors under different configurations. The results demonstrate that 60% truncated CPC coupled with SFT receiver suffered high gap losses, especially at smaller incidence angles which were significantly alleviated by the CT receiver due to the reduced gap between the absorber and the reflector cusp by extended flat fins. For N-S installation, instantaneous optical power collection was improved by 70% at midday by employing the CT receiver while 34% more power was collected in the E-W arrangement as compared to the SFT receiver. Similarly, daily energy collection by a CPC paired with the CT receiver was 35% and 43% higher than for the SFT receiver during the selected time span (from 10:00 to 17:00 h) for N-S and E-W installations, respectively.

The midday optical efficiency of CT receiver coupled with a truncated CPC placed in the E-W direction was almost 20% higher than a SFT receiver in the E-W as well as in a N-S arrangement at the spring and autumn equinoxes. Similarly, E-W installation of a CPC with the CT receiver achieved 15% higher efficiency than a N-S oriented SFT and CT receivers at the summer solstice. At the winter solstice, a CT receiver with CPC in the E-W orientation was almost 40% and 25% more efficient than a N-S installation of SFT and CT receivers, respectively. Overall, the optical efficiency in case of the CT receiver coupled with CPC was higher in all configurations except at summer solstice where the SFT receiver placed in the E-W direction surpassed other arrangments. The experiments conducted on a truncated CPC with CT receiver at different inlet temperatures demonstrated the superior performance of N-S installation at relatively lower temperatures, while E-W installation was more efficient at elevated inlet temperatures. Thus, the experimental results validate the simulation study by following similar trends in both E-W and N-S arrangments which endorse the presented performance prediction method as instrumental for decision making to choose the best design and configuration of CPC collectors for medium temperature heat supply.