A Thermo-Electric Apparatus for Thermal Diffusivity and Thermal Conductivity Measurements

Abstract

In this study, a one-dimensional heat transfer measurement device is developed based on the mathematical theory of the Angstrom method. To conform to the mathematical assumption, it is required that the device precisely controls the heat source to generate sinusoidal temperature signal. A thermo-electric module is used as the heat source for the measurement platform. This module is connected to a computer for program control, such that the temperature can be controlled quickly, precisely, and dynamically. In this study, five common heat-conducting materials are tested to verify the proposed one-dimensional heat transfer measurement device. By substituting the experimental results into the mathematical model of the Angstrom method, the thermal diffusion and thermal conductivity of the test material is calculated. The experimental results are compared with the physical properties of the materials, and the accuracy error is extremely low. This study confirmed that the Angstrom method theory applied thermal diffusivity and thermal conductivity measurement, which can be realized by thermo-electric temperature control technology.

1. Introduction

With the recent advancements in technology, 3C (computer, communication, and consumer electronics) products, including smartphones, laptops, and wearable electronic products, are becoming thinner and lighter. The use of small electronic chips is resulting in a significant increase in their heat generation per unit volume. The traditional method of heat dissipation in electronic devices is to use fins, which cannot be employed in thin electronic products. It is often necessary to rely on one-dimensional heat-conducting components to transfer heat to the environment. Therefore, measuring the thermal conductivity of materials is important in both materials science and engineering applications.

The mathematical model of the Angstrom method was proposed by A.J. Angstrom in 1861 [1]. It is based on one-dimensional Fourier’s law of heat conduction. It mainly assumes that the heat source is a sine wave, which simplifies the mathematical equation. Therefore, the control accuracy of the sine-wave temperature of heat source is very crucial [2,3].

At present, devices used to measure the thermal conductivity of materials include those based on the transient plane heat source method and the thermal diffusivity by the flash method. Their experimental setup is shown in Figure 1. The transient plane heat source method adopts a hot disk as the measurement sensor. The variations in electric resistance as a function of time during heating are recorded. The slope of the resulting data is used to calculate thermal conductivity and diffusivity [4]. Thermal diffusivity by the flash method is theoretically based on the half-time method. In other words, the method utilizes a laser at the bottom as the heat source. The time required for heat to penetrate the sample is measured to compute the thermal diffusivity [5].

Based on the Angstrom method, we developed a simpler measurement device that can rapidly measure the thermal conductivity of materials [6,7]. A therm based on the Angstrom method, we designed an experimental device to measure the thermal conductivity of materials rapidly [8]. A thermo-electric cooling (TEC) module is used as the heat source of the measurement platform. It is connected to a computer for program control, thereby achieving a dynamic operation of the sine-wave temperature [9,10,11]. The thermal conductivities of five common heat-conducting materials used in electronics, namely red copper, brass, silver, aluminium alloy (1050), and non-metallic aluminium nitride ceramic, are measured. The obtained parameters are substituted in the mathematical model of the Angstrom method to verify the measurement results of the device.

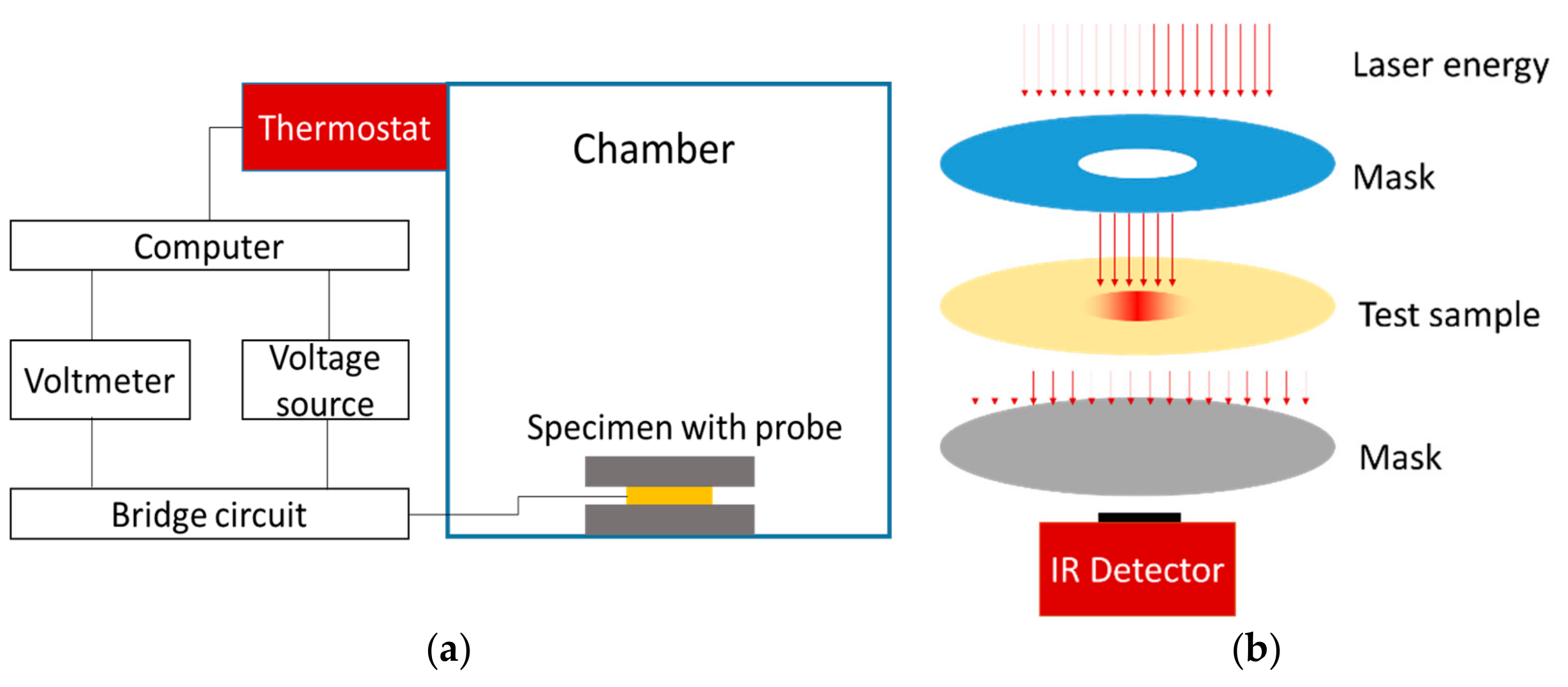
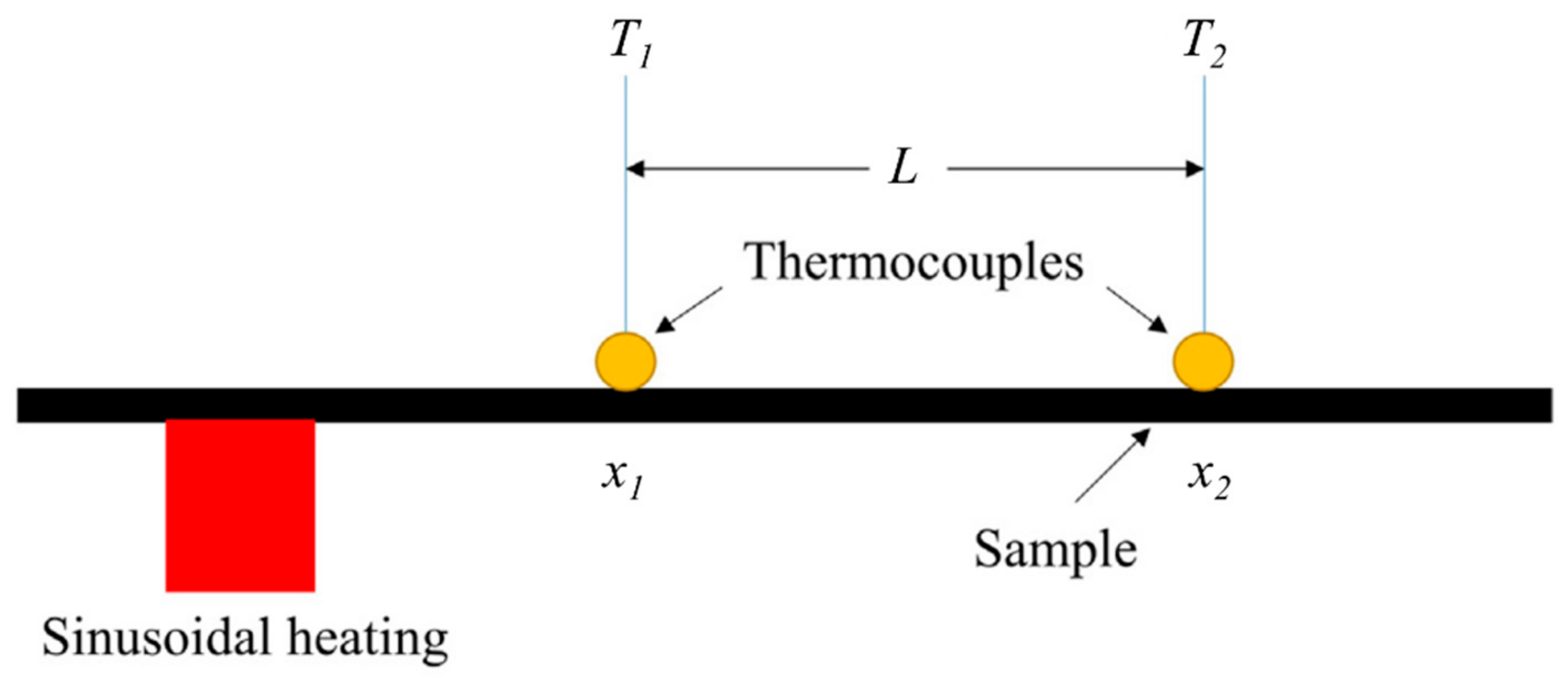
2. Principle and Experimental

The use of steady-state temperature oscillations to determine thermal diffusivity α was first described by Angstrom in 1861 and is generally known as the Angstrom method. This method is based on the one-dimensional Fourier equation. First, the heat source is configured to generate sine-wave temperature. When a sinusoidal heating flux is transmitted down the sample from one end, the temperature values at any point in the interior of the sample present periodic fluctuations [12,13]. Measuring the temperature distribution at two separate points (as shown in Figure 2) gives us two waves with different amplitudes and temporal phases. In this study considering the case for which losses from the sides of the sample are negligible. Then the one dimensional heat conduction Equation is

$$\frac{{\partial }^{2}T}{\partial x}-\frac{1}{\alpha } \frac{\partial T}{\partial t}=0$$

(1)

where T is the temperature, x the one-dimensional coordinate axis and α the thermal diffusivity. The derivation of the Angstrom Method is as follows.

Let the heat source be a sinusoidal source with a frequency of: $f=\frac{w}{2\pi }$ ($w$: Angular velocity). The equation that relates amplitude (temperature) to frequency is

$$\Delta T=B\left(x\right)e^{iwt}$$

(2)

Substituting Equation (1) into Equation (2) yields

$$\frac{d^{2}B\left(x\right)}{d{x}^2}=\left(\frac{iw}{\alpha }\right)B\left(x\right)$$

(3)

Suppose that:

$$B\left(x\right)=B_0{e}^{-\sqrt{\lambda x}} ; \sqrt{\lambda }=a+ib$$

where $\lambda$ is the sinusoidal wavelength. Equation (3) may then be simplified to

$$\alpha =\frac{w}{2ab}$$

(4)

Select two points (x₁ and x₂) on the experimental material (as shown in Figure 2); Equation (2) and Equation (3) can be rearranged as

$$T_n=B_n{e}^{-a_{n}x}$$

(5)

Then

$$\frac{M}{N}=e^{-a_n\left(x_1-x_2\right)}$$

(6)

Let $x_1-x_2=L$, and

$$a_n=\frac{\ell n\left(M/N\right) }{L};\hspace{1em}{b}_n=\frac{\left({\varphi }_1-{\varphi }_2\right)}{\left(L\right)}$$

By determining the components of the Fourier series of the temperature at x₁ and x₂ for the nth harmonic, an and bn can both be determined:

$$\alpha =\frac{w}{2ab}=\frac{w}{2\frac{\ell n\left(\frac{M}{N}\right) }{L}\frac{\left({\varphi }_1-{\varphi }_2\right)}{\left(L\right)}}=\frac{L^2}{2\Delta t\ell n\left(M/N\right)}$$

(7)

As shown in Figure 2, two points, x₁ and x₂, are selected on the sample, separated by distance L, Δt is the time difference between the sine-wave temperatures at T₁ and T₂, and M and N are temperature amplitudes at T₁ and T₂, respectively.

The thermal diffusivity α is defined as the ratio of thermal conductivity k and thermal capacitance ρC_p, where ρ is the density and C_p is the specific heat of the material. Therefore, from the results measured using the test proposed in this study, the thermal conductivity of the material to be tested can be derived as follows:

$$k=\alpha \rho C_p$$

(8)

Based on the Angstrom method, we developed a one-dimensional heat transfer measurement device. The hardware setup mainly consists of three parts: (1) power supply: Twintex TPS-3605 (Twintex Instrument, Shenzhen, China), (2) thermo-electric temperature control platform(The software of measurement device is edited by our laboratory), and (3) NI 6009 controller ( National Instruments Debrecen, Hatvan Hungary). To obtain the desired sinusoidal heating curve, the NI 6009 controller is used to control the power supply to generate sine waves, thereby achieving the desired output power [14]. By using the TEC platform, a dynamic control on temperature can be achieved quickly and precisely to produce heating and cooling effects. The red dotted-line area in Figure 3 represents the test area of the material. The sample to be tested is placed in this area, and its thermal conductivity is measured. Multiple sets of thermocouples with adjustable distances are placed above the test area. T₁ and T₂ are the temperature measurement points, where T₁ is near the heat source, and T₂ is 30 mm away from T₁. The thermocouple signal is connected to a USB-4718 reader. Multiple sets of temperature data can be recorded every 0.1 s. The analogue thermocouple signals are converted to digital signals and transmitted to the dedicated program developed for the measurement. The data retrieval interface is shown in Figure 4. The x-axis represents the elapsed time, and the y-axis represents the temperature. The red and blue lines represent the temperature changes at T₁ and T₂, respectively, with the heating cycle.

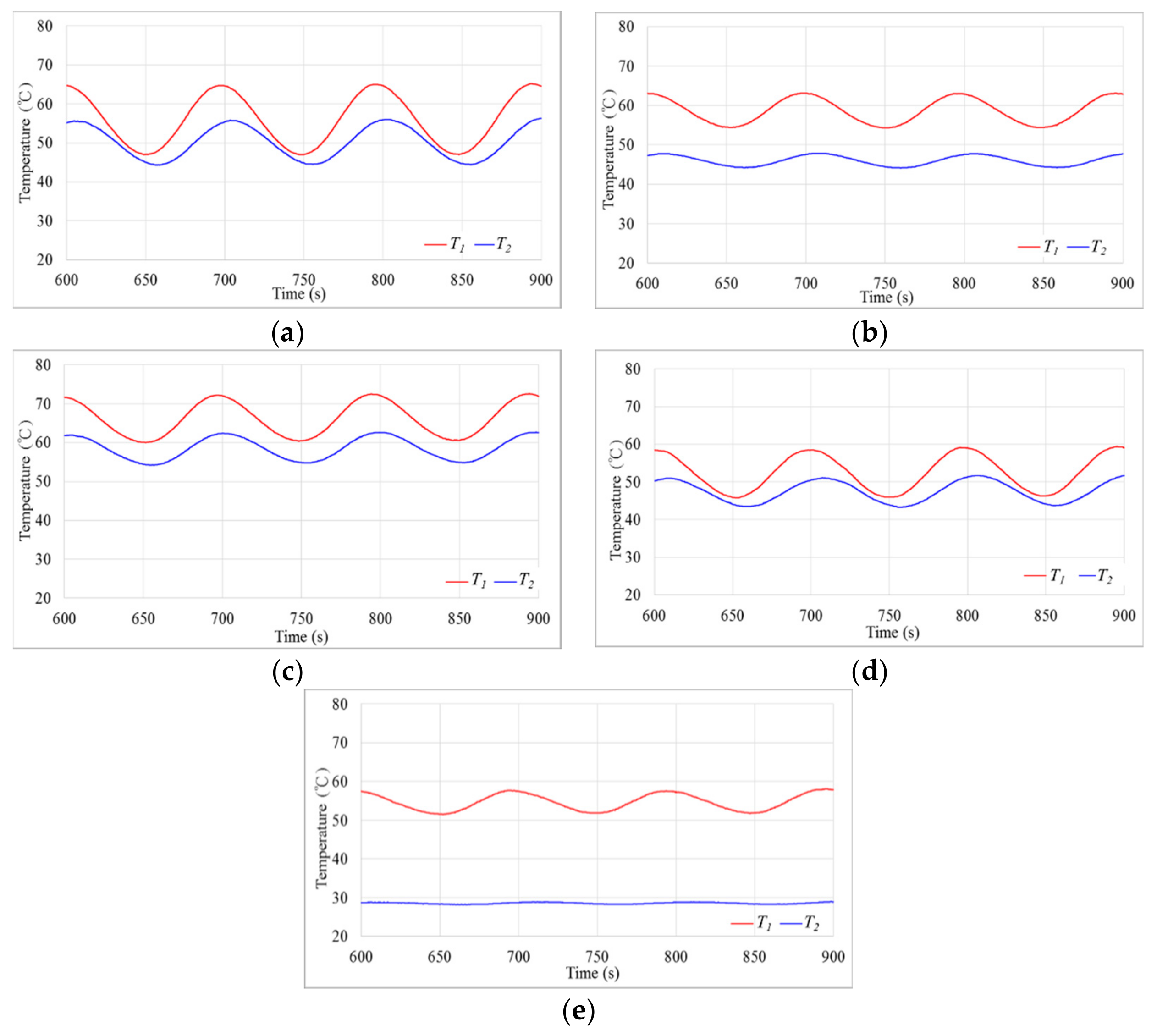
3. Results and Discussion

Based on the Angstrom theory, we designed a set of experimental instruments as a measurement device to measure thermal conductivity rapidly. A TEC module is used as the heat source for the measurement platform. It is connected to a computer for program control, thereby achieving the dynamic operation of the sine-wave temperature [15,16,17,18]. The thermal conductivities of five common heat-conducting materials used in electronics, namely red copper, brass, silver, aluminium alloy (1050), and non-metallic aluminium nitride ceramic, are measured. The obtained parameters are substituted in the mathematical model of the Angstrom method to verify the measurement results of the proposed device.

Standard samples with known thermal conductivity values are used in the experiment. The physical properties of the selected materials are listed in

Table 1. Physical properties of the materials.

Test Material	$\mathsf{\rho } \left[\raisebox{1ex}{$g$}\!\left/ \!\raisebox{-1ex}{$c{m}^3$}\right.\right]$	$\mathbf{Cp} [\raisebox{1ex}{$ \mathbf{J}$}\!\left/ \!\raisebox{-1ex}{$\mathbf{g} °\mathbf{c}$}\right.]$	$\mathbf{K}1 \left[\raisebox{1ex}{$\mathbf{w}$}\!\left/ \!\raisebox{-1ex}{$\mathbf{m}·\mathbf{k}$}\right.\right]$
Red copper (Cu)	8.96	0.39	398
Brass (Bs)	8.21	0.38	105
Silver (Ag)	10.49	0.23	429
Aluminium (AL1050)	2.68	0.91	237
Aluminium Nitride (AlN)	3.26	0.74	140

. A schematic representation of the sample dimensions is shown in Figure 5 shows the test samples of the five heat-conducting materials used in our experiment. The measurements performed on these test samples are the basis for the experimental analysis. Thin strip samples with a uniform size of W = 10 mm, D = 100 mm, and H = 1 mm are used for all the materials.

The complete setup is shown in Figure 6. T₁ and T₂ are the temperature measuring points. T₁ is above the heat source, and T₂ is 30 mm away from T₁. After the setup is complete, changing input power is provided by the programmable power supply. The temperature change is monitored in real time. The TEC is controlled to match a sine-wave temperature change, as shown in Figure 4. After 600 s, when the temperature change of the test sample stabilises, the temperature curve is recorded and analysed by the program. After storing the results, the required parameters are recorded. Figure 7 shows the experimental results of the five materials. The thermal diffusivity α is then calculated according to the Angstrom method theoretical equation (Equation (7)). The thermal conductivity of the test sample is calculated using Equation (8).

The results measured by the device for all the test samples are listed in

Table 2. Sample measurement results.

Test Material	M [℃]	N [℃]	Δt [s]	α [mm2/s]	K2 $\left[\raisebox{1ex}{$\mathit{w}$}\!\left/ \!\raisebox{-1ex}{$\mathit{m}·\mathit{k}$}\right.\right]$
Red copper (Cu)	4.8	2.5	6.0	114.97	401.76
Brass (Bs)	3.7	1.1	12.2	30.40	94.87
Silver (Ag)	7.9	3.9	3.6	177.08	427.24
Aluminium (AL1050)	7.4	2.7	5.0	89.27	217.70
Aluminium Nitride (AlN)	3.0	1.3	9.0	59.79	144.24

. The measured parameters include the amplitudes M and N of the two different points in a heating cycle and sine wave delay time Δt. By substituting the parameters into the mathematical model of the Angstrom method, the thermal diffusivity α is calculated.

The physical properties such as density ρ and specific heat C_p of the test materials used in this experiment can be obtained by referring to the physical property table. Therefore, the thermal conductivity of test material can be derived by substituting the measured thermal diffusivity α into Equation (8). The materials selected in this study are common heat-conducting materials used in electronics. The relative error (%) between the measured results and actual values can be obtained by comparing with the physical property table. The accuracy errors of the measurements are calculated. The verification results are listed in

Table 3. Comparison of thermal conductivity between measured and actual values.

Test Material	$\mathbf{K}1 \left[\raisebox{1ex}{$\mathit{w}$}\!\left/ \!\raisebox{-1ex}{$\mathit{m}·\mathit{k}$}\right.\right]$	$\mathbf{K}2 [\raisebox{1ex}{$\mathit{w}$}\!\left/ \!\raisebox{-1ex}{$\mathit{m}·\mathit{k}$}\right.]$	(±) Error	Standard Error (%)
Red copper (Cu)	398	401.76	3.76	0.94
Brass (Bs)	105	94.87	10.13	9.65
Silver (Ag)	429	427.24	1.76	0.41
Aluminium (AL1050)	237	217.70	19.30	8.14
Aluminium Nitride (AlN)	140	144.24	4.24	3.03

. It is evident from the results that compared to the actual thermal conductivities mentioned in the physical property table, the accuracy errors of the measured results are below 10%.

4. Conclusions

In this study, a one-dimensional heat transfer measurement device is developed based on the mathematical theory of the Angstrom Method. To conform to the mathematical assumption, it is required that the device precisely controls the heat source to generate sine-wave temperature. A TEC module is used as the heat source for the measurement platform. It is connected with a computer for program control, such that the temperature can be quickly, precisely, and dynamically controlled. The experiment verified the thermal conductivities of five common heat-conducting materials, namely red copper, brass, silver, aluminium alloy (1050), and non-metallic aluminium nitride ceramic. The experimental results were substituted in the mathematic model of the Angstrom method to calculate the thermal conductivities of the test materials.

The experimental results are compared with the values of the material physical property table. The one-dimensional heat transfer device developed in this study was used to test the common heat-conducting materials. The measured results of thermal conductivities (W/m·K) are red copper: 401.76, brass: 94.87, silver: 427.24, aluminium alloy (1050): 217.70, and aluminium nitride ceramic: 144.24. A comparison with the material physical property table shows that the accuracy errors of the measured results are below 10%.