Computationally Efficient Method of Co-Energy Calculation for Transverse Flux Machine Based on Poisson Equation in 2D
Abstract
:1. Introduction
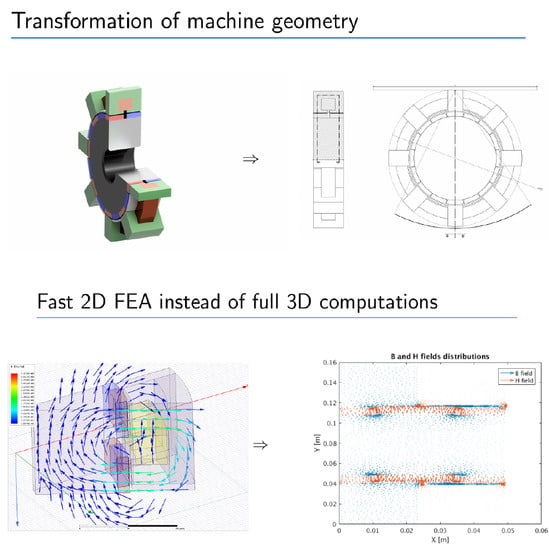
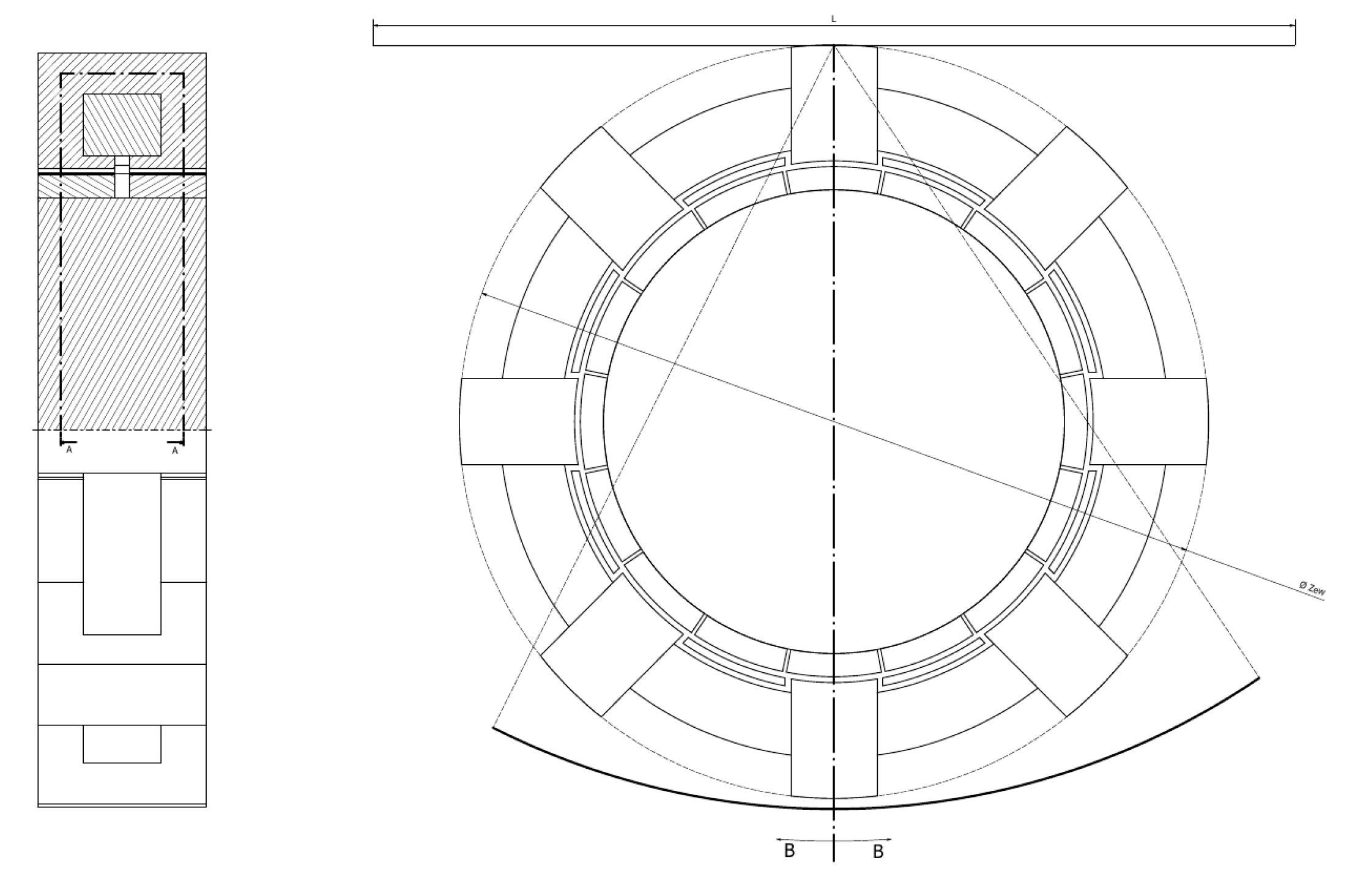
2. Description of the Method for Creating a Machine 2D Model
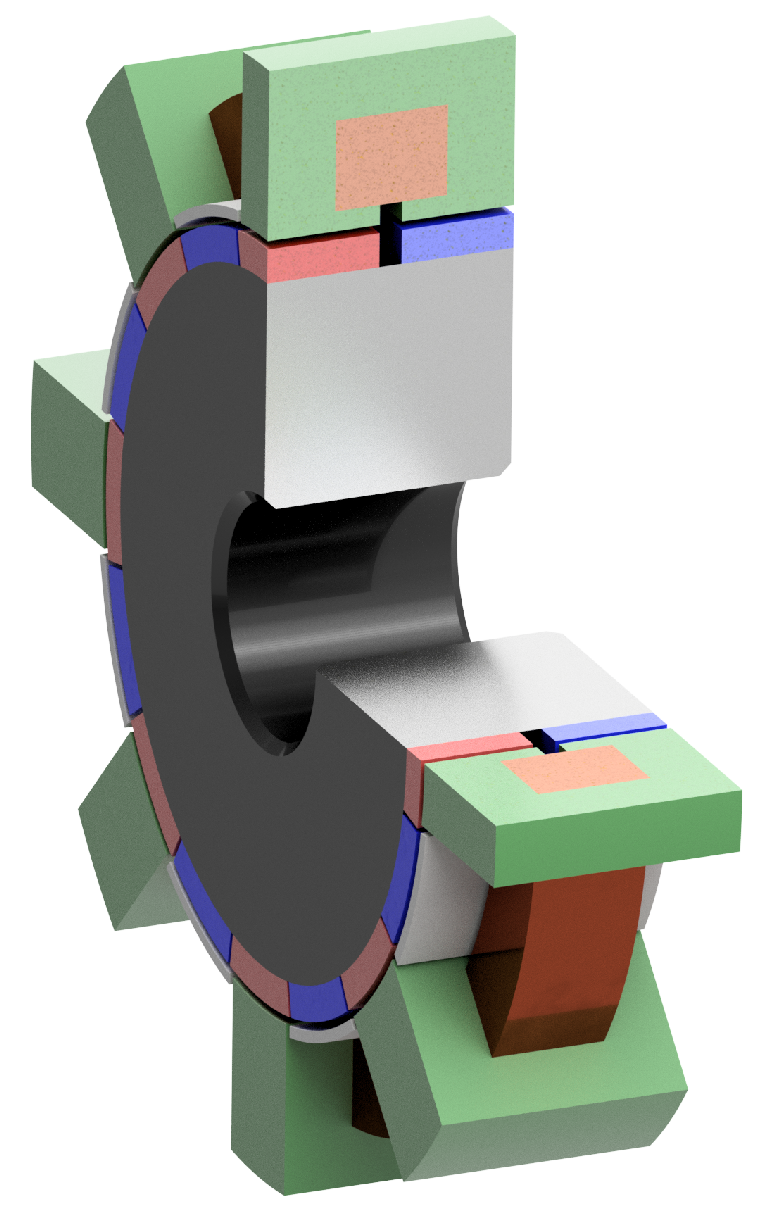
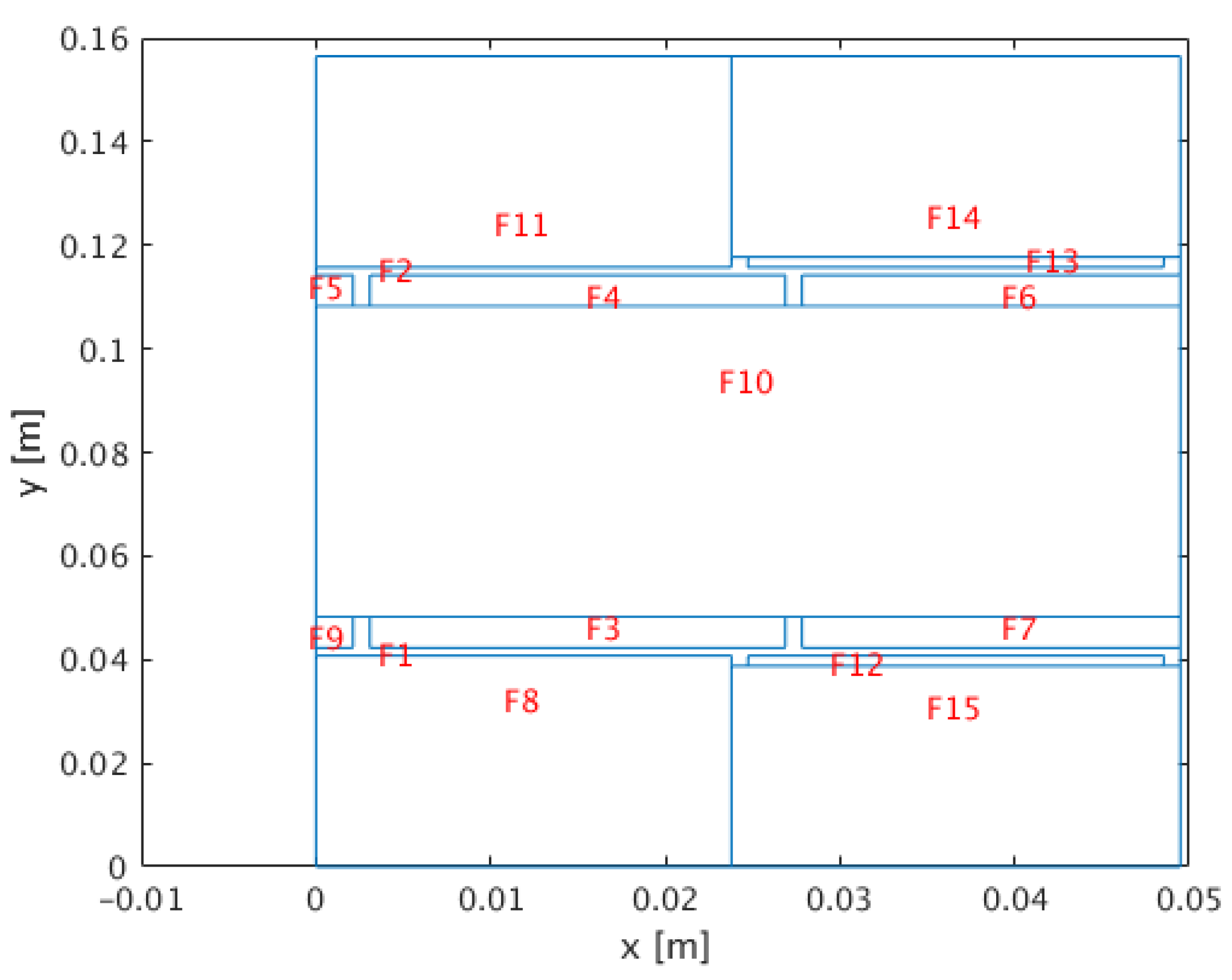
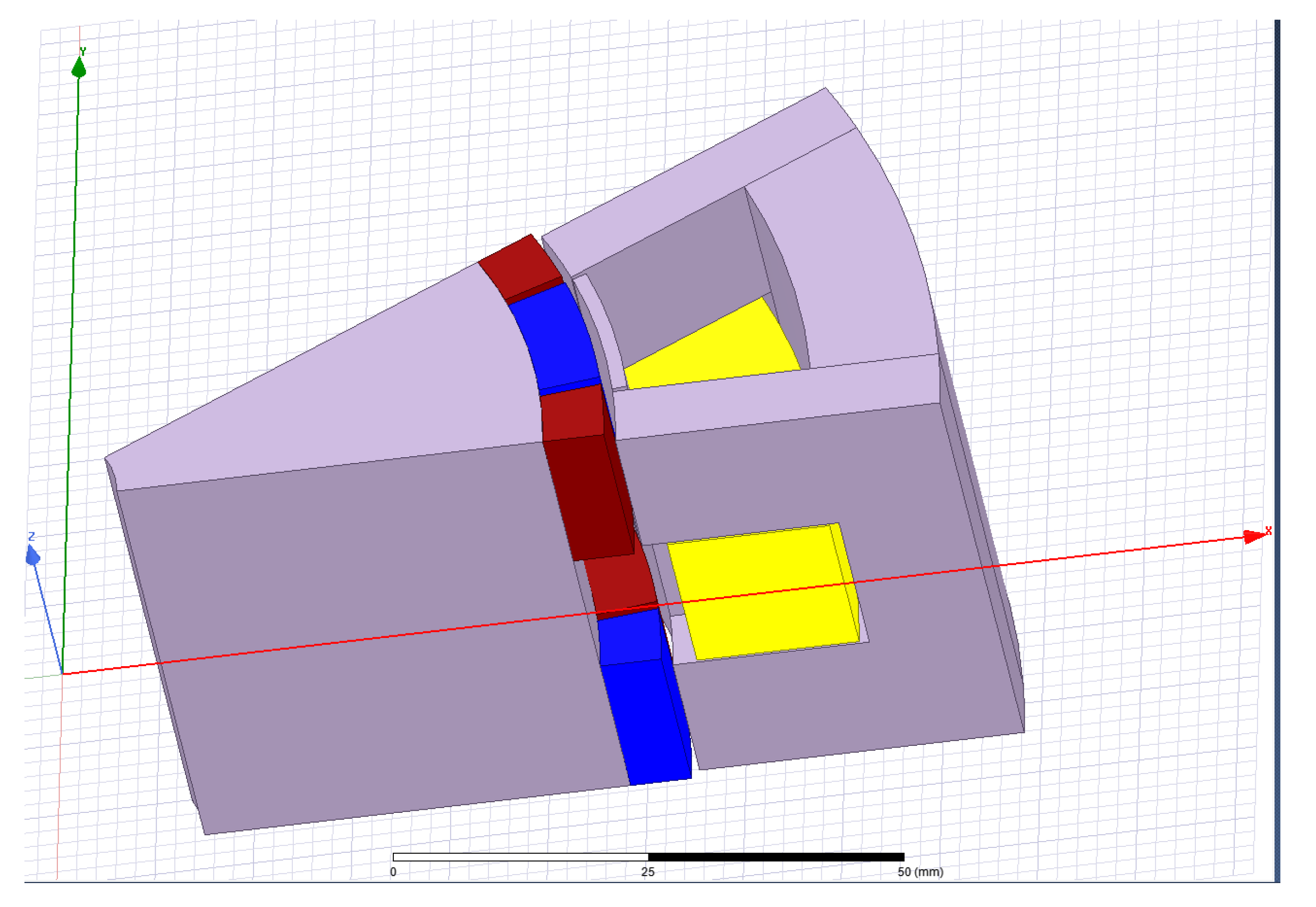
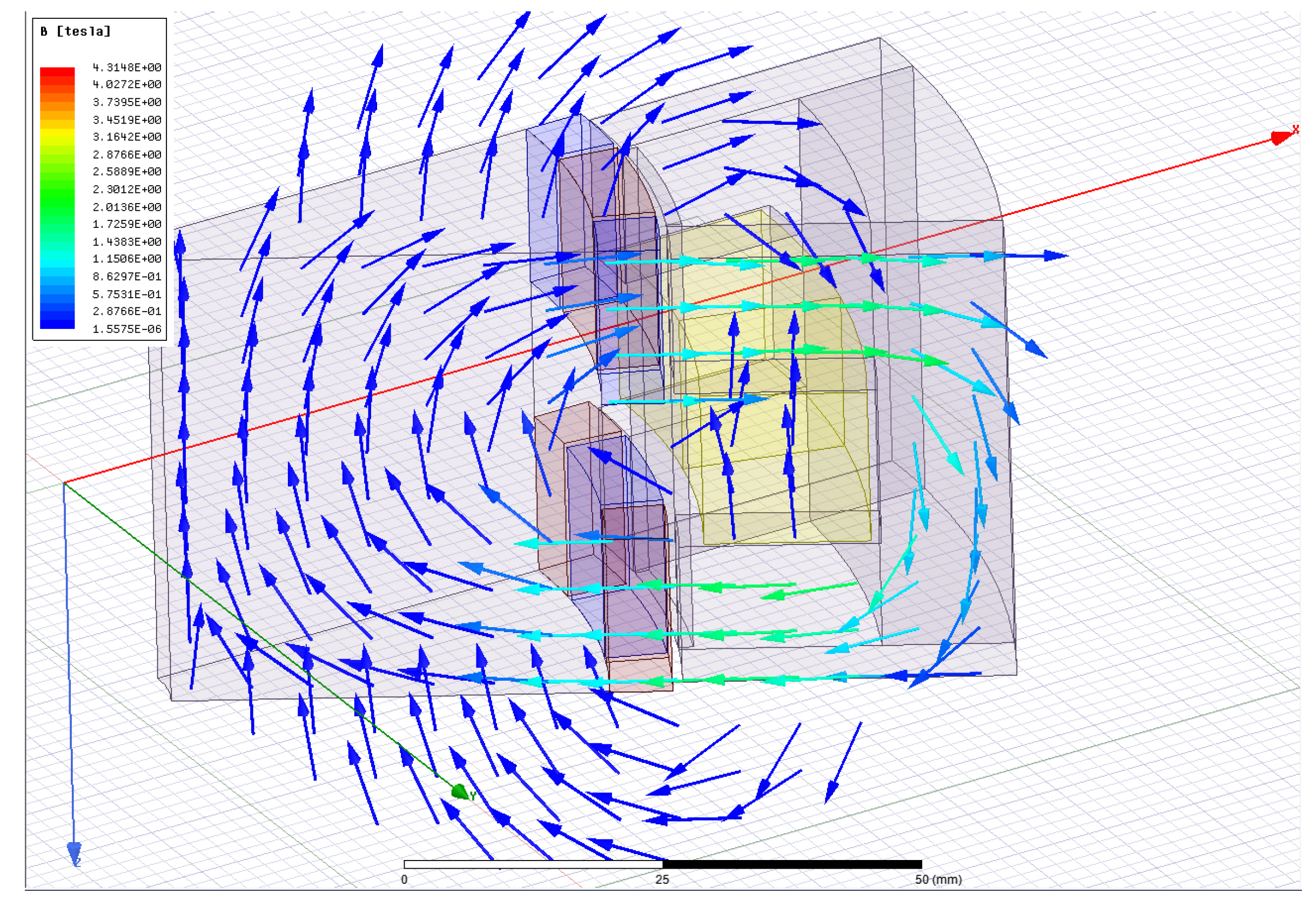
- Reflect ways on which the magnetic field closes in a studied machine for one phase it is 8 systems that comprise of a pair of permanent magnets, stator yoke, as well as rotor parts (see Figure 1)
- provide a possibility to consider the presence of magnetic field that comes from stator winding phase coil current
3. Description of the Computational Problem
- —stator phase winding current,
- —equivalent magnetizing current
- —magnetic field strength vector
4. Imposition of a Boundary Condition
4.1. Requirements Concerning the Imposed Boundary Conditions
4.2. The Method of Imposing Boundary Conditions
- denotes the value of vector potential in a given nod located on the upper boundary, selected as subordinate (arbitrary)
- denotes the value of vector potential in a given nod located on the bottom boundary, selected as the dominant one
- D denotes a value of difference in potentials, enforced between the left and the right area boundaries.
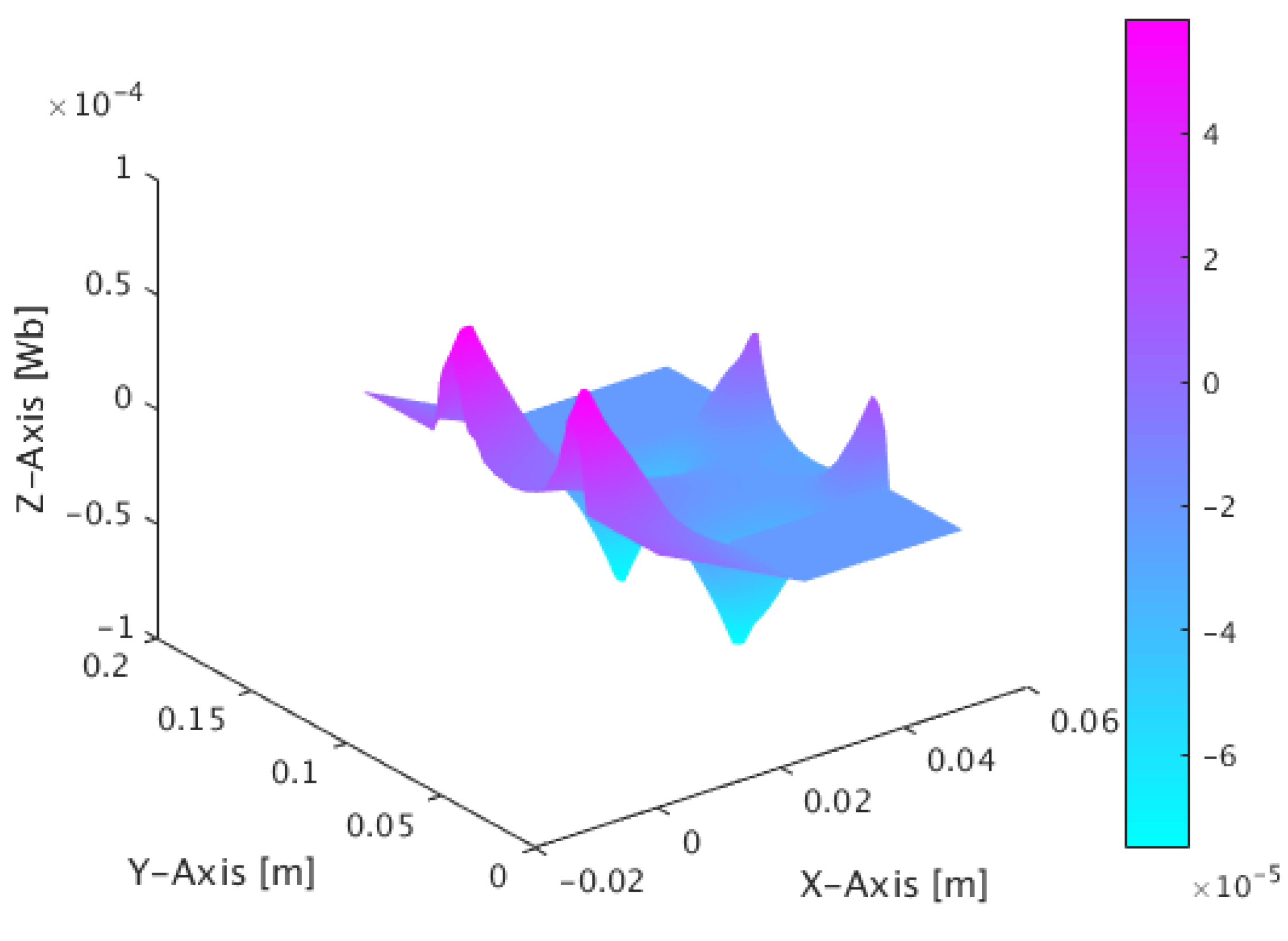
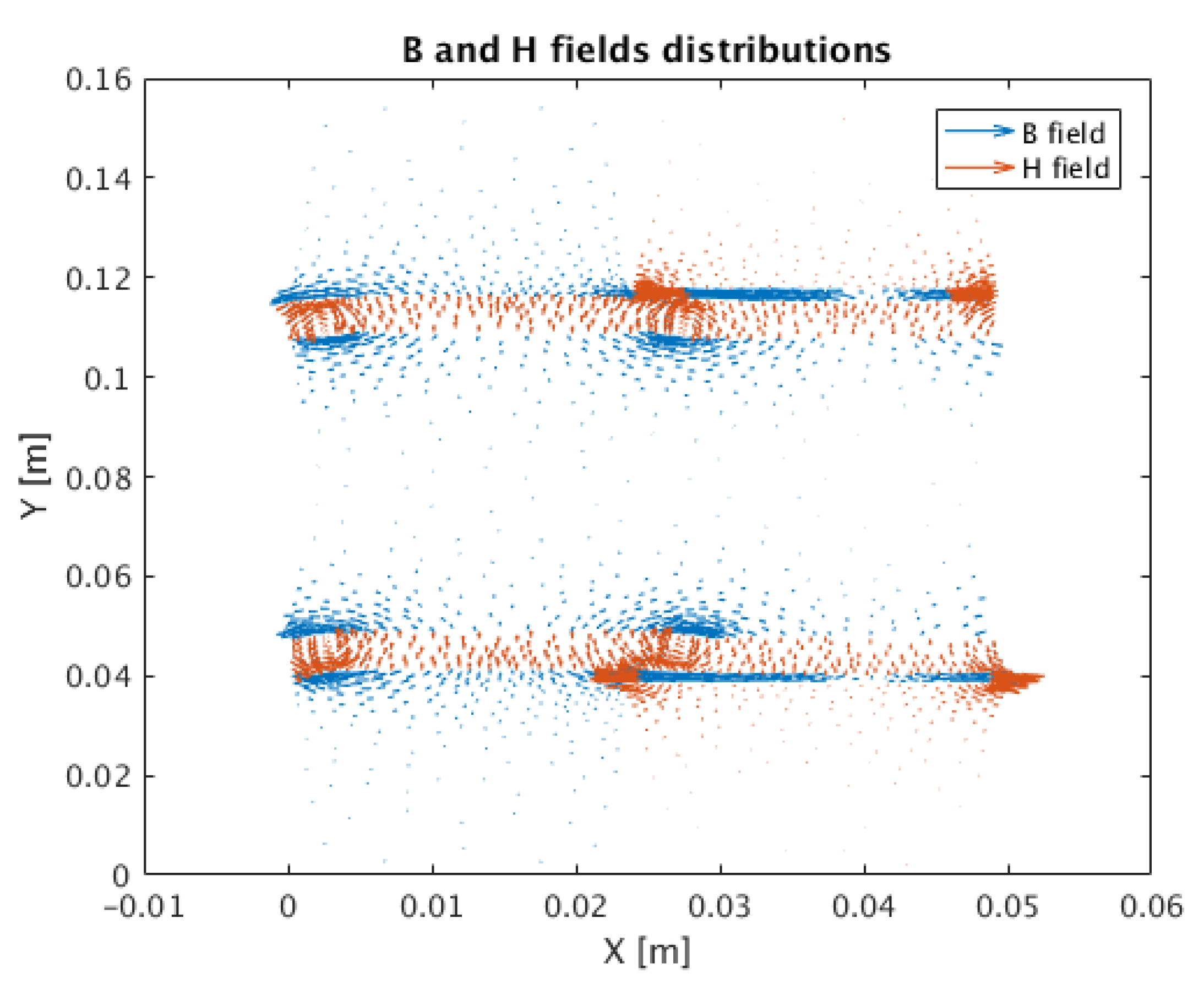
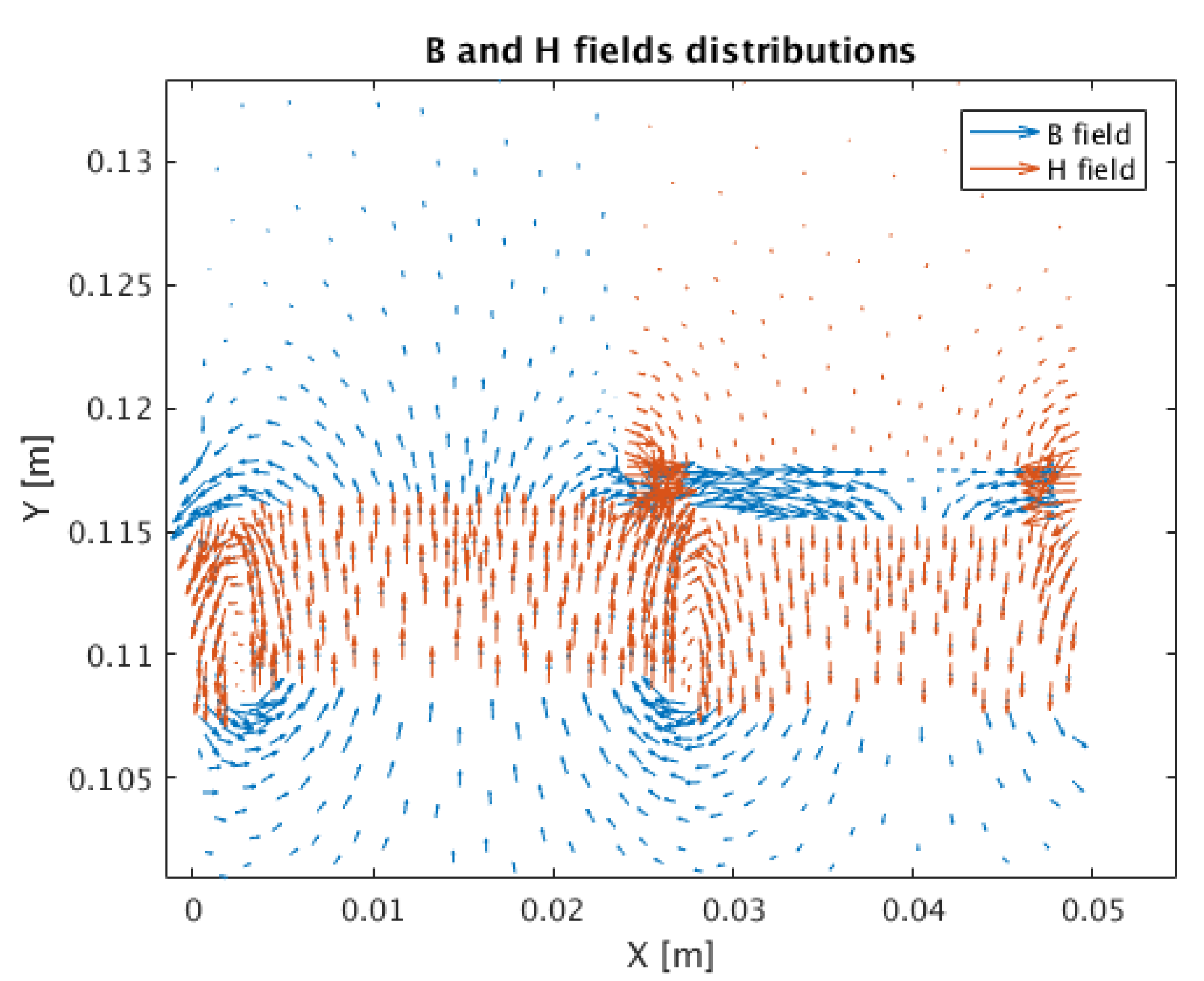
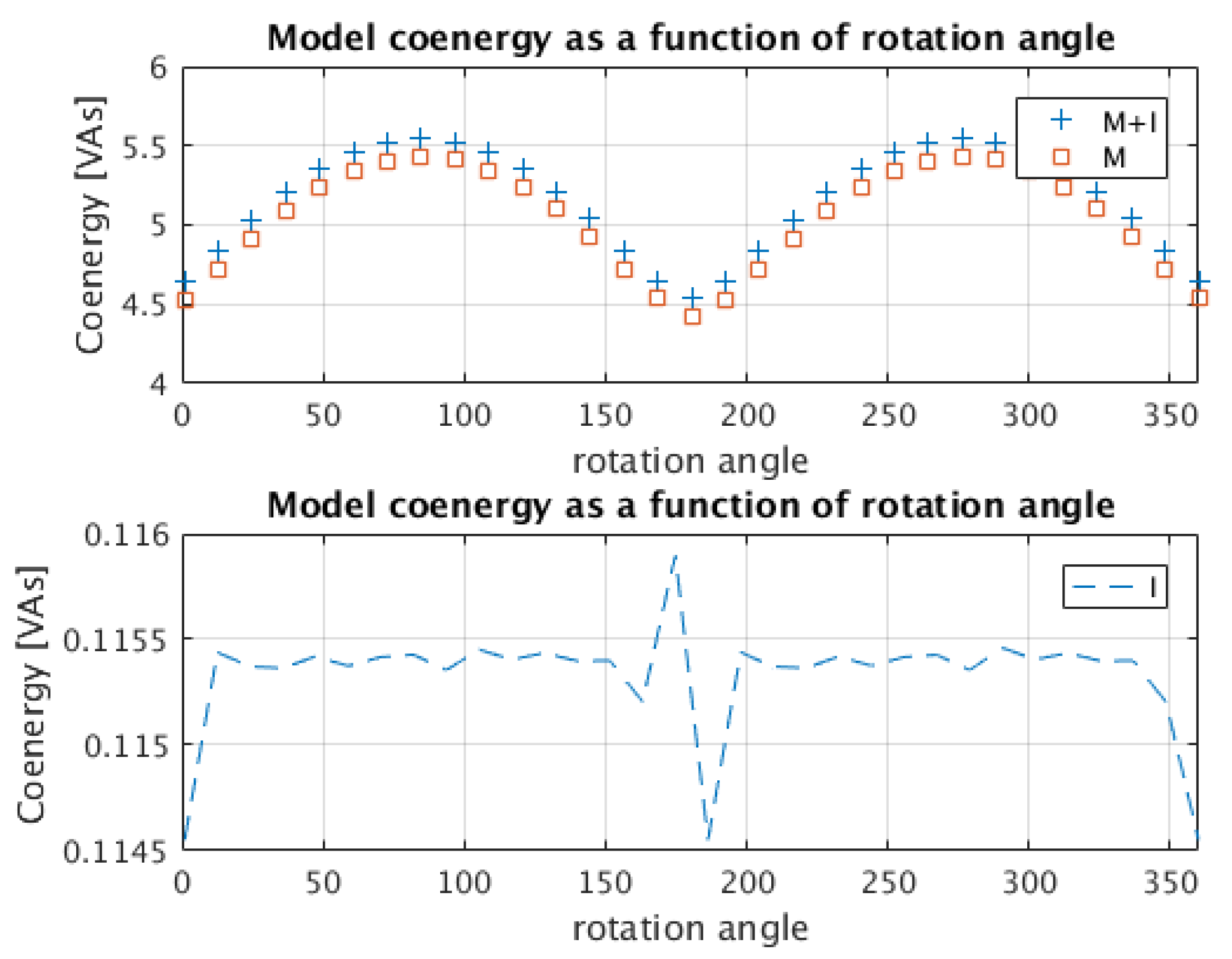
5. Results of Calculations Performed with the Presented Method
- There is only magnetic field from permanent magnets
- Magnetic fields from permanent magnets and phase winding current are considered
- There occurs only magnetic field from phase winding current.
- z—indicates the number of coil windings of phase winding
- —is the amperage of the current flowing through this winding.
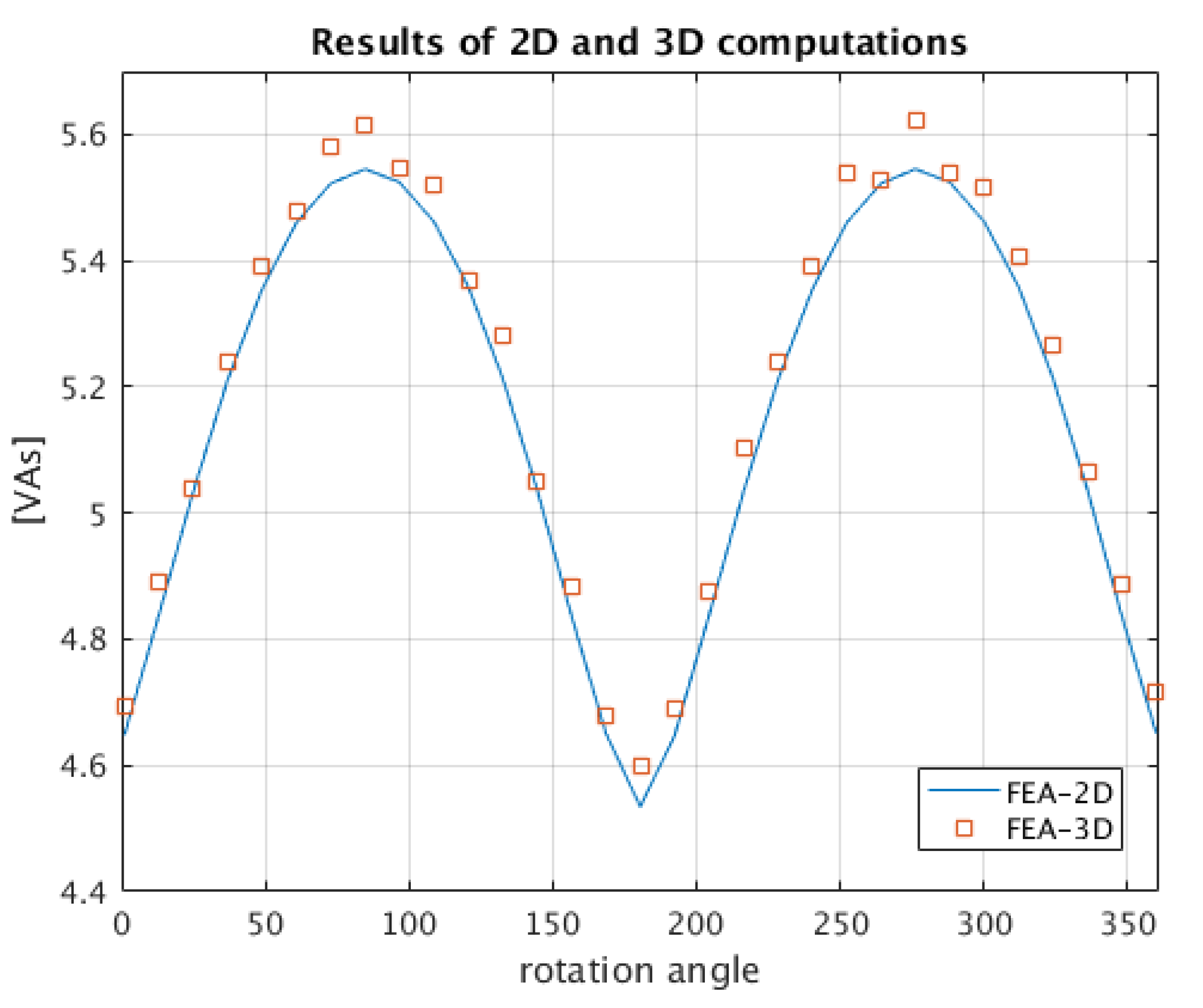
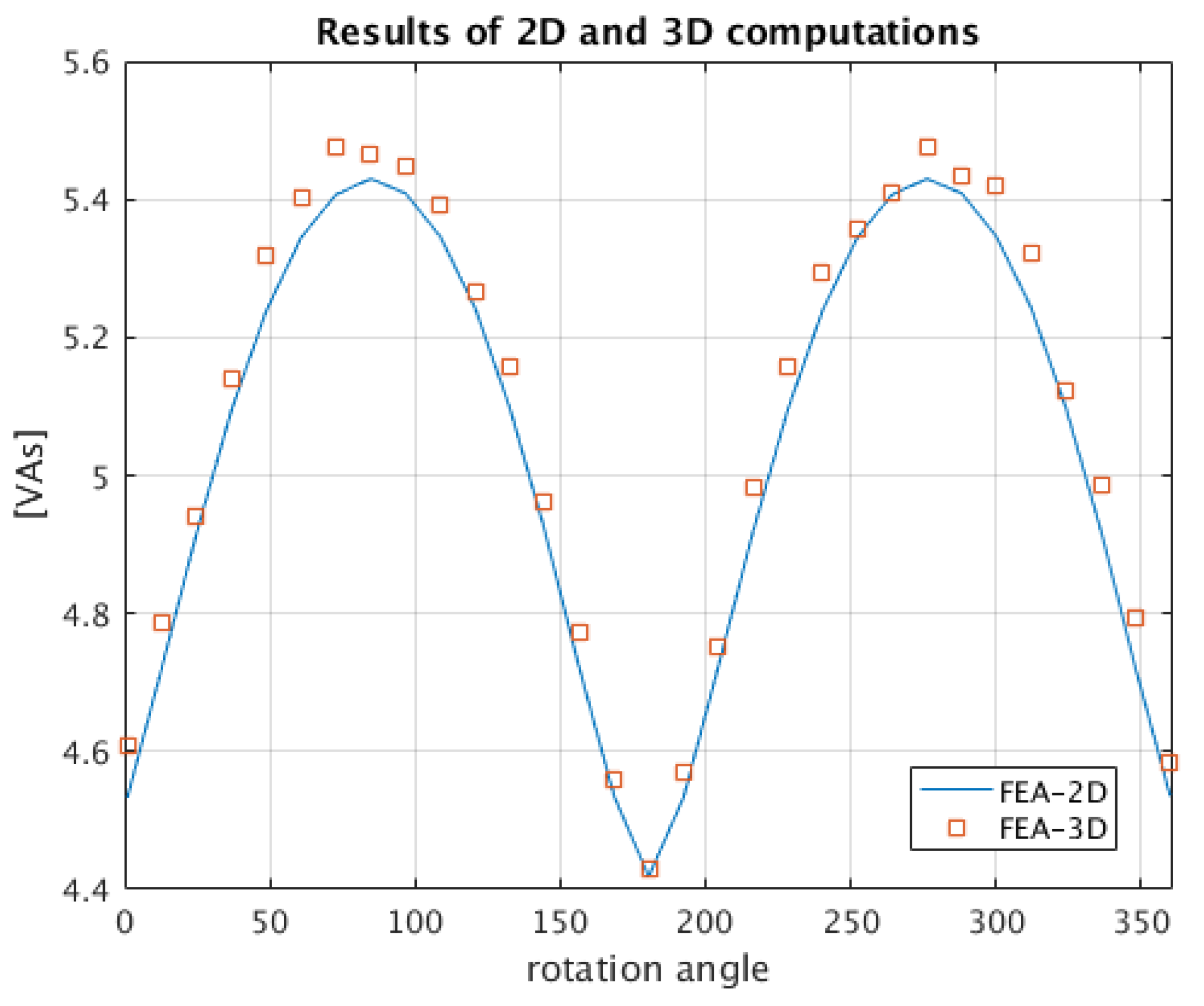
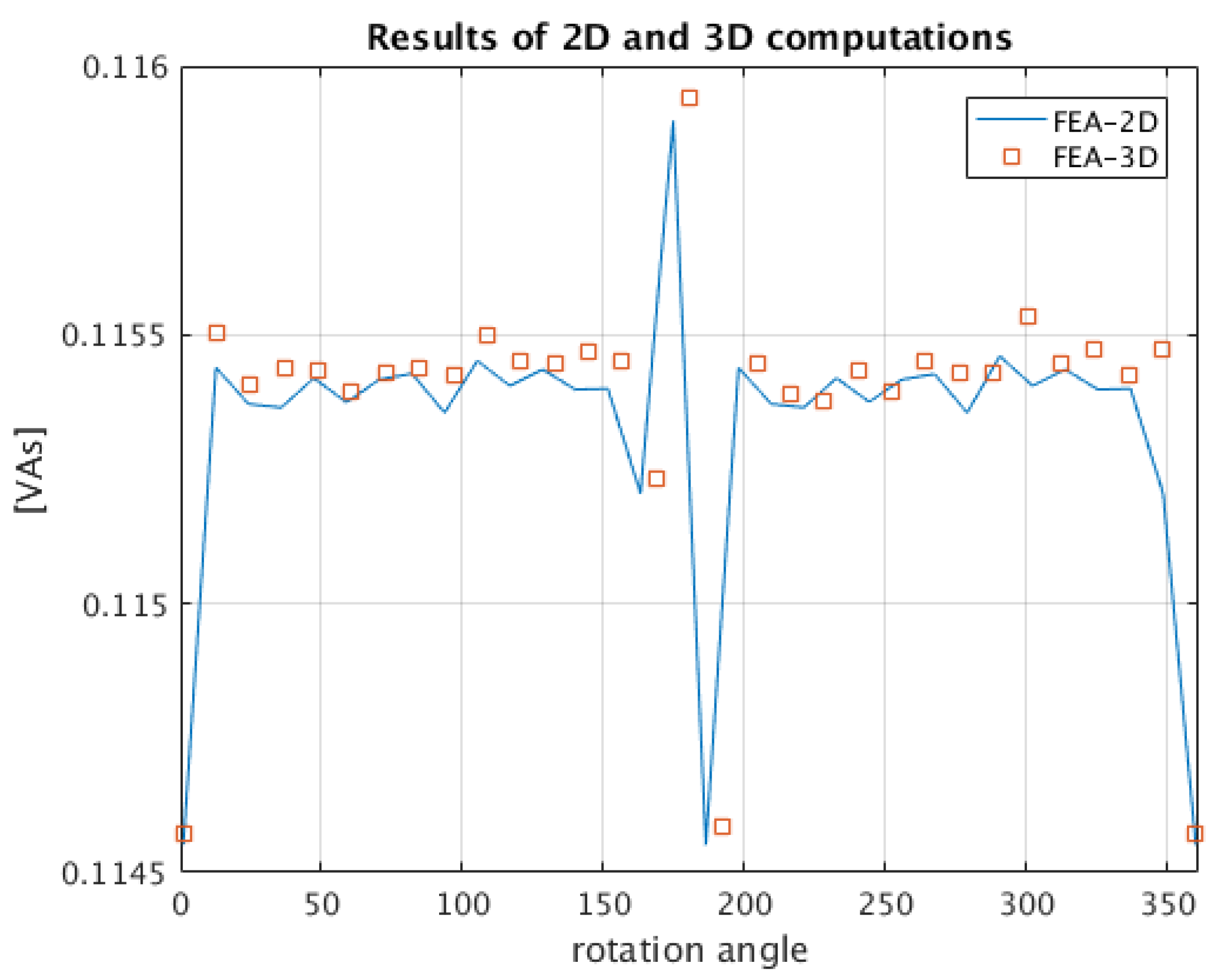
6. Validation of Developed Method
- -indicates the resulting co-energy value obtained by 3D FEM for a certain angular position of rotor, denoted by index k
- -indicates the corresponding result obtained by proposed method.
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kappatou, J.; Zalokostas, G.; Spyratos, D. 3-D FEM Analysis, Prototyping and Tests of an Axial Flux Permanent-Magnet Wind Generator. Energies 2017, 10, 1269. [Google Scholar] [CrossRef]
- Bang, D.; Polinder, H.; Shresthan, G.; Ferreira, J.A. Ring shaped transverse flux PM generator for large direct drive wind turbines. In Proceedings of the International Conference on Power Electronic and Drive Systems, Taipei, Taiwan, 2–5 November 2009; pp. 61–66. [Google Scholar]
- Svechkarenko, D.; Soulard, J.; Sadarangani, C. Parametric study of a transversal flux wind generator at no-load using three-dimensional finite element analysis. In Proceedings of the International Conference on Electrical Machines and Systems, Tokyo, Japan, 15–18 November 2009; pp. 1–6. [Google Scholar]
- Hasubek, B.E.; Nowicki, E.P. Design limitations of reduced magnet material passive rotor transverse flux motors investigate using 3D finite element analysis. In Proceedings of the IEEE Canadian Conference Electrical and Computer Engineering, Halifax, NS, Canada, 7–10 May 2000; pp. 365–369. [Google Scholar]
- Azarinfar, H.; Aghaebrahimi, M. Design Analysis and Fabrication of a Novel Transverse Flux Permanent Magnet Machine with Disk Rotor. Appl. Sci. 2017, 7, 860. [Google Scholar] [CrossRef]
- Zheng, P.; Zhao, Q.; Bai, J.; Yu, B.; Song, Z.; Shang, J. Analysis and Design of a Transverse-Flux Dual Rotor Machine for Power-Split Hybrid Electric Vehicle Applications. Energies 2013, 6, 6548–6568. [Google Scholar] [CrossRef]
- Wu, Y.; Kang, J.; Zhang, Y.; Jing, S.; Hu, D. Study of reliability and accelerated life test of electric drive system. In Proceedings of the IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009. [Google Scholar]
- Zhao, J.; Han, Q.; Dai, Y.; Hua, M. Study on the Electromagnetic Design and Analysis of Axial Flux Permanent Magnet Synchronous Motors for Electric Vehicles. Energies 2019, 12, 3451. [Google Scholar] [CrossRef]
- Peng, G.; Wei, J.; Shi, Y.; Shao, Z.; Jian, L. A Novel Transverse Flux Permanent Magnet Disk Wind Power Generator with H-Shaped Stator Cores. Energies 2018, 11, 810. [Google Scholar] [CrossRef]
- Zhu, S.; Zheng, P.; Yu, B.; Cheng, L.; Wang, W. Performance Analysis and Modeling of a Tubular Staggered-Tooth Transverse-Flux PM Linear Machine. Energies 2016, 9, 163. [Google Scholar] [CrossRef]
- Yang, X.; Kou, B.; Luo, J.; Zhou, Y.; Xing, F. Torque Characteristic Analysis of a Transverse Flux Motor Using a Combined-Type Stator Core. Appl. Sci. 2016, 6, 342. [Google Scholar] [CrossRef]
- Dobzhanskyi, O.; Mendrela, E.; Trznadlowski, A. Analysis of leakage flux losses in transverse flux PM synchronous generator. In Proceedings of the IEEE Green Technology Conference, Baton Rouge, LA, USA, 14–15 April 2011. [Google Scholar]
- Gieras, J.F. Transverse Flux Machine. U.S. Patent 7,830,057, 4 March 2010. [Google Scholar]
- Yu, B.; Zhang, S.; Yan, J.; Cheng, L.; Zheng, P. Thermal Analysis of a Novel Cylindrical Transverse-Flux Permanent-Magnet Linear Machine. Energies 2015, 8, 7874–7896. [Google Scholar] [CrossRef]
- Wang, W.; Zhou, S.; Mi, H.; Wen, Y.; Liu, H.; Zhang, G.; Guo, J. Sensitivity Analysis and Optimal Design of a Stator Coreless Axial Flux Permanent Magnet Synchronous Generator. Sustainability 2019, 11, 1414. [Google Scholar] [CrossRef]
- Wang, W.; Wang, W.; Mi, H.; Mao, L.; Zhang, G.; Liu, H.; Wen, Y. Study and Optimal Design of a Direct-Driven Stator Coreless Axial Flux Permanent Magnet Synchronous Generator with Improved Dynamic Performance. Energies 2018, 11, 3162. [Google Scholar] [CrossRef]
- Boldea, I.; Wang, C.X.; Yang, B.; Nasar, S.A. Analysis and design of flux reversal linear permanent magnet oscillating machine. In Proceedings of the 1998 Industry Applications Conference, 33th IAS Annual Meeting, St. Loius, MO, USA, 12–15 October 1998; pp. 136–143. [Google Scholar]
- Kou, B.Q.; Lou, J.; Yang, X.B.; Zhang, L. Modeling and analysis of novel transverse-flux flux reversal linear motor for long-stroke applications. IEEE Trans. Ind. Electron. 2016, 63, 6238–6248. [Google Scholar] [CrossRef]
- Wang, Q.; Zou, J.M.; Zou, J.B.; Zhao, M. Analysis and computer aided simulation of cogging force characteristic of a linear electromagnetic launcher with tubular transverse flux machine. IEEE Trans. Plasma Sci. 2011, 39, 157–161. [Google Scholar] [CrossRef]
- Dong, D.; Huang, W.; Bu, F.; Wang, Q.; Jiang, W.; Lin, X. Modeling and Static Analysis of Primary Consequent-Pole Tubular Transverse-Flux Flux-Reversal Linear Machines. Energies 2017, 10, 1479. [Google Scholar] [CrossRef]
- Hasanien, H.M.; bd-Rabou, A.S.; Sakr, S.M. Design optimization of transverse flux linear motor for weight reduction and performance improvement using response surface methodology and genetic algorithms. IEEE Trans. Energy Convers. 2010, 25, 598–605. [Google Scholar] [CrossRef]
- Marsden, J.E.; Tromba, A. Vector Calculus, 6th ed.; W.H. Freeman and Company: New York, NY, USA, 2012. [Google Scholar]
- Engwirda, D. Locally-Optimal Delaunay-Refinement and Optimisation-Based Mesh Generation. Ph.D. Thesis, School of Mathematics and Statistics, The University of Sydney, Sydney, Australia, 2014. Available online: http://hdl.handle.net/2123/13148 (accessed on 15 October 2019).
- Berhausen, S.; Paszek, S. Use of the finite element method for parameter estimation of the circuit model of a high power synchronous generator. Biul. Pol. Acad. Sci. Tech. Sci. 2015, 63, 575–582. [Google Scholar] [CrossRef]
- Vanoost, D.; Gersem, H.D.; Peuteman, J.; Gielen, G.; Pissort, D. Two Dimensional Magnetic Finite-Element Simulation for Devices With a Radial Symmetry. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Silvester, P.P.; Ferrari, R.L. Finite Elements for Electrical Engineers, 3rd ed.; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Jin, J.M. The Finite Element Method in Electromagnetics, 3rd ed.; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Sadiku, M.N.O. Numerical Techniques in Electromagnetics with MATLAB, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Li, J.; Chen, Y. Computational Partial Differential Equations Using Matlab; Springer: Berlin, Germany, 2010. [Google Scholar]
- Smoleń, A.; Gołębiowski, M. Computationally efficient method for determining the most important electrical parameters of Axial Field Permanent Magnet machine. BIuletin Yhe Pol. Acad. Sci. Tech. Sect. 2018, 66, 947–959. [Google Scholar]
| Case | Value of Error Norm |
|---|---|
| Both current and permanent magnets are included | 0.0091 |
| Only permanent magnets are included | 0.0099 |
| Only stator current is included | 0.0012 |
| Parameter | 2D Calculations | 3D Calculations |
|---|---|---|
| Number of elements | 3753 | 230,000 |
| Total computational time | 2 min 32 sec | 6 h 24 min |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smoleń, A.; Gołębiowski, L.; Gołębiowski, M.; Mazur, D. Computationally Efficient Method of Co-Energy Calculation for Transverse Flux Machine Based on Poisson Equation in 2D. Energies 2019, 12, 4340. https://doi.org/10.3390/en12224340
Smoleń A, Gołębiowski L, Gołębiowski M, Mazur D. Computationally Efficient Method of Co-Energy Calculation for Transverse Flux Machine Based on Poisson Equation in 2D. Energies. 2019; 12(22):4340. https://doi.org/10.3390/en12224340
Chicago/Turabian StyleSmoleń, Andrzej, Lesław Gołębiowski, Marek Gołębiowski, and Damian Mazur. 2019. "Computationally Efficient Method of Co-Energy Calculation for Transverse Flux Machine Based on Poisson Equation in 2D" Energies 12, no. 22: 4340. https://doi.org/10.3390/en12224340
APA StyleSmoleń, A., Gołębiowski, L., Gołębiowski, M., & Mazur, D. (2019). Computationally Efficient Method of Co-Energy Calculation for Transverse Flux Machine Based on Poisson Equation in 2D. Energies, 12(22), 4340. https://doi.org/10.3390/en12224340