Simulation of Synchronized-Switching Method Energy Harvester Including Accurate Piezoceramic Nonlinear Behavior
Abstract
1. Introduction
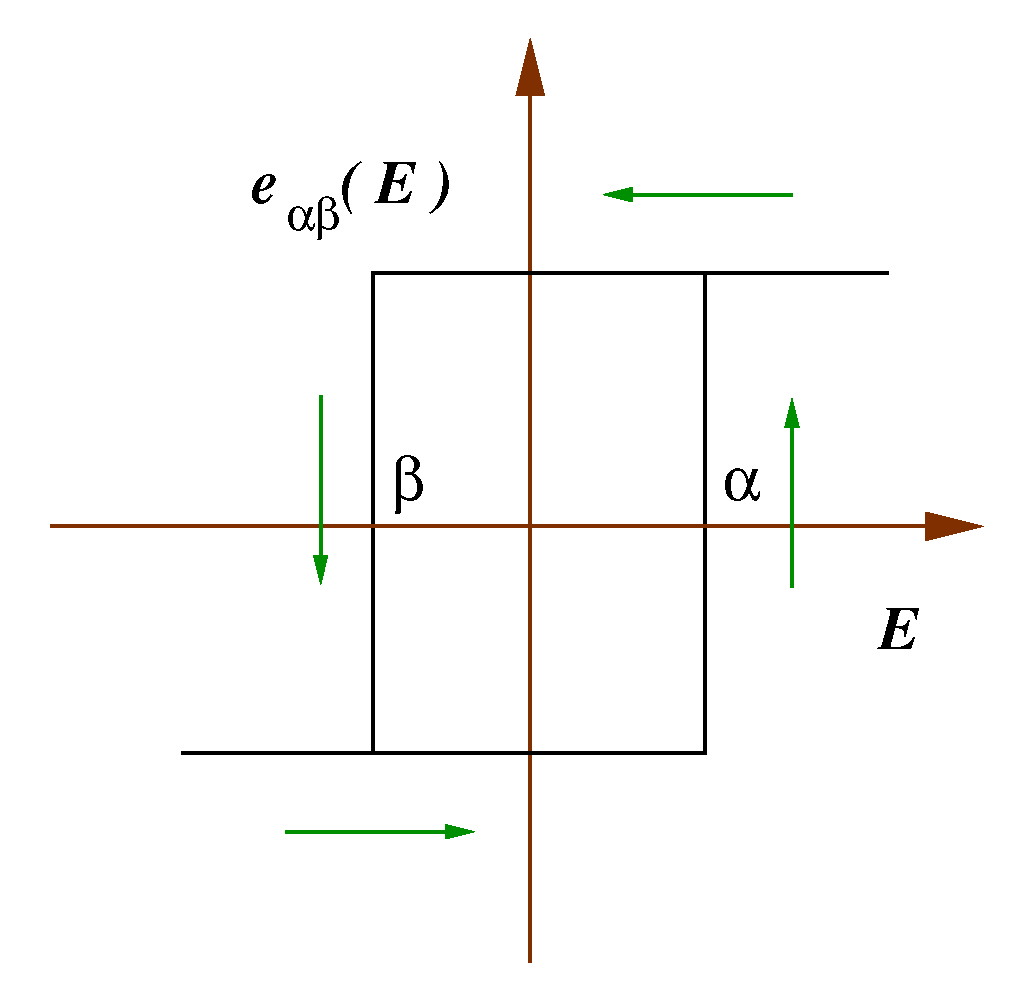
2. Hysteresis Model of Ferroelectrics Transducers
2.1. Quasistatic Contribution
2.2. Dynamic Contribution
2.3. Mechanical-Stress Consideration
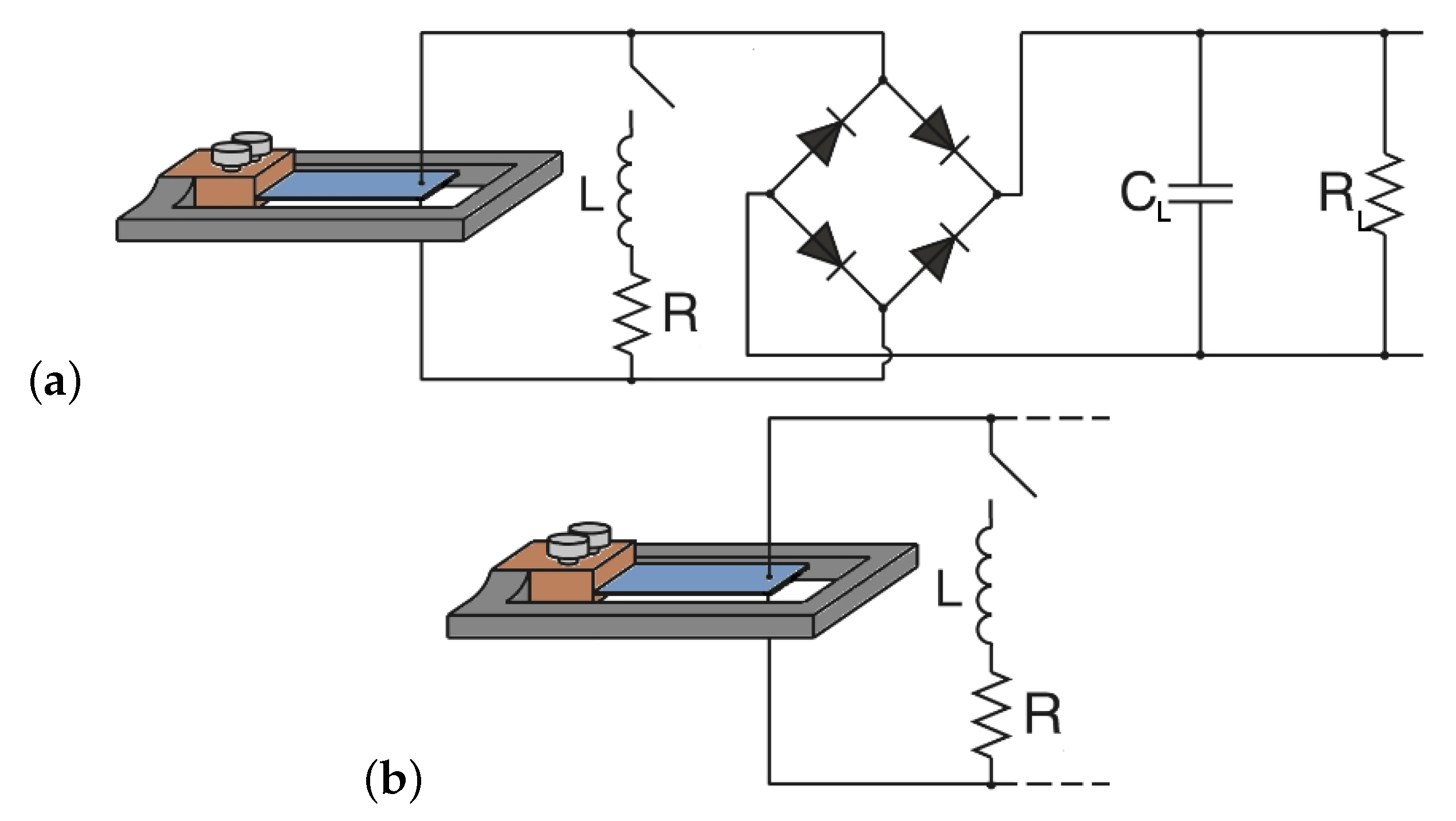
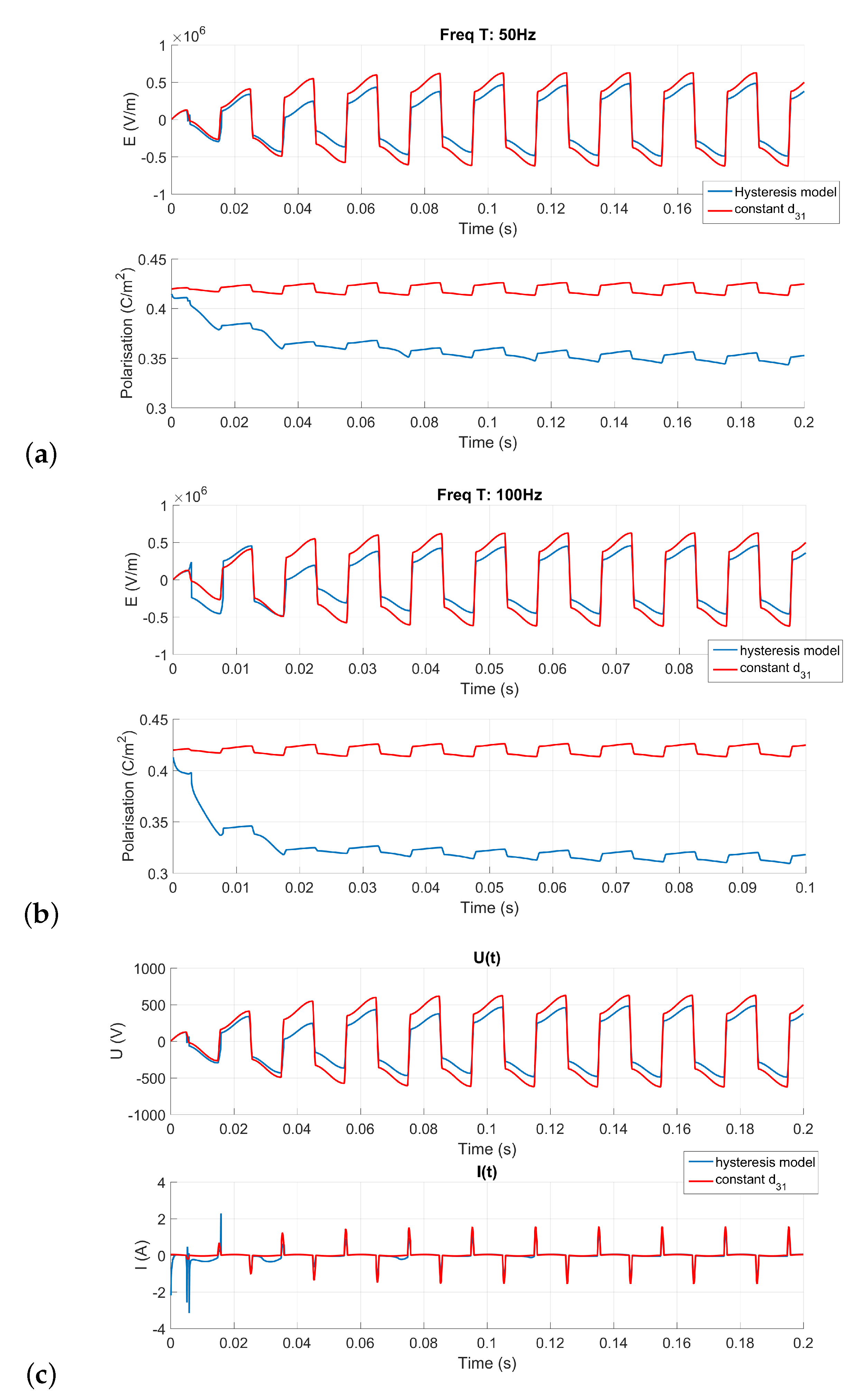
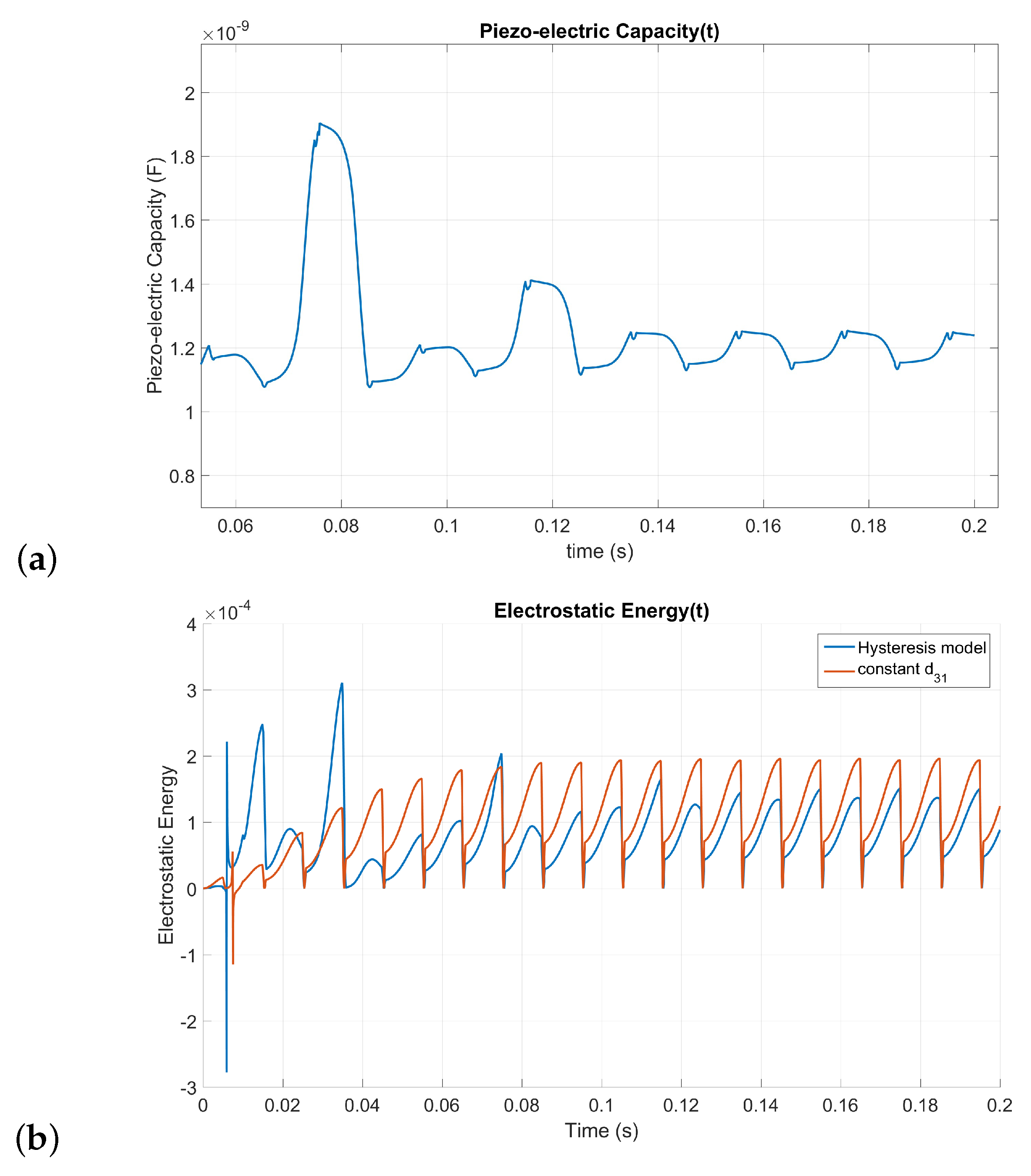
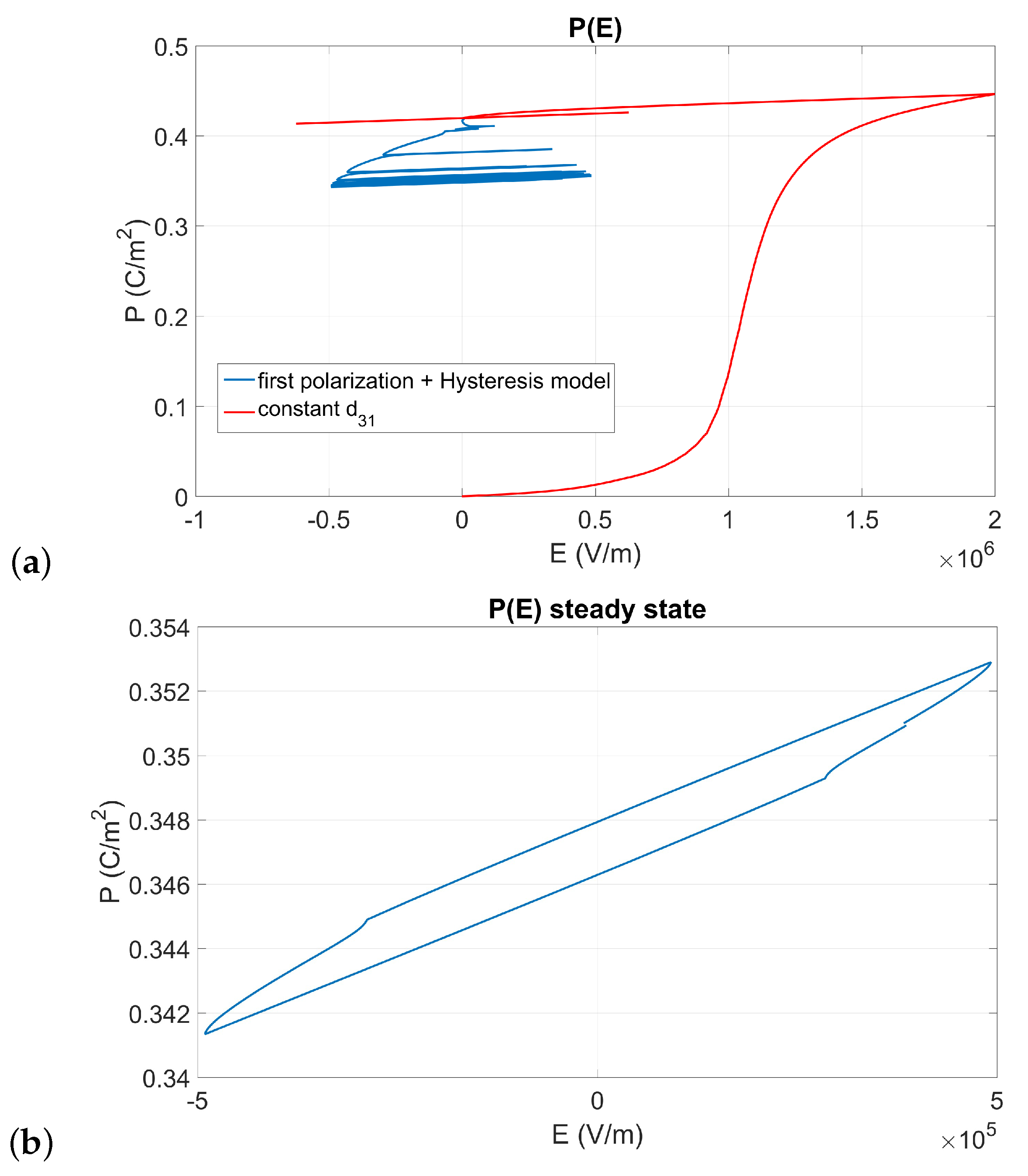
3. SSHI Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mitcheson, P.D.; Yeatman, E.M.; Rao, G.K.; Holmes, A.S.; Green, T.C. Energy harvesting from human and machine motion for wireless electronic devices. Proc. IEEE 2008, 96, 1457–1486. [Google Scholar] [CrossRef]
- Litak, G.; Manoach, E. Dynamics of composite nonlinear systems and materials for engineering applications and energy harvesting—The role of nonlinear dynamics and complexity in new developments. Eur. Phys. J. Spec. Top. 2013, 222, 1479–1482. [Google Scholar] [CrossRef]
- Litak, G.; Manoach, E.; Halvorsen, E. Nonlinear and multiscale dynamics of smart materials in energy harvesting. Eur. Phys. J.-Spec. Top. 2015, 224, 2671–2673. [Google Scholar] [CrossRef][Green Version]
- Harne, R.L.; Wang, K.W. A review of the recent research on vibration energy harvesting via bistable systems. Smart Mat. Struct. 2013, 22, 023001. [Google Scholar] [CrossRef]
- Pellegrini, S.P.; Tolou, N.; Schenk, M.; Herder, J.L. Bistable vibration energy harvesters: A review. J. Intell. Mater. Syst. Struct. 2013, 24, 1303–1312. [Google Scholar] [CrossRef]
- Twiefel, J.; Westermann, H. Survey on broadband techniques for vibration energy harvesting. J. Intell. Mater. Syst. Struct. 2013, 24, 1291–1302. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Masana, R.; Erturk, A.; Quinn, D.D. On the role of nonlinearities in vibratory energy harvesting: A critical review and discussion. Appl. Mech. Rev. 2014, 66, 040801. [Google Scholar] [CrossRef]
- Huguet, T.; Badel, A.; Druet, O.; Lallart, M. Drastic bandwidth enhancement of bistable energy harvesters: Study of subharmonic behaviors and their stability robustness. Appl. Energy 2018, 226, 607–617. [Google Scholar] [CrossRef]
- Huang, D.; Zhou, S.; Litak, G. Theoretical analysis of multi-stable energy harvesters with high order stiffness terms. Commun. Nonlinear Sci. Numer. Simul. 2019, 69, 270–286. [Google Scholar] [CrossRef]
- Lallart, M.; Lefeuvre, E.; Richard, C.; Guyomar, D. Self-powered circuit for broadband, multimodal piezoelectric vibration control. Sens. Actuator A 2008, 143, 377–382. [Google Scholar] [CrossRef]
- Guyomar, D.; Richard, C.; Mohammadi, S. Damping behavior of semi-passive vibration control using shunted piezoelectric materials. J. Intell. Mater. Syst. Struct. 2008, 19, 977–985. [Google Scholar] [CrossRef]
- Kelley, C.R.; Kauffman, J.L. Adaptive synchronized switch damping on an inductor: A self-tuning switching law. Smart Mater. Struct. 2017, 26, 035032. [Google Scholar] [CrossRef]
- Zouari, M.; Naifar, S.; Bouattour, G.; Derbel, N.; Kanoun, O. Energy management based on fractional open circuit and P-SSHI techniques for piezoelectric energy harvesting. tm-Technisches Messen 2019, 86, 14–24. [Google Scholar] [CrossRef]
- Qureshi, E.M.; Shen, X.; Chen, J. Vibration control laws via shunted piezoelectric transducers: A review. Int. J. Aeronaut. Space Sci. 2014, 15, 1–19. [Google Scholar] [CrossRef]
- Badel, A.; Guyomar, D.; Lefeuvre, E.; Richard, C. Piezoelectric Energy Harvesting using a Synchronized Switch Technique. J. Intell. Mater. Syst. Struct. 2006, 17, 831–839. [Google Scholar] [CrossRef]
- Badel, A.; Benayad, A.; Lefeuvre, E.; Lebrun, L.; Richard, C.; Guyomar, D. Single Crystals and Nonlinear Process for Outstanding Vibration Powered Electrical Generators. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 2006, 53, 673–684. [Google Scholar] [CrossRef]
- Lefeuvre, E.; Sebald, G.; Guyomar, D.; Lallart, M.; Richard, C. Materials, structures and power interfaces for efficient piezoelectric energy harvesting. J. Electroceram 2009, 22, 171–179. [Google Scholar] [CrossRef]
- Guyomar, D.; Badel, A.; Lefeuvre, E.; Richard, C. Toward Energy Harvesting Using Active Materials and Conversion Improvement by Nonlinear Processing. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 2005, 52, 584–595. [Google Scholar] [CrossRef]
- Lefeuvre, E.; Badel, A.; Richard, C.; Petit, L.; Guyomar, D.A. Comparison between several vibration-powered piezoelectric generators for standalone systems. Sens. Actuator A Phys. 2006, 126, 405–416. [Google Scholar] [CrossRef]
- Ducharne, B.; Guyomar, D.; Sebald, G. Low frequency modelling of hysteresis behavior and dielectric permittivity in ferroelectric ceramics under electric field. J. Phys. D Appl. Phys. 2007, 40, 551–555. [Google Scholar] [CrossRef]
- Priya, S. Advances in energy harvesting using low profile piezoelectric transducers. J. Electroceram. 2007, 19, 167–184. [Google Scholar] [CrossRef]
- Zhang, B.; Ducharne, B.; Guyomar, D.; Sebald, G. Energy harvesting based on piezoelectric Ericsson cycles in a piezoceramic material. Eur. Phys. J.-Spec. Top. 2013, 222, 1733–1743. [Google Scholar] [CrossRef]
- Zhang, B.; Ducharne, B.; Gupta, B.; Sebald, G.; Guyomar, D.; Gao, J. Experimental sea wave energy extractor based on Piezoelectric Ericsson cycles. J. Int. Mater. Syst. Struct. 2017, 26, 1102–1112. [Google Scholar] [CrossRef]
- Zhang, B.; Ducharne, B.; Sebald, G.; Guyomar, D. Characterization of fractional order for high-frequency bandwidth model of dielectric ferroelectrics. J. Intell. Mater. Syst. Struct. 2016, 27, 437–443. [Google Scholar] [CrossRef]
- Wang, D.; Wang, L.; Melnik, R. Vibration energy harvesting based on stress-induced polarization switching: A phase field approach. Smart Mater. Stuct. 2017, 26, 065022. [Google Scholar] [CrossRef]
- Mayergoyz, I.D. Mathematical Models of Hysteresis and Their Applications, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Preisach, F. Über die magnetische Nachwirkung. Zeitschrift Physik. 1935, 94, 277–302. [Google Scholar] [CrossRef]
- Sutor, A.; Rupitsch, S.J.; Lerch, R. A Preisach based hysteresis model for magnetic and ferroelectric hysteresis. Appl. Phys. A 2010, 100, 425–430. [Google Scholar] [CrossRef]
- Bernard, Y.; Maalej, H.; Lebrun, L.; Ducharne, B. Preisach modelling of ferroelectric behavior. Int. J. Appl. Electr. Mech. 2007, 25, 729–733. [Google Scholar]
- Bernard, Y.; Mendes, E.; Ren, Z. Determination of the distribution function of Preisach’s model using centred cycles. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2000, 19, 997–1006. [Google Scholar] [CrossRef]
- Biorci, G.; Pescetti, D. Some Remarks on Hysteresis. J. Appl. Phys. 1966, 37, 425–427. [Google Scholar] [CrossRef]
- Zhang, B.; Gupta, B.; Ducharne, B.; Sebald, G.; Uchimoto, T. Preisach’s model extended with dynamic fractional derivation contribution. IEEE Trans. Magn. 2017, 54, 6100204. [Google Scholar] [CrossRef]
- Guyomar, D.; Ducharne, B.; Sebald, G. High frequency bandwidth polarization and strain control using a fractional derivative inverse model. Smart Mater. Struct. 2010, 19, 045010. [Google Scholar] [CrossRef]
- Ducharne, B.; Zhang, B.; Guyomar, D.; Sebald, G. Fractional derivative operators for modeling piezo ceramic polarization behaviors under dynamic mechanical stress excitation. Sens. Actuator A-Phys. 2013, 189, 74–79. [Google Scholar] [CrossRef]
- Guyomar, D.; Ducharne, B.; Sebald, G. The use of fractional derivation in modeling ferroelectric dynamic hysteresis behavior over large frequency bandwidth. J. Appl. Phys. 2010, 107, 114108. [Google Scholar] [CrossRef]
- Guyomar, D.; Ducharne, B.; Sebald, G.; Audigier, D. Fractional derivative operator for modeling dynamical polarization behaviour as a function of frequency and electric field amplitude. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 437–443. [Google Scholar] [CrossRef] [PubMed]
- Alik, H.; Hughes, T.J.R. Finite element method for piezoelectric vibration. Int. J. Numer. Methods Eng. 1970, 2, 151–157. [Google Scholar] [CrossRef]




| Parameter | n | A | l | L | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Value | 0.03 | 0.56 | 20,000 | 0.001 | 0.1 | 160 | ||||
| Units | V N C m | - | V S C m | m | mm | N m | rad s | rad s | s | H |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ducharne, B.; Gupta, B.; Litak, G. Simulation of Synchronized-Switching Method Energy Harvester Including Accurate Piezoceramic Nonlinear Behavior. Energies 2019, 12, 4466. https://doi.org/10.3390/en12234466
Ducharne B, Gupta B, Litak G. Simulation of Synchronized-Switching Method Energy Harvester Including Accurate Piezoceramic Nonlinear Behavior. Energies. 2019; 12(23):4466. https://doi.org/10.3390/en12234466
Chicago/Turabian StyleDucharne, Benjamin, Bhaawan Gupta, and Grzegorz Litak. 2019. "Simulation of Synchronized-Switching Method Energy Harvester Including Accurate Piezoceramic Nonlinear Behavior" Energies 12, no. 23: 4466. https://doi.org/10.3390/en12234466
APA StyleDucharne, B., Gupta, B., & Litak, G. (2019). Simulation of Synchronized-Switching Method Energy Harvester Including Accurate Piezoceramic Nonlinear Behavior. Energies, 12(23), 4466. https://doi.org/10.3390/en12234466






