Analysis of Ripple Current in the Capacitors of Active Power Filters
Abstract
1. Introduction
- (1)
- Component forced by the usually distorted mains voltage;
- (2)
- Component forced by the nonlinear load current harmonics and harmonics in the output current of the PAPF that compensates them;
- (3)
- Component forced by the inverters of the PAPF and containing carrier and sideband harmonics (for equal and different inductances on the converter side).
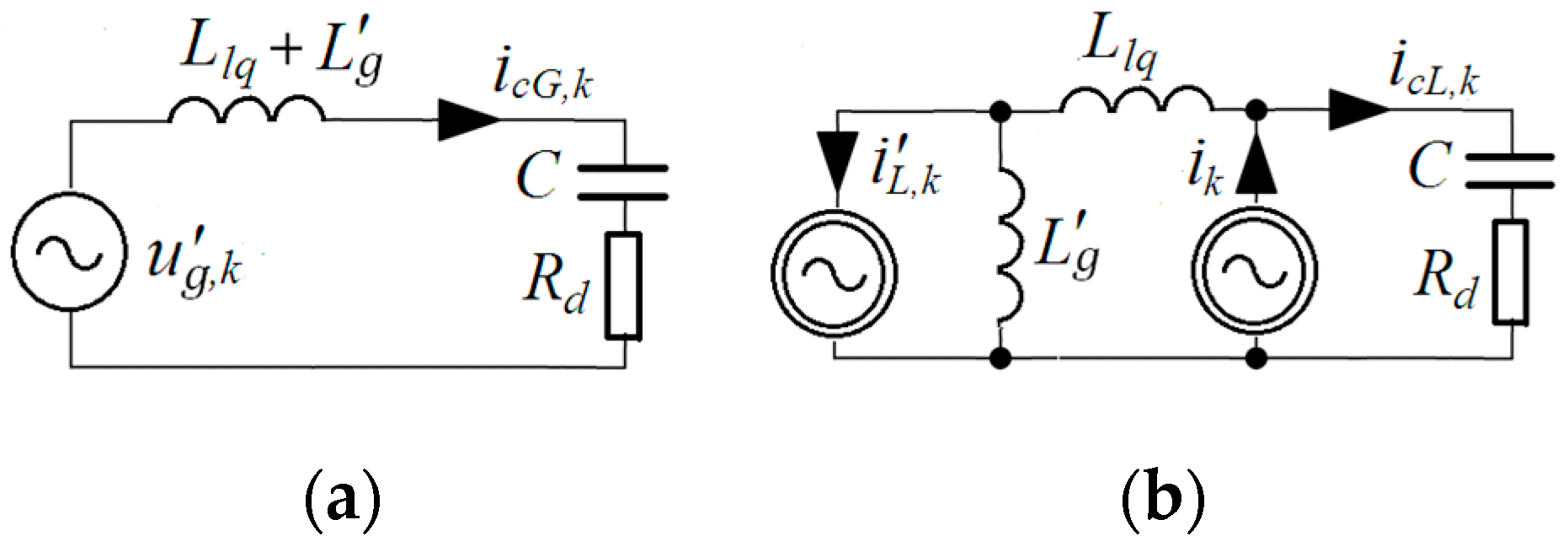
2. Description of the Input Circuit of PAPF
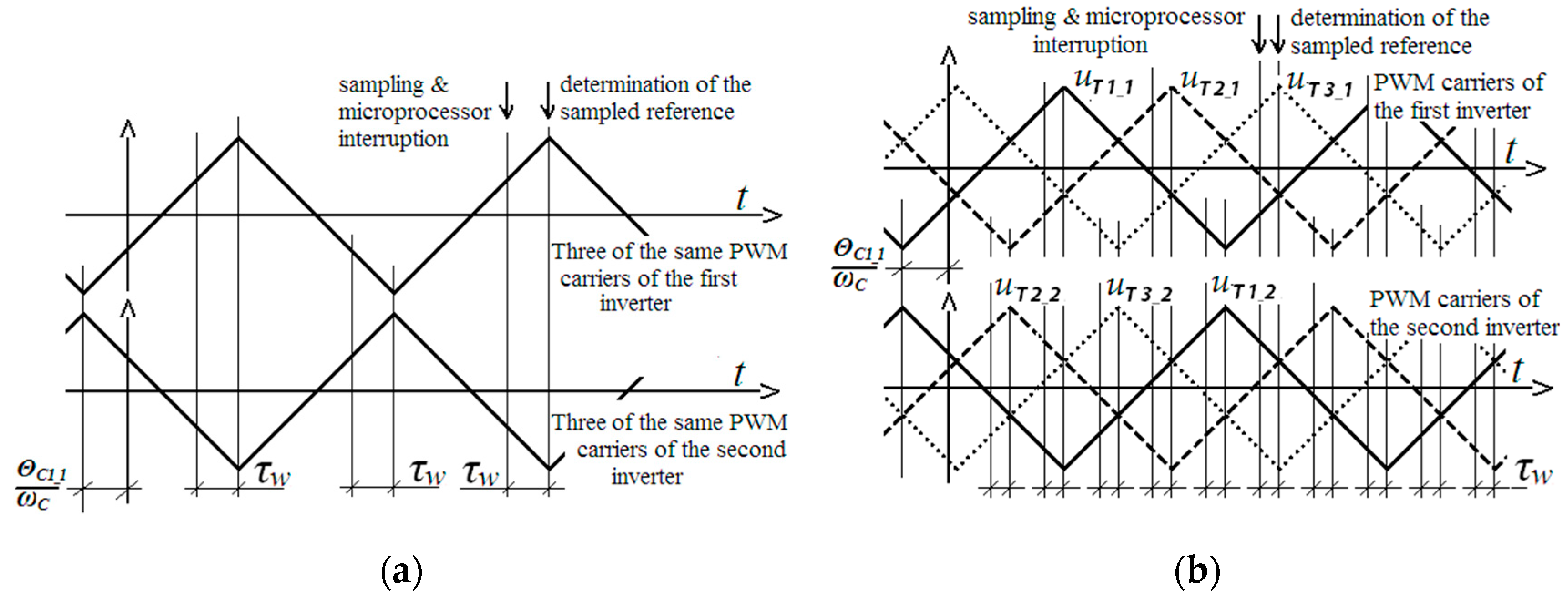
3. Inverter Output Voltage with Asymmetrical Regular-Sampled PWM
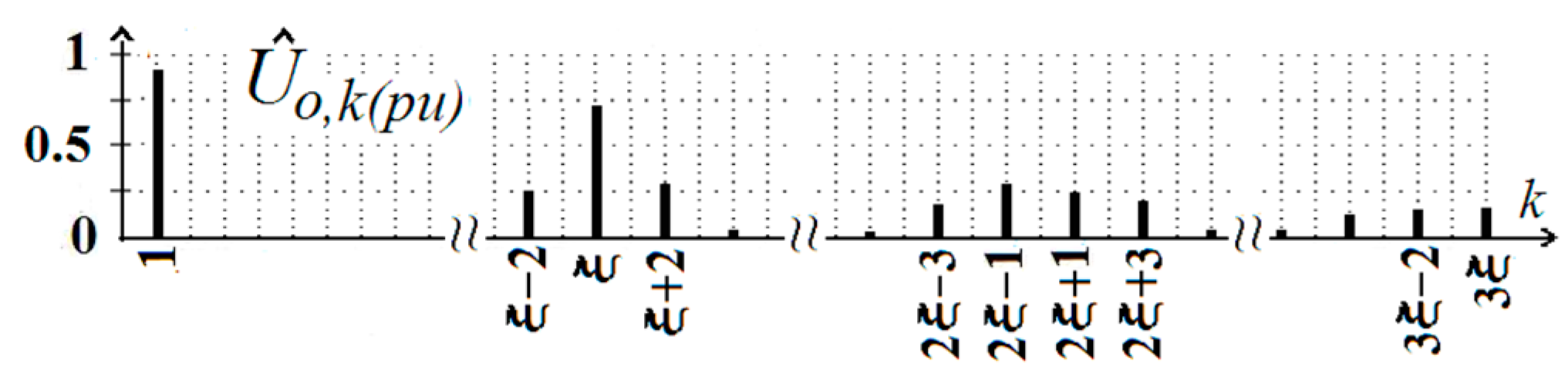
4. LCL System Capacitor Current
4.1. Rms of Capacitor C Current Component
4.2. Rms of Capacitor C Current Component
4.3. Rms of Capacitor C Current Ripple
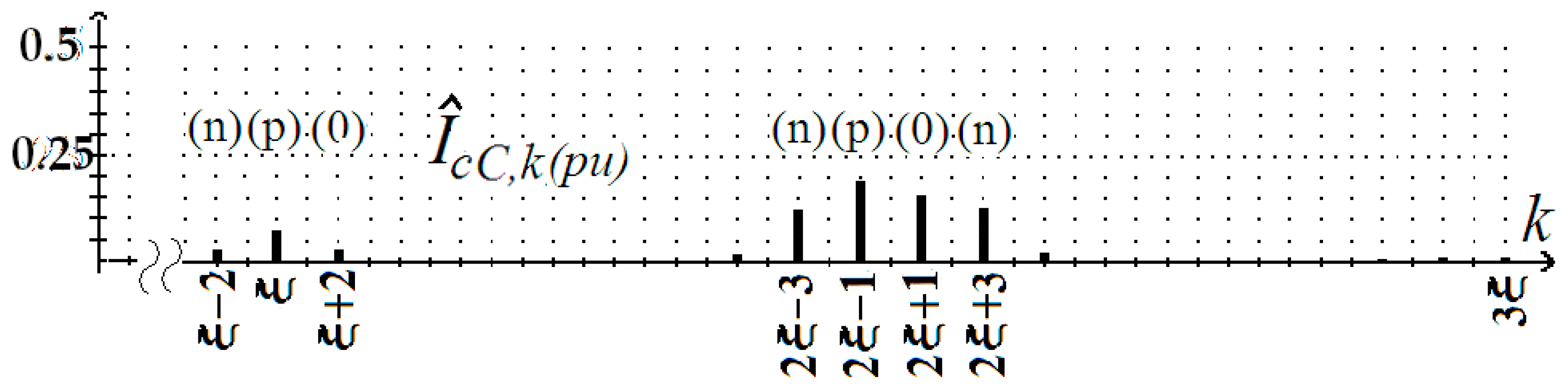
5. The Ripple Current in Dc-Link Capacitors
5.1. Current icp
5.2. Dc-Link Capacitor Current Component idcC
6. Simulation Tests of the Power Supply System
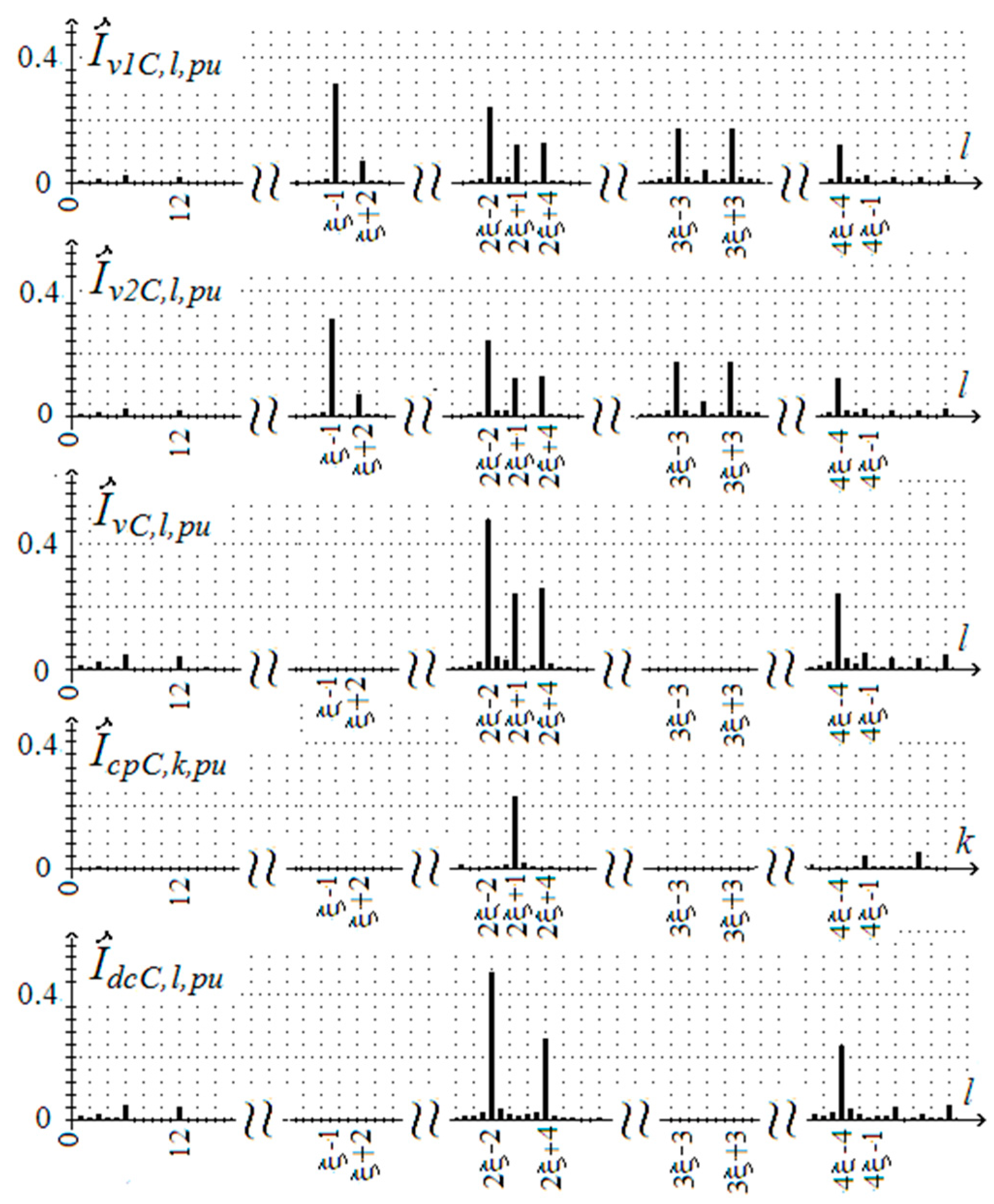
6.1. Rms of Capacitor C Current
6.2. Rms Value of Ripple Current in Dc-Link Capacitors
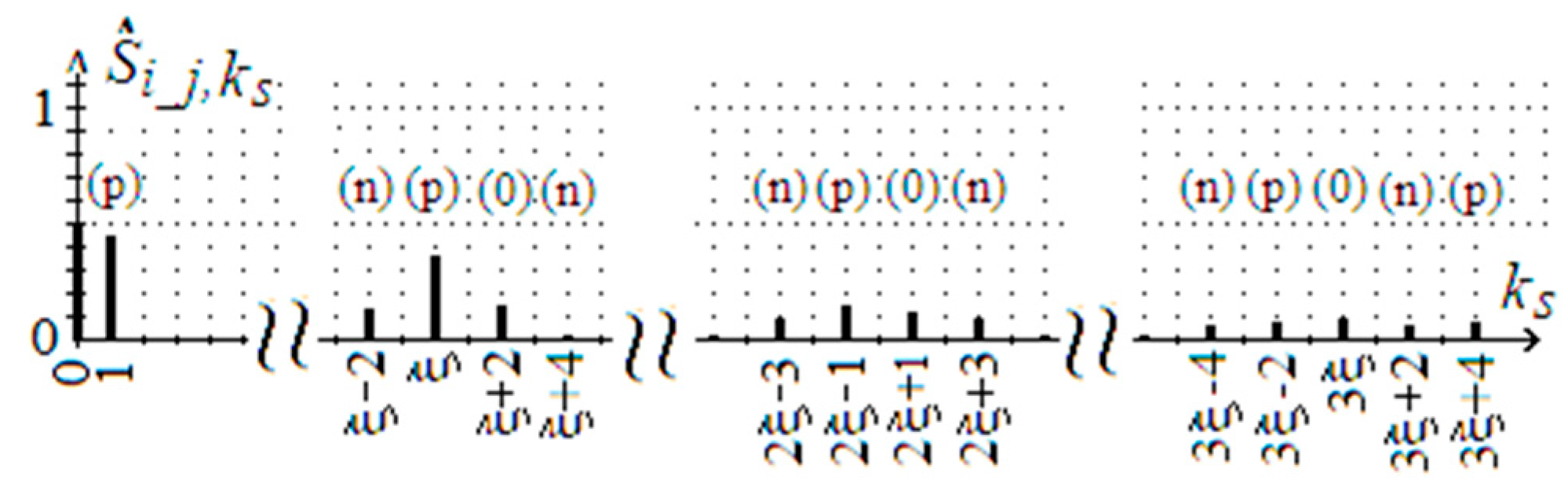
6.3. The Currents of LCL-Ripple Filter and Dc-Link Capacitors in a PAPF with One and Two Voltage Source Inverters for Positive and Negative Sequence Carriers
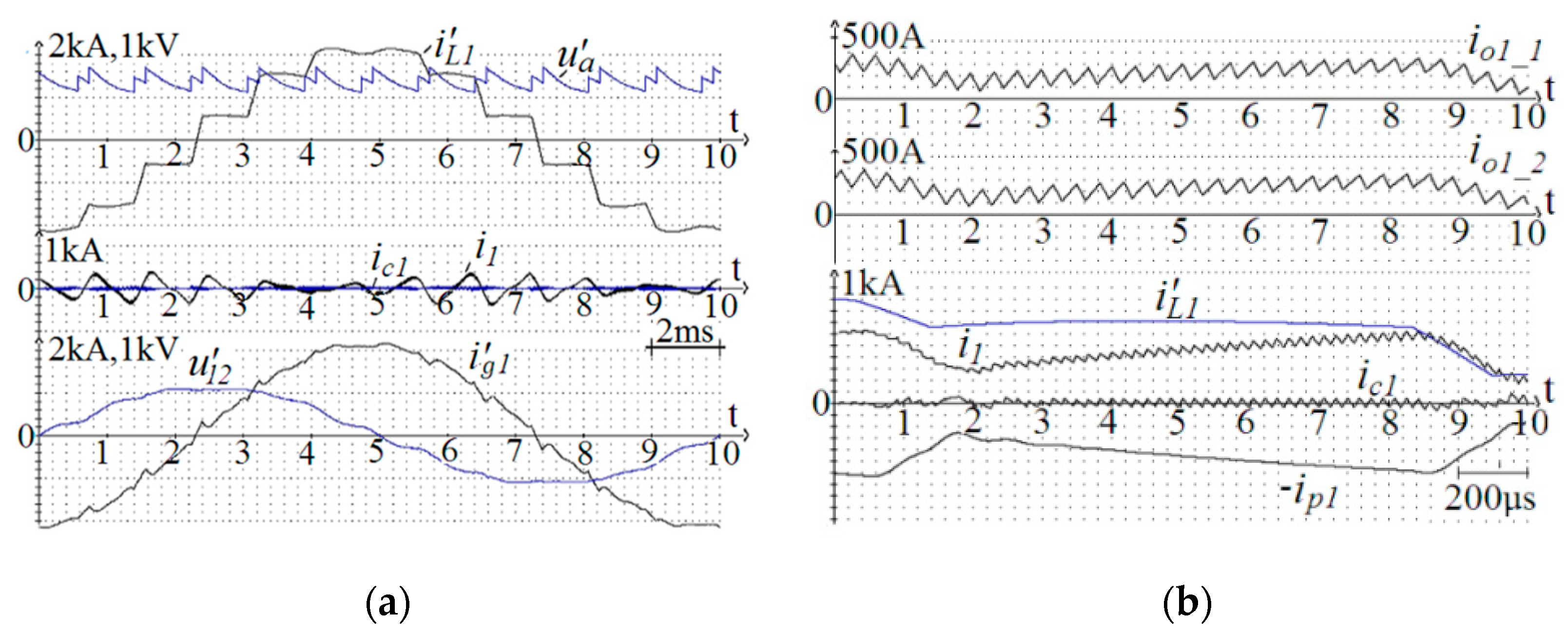
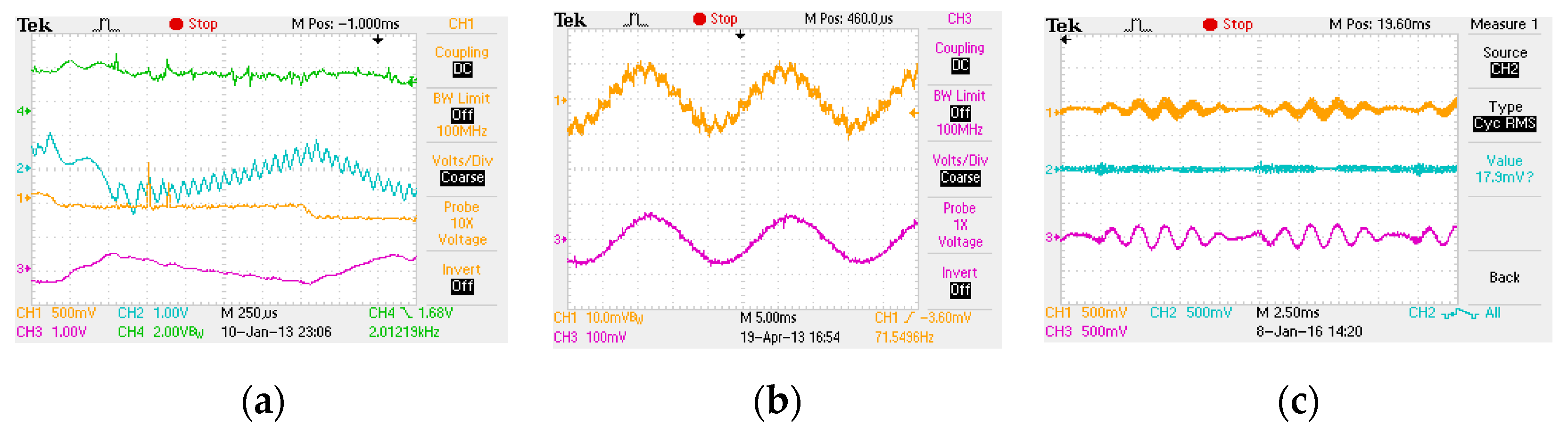
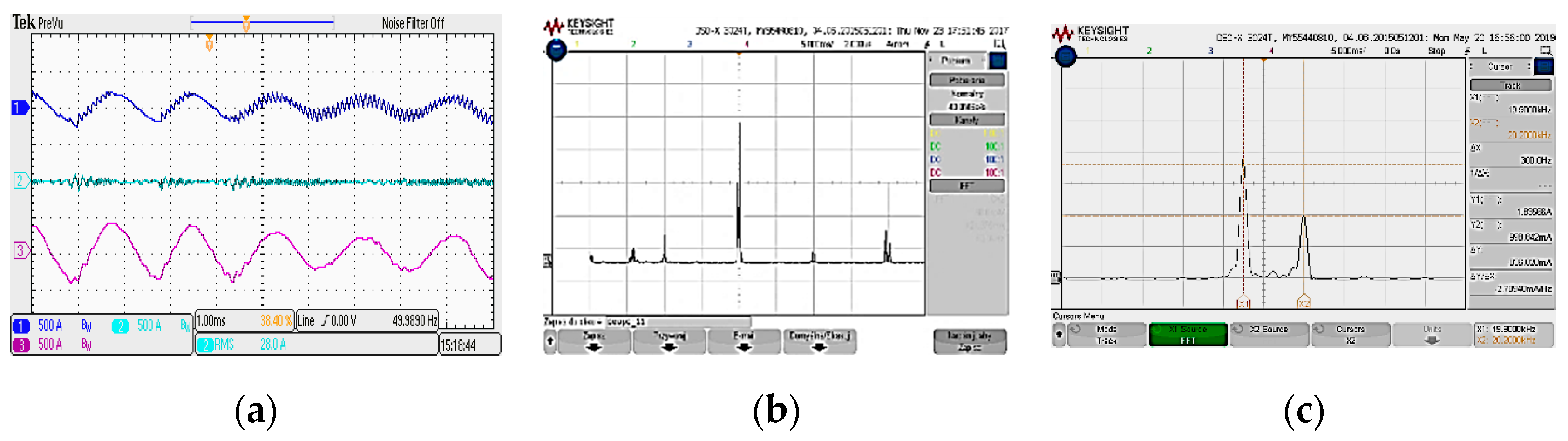
7. Experimental Results
8. Conclusions
- the rms values of currents in LCL filter capacitors in PAPF systems with double interleaved PWM carriers and double three interleaved PWM are similar, with accuracy of 1.5%; and
- the rms values of total currents in LCL filter capacitors and dc-link capacitors in PAPF systems with a current control system with asymmetrical and symmetrical regular-sampled PWM are similar, with accuracy of 6%.
Funding
Conflicts of Interest
Nomenclature
| , , , , | Fourier harmonic coefficients |
| , , , , , , | Amplitudes of harmonic coefficients |
| , | Amplitudes of voltage and current harmonics brought to terminals 1, 2, 3 of Tr1 transformer primary side |
| , | rms value of current harmonics |
| , | The circuit impedances for harmonics of positive and negative sequence and of zero sequence, respectively |
| The harmonic current component of the ks ± k order | |
| The phase angles for harmonics of positive and negative sequence and of zero sequence, respectively | |
| N | The number of operations in the microprocessor interruption service routine |
| λ | Harmonic attenuation factor |
| υz | Transformer turns ratio |
Appendix A
| M | −H2ξ − 2 | H2ξ + 4 | −H4ξ − 4 | −H4ξ + 2 | −H6ξ±6 | H6ξ | −H8ξ − 8 | H8ξ − 2 | H8ξ + 4 | H8ξ + 10 | H10ξ + 2 | H12ξ | H14ξ + 4 | H18ξ | G(M) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.486 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | −0.246 | 0.000 | 0.158 | 0.567 |
| 0.05 | 0.005 | 0.000 | 0.000 | 0.009 | 0.000 | 0.458 | 0.000 | 0.018 | −0.000 | 0.000 | −0.022 | −0.195 | 0.001 | 0.092 | 0.507 |
| 0.10 | 0.019 | 0.000 | 0.000 | 0.036 | 0.000 | 0.381 | 0.000 | 0.063 | −0.002 | 0.000 | −0.073 | −0.074 | 0.010 | −0.023 | 0.403 |
| 0.15 | 0.042 | 0.000 | 0.002 | 0.076 | 0.000 | 0.268 | 0.000 | 0.118 | −0.011 | 0.000 | −0.122 | 0.040 | 0.036 | −0.054 | 0.338 |
| 0.20 | 0.073 | 0.001 | 0.005 | 0.126 | 0.001 | 0.140 | 0.000 | 0.158 | −0.028 | 0.000 | −0.137 | 0.085 | 0.068 | 0.002 | 0.312 |
| 0.25 | 0.110 | 0.002 | 0.012 | 0.178 | 0.002 | 0.018 | 0.000 | 0.167 | −0.056 | 0.000 | −0.105 | 0.055 | 0.077 | 0.038 | 0.311 |
| 0.30 | 0.151 | 0.005 | 0.023 | 0.227 | 0.005 | −0.079 | 0.001 | 0.139 | −0.088 | 0.000 | −0.039 | −0.008 | 0.047 | 0.009 | 0.335 |
| 0.35 | 0.195 | 0.008 | 0.039 | 0.267 | 0.011 | −0.140 | 0.002 | 0.082 | −0.115 | 0.000 | 0.030 | −0.051 | −0.006 | −0.027 | 0.393 |
| 0.40 | 0.238 | 0.014 | 0.060 | 0.294 | 0.020 | −0.159 | 0.005 | 0.014 | −0.128 | 0.001 | 0.072 | −0.047 | −0.042 | −0.014 | 0.446 |
| 0.45 | 0.280 | 0.022 | 0.084 | 0.304 | 0.034 | −0.143 | 0.005 | −0.044 | −0.121 | 0.003 | 0.071 | −0.011 | −0.036 | 0.017 | 0.474 |
| 0.50 | 0.317 | 0.033 | 0.112 | 0.297 | 0.051 | −0.102 | 0.017 | −0.076 | −0.092 | 0.006 | 0.035 | 0.025 | −0.002 | 0.016 | 0.485 |
| 0.55 | 0.349 | 0.046 | 0.140 | 0.275 | 0.071 | −0.050 | 0.027 | −0.078 | −0.049 | 0.011 | −0.009 | 0.035 | 0.026 | −0.009 | 0.493 |
| 0.60 | 0.374 | 0.063 | 0.166 | 0.240 | 0.091 | 0.000 | 0.038 | −0.055 | −0.001 | 0.019 | −0.038 | 0.019 | 0.025 | −0.015 | 0.504 |
| 0.65 | 0.392 | 0.081 | 0.189 | 0.197 | 0.110 | 0.037 | 0.050 | −0.021 | 0.038 | 0.030 | −0.042 | −0.006 | 0.003 | 0.001 | 0.517 |
| 0.70 | 0.401 | 0.102 | 0.206 | 0.150 | 0.123 | 0.057 | 0.050 | 0.011 | 0.060 | 0.043 | −0.025 | −0.019 | −0.016 | 0.012 | 0.529 |
| 0.75 | 0.401 | 0.125 | 0.215 | 0.105 | 0.127 | 0.060 | 0.064 | 0.028 | 0.061 | 0.056 | −0.001 | −0.015 | −0.015 | 0.004 | 0.531 |
| 0.80 | 0.394 | 0.148 | 0.217 | 0.065 | 0.121 | 0.050 | 0.063 | 0.030 | 0.046 | 0.066 | 0.017 | −0.003 | −0.002 | −0.006 | 0.521 |
| 0.85 | 0.379 | 0.171 | 0.209 | 0.034 | 0.105 | 0.034 | 0.057 | 0.020 | 0.023 | 0.072 | 0.020 | 0.005 | 0.007 | −0.006 | 0.501 |
| 0.90 | 0.358 | 0.193 | 0.194 | 0.013 | 0.083 | 0.019 | 0.046 | 0.006 | −0.001 | 0.072 | 0.013 | 0.005 | 0.006 | 0.001 | 0.475 |
| 0.95 | 0.332 | 0.214 | 0.171 | 0.004 | 0.059 | 0.012 | 0.046 | −0.002 | −0.016 | 0.065 | 0.004 | 0.002 | 0.001 | 0.004 | 0.445 |
| 1.00 | 0.301 | 0.232 | 0.143 | 0.007 | 0.038 | 0.014 | 0.018 | −0.001 | −0.019 | 0.053 | 0.001 | 0.000 | 0.001 | 0.002 | 0.414 |
References
- Liserre, M.; Blaabjerg, F.; Hansen, S. Design and Control of an LCL-Filter-Based Three-Phase Active Rectifier. IEEE Trans. Ind. Appl. 2005, 41, 1281–1291. [Google Scholar] [CrossRef]
- Jeong, H.G.; Yoon, D.-K.; Lee, K.B. Design of an LCL-Filter for Three-Parallel Operation of Power Converters in Wind Turbines. J. Power Electron. 2013, 13, 437–445. [Google Scholar] [CrossRef]
- Asiminoaei, L.; Aeloiza, E.; Enjeti, P.; Blaabjerg, F. Shunt Active-Power_Filter Topology Based on Parallel Interleaved Inverters. IEEE Trans. Ind. Electron. 2008, 55, 1175–1189. [Google Scholar] [CrossRef]
- Jalili, K.; Bernet, S. Design of LCL Filters of Active-Front-End Two-Level Voltage-Source Converters. IEEE Trans. Ind. Electron. 2009, 56, 1674–1689. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Shahani, A.; Basu, K.; Mohan, N. LCL filter design for grid-connected inverters by analytical estimation of PWM ripple voltage. In Proceedings of the 2014 Twenty-Ninth Annual Applied Power Electronics Conference and Exposition (APEC), Fort Worth, TX, USA, 16–20 March 2014; pp. 1281–1286. [Google Scholar]
- Tang, Y.; Loh, P.C.; Wang, P.; Choo, F.H.; Gao, F.; Blaabjerg, F. Generalized design of high performance shunt active power filter with output LCL filter. IEEE Trans. Ind. Electron. 2012, 59, 1443–1452. [Google Scholar] [CrossRef]
- Vodyakho, O.; Mi, C.C. Three-level inverter-based shunt active power filter in three-phase three-wire and four-wire system. IEEE Trans. Power Electron. 2009, 24, 1350–1363. [Google Scholar] [CrossRef]
- McGrath, B.P.; Holmes, D.G. A general analytical method for calculating inverter DC-link current harmonics. IEEE Trans. Ind. Appl. 2009, 45, 1851–1859. [Google Scholar] [CrossRef]
- Kolar, J.W.; Wolbank, T.M.; Schrödl, M. Analytical calculation of the RMS current stress on the DC link capacitor of voltage DC link PWM converter systems. IEE Proc. Electr. Power Appl. 2006, 153, 535–543. [Google Scholar] [CrossRef]
- Zhang, H.; Wheeler, N.; Grant, D. Switching harmonics in the DC link current in a PWM AC-DC-AC converter. In Proceedings of the IAS ′95. Conference Record of the 1995 IEEE Industry Applications Conference Thirtieth IAS Annual Meeting, Orlando, FL, USA, 8–12 October 1995; pp. 2649–2655. [Google Scholar]
- Zhang, D.; Wang, F.; Burgos, R.; Lai, R.; Boroyevich, D. DC-link ripple current reduction for paralleled three-phase voltage-source converters with interleaving. IEEE Trans. Power Electron. 2011, 26, 1741–1753. [Google Scholar] [CrossRef]
- Ye, H.; Emadi, A. An interleaving scheme to reduce DC-link current harmonics of dual traction inverters in hybrid electric vehicles. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition-APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 3205–3211. [Google Scholar]
- Quan, Z.; Li, Y. Impact of Carrier Phase Shift PWM on the DC Link Current of Single and Interleaved Three-Phase Voltage Source Converters. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 3851–3855. [Google Scholar]
- Smolenski, R.; Jasinski, M.; Jarnut, M.; Bojarski, J.; Cecati, C. Compensation of CM voltage in systems consisting of interleaved AC-DC converters. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 1996–2001. [Google Scholar]
- Malinowski, M.; Bernet, S. A Simple Voltage Sensorless Active Damping Scheme for Three Phase PWM Converters with an LCL Filter. IEEE Trans. Ind. Electron. 2008, 55, 1876–1880. [Google Scholar] [CrossRef]
- Wu, D.; Chen, Y.; Hong, S.; Zhao, X.; Luo, J.; Gu, Z. Mathematical model analysis and LCL Filter Design of VSC. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012; pp. 2799–2804. [Google Scholar]
- Lang, Y.; Xu, D.; Hadianamrei, S.R.; Ma, H. A novel design method of LCL type utility interface for three-phase voltage source rectifier. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Recife, Brazil, 16 June 2005; pp. 313–317. [Google Scholar]
- Shen, G.; Zhu, X.; Zhang, J.; Xu, D. A New Feedback Method for PR Current Control of LCL-Filter-Based Grid-Connected Inverter. IEEE Trans. Ind. Electron. 2010, 57, 2033–2041. [Google Scholar] [CrossRef]
- Pei, X.; Zhou, W.; Kang, Y. Analysis and calculation of DC-link current and voltage ripples for three-phase inverter with unbalanced load. IEEE Trans. Power Electron. 2015, 30, 5401–5412. [Google Scholar] [CrossRef]
- Lascu, C.; Asiminoaei, L.; Boldea, L.; Blaabjerg, F. Frequency response analysis of current controllers for selective harmonic compensation in active power filters. IEEE Trans. Ind. Electron. 2009, 56, 337–347. [Google Scholar] [CrossRef]
- Ben-Sheng, C.; Yuan-Yih, H. A minimal harmonic controller for a STATCOM. IEEE Trans. Ind. Electron. 2008, 55, 655–664. [Google Scholar]
- Platek, T.; Osypinski, T. Current Control with Asymmetrical Regular Sampled PWM Modulator Applied for Parallel Active Filter. Bull. Pol. Acad. Sci. Tech. 2016, 64, 287–300. [Google Scholar]
- Holmes, D.G.; Lipo, T.A. Pulse Width Modulation For Power Converters; IEEE PRESS: Hoboken NJ 07030 USA, Willey-Interscience; 2003. [Google Scholar]
- Zhang, D.; Wang, F.; Burgos, R.; Lai, R.; Boroyevich, D. Impact of interleaving on ac passive components of paralleled three-phase voltage-source converters. IEEE Trans. Ind. Appl. 2010, 46, 1042–1054. [Google Scholar] [CrossRef]
- Rockhill, A.A.; Liserre, M.; Teodorescu, R.; Rodriguez, P. Grid-Filter Design for a Multimegawatt Medium-Voltage Voltage-Source Inverter. IEEE Trans. Ind. Electron. 2011, 58, 1205–1217. [Google Scholar] [CrossRef]
- Shang, Y. Synchronization in networks of coupled harmonic oscillators with stochastic perturbation and time delays. Ann. Acad. Rom. Sci. Ser. Math. Appl. 2012, 4, 44–58. [Google Scholar]
- Holmes, D.G.; Lipo, T.A.; McGrath, B.P.; Kong, W.Y. Optimized design of stationary frame three phase AC current regulators. IEEE Trans. Power Electron. 2009, 24, 2417–2426. [Google Scholar] [CrossRef]
- Liu, F.; Zha, X.; Zhou, Y.; Duan, S. Design and research on parameter of LCL filter in three-phase grid-connected inverter. In Proceedings of the 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 2174–2177. [Google Scholar]
- Liu, Y.; Lai, C.M. LCL Filter Design with EMI Noise Consideration for Grid-Connected Inverter. Energies 2018, 11, 1646. [Google Scholar] [CrossRef]
- Abusara, M.A.; Jamil, M.; Sharkh, S.M. Repetitive current control of an interleaved grid connected inverter. In Proceedings of the 2012 3rd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aalborg, Denmark, 25-28 June 2012; pp. 558–563. [Google Scholar]
- Jiang, Y.; Ekström, A. General Analysis of Harmonic Transfer Through Converters. IEEE Trans. Power Electron. 1997, 12, 287–293. [Google Scholar] [CrossRef]
- Kimball, J.W.; Zawodniok, M. Reducing Common-Mode Voltage in Three-Phase Sine-Triangle PWM with Interleaved Carriers. In Proceedings of the 2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, CA, USA, 21–25 February 2010; Volume 26, pp. 2229–2236. [Google Scholar]
- Shang, Y. Resilient Multiscale Coordination Control against Adversarial Nodes. Energies 2018, 11, 1844. [Google Scholar] [CrossRef]



| Matrix A | |||||
|---|---|---|---|---|---|
| A = |
| The Sequence of the Individual Harmonic Voltages of the Three-Phase Outputs uo1_1, uo2_1, uo3_1 and uo1_2, uo2_2, uo3_2 | |||
|---|---|---|---|
| - | positive sequence (p) | negative sequence (n) | zero sequence (0) |
| the same sequence | m + n = −5, −2,1,4,7… | m + n = −4, −1, 2, 5… | m + n = −6, −3, 0, 3, 6… |
| opposite sequence | m − n = –4, −1,2,5… | m − n = −5, −2, 1, 4, 7… | m − n = −6, −3, 0, 3, 6… |
| Functions | Values | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| M | 0.00 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
| 0.05 | 0.15 | 0.25 | 0.35 | 0.45 | 0.55 | 0.65 | 0.75 | 0.85 | 0.95 | ||
| J0(πM/2) | 1.000 | 0.994 | 0.975 | 0.945 | 0.904 | 0.852 | 0.790 | 0.720 | 0.643 | 0.559 | 0.472 |
| 0.998 | 0.986 | 0.962 | 0.926 | 0.879 | 0.822 | 0.756 | 0.682 | 0.602 | 0.516 | ||
| 0.000 | 0.155 | 0.299 | 0.421 | 0.514 | 0.571 | 0.592 | 0.579 | 0.540 | 0.487 | 0.438 | |
| 0.078 | 0.229 | 0.363 | 0.471 | 0.547 | 0.586 | 0.589 | 0.562 | 0.515 | 0.461 | ||
| Input, Output Parameters | Existing Conditions for Current Harmonics iv,k | No Harmonics | ||||||
|---|---|---|---|---|---|---|---|---|
| Sequence of ioi_j,k | (p) | (n) | (0) | (p) | (n) | (0) | (0) | (p), (n) |
| Sequence of si_j,ks | (p) | (n) | (0) | (n) | (p) | (0) | (p), (n) | (0) |
| Conditions | ms ± m = −6, −4, −2, 0, 2, 4, 6… | Do not exist | ||||||
| (ms ± ns) − (m ± n) = 0, ±3, ±6… | (ms ± m) + (ns ± n) = 0, ±3, ±6… | |||||||
| Order of harm. of | abs(k − ks) | k + ks | ||||||
| ms = 1, ns = 0 (p) | m = 1, n = −2 (n) | ms + m = 2, ns + n = −2 (ss) | |
| ms = 1, ns = 0 (n) | m = 1, n = 2 (p) | ms + m = 2, ns + n = 2 (os) | |
| ms = 1, ns = −2(n) | m = 1, n = 0 (p) | ms + m = 2, ns + n = −2 (ss) | |
| ms = 1, ns = 2 (p) | m = 1, n = 0 (n) | ms + m = 2, ns + n = −2 (os) | |
| ms = 0, ns = 1 (p) | m = 2, n = −1 (p) | m − ms = 2, n − ns = −2 (ss) | |
| ms = 0, ns = 1 (p) | m = 2, n = 1 (n) | m + ms = 2, n + ns = 2 (os) | |
| ms = 0, ns = 1 (p) | m = 2, n = −3 (n) | m + ms = 2, n + ns = −2 (ss) | |
| ms = 0, ns = 1 (p) | m = 2, n = 3 (p) | m − ms = 2, n − ns = 2 (os) | |
| ms = 1, ns = 0 (p) | m = 3, n = −2 (p) | m − ms = 2, n − ns = −2 (ss) | |
| ms = 1, ns = 0 (n) | m = 3, n = 2 (n) | m − ms = 2, n − ns = 2 (os) | |
| ms = 3, ns = −4(n) | m = 1, n = −2 (n) | ms − m = 2, ns − n = −2 (ss) | |
| ms = 3, ns = 4 (p) | m = 1, n = 2 (p) | ms − m = 2, ns − n = 2 (os) | |
| ms = 1, ns = −(n) | m = 3, n = −4 (n) | m − ms = 2, n − ns = −2 (ss) | |
| ms = 1, ns = 2 (p) | m = 3, n = 4 (p) | m − ms = 2, n − ns = 2 (os) | |
| ms = 3, ns = −2(p) | m = 1, n = 0 (p) | ms − m = 2, ns − n = −2 (ss) | |
| ms = 3, ns = 2 (n) | m = 1, n = 0 (n) | ms − m = 2, ns − n = 2 (os) | |
| ms = 3, ns = 0 (0) | m = 1, n = 2 (0) | ms − m = 2, ns − n = −2; (ss) | |
| ms = 3, ns = 0 (0) | m = 1, n = −2 (0) | ms − m = 2, ns − n = 2; (os) | |
| ms = 1, ns = 2 (0) | m = 3, n = 0 (0) | m − ms = 2, n − ns = −2 (ss) | |
| ms = 1, ns = −2 (0) | m = 3, n = 0 (0) | m − ms = 2, n − ns = 2 (os) | |
| ms = 2, ns = −1(p) | m = 4, n = −3 (p) | m − ms = 2, n − ns = −2 (ss) | |
| ms = 2, ns = 1 (n) | m = 4, n = 3 (n) | m − ms = 2, n − ns = −2 (os) | |
| ms = 4, ns = −3 (p) | m = 2, n = −1 (p) | ms − m = 2, ns − n = −2 (ss) | |
| ms = 4, ns = 3 (n) | m = 2, n = 1 (n) | ms − m = 2, ns − n = 2 (os) | |
| Parameter | Value |
|---|---|
| fg (grid dispersion inductance) | 50 Hz, 3 μH |
| Tr1, υz | Dy5 (400 V/400 V), √3 |
| Tr2 | Dd0y5 (400 V/400 V/400 V) |
| L’lq2 (Th1– Th12 rectifier side dispersion inductance of Tr2) | 80 μH |
| , ,, | 300 μH, 3 mΩ, 1035 A, 644 V |
| Firing angle of SCR converter α | 50° |
| ,Cdc | 720 V, 2.7 mF |
| L_1, L_2, L | 76 μH, 84 μH, 80 μH |
| C, Rd, Llq (APF side dispersion inductance of Tr1) | 0 μF, 180 mΩ, 20 μH |
| Control system: | |
| fC (carrier frequency) | 10 kHz, 15 kHz |
| fsamp (carrier frequency and sampling frequency) | 20 kHz, 30 kHz |
| k,l | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| V | rad | A | A | rad | A | rad | A | A | A | A | A | |
| 1 | 326.6 | 0.000 | 2162.3 | 2156.6 | −0.926 | 5.9 | 1.398 | 2.8 | 5.1 | 0.0 | 0.2 | 0.2 |
| 2 | 0.0 | 0.000 | 0.1 | 0.2 | 1.710 | 0.3 | 1.173 | 0.2 | 0.0 | 0.0 | 0.2 | 0.2 |
| 3 | 0.0 | 0.000 | 1.0 | 1.1 | 2.154 | 1.2 | 2.769 | 0.6 | 0.2 | 0.3 | 1.3 | 1.2 |
| 4 | 0.0 | 0.000 | 0.3 | 0.1 | 1.524 | 0.5 | 2.193 | 0.2 | 0.0 | 0.0 | 0.4 | 0.4 |
| 5 | 0.0 | 0.000 | 17.9 | 18.7 | 2.716 | 2.7 | −2.90 | 1.4 | 0.0 | 0.0 | 0.3 | 0.4 |
| 6 | 0.0 | 0.000 | 0.4 | 0.1 | 0.000 | 0.5 | 2.727 | 0.2 | 0.0 | 0.0 | 4.4 | 4.4 |
| 7 | 0.0 | 0.000 | 5.8 | 10.5 | −0.900 | 4.6 | −0.391 | 2.4 | 0.0 | 0.0 | 0.3 | 0.4 |
| 8 | 0.0 | 0.000 | 0.7 | 0.1 | 0.000 | 0.6 | 2.510 | 0.4 | 0.0 | 0.1 | 0.3 | 0.4 |
| 9 | 0.0 | 0.000 | 2.0 | 1.5 | −0.398 | 2.4 | 1.761 | 1.1 | 1.0 | 1.5 | 2.8 | 2.5 |
| 10 | 0.0 | 0.000 | 0.8 | 0.2 | −1.507 | 0.7 | 1.981 | 0.5 | 0.0 | 0.1 | 0.2 | 0.2 |
| 11 | 12.0 | −2.967 | 53.5 | 206.7 | −0.719 | 169.1 | −1.462 | 84.6 | 4.0 | 0.1 | 0.5 | 0.5 |
| 12 | 0.0 | 0.000 | 0.6 | 0.1 | 0.000 | 0.1 | −0.275 | 0.2 | 0.1 | 0.2 | 163.5 | 163.6 |
| 13 | 8.0 | −0.349 | 5.8 | 129.6 | 0.440 | 124.3 | 0.909 | 62.4 | 3.4 | 0.2 | 0.6 | 0.7 |
| 14 | 0.0 | 0.000 | 0.4 | 0.1 | −2.398 | 0.7 | 1.858 | 0.3 | 0.1 | 0.1 | 0.6 | 0.7 |
| 15 | 0.0 | 0.000 | 1.3 | 1.4 | −2.762 | 2.2 | −0.757 | 1.0 | 1.8 | 2.8 | 3.8 | 2.5 |
| 16 | 0.0 | 0.000 | 0.3 | 0.1 | 2.915 | 0.2 | 1.778 | 0.2 | 0.1 | 0.1 | 0.7 | 0.8 |
| 17 | 0.0 | 0.000 | 14.5 | 10.4 | −1.839 | 4.0 | 0.376 | 2.0 | 0.1 | 0.0 | 0.9 | 0.9 |
| 18 | 0.0 | 0.000 | 1.3 | 0.0 | 0.000 | 1.2 | −2.740 | 0.6 | 0.1 | 0.1 | 4.5 | 4.6 |
| 19 | 0.0 | 0.000 | 12.1 | 8.5 | −0.423 | 3.7 | 3.070 | 2.0 | 0.3 | 0.3 | 1.1 | 0.9 |
| 20 | 0.0 | 0.000 | 0.9 | 0.1 | 0.000 | 0.7 | −2.559 | 0.3 | 0.4 | 0.5 | 1.1 | 0.6 |
| 21 | 0.0 | 0.000 | 1.8 | 1.3 | 1.039 | 1.9 | −1.155 | 0.9 | 1.2 | 1.9 | 2.5 | 1.6 |
| 22 | 0.0 | 0.000 | 0.5 | 0.2 | −0.092 | 1.4 | −1.177 | 0.5 | 0.3 | 0.5 | 1.0 | 0.9 |
| 23 | 0.0 | 0.000 | 10.0 | 70.5 | 0.663 | 56.6 | 0.159 | 28.2 | 3.1 | 0.2 | 2.0 | 2.2 |
| 24 | 0.0 | 0.000 | 1.3 | 0.1 | 0.000 | 1.2 | −1.442 | 0.7 | 0.3 | 0.5 | 33.1 | 33.0 |
| 25 | 0.0 | 0.000 | 14.7 | 57.9 | 1.957 | 40.6 | 2.568 | 20.3 | 3.3 | 0.7 | 1.9 | 2.4 |
| 298 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.1 | 1.171 | 13.1 | 0.1 | 0.0 | 0.1 | 0.1 |
| 299 | 0.0 | 0.000 | 0.4 | 0.3 | −2.041 | 0.1 | 0.000 | 1.2 | 0.0 | 0.0 | 0.0 | 0.0 |
| 300 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.0 | 0.000 | 32.9 | 0.0 | 0.0 | 0.2 | 0.2 |
| 301 | 0.0 | 0.000 | 0.5 | 0.4 | −0.816 | 0.1 | 0.000 | 1.2 | 0.0 | 0.1 | 0.2 | 0.0 |
| 302 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.1 | 0.000 | 11.5 | 0.1 | 0.1 | 0.2 | 0.1 |
| 550 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.2 | 0.170 | 0.2 | 0.2 | 0.0 | 6.3 | 6.2 |
| 562 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.6 | −0.330 | 0.3 | 0.6 | 0.2 | 9.4 | 9.6 |
| 568 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.5 | −1.247 | 0.3 | 0.5 | 0.3 | 7.4 | 7.1 |
| 574 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.3 | 3.123 | 0.2 | 0.3 | 0.3 | 6.9 | 6.9 |
| 580 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.2 | −0.967 | 0.1 | 0.2 | 0.2 | 6.4 | 6.5 |
| 589 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 2.6 | 0.977 | 1.3 | 2.6 | 4.2 | 4.7 | 0.5 |
| 592 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.1 | −0.017 | 0.1 | 0.2 | 0.4 | 17.0 | 16.8 |
| 595 | 0.0 | 0.000 | 0.1 | 0.1 | 0.000 | 2.2 | −0.410 | 1.1 | 2.2 | 3.5 | 2.8 | 0.6 |
| 597 | 0.0 | 0.000 | 0.4 | 0.0 | 0.000 | 7.5 | −2.483 | 3.8 | 7.8 | 0.4 | 1.2 | 1.5 |
| 598 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 1.2 | 1.269 | 0.6 | 1.3 | 0.5 | 30.3 | 30.8 |
| 599 | 0.0 | 0.000 | 0.5 | 0.0 | 0.000 | 9.8 | 1.862 | 4.9 | 10.1 | 0.6 | 2.7 | 2.1 |
| 600 | 0.0 | 0.000 | 0.1 | 0.0 | 0.000 | 0.2 | 0.407 | 0.1 | 0.2 | 0.9 | 2.2 | 1.3 |
| 601 | 0.0 | 0.000 | 0.1 | 0.1 | 0.000 | 11.4 | 2.807 | 5.7 | 11.4 | 17.9 | 18.5 | 1.1 |
| 602 | 0.0 | 0.000 | 0.1 | 0.0 | 0.000 | 1.4 | 0.058 | 0.7 | 1.4 | 1.2 | 0.9 | 0.4 |
| 603 | 0.0 | 0.000 | 0.3 | 0.0 | 0.000 | 7.6 | 0.767 | 3.8 | 7.9 | 0.5 | 0.6 | 0.9 |
| 604 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.5 | −1.395 | 0.2 | 0.5 | 0.2 | 12.1 | 12.3 |
| 609 | 0.0 | 0.000 | 0.1 | 0.0 | 0.000 | 2.3 | 1.266 | 1.2 | 2.4 | 0.1 | 1.7 | 1.7 |
| 610 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.3 | −2.500 | 0.2 | 0.3 | 0.0 | 25.1 | 25.1 |
| 613 | 0.0 | 0.000 | 0.1 | 0.1 | 0.000 | 3.0 | −0.720 | 1.5 | 3.0 | 4.5 | 3.9 | 0.7 |
| 616 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.2 | −2.064 | 0.1 | 0.2 | 0.3 | 22.3 | 22.3 |
| 622 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.2 | 1.651 | 0.1 | 0.3 | 0.2 | 21.5 | 21.4 |
| 628 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.2 | −0.442 | 0.1 | 0.2 | 0.0 | 5.3 | 5.3 |
| 634 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.3 | 2.551 | 0.2 | 0.3 | 0.1 | 8.6 | 8.6 |
| 640 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.3 | 2.546 | 0.2 | 0.3 | 0.1 | 6.8 | 7.0 |
| 646 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.1 | 0.000 | 0.1 | 0.1 | 0.1 | 7.2 | 7.3 |
| 652 | 0.0 | 0.000 | 0.0 | 0.0 | 0.000 | 0.1 | 0.519 | 0.1 | 0.1 | 0.1 | 5.8 | 5.8 |
| 1531 A | 155.1 A | −0.93 rad | 18.4 A | 138 A | 1536 A | 397 V | 231 V |
| THDiL1 = 12.3% | THDig1 = 4.36% | THDu12 = 4.62% | THDug1 = 4.42% | ||||
| Results of Simulation Research | Results of Calculations | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| k | Û’g1,k | Ψ’g1,k | Î’L1,k | φ’L1,k | Ic1,k(rms) | λk | ÎcG1,k | ÎcL1,k | IcGL1,k(rms) |
| - | V | rad | A | rad | A | - | A | A | A |
| 1 | 327 | 0 | 2156.6 | −0.93 | 3.6 | 0 | 5.13 | 0.032 | 3.64 |
| 11 | 12 | −2.97 | 206.7 | −0.72 | 2.8 | 0.82 | 2.1 | 1.98 | 2.72 |
| 13 | 8 | −0.35 | 129.6 | 0.44 | 2.4 | 0.96 | 1.66 | 2.1 | 2.46 |
| 23 | 0 | 70.5 | 0.66 | 2.2 | 0.8 | 0 | 3.0 | 2.12 | |
| 25 | 0 | 57.9 | 2.00 | 2.33 | 0.7 | 0 | 2.52 | 1.78 | |
| Results of Simulation Research/Results of Calculations | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| fC [kHz] | 15 | 10 | 15 | 10 | 15 | 10 | 15 | 10 | 15 | 10 | 15 | 10 | 15 | 10 |
| M= 0.9 | 34.9/ 34.2 | 50.1/ 51.3 | 19.0/ 18.4 | 29.1/ 27.7 | 17.7/ 18.5 | 26.5/ 27.8 | 2.8/ 1.2 | 2.8/ 1.9 | 10.0/ 7.9 | 14.3/ 11.9 | 2.6/ 1.8 | 3.7/ 2.7 | 9.8/ 7.9 | 13.8/ 11.9 |
| M= 0.45 | 25.7/ 26.7 | 39.8/ 40.1 | 2.1/ 2.1 | 3.6/ 3.2 | 7.7/ 8.0 | 12.5/ 12.0 | 30.0/ 29.0 | 45.4/ 43.5 | 3.5/ 3.3 | 5.4/ 4.9 | 14.7/ 13.7 | 22.1/ 20.5 | 3.5/ 3.3 | 5.1/ 4.9 |
| M= 0.05 | 1.06/ 0.5 | 1.4/ 0.7 | 0.07/ 0 | 0.1/ 0 | 0.07/ 0 | 0.0/ 0 | 1.35/ 0.9 | 1.7/ 1.3 | 0.2/ 0 | 0.5/ 0 | 45.5/ 43.7 | 67.7/ 65.6 | 0.2/ 0 | 0.5/ 0 |
| fC = 15 kHz | Results for Asymmetrical Regular Sampled PWM/Results for Symmetrical Regular Sampled PWM | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PAPF with One Three-Phase Voltage Source Inverter | PAPF with Two Paralleled Three-Phase Voltage Source Inverters | |||||||||||
| Converter-Side Inductances | L/2 | L | ||||||||||
| Carrier Based PWM Strategies | Single PWM Carrier | Three Interleaved PWM Carriers [32] | Single PWM Carrier | Double Interleaved PWM Carriers [3] | Double Three Interleaved PWM Carriers [13] | |||||||
| Positive Sequence Carrier | Negative Sequence Carrier | |||||||||||
| M | 0.9 | 0.9 | 0.675 | 0.45 | 0.05 | 0.9 | 0.675 | 0.45 | 0.05 | 0.9 | ||
| Ic,rms [A] | 61.9/ 61.8 | 67.37/ 67.24 | 62.0/ 61.7 | 17.0/ 16.3 | 19.2/ 19.2 | 18.0/ 18.0 | 2.88/ 3.4 | 17.1/ 16.3 | 19.0/ 19.0 | 17.8/ 17.8 | 2.88/ 3.4 | 17.0/ 16.3 |
| Idc,rms [A] | 53.1/ 52.4 | 56.12/ 55.06 | 53.3/ 52.4 | 31.3/ 30.2 | 41.2/ 41.3 | 64.9/ 64.9 | 123/ 121 | 36.2/ 35.2 | 40.43/ 39.38 | 36.8/ 36.9 | 37.7/ 37.4 | 36.4/ 36.2 |
| CMVrms [V] | 14.4/ 15.2 | 6.32/ 7.99 | 14.4/ 15.2 | 4.4/ 8.9 | 1.17/ 8.26 | 0.60/ 8.22 | 0.04/ 8.25 | 4.33/ 8.79 | 2.57/ 8.6 | 2.5/ 8.56 | 0.39/ 8.25 | 4.3/ 8.89 |
| N | 3 | 1 | 6 | 6 | 2 | |||||||
| M | ||||||||
|---|---|---|---|---|---|---|---|---|
| L_1 = 80µH, L_2 = 80µH | L_1 = 76µH, L_2 = 84µH | L_1 = 76µH L_2 = 84 µH | ||||||
| IcC1,rms | IdcC,rms | IcC1,rms | IdcC,rms | IcC1,rms | IcC2,rms | IcC3,rms | IdcC,rms | |
| Results of Calculations/Results of Simulations Studies | Results of Simulations Studies | |||||||
| 0.9 | 22.2/25.15 | 53.0/53.5 | 22.88/26.02 | 53.77 | 24.18 | 26.42 | 26.51 | 56.77 |
| 0.45 | 24.94/27.58 | 53.0/55.48 | 26.41/29.13 | 55.63 | 29.77 | 28.99 | 28.99 | 56.24 |
| 0.05 | 3.55/4.42 | 56.5/56.58 | 10.47/11.30 | 56.75 | 11.41 | 11.27 | 11.26 | 56.64 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Platek, T. Analysis of Ripple Current in the Capacitors of Active Power Filters. Energies 2019, 12, 4493. https://doi.org/10.3390/en12234493
Platek T. Analysis of Ripple Current in the Capacitors of Active Power Filters. Energies. 2019; 12(23):4493. https://doi.org/10.3390/en12234493
Chicago/Turabian StylePlatek, Tadeusz. 2019. "Analysis of Ripple Current in the Capacitors of Active Power Filters" Energies 12, no. 23: 4493. https://doi.org/10.3390/en12234493
APA StylePlatek, T. (2019). Analysis of Ripple Current in the Capacitors of Active Power Filters. Energies, 12(23), 4493. https://doi.org/10.3390/en12234493





