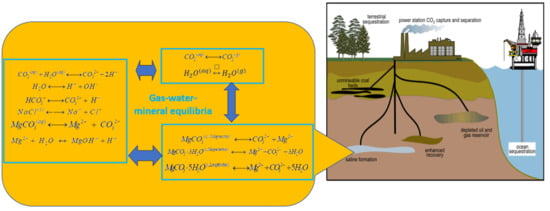
Numerical Modeling of CO2, Water, Sodium Chloride, and Magnesium Carbonates Equilibrium to High Temperature and Pressure
Abstract
:1. Introduction
2. Phenomenological Description and Geochemical Modeling
2.1. Equilibrium Constant
2.2. Activity Model and Fugacity Model
2.3. Calculation Routine
- (1)
- Initialize the system with molality of each component and species at given pressure and temperature.
- (2)
- Calculate the equilibrium constant of each reaction.
- (3)
- Calculate activity coefficient of each aqueous species and fugacity coefficient of each gaseous species with current molality of each species of the system.
- (4)
- Solve mass and charge conservation equations and linearized reaction equilibrium equations. Update the molality and activity/fugacity coefficient of each species.
- (5)
- Calculate the absolute relative difference of molality of each species and activity coefficient. If both are smaller than tolerance, stop the calculation and output the final results. Otherwise, go to step (3).
3. Results
3.1. Comparisons of MgCO3 Mineral Solubility: Model Calculations and Experiments
3.2. CO2 Solubility
3.3. Model Predictions
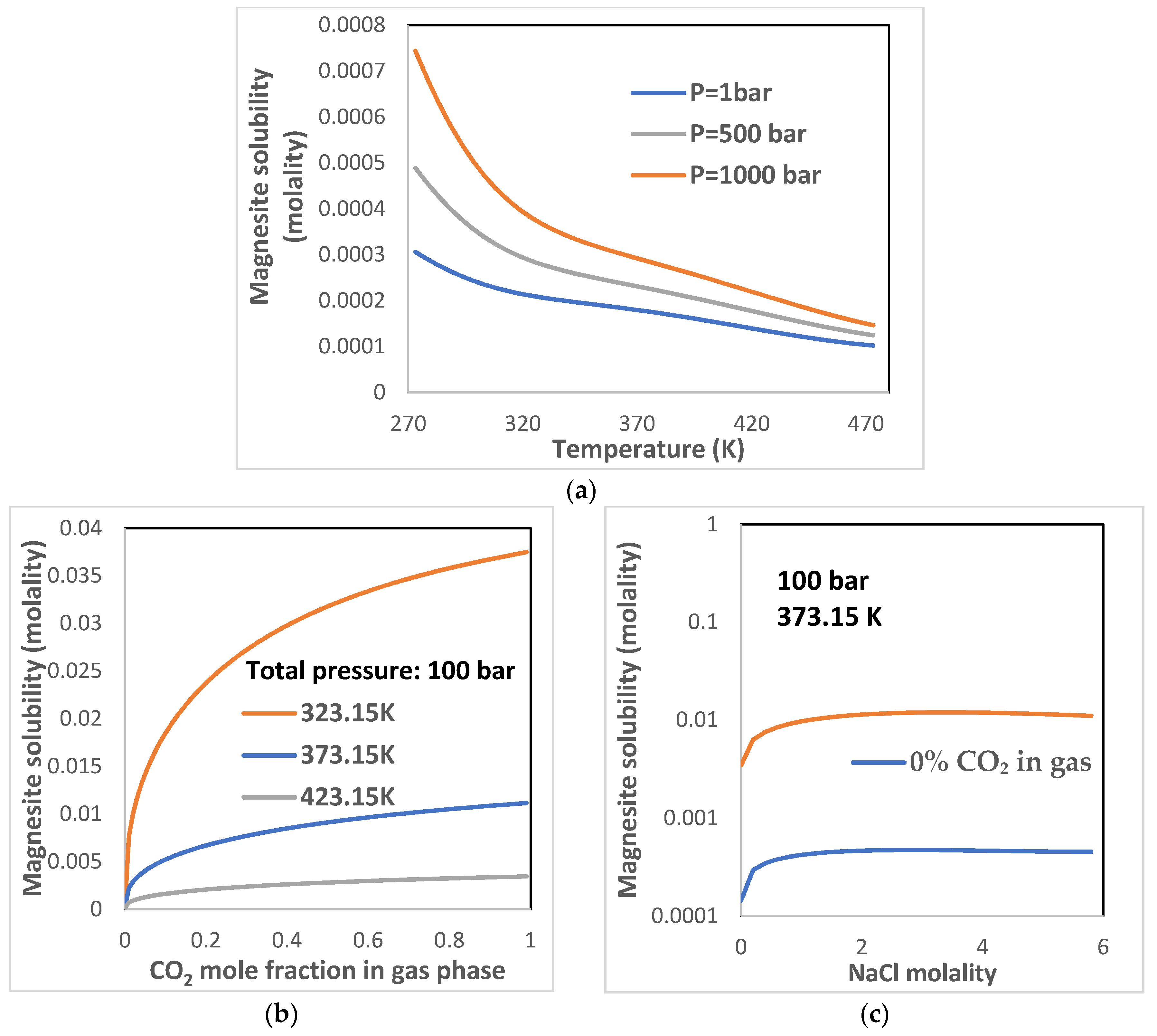
3.3.1. MgCO3 Mineral Solubility
3.3.2. Solution Properties
4. Conclusions
- (1)
- Temperature usually decreases the mineral solubilities, and pressure usually increases the solubility. However, for nesquehonite, the solubility decreases with temperature when the temperature is less than about 100 °C and increases when the temperature is higher than 100 °C. For lansfordite, the solubility increases with temperature from 0–200 °C.
- (2)
- The presence of CO2 in aqueous solution or gases phase will significantly enhance the dissolution of MgCO3 minerals.
- (3)
- For CO2 saturated solutions, the dissolution of MgCO3 minerals will increase the pH of the solutions at different temperature and pressure conditions. MgCO3 minerals can be treated as “buffer minerals”.
- (4)
- The influences of MgCO3 minerals on CO2 solubility are insignificant. However, the concentrations of carbon-bearing ions in the solutions are significantly increased by the dissolution of MgCO3 minerals.
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, H.; Liao, X.; Chen, Y.; Zhao, X. Sensitivity analysis of CO2 sequestration in saline aquifers. Pet. Sci. 2010, 7, 372–378. [Google Scholar] [CrossRef]
- Li, J.; Ahmed, R.; Li, X. Thermodynamic modeling of CO2-N2-O2-Brine-Carbonates in conditions from surface to high temperature and pressure. Energies 2018, 11, 2627. [Google Scholar] [CrossRef]
- Bénézeth, P.S.; Saldi, G.D.; Dandurand, J.-L.; Schott, J. Experimental determination of the solubility product of magnesite at 50 to 200 °C. Chem. Geol. 2011, 286, 21–31. [Google Scholar] [CrossRef]
- Li, J.; Li, X. Analysis of u-tube sampling data based on modeling of CO2 injection into CH4 saturated aquifers. Greenh. Gases: Sci. Technol. 2015, 5, 152–168. [Google Scholar] [CrossRef]
- Wagner, R. Ueber die löslichkeit einiger erd-und metallcarbonate in kohlensäurehaltigem wasser. J. Anal. Chem. 1867, 6, 233–238. [Google Scholar] [CrossRef]
- Cameron, F.K.; Briggs, L.J. Equilibrium between carbonates and bicarbonates in aqueous solution. J. Phys. Chem. 1901, 5, 537–555. [Google Scholar] [CrossRef]
- Wells, R.C. The solubility of magnesium carbonate in natural waters.2. J. Am. Chem. Soc. 1915, 37, 1704–1707. [Google Scholar] [CrossRef]
- Bär, O. Beitrag zum thema dolomitentstehung. Zentr. Mineral. Geol. Palaontol. Abt. A 1932, 1932, 46–62. [Google Scholar]
- Halla, F.; Chilingar, G.V.; Bissell, H.J. Thermodynamic studies on dolomite formation and their geologic implications: An interim report. Sedimentology 1962, 1, 296–303. [Google Scholar] [CrossRef]
- Berg, L.G.; Borisova, L.A. Solubility isotherms of the ternary systems Mg2+, Ca2+//CO32−, H2O, Na+, Ca2+//CO32−, H2O and Na+, Mg2+//CO32−, H2O at 25 °C and PCO2 = 1 atmosphere. Russ. J. Inorg. Chem. 1960, 5, 618–620. [Google Scholar]
- Christ, C.L.; Hostetler, P.B. Studies in the system MgO-SiO2-CO2-H2O (ii); the activity-product constant of magnesite. Am. J. Sci. 1970, 268, 439–453. [Google Scholar] [CrossRef]
- Cameron, F.K.; Seidell, A. The solubility of magnesium carbonate in aqueous solutions of certain electrolytes. J. Phys. Chem. 2002, 7, 578–590. [Google Scholar] [CrossRef]
- Engel, M. Sur la solubilité des sels en présence des acides, des bases et de sels. Ann. Chim. Phys. 1889, 17, 349–369. [Google Scholar]
- Königsberger, E.; Königsberger, L.-C.; Gamsjäger, H. Low-temperature thermodynamic model for the system Na2CO3−MgCO3−CaCO3−H2O. Geochim. Cosmochim. Acta 1999, 63, 3105–3119. [Google Scholar] [CrossRef]
- Kline, W.D. The solubility of magnesium carbonate (nesquehonite) in water at 25 °C and pressures of carbon dioxide up to one atmosphere1. J. Am. Chem. Soc. 1929, 51, 2093–2097. [Google Scholar] [CrossRef]
- Mitchell, A.E. Ccxii.—studies on the dolomite system.—Part ii. J. Chem. Soc. Trans. 1923, 123, 1887–1904. [Google Scholar] [CrossRef]
- Haehnel, O. Über die löslichkeit des magnesiumcarbonats in kohlensäurehaltigem wasser unter höheren kohlendioxyddrucken und über die eigenschaften solcher magnesiumbicarbonatlösungen. J. für Prakt. Chem. 1924, 108, 61–74. [Google Scholar] [CrossRef]
- Yanat’eva, O.K. Solubility of the system Ca, Mg-CO3, SO4-H2O at 25 °C and PCO2 of 0.0012 atm. Zh. Neorgan. Khim. 1957, 2, 2183–2187. [Google Scholar]
- Takahashi, G. Investigation on the synthesis of potassium carbonate by Mr. Engel. Bull. Imp. Hyg. Lab. (Tokyo) 1927, 29, 165–262. [Google Scholar]
- Ponizovskii, A.M.; Vladimirova, N.M.; Gordon-Yanovskii, F.A. The solubility relation in the system Na, Mg-Cl, HCO3-H2O at 0°C with carbon dioxide at 4 and 10 kg/cm2. Russ. J. Inorg. Chem. 1960, 5, 1250–1252. [Google Scholar]
- Yanat’eva, O.K.; Rassonskaya, I.S. Metastable equilibria and solid phases in the CaCO3-MgCO3-H2O system. Russ. J. Inorg. Chem. 1961, 6, 730–733. [Google Scholar]
- Harvie, C.E.; Weare, J.H. The prediction of mineral solubilities in natural waters: The Na-K-Mg-Ca-Cl-SO4-H2O system from zero to high concentration at 25 °C. Geochim. Cosmochim. Acta 1980, 44, 981–997. [Google Scholar] [CrossRef]
- Harvie, C.E.; Møller, N.; Weare, J.H. The prediction of mineral solubilities in natural waters: The Na-K-Mg-Ca-H-Cl-SO4-OH-HCO3-CO3-CO2-H2O system to high ionic strengths at 25 °C. Geochim. Cosmochim. Acta 1984, 48, 723–751. [Google Scholar] [CrossRef]
- Pitzer, K.S. Thermodynamics of electrolytes. I. Theoretical basis and general equations. J. Phys. Chem. 1973, 77, 268–277. [Google Scholar] [CrossRef]
- Pitzer, K.S.; Mayorga, G. Thermodynamics of electrolytes. II. Activity and osmotic coefficients for strong electrolytes with one or both ions univalent. J. Phys. Chem. 1973, 77, 2300–2308. [Google Scholar] [CrossRef]
- Pitzer, K.S.; Kim, J.J. Thermodynamics of electrolytes. IV. Activity and osmotic coefficients for mixed electrolytes. J. Am. Chem. Soc. 1974, 96, 5701–5707. [Google Scholar] [CrossRef]
- Pitzer, K.S. Thermodynamic properties of aqueous sodium chloride solutions. J. Phys. Chem. Ref. Data 1984, 13, 1–102. [Google Scholar] [CrossRef]
- Møller, N. The prediction of mineral solubilities in natural waters: A chemical equilibrium model for the Na-Ca-Cl-SO4-H2O system, to high temperature and concentration. Geochim. Cosmochim. Acta 1988, 52, 821–837. [Google Scholar] [CrossRef]
- Greenberg, J.P.; Møller, N. The prediction of mineral solubilities in natural waters: A chemical equilibrium model for the Na-K-Ca-Cl-SO4-H2O system to high concentration from 0 to 250 °C. Geochim. Cosmochim. Acta 1989, 53, 2503–2518. [Google Scholar] [CrossRef]
- Christov, C.; Moller, N. Chemical equilibrium model of solution behavior and solubility in the H-Na-K-OH-Cl-HSO4-SO4-H2O system to high concentration and temperature.11 associate editor: Wesolowski. D. J. Geochim. Cosmochim. Acta 2004, 68, 1309–1331. [Google Scholar] [CrossRef]
- Duan, Z.; Sun, R. An improved model calculating CO2 solubility in pure water and aqueous NaCl solutions from 273 to 533 K and from 0 to 2000 bar. Chem. Geol. 2003, 193, 257–271. [Google Scholar] [CrossRef]
- Duan, Z.; Li, D. Coupled phase and aqueous species equilibrium of the H2O–CO2–NaCl–CaCO3 system from 0 to 250 °C, 1 to 1000 bar with NaCl concentrations up to saturation of halite. Geochim. Cosmochim. Acta 2008, 72, 5128–5145. [Google Scholar] [CrossRef]
- Li, D.; Duan, Z. The speciation equilibrium coupling with phase equilibrium in the H2O–CO2–NaCl system from 0 to 250 °C, from 0 to 1000 bar, and from 0 to 5 molality of NaCl. Chem. Geol. 2007, 244, 730–751. [Google Scholar] [CrossRef]
- Li, J.; Duan, Z. A thermodynamic model for the prediction of phase equilibria and speciation in the H2O–CO2–NaCl–CaCO3–CaSO4 system from 0 to 250 °C, 1 to 1000 bar with NaCl concentrations up to halite saturation. Geochim. Cosmochim. Acta 2011, 75, 4351–4376. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. User’s guide to PHREEQC (Version 2)—A computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations. Water-Resour. Investig. Rep. 1999, 99, 312. [Google Scholar]
- Xu, T.; Spycher, N.; Sonnethal, E.; Zhang, G.; Zheng, L.; Pruess, K. TOUGHREACT Version 2.0: A simulator for subsurface reactive transport under non-isothermal multiphase flow conditions. Comput. Geosci. 2011, 37, 763–774. [Google Scholar] [CrossRef]
- Su, D.; Mayer, K.U.; MacQuarrie, K.T. Parallelization of MIN3P-THCm: A high performance computational framework for subsurface flow and reactive transport simulation. Environ. Model. Softw. 2017, 95, 271–289. [Google Scholar] [CrossRef]
- Wolery, T.J. EQ3/6 A Software Package for Geochemical Modeling (Version 05). Report Number: LLNL-CODE-638958. Available online: https://www.osti.gov//servlets/purl/1231666 (accessed on 28 November 2019).
- Zhu, C.; Burden, D.S. Mineralogical compositions of aquifer matrix as necessary initial conditions in reactive contaminant transport models. J. Contam. Hydrol. 2001, 51, 145–161. [Google Scholar] [CrossRef]
- Dobson, P.; Salah, S.; Spycher, N.; Sonnenthal, E.L. Simulation of Water-Rock interaction in the Yellowstone Geothermal system using TOUGHREACT. Geochermics 2004, 33, 493–502. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Shi, W.; Li, J.; Deng, G.; Chang, Y.; Li, Z. Application of geochemical code EQ3/6 to leaching technique of hard rock uranium deposit. J. East. China Geol. Inst. 1997, 20, 362–367. [Google Scholar]
- Computer Modeling Group (CMG), User Technical Manual; Computer Modelling Group Ltd.: Calgary, Canada, 2016.
- Wei, L. Sequential Coupling of Geochemical Reactions With Reservoir Simulations for Waterflood and EOR Studies. SPE J. 2012, 17, 469–484. [Google Scholar] [CrossRef]
- Adegbite, J.O.; Al-Shalabi, E.W.; Ghosh, B. Modeling the Effect of Engineered Water Injection on Oil Recovery from Carbonate Cores. In Proceedings of the SPE International Conference on Oilfield Chemistry, Montgomery, TX, USA, 3–5 April 2017. [Google Scholar] [CrossRef]
- Li, X.; Wei, L.; Zhang, H. Improving Reactive Transport Modeling Predictivity for ASP Flooding Simulations. In Proceedings of the SPE EOR Conference at Oil and Gas West Asia, Muscat, Oman, 21–23 March 2016; pp. 1–20. [Google Scholar] [CrossRef]
- Li, J.; Wei, L.; Li, X. An improved cubic model for the mutual solubilities of CO2–CH4–H2S–brine systems to high temperature, pressure and salinity. Appl. Geochem. 2015, 54, 1–12. [Google Scholar] [CrossRef]
- Appelo, C.A.J.; Parkhurst, D.L.; Post, V.E.A. Equations for calculating hydrogeochemical reactions of minerals and gases such as CO2 at high pressures and temperatures. Geochim. Cosmochim. Acta 2014, 125, 49–67. [Google Scholar] [CrossRef]
- Helgeson, H.C.; Kirkham, D.H.; Flowers, G.C. Theoretical prediction of the thermodynamic behavior of aqueous electrolytes at high pressures and temperatures: Calculation of activity coefficients, osmotic coefficients, and apparent molal and standard and relative partial modal properties to 600 °C and 5 Kb. Am. J. Sci. 1981, 281, 1249–1516. [Google Scholar] [CrossRef]
- Duan, Z.; Sun, R.; Zhu, C.; Chou, I.M. An improved model for the calculation of CO2 solubility in aqueous solutions containing Na+, K+, Ca2+, Mg2+, Cl−, and SO42−. Mar. Chem. 2006, 98, 131–139. [Google Scholar] [CrossRef]
- Peng, D.-Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Michelsen, M.L.; Mollerup, J.M. Thermodynamic models: Fundamentals & Computational Aspects, 2nd ed.; TIE-LINE Publications: Herning, Denmark, 2007. [Google Scholar]
- Visscher, A.D.; Vanderdeelen, J.; Königsberger, E.; Churagulov, B.R.; Ichikuni, M.; Tsurumi, M. Iupac-nist solubility data series. 95. Alkaline earth carbonates in aqueous systems. Part 1. Introduction, be and mg. J. Phys. Chem. Ref. Data. 2012, 41, 013105. [Google Scholar] [CrossRef] [Green Version]








| Reaction | A0 | A1 | A2 | A3 | A4 | A5 | |
|---|---|---|---|---|---|---|---|
| (7) | 7.267 | −0.033918 | −1476.604 | 0 | 0 | 0 | 28.3 |
| (8) | −6.008 | −0.00688 | 873.4 | 0 | 0 | 0 | 74.789 |
| (9) | −4.85 | 0 | 0 | 0 | 0 | 0 | 100.81 |
| (10) | −0.5837 | −9.2067 | −2.3984 | −0.03 | 0 | 0 | Helgson et al. [48] |
| (11) a | −11.809 | 0 | 0 | 0 | 0 | 0 | 0 |
| , , , , , , , , , , , , , , | Li and Duan [33], Duan and Li [32] |
| , , , , , , , , , , , , , , | Greenburg et al. [29]; Moller 1988 [28] Christov and Moller [30]; |
| , , , , , | Set to 0.0 |
| , , , | Duan and Sun [31]; Duan et al. [49] |
| Reference | Data Points | T (°C) | PCO2 (atm) | AAD% |
|---|---|---|---|---|
| Wells [7] | 1 | 20 | 0.00029 | 3.8 |
| Bar [8] | 2 | 18 | 0.00031 | 13.3 |
| Halla [9] | 2 | 25–38.8 | 0.932–0.955 | 8.75 |
| Berg and Borisova [10] | 1 | 25 | 0.987 | 11.6 |
| Christ and Hostetler [11] | 3 | 90.3–91 | 0.0274–0.312 | 9.61 |
| Benezeth et al. [3] | 11 | 120–200 | 12–30 | 13.17 |
| Reference | Data Points | T (°C) | PCO2 (atm) | AAD% |
|---|---|---|---|---|
| Engel [13] | 14 | 3.5–50 | 0.878–5.986 | 2.09 |
| Wells [7] | 2 | 20 | 0.00029 | 9.41 |
| Mitchell [16] | 6 | 25 | 6–21 | 5.22 |
| Haehnel [17] | 12 | 5–60 | 1 | 1.13 |
| Yanat and Rassonskaya [21] | 10 | 0–53.5 | 1 | 2.91 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Li, X. Numerical Modeling of CO2, Water, Sodium Chloride, and Magnesium Carbonates Equilibrium to High Temperature and Pressure. Energies 2019, 12, 4533. https://doi.org/10.3390/en12234533
Li J, Li X. Numerical Modeling of CO2, Water, Sodium Chloride, and Magnesium Carbonates Equilibrium to High Temperature and Pressure. Energies. 2019; 12(23):4533. https://doi.org/10.3390/en12234533
Chicago/Turabian StyleLi, Jun, and Xiaochun Li. 2019. "Numerical Modeling of CO2, Water, Sodium Chloride, and Magnesium Carbonates Equilibrium to High Temperature and Pressure" Energies 12, no. 23: 4533. https://doi.org/10.3390/en12234533
APA StyleLi, J., & Li, X. (2019). Numerical Modeling of CO2, Water, Sodium Chloride, and Magnesium Carbonates Equilibrium to High Temperature and Pressure. Energies, 12(23), 4533. https://doi.org/10.3390/en12234533