Study on Dust Deposition Mechanics on Solar Mirrors in a Solar Power Plant
Abstract
:Highlights
- The effects of the environmental conditions, solar mirror conditions, and particle self-factors on dust deposition weight have been systematic studied.
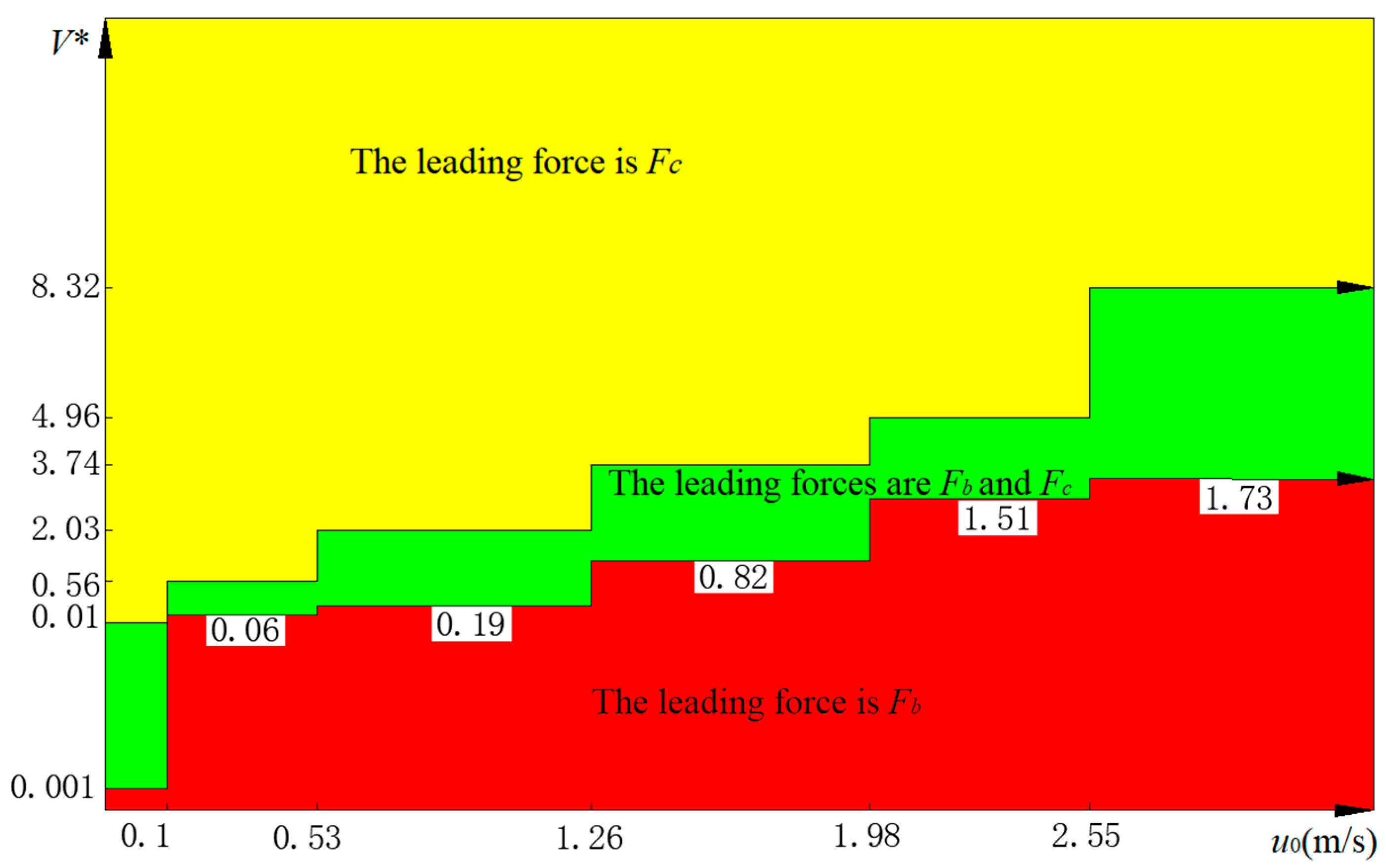
- The leading forces during the motion process of dust particles are Fc or Fb based on Equations (14)–(16). When the leading forces are Fc, or Fc and Fb, the dust particles will be deposited on the solar mirror.
1. Introduction
2. Model Description
2.1. Particle Motion Balance
2.2. Model Assumptions and Simulation Conditions
3. Results and Discussion
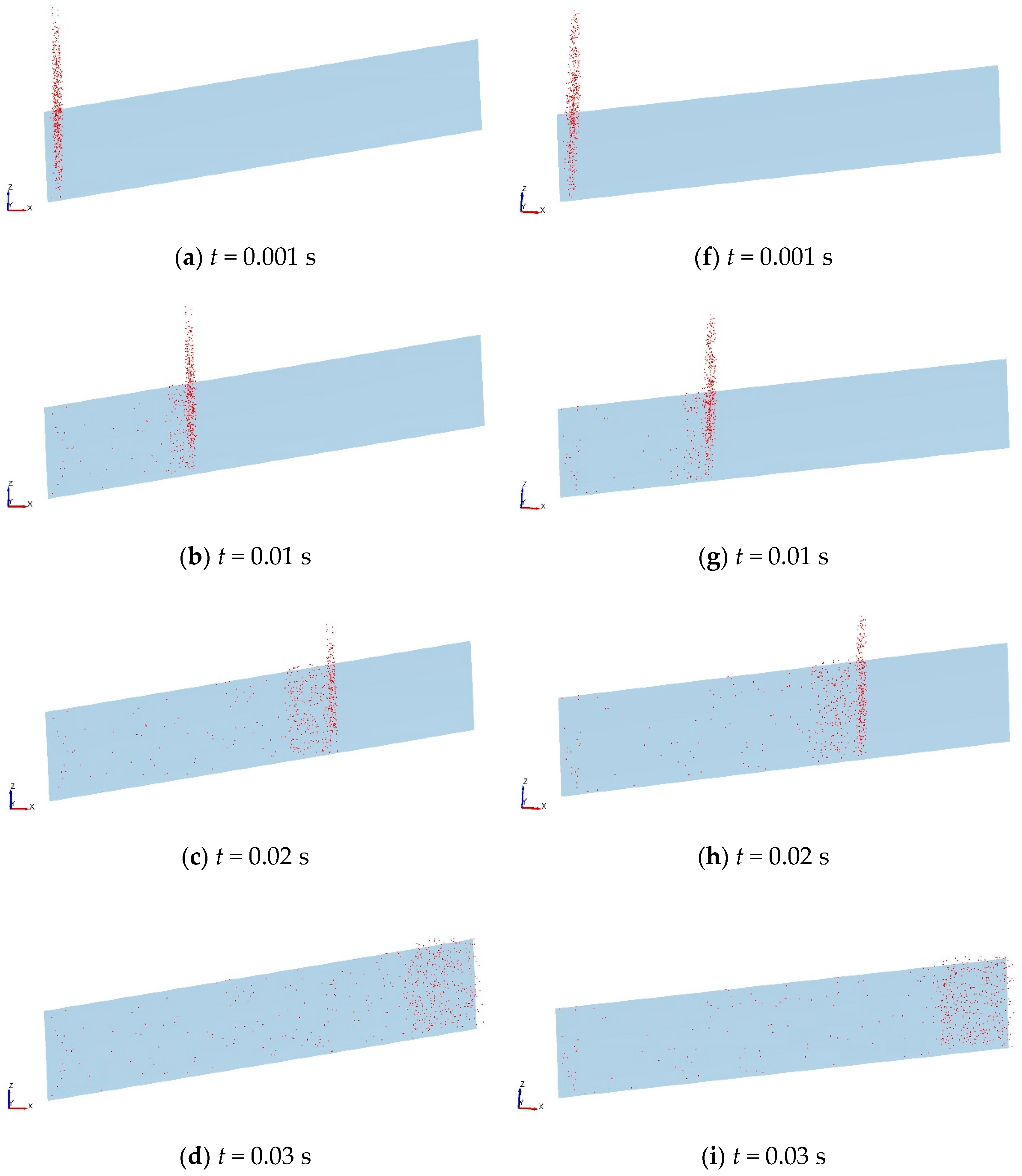
3.1. Motion Characteristics of Dust Particle
3.1.1. Motion Behaviors of Dust Particle
3.1.2. Analysis of Forces Acting on Dust Particle
3.2. Dust Deposition Weight on Solar Mirror
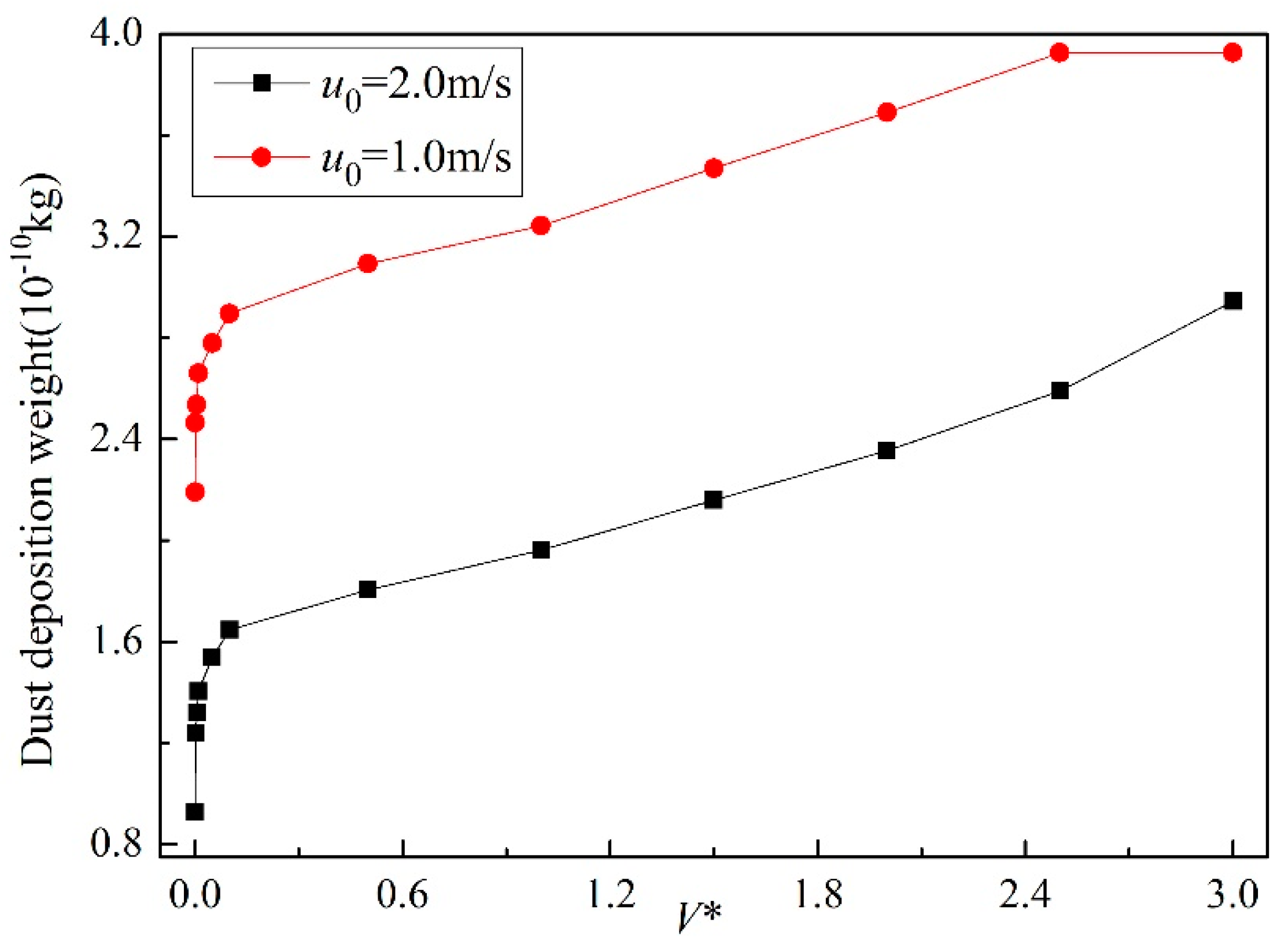
3.2.1. Environmental Condition (EC)
3.2.2. Solar Mirror Conditions (SMC)
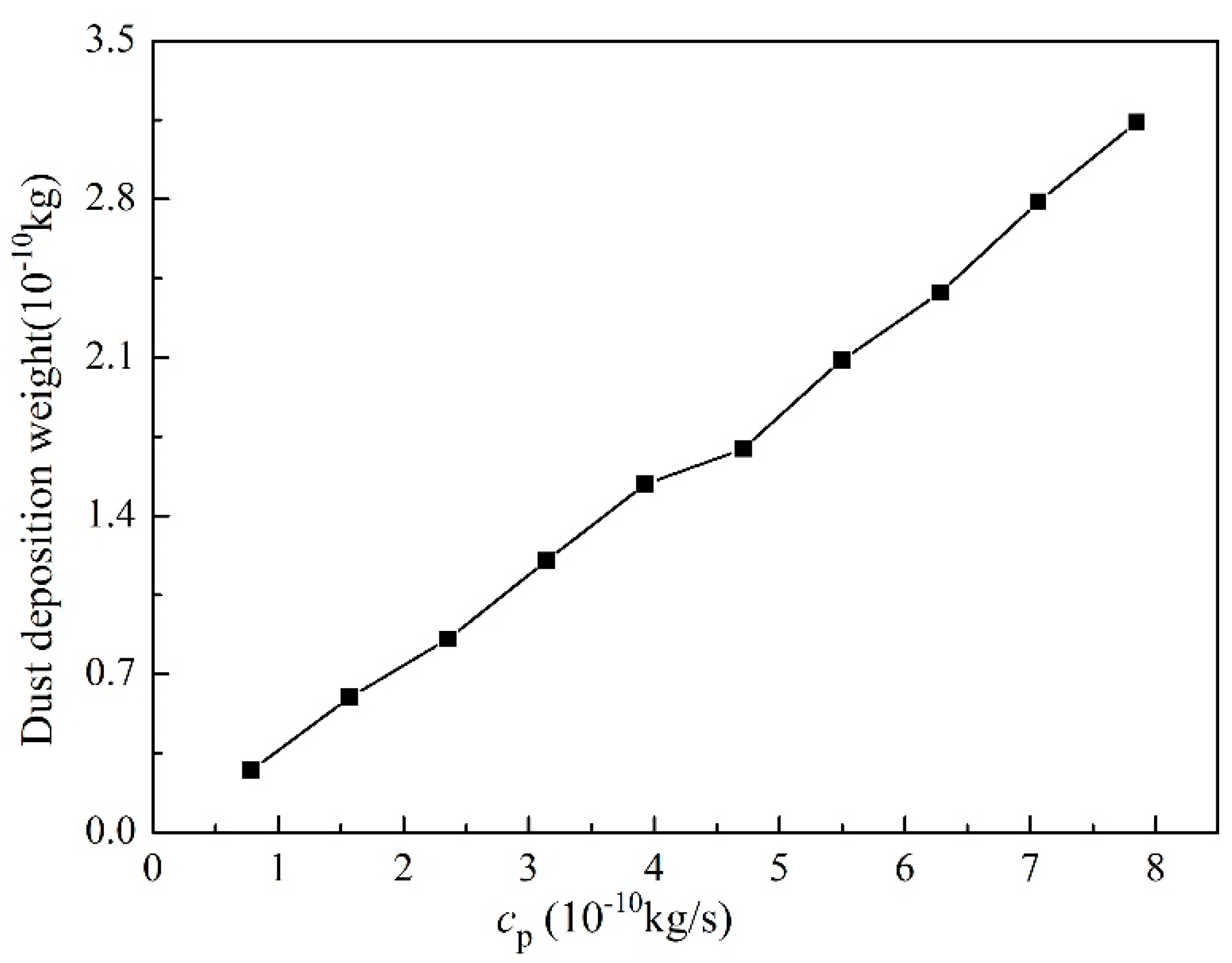
3.2.3. Particle Self-Factors (PSF)
3.3. Comparison of Dust Deposition Weight Among EC, SMC, and PSF
4. Conclusions
- No matter whether the mirror is clear or dusty, the phenomenon that a considerable number of dust particles are deposited on the solar mirror can be found. The dust deposition weight will be underestimated without the consideration of the liquid bridge force (Fc).
- Dust particles after particle collision either immediately adhere to the mirror, rebound and finally flow away from the mirror, remain stationary after making some relative motion, or glide for some distance and finally stay on the mirror or leave from the system. Whether dust particles are deposited on the solar mirror or not depends on the leading force. The leading forces are the force Fc or the contact force (Fb).
- Dust deposition weight on solar mirror can be controlled by altering the environmental condition, solar mirror conditions, and particle self-factors. The reasonable design of θ, increasing the parameter u0, and decreasing the degree of dust, V*, dp, and cp, can make more dust particles flow away from the solar mirror. Meanwhile, in essence, dust deposition weight on solar mirrors decreases when decreasing the leading force Fc or increasing the leading force Fb.
- The leading forces can be different at different ranges of u0 and V*, based on Equations (14)–(16). The lower and upper limit value of V* can be found at a corresponding range of u0 when the unique leading force is Fc or Fb. When the leading forces are Fc, or Fc and Fb, the dust particles will be deposited on the solar mirror.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbol | Comment | Unit |
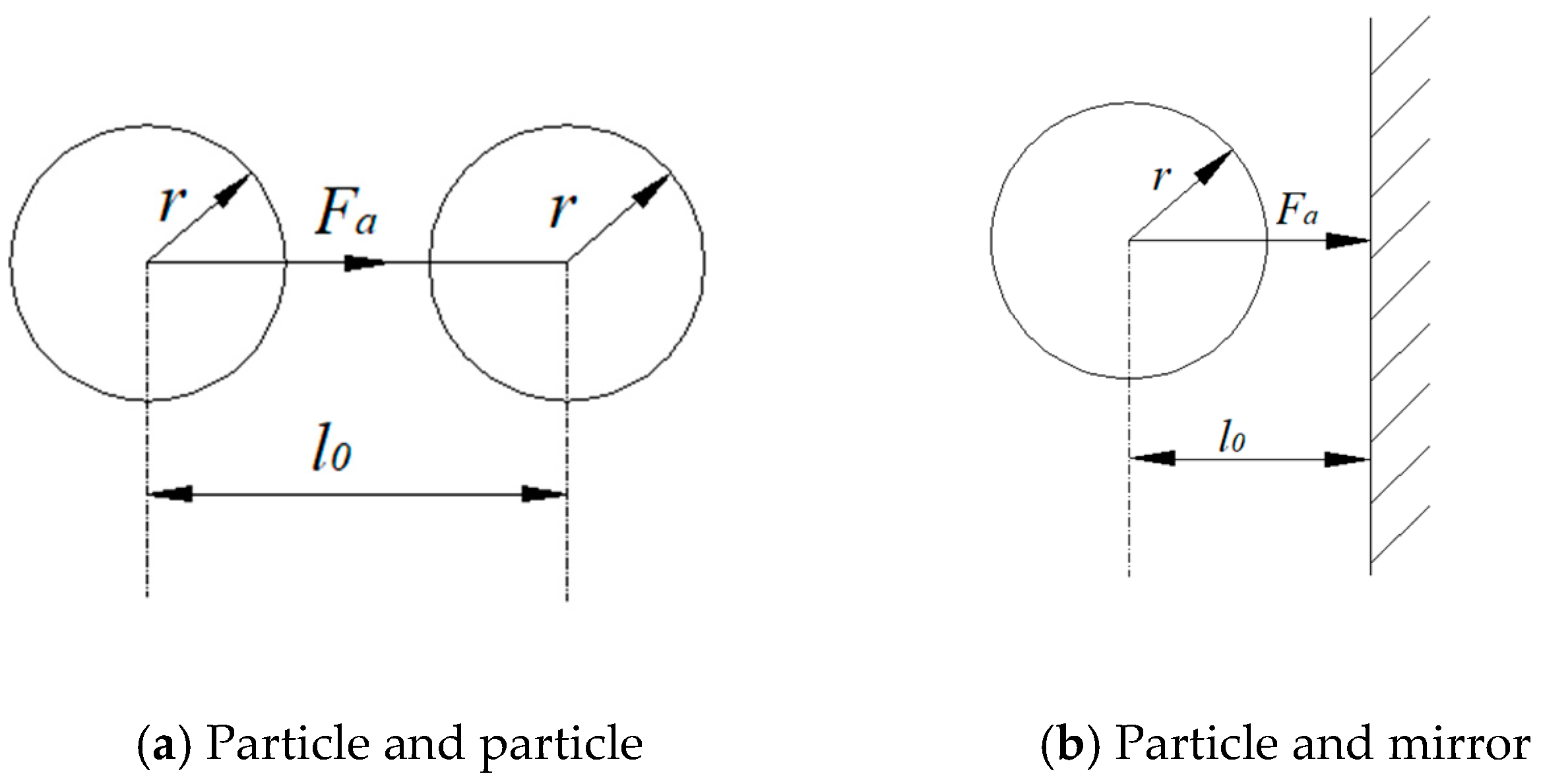
| Fa | Van Der Waals force | N |
| Fg | Gravity force | N |
| Fe | Electrostatic force | N |
| Fd | Buoyant force | N |
| Fc | Liquid bridge force | N |
| Fb | Contact force | N |
| r | Radius of dust particle | m |
| ϖ | Lifshitz constant | - |
| l0 | Average distance between molecules | m |
| m | Dust particle mass | kg |
| g | Gravitational acceleration | m2/s |
| V* | Dimensionless liquid bridge volume | - |
| θ | Inclination angle of solar mirror | ° |
| Fchs | Electrostatic image force | N |
| Fchl | Electrical double layer force | N |
| Fche | Electrostatic image force | N |
| Q | Electric charge of dust particle | C |
| ε | Dielectric constant between dielectrics | - |
| ε0 | Absolute dielectric constant | - |
| Fbn | The normal component of Fb | N |
| Fbt | The tangential component of Fb | N |
| Fbnij | Fbn between particles “i” and “j” | N |
| Fbtij | Fbt between particles “i” and “j” | N |
| α | Normal displacement | m |
| δ | Tangential displacement | m |
| kn | Spring constant in normal direction | - |
| kt | Spring constant in tangential direction | - |
| cn | Damping coefficient in normal direction | - |
| ct | Damping coefficient in tangential direction | - |
| μs | Friction coefficient | - |
| n | Vector from the particles “i” to the particles “j” | - |
| vct | Sliding velocity vector | m/s |
| Fx | Other forces acting on the dust particle | N |
| u0 | Wind speed | m/s |
| vij | Relative velocity between particles “i” and “j” | m/s |
| U | Contact potential difference | V |
| σ | Surface charge density of the solar mirror | C |
| γ | Liquid surface tension | Pa |
| t | Time | s |
| dp | Diameter of dust particle | m |
| ρp | Density of dust particle | kg/m3 |
| cp | Initial concentration of dust particle | kg/s |
| EC | Environmental condition | - |
| SMC | Solar mirror conditions | - |
| V | Dust particle volume | m3 |
| ρair | Air density | kg/m3 |
| PSF | Particle self-factors | - |
References
- Mekhilef, S.; Saidur, R.; Safari, A. A review on solar energy use in industries. Renew. Sustain. Energy Rev. 2011, 15, 1777–1790. [Google Scholar] [CrossRef]
- Yaghoubi, M.; Niknia, I.; Kanaan, P.; Mahmoodpoor, A.R. Experimental study of dust deposition effect on the performances of parabolic trough collectors. In Proceedings of the Solar PACES 2011: 17th Solar Paces Conference, Granada, Spain, 20–23 September 2011. [Google Scholar]
- Şahin, A.D. A new formulation for solar irradiation and sunshine duration estimation. Int. J. Energy Res. 2007, 31, 109–118. [Google Scholar] [CrossRef]
- Sansoni, P.; Fontani, D.; Fransini, F.; Giannuzzi, A.; Sani, E.; Mercatelli, L.; Jafrancesco, D. Optical collection efficiency and orientation of a solar trough medium-power plant installed in Italy. Renew. Energy 2011, 36, 2341–2347. [Google Scholar] [CrossRef]
- Ahmed, O.K.; Mohammed, Z.A. Dust effect on the performance of the hybrid PV/Thermal collector. Therm. Sci. Eng. Prog. 2017, 3, 114–122. [Google Scholar] [CrossRef]
- Ajadi, D.A.; Fajinmi, G.R.; Sanusi, Y.K. Effect of dust on the Performance of a locally Designed Solar Dryer. Res. J. Appl. Sci. 2007, 2, 251–254. [Google Scholar]
- Jing, Z.; Zhiping, W.; Kezhen, W.; Jianbo, L. Dust effect on thermal performance of flat plate solar collectors. J. Sol. Energy Eng. 2015, 137, 14502. [Google Scholar] [CrossRef]
- Ahmed, O.K. Effect of dust on the performance of solar water collectors in Iraq. Int. J. Renew. Energy Dev. 2016, 5, 65–72. [Google Scholar] [CrossRef]
- Yadav, N.K.; Pala, D.; Chandra, L. On the understanding and analyses of dust deposition on heliostat. Energy Proced. 2014, 57, 3004–3013. [Google Scholar] [CrossRef]
- Kaldellis, J.K.; Kokala, A. Quantifying the decrease of the photovoltaic panels’ energy yield due to phenomena of natural air pollution disposal. Energy 2010, 35, 4862–4869. [Google Scholar] [CrossRef]
- Imad, J.K.; Imad, J.M.; Imad, M.M. Periodic Cleaning Effect on the Output Power of Solar Panels; 2nd Scientific Conference; Karbala university: Karbala, Iraq, 2014; pp. 116–122. [Google Scholar]
- Niknia, I.M.; Yaghoubi, M.; Hessami, R. A novel experimental method to find dust deposition effect on the performance of parabolic trough solar collectors. Int. J. Environ. Stud. 2012, 69, 233–252. [Google Scholar] [CrossRef]
- Kaldellis, J.K.; Fragos, P.; Kapsali, M.; Zafirakis, D.; Spyropoulos, G. Dust deposition impact on photovoltaic-assisted water pumping systems. In Proceedings of the WREC XI: 11th World Renewable Energy Congress, Abu Dhabi, UAE, 25–30 September 2010; pp. 1117–1122. [Google Scholar]
- Sayyah, A.; Horenstein, M.N.; Mazumder, M.K. Energy yield loss caused by dust deposition on photovoltaic panels. Sol. Energy 2014, 107, 576–604. [Google Scholar] [CrossRef]
- Elminir, H.K.; Ghitas, A.E.; Hamid, R.H.; El-Hussainy, F.; Beheary, M.M.; Abdel-Moneim, K.M. Effect of dust on the transparent cover of solar collectors. Energy Convers. Manag. 2006, 47, 3192–3203. [Google Scholar] [CrossRef]
- Garcı´a, M.; Marroyo, L.; Lorenzo, E.; Pe´rez, M. Soiling and otheroptical losses in solar-tracking PV plants in Navarra. Progr. Photovolt. Res. Appl. 2011, 19, 211–217. [Google Scholar] [CrossRef]
- Hanai, T.A.; Hashim, R.B.; Chaar, L.E.; Lamont, L.A. Environmental effects on a grid connected 900 W photovoltaic thin-film amorphous silicon system. Renew. Energy 2011, 36, 2615–2622. [Google Scholar] [CrossRef]
- Appels, R.; Muthirayan, B.; Beerten, A.; Paesen, R.; Driesen, J.; Poortmans, J. The effect of dust deposition on photovoltaic modules. In Proceedings of the 38th IEEE Photovoltaic Specialists Conference (PVSC), Austin, TX, USA, 3–8 June 2011; pp. 001886–001889. [Google Scholar]
- AlBusairi, H.A.; Mo¨ller, H.J. Performance evaluation of CdTe PV modules under natural outdoor conditions in Kuwait. In Proceedings of the 25th European Photovoltaic Solar Energy Conference and Exhibition/5th World Conference on Photovoltaic Energy Conversion, Valencia, Spain, 6–10 September 2010; pp. 3468–3470. [Google Scholar]
- Lu, H.; Zhang, L.Z. Numerical study of dry deposition of monodisperse and polydisperse dust on building-mounted solar photovoltaic panels with different roof inclinations. Sol. Energy 2018, 176, 535–544. [Google Scholar] [CrossRef]
- Lu, J.; Hajimirza, S. Optimizing sun-tracking angle for higher irradiance collection of PV panels using a particle-based dust accumulation model with gravity effect. Sol. Energy 2017, 158, 71–82. [Google Scholar] [CrossRef]
- Lu, H.; Lu, L.; Wang, Y. Numerical investigation of dust pollution on a solar photovoltaic (PV) system mounted on an isolated building. Appl. Energy 2016, 180, 27–36. [Google Scholar] [CrossRef]
- Boddupalli, N.; Goenka, V.; Chandra, L. Fluid Flow Analysis Behind Heliostat Using LES and RANS: A Step Towards Optimized Field Design in Desert Regions. In Proceedings of the 22nd International Conference on Concentrating Solar Power and Chemical Energy Systems (SOLARPACES), Abu Dhabi, UAE, 11–14 October 2016. [Google Scholar]
- Brosh, T.; Levy, A. Modeling of Heat Transfer in Pneumatic Conveyer Using a Combined DEM-CFD Numerical Code. Dry. Technol. 2010, 28, 155–164. [Google Scholar] [CrossRef]
- Sumol, S.H.; Thanit, S.; Mana, A. Investigation of Temperature Distribution and Heat Transfer in Fluidized Bed Using a Combined CFD-DEM Model. Dry. Technol. 2011, 29, 697–708. [Google Scholar]
- Xu, B.H.; Yu, A.B. Numerical simulation of the gas-solid flow in a fluidized bed by combining discrete particle method with computational fluid dynamics. Chem. Eng. Sci. 1997, 52, 2785–2809. [Google Scholar] [CrossRef]
- Liu, X.; Yue, S.; Lu, L.; Gao, W.; Li, J. Numerical simulations of gas-solid two-phase impinging streams with dynamic inlet flow. Energies 2018, 11, 1913. [Google Scholar] [CrossRef]
- Zhong, W.; Xiong, Y.; Yuan, Z.; Zhang, M. DEM simulation of gas-solid flow behaviors in spout-fluid bed. Chem. Eng. Sci. 2006, 61, 1571–1584. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I.E.; Lifshitz, E.M.; Pitaevskii, L.P. The general theory of van der Waals forces. Adv. Phys. 1961, 10, 165–209. [Google Scholar] [CrossRef]
- Khomwachirakul, P.; Devahastin, S.; Swasdisevi, T.; Soponronnarit, S. Simulation of flow and drying characteristics of high-moisture particles in an impinging stream dryer via CFD-DEM. Dry. Technol. 2016, 34, 403–419. [Google Scholar] [CrossRef]
- Mikami, T.; Kamiya, H.; Horio, M. Numerical simulation of cohesive powder behavior in a fluidized bed. Chem. Eng. Sci. 1998, 53, 1927–1940. [Google Scholar] [CrossRef]
- Bowling, R.A. An analysis of particle adhesion on semiconductor surfaces. J. Electrochem. Soc. 1985, 132, 2208–2214. [Google Scholar] [CrossRef]
- Behrens, S.H.; Grier, D.G. The charge of glass and silica surfaces. J. Chem. Phys. 2001, 115, 6716–6721. [Google Scholar] [CrossRef] [Green Version]
- Meng, G. Research on Mechanism of Dust Particle Adhesion and Removal from Solar Panel Surface in Desert Area. Master’s Thesis, Qinghai University, Qinghai, China, 2015. [Google Scholar]










| Parameters | Discrete Element Method (DEM) |
|---|---|
| Poisson’s ratio (dust particle/solar mirror) | 0.4/0.23 |
| Shear modulus (dust particle/solar mirror) | 2 × 106/2 × 1010 |
| Density of the dust particle (ρp) | 1400 kg/m3 |
| Density of the solar mirror | 2458 |
| Coefficient of recovery (dust particle/solar mirror) | 0.5/0.4 |
| Rolling friction coefficient (dust particle/solar mirror) | 0.5/0.7 |
| Static friction coefficient (dust particle/solar mirror) | 0.1/0.5 |
| Liquid surface tension | 0.07275 N/m |
| Liquid viscosity | 0.03 Pa·s |
| Solid-liquid contact angle | 0 |
| Surface conditions of solar mirror | Clear or dusty solar mirror |
| Incline angle of solar mirror (θ) | 10°–60° |
| Wind speed (u0) | 2–10 m/s |
| Dimensionless liquid bridge volume (V*) | 0.001–2.64 |
| Diameter of dust particle (dp) | 1.0 × 10−5−1 × 10−4 m |
| Initial concentration of dust particle (cp) | 7.85 × 10−11−7.85 × 10−10 kg/s |
| Conditions | Leading Force | Final Motion State |
|---|---|---|
| Equation (14) | Fc | On the solar mirror |
| Equation (16) | Fc and Fb | On the solar mirror |
| Equation (15) | Fb | Off the solar mirror |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Yue, S.; Lu, L.; Li, J. Study on Dust Deposition Mechanics on Solar Mirrors in a Solar Power Plant. Energies 2019, 12, 4550. https://doi.org/10.3390/en12234550
Liu X, Yue S, Lu L, Li J. Study on Dust Deposition Mechanics on Solar Mirrors in a Solar Power Plant. Energies. 2019; 12(23):4550. https://doi.org/10.3390/en12234550
Chicago/Turabian StyleLiu, Xueqing, Song Yue, Luyi Lu, and Jianlan Li. 2019. "Study on Dust Deposition Mechanics on Solar Mirrors in a Solar Power Plant" Energies 12, no. 23: 4550. https://doi.org/10.3390/en12234550
APA StyleLiu, X., Yue, S., Lu, L., & Li, J. (2019). Study on Dust Deposition Mechanics on Solar Mirrors in a Solar Power Plant. Energies, 12(23), 4550. https://doi.org/10.3390/en12234550




