Assessing the Performance of the European Natural Gas Network for Selected Supply Disruption Scenarios Using Open-Source Information
Abstract
1. Introduction
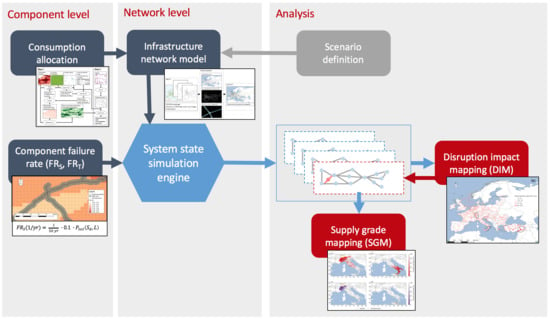
2. Materials and Methods
2.1. System and Data
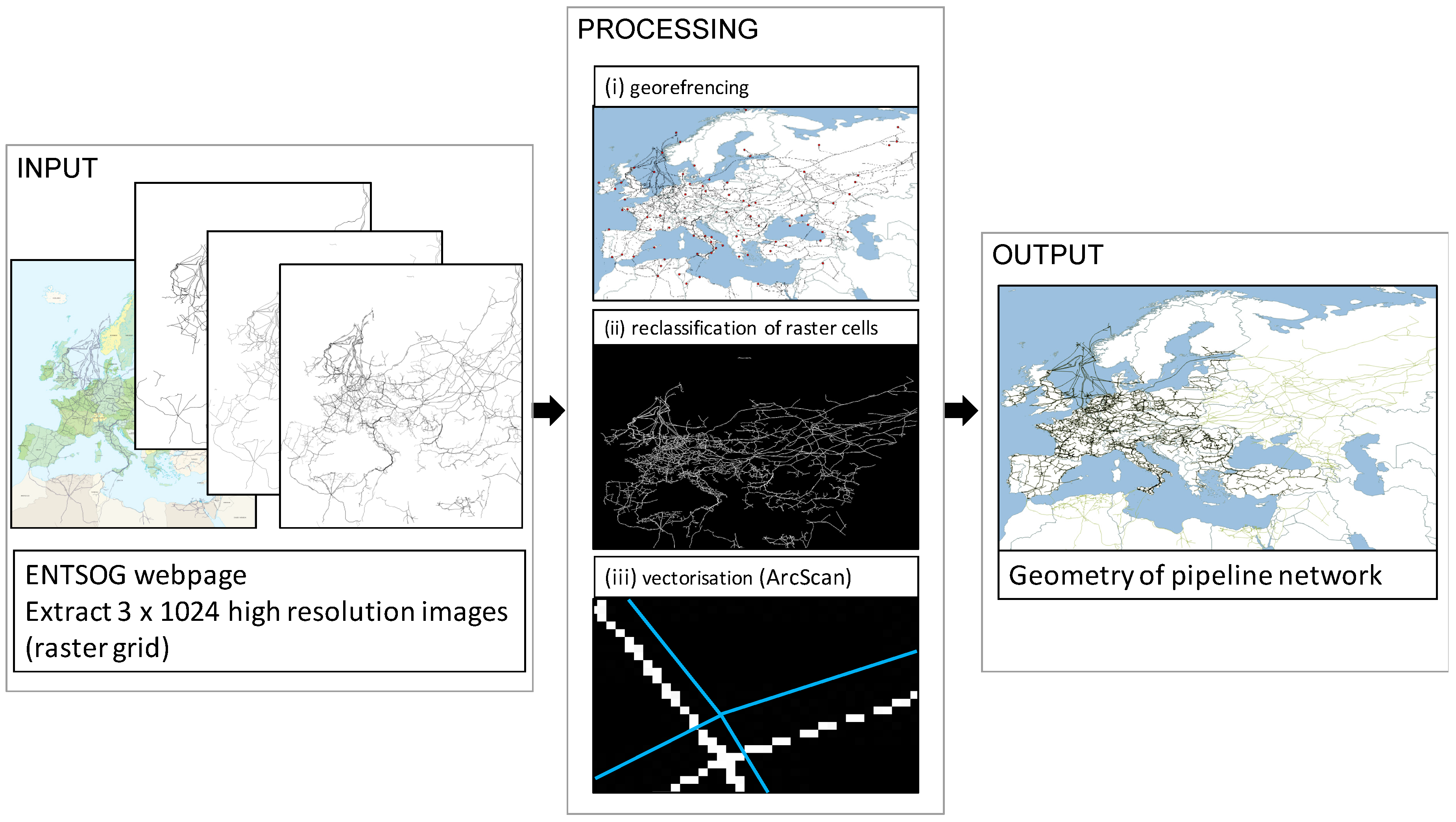
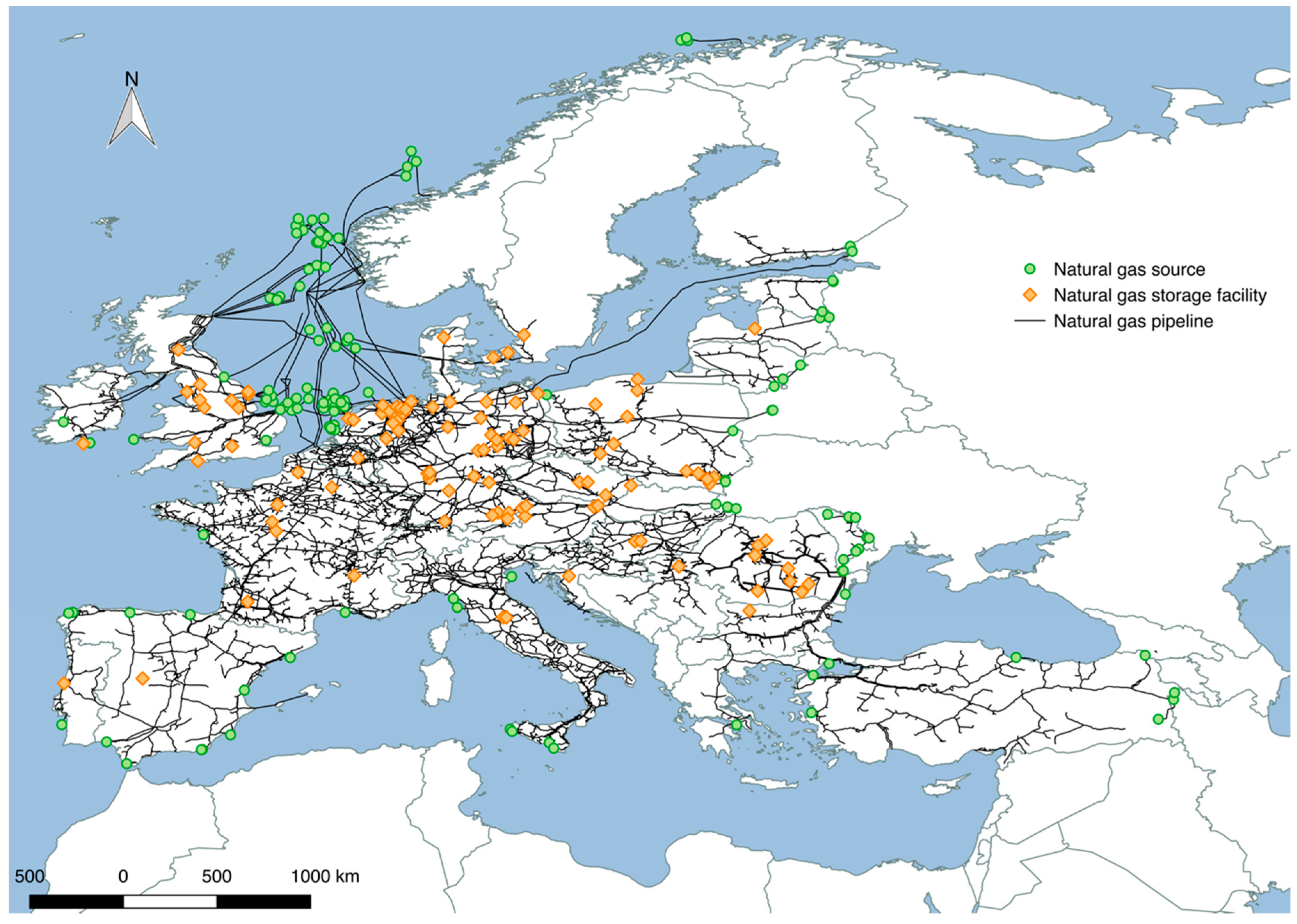
2.1.1. Infrastructure Network Data
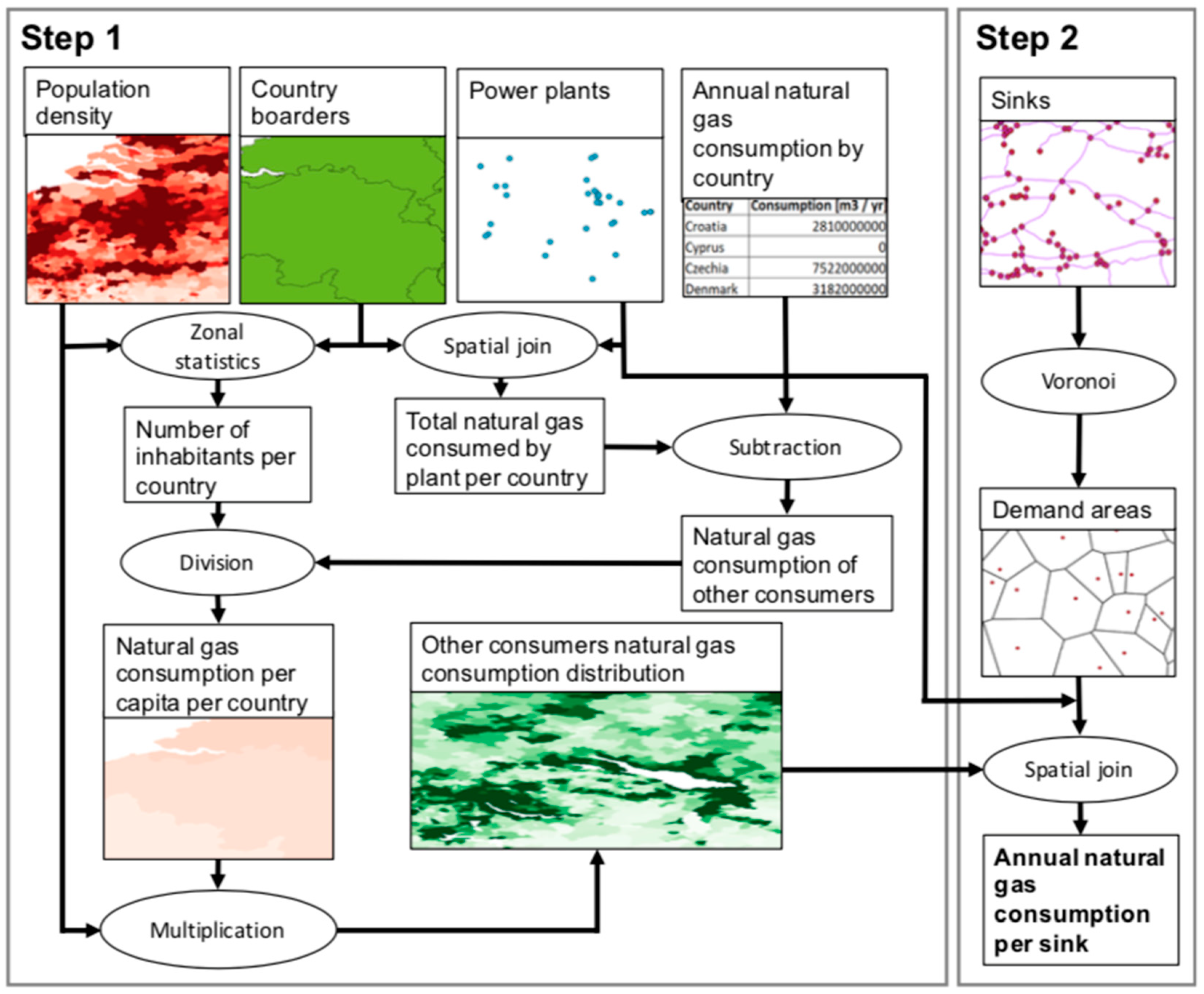
2.1.2. Data to Allocate the Natural Gas Consumption
2.1.3. Natural Hazard and Technical Failure Data
2.2. Methods
2.2.1. Consumption Allocation
2.2.2. Infrastructure Network Model
2.2.3. Component Failure Rate
2.2.4. System State Simulation Engine
2.2.5. Disruption Impact and Supply Grade Mapping
3. Results and Discussion
3.1. Disruption Impact Mapping
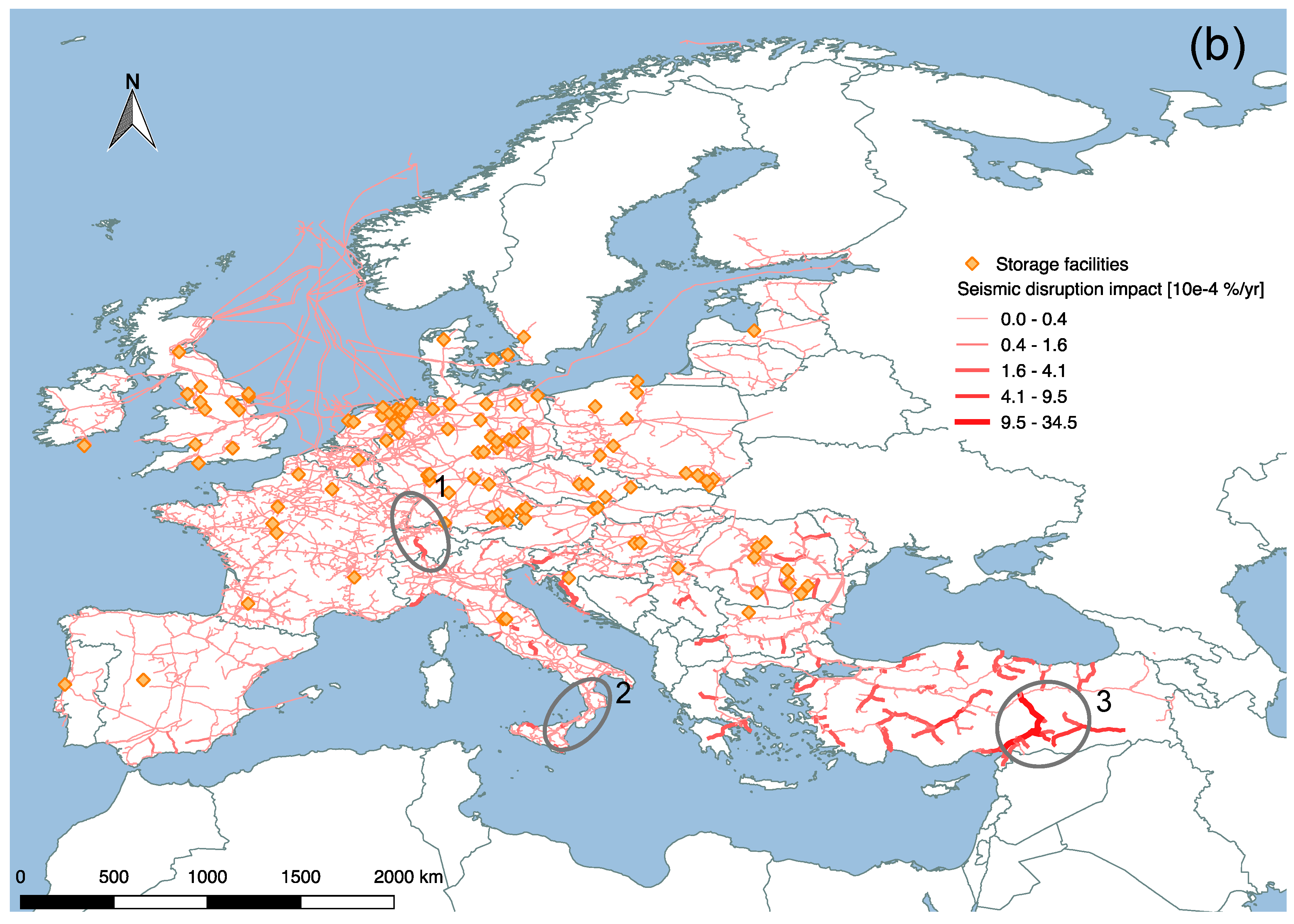
3.1.1. Seismic Disruption Impact Mapping
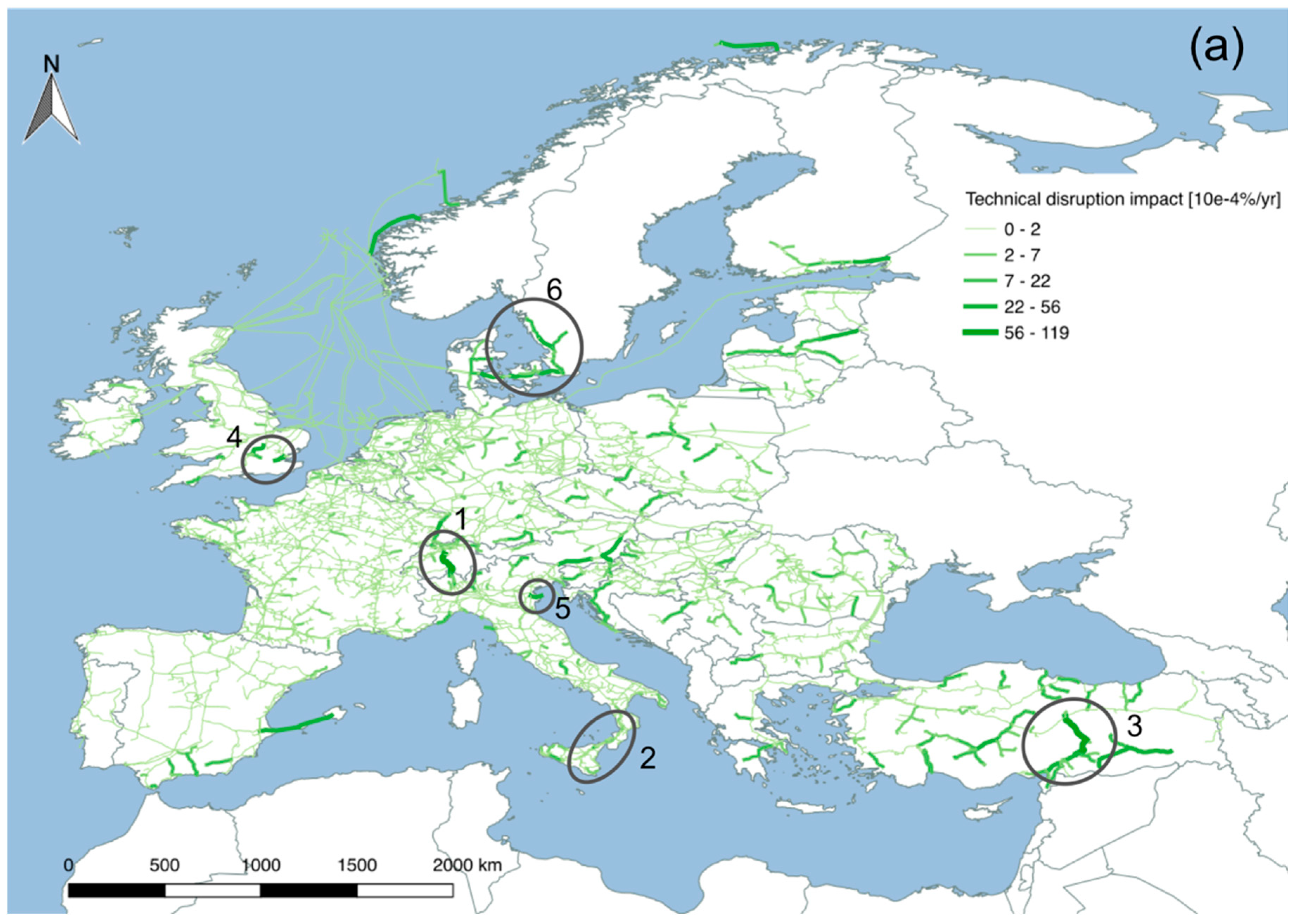
3.1.2. Technical Failure Disruption Impact Mapping
3.1.3. Comparison of Seismic and Technical Failure Rates
3.2. Supply Grade Mapping
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| API | Application Programming Interface |
| DIM | Disruption Impact |
| E-PRTR | European Pollutant Release and Transfer Register |
| ENSAD | Energy-related Severe Accident Database |
| ENTSOG | European Network of Transmission System Operators for Gas |
| EGIG | European Gas pipeline Incident data Group |
| ESHM13 | European Seismic Hazard Model |
| FRS | Seismic hazard failure rate |
| FRT | Technical failure rate |
| GIS | Geographic Information Systems |
| IEA | International Energy Agency |
| LNG | Liquefied Natural Gas |
| OC | Other Consumers |
| PGA | Peak Ground Acceleration |
| PGV | Peak Ground Velocity |
| PGM | Peak Ground Motion |
| PSI | Paul Scherrer Institute |
| SGM | Supply grade |
References
- IEA. World Energy Statistics and Balances; International Energy Agency: Paris, France, 2017. [Google Scholar]
- IEA. Outlook for Natural Gas; International Energy Agency (IEA): Paris, France, 2017. [Google Scholar]
- Carvalho, R.; Buzna, L.; Bono, F.; Masera, M.; Arrowsmith, D.K.; Helbing, D. Resilience of natural gas networks during conflicts, crises and disruptions. PLoS ONE 2014, 9, e90265. [Google Scholar] [CrossRef] [PubMed]
- Austvik, O.G. The energy union and security-of-gas supply. Energy Policy 2016, 96, 372–382. [Google Scholar] [CrossRef]
- Tirone, J.; Wabl, M. Austrian gas pipeline explosion disrupts key EU supply hub. In Bloomberg Markets; Bloomberg: New York, NY, USA, 2017. [Google Scholar]
- Carvalho, R.; Buzna, L.; Bono, F.; Gutiérrez, E.; Just, W.; Arrowsmith, D. Robustness of trans-European gas networks. Phys. Rev. E 2009, 80, 016106. [Google Scholar] [CrossRef] [PubMed]
- Poljansek, K.; Bono, F.; Gutiérrez, E. Seismic risk assessment of interdependent critical infrastructure systems: The case of european gas and electricity networks. Earthq. Eng. Struct. Dyn. 2012, 41, 61–79. [Google Scholar] [CrossRef]
- Poljansek, K.; Bono, F.; Gutiérrez, E. Gis-Based Method to Assess Seismic Vulnerability of Interconnected Infrastructure: A Case of EU Gas and Electricity Networks; No. JRC57064; Publications Office of the European Union JRC: Geel, Belgium, 2010. [Google Scholar]
- Kaplan, S.; Garrick, B.J. On the quantitative definition of risk. Risk Anal. 1981, 1, 11–27. [Google Scholar] [CrossRef]
- Heinimann, H.R. A generic framework for resilience assessment. In Resource Guide on Resilience; EPFL International Risk Governance Center: Lausanne, Switzerland, 2016. [Google Scholar]
- Hosseini, S.; Barker, K.; Ramirez-Marquez, J.E. A review of definitions and measures of system resilience. Reliab. Eng. Syst. Saf. 2016, 145, 47–61. [Google Scholar] [CrossRef]
- Heinimann, H.R.; Hatfield, K. Infrastructure resilience assessment, management and governance—State and perspectives. In Resilience-Based Approaches to Critical Infrastructure Safeguarding; NATO: Ponta Delgada, Portugal, 2017. [Google Scholar]
- Ganin, A.A.; Massaro, E.; Gutfraind, A.; Steen, N.; Keisler, J.M.; Kott, A.; Mangoubi, R.; Linkov, I. Operational resilience: Concepts, design and analysis. Sci. Rep. 2016, 6, 19540. [Google Scholar] [CrossRef]
- Didier, M.; Broccardo, M.; Esposito, S.; Stojadinovic, B. A compositional demand/supply framework to quantify the resilience of civil infrastructure systems (Re-CoDeS). Sustain. Resilient Infrastruct. 2017, 3, 86–102. [Google Scholar] [CrossRef]
- Gasser, P.; Lustenberger, P.; Cinelli, M.; Kim, W.; Spada, M.; Burgherr, P.; Hirschberg, S.; Stojadinovic, B.; Sun, T.Y. A review on resilience assessment of energy systems. Sustain. Resilient Infrastruct. 2019, 1–27. [Google Scholar] [CrossRef]
- Burgherr, P.; Giroux, J.; Spada, M. Accidents in the energy sector and energy infrastructure attacks in the context of energy security. Eur. J. Risk Regul. 2015, 6, 271–283. [Google Scholar] [CrossRef]
- Blaikie, P.; Cannon, T.; Davis, I.; Wisner, B. At Risk: Natural hazards, People’s Vulnerability and Disasters; Routledge: Abingdon, UK, 2004. [Google Scholar]
- HAZUS. Multi-Hazard Loss Estimation Methodology—Hurricane Model; FEMA: Washington, DC, USA, 2003.
- HAZUS. Multi-Hazard Loss Estimation Methodology—Earthquake Model; FEMA: Washington, DC, USA, 2003.
- HAZUS. Multi-Hazard Loss Estimation Methodology—Flood Model; FEMA: Washington, DC, USA, 2003.
- GEM. Gem Physical Vulnerability Functions Database. 2016. Available online: https://www.globalquakemodel.org (accessed on 9 December 2019).
- Hirschberg, S.; Spiekerman, G.; Dones, R. Severe Accidents in the Energy Sector; Paul Scherrer Institut, Villigen PSI: Villigen, Switzerland, 1998; p. 340. [Google Scholar]
- Kim, W.; Burgherr, P.; Spada, M.; Lustenberger, P.; Kalinina, A.; Hirschberg, S. Energy-related severe accident database (ensad): Cloud-based geospatial platform. Big Earth Data 2019, 2, 368–394. [Google Scholar] [CrossRef]
- Gao, J.; Liu, X.; Li, D.; Havlin, S. Recent progress on the resilience of complex networks. Energies 2015, 8, 12187–12210. [Google Scholar] [CrossRef]
- Mieler, M.; Stojadinovic, B.; Budnitz, R.; Comerio, M.; Mahin, S. A framework for linking community-resilience goals to specific performance targets for the built environment. Earthq. Spectra 2015, 8, 12187–12210. [Google Scholar] [CrossRef]
- Helbing, D. Globally networked risks and how to respond. Nature 2013, 497, 51–59. [Google Scholar] [CrossRef]
- Voropai, N.I.; Senderov, S.M.; Edelev, A.V. Detection of “bottlenecks” and ways to overcome emergency situations in gas transportation networks on the example of the European gas pipeline network. Energy 2012, 42, 3–9. [Google Scholar] [CrossRef]
- Yu, W.; Song, S.; Li, Y.; Min, Y.; Huang, W.; Wen, K.; Gong, J. Gas supply reliability assessment of natural gas transmission pipeline systems. Energy 2018, 162, 853–870. [Google Scholar] [CrossRef]
- Gjorgiev, B.; Antenucci, A.; Volkanovski, A.; Sansavini, G. An FTA method for the unavailability of supply in gas networks supported by physical models. IEEE Trans. Reliab. 2019. [Google Scholar] [CrossRef]
- Su, H.; Zhang, J.; Zio, E.; Yang, N.; Li, X.; Zhang, Z. An integrated systemic method for supply reliability assessment of natural gas pipeline networks. Appl. Energy 2018, 209, 489–501. [Google Scholar] [CrossRef]
- Praks, P.; Kopustinskas, V.; Masera, M. Monte-carlo-based reliability and vulnerability assessment of a natural gas transmission system due to random network component failures. Sustain. Resilient Infrastruct. 2017, 2, 97–107. [Google Scholar] [CrossRef]
- Kopustinskas, V.; Praks, P. Probabilistic gas transmission network simulator and application to the EU gas transmission system. In Summer Safety & Reliability Seminars SSARS 2015; SSARS: Gdańsk/Sopot, Poland, 2015. [Google Scholar]
- Praks, P.; Kopustinskas, V.; Masera, M. Probabilistic modelling of security of supply in gas networks and evaluation of new infrastructure. Reliab. Eng. Syst. Saf. 2015, 144, 254–264. [Google Scholar] [CrossRef]
- Sacco, T.; Compare, M.; Zio, E.; Sansavini, G. Portfolio decision analysis for risk-based maintenance of gas networks. J. Loss Prev. Process Ind. 2019, 60, 269–281. [Google Scholar] [CrossRef]
- Hauser, P.; Hobbie, H.; Möst, D. Resilience in the German natural gas network: Modelling approach for a high-resolution natural gas system. In Proceedings of the 2017 14th International Conference on the European Energy Market (EEM), Dresden, Germany, 6–9 June 2017. [Google Scholar]
- Hauser, P.; Heidari, S.; Weber, C.; Möst, D. Does increasing natural gas demand in the power sector pose a threat of congestion to the german gas grid? A model-coupling approach. Energies 2019, 1, 2159. [Google Scholar] [CrossRef]
- Jensen, T.V.; Pinson, P. Re-europe, a large-scale dataset for modeling a highly renewable European electricity system. Sci. Data 2017, 4, 170175. [Google Scholar] [CrossRef] [PubMed]
- Pfenninger, S.; DeCarolis, J.; Hirth, L.; Quoilin, S.; Staffell, I. The importance of open data and software: Is energy research lagging behind? Energy Policy 2017, 101, 211–215. [Google Scholar] [CrossRef]
- Swiss, Re. China’s Belt & Road Initiative: The Impact on Commercial Insurance in Participating Regions. In Sigma; Swiss Re: Zurich, Switzerland, 2017. [Google Scholar]
- Spada, M.; Burgherr, P. A hierarchical approximate bayesian computation (habc) for accident risk in the energy sector triggered by natural events. In Proceedings of the European Safety and Reliability Conference (ESREL), Hannover, Germany, 22–26 September 2019. [Google Scholar]
- Lustenberger, P.; Kim, W.; Schumacher, F.; Spada, M.; Burgherr, P.; Hirschberg, S.; Stojadinovic, B. Network analysis of the European natural gas infrastructure to quantify its performance in long-term pipeline shutdown scenarios. In Proceedings of the European Safety and Reliability Conference (ESREL), Trondheim, Norway, 17–21 June 2018. [Google Scholar]
- ENTSOG. Entsog Transparancy Platform. 2016. Available online: http://www.entsog.eu/ (accessed on 15 October 2017).
- El-Shiekh, T. The optimal design of natural gas transmission pipelines. Energy Sources Part B Econ. Plan. Policy 2013, 8, 7–13. [Google Scholar] [CrossRef]
- Martin, A.; Möller, M.; Moritz, S. Mixed integer models for the stationary case of gas network optimization. Math. Program. 2005, 105, 563–582. [Google Scholar] [CrossRef]
- Perner, J. Die Langfristige Erdgasversorgung Europas: Analysen und Simulationen Mit dem Angebotsmodell Eugas; Zeitschrift für Energiewirtschaft, Springer: Berlin, Germany, 2002. [Google Scholar]
- IEA. North American Energy Industrial Complex—Pipelines; IEA: Paris, France, 2017. [Google Scholar]
- FNB. Transmission System—Facts and Figures; FNB: Pittsburgh, PA, USA, 2017; Available online: http://www.fnb-gas.de/en/transmission-systems/facts-and-figures/facts-and-figures.html (accessed on 15 October 2017).
- Zhao, Y.; Rui, Z. Pipeline compressor station construction cost analysis. Int. J. Oil Gas Coal Technol. 2014, 8, 41–61. [Google Scholar] [CrossRef]
- Messersmith, D.; Brockett, D.; Loveland, D. Understanding Natural Gas Compressor Stations. 2015. Available online: https://extension.psu.edu/downloadable/download/sample/sample_id/755/ (accessed on 15 October 2017).
- QGIS Development Team. Qgis Geographic Information System 2.18; QGIS Development Team: ’s-Hertogenbosch, The Netherlands, 2016. [Google Scholar]
- BP. Statistical Review of World Energy; BP: London, UK, 2018. [Google Scholar]
- Enipedia. 2017. Available online: http://enipedia.tudelft.nl/wiki/Main_Page (accessed on 1 July 2017).
- GlobalEnergyObservatory. 2017. Available online: http://www.globalenergyobservatory.com/ (accessed on 1 July 2017).
- European Environment Agency (EEA). European Pollutant Release and Transfer Register (E-Prtr); European Environment Agency: København, Denmark, 2017; Available online: https://prtr.eea.europa.eu/-/home (accessed on 1 July 2017).
- Center for International Earth Science Information Network—CIESIN—Columbia University. Gridded Population of the World, Version 4 (gpwv4): Population Count Adjusted to Match 2015 Revision of Un Wpp Country Totals, Revision 10; NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2017. [Google Scholar]
- GADM. Gadm Database of Global Administrative Areas (v3.6). 2017. Available online: http://www.gadm.org/ (accessed on 15 October 2017).
- Woessner, J.; Laurentiu, D.; Giardini, D.; Crowley, H.; Cotton, F.; Grünthal, G.; Valensise, G.; Arvidsson, R.; Basili, R.; Demircioglu, M.B.; et al. The 2013 European seismic hazard model: Key components and results. Bull. Earthq. Eng. 2015, 13, 3553–3596. [Google Scholar] [CrossRef]
- CEN. Eurocode 8: Design of Structures for Earthquake Resistance, in Part 1: General Rules, Seismic Actions and Rules for Buildings; CEN: Brussels, Belgium, 2004. [Google Scholar]
- Burgherr, P.; Hirschberg, S. Comparative risk assessment of severe accidents in the energy sector. Energy Policy 2014, 74, S45–S56. [Google Scholar] [CrossRef]
- Felder, F. A critical assessment of energy accident studies. Energy Policy 2009, 37, 5744–5751. [Google Scholar] [CrossRef]
- Burgherr, P.; Spada, M.; Kalinina, A.; Hirschberg, S.; Kim, W.; Gasser, P.; Lustenberger, P. The Energy-Related Severe Accident Database (ENSAD) for Comparative Risk Assessment of Accidents in the Energy Sector. In European Safety and Reliability Conference (ESREL); CRC Press, Taylor & Francis Group: London, UK, 2017. [Google Scholar]
- Henry, D.; Ramirez-Marquez, J.E. Generic metrics and quantitative approaches for system resilience as a function of time. Reliab. Eng. Syst. Saf. 2012, 99, 114–122. [Google Scholar] [CrossRef]
- Nan, C.; Sansavini, G.; Kröger, W. Building an Integrated Metric for Quantifying the Resilience of Interdependent Infrastructure Systems; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Kyriakidis, M.; Lustenberger, P.; Burgherr, P.; Dang, V.N.; Hirschberg, S. Quantifying energy systems resilience—A simulation approach to assess recovery. Energy Technol. 2018, 6, 1700–1706. [Google Scholar] [CrossRef]
- Eurogas. Eurogas Statisitcal Report 2016; Eurogas: Bruxelles, Belgium, 2016. [Google Scholar]
- Pustišek, A.; Karasz, M. Natural Gas: A Commercial Perspective; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Moran, M.J.; Shapiro, H.N.; Boettner, D.D.; Bailey, M.B. Fundamentals of Engineering Thermodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Eurostat. Simplified Energy Balances—Annual Data; Eurostat: Bruxelles, Belgium, 2018. [Google Scholar]
- Aurenhammer, F. Voronoi diagrams—A survey of a fundamental geometric data structure. ACM Comput. Surv. (CSUR) 1991, 23, 345–405. [Google Scholar] [CrossRef]
- Lustenberger, P.; Sun, T.; Gasser, P.; Kim, W.; Spada, M.; Burgherr, P.; Hirschberg, S.; Stojadinović, B. Potential Impacts of Selected Natural Hazards and Technical Failures on the Natural Gas Tranmission Network in Europe, in European SAFETY and Reliability Conference (ESREL); Taylor & Francis: Portoroz, Slovenia, 2017. [Google Scholar]
- Ford, L.; Fulkerson, D. Maximal flow through a network. Can. J. Math. 1956. [Google Scholar] [CrossRef]
- Boykov, Y.; Kolmogorov, V. An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1124–1137. [Google Scholar] [CrossRef]
- MATLAB. Versin r2015b; The MathWorks Inc.: Natick, MA, USA, 2015. [Google Scholar]
- Csardi, G.; Nepusz, T. The igraph software package for complex network research. InterJournal Complex Syst. 2006, 1695, 1–9. [Google Scholar]
- Caprio, M.; Tarigan, B.; Worden, C.B.; Wiemer, S.; Wald, D.J. Ground motion to intensity conversion equations (gmices): A global relationship and evaluation of regional dependency. Bull. Seismol. Soc. Am. 2015, 105, 1476–1490. [Google Scholar] [CrossRef]
- EGIG. 9th Report of the European Gas Pipeline Incident Data Group (Period 1970–2013); EGIG: Groningen, The Netherlands, 2015. [Google Scholar]
- Nicholson, C.D.; Barker, K.; Ramirez-Marquez, J.E. Flow-based vulnerability measures for network component importance: Experimentation with preparedness planning. Reliab. Eng. Syst. Saf. 2016, 145, 62–73. [Google Scholar] [CrossRef]
- Docker Inc. Docker; Docker Inc.: San Francisco, CA, USA, 2019. [Google Scholar]
- Grünthal, G.; Wahlström, R. The European-mediterranean earthquake catalogue (EMEC) for the last millennium. J. Seismol. 2012, 16, 535–570. [Google Scholar] [CrossRef]
- Transitgas. The Pipeline System. 2017. Available online: http://www.transitgas.org/EN/ (accessed on 15 October 2017).
- Transmed. Gas Transportation System. 2017. Available online: http://www.transmed-spa.it/?lingua=2 (accessed on 10 October 2017).
- GreenStream. The Greenstream Pipeline. 2017. Available online: http://www.greenstreambv.com/en/pages/home.shtml (accessed on 10 October 2017).
- ETNSOG. Union-Wide Simulation of Gas Supply and Infrastructure Disruption Scenarios (SOS Simulation); ENTSOG: Bruxelles, Belgium, 2017. [Google Scholar]
- TANAP. Trans Anatolian Natural Gas Pipeline Project. 2017. Available online: http://www.tanap.com/ (accessed on 10 October 2017).
- AdriaticLNG. Cavarzere Porto Levante. 2017. Available online: http://www.adriaticlng.it/en/home/ (accessed on 10 October 2017).
- Tsionis, G.; Pinto, A.; Giardini, D.; Mignan, A.; Cotton, F.; Danciu, L.; Iervolino, I.; Pitilakis, K.; Stojadinovic, B.; Zwicky, P. Harmonized Approach to Stress Tests for Critical Infrastructures Against Natural Hazards; Joint Research Centre (JRC): Luxembourg, 2016. [Google Scholar]
- Vainio, J. An Explosion in the Heart of the European Gas System: What does the Baumgarten Case Tell about the Resiliency of the System? 2017. Available online: https://www.enseccoe.org/data/public/uploads/2017/12/sardines-2017_512_baumgarten-explosion-and-gas-system-resiliency-in-europe.pdf (accessed on 20 January 2018).
- UN General Assembly. The Sendai Framework for Disaster Risk Reduction; UN General Assembly: New York, NY, USA, 2015; pp. 2015–2030. [Google Scholar]










| Study | Methodologies | Case Study | ||||||
|---|---|---|---|---|---|---|---|---|
| Topological Analysis | Thermal-Hydraulic Flow Computation | Economic Models | Stochastic Failure Estimation | Europe | Great Britain | Germany | “Fictitious” Real World Network | |
| Carvalho et al., 2009 [6] | X | X | X | |||||
| Carvalho et al., 2014 [3] | X | X | ||||||
| Gjorgiev et al., 2019 [29] | X | X | X | |||||
| Hauser et al., 2017 [35] | X | X | ||||||
| Hauser et al., 2019 [36] | X | X | ||||||
| Kopustinskas and Praks 2015 [32] | X | X | ||||||
| Poljansek et al., 2012 [7] | X | X | X | |||||
| Praks et al., 2017 [31] | X | X | ||||||
| Praks et al., 2015 [33] | X | X | ||||||
| Sacco et al., 2019 [34] | X | X | X | |||||
| Su et al., 2018 [30] | X | X | X | X | ||||
| Voropai et al., 2012 [27] | X | X | ||||||
| Yu et al., 2018 [28] | X | X | X | |||||
| Dataset | Type | Source | Description |
|---|---|---|---|
| Natural gas pipelines | Shapefile (Polyline) | ENTSOG 2016 [42] | European natural gas pipelines categorized in three diameter classes (8157 pipelines, 197,612 km) |
| Natural gas storage facilities | Shapefile (Points) | ENTSOG 2016 [42] | European natural gas storage facilities with location, facility name and storage volume (152 entries) |
| Natural gas sources | Shapefile (Points) | ENTSOG 2016 [42] | European natural gas sources (LNG ports, production platforms and cross-border interconnection points) |
| Pipeline Diameter Category | Diameter d (inch) | Capacity C (109 m3/yr) |
|---|---|---|
| Small pipelines | d ≤ 24 | C < 3.942 |
| Medium pipelines | 24 < d ≤ 36 | 3.942 ≤ C < 8.76 |
| Large pipelines | 36 < d | 8.76 ≤ C < 87.6 |
| Dataset | Type | Source | Description |
|---|---|---|---|
| Population count | Geotiff, Raster (30 arc-seconds) | Center for International Earth Science Information Network -CIESIN-Columbia University 2017 [55] | The population count per pixel from UN WPP-Adjusted Population Count, v4.10 (2015) |
| Country boundaries | Shapefile (Polygon) | GADM 2017 [56] | Worldwide country boundaries (administrative level 0) |
| Natural gas power plants | Shapefile (Points) | Enipedia [52] | European natural gas power plants with associated annual carbon dioxide emissions (565 with complete information) |
| National natural gas consumption | Table | IEA 2017 [1] | Annual natural gas production, imports and exports on country level (reference year 2015) |
| PGM | α1 | α2 | β1 | β2 | tPGM |
|---|---|---|---|---|---|
| PGA | 2.270 | −1.361 | 1.647 | 3.822 | 1.6 |
| PGV | 4.424 | 4.018 | 1.589 | 2.671 | 0.3 |
| Pipeline Index | ΔFmax,i (%) |
|---|---|
| 1 | 4.6 |
| 2 | 3.5 |
| 3 | 1.8 |
| 4 | 1.8 |
| 5 | 1.8 |
| 6 | 1.1 |
| Seismic | Technical | |||||||
|---|---|---|---|---|---|---|---|---|
| min | max | mean | std | min | max | mean | std | |
| Maximum pipeline failure rate (10–3/year) | 0 | 2 | 0.1 | 0.25 | 0 | 77 | 0.94 | 1.69 |
| Maximum disruption impact (10–4%/year) | 0 | 34.5 | 0.07 | 0.69 | 0 | 118 | 0.44 | 3.26 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lustenberger, P.; Schumacher, F.; Spada, M.; Burgherr, P.; Stojadinovic, B. Assessing the Performance of the European Natural Gas Network for Selected Supply Disruption Scenarios Using Open-Source Information. Energies 2019, 12, 4685. https://doi.org/10.3390/en12244685
Lustenberger P, Schumacher F, Spada M, Burgherr P, Stojadinovic B. Assessing the Performance of the European Natural Gas Network for Selected Supply Disruption Scenarios Using Open-Source Information. Energies. 2019; 12(24):4685. https://doi.org/10.3390/en12244685
Chicago/Turabian StyleLustenberger, Peter, Felix Schumacher, Matteo Spada, Peter Burgherr, and Bozidar Stojadinovic. 2019. "Assessing the Performance of the European Natural Gas Network for Selected Supply Disruption Scenarios Using Open-Source Information" Energies 12, no. 24: 4685. https://doi.org/10.3390/en12244685
APA StyleLustenberger, P., Schumacher, F., Spada, M., Burgherr, P., & Stojadinovic, B. (2019). Assessing the Performance of the European Natural Gas Network for Selected Supply Disruption Scenarios Using Open-Source Information. Energies, 12(24), 4685. https://doi.org/10.3390/en12244685