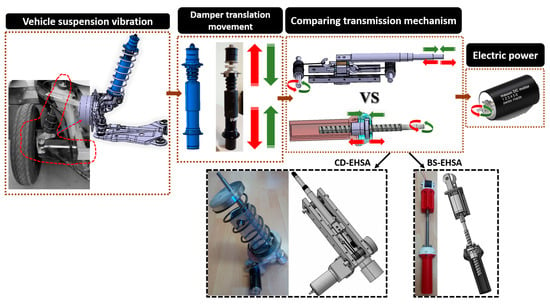
Design and Potential Power Recovery of Two Types of Energy Harvesting Shock Absorbers
Abstract
:1. Introduction
- The design, manufacture, and mathematical modeling of the systems: BS-EHSA and CD-EHSA.
- The results, experimental and simulation of the electrical power that is generated with both technologies for different conditions. Taking as reference the characteristic curves of the damper of a Renault Twizy and Ford Focus.
- The results shown in this work, both for the BS-EHSA and for the CD-EHSA, make it possible to compare each other because they share the same initial conditions.
- Qualitative analysis of both technologies for their future application in vehicle suspension systems.
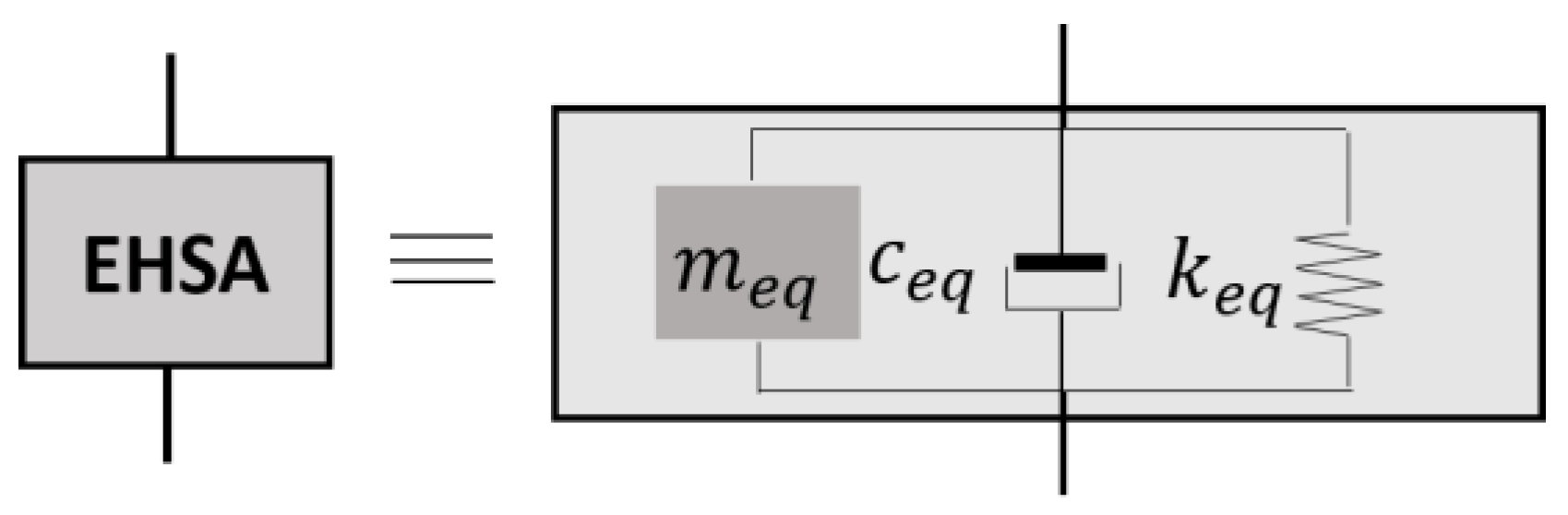
2. Framework to Analyze the Performance of the BS-EHSA and CD-EHSA
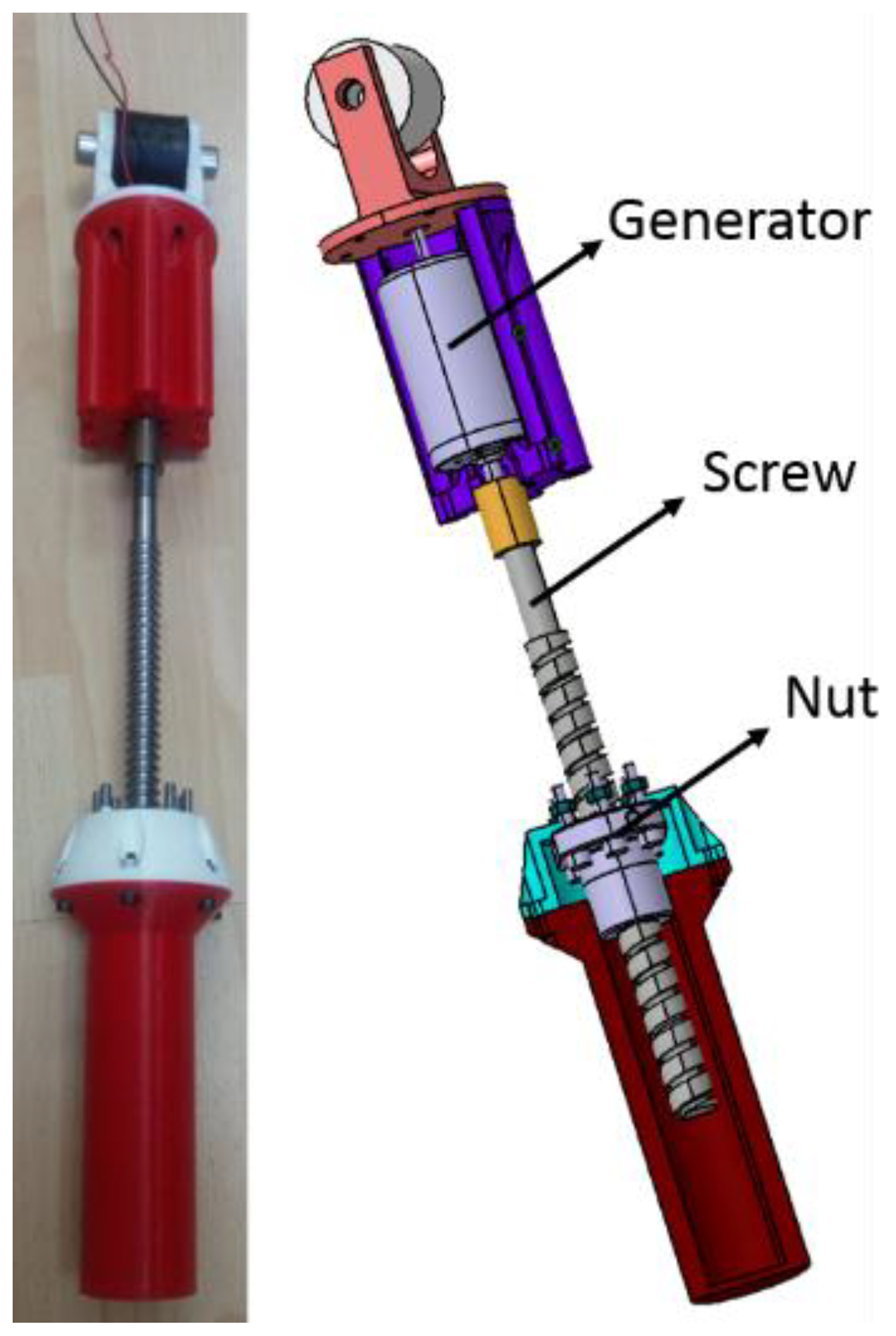
3. Ball-Screw Energy Harvesting Shock Absorber (BS-EHSA)
3.1. Design Principle and Prototype
3.2. Mathematical Model
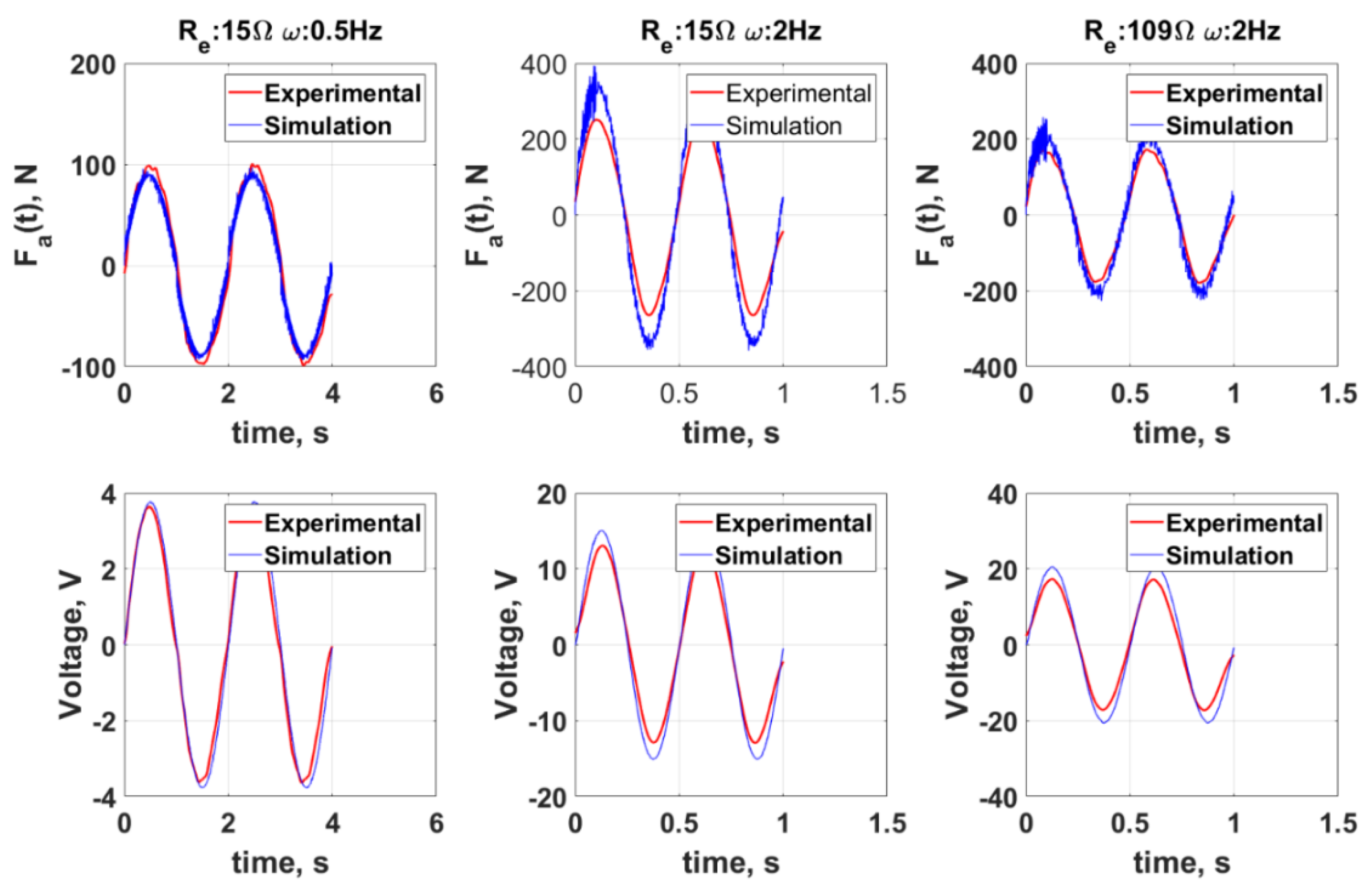
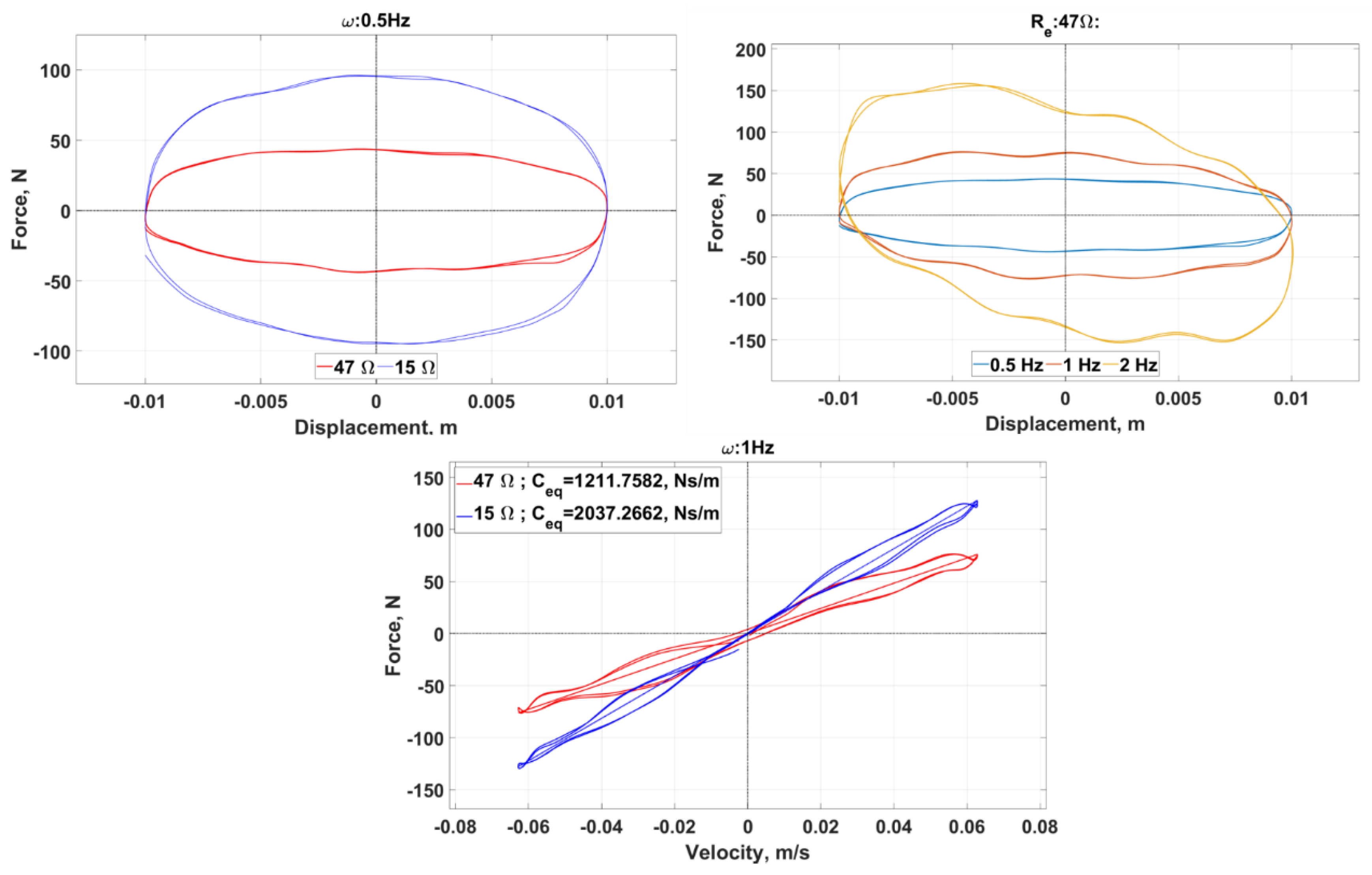
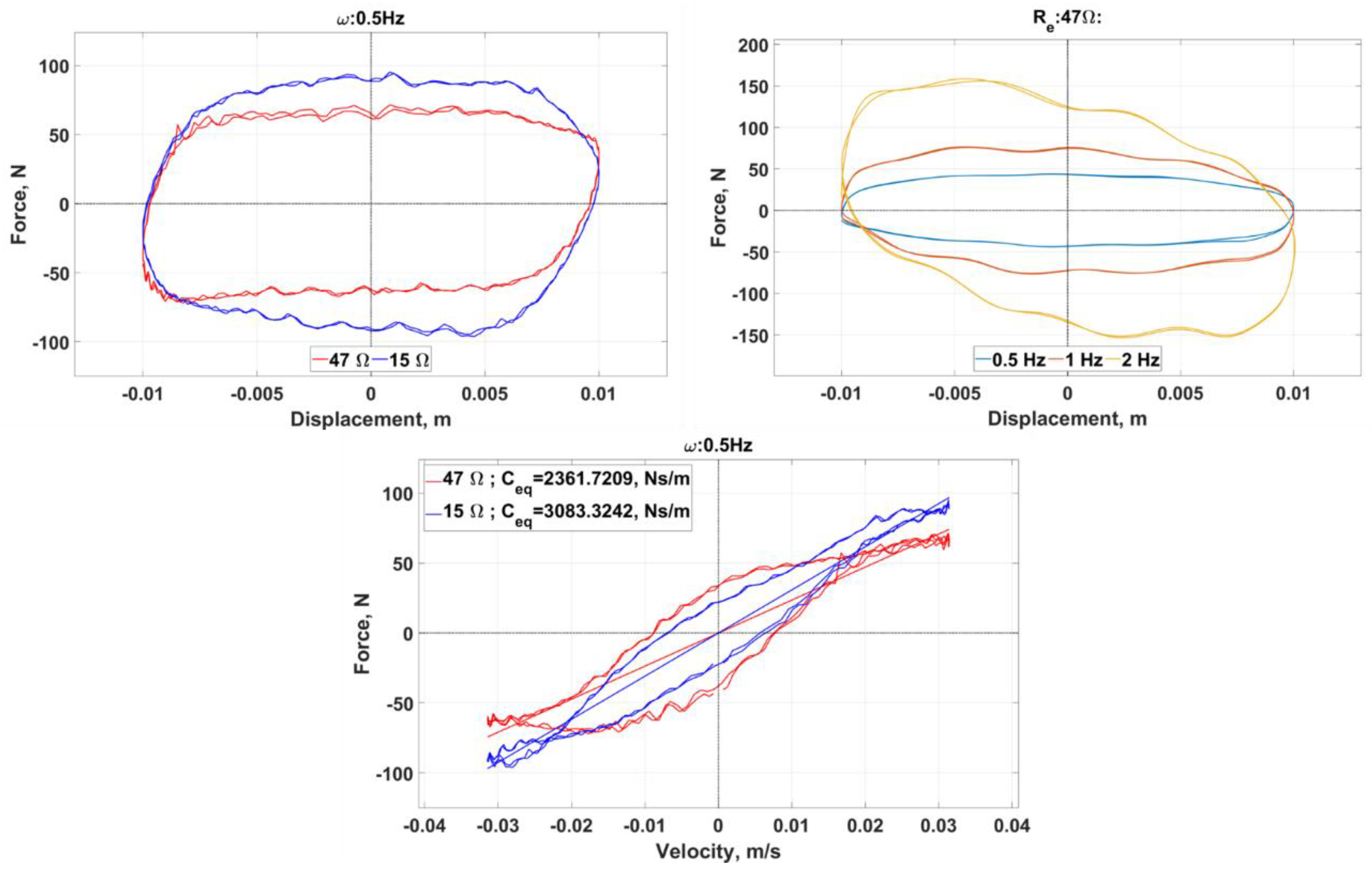
3.3. Comparison of Simulations and Experiments
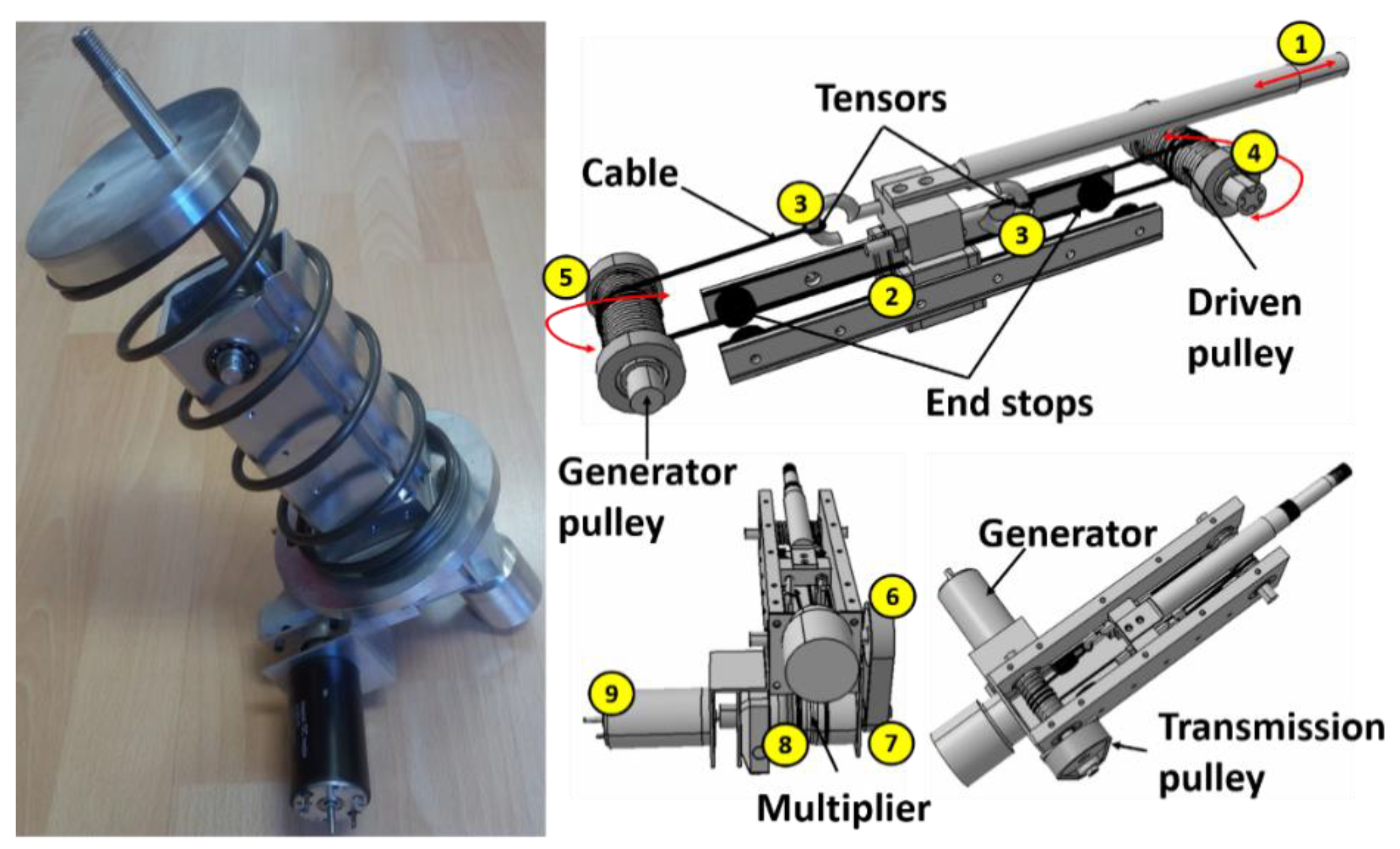
4. Cable-Dynamics Energy Harvesting Shock Absorber (CD-EHSA)
4.1. Design Principle and Prototype
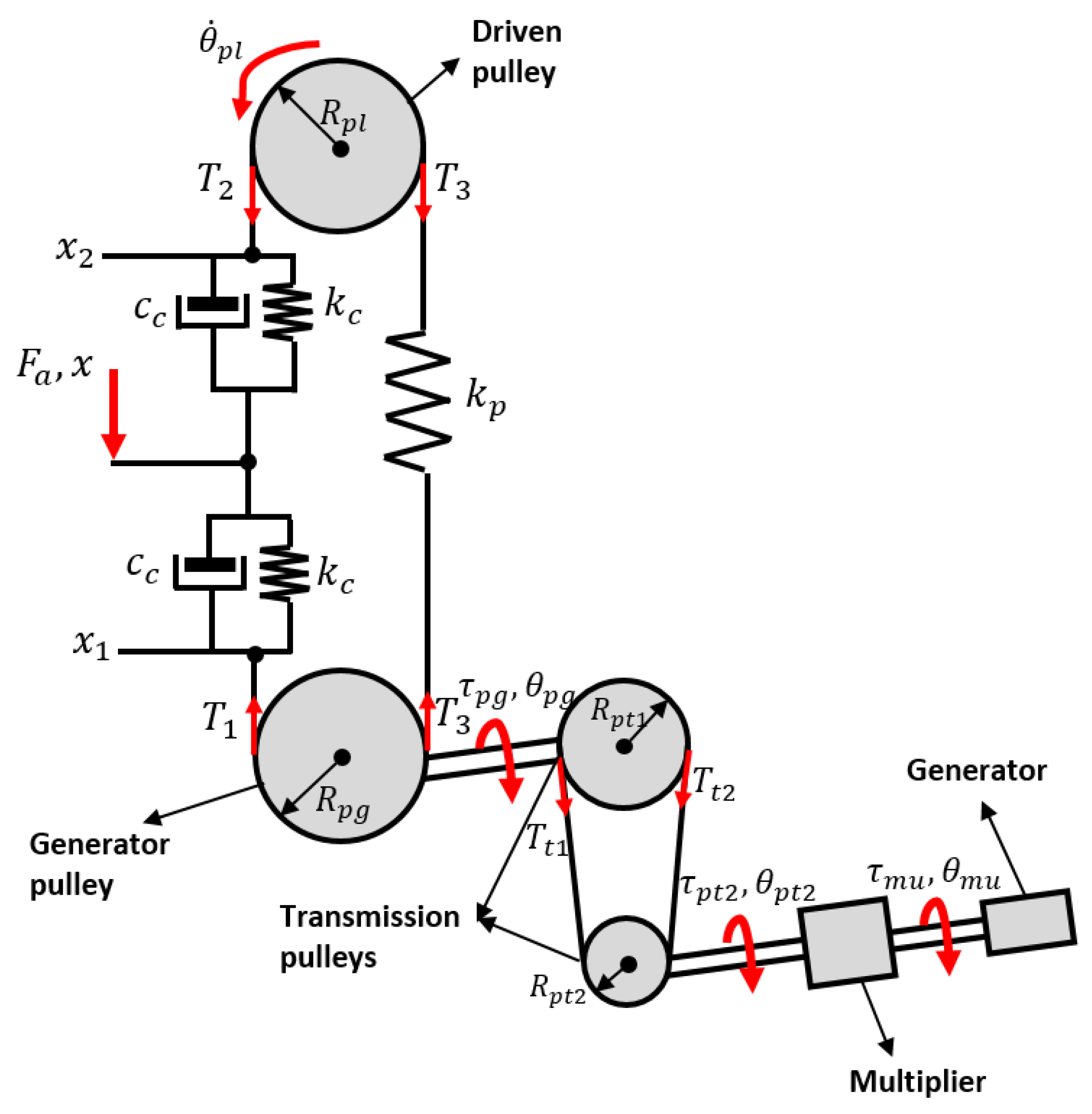
4.2. Mathematical Model
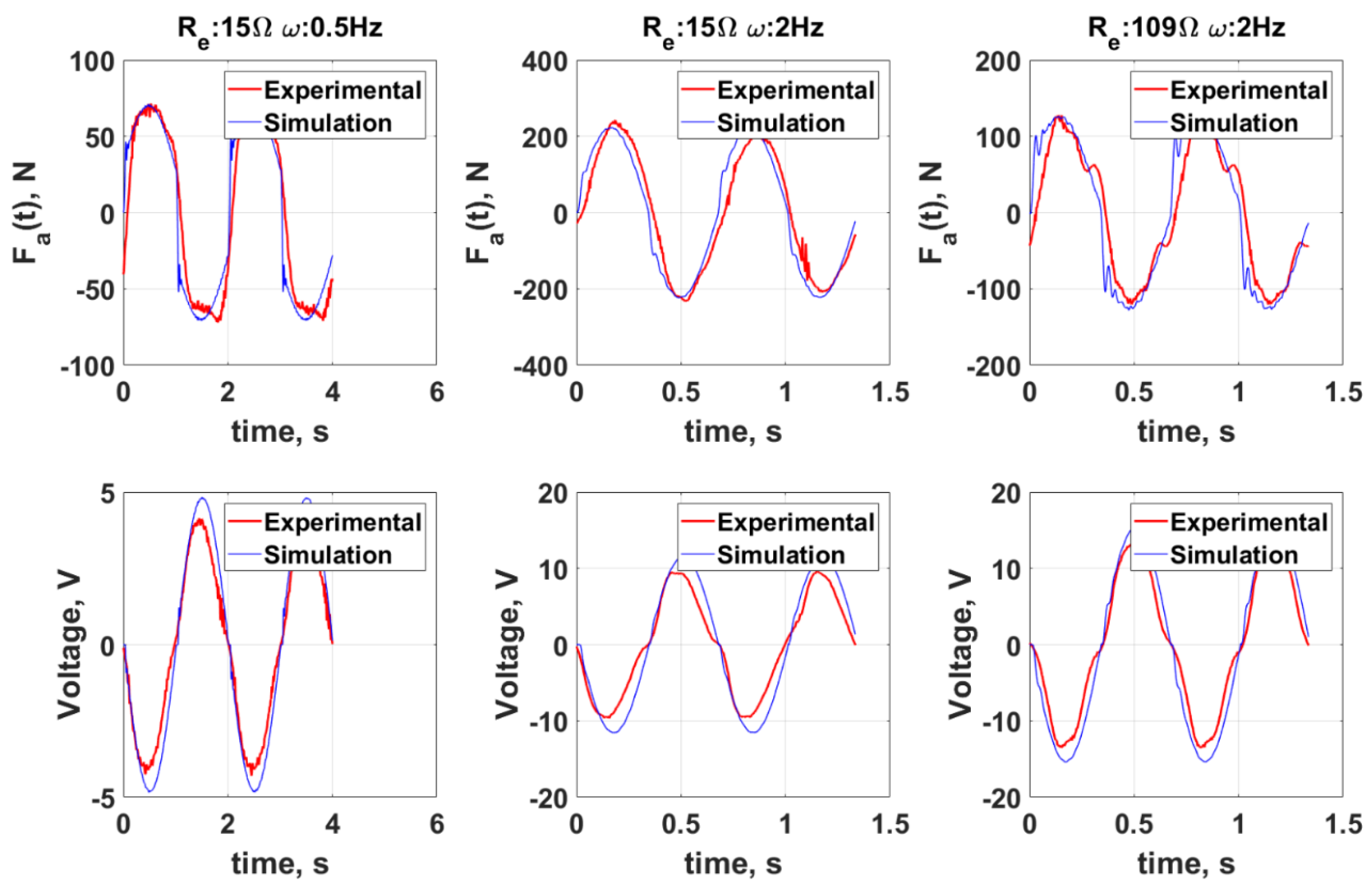
4.3. Comparison of Simulations and Experiments
5. Numerical Simulation using BS-EHSA and CD-EHSA
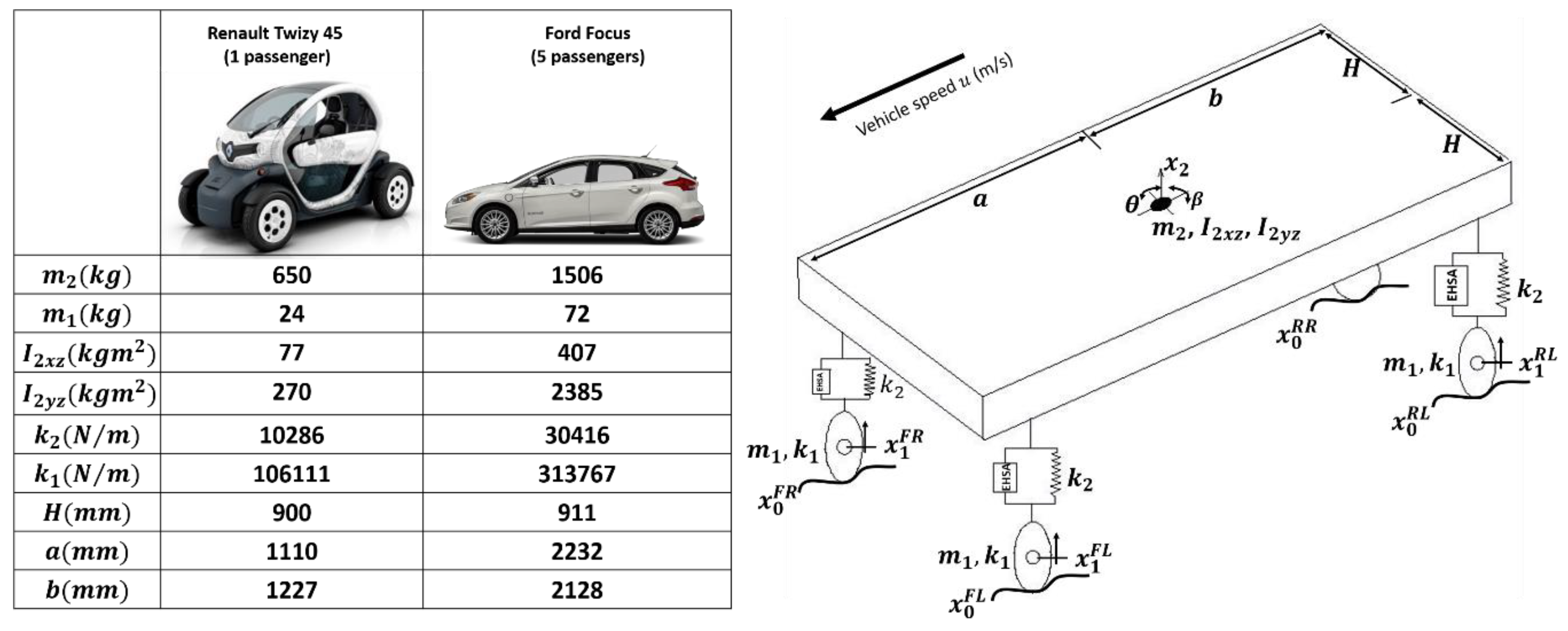
5.1. Vehicle Parameters and Modelling
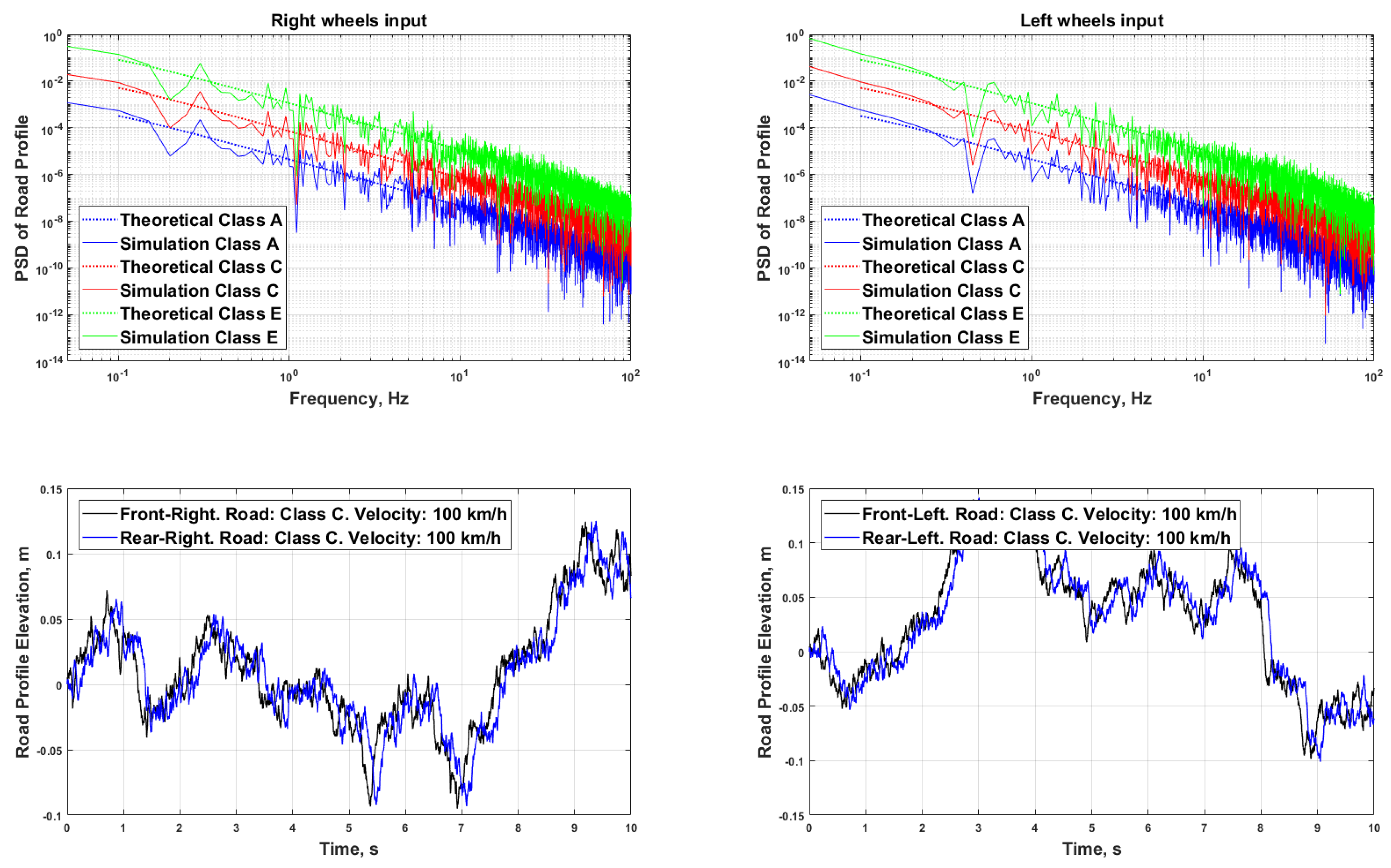
5.2. Input Signals Generation
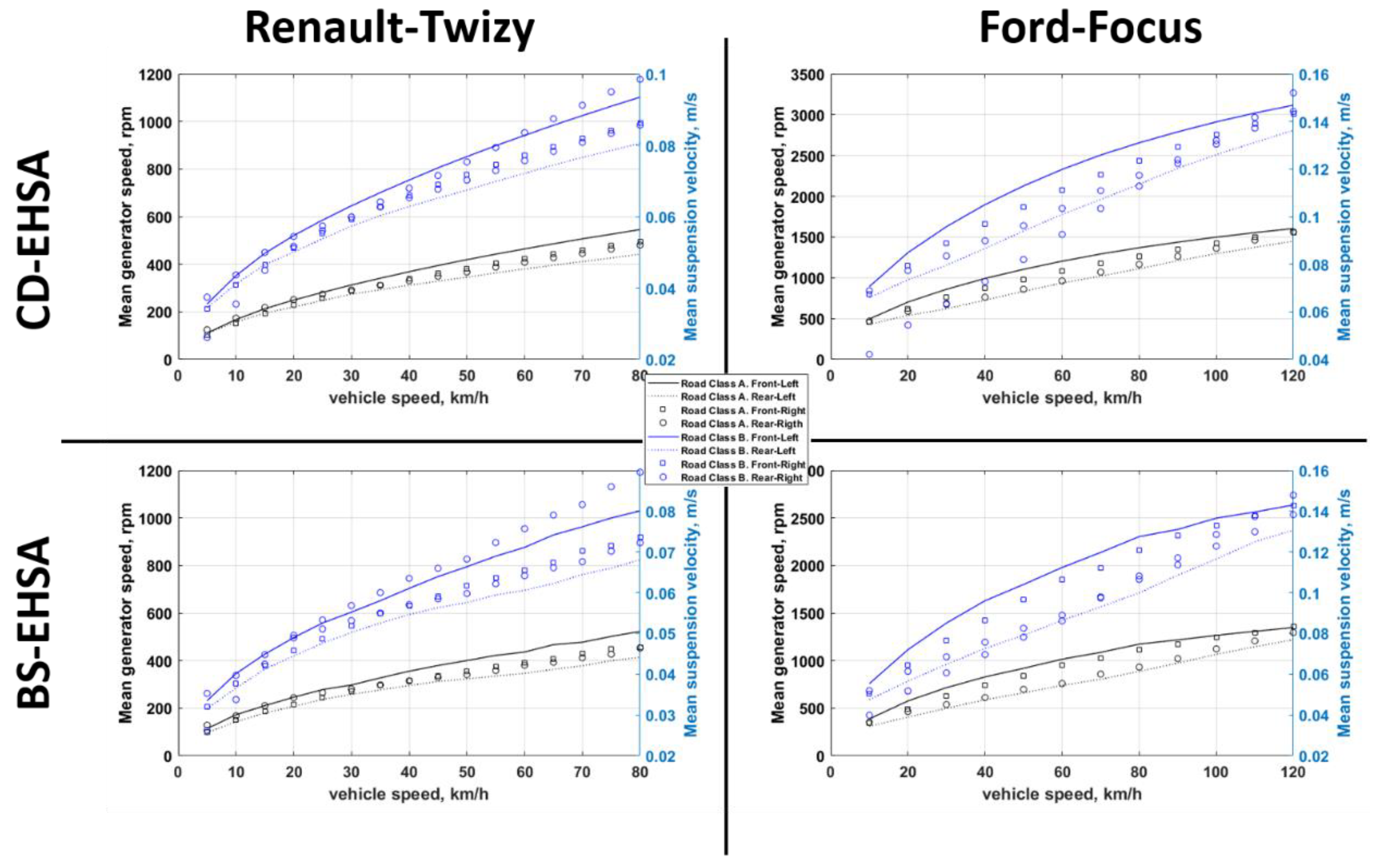
5.3. EHSA Design
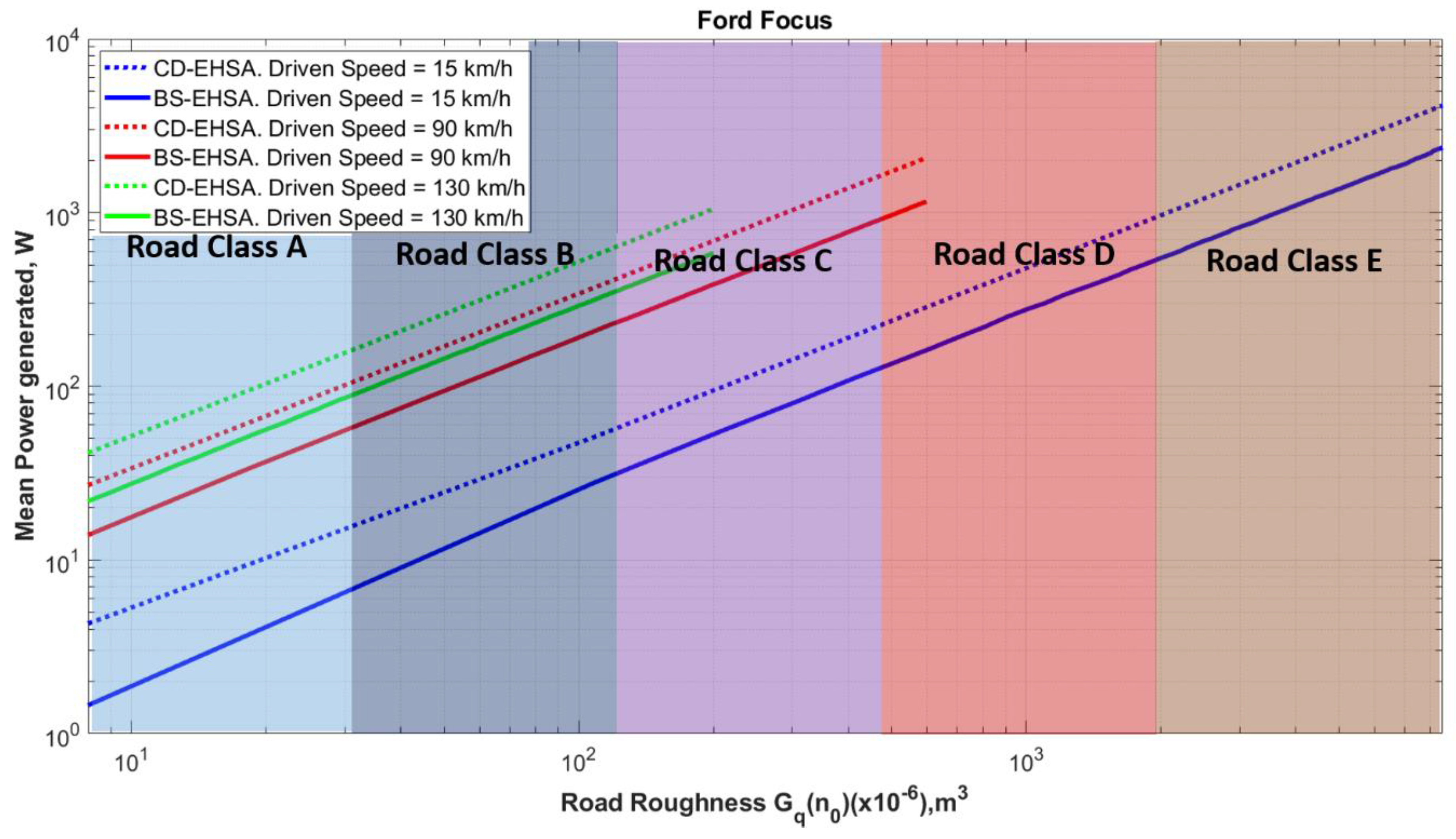
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Orr, B.; Akbarzadeh, A.; Mochizuki, M.; Singh, R. A review of car waste heat recovery systems utilising thermoelectric generators and heat pipes. Appl. Therm. Eng. 2016, 101, 490–495. [Google Scholar] [CrossRef]
- Liu, X.; Li, C.; Deng, Y.D.; Su, C.Q. An energy-harvesting system using thermoelectric power generation for automotive application. Int. J. Electr. Power Energy Syst. 2015, 67, 510–516. [Google Scholar] [CrossRef]
- Kim, T.Y.; Negash, A.a.; Cho, G. Waste heat recovery of a diesel engine using a thermoelectric generator equipped with customized thermoelectric modules. Energy Convers. Manag. 2016, 124, 280–286. [Google Scholar] [CrossRef]
- Rahman, A.; Razzak, F.; Afroz, R.; Mohiuddin, A.K.M.; Hawlader, M.N.A. Power generation from waste of IC engines. Renew. Sustain. Energy Rev. 2015, 51, 382–395. [Google Scholar] [CrossRef]
- Saidur, R.; Rezaei, M.; Muzammil, W.K.; Hassan, M.H.; Paria, S.; Hasanuzzaman, M. Technologies to recover exhaust heat from internal combustion engines. Renew. Sustain. Energy Rev. 2012, 16, 5649–5659. [Google Scholar] [CrossRef]
- Lv, C.; Zhang, J.; Li, Y.; Yuan, Y. Mechanism analysis and evaluation methodology of regenerative braking contribution to energy efficiency improvement of electrified vehicles. Energy Convers. Manag. 2015, 92, 469–482. [Google Scholar] [CrossRef]
- Qiu, C.; Wang, G. New evaluation methodology of regenerative braking contribution to energy efficiency improvement of electric vehicles. Energy Convers. Manag. 2016, 119, 389–398. [Google Scholar] [CrossRef]
- Jin, L.; Chen, P.; Liu, Y. An Analysis of Regenerative Braking and Energy Saving for Electric Vehicle with In-Wheel Motors. Int. J. Control. Autom. 2014, 7, 219–230. [Google Scholar] [CrossRef]
- Clegg, S.J. A Review of Regenerative Braking Systems; University of Leeds: Leeds, UK, 1996; p. 24. [Google Scholar]
- Lee, J.; Choi, B. Development of a piezoelectric energy harvesting system for implementing wireless sensors on the tires. Energy Convers. Manag. 2014, 78, 32–38. [Google Scholar] [CrossRef]
- Zhu, B.; Han, J.; Zhao, J.; Deng, W. Practical design of an energy harvester considering wheel rotation for powering intelligent tire systems. J. Electron. Mater. 2017, 46, 2483–2493. [Google Scholar] [CrossRef]
- Decoupler, P.Z.T. Vibration energy harvesting from a hydraulic engine mount via PZT decoupler. In Proceedings of the ASME 2010 International Mechanical Engineering Congress & Exposition IMECE2010, Vancouver, BC, Canada , 12–18 November 2010. [Google Scholar]
- Mohareri, O.; Arzanpour, S. Energy harvesting from vibration of a hydraulic engine mount using a turbine. In Proceedings of the 2011 IEEE International Conference on Mechatronics, Istanbul, Turkey, 13–15 April 2011; pp. 1–6. [Google Scholar]
- Ning, D.; Sun, S.; Du, H.; Li, W.; Zhang, N. Vibration control of an energy regenerative seat suspension with variable external resistance. Mech. Syst. Signal Process. 2017, 106, 94–113. [Google Scholar] [CrossRef] [Green Version]
- Bowen, L.; Vinolas, J.; Olazagoitia, J.L. Methodology for comparing the functional performance of energy harvesting shock absorbers. Int. J. Appl. Electromagn. Mech. 2017, 55, 545–564. [Google Scholar] [CrossRef]
- Abdelkareem, M.A.A.; Xu, L.; Ali, M.K.A.; Elagouz, A.; Mi, J.; Guo, S.; Liu, Y.; Zuo, L. Vibration energy harvesting in automotive suspension system: A detailed review. Appl. Energy 2018, 229, 672–699. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, X.; John, S. A comprehensive review of the techniques on regenerative shock absorber systems. Energies 2018, 11, 1167. [Google Scholar] [CrossRef] [Green Version]
- Tang, X.; Lin, T.; Zuo, L. Design and optimization of a tubular linear electromagnetic vibration energy harvester. IEEE/ASME Trans. Mechatron. 2014, 19, 615–622. [Google Scholar] [CrossRef]
- Singh, S.; Satpute, N.V. Design and analysis of energy-harvesting shock absorber with electromagnetic and fluid damping. J. Mech. Sci. Technol. 2015, 29, 1591–1605. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, X.; Liu, Z. A novel regenerative shock absorber with a speed doubling mechanism and its Monte Carlo simulation. J. Sound Vib. 2018, 417, 260–276. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, X.; Chen, W.; Rasim, Y.; Salman, W.; Pan, H.; Yuan, Y.; Wang, C. A high-efficiency energy regenerative shock absorber using supercapacitors for renewable energy applications in range extended electric vehicle. Appl. Energy 2016, 178, 177–188. [Google Scholar] [CrossRef]
- Zhang, X.; Pan, H.; Qi, L.; Zhang, Z.; Yuan, Y.; Liu, Y. A renewable energy harvesting system using a mechanical vibration rectifier (MVR) for railroads”. Appl. Energy 2017, 204, 1535–1543. [Google Scholar]
- Li, P.; Zuo, L. Influences of the electromagnetic regenerative dampers on the vehicle suspension performance. J. Automob. Eng. 2017, 231, 383–394. [Google Scholar] [CrossRef]
- Galluzzi, R.; Xu, Y.; Amati, N.; Tonoli, A. Optimized design and characterization of motor-pump unit for energy-regenerative shock absorbers. Appl. Energy 2017, 210, 16–27. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, H.; Guo, K.; Zhang, X.; Li, S.E. Electro-hydraulic damper for energy harvesting suspension: Modeling, prototyping and experimental validation. Appl. Energy 2017, 199, 1–12. [Google Scholar] [CrossRef]
- Guo, S.; Lin, X.; Liu, Y.; Zuo, L. Modeling and experiments of a hydraulic electromagnetic energy harvesting shock absorber. IEEE/ASME Trans. Mechatron. 2017, 22, 11. [Google Scholar] [CrossRef]
- Zou, J.; Guo, X.; Xu, L.; Tan, G.; Zhang, C.; Zhang, J. Design, modeling, and analysis of a novel hydraulic energy-regenerative shock absorber for vehicle suspension. Shock Vib. 2017, 2017, 1–12. [Google Scholar] [CrossRef]
- Peng, M.; Guo, X.; Zou, J.; Zhang, C.M. Simulation Study on Vehicle Road Performance with Hydraulic Electromagnetic Energy-Regenerative Shock Absorber Hydraulic Electromagnetic Energy-Regenerative; SAE International: Warrendale, PA, USA, 2016; p. 10. [Google Scholar]
- Wang, R.; Gu, F.; Cattley, R.; Ball, A.D. Modelling, testing and analysis of a regenerative hydraulic shock absorber system. Energies 2016, 9, 386. [Google Scholar] [CrossRef] [Green Version]
- Xie, L.; Li, J.; Li, X.; Huang, L.; Cai, S. Damping-tunable energy-harvesting vehicle damper with multiple controlled generators: Design, modeling and experiments. Mech. Syst. Signal Process. 2017, 99, 859–872. [Google Scholar] [CrossRef]
- Bowen, L.; Vinolas, J.; Olazagoitia, J.L. Banco de ensayo para validar el modelo computacional de un cuarto de coche con amortiguador recuperador de energía. Dyna 2017, 93, 82–95. [Google Scholar] [CrossRef]
- Xie, L.; Li, J.; Cai, S.; Li, X. Electromagnetic energy-harvesting damper with multiple independently controlled transducers: On-demand damping and optimal energy regeneration. IEEE/ASME Trans. Mechatron. 2017, 22, 2705–2713. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, L.; Zuo, L. Design, Modeling, Lab and Field Tests of a Mechanical-motion-rectifier-based Energy harvester using a ball-screw mechanism. IEEE/ASME Trans. Mechatron. 2017, 22, 1933–1943. [Google Scholar] [CrossRef]
- Sabzehgar, R.; Maravandi, A.; Moallem, M. Energy regenerative suspension using an algebraic screw linkage mechanism. IEEE/ASME Trans. Mechatron. 2013, 19, 1251–1259. [Google Scholar] [CrossRef]
- Maravandi, A.; Moallem, M. Regenerative shock absorber using a two-leg motion conversion mechanism. IEEE/ASME Trans. Mechatron. 2015, 20, 2853–2861. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, X.; al Shami, E.; John, S.; Zuo, L.; Wang, C.H. A novel indirect-drive regenerative shock absorber for energy harvesting and comparison with a conventional direct-drive regenerative shock absorber. Appl. Energy 2018, 229, 111–127. [Google Scholar] [CrossRef]
- Li, Z.; Zuo, L.; Luhrs, G.; Lin, L.; Qin, Y. Electromagnetic energy-harvesting shock absorbers: Design, modeling, and road tests. IEEE Trans. Veh. Technol. 2012, 62, 1065–1074. [Google Scholar] [CrossRef]
- Smith, M.C. Synthesis of mechanical networks: The inerter. IEEE Trans. Automat. Contr. 2002, 47, 1648–1662. [Google Scholar] [CrossRef] [Green Version]
- Armstrong, B.; de Wit, C.C. Friction modeling and compensation. In the Control Handbook; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Abdelkareem, M.A.A.; Xu, L.; Guo, X.; Ali, M.K.A.; Elagouz, A.; Hassan, M.A.; Essa, F.A.; Zou, J. Energy harvesting sensitivity analysis and assessment of the potential power and full car dynamics for different road modes. Mech. Syst. Signal Process. 2018, 110, 307–332. [Google Scholar] [CrossRef]
- Ren, H.; Chen, S.; Wu, Z. Model of excitation of random road profile in time domain for a vehicle with four wheels. In Proceedings of the 2011 International Conference on Mechatronic Science, Electric Engineering and Computer (MEC), Jilin, China, 19–22 August 2011; pp. 2332–2335. [Google Scholar]
- Múčka, P. Simulated road profiles according to ISO 8608 in vibration analysis. J. Test. Eval. 2017, 46, 405–418. [Google Scholar] [CrossRef]






| Rated Voltage | Rated Speed | Max Permissible Speed | Rated/Max Current | Internal Resistor Ri | Internal Inductance Li | Torque Constant Kt | Voltage Constant 1/Kre |
|---|---|---|---|---|---|---|---|
| 48 V | 2700 r/min | 12,000 rpm | 1.38 A | 6.6 Ω | 1.7 mH | 0.137 nm/A | 69.7 rpm/V |
| Parameters | Value | Units | |
|---|---|---|---|
| Inertia of motor | Jm | 121 | gcm2 |
| Inertia of screw | Js | 180 | gcm2 |
| Ball center-to-center diameter | ds | 16 | mm |
| Screw lead | τ | 5 | mm/rev |
| Parameters | Value | Units | |
|---|---|---|---|
| Inertia of motor | Jm | 121 | gcm2 |
| Inertia of the multiplier | Jmu | 100 | gcm2 |
| Inertia of the 1st pulley | Jpt1 | 233 | gcm2 |
| Inertia of the 2nd pulley | Jpt2 | 81 | gcm2 |
| Multiplier ratio | kmu | 5 | |
| Generator pulley radius | Rpg | 8 | mm |
| Cable stiffness coefficient | kc | 1104 | kN/m |
| Cable damping coefficient | cc | 100 | N/(m/s) |
| Road Level | Gq(n0)(x10−6)m3 n0 = 0.1 m−1 | ||
|---|---|---|---|
| Lower Limit | Average | Upper Limit | |
| A | 8 | 16 | 32 |
| B | 32 | 62 | 128 |
| C | 128 | 256 | 512 |
| D | 512 | 1024 | 2048 |
| E | 2048 | 4096 | 8492 |
| F | 8192 | 16,384 | 32,768 |
| BS-EHSA | CD-EHSA | |||||||
|---|---|---|---|---|---|---|---|---|
| Transmission Factor (mm/rev) | External Load Re (Ω) | Generator Model | Transmission Factor (mm/rev) | External Load Re (Ω) | Generator Model | |||
| Compression | Extension | Compression | Extension | |||||
| Ford-Focus | 3.5 | 0.6 | 1000 | Maxon 136210 | 3 | 3 | 0.7 | Maxon 136210 |
| Renault-Twizy | 6 | 3 | 1300 | Maxon 218010 | 6 | 2 | 40 | Maxon 218010 |
| Rated Voltage | Rated Speed | Max Permissible Speed | Rated/Max Current | Internal Resistor Ri | Internal Inductance Li | Torque Constant kt | Voltage Constant 1/kre |
|---|---|---|---|---|---|---|---|
| 24 V | 7970 r/min | 12,000 r/min | 12.5 A | 0.143 Ω | 0.056 mH | 0.0263 nm/A | 364 rpm/V |
| CD-EHSA | BS-EHSA | ||
|---|---|---|---|
| Advantages | Disadvantages | Advantages | Disadvantages |
| ● The backlashes decrease in the change of direction when using a cable transmission. | ● Its damping coefficient has a greater dependence on the excitation frequency compared to other EHSA technology. | ● Its design and manufacturing is simpler. | ● The speed of rotation is limited by the wear of the inner balls in the nut. |
| ● Inertial values can be reduced by using a cable and a pulley as the main element. | ● There are not many works in EHSA literature using cable transmission. It is a solution still in the maturation phase. | ● It allows a more compact design. | ● Its durability in the use of suspensions is affected by the impacts that may exist internally between the nut and the screw in the change of direction. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bowen, L.; Vinolas, J.; Olazagoitia, J.L. Design and Potential Power Recovery of Two Types of Energy Harvesting Shock Absorbers. Energies 2019, 12, 4710. https://doi.org/10.3390/en12244710
Bowen L, Vinolas J, Olazagoitia JL. Design and Potential Power Recovery of Two Types of Energy Harvesting Shock Absorbers. Energies. 2019; 12(24):4710. https://doi.org/10.3390/en12244710
Chicago/Turabian StyleBowen, Lincoln, Jordi Vinolas, and José Luis Olazagoitia. 2019. "Design and Potential Power Recovery of Two Types of Energy Harvesting Shock Absorbers" Energies 12, no. 24: 4710. https://doi.org/10.3390/en12244710
APA StyleBowen, L., Vinolas, J., & Olazagoitia, J. L. (2019). Design and Potential Power Recovery of Two Types of Energy Harvesting Shock Absorbers. Energies, 12(24), 4710. https://doi.org/10.3390/en12244710