Next Article in Journal
Ammonium Sulphate from a Bio-Refinery System as a Fertilizer—Agronomic and Economic Effectiveness on the Farm Scale
Previous Article in Journal
Reduction in Sunshine Duration and Related Factors over Mainland China during 1961–2016
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 12
Issue 24
10.3390/en12244719
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Dispersive Optical Systems for Highly-Concentrated Solar Spectrum Splitting: Concept, Design, and Performance Analyses

by
Si Kuan Thio
1 and
Sung-Yong Park
2,*
1
Department of Mechanical Engineering, National University of Singapore, Singapore 117575, Singapore
2
Department of Mechanical Engineering, San Diego State University, San Diego, CA 92182-1323, USA
*
Author to whom correspondence should be addressed.
Energies 2019, 12(24), 4719; https://doi.org/10.3390/en12244719
Submission received: 16 November 2019 / Revised: 7 December 2019 / Accepted: 9 December 2019 / Published: 11 December 2019
(This article belongs to the Section A2: Solar Energy and Photovoltaic Systems)
Browse Figures
Versions Notes

Abstract

:
We present a concept design of a solar spectrum splitting system that enables highly-concentrated solar energy harvesting over the entire AM1.5 spectral range. After passing through an array of the dispersive optical system (DOS) module composed of a grating structure and dispersive prisms below a concentrating lens, incident sunlight can be separated into two wavelength bands of visible (VIS) and infrared (IR) ranges, which can then be focused onto corresponding solar receivers. Based on the spectral response of typical crystalline silicon solar cells, the VIS wavelength band is selected from 0.4 μm to 1.2 μm to contribute to photovoltaic (PV) conversion to generate electricity. Meanwhile, the IR band in longer wavelength ranges (1.2 μm ≤ λ ≤ 2.5 μm), which does not contribute to PV conversion, can be simultaneously used for solar thermal applications such as water heating and thermoelectricity. In this paper, various design parameters (e.g., focal length of a concentrating lens, groove density of a grating, geometry of dispersive prisms, material combination of optical components, etc.) have been investigated to determine an optimum set of system configurations, using optical design software (Zemax OpticStudio 14.2). Our simulation studies validate that the DOS is able to split incident AM1.5 solar irradiance into the two wavelength bands of the VIS and IR ranges and focus each wavelength band with concentration factors as high as 798× and 755× on the same focal plane, respectively. Such high concentration factors for both wavelength bands can be actualized due to the additional optical components used—a grating structure and dispersive prisms, which allow to minimize optical aberrations through both diffraction and refraction. The proposed DOS, designed with commercially available optical components, has the potential to widen the use of the sun’s spectrum by allowing effective PV conversion of solar cells under high concentration with tolerable optical system losses and concurrently converting the remaining solar irradiation into useful energy for a broad range of thermal applications.

Graphical Abstract

1. Introduction

Due to limited supply of fossil energy sources and climate change, solar energy has been foreseen as one of the promising sustainable energy solutions. When sunlight reaches the earth in the form of electromagnetic radiation, its optical path length through the earth’s atmosphere is defined as the air mass (AM) coefficient relative to the vertical path length. The AM1.5 solar spectrum, which is mainly confined between 0.3 μm ≤ λ ≤ 2.5 μm, has been universally used to characterize the solar spectrum [1,2]. Solar irradiance from the AM1.5 can be typically converted into useful electrical and thermal energy forms using a wide range of solar power technologies such as photovoltaics [3,4,5], solar thermo-chemical reaction [6,7], and concentrated solar power (CSP) [8,9,10,11,12].
Among these solar power technologies, photovoltaic (PV) methods have been conveniently used because radiative solar energy can be directly converted to electricity with solar cells. Incident sunlight is absorbed by the semiconducting materials of a solar cell and excites electrons to a higher energy state to generate electricity [13]. This PV process indicates that the energy bandgap of the semiconducting materials used in a solar cell inherently limits their spectral response [14,15]. For example, a crystalline silicon (c-Si) solar cell, which is most popularly used in PV markets [16,17,18,19], has the energy bandgap around 1.12 eV that typically corresponds to the narrow solar spectral response within 0.4 μm ≤ λ < 1.2 μm [15]. This indicates that photons in lower energy states are not able to contribute to forming electron-hole pairs and generating electricity [20,21]. In order to cover a wide range of solar spectrum, multi-junction solar cells have been developed by stacking several different semiconducting materials in a series connection [22]. Each of the semiconducting materials responds to different energy bandgaps and allows the absorption of wide solar spectrum, resulting in the increase of the solar cell’s efficiency [22,23]. Although the simultaneous use of multiple junctions in a solar cell is able to utilize a broader range of the solar spectrum [24], several issues are raised in stacking different semiconducting materials together. Due to the issue of spectral and lattice matching between adjacent junctions, the choice of semiconducting materials is limited to cost-ineffective ones such as gallium arsenide (GaAs) and germanium (Ge) [25,26]. This also leads to complex and expensive fabrication processes, e.g. wafer bonding and metal organic chemical vapor deposition (MOCVD) [19,27,28].
In recent years, solar spectrum splitting technologies have been alternatively proposed to harvest wide-spectral solar energy [29,30,31,32,33,34,35,36,37,38,39,40,41,42]. Using spectral splitting dichroic filters, a portion of the infrared radiation is separated from a wide solar spectrum and the sunlight in the only visible range is then directed to solar cells for PV conversion [29,30,31,32,33,34,35,36]. Not only can excessive heating be removed from solar cells to improve their PV performance, but also the filtered solar spectrum in the infrared range is simultaneously used for other solar thermal applications such as water heating and thermoelectricity [26,30,43]. However, the filters used for such hybrid photovoltaic/thermal systems typically make the incoming sunlight spatially redirected to achieve solar slitting, before it is focused onto each of solar receivers (e.g., PV cells and thermal absorbers). As a result, hybrid systems significantly lose solar concentration performance, to as small as 8.7× [24,25,43]. To provide higher concentration, more complicated systems have been investigated using solar towers illuminated by heliostats, leading to large system sizes as well as increased cost [37,38,39,40,41,42].
In this study, we present conceptual demonstrations of a dispersive optical system (DOS) that enables highly-concentrated spectral splitting to effectively harvest wide-spectrum solar energy for potential photovoltaic/thermal applications. The DOS module is designed to be compact with commercially-available optical components such as a diffractive grating and dispersive prisms that are placed below a low-cost Fresnel lens. While incoming sunlight in a wide spectral range passes through an array of the DOS module, it undergoes both light diffraction and refraction such that optical aberrations are minimized. As a result, two wavelength bands split into the visible (VIS) and infrared (IR) ranges can be effectively focused onto corresponding solar receivers positioned on the same focal plane without spatial redirection that has been typically observed for previous solar spitting technologies. Our simulation studies validate that the VIS range of the sunlight can be focused onto a solar cell with a concentration factor as high as 798× for effective PV energy harvesting. Concurrently, the separated IR irradiation, which does not contribute to PV conversion, can also be used for possible solar thermal applications such as water heating and thermoelectricity under a concentration factor of 755×. Concept and design issues of the DOS module were discussed in this paper. Using the optical design software (OpticStudio 14.2, Zemax LLC, Kirkland, WA, USA), the optical performance was also investigated with varying the focal length of an external Fresnel and various DOS parameters (e.g., prism materials and geometry, a grating component, etc.) to understand their effects on spectrum splitting and solar concentration. The proposed DOS optical system is conveniently scalable in size and designed with commercially-available optical components for cost effectiveness. Our solar splitting technology offers the potential to widen the use of the sun’s spectrum to allow effective PV conversion and concurrently converting the remaining solar irradiation into useful thermal applications under high concentration.

2. Overview of Sunlight Separation System

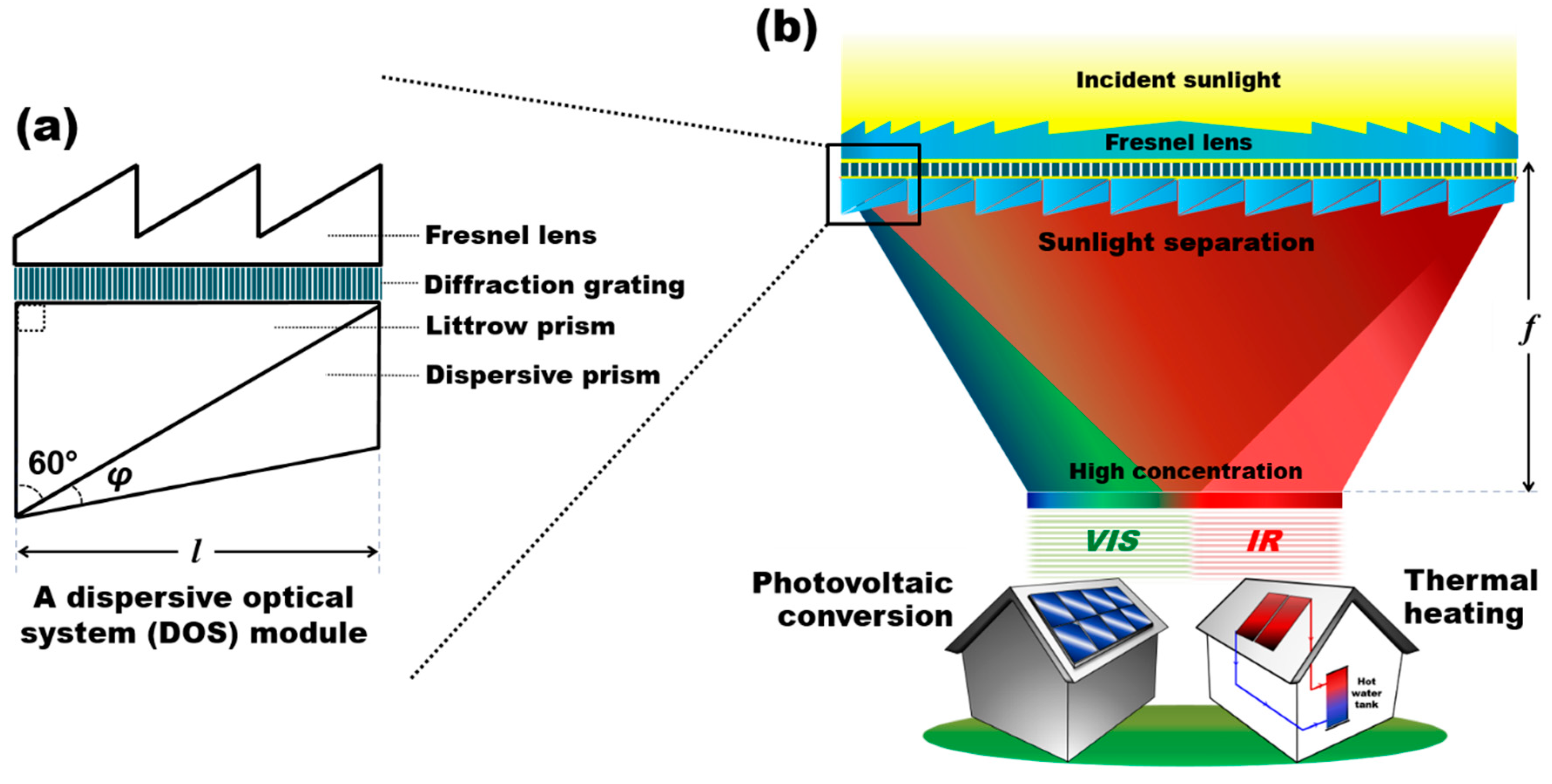
Figure 1 shows a schematic of the DOS array placed underneath a Fresnel lens to achieve highly-concentrated solar spectrum splitting. The DOS module mainly consists of three commercially-available optical components in the design (Figure 1a): a layer of diffraction grating, followed by compound prisms of a low-dispersion Littrow prism and another triangular high-dispersion prism, similar to the concept of an Amici prism [44,45].
As illustrated in Figure 1, sunlight is focused by the Fresnel lens before entering the interface of the DOS, where it undergoes dispersion through diffraction by a grating layer, followed by refraction in the two layers of arrayed dispersive compound prisms. In this study, the solar spectrum separated by the DOS array is based on the spectral response of the crystalline silicon (c-Si) solar cell that is the most commonly used one in PV markets [16,17,18,19]. Here, we classified the solar spectrum into two wavelength bands. The first wavelength band selected is the VIS range of 0.4 μm ≤ λ < 1.2 μm, mainly contributing to PV conversion of the c-Si solar cells. Thereon, the other wavelength band is chosen as the IR range of 1.2 μm ≤ λ ≤ 2.5 μm, forming the majority portion of the AM1.5 solar spectrum not absorbed by the c-Si cells for PV conversion [46].
It is also important to note that the focal length of the external Fresnel lens, as its feature of the optical distance where light rays converge, has a key influence on the optical performance achieved by the DOS. Typically, the focal length of a commercial optical lens is defined at a specific wavelength designed by manufacturers, although not all the rays converge to a single point at the defined focal length due to optical aberrations. Moreover, the function of the DOS is to spilt sunlight into two wavelength bands on the given focal plane. Therefore, our study defines the focal plane horizontally drawn at the focal point of the rays at λ = 1.2 μm in order to have a clear distinction between the two wavelength bands that are separated at λ = 1.2 μm. Hence, the minimum footprint size of the respective solar receivers is determined on the given focal plane. The concentration performance of each VIS and IR wavelength band achieved by the DOS can be estimated by the area reduction ratio between solar input and focused output as:
Concentration   factor = An   area   of   input   light An   area   of   focused   output   light .
In the following subsections, we will describe how each of the DOS components works for achieving solar spectrum separation with high concentration.

2.1. A diffraction Grating

Figure 2 illustrates a transmissive diffraction grating which is used as the first optical element to diffract sunlight into its individual wavelengths. When light emits from the grating, it is dispersed into fringes on the opposite side of the grating at a fixed diffracted angle, based on the grating’s diffraction order. The diffraction angle of a light beam can be determined by the well-known transmissive diffraction grating equation as [47]:
2 d ( sin θ m + sin θ i ) = m λ ,
where θi and θm are the angles of the incident and diffracted beam, m is an integer representing the diffraction order (i.e., m = 0, ±1, ±2 …), λ is the wavelength of light, and d is the distance between the grating grooves, which can be characterized by the density of the grooves (dg), i.e., the number of grooves per unit length (grooves/mm). Equation (2) ensures that light beams entering the grating structure are diffracted into its constituent wavelength components (where λ1 > λ2 > λ3 …) with the respective diffraction angle of θm at each individual order of m.
As shown in Figure 2, when light undergoes diffraction through the grating to form a light spectrum, the ray at the diffraction order of m = 0 does not experience diffraction. For m = ±1, however, the ray at a longer wavelength (e.g., λ1) diffracts more than a shorter wavelength (e.g., λ3) and results in having a larger diffraction angle [48]. Similarly, high diffraction orders for |m| ≥ 2 are also formed into fringes, but they typically possess very little optical power (<3%) [49].
Figure 3a illustrates the ray tracing when incoming light passes through the stack of a Fresnel lens and a grating structure. For the rays at the 0th diffraction order, a spectrum of chromatic aberration is created by the concentrating lens without diffraction, while the rays at m = ±1 experience both concentration and diffraction, thus forming an asymmetrical Petzval field curvature (to be further discussed in Section 3.1). This ray tracing based on the combination of light concentration and diffraction (see Figure 3a) does not show any sunlight separation at m = 0 as well as very poor concentration performances for the rays at m = ±1. Therefore, this optical design is truly undesirable to obtain highly-concentrated sunlight separation. To address this issue, a different type of the grating structure was proposed to allow a very high diffraction efficiency in a specific order [48]. For our study, the concept of a blazed grating structure was used to create the diffraction efficiency maximized at the +1st diffraction order, while minimizing the residual power in the other orders. To provide a blazed surface (i.e. triangular grooves), an array of Littrow prisms is placed after the grating structure, as shown in Figure 3b. This indicates that incident light experiences the refraction through the blazed surface by the Littrow prisms after concentration and diffraction. As a result, the majority of input optical power can be focused in the 0th and +1st diffraction orders [49].

2.2. Dispersive Compound Prisms

The secondary dispersion mechanism is based on an array of compound prisms. When light passes through a prism, it will be dispersed into its constituent wavelengths with each wavelength of light having its individual refractive index [48]. Therefore, a dispersed light ray of any specific wavelength can be traced by determining its refraction angle, which can be expressed using Snell’s law of refraction as:
θ r = sin − 1 [ n 1 n 2 sin θ i ] ,
where θi represents the incident angle of incoming light ray, θr is its refracted angle as it emerges out of the prism, n1 and n2 indicate the refractive indices of the two media that the light passes through. As discussed in the previous section, the first layer of prisms has been selected as a Littrow prism that is able to provide a blazed surface to focus the majority of the input light closer together via refraction (Figure 3b). While it is possible to use prisms with intricate angles, commercially available Littrow prisms with fixed prism angles of 30°/60°/90° have been chosen as they can be easily manufactured, which will also help us to keep overall system cost as low as possible. In addition, it is also suggested that the Littrow prism is made of the same low-dispersion material as the grating structure to reduce possible reflection losses.
Compared to the situation of Figure 3a, the optical performance can be much improved by using a layer of Littrow prisms after a grating (Figure 3b). However, due to optical aberrations caused by the grating structure and the array of Littrow prisms, a Petzval field curvature is almost vertically formed and solar concentration performance remained poor. To further improve it, the second layer of high-dispersion prisms with the prism angle of φ was implemented (refer to Figure 1a), where incident light undergoes effective dispersion. Figure 3c illustrates the combination of both two layers of the prisms in contact, resembling the concept of an Amici prism [44,45]. The material of the second prisms has been selected such that they have a similar refractive index as the first Littrow prisms at the Fraunhofer “D” line of 589.3 nm (i.e., n1 ≈ n2 where 1 and 2 denote the first Littrow prism and the second triangular prism), but different Abbe numbers (VD1 ≠ VD2) such that the center wavelength of light can emerge from the compound prisms as nearly parallel to the entrance light beam as possible, i.e., the minimum ray deviation. The rays at the remaining wavelengths are consequently refracted at the angles relative to the materials’ Abbe numbers such that the light dispersion eventuates to an optical spectrum. Selecting materials with a similar refractive index between two prisms can also be beneficial to minimize geometric optical losses and compensate beam deviation while maintaining chromatic dispersion, i.e., minimizing comatic aberration along the Petzval field curvature [50,51]. The dispersive compound prisms make use of Snell’s law of refraction to disperse the white light chromatically in accordance to their wavelengths derived from the Fermat’s principle [52]. A shorter wavelength of light will deviate more from its original path than the one with a longer wavelength.
Although both diffraction grating and prism components in the DOS module serve to disperse sunlight, they operate on very different mechanisms, i.e. one makes diffraction and another induces refraction. When light undergo diffraction through the grating structure to form a light spectrum, a ray at a longer wavelength (e.g., λ1) will diffract more than that of a shorter wavelength (e.g., λ3) and have a larger diffraction angle θm, as presented in Figure 2. However, when light undergoes dispersion through refractive optical media, shorter wavelengths of light will refract more than longer wavelengths of light. Hence, each wavelength of light in a diffraction spectrum is said to be in transposition to its corresponding wavelength of light in a refractive spectrum. Such phenomenon can greatly enhance the optical performances of the DOS by adding the second layer of high-dispersion triangular prisms. When sunlight undergoes separation through the DOS, the combination of the diffraction grating component and Littrow prisms allows high diffraction efficiency in the 0th and 1st orders, but it still causes optical aberrations as shown in Figure 3b. By adding the second layer of high-dispersion prisms, the aberrations can be corrected through refraction. Figure 3c illustrates how the DOS array can undergo effective sunlight separation and, at the same time, minimize comatic aberrations to achieve high solar concentrations. The illustrated beam pathways discussed in Figure 3 are supported by ZEMAX simulation results presented in a supplement document.

3. Performance Analyses

The DOS enables highly-concentrated solar spectrum splitting into two wavelength bands. The VIS wavelength band of 0.4 μm ≤ λ < 1.2 μm mainly contributes to PV conversion of the c-Si solar cells, while the IR band of 1.2 μm ≤ λ ≤ 2.5 μm is simultaneously used for alternative thermal heating applications. Solar performance achieved by the DOS relies on various parametric combinations (e.g., a focal length of the external concentrator, prism materials and geometry, a grating component, and so on). In this section, we used optical design software (OpticStudio 14.2, ZEMAX) to investigate how each parameter can be varied to meet the design criteria of the DOS—to realize separation of sunlight into VIS and IR wavelength bands while achieving high solar concentration for both wavelength bands by ensuring the minimum footprint sizes of the solar receivers, respectively. To simulate solar irradiance, the input light source was assumed to provide collimated light covering the AM1.5 spectrum ranging from 0.4 µm to 2.5 µm. For the simulation simplification, this solar input was chosen as a total of 10,000 rays with an aperture size of 50 × 1 mm2. This couples the solar input with a linear array of 50 DOS modules and a cylindrical Fresnel lens, so that light rays can cover every spot along one axis. Parametric studies with varying inputs are discussed in the following subsections.

3.1. Effect of the Focal Length

The effect of the focal length (f) given by an external Fresnel lens has been first studied. To evaluate the concentration performance (i.e., the minimum footprint size of respective solar receivers), we select a common focal plane horizontally drawn at the focal point of the rays at λ = 1.2 μm, where the two wavelength bands can be clearly separated. Therefore, their concentration factors can be subsequently estimated on the given focal plane by using Equation (1). For this study, the external lens’s focal length was varied from 50 mm to 200 mm, while other control parameters were set to be the grating density as dg = 12 grooves/mm and the apex angle of the second prism as φ = 19°. The length of each prisms (refer to Figure 1a) was set as l = 1 mm, while their materials were selected as low-dispersion BK7 (VD2 = 64.17) for the Littrow prism and high-dispersion F2 (VD2 = 36.37) for the second triangular prism (justifications for choice of materials are discussed in Section 3.3).
Figure 4 shows simulation results of the concentration factor for both VIS and IR wavelength bands. An opposite trend is observed for each wavelength band; one increases but another decreases as the increase of the lens’s focal length. To help understand such simulation results in solar concentration performance varied by the focal length, a concept of the Petzval field curvature is introduced [50]. Due to optical aberrations, each wavelength of light cannot be brought into focus on a common flat plane. Typically, rays at shorter wavelengths (e.g., λ = 0.4 µm) have much shorter focal points than the ones at longer wavelengths (e.g., λ = 2.5 µm). Such a curve collecting these focal points varied by the rays’ wavelengths is called the Petzval field curvature, where every focal point is asymmetrically distributed.
The illustration in Figure 5a presents how the Petzval field curvature is formed when sunlight undergoes dispersion after passing through the DOS array, where λL and λR denote the wavelengths of light rays emitting from the leftmost and rightmost DOS module, respectively. The rays at the same wavelength but different incident locations (e.g., λ = λL = λR = 0.4 µm) come across their pathways at a focal point on the Petzval field curvature and followed by diverging onto the focal plane. Therefore, the minimum footprint size of each solar receiver can be determined by how far this Petzval field curvature is away from the focal plane at specific wavelengths. It is interestingly found that the lens’ focal length (f) has an influence on the formation of the field curvature. As shown in Figure 5a, when the Fresnel lens with a short focal length is used, the field curvature is formed far away from the focal plane particularly at short wavelengths (e.g., λ = 0.4 µm). This results in the rays diverging upon passing through their focal point and being incident on the focal plane with the extreme left at λR = 0.4 µm. Consequently, the footprint size for the VIS wavelength band covering the spectrum of 0.4 μm ≤ λ < 1.2 μm becomes very large with poor concentration performance, while the IR range of 1.2 μm ≤ λ ≤ 2.5 μm can have relatively high concentration. In contrast, when f is long (refer to Figure 5b), the field curvature is formed far away from the focal plane particularly at longer wavelengths (e.g., λ = 2.5 µm), oppositely losing the concentration performance for the IR wavelength bands. The illustrated beam pathways discussed in Figure 5 are also supported by ZEMAX simulation results presented in a supplement document. Based on this understanding, solar concentration performance achieved by the DOS relies on how the Peztval field curvature is formed, which is varied by the external lens’s focal length selected by a system designer as presented in Figure 4.

3.2. Effects of the Grating Density and the Prism Angle

This section has investigated the dependency of the groove density (dg) of the diffraction grating and the apex angle (φ) of the second prism on system performance achieved by the DOS. For these studies, the groove density of a grating structure has been varied from 6 to 18 grooves/mm with several different values of the second prism angle (φ) ranging from 15° to 21°. All other control parameters such as f = 100 mm and prism length and materials are kept the same as the previous study.
Figure 6a presents their effects on the concentration factor for the IR wavelength band with various prism angles. The performance of solar concentration generally decreases with the increase of dg. This result can be explained based on the grating equation in Equation (2). The high values of dg in a grating represents dense grooves with the short distance (d) between the grooves.
As indicated in Figure 2, for low values of d with a given θi, Equation (2) expresses large beam diffraction in IR ranges (i.e., large θm), where the Petzval field curvature is formed far away from the focal plane for longer wavelengths of light and leads to a loss in concentration effect. It is also observed from Figure 6a that the solar concentration increases with higher prism angles (φ). As light emerges from the last interface of the second prism, a larger φ causes a wider angle of refraction, in accordance to Snell’s law. As light at shorter wavelengths refracts more when compared to longer wavelengths within the IR wavelength band, every wavelength’s focal point within the wavelength band becomes closer together along the Petzval field curvature, resulting in a smaller footprint and thus a higher concentration factor.
On the contrary to the IR wavelength band, Figure 6b shows that the concentration factor for the VIS band at shorter wavelengths is less reliant on the groove density (dg). This observation has also been discussed in Figure 2. The VIS concentration is more dominantly influenced by the apex angle of the second prism. The same reasoning used in the performance of IR concentration can be applicable to explain this similar observation for VIS. A wider refraction angle causes light at shorter wavelengths to converge onto the longer wavelengths within each respective wavelength bands, resulting in a smaller footprint and thus a higher concentration factor. One interesting point in Figure 6b, however, is the peak in concentration performance in the VIS wavelength band at dg = 13.5 grooves/mm when the prism is at φ = 21°. This is because the focal points of the light in the VIS range are found to be close to one another along the Petzval field curvature. Comatic aberration in the VIS ranges is said to be lowest at the given parameters, resulting in a very small VIS footprint and hence, such high concentration factor.
However, while certain groove densities at specific prism angles provide high solar concentrations in either VIS or IR, not every set of parameters can be taken into consideration. This is because a fraction of the VIS wavelength band at notably short wavelengths (e.g., λL = 0.4 µm) is overlapped into the IR wavelength band at various grating densities and prism angles, as referred to the inset image of Figure 6c. Overlapping of these rays occurs when the field curvature becomes severe at the short wavelength ranges. As a result, the rays at λL = 0.4 µm continue to diverge after passing through their focal point and a fraction of these rays will eventually overlap with the footprint of the IR wavelength band on the common plane. This overlapping phenomenon is undesirable as a portion of the VIS wavelength band cannot contribute to PV conversion process. Figure 6c shows the percentage of the overlapped outmost λL = 0.4 µm ray in the IR wavelength band with respect to the footprint size of the IR band of the particular configuration. Positive values in Figure 6c signify that a portion of the VIS wavelength band is overlapped with the IR, as shown in an inset image of Figure 6c, while negative values signify that two wavelength bands are completely separated at the focal point of the rays at λ = 1.2 μm, as shown in the illustrations of Figure 5.
The marked data points (I, II, and III) in Figure 6 can be used to analyze the design choice of groove density and prism angle. Firstly, the point I (dg = 6 grooves/mm and φ = 21°) in the graphs of Figure 6 indicates a high concentration factor at above 1700× for the IR band. However, a much lower concentration factor of 500× is observed in the VIS band. Furthermore, this set of parameters causes the largest overlap between two wavelength bands at 110% as presented in Figure 6c. Secondly, the point II (dg = 13.5 grooves/mm, φ = 21°) reflects the highest VIS concentration factor of 940× in Figure 6b, while Figure 6a highlighted a slightly lower concentration factor of 738× for IR wavelength band. However, Figure 6c also shows a positive value of 4%, verifying an overlap between the two wavelength bands. Lastly, the point III (dg = 12 grooves/mm, φ = 19°) demonstrates similarly high concentration factors of 798× and 755× for VIS and IR wavelength bands, respectively. A negative value of −0.1% in Figure 6c has indicated no overlapping between the two wavelength bands. Therefore, while this study has shown that low groove densities and large prism angles can achieve high solar concentrations of either VIS or IR, the tradeoff comes with an increase in the overlapped percentage between two wavelength bands. Finally, a point III shows balanced concentration performances for both VIS and IR bands without the overlapping.

3.3. Effect of Prism Material

As the wide-spectrum sunlight passes through the DOS, it undergoes dispersion with the longer wavelengths travelling through the prism faster than the shorter wavelengths, resulting in chromatic dispersion. The Abbe number (VD) indicates the level of the prism materials for optical dispersion, according to the variation of its refractive index with respect to the wavelength. Low dispersive materials have the high value of VD, while the low VD indicates the materials with high dispersion. To understand the effect of the prism materials on system performance, we define the ratio (Vr) of the Abbe number between the two prism materials as:
V r = V D 1 / V D 2 ,
where VD1 and VD2 are the Abbe numbers for the first Littrow prism and the second dispersive prism, respectively. Based on such a definition, it is noted that a higher value of Vr signifies more dispersion of the rays. For this study, several prism materials are selected based on their similarities in refractive indices but differences in the Abbe number. The material for the first layer (i.e., a Littrow prism) is identified as BK7, which is also the same material used for the Fresnel lens and grating structure to reduce possible optical losses at their interface. The material of BK7 also offers a high Abbe number of VD1 = 64.17 to minimize the ray deviation, hence the less effect of comatic aberration to achieve high solar concentration [50,51]. With the given first material, the Vr value was varied from 0.70 to 1.76 by possibly selecting several materials for the second dispersive prism as N-FK58 (VD2 = 90.90), N-PK51 (VD2 = 76.97), BK7 (VD2 = 64.17), KZFS4 (VD2 = 44.49), and F2 (VD2 = 36.37). These materials were chosen based on the proximity of their refractive indices as compared to the one for BK7 to minimize the ray deviation due to comatic aberrations. In this study, other control parameters were set to be as f = 100 mm, l = 1 mm, φ = 19°, and dg = 12 grooves/mm.
Figure 7 presents simulation results of the concentration factors for the VIS and IR wavelength bands. At Vr = 1.0, indicating that the two prisms are made of the same material and hence the minimum spectral dispersion, the lowest concentration performance is obtained for both the VIS and IR wavelength bands. While | Vr | > 1.0, the concentration factor increases due to the high value of Vr dominantly refracting incoming rays. The study in Figure 7 notes us that it is beneficial to have a large Vr for material combination. With the Littrow prism assumed to be made of a low-dispersion material of BK7, the second dispersive prism is recommended to be made of a high-dispersion material (i.e., low VD2). Based on the study indicated in Figure 7, the DOS is able to split the wide solar spectrum into the two wavelength bands to achieve the concentration factors as high as 798× and 755× for both VIS and IR bands at Vr = 1.76.

3.4. Reflection Loss

Fundamentally, reflection loss, which occurs when light is incident onto the interface shared by two different media of different refractive indices, is one of the performance metrics to be concerned [53,54]. A reflection loss could be accumulated at the interfaces across the 3 optical components of the DOS, which is dependable on incident angles of incoming light as well as the refractive index ratio between the two media. After the Fresnel lens, the rays are focused with various incident angles along the grating structure, before reaching the two layers of prisms. Maximum reflection loss occurs for the rays being incident at the extreme ends of the DOS, where incident angles of incoming concentrated light are highest.
For this study, a ray tracing software (Zemax OpticStudio 14.2) was used to measure the total optical power before and after the interfaces of the DOS for both VIS and IR wavelength bands. High solar concentrations can be achieved by placing the DOS underneath a Fresnel lens, which has been widely used in regular concentrating solar applications such as concentrated photovoltaics (CPV) and concentrated solar power (CSP). Optical losses by reflection occurring in the Fresnel lens are inevitable for any optical system (i.e., DOS, CPV/CSP systems). By using only the Fresnel lens (f = 100 mm) without any dispersion mechanism attached for comparison, a typical CPV/CSP system is simulated to have a solar concentration only 38× (Zemax simulation results presented in a supplement document), due to chromatic aberrations over the whole sunlight spectrum. However, by additionally attaching the DOS underneath the concentrating lens, solar spectrum separation with higher solar concentration factors can be achieved for both VIS (798×) and IR (755×) wavelength bands with only an additional 5.8% in overall reflection losses of the system. Moreover, reflection losses can be further reduced around 2.7% by applying a thin film of a matching refractive index based on the principle of Rayleigh’s film [48] between the two layers of dispersive arrayed prisms.

4. Optimum System Configuration for Balanced Performance

Based on the parametric studies discussed in the previous sections, different permutations of parameters can be chosen to fulfill the established design requirements of the DOS system. System performance is entirely up to one’s discretion. In this paper, we determined an optimized system to have similar weightages in concentration performances for VIS and IR wavelength bands. As the VIS wavelength band ranging, 0.4 μm ≤ λ < 1.2 μm, is designated to PV conversion of c-Si solar cells, having a high concentration offers advantages such as cost reduction in material and higher conversion cell efficiency [55]. On the other hand, IR wavelength band covering 1.2 μm ≤ λ ≤ 2.5 μm is being converted for solar thermal applications, where high concentration factors are critically required for effective thermal energy harvesting. Therefore, we optimized the DOS for both VIS and IR to have equally high concentration performances.
By referring to Figure 4, we recognized that the increase of the lens’ focal length results in an increase in the DOS’ performance of solar concentration in the VIS wavelength band, but at the expense of a decrease in performance of solar concentration in the IR wavelength band. In order for both VIS and IR wavelength bands to have similar weightages in solar concentration, keeping in view of the optical components’ commercial availability for low-cost systems, an external Fresnel lens with a focal length of f = 100 mm has been suggested. Additionally, from Figure 6, we observed that having small dg and large φ is necessary to achieve high VIS and IR concentration factors required for effective energy harvesting. However, a small dg and a large φ will have an undesirable overlapping between two wavelength bands, as the case of the point I indicated in Figure 6. Moreover, Figure 6b,c demonstrated extremely high VIS concentration factor without the overlapping of two wavelength bands when dg = 13.5 grooves/mm and φ = 21° (as the case of the point II indicated in Figure 6). However, the concentration factor of the IR range is found to be significantly lower, which did not satisfy the design criterion with similar weights in concentration performance for both wavelength bands. Consequently, the DOS module has been established to have a diffraction grating layer of groove density, dg = 12 grooves/mm, followed by the dispersive compound prism geometrics of 30°/60°/90° prism angles for the first Littrow prism and φ = 19° the second triangular dispersive prism, as the case of point III in Figure 6. Finally, based on the results presented in Figure 7, it was understood that a large value of Vr is preferred to achieve high solar concentration. As such, the dispersive compound prism in each DOS module with a material combination as high as Vr = 1.76 is preferred, where the Littrow prism is made of BK7 while the second triangular dispersive prism is made of F2.
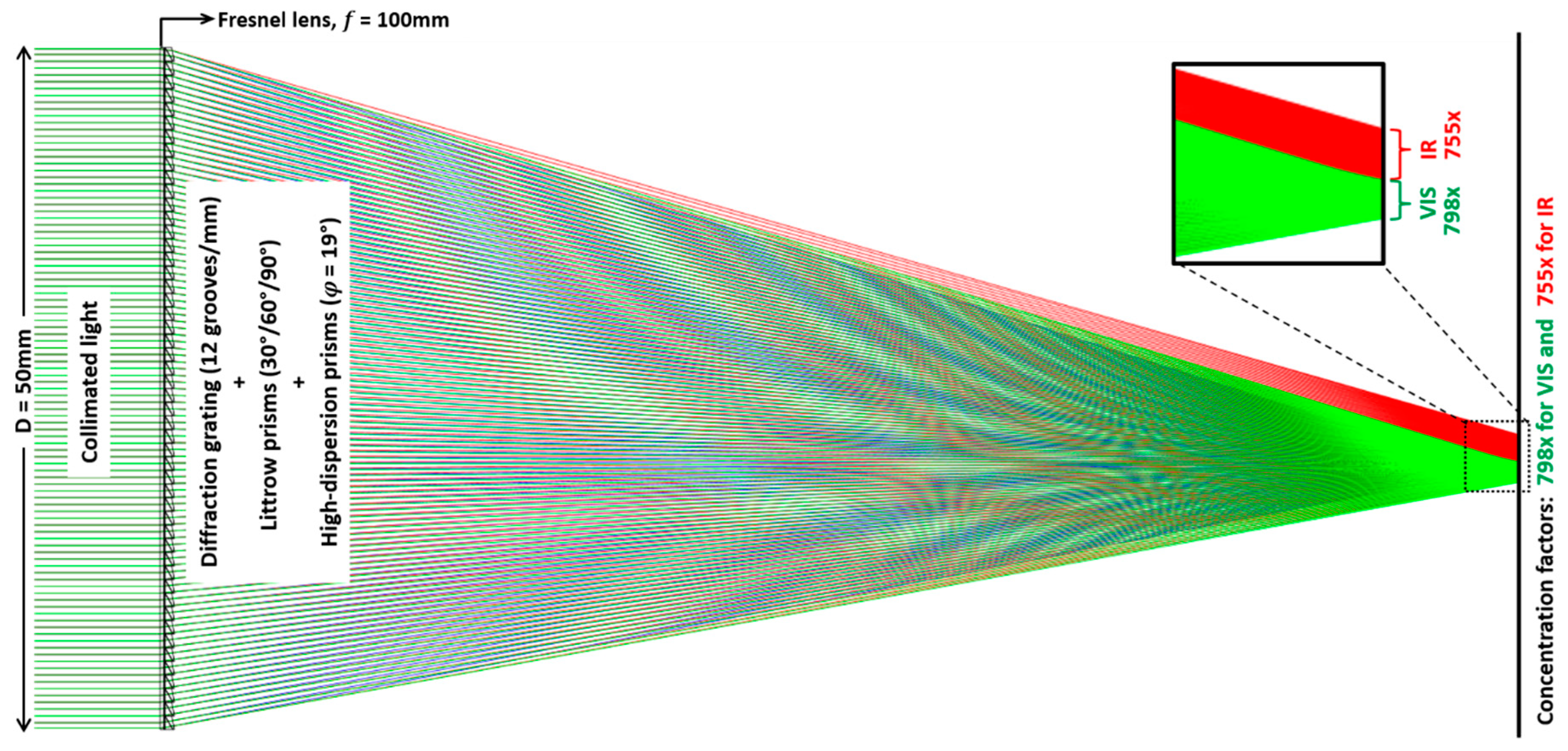
In summary, Figure 8 illustrates a ray tracing result of the system performance achieved by placing the DOS array below an external concentrating lens with the established parameters. Firstly, a commercially-available Fresnel lens (diameter, D = 50 mm) with f = 100 mm is chosen. Below the lens, the DOS is assembled with its first optical component as a grating layer with the groove density of dg = 12 grooves/mm. Subsequently, a Littrow prism array with the prism angles of 30°/60°/90° and the length of l = 1 mm is modelled for each prism after the grating layer as the second optical component (refer to Figure 1). An array of triangular dispersive prism (φ = 19°) with the length of l = 1 mm for each prism is also attached as the last component of the DOS. The Littrow prism is selected with a low-dispersion material, BK7 (n1 = 1.52 and VD1 = 64.17) while the second triangular dispersive prism is assumed to be made of a high-dispersion material, F2 (n2 = 1.62 and VD2 = 36.37). Similar to previous studies, the input light source emits collimated light covering AM 1.5 solar spectrum from 0.4 µm to 2.5 µm to simulate solar irradiance. A total of 10,000 rays is firstly being focused by the Fresnel lens and then dispersed spectrally after passing through the combined DOS system, separating into two wavelength bands in the VIS and IR ranges with similar concentration factors at the focal plane defined by the focal point of the λ = 1.2 μm rays. The VIS wavelength band (0.4 μm ≤ λ < 1.2 μm) separated by the DOS is designated for PV conversion of the c-Si solar cells with the solar concentration as high as 798×. Likewise, the DOS can utilize the IR wavelength band (1.2 μm ≤ λ ≤ 2.5 μm) concurrently for various thermal applications with similar concentration performance of 755. While poor concentration performance of a typical CPV system is largely dominated by chromatic aberration, high solar performances are achievable by adding the DOS array because sunlight is being focused and then subsequently separated into two highly concentrated wavelength bands (VIS or IR) with minimum optical aberrations.
An additional comparative study has been also conducted to determine the concentration performances for an ordinary system comprising of only a single Fresnel lens with an identical focal length (f = 100 mm) without the DOS array, presented in a supplement document. First, an input light source was set to be incident onto the only Fresnel lens using only wavelengths in VIS range (0.4 μm ≤ λ < 1.2 μm) and a following study was conducted with only wavelengths in the IR range (1.2 μm ≤ λ ≤ 2.5 μm). The ray tracing results estimated concentration factors of just 38× and 65× for VIS and IR ranges respectively, validating the poor concentration performances due to chromatic aberrations caused by using the only Fresnel lens. Clearly, by additionally placing the DOS array composed of a diffraction grating and dispersive prisms below the lens, we can realize much higher concentrations of 798× and 755× for both VIS and IR respectively, as much as 21.0 folds (VIS band) and 11.6 folds (IR band) higher than what are achieved in ordinary systems with a single Fresnel lens.

5. Conclusions

We present a novel dispersive optical system (DOS) that enables highly-concentrated spectral splitting to effectively harvest solar energy over the entire AM1.5 spectrum. By separating sunlight into two wavelength bands, VIS and IR, the concept of the DOS can help widen the usage of the whole sunlight spectrum, for photovoltaic conversion of solar cells, while at the same time harvesting energy from the rest of the sunlight spectrum for other thermal applications. A reasonably low reflection loss caused by the optical components in the DOS is estimated with only an additional loss about 2.7% by using a Rayleigh’s film as compared to regular single concentrating lens solar applications.
By attaching to an external Fresnel lens (f = 100 mm), the DOS system used a grating structure (dg = 12 grooves/mm), followed by a layer of 30°/60°/90° Littrow prisms of the same material, which served as a blazed surface to focus light from the 0th and 1st diffraction orders close together with minimum reflection losses. Thereafter, another layer of high-dispersion prisms with an apex angle of φ = 19° is recommended to minimize comatic aberration and the Petzval field curvature through refraction, and achieve high but similar concentrations for both VIS and IR wavelength bands. In fact, the combination of a grating structure and prisms is able to achieve concentration performance at least 20-fold (VIS band) and 11-fold (IR band) higher than regular concentrated solar applications that typically make use of a single concentrating lens. In addition, the materials used for the arrayed compound prisms should have a large difference in their Abbe numbers with the recommended selection to be BK7 for Littrow prisms and F2 for the second layer of triangular prisms. These chosen parameters are able to achieve very high solar concentration factor of 798× and 755× for both VIS and IR wavelength bands. The optical components in the DOS are designed based on their commercial availability to propose a low-cost optical system, and can be conveniently scalable in size. Upon successful implementation, the DOS has the potential to harvest solar energy under high concentrations over the entire AM1.5 spectrum with c-Si solar cells converting 0.4 μm ≤ λ < 1.2 μm of light into electricity, while the rest of the solar radiation (1.2 μm ≤ λ ≤ 2.5 μm) can be converted into useful energy for a wide variety of thermal applications such as water heating and thermoelectricity. This system can be economically viable, sustainable and practical for both industrial and domestic usage.

Supplementary Materials

The following are available online at https://www.mdpi.com/1996-1073/12/24/4719/s1, Figure S1: ZEMAX simulations of the beam pathways illustrated in Figure 3 for an improved solar performance, Figure S2: ZEMAX simulations on the conceptual demonstrations of the shift in Petzval curvature presented in Figure 5, Figure S3: ZEMAX simulations of only a Fresnel lens with f = 100 mm.

Author Contributions

S.K.T. worked on performance analysis and simulation-based concept demonstration. S.-Y.P. guided study concept and revised the manuscript.

Funding

This work is gratefully supported by the start-up funding from the San Diego State University, USA and the research grants from the Ministry of Education (R-265-000-588-114, R-265-000-597-112), Singapore.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Gueymard, C.; Myers, D.; Emery, K. Proposed reference irradiance spectra for solar energy systems testing. Sol. Energy 2002, 73, 443–467. [Google Scholar] [CrossRef]
  2. Gueymard, C.A. The sun’s total and spectral irradiance for solar energy applications and solar radiation models. Sol. Energy 2004, 76, 423–453. [Google Scholar] [CrossRef]
  3. Schmidt-Mende, L.; Fechtenkötter, A.; Müllen, K.; Moons, E.; Friend, R.H.; MacKenzie, J.D. Self-organized discotic liquid crystals for high-efficiency organic photovoltaics. Science 2001, 293, 1119–1122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Baran, D.; Ashraf, R.S.; Hanifi, D.A.; Abdelsamie, M.; Gasparini, N.; Röhr, J.A.; Holliday, S.; Wadsworth, A.; Lockett, S.; Neophytou, M.; et al. Reducing the efficiency–stability–cost gap of organic photovoltaics with highly efficient and stable small molecule acceptor ternary solar cells. Nat. Mater. 2016, 16, 363. [Google Scholar] [CrossRef] [PubMed]
  5. Cheng, J.; Park, S.-Y.; Chen, C.-L. Optofluidic solar concentrators using electrowetting tracking: Concept, design, and characterization. Sol. Energy 2013, 89, 152–167. [Google Scholar] [CrossRef]
  6. Pasamontes, M.; Álvarez, J.; Guzman, J.; Berenguel, M.; Camacho, E. Hybrid modeling of a solar-thermal heating facility. Sol. Energy 2013, 97, 577–590. [Google Scholar] [CrossRef]
  7. Maurer, C.; Baumann, T.; Hermann, M.; Di Lauro, P.; Pavan, S.; Michel, L.; Kuhn, T.E. Heating and cooling in high-rise buildings using facade-integrated transparent solar thermal collector systems. J. Build. Perform. Simul. 2013, 6, 449–457. [Google Scholar] [CrossRef]
  8. Barlev, D.; Vidu, R.; Stroeve, P. Innovation in concentrated solar power. Sol. Energy Mater. Sol. Cells 2011, 95, 2703–2725. [Google Scholar] [CrossRef]
  9. Slocum, A.H.; Codd, D.S.; Buongiorno, J.; Forsberg, C.; McKrell, T.; Nave, J.-C.; Papanicolas, C.N.; Ghobeity, A.; Noone, C.J.; Passerini, S. Concentrated solar power on demand. Sol. Energy 2011, 85, 1519–1529. [Google Scholar] [CrossRef] [Green Version]
  10. Guerrero-Lemus, R.; Martínez-Duart, J.M. Concentrated solar power. In Renewable Energies and CO2; Springer: Berlin/Heidelberg, Germany, 2013; pp. 135–151. [Google Scholar]
  11. Vignarooban, K.; Xu, X.; Arvay, A.; Hsu, K.; Kannan, A. Heat transfer fluids for concentrating solar power systems—A review. Appl. Energy 2015, 146, 383–396. [Google Scholar] [CrossRef]
  12. Narasimhan, V.; Jiang, D.; Park, S.-Y. Design and optical analyses of an arrayed microfluidic tunable prism panel for enhancing solar energy collection. Appl. Energy 2016, 162, 450–459. [Google Scholar] [CrossRef]
  13. Pearson, G. Conversion of solar to electrical energy. Am. J. Phys. 1957, 25, 591–598. [Google Scholar] [CrossRef]
  14. Dirnberger, D.; Blackburn, G.; Müller, B.; Reise, C. On the impact of solar spectral irradiance on the yield of different pv technologies. Sol. Energy Mater. Sol. Cells 2015, 132, 431–442. [Google Scholar] [CrossRef]
  15. Santbergen, R.; van Zolingen, R.C. The absorption factor of crystalline silicon pv cells: A numerical and experimental study. Sol. Energy Mater. Sol. Cells 2008, 92, 432–444. [Google Scholar] [CrossRef]
  16. Treble, F. Milestones in the development of crystalline silicon solar cells. Renew. Energy 1998, 15, 473–478. [Google Scholar] [CrossRef]
  17. Ba, B.; Kane, M. Spectral response of a polycrystalline silicon solar cell. NASA STI/Recon Tech. Rep. N 1994, 95, 1–12. [Google Scholar]
  18. Mickelsen, R.A.; Chen, W.S.; Hsiao, Y.R.; Lowe, V.E. Polycrystalline thin-film cuinse 2/cdzns solar cells. IEEE Trans. Electron Devices 1984, 31, 542–546. [Google Scholar] [CrossRef]
  19. Roman, J.M. State-of-the-art of iii-v solar cell fabrication technologies, device designs and applications. Adv. Photovolt. Cell Des. 2004, 4, 1–8. [Google Scholar]
  20. Karp, J.H.; Ford, J.E. Multiband Solar Concentrator Using Transmissive Dichroic Beamsplitting. In Proceedings of the SPIE—The International Society for Optical Engineering, San Diego, CA, USA, 11–12 August 2008; p. 7043. [Google Scholar] [CrossRef]
  21. Shockley, W.; Queisser, H.J. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 1961, 32, 510. [Google Scholar] [CrossRef]
  22. Fraas, L.M.; Avery, J.E.; Martin, J.; Sundaram, V.S.; Girard, G.; Dinh, V.T.; Davenport, T.M.; Yerkes, J.; O’neil, M. Over 35-percent efficient gaas/gasb tandem solar cells. IEEE Trans. Electron Devices 1990, 37, 443–449. [Google Scholar] [CrossRef]
  23. Luque, A.; Hegedus, S. Handbook of Photovoltaic Science and Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
  24. Imenes, A.; Mills, D. Spectral beam splitting technology for increased conversion efficiency in solar concentrating systems: A review. Sol. Energy Mater. Sol. Cells 2004, 84, 19–69. [Google Scholar] [CrossRef]
  25. Barnett, A.; Kirkpatrick, D.; Honsberg, C.; Moore, D.; Wanlass, M.; Emery, K.; Schwartz, R.; Carlson, D.; Bowden, S.; Aiken, D.; et al. Very high efficiency solar cell modules. Prog. Photovolt. Res. Appl. 2009, 17, 75–83. [Google Scholar] [CrossRef]
  26. Mojiri, A.; Taylor, R.; Thomsen, E.; Rosengarten, G. Spectral beam splitting for efficient conversion of solar energy—A review. Renew. Sustain. Energy Rev. 2013, 28, 654–663. [Google Scholar] [CrossRef]
  27. Stefancich, M.; Zayan, A.; Chiesa, M.; Rampino, S.; Roncati, D.; Kimerling, L.; Michel, J. Single element spectral splitting solar concentrator for multiple cells cpv system. Opt. Express 2012, 20, 9004–9018. [Google Scholar] [CrossRef] [PubMed]
  28. Arimochi, M.; Watanabe, T.; Yoshida, H.; Tange, T.; Nomachi, I.; Ikeda, M.; Dai, P.; He, W.; Ji, L.; Lu, S. Iii–v compound semiconductor multi-junction solar cells fabricated by room-temperature wafer-bonding technique. Jpn. J. Appl. Phys. 2015, 54, 056601. [Google Scholar] [CrossRef]
  29. Otanicar, T.P.; Chowdhury, I.; Prasher, R.; Phelan, P.E. Band-gap tuned direct absorption for a hybrid concentrating solar photovoltaic/thermal system. J. Sol. Energy Eng. 2011, 133, 041014. [Google Scholar] [CrossRef]
  30. Zhao, J.; Luo, Z.; Zhang, Y.; Shou, C.; Ni, M. Optimal design and performance analysis of a low concentrating photovoltaic/thermal system using the direct absorption collection concept. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference (APPEEC), Chengdu, China, 28–31 March 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–6. [Google Scholar]
  31. Crisostomo, F.; Becker, J.; Mesgari, S.; Hjerrild, N.; Taylor, R.A. Desing and on-sun testing of a hybrid pvt prototype using a nanofluid-based selective absorption filter. In Proceedings of the 2015 12th International Conference on the European Energy Market (EEM), Lisbon, Portugal, 19–22 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
  32. Looser, R.; Vivar, M.; Everett, V. Spectral characterisation and long-term performance analysis of various commercial heat transfer fluids (htf) as direct-absorption filters for cpv-t beam-splitting applications. Appl. Energy 2014, 113, 1496–1511. [Google Scholar] [CrossRef]
  33. Taylor, R.A.; Otanicar, T.; Rosengarten, G. Nanofluid-based optical filter optimization for pv/t systems. Light Sci. Appl. 2012, 1, e34. [Google Scholar] [CrossRef] [Green Version]
  34. Sabry, M.; Gottschalg, R.; Betts, T.R.; Shaltout, M.; Hassan, A.; El-Nicklawy, M.; Infield, D. Optical filtering of solar radiation to increase performance of concentrator systems. In Proceedings of the 2002 Conference Record of the Twenty-Ninth IEEE Photovoltaic Specialists Conference, New Orleans, LA, USA, 19–24 May 2002; IEEE: Piscataway, NJ, USA, 2003; pp. 1588–1591. [Google Scholar]
  35. Jiang, S.-L.; Hu, P.; Mo, S.-P.; Chen, Z.-S. Modeling for two-stage dish concentrating spectral beam splitting photovoltaic/thermal system. In Proceedings of the 2009 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 27–31 March 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–4. [Google Scholar]
  36. Crisostomo, F.; Taylor, R.A.; Zhang, T.; Perez-Wurfl, I.; Rosengarten, G.; Everett, V.; Hawkes, E.R. Experimental testing of sinx/sio2 thin film filters for a concentrating solar hybrid pv/t collector. Renew. Energy 2014, 72, 79–87. [Google Scholar] [CrossRef]
  37. Segal, A.; Epstein, M.; Yogev, A. Hybrid concentrated photovoltaic and thermal power conversion at different spectral bands. Sol. Energy 2004, 76, 591–601. [Google Scholar] [CrossRef]
  38. Imenes, A.G.; Buie, D.; Mills, D.R.; Schramek, P.; Bosi, S.G. A new strategy for improved spectral performance in solar power plants. Sol. Energy 2006, 80, 1263–1269. [Google Scholar] [CrossRef]
  39. Imenes, A.; Buie, D.; McKenzie, D. The design of broadband, wide-angle interference filters for solar concentrating systems. Sol. Energy Mater. Sol. Cells 2006, 90, 1579–1606. [Google Scholar] [CrossRef]
  40. Imenes, A.; Mills, D. Electricity replacement benefits of various receiver combinations in a multi tower solar array distributed chp plant. In Proceedings of the ISES Solar World Congress—Solar Energy for a Sustainable Future, Gothenburg, Sweden, 14–19 June 2003. [Google Scholar]
  41. Yogev, A.; Krupkin, V.; Epstein, M. Solar Energy Plant; Google Patents: Washington, DC, USA, 1996. [Google Scholar]
  42. Zamfirescu, C.; Dincer, I. Assessment of a new integrated solar energy system for hydrogen production. Sol. Energy 2014, 107, 700–713. [Google Scholar] [CrossRef]
  43. Ju, X.; Xu, C.; Han, X.; Du, X.; Wei, G.; Yang, Y. A review of the concentrated photovoltaic/thermal (cpvt) hybrid solar systems based on the spectral beam splitting technology. Appl. Energy 2017, 187, 534–563. [Google Scholar] [CrossRef]
  44. Hagen, N.; Tkaczyk, T.S. Compound prism design principles, i. Appl. Opt. 2011, 50, 4998–5011. [Google Scholar] [CrossRef] [Green Version]
  45. Duarte, F. Tunable laser optics: Applications to optics and quantum optics. Prog. Quantum Electron. 2013, 37, 326–347. [Google Scholar] [CrossRef]
  46. Gouvêa, E.C.; Sobrinho, P.M.; Souza, T.M. Spectral response of polycrystalline silicon photovoltaic cells under real-use conditions. Energies 2017, 10, 1178. [Google Scholar] [CrossRef] [Green Version]
  47. Gaylord, T.K.; Moharam, M. Analysis and applications of optical diffraction by gratings. Proc. IEEE 1985, 73, 894–937. [Google Scholar] [CrossRef]
  48. Hecht, E. Optics, 5th ed.; Pearson Education, Incorporated: San Francisco, CA, USA, 2016. [Google Scholar]
  49. Languy, F. Achromatization of Nonimaging Fresnel Lenses for Photovoltaic Solar Concentration Using Refractive and Diffractive Patterns; Université de Liège: Liège, Belgique, 2012. [Google Scholar]
  50. Riedl, M.J. Optical Design Fundamentals for Infrared Systems; SPIE Press: Bellingham, WA, USA, 2001; Volume 48. [Google Scholar]
  51. Russo, J.M.; Zhang, D.; Gordon, M.; Vorndran, S.D.; Wu, Y.; Kostuk, R.K. Grating-Over-Lens Concentrating Photovoltaic Spectrum Splitting Systems with Volume Holographic Optical Elements. In Proceedings of the SPIE—The International Society for Optical Engineering, San Diego, CA, USA, 27 August 2013; p. 882106. [Google Scholar]
  52. Katz, M.G.; Schaps, D.M.; Shnider, S. Almost equal: The method of adequality from diophantus to fermat and beyond. Perspect. Sci. 2013, 21, 283–324. [Google Scholar] [CrossRef] [Green Version]
  53. Remillard, J.; Everson, M.; Weber, W. Loss mechanisms in optical light pipes. Appl. Opt. 1992, 31, 7232–7241. [Google Scholar] [CrossRef] [PubMed]
  54. Rubin, M. Optical properties of soda lime silica glasses. Sol. Energy Mater. 1985, 12, 275–288. [Google Scholar] [CrossRef] [Green Version]
  55. Garboushian, V.; Yoon, S.; Turner, G.; Gunn, A.; Fair, D. A novel high-concentration pv technology for cost competitive utility bulk power generation. In Proceedings of the 1994 IEEE 1st World Conference on Photovoltaic Energy Conversion—WCPEC (A Joint Conference of PVSC, PVSEC and PSEC), Waikoloa, HI, USA, 5–9 December 1994; IEEE: Piscataway, NJ, USA, 2002; pp. 1060–1063. [Google Scholar]
Energies 12 04719 g001 550
Figure 1. A schematic of the dispersive optical system (DOS) enabling both solar spectrum splitting and high concentration with the minimum optical aberration and its potential applications to harvest a wide range of solar spectrum. (a) The DOS module is composed of three compact optical components placed below a low-cost Fresnel lens: a diffraction grating layer, and compound prisms made of a low-dispersion Littrow prism and a high-dispersion triangular prism. (b) Incoming sunlight is being focused by the external concentrator, split into two wavelength bands of visible (VIS) and infrared (IR) light via an array of the DOS module, before reaching corresponding solar receivers such as solar cells and thermal absorbers positioned on the same focal plane. The only VIS range of the sunlight can be focused onto solar cells with a concentration factor of 798× to enhance its photovoltaic (PV) conversion. At the same time, the separated IR irradiation can be also used for possible solar thermal applications such as water heating and thermoelectricity with the concentration factor as high as 755×. Such high concentration performance for both wavelength bands can be achieved by using the additional optical components - a diffraction grating structure and dispersive prisms, which allow to minimize optical aberrations through both diffraction and refraction and result in highly-concentrated sunlight separation. Additionally, a regular solar tracker can be externally integrated to ensure an optimum position of the whole system for daily and seasonal operations. The proposed low-cost solar splitting technology is not only able to achieve the high solar concentration to minimize the footprint size of solar receivers for both VIS and IR wavelength bands, but also lessen thermal degradation of solar cells by rejecting IR radiation, while using commercially-available Fresnel lens and DOS components.
Figure 1. A schematic of the dispersive optical system (DOS) enabling both solar spectrum splitting and high concentration with the minimum optical aberration and its potential applications to harvest a wide range of solar spectrum. (a) The DOS module is composed of three compact optical components placed below a low-cost Fresnel lens: a diffraction grating layer, and compound prisms made of a low-dispersion Littrow prism and a high-dispersion triangular prism. (b) Incoming sunlight is being focused by the external concentrator, split into two wavelength bands of visible (VIS) and infrared (IR) light via an array of the DOS module, before reaching corresponding solar receivers such as solar cells and thermal absorbers positioned on the same focal plane. The only VIS range of the sunlight can be focused onto solar cells with a concentration factor of 798× to enhance its photovoltaic (PV) conversion. At the same time, the separated IR irradiation can be also used for possible solar thermal applications such as water heating and thermoelectricity with the concentration factor as high as 755×. Such high concentration performance for both wavelength bands can be achieved by using the additional optical components - a diffraction grating structure and dispersive prisms, which allow to minimize optical aberrations through both diffraction and refraction and result in highly-concentrated sunlight separation. Additionally, a regular solar tracker can be externally integrated to ensure an optimum position of the whole system for daily and seasonal operations. The proposed low-cost solar splitting technology is not only able to achieve the high solar concentration to minimize the footprint size of solar receivers for both VIS and IR wavelength bands, but also lessen thermal degradation of solar cells by rejecting IR radiation, while using commercially-available Fresnel lens and DOS components.
Energies 12 04719 g001
Energies 12 04719 g002 550
Figure 2. A schematic illustration of a transmissive diffraction grating structure. With the grating groove’s distance (d) apart, incident light impinges on the grating and emerges separated for each wavelength λ, where λ1 > λ2 > λ3. When light undergoes diffraction through the grating structure to form a light spectrum, longer wavelengths of light (e.g., λ1) will diffract more than shorter wavelengths of light (e.g., λ3). As a result, a ray at λ1 has a larger diffraction angle θm than the one at λ3.
Figure 2. A schematic illustration of a transmissive diffraction grating structure. With the grating groove’s distance (d) apart, incident light impinges on the grating and emerges separated for each wavelength λ, where λ1 > λ2 > λ3. When light undergoes diffraction through the grating structure to form a light spectrum, longer wavelengths of light (e.g., λ1) will diffract more than shorter wavelengths of light (e.g., λ3). As a result, a ray at λ1 has a larger diffraction angle θm than the one at λ3.
Energies 12 04719 g002
Energies 12 04719 g003 550
Figure 3. Schematic illustrations of the ray tracing passing through a Fresnel lens and (a) a transmissive diffraction grating structure, (b) a combination of a grating structure and an arrayed Littrow prisms, and (c) a combination of a grating structure, arrayed Littrow prisms, and high-dispersion triangular prisms. (a) Incoming rays first undergo light concentration and then diffraction. For the rays at m = ±1, a Petzval field curvature is separately formed far away from the focal plane, while the rays at the 0th diffraction order experiences a chromatic aberration caused by the concentrating lens without diffraction. As a result, very poor concentration performance and no clear sunlight separation have been noted. (b) Beam pathway of incoming light when an array of a Littrow prism, made of the same material as the grating structure, featuring 30°/60°/90° angles is placed after the grating structure. The constructed blazed surface is able to focus light from the 0th and 1st order diffraction close together. However, a high Petzval field curvature can still be observed, producing optical aberrations which still lead to poor concentration performance. (c) Beam pathway of an incoming light passing through a grating followed by a Littrow prism and then a triangular prism. Light dispersion first occurs via diffraction in the grating layer with the 0th and 1st order diffracted rays being refracted close together by the Littrow prisms. The next layer of triangular prisms is responsible for correcting the comatic aberrations through refraction. As a result, a lower Petzval curvature is formed, minimizing aberrations and further improving solar concentration performances.
Figure 3. Schematic illustrations of the ray tracing passing through a Fresnel lens and (a) a transmissive diffraction grating structure, (b) a combination of a grating structure and an arrayed Littrow prisms, and (c) a combination of a grating structure, arrayed Littrow prisms, and high-dispersion triangular prisms. (a) Incoming rays first undergo light concentration and then diffraction. For the rays at m = ±1, a Petzval field curvature is separately formed far away from the focal plane, while the rays at the 0th diffraction order experiences a chromatic aberration caused by the concentrating lens without diffraction. As a result, very poor concentration performance and no clear sunlight separation have been noted. (b) Beam pathway of incoming light when an array of a Littrow prism, made of the same material as the grating structure, featuring 30°/60°/90° angles is placed after the grating structure. The constructed blazed surface is able to focus light from the 0th and 1st order diffraction close together. However, a high Petzval field curvature can still be observed, producing optical aberrations which still lead to poor concentration performance. (c) Beam pathway of an incoming light passing through a grating followed by a Littrow prism and then a triangular prism. Light dispersion first occurs via diffraction in the grating layer with the 0th and 1st order diffracted rays being refracted close together by the Littrow prisms. The next layer of triangular prisms is responsible for correcting the comatic aberrations through refraction. As a result, a lower Petzval curvature is formed, minimizing aberrations and further improving solar concentration performances.
Energies 12 04719 g003
Energies 12 04719 g004 550
Figure 4. The effect of the focal length (f) on the solar concentration performance for the VIS and IR wavelength bands. Concentration factors for each wavelength band have an inverse relationship.
Figure 4. The effect of the focal length (f) on the solar concentration performance for the VIS and IR wavelength bands. Concentration factors for each wavelength band have an inverse relationship.
Energies 12 04719 g004
Energies 12 04719 g005 550
Figure 5. Conceptual demonstration of the shift in Petzval field curvature with the change in the focal length (f) of a Fresnel lens after sunlight splitting by the DOS, where λL and λR denote the wavelengths of light rays emitting from the leftmost and rightmost DOS module, respectively. To clearly separate the two wavelength bands, a focal plane is defined as the plane horizontally drawn at the focal point of the rays at λ = 1.2 µm, where the concentration performance of each VIS and IR spectral range can be estimated by the area reduction ratio between solar input and focused output. After spectrum splitting, optical aberrations cause each wavelength of light to have its focal point asymmetrically distributed along a Petzval field curvature. The curvature’s radius differs with different f, across different wavelengths of light. (a) When a Fresnel lens with a short f is used, a higher curvature can be observed with short wavelengths, shown by the smaller radius of curvature at λ = 0.4 µm as compared to the larger radius of curvature at λ = 2.5µm. As the λ = 0.4 µm solar rays have a much shorter focal point, they start diverging towards the focal plane, resulting in a large footprint size for the VIS wavelength band. (b) When a Fresnel lens with a long f is used, the Petzval field curvature is lower with the short wavelengths, illustrated by the larger radius of curvature at λ = 0.4 µm. A higher curvature can then be observed with long wavelengths, resulting in the smaller radius of curvature (i.e., a shorter focal point) at λ = 2.5 µm. Now, the λ = 2.5 µm solar rays start diverging towards the focal plane, resulting in a large footprint size for the IR wavelength band.
Figure 5. Conceptual demonstration of the shift in Petzval field curvature with the change in the focal length (f) of a Fresnel lens after sunlight splitting by the DOS, where λL and λR denote the wavelengths of light rays emitting from the leftmost and rightmost DOS module, respectively. To clearly separate the two wavelength bands, a focal plane is defined as the plane horizontally drawn at the focal point of the rays at λ = 1.2 µm, where the concentration performance of each VIS and IR spectral range can be estimated by the area reduction ratio between solar input and focused output. After spectrum splitting, optical aberrations cause each wavelength of light to have its focal point asymmetrically distributed along a Petzval field curvature. The curvature’s radius differs with different f, across different wavelengths of light. (a) When a Fresnel lens with a short f is used, a higher curvature can be observed with short wavelengths, shown by the smaller radius of curvature at λ = 0.4 µm as compared to the larger radius of curvature at λ = 2.5µm. As the λ = 0.4 µm solar rays have a much shorter focal point, they start diverging towards the focal plane, resulting in a large footprint size for the VIS wavelength band. (b) When a Fresnel lens with a long f is used, the Petzval field curvature is lower with the short wavelengths, illustrated by the larger radius of curvature at λ = 0.4 µm. A higher curvature can then be observed with long wavelengths, resulting in the smaller radius of curvature (i.e., a shorter focal point) at λ = 2.5 µm. Now, the λ = 2.5 µm solar rays start diverging towards the focal plane, resulting in a large footprint size for the IR wavelength band.
Energies 12 04719 g005
Energies 12 04719 g006 550
Figure 6. The effect of the grating groove density (dg) and the apex angle (φ) of the second prism on system performance achieved by the DOS. (a) Concentration factor of IR wavelength band as a function of grating groove density, dg. (b) Concentration factor of VIS wavelength band as a function of grating groove density, dg. (c) Percentage length of overlap, lo, of the outmost λL = 0.4 µm ray into the IR band with respect to that particular IR footprint size as a function of grating groove density, dg. Having concluded in the previous study that f = 100 mm is suggested for a balanced performance in both VIS (intensity of energy for photovoltaic conversion) and IR (intensity of thermal energy), simulations for different values of φ ranging from 15° ≤ φ ≤ 21° have further derived the conclusions that lower values of dg and higher values of φ will result in a higher concentration ratio for both cases of VIS and IR, but there is an increase in lo as a tradeoff. The optimum parameters have been chosen as dg = 7.5 grooves/mm and φ = 19° (point III) to achieve similarly high concentration factors of 798×.
Figure 6. The effect of the grating groove density (dg) and the apex angle (φ) of the second prism on system performance achieved by the DOS. (a) Concentration factor of IR wavelength band as a function of grating groove density, dg. (b) Concentration factor of VIS wavelength band as a function of grating groove density, dg. (c) Percentage length of overlap, lo, of the outmost λL = 0.4 µm ray into the IR band with respect to that particular IR footprint size as a function of grating groove density, dg. Having concluded in the previous study that f = 100 mm is suggested for a balanced performance in both VIS (intensity of energy for photovoltaic conversion) and IR (intensity of thermal energy), simulations for different values of φ ranging from 15° ≤ φ ≤ 21° have further derived the conclusions that lower values of dg and higher values of φ will result in a higher concentration ratio for both cases of VIS and IR, but there is an increase in lo as a tradeoff. The optimum parameters have been chosen as dg = 7.5 grooves/mm and φ = 19° (point III) to achieve similarly high concentration factors of 798×.
Energies 12 04719 g006
Energies 12 04719 g007 550
Figure 7. The effect of the prism mateirals on the solar concentration performance for the VIS and IR wavelength bands by varying the Abbe number ratio (Vr = VD1/VD2) of the compound prism materials.
Figure 7. The effect of the prism mateirals on the solar concentration performance for the VIS and IR wavelength bands by varying the Abbe number ratio (Vr = VD1/VD2) of the compound prism materials.
Energies 12 04719 g007
Energies 12 04719 g008 550
Figure 8. Simulation results show effective solar splitting as well as high concentration up to 798× for VIS wavelength band and 755 factor for IR wavelength band on the focal plane, f = 100 mm, given by an external Fresnel lens. Simulation results based on the following DOS parameters: a diffraction grating with the groove density of dg = 12 grooves/mm, the 1-mm height of each compound prism module. The first layer of Littrow prism has an apex angle of φ = 30° and is made of a low dispersion material BK7 (n = 1.52, VD = 64.17), while the second layer is a triangular prism with a corresponding apex angle of φ = 19° and made of a high dispersion material F2 (n = 1.62, VD = 36.37).
Figure 8. Simulation results show effective solar splitting as well as high concentration up to 798× for VIS wavelength band and 755 factor for IR wavelength band on the focal plane, f = 100 mm, given by an external Fresnel lens. Simulation results based on the following DOS parameters: a diffraction grating with the groove density of dg = 12 grooves/mm, the 1-mm height of each compound prism module. The first layer of Littrow prism has an apex angle of φ = 30° and is made of a low dispersion material BK7 (n = 1.52, VD = 64.17), while the second layer is a triangular prism with a corresponding apex angle of φ = 19° and made of a high dispersion material F2 (n = 1.62, VD = 36.37).
Energies 12 04719 g008

Share and Cite

MDPI and ACS Style

Thio, S.K.; Park, S.-Y. Dispersive Optical Systems for Highly-Concentrated Solar Spectrum Splitting: Concept, Design, and Performance Analyses. Energies 2019, 12, 4719. https://doi.org/10.3390/en12244719

AMA Style

Thio SK, Park S-Y. Dispersive Optical Systems for Highly-Concentrated Solar Spectrum Splitting: Concept, Design, and Performance Analyses. Energies. 2019; 12(24):4719. https://doi.org/10.3390/en12244719

Chicago/Turabian Style

Thio, Si Kuan, and Sung-Yong Park. 2019. "Dispersive Optical Systems for Highly-Concentrated Solar Spectrum Splitting: Concept, Design, and Performance Analyses" Energies 12, no. 24: 4719. https://doi.org/10.3390/en12244719

APA Style

Thio, S. K., & Park, S. -Y. (2019). Dispersive Optical Systems for Highly-Concentrated Solar Spectrum Splitting: Concept, Design, and Performance Analyses. Energies, 12(24), 4719. https://doi.org/10.3390/en12244719

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop