Tie-Line Reserve Power Probability Margin for Day-Ahead Dispatching in Power Systems with High Proportion Renewable Power Sources
Abstract
:1. Introduction
2. Grid Area Division Based on Power Source Properties
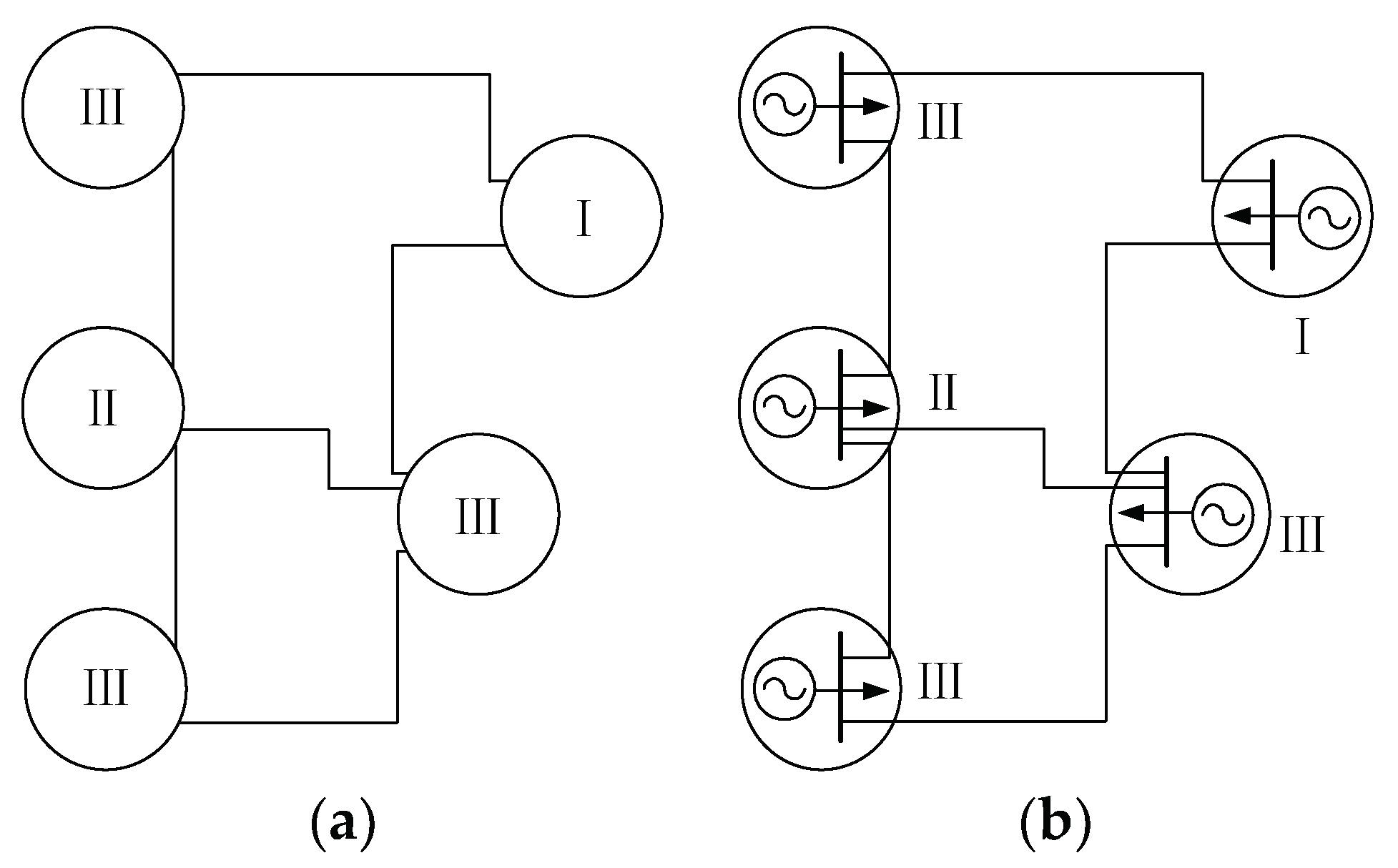
2.1. Types of Grid Area Division Based on Power Source Properties
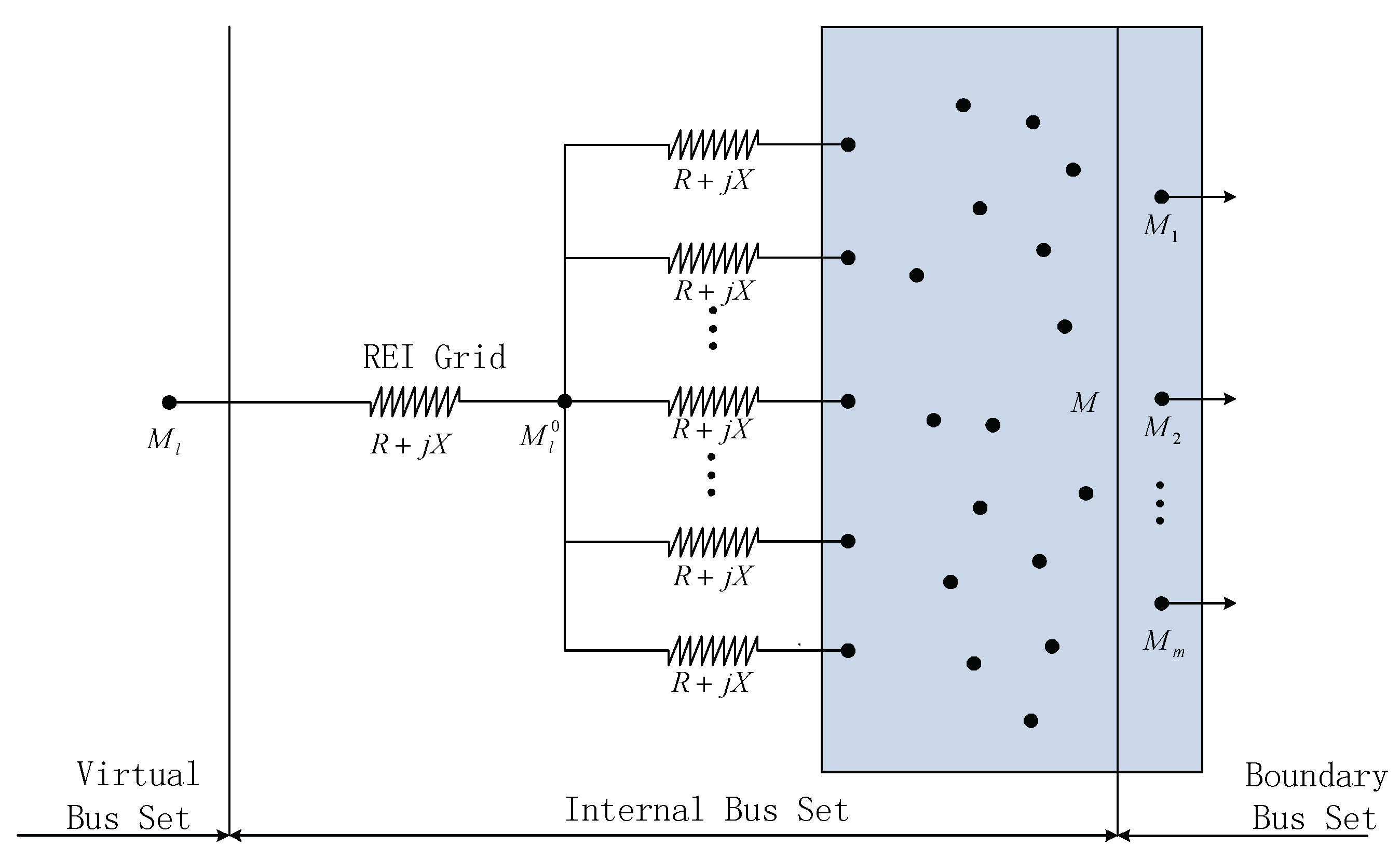
2.2. Equivalent Parameters of Power Grid Area
3. Prediction Error Probability Optimal Power Flow for Day-Ahead Dispatching
3.1. DPEPOPF Based on Grid Area Division
3.2. Inter-Area DPEPOPF
3.2.1. Prediction Error Probability Optimal Power Flow Mathematical Model
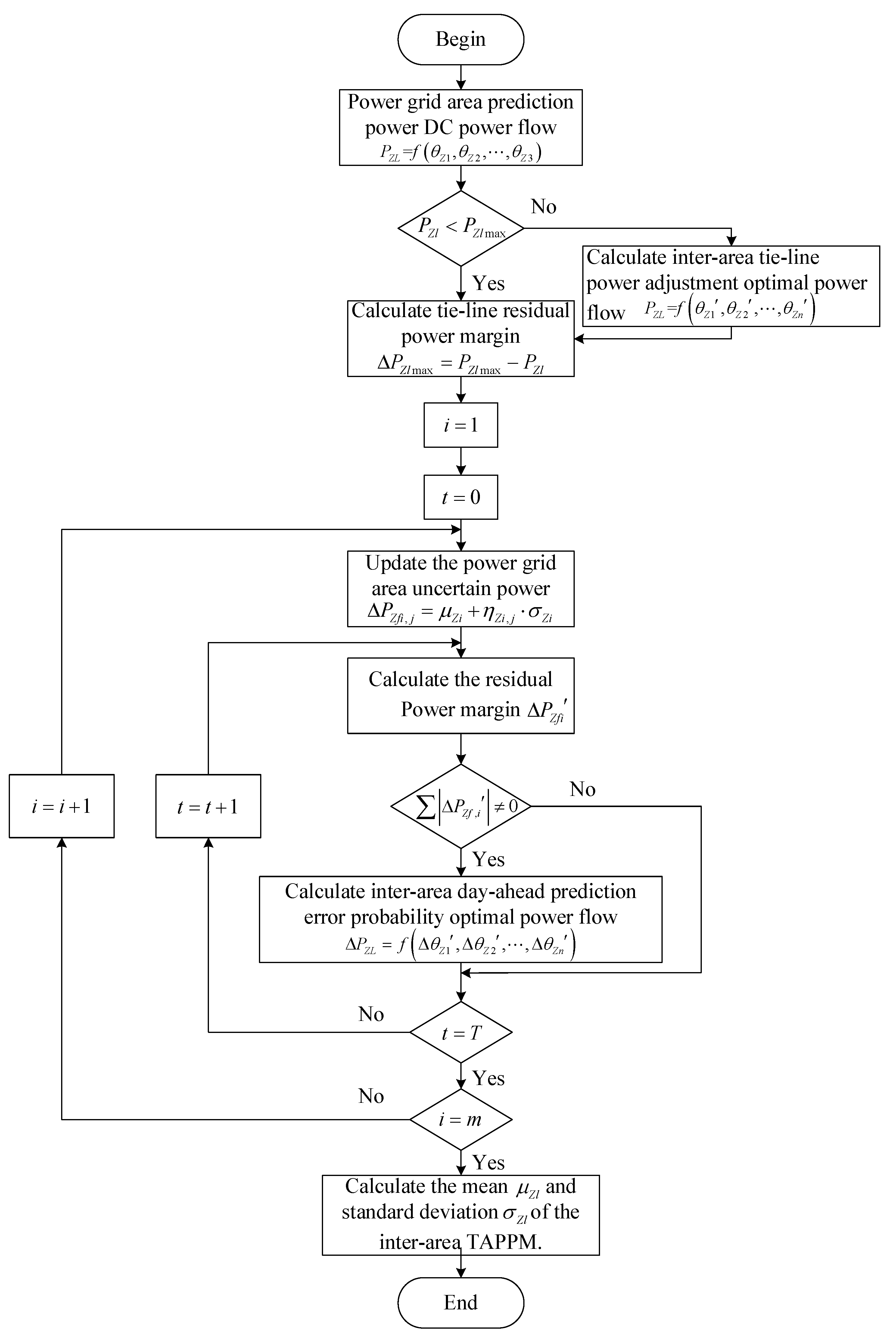
3.2.2. Inter-Area Point Estimation Optimization Algorithm for DPEPOPF
- (1)
- According to Equation (23), the inter-area tie-line power is calculated using the power grid area uncertainty power source predicted value:
- (2)
- Whether any tie-line exceeds the upper limit power is detected according to Equation (24); if the upper limit is exceeded, the third step will be executed; otherwise, the fourth step will be executed:
- (3)
- According to Equation (12), the mathematical model of the inter-area tie-line power adjustment power flow is used to adjust the tie-line power.
- (4)
- The inter-area tie-line residual power margin is calculated according to Equation (25):
- (5)
- According to the point estimation optimization algorithm for the DPEPOPF, the variables are selected in turn.
- (6)
- The power grid area uncertain power generation probability variable is updated according to Equation (19).
- (7)
- After the power grid area is self-accommodated, the residual power margin of power grid area is calculated.
- (8)
- According to Equation (11), the inter-area DPEPOPF is calculated.
- (9)
- The mean and standard deviation of the inter-area TRPPM are calculated.
3.3. Intra-Area DPEPOPF
3.3.1. Prediction Error Probability Optimal Power Flow Mathematical Model
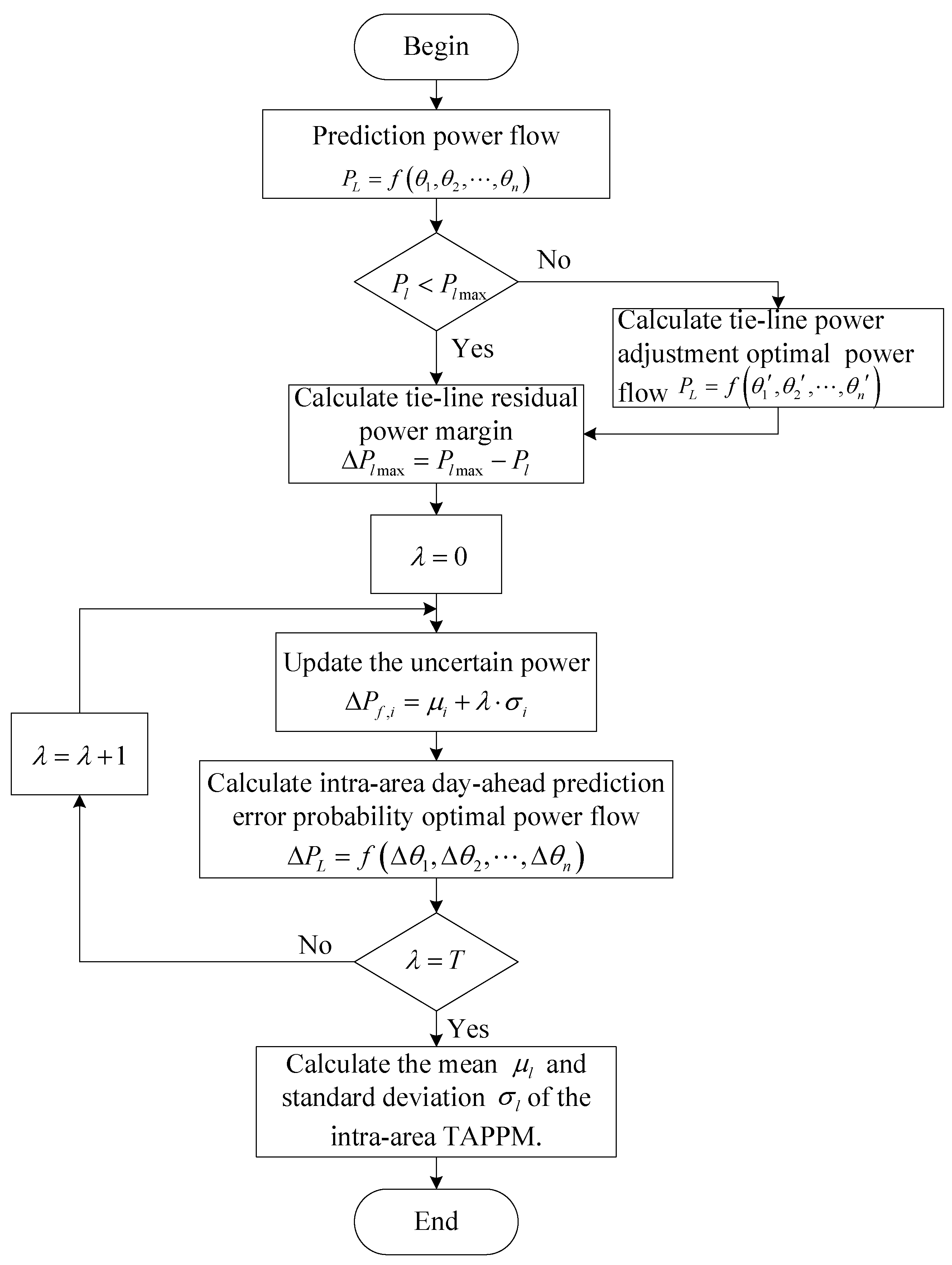
3.3.2. Intra-Area DPEPOPF
- (1)
- According to Equation (36), the tie-line power is calculated using the uncertainty power source predicted value:
- (2)
- Detecting whether each tie-line power exceeds the upper limit according to Equation (37). If the upper limit is exceeded, the third step will be executed, otherwise the fourth step will be executed.
- (3)
- According to Equation (29), a mathematical model of the intra-area tie-line power adjustment power flow is used to adjust the tie-line power.
- (4)
- Each value of the tie-line residual power margin is calculated according to Equation (38):
- (5)
- Update the uncertain power generation probability variable according to Equation (35).
- (6)
- According to Equation (28), the intra-area DPEPOPF is calculated.
- (7)
- Calculate the mean and standard deviation of the intra-area TRPPM.
4. Simulation Results
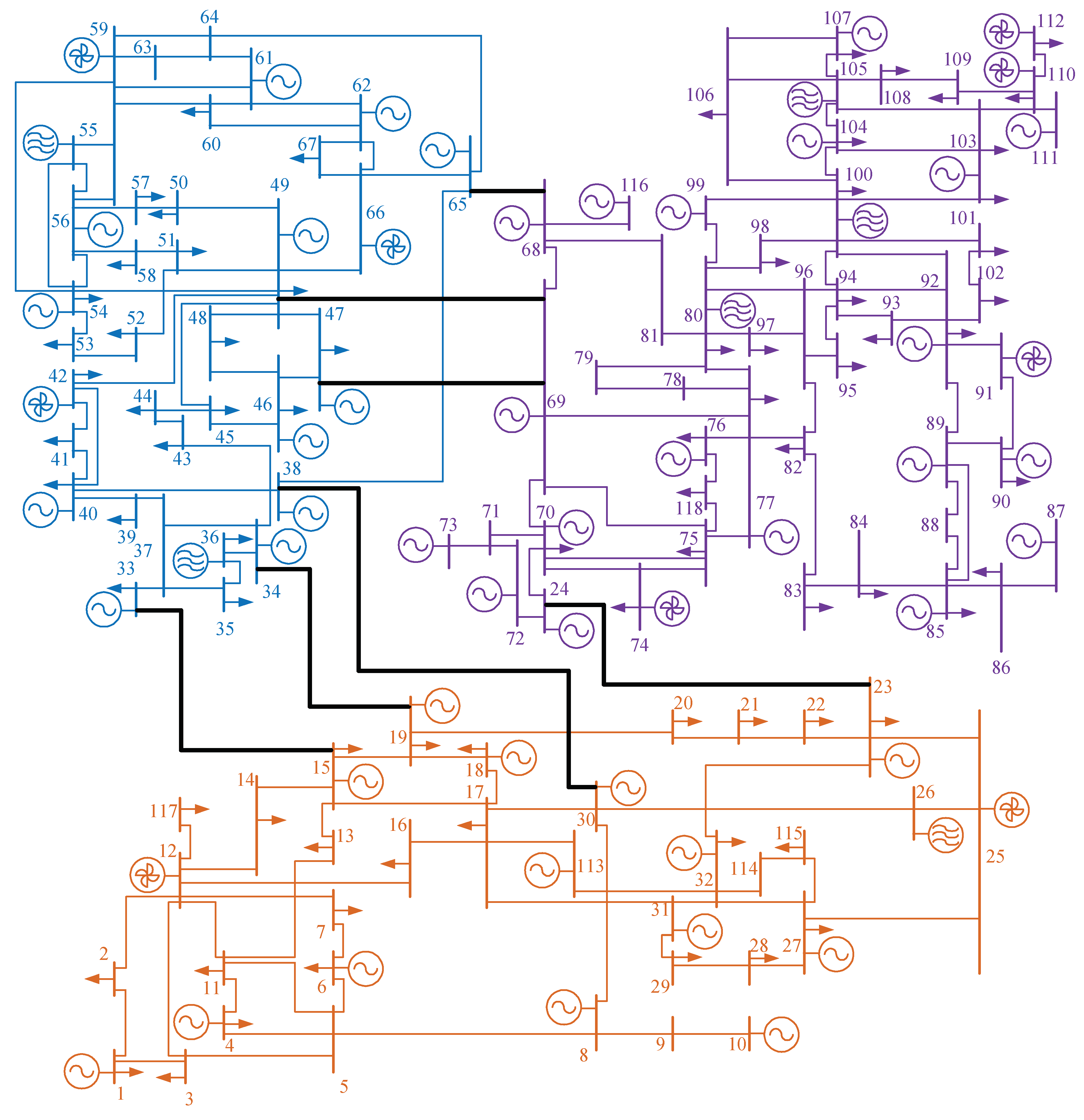
4.1. Modified IEEE 118 Bus Test System Raw Data
4.2. Simulation Results of Inter-Area TRPPM
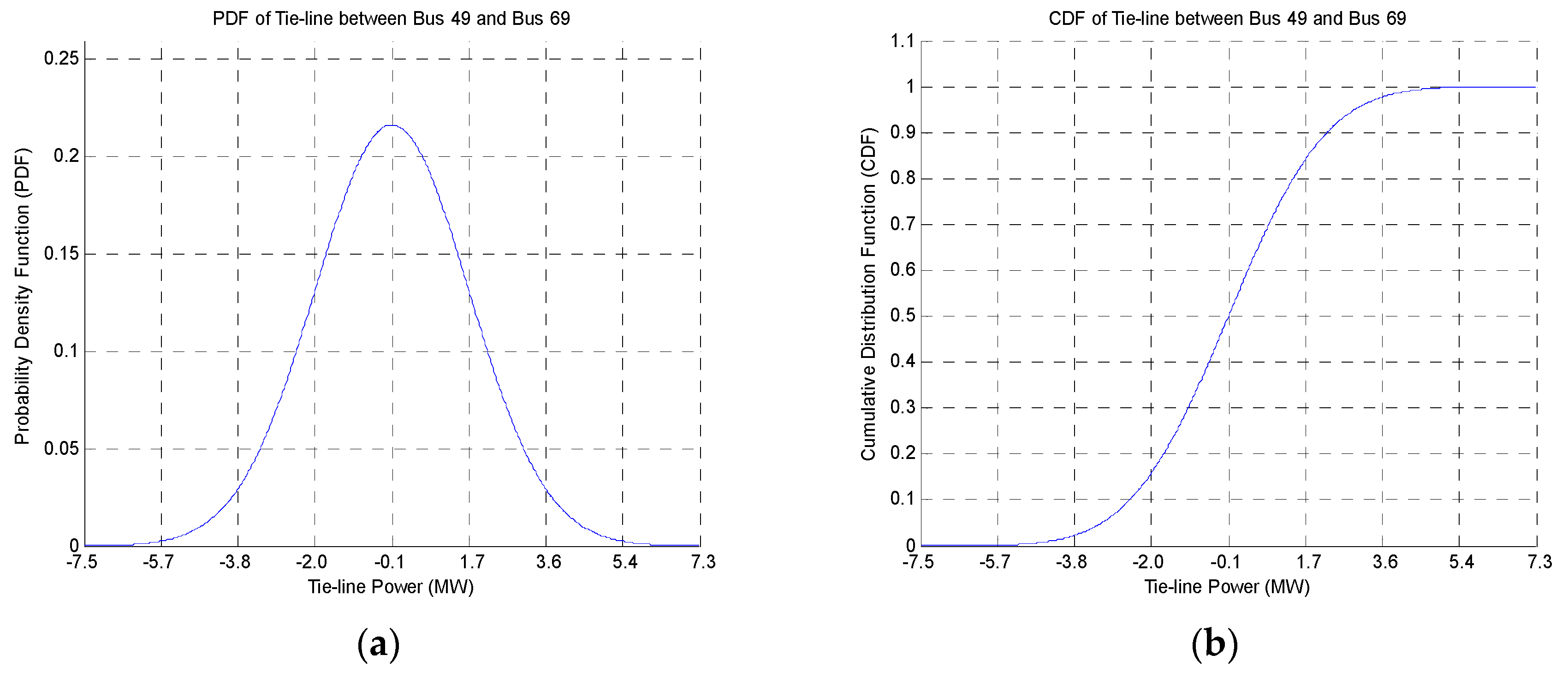
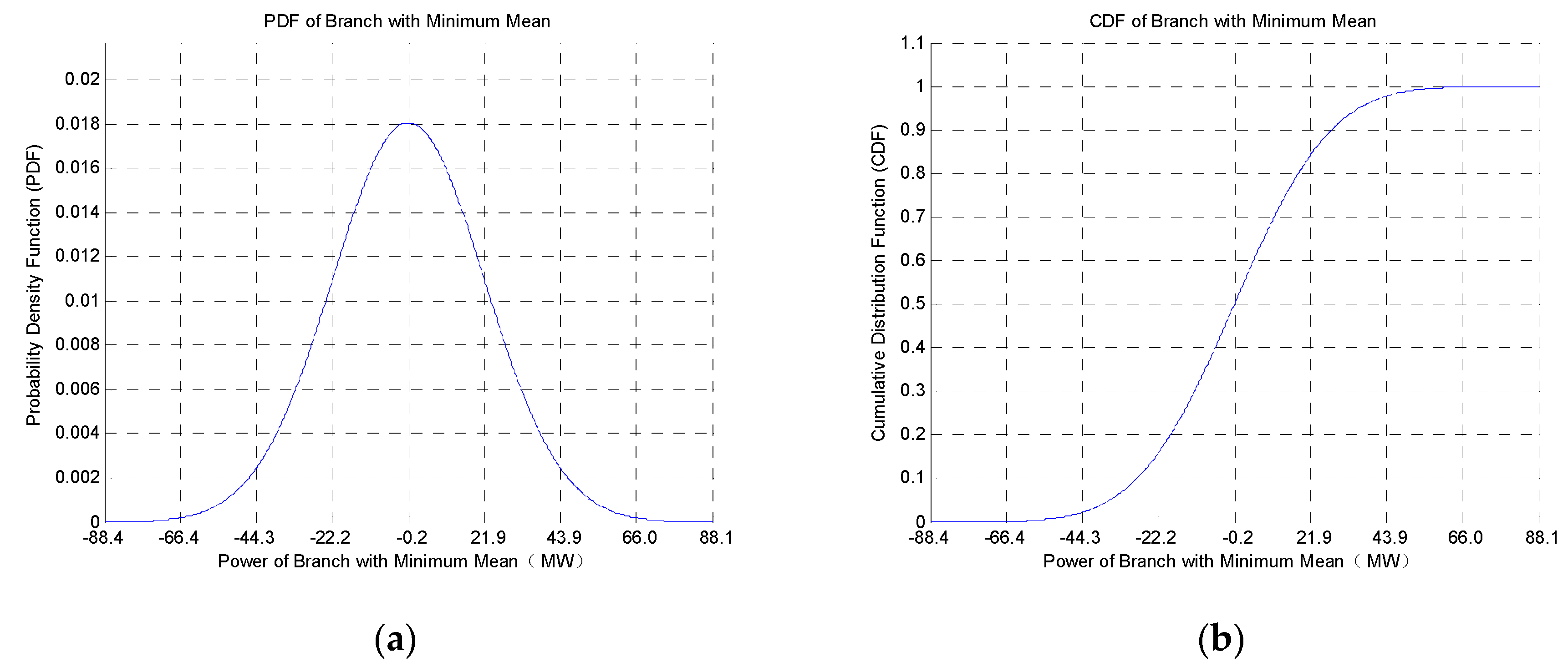
4.3. Simulation Results of Intra-Area TRPPM
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| PSHPRPSs | Power systems with a high proportion of renewable power sources |
| DPEPOPF | Day-ahead prediction error probability optimal power flow |
| TRPPM | Tie-line reserve power probability margin |
| DCS | Dispatch control system |
| AGC | Automatic generation control |
| CDF | Cumulative distribution function |
| Probability density function | |
| IEEE | Institute of Electrical and Electronics Engineers |
| DC | Direct current |
| REI | Radial equivalent independent |
| AC | Alternating current |
| Equivalent bus | |
| Active power of the equivalent bus | |
| Active power of each power source | |
| Power of each load | |
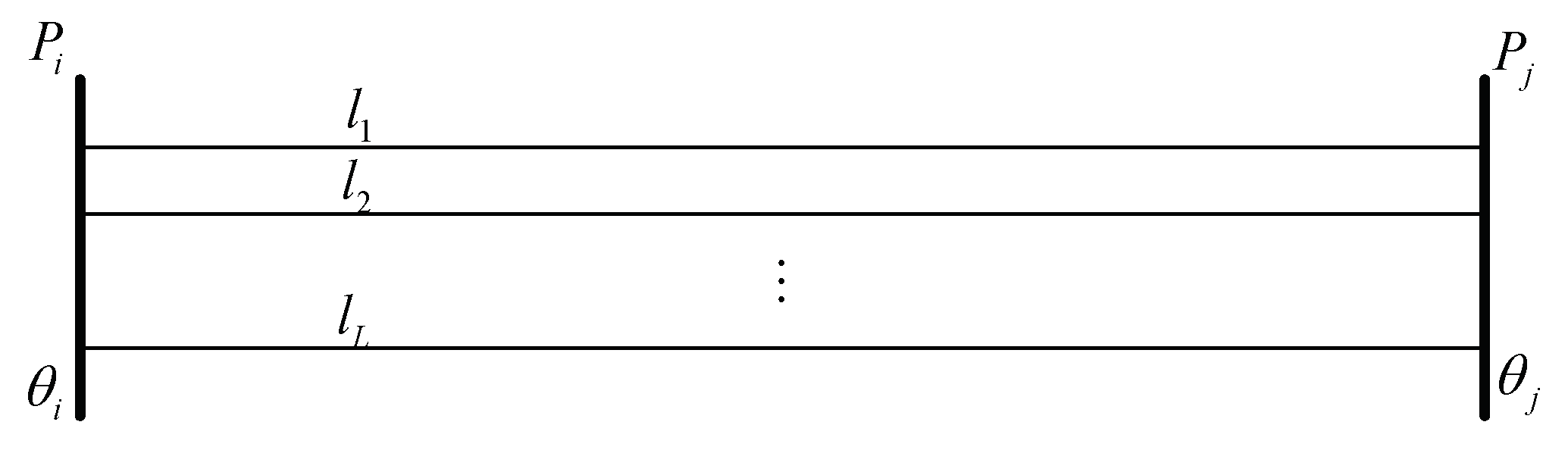
| Total power of tie-line | |
| Power of tth tie-line | |
| Reactance of the tth tie-line | |
| Power variation of equivalent bus | |
| Active power of the equivalent bus | |
| Phase angle variable of the equivalent bus | |
| Calculated value of equivalent bus active power | |
| Admittance between bus i and the zero-potential bus | |
| Conductance between bus i and bus j | |
| Represents the reactance between bus i and bus j | |
| Power margin of inter-area tie-line | |
| Day-ahead power prediction error | |
| Reserve power | |
| Line residual power margin | |
| Reserve power of the ith power grid area | |
| Reserve power function | |
| Accommodation capacity of a type I grid | |
| Accommodation capacity of a type III grid | |
| Uncertain power generation of the ith regional power grid | |
| Standard location coefficient | |
| Central moments | |
| Mean | |
| Standard deviation | |
| PDF of the power grid area uncertainty power generation | |
| Power prediction error of uncertainty power source | |
| Inter-area tie-line residual power margin | |
| Intra-area uncertain generating power | |
| Total reserve power | |
| Percentage error of the simulation result | |
| Simulation result of the AC power flow model | |
| Simulation result of the DPEPOPF mathematical model | |
| Average percentage error |
Appendix A
| Bus | Mean | Standard Deviation | Area |
|---|---|---|---|
| 12 | 0.0555 | 0.407 | 1 |
| 25 | 0.096 | 0.64 | 1 |
| 26 | 0.0828 | 0.7452 | 1 |
| 36 | 0.015 | 0.18 | 2 |
| 42 | 0.03 | 0.205 | 2 |
| 55 | 0.02 | 0.20 | 2 |
| 59 | 0.102 | 0.51 | 2 |
| 66 | 0.0984 | 0.984 | 2 |
| 74 | 0.02 | 0.20 | 3 |
| 80 | 0.1154 | 1.154 | 3 |
| 91 | 0.015 | 0.18 | 3 |
| 100 | 0.1056 | 0.704 | 3 |
| 105 | 0.035 | 0.195 | 3 |
| 110 | 0.04 | 0.17 | 3 |
| 112 | 0.025 | 0.205 | 3 |
Appendix B
| From-Bus | To-Bus | Mean | Standard Deviation | From-Bus | To-Bus | Mean | Standard Deviation |
|---|---|---|---|---|---|---|---|
| 2 | 1 | 0.60 | 5.28 | 20 | 19 | 1.58 | 17.31 |
| 3 | 1 | −0.59 | 4.72 | 15 | 19 | −1.40 | 10.62 |
| 5 | 4 | −2.45 | 5.25 | 21 | 20 | 1.58 | 17.31 |
| 5 | 3 | −1.35 | 0.64 | 22 | 21 | 1.58 | 17.31 |
| 5 | 6 | −2.46 | 5.37 | 23 | 22 | 1.58 | 17.31 |
| 6 | 7 | −2.46 | 5.37 | 25 | 23 | 3.56 | 34.59 |
| 9 | 8 | −23.43 | 26.57 | 26 | 25 | −3.39 | 4.66 |
| 8 | 5 | −9.02 | 3.65 | 25 | 27 | 2.65 | 24.75 |
| 10 | 9 | −23.43 | 26.57 | 27 | 28 | 1.02 | 10.15 |
| 4 | 11 | −2.45 | 4.75 | 28 | 29 | 1.02 | 10.15 |
| 5 | 11 | −2.76 | 4.18 | 30 | 17 | −2.74 | 38.83 |
| 11 | 12 | −4.05 | 15.26 | 30 | 8 | 14.41 | 32.92 |
| 12 | 2 | 0.60 | 5.28 | 26 | 30 | 11.67 | 79.18 |
| 12 | 3 | 0.76 | 4.08 | 17 | 31 | −2.42 | 14.71 |
| 7 | 12 | −2.46 | 5.37 | 31 | 29 | −1.02 | 10.15 |
| 11 | 13 | −1.16 | 6.34 | 23 | 32 | 1.98 | 17.28 |
| 12 | 14 | −1.08 | 8.70 | 32 | 31 | 1.39 | 14.57 |
| 15 | 13 | 1.16 | 6.34 | 27 | 32 | 1.07 | 9.62 |
| 15 | 14 | 1.08 | 8.70 | 113 | 17 | 2.21 | 7.31 |
| 16 | 12 | 1.23 | 2.01 | 32 | 113 | 2.21 | 17.31 |
| 17 | 15 | 0.84 | 40.80 | 32 | 114 | −0.55 | 4.98 |
| 17 | 16 | 1.23 | 2.01 | 27 | 115 | 0.55 | 4.98 |
| 17 | 18 | −0.18 | 22.06 | 114 | 115 | −0.55 | 4.98 |
| 18 | 19 | −0.18 | 22.06 | 12 | 117 | 0.00 | 0.00 |
| From-Bus | To-Bus | Mean | Standard Deviation | From-Bus | To-Bus | Mean | Standard Deviation |
|---|---|---|---|---|---|---|---|
| 36 | 35 | 0.78 | 1.81 | 49 | 54 | −2.48 | 22.40 |
| 37 | 35 | −0.78 | 1.81 | 54 | 55 | −0.64 | 6.03 |
| 37 | 33 | 0.00 | 0.00 | 54 | 56 | −1.41 | 12.95 |
| 36 | 34 | 0.72 | 16.19 | 56 | 55 | −2.10 | 20.03 |
| 37 | 34 | −2.90 | 34.62 | 57 | 56 | −1.22 | 11.03 |
| 38 | 37 | 10.80 | 36.20 | 50 | 57 | −1.22 | 11.03 |
| 37 | 39 | 7.28 | 1.70 | 58 | 56 | −1.02 | 9.18 |
| 37 | 40 | 7.21 | 10.01 | 51 | 58 | −1.02 | 9.18 |
| 39 | 40 | 7.28 | 10.05 | 59 | 54 | 0.89 | 7.55 |
| 40 | 41 | −6.02 | 10.01 | 59 | 56 | 1.55 | 13.14 |
| 42 | 40 | 6.04 | 0.81 | 59 | 55 | 0.73 | 6.05 |
| 42 | 41 | 6.02 | 0.81 | 60 | 59 | −1.31 | 4.54 |
| 44 | 43 | 2.18 | 0.81 | 61 | 59 | −1.35 | 4.67 |
| 34 | 43 | −2.18 | 12.73 | 61 | 60 | −0.91 | 3.11 |
| 45 | 44 | 2.18 | 20.81 | 62 | 60 | −0.40 | 1.43 |
| 46 | 45 | 0.95 | 16.46 | 61 | 62 | 0.26 | 1.02 |
| 47 | 46 | 0.53 | 20.81 | 63 | 59 | −4.37 | 15.04 |
| 48 | 46 | 0.42 | 16.46 | 64 | 63 | −4.37 | 15.04 |
| 49 | 47 | 0.53 | 20.81 | 64 | 61 | −2.00 | 6.76 |
| 49 | 42 | 9.05 | 0.43 | 65 | 38 | 10.80 | 36.20 |
| 49 | 45 | 1.23 | 11.92 | 65 | 64 | −6.37 | 21.80 |
| 49 | 48 | 0.42 | 16.46 | 66 | 49 | 6.06 | 86.46 |
| 49 | 50 | −1.22 | 11.03 | 66 | 62 | −0.33 | 1.23 |
| 49 | 51 | −1.47 | 13.32 | 67 | 62 | −0.33 | 1.23 |
| 51 | 52 | −0.46 | 4.13 | 65 | 66 | −4.43 | 14.40 |
| 52 | 53 | −0.46 | 4.13 | 66 | 67 | −0.33 | 1.23 |
| 54 | 53 | 0.46 | 4.13 |
| From-Bus | To-Bus | Mean | Standard Deviation | From-Bus | To-Bus | Mean | Standard Deviation |
|---|---|---|---|---|---|---|---|
| 68 | 69 | 12.60 | 54.03 | 93 | 94 | 0.53 | 17.92 |
| 69 | 70 | 16.15 | 41.86 | 94 | 95 | 4.37 | 11.13 |
| 70 | 24 | 17.80 | 21.16 | 96 | 80 | 2.62 | 5.11 |
| 70 | 71 | 17.80 | 63.24 | 96 | 82 | 4.06 | 33.91 |
| 72 | 24 | 17.80 | 6.75 | 94 | 96 | 4.93 | 12.56 |
| 71 | 72 | 17.80 | 43.25 | 97 | 80 | 2.62 | 5.11 |
| 71 | 73 | 0.00 | 20.00 | 98 | 80 | 4.82 | 12.60 |
| 70 | 74 | −8.99 | 30.68 | 99 | 80 | 4.82 | 12.58 |
| 75 | 70 | 10.45 | 31.86 | 92 | 100 | −1.34 | 21.31 |
| 69 | 75 | 4.73 | 6.75 | 94 | 100 | −8.24 | 59.54 |
| 75 | 74 | 6.99 | 10.68 | 95 | 96 | 4.37 | 11.13 |
| 77 | 76 | 5.64 | 15.89 | 96 | 97 | 2.62 | 5.11 |
| 77 | 69 | 8.28 | 31.25 | 100 | 98 | 4.82 | 12.60 |
| 77 | 75 | 7.07 | 19.91 | 100 | 99 | 4.82 | 12.58 |
| 77 | 78 | −3.27 | 18.04 | 101 | 100 | −1.34 | 21.37 |
| 79 | 78 | 3.27 | 18.04 | 92 | 102 | −1.34 | 21.37 |
| 80 | 77 | 10.56 | 58.29 | 102 | 101 | −1.34 | 21.37 |
| 80 | 79 | 3.27 | 18.04 | 100 | 103 | −5.95 | 33.98 |
| 81 | 68 | 12.60 | 54.03 | 100 | 104 | −2.11 | 11.98 |
| 80 | 81 | 12.60 | 54.03 | 103 | 104 | −0.74 | 4.17 |
| 82 | 77 | 7.18 | 9.29 | 103 | 105 | −1.38 | 7.82 |
| 83 | 82 | 3.11 | 43.20 | 100 | 106 | −1.94 | 11.04 |
| 84 | 83 | 1.34 | 18.58 | 104 | 105 | −2.85 | 16.15 |
| 85 | 83 | 1.78 | 24.62 | 105 | 106 | 1.69 | 9.61 |
| 85 | 84 | 1.34 | 18.58 | 105 | 107 | 0.25 | 1.44 |
| 85 | 86 | 0.00 | 50.00 | 105 | 108 | −2.67 | 15.50 |
| 87 | 86 | 0.00 | 50.00 | 106 | 107 | −0.25 | 1.44 |
| 88 | 85 | 1.56 | 13.39 | 108 | 109 | −2.67 | 15.50 |
| 89 | 85 | 1.56 | 13.41 | 103 | 110 | −3.83 | 22.00 |
| 89 | 88 | 1.56 | 13.39 | 109 | 110 | −2.67 | 15.50 |
| 89 | 90 | −0.99 | 19.04 | 111 | 110 | 0.00 | 0.00 |
| 90 | 91 | −0.99 | 19.04 | 110 | 112 | −2.50 | 20.50 |
| 89 | 92 | −2.13 | 77.48 | 68 | 116 | 0.00 | 0.00 |
| 91 | 92 | 0.51 | 1.04 | 75 | 118 | −5.64 | 15.89 |
| 92 | 93 | 0.53 | 17.92 | 76 | 118 | 5.64 | 15.89 |
| 92 | 94 | 0.53 | 17.92 |
References
- Wang, Z.; Guo, Z. On Critical Timescale of Real-Time Power Balancing in Power Systems with Intermittent Power Sources. Electr. Power Syst. Res. 2018, 155, 246–253. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, W.; Zheng, T.; Sun, H. Design of a Multi-Time Scale Coordinated Active Power Dispatching System for Accommodating Large Scale Wind Power Penetration. Autom. Electr. Power Syst. 2011, 35, 1–6. [Google Scholar]
- Zhai, J.; Ren, J.; Zhou, M.; Li, Z. Multi-Time Scale Fuzzy Chance Constrained Dynamic Economic Dispstch Model for Power System with Wind Power. Power Syst. Technol. 2016, 40, 1094–1099. [Google Scholar]
- Shang, J. Coordination Model and Algorithm of Energy-Saving Power Generation Dispatching Based on Time Scale. Power Syst. Technol. 2008, 32, 56–61. [Google Scholar]
- Happ, H.H. Optimal Power Dispatch-A Comprehensive Survey. IEEE Trans. Appar. Syst. 1977, 96, 841–854. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, B.; Yan, D.; Li, Y.; Luo, T. A Multi-Time Scale Rolling Coordination Scheduling Method for Power Grid Integrated with Large Scale Wind Farm. Power Syst. Technol. 2014, 38, 2434–2440. [Google Scholar]
- Liu, C.; Chao, Q.; Wei, L. Wind-Storage Coupling Based on Actual Data and Fuzzy Control in Multiple Time Scales for Real-Time Rolling Smoothing of Fluctuation. Electr. Power Autom. Equip. 2015, 35, 35–41. [Google Scholar]
- Wang, H.; He, C.; Fang, G.; Fu, L. A Gradual Optimization Model of Dispatching Schedule Taking Account of Wind Power Prediction Error Bands. Autom. Electr. Power Syst. 2011, 35, 131–135. [Google Scholar]
- Cheng, C.; Li, G.; Cheng, X.; Shen, J.; Lu, J. Large-Scale Ultra Voltage Direct Current Hydropower Absorption and Its Experiences. Proc. CSEE 2015, 35, 549–560. [Google Scholar]
- Huang, C.; Ding, J.; Tian, G.; Tang, H. Hydropower Operation Modes of Large-Scale Wind Power Grid Integration. Autom. Electr. Power Syst. 2011, 35, 37–40. [Google Scholar]
- Zhang, G.; Zhang, B. Optimal Power Flow Approach Consider Secondary Reserve Demand with Wind Power Integration. Autom. Electr. Power Syst. 2009, 33, 25–28. [Google Scholar]
- Liu, J.; Yu, J.; Liu, Z. An Intelligent Optimal Dispatch Strategy for Spinning Reserve Coping with Wind Intermittent Disturbance. Proc. CSEE 2013, 33, 163–170. [Google Scholar]
- Qadrdan, M.; Wu, J.; Jenkins, N.; Ekanayake, J. Operating Strategies for a GB Integrated Gas and Electricity Network Considering the Uncertainty in Wind Power Forecasts. IEEE Trans. Sustain. Energy 2014, 5, 128–138. [Google Scholar] [CrossRef]
- Dai, X.; Deng, Z.; Liu, G.; Tang, X.; Zhang, F.; Deng, Z. Review on Advanced Flywheel Energy Storage System with Large Scale. Trans. China Electrotech. Soc. 2011, 26, 133–140. [Google Scholar]
- Hou, Y.; Jiang, X.; Jiang, J. SMES Based Unified Power Quality Conditioner and Control Strategy. Autom. Electr. Power Syst. 2003, 27, 49–53. [Google Scholar]
- Huang, X.; Zhang, L.; Zheng, Q.; Alfred, R. Optimization Design of Electricity Saving Device in Hybrid Energy Storage System Based on Compressed Air and Supercapacitors. J. Power Supply 2013, 50, 72–78. [Google Scholar]
- Yang, N.; Wang, B.; Liu, D.; Zhao, J.; Wang, H. An Integrated Supply-Demand Stochastic Optimization Method Considering Large-Scale Wind Power and Flexible Load. Proc. CSEE 2013, 33, 63–69. [Google Scholar]
- Wang, B.; Liu, X.; Li, Y. Day-Ahead Generation Scheduling and Operation Simulation Considering Demand Response in Large-Capacity Wind Power Integrated Systems. Proc. CSEE 2013, 33, 35–44. [Google Scholar]
- Yu, D.; Song, S.; Zhang, B.; Han, X. Synergistic Dispatch of PEVs Charging and Wind Power in Chinese Regional Power Grids. Autom. Electr. Power Syst. 2011, 35, 24–29. [Google Scholar]
- Xiao, X.; Chen, Z.; Liu, N. Integrated Mode and Key Issues of Renewable Energy Sources and Electric Vehicles’ Charging and Discharging Facilities in Microgrid. Trans. China Electrotech. Soc. 2013, 28, 1–14. [Google Scholar]
- Dong, Z.; Yang, D.; Reindl, T.; Walsh, W.M. Satellite Image Analysis and a Hybrid ESSS/ANN Model to Forecast Solar Irradiance in the Tropics. Energy Convers. Manag. 2014, 79, 66–73. [Google Scholar] [CrossRef]
- Ding, M.; Yang, R. Research on Short-Term Prediction of PV Output Power Based on Weather Forecast. Renew. Energy Resour. 2014, 32, 385–391. [Google Scholar]
- Dong, Y.; Guo, H.; Wu, S.; Wang, Z.; Ming, F.A.N. Model Prediction Tree for Forecasting Photovoltaic Power Generation. Renew. Energy Resour. 2014, 32, 253–258. [Google Scholar]
- Yang, X.; Xiao, Y.; Chen, S. Wind Speed and Generated Power Forecasting Wind Farm. Proc. CSEE 2005, 25, 1–5. [Google Scholar]
- Wang, S.; Yu, J. Joint Conditions Probability Forecast Method for Wind Speed and Wind Power. Proc. CSEE 2011, 31, 7–15. [Google Scholar]
- Elena Dragomir, O.; Dragomir, F.; Stefan, V.; Minca, E. Adaptive Neuro-Fuzzy Inference Systems as a Strategy for Predicting and Controling the Energy Produced from Renewable Sources. Energies 2015, 8, 13047–13061. [Google Scholar] [CrossRef] [Green Version]
- Monteiro, C.; Santos, T.; Fernandez-Jimenez, L.A.; Ramirez-Rosado, I.J.; Terreros-Olarte, M.S. Short-Term Power Forecasting Model for Photovoltaic Plants Based on Historical Similarity. Energies 2013, 6, 2624–2643. [Google Scholar] [CrossRef]
- Niya, C.; Zheng, Q.; Ian, T.N. Wind Power Forecasts Using Gaussian Processes and Numerical Weather Prediction. IEEE Trans. Power Syst. 2014, 29, 656–665. [Google Scholar]
- Wang, F.; Mi, Z.; Su, S.; Zhao, H. Short-Term Solar Irradiance Forecasting Model Based on Artificial Neural Network Using Statistical Feature Parameters. Energies 2012, 5, 1355–1370. [Google Scholar] [CrossRef] [Green Version]
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Idna Idris, M.Y.; Mekhilef, S.; Horan, B.; Stojcevski, A. SVR-Based Model to Forecast PV Power Generation under Different Weather Conditions. Energies 2017, 10, 876. [Google Scholar] [CrossRef]
- Dong, J.; Yang, P.; Nie, S. Day-Ahead Scheduling Model of the Distributed Small Hydro-Wind-Energy Storage Power System Based on Two-Stage Stochastic Robust Optimization. Sustainability 2019, 11, 2829. [Google Scholar] [CrossRef] [Green Version]
- Papari, B.; Edrington, C.S.; Bhattacharya, I.; Rudman, G. Effective Energy Management of Hybrid AC-DC Microgrids with Storage Devices. IEEE Trans. Smart Grid 2019, 10, 193–203. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, Q.; Xiong, X.; Ouyang, J.; Xuan, P.; Xie, P.; Zou, J. Multi-time-scale robust economic dispatching method for the power system with clean energy. J. Eng. 2019, 2019, 1377–1381. [Google Scholar] [CrossRef]
- Papari, B.; Edrington, C.S.; Kavousi-Fard, F. An Effective Fuzzy Feature Selection and Prediction Method for Modeling Tidal Current: A Case of Persian Gulf. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4956–4961. [Google Scholar] [CrossRef]
- Jabr, R.A.; Pal, B.C. Intermittent wind generation in optimal power flow dispatching. IET Gener. Transm. Distrib. 2009, 3, 66–74. [Google Scholar] [CrossRef]
- Wang, Z.; Bian, Q.; Xin, H.; Gan, D. A Distributionally Robust Co-Ordinated Reserve Scheduling Model Considering CVaR-Based Wind Power Reserve Requirements. IEEE Trans. Sustain. Energy 2016, 7, 625–636. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, Q.; Li, F. Probabilistic Model of Payment Cost Minimization Considering Wind Power and Its Uncertainty. IEEE Trans. Sustain. Energy 2013, 4, 716–724. [Google Scholar] [CrossRef]
- Dobson, I.; Greene, S.; Rajaraman, R.; DeMarco, C.L.; Alvarado, F.L.; Glavic, M.; Zhang, J.; Zimmerman, R. Electric Power Transfer Capability: Concepts, Applications, Sensitivity and Uncertainty; PSERC Publication: Tempe, AZ, USA, 2001; pp. 1–34. [Google Scholar]
- Zhizhong, G. Power Network Analytic Wheel; Science Press: Beijing, China, 2008; pp. 262–279. [Google Scholar]
- Liu, B.; Zhou, J.; Zhou, H.; Liu, K. An Improved Model for Wind Power Forecast Error Distribution. East China Electr. Power 2012, 40, 286–291. [Google Scholar]
- Nan, X.; Li, Q. Energy Storage Power and Capacity Allocation Based on Wind Power Forecasting Error Distribution. Electr. Power Autom. Equip. 2013, 33, 117–122. [Google Scholar]
- Aidan, T.; Eleanor, D.; Mark, O. Rolling Unit Commitment for Systems with Significant Installed Wind Capacity. In Proceedings of the 2007 IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007. [Google Scholar]
- Makarov, Y.V.; Etingov, P.V.; Ma, J.; Huang, Z.; Subbarao, K. Incorporating Uncertainty of Wind Power Generation Forecast into Power System Operation, Dispatch, and Unit Commitment Procedures. IEEE Trans. Sustain. Energy 2011, 2, 433–442. [Google Scholar] [CrossRef]
- Pappala, V.S.; Erlich, I.; Rohrig, K.; Dobschinski, J. A Stochastic Model for the Optimal Operation of a Wind-Thermal Power System. IEEE Trans. Power Syst. 2009, 24, 940–950. [Google Scholar] [CrossRef]
- Tewari, S.; Geyer, C.J.; Mohan, N. A Statistical Model for Wind Power Forecast Error and its Application to the Estimation of Penalties in Liberalized Markets. IEEE Trans. Power Syst. 2011, 26, 2031–2039. [Google Scholar] [CrossRef]
- Morales, J.M.; Perez-Ruiz, J. Point Estimate Schemes to Solve the Probabilistic Power Flow. IEEE Trans. Power Syst. 2007, 22, 1594–1601. [Google Scholar] [CrossRef]
- Wang, J.; Shahidehpour, M.; Li, Z. Security-Constrained Unit Commitment with Volatile Wind Power Generation. IEEE Trans. Power Syst. 2008, 23, 1319–1327. [Google Scholar] [CrossRef]
- Pei, Z.; Lee, S.T. Probabilistic load flow computation using the method of combined cumulants and Gram-Charlier expansion. IEEE Trans. Power Syst. 2004, 19, 676–682. [Google Scholar]

| From-Bus | To-Bus | Mean | Standard Deviation |
|---|---|---|---|
| 15 | 33 | −1.36 | 21.17 |
| 19 | 34 | −0.68 | 10.66 |
| 30 | 38 | −3.12 | 48.77 |
| 23 | 24 | −2.65 | 41.38 |
| 47 | 69 | −0.14 | 2.15 |
| 65 | 68 | −2.39 | 37.38 |
| 49 | 69 | −0.12 | 1.85 |
| Condition | From-Bus | To-Bus | Mean | Standard Deviation |
|---|---|---|---|---|
| Minimum mean | 18 | 19 | −0.1840 | 22.0614 |
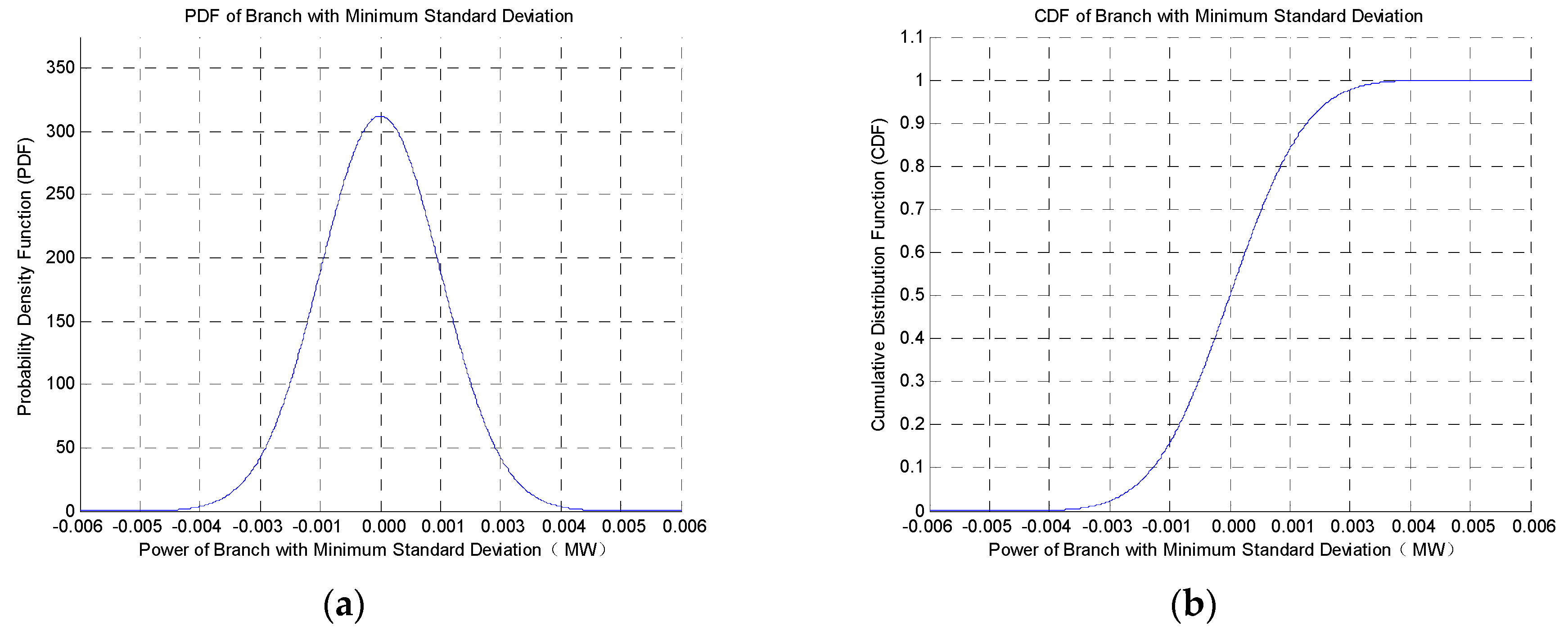
| Minimum standard deviation | 68 | 116 | 0 | 0.0013 |
| Power Flow Model | DPEPOPF Model | DC Power Flow Model |
|---|---|---|
| 0.396% | 11.05% |
| Model | DPEPOPF Model | DC Power Flow Model | AC Power Flow Model |
|---|---|---|---|
| Operation time (s) | 0.076 | 0.023 | 0.270 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Guo, Z.; Tadie, A.T.; Li, H.; Wang, G.; Hou, Y. Tie-Line Reserve Power Probability Margin for Day-Ahead Dispatching in Power Systems with High Proportion Renewable Power Sources. Energies 2019, 12, 4742. https://doi.org/10.3390/en12244742
Chen Y, Guo Z, Tadie AT, Li H, Wang G, Hou Y. Tie-Line Reserve Power Probability Margin for Day-Ahead Dispatching in Power Systems with High Proportion Renewable Power Sources. Energies. 2019; 12(24):4742. https://doi.org/10.3390/en12244742
Chicago/Turabian StyleChen, Yue, Zhizhong Guo, Abebe Tilahun Tadie, Hongbo Li, Guizhong Wang, and Yingwei Hou. 2019. "Tie-Line Reserve Power Probability Margin for Day-Ahead Dispatching in Power Systems with High Proportion Renewable Power Sources" Energies 12, no. 24: 4742. https://doi.org/10.3390/en12244742
APA StyleChen, Y., Guo, Z., Tadie, A. T., Li, H., Wang, G., & Hou, Y. (2019). Tie-Line Reserve Power Probability Margin for Day-Ahead Dispatching in Power Systems with High Proportion Renewable Power Sources. Energies, 12(24), 4742. https://doi.org/10.3390/en12244742






