Application of Artificial Neural Network for the Optimum Control of HVAC Systems in Double-Skinned Office Buildings
Abstract
:1. Introduction
2. Simulation Modeling
2.1. Simulation Program
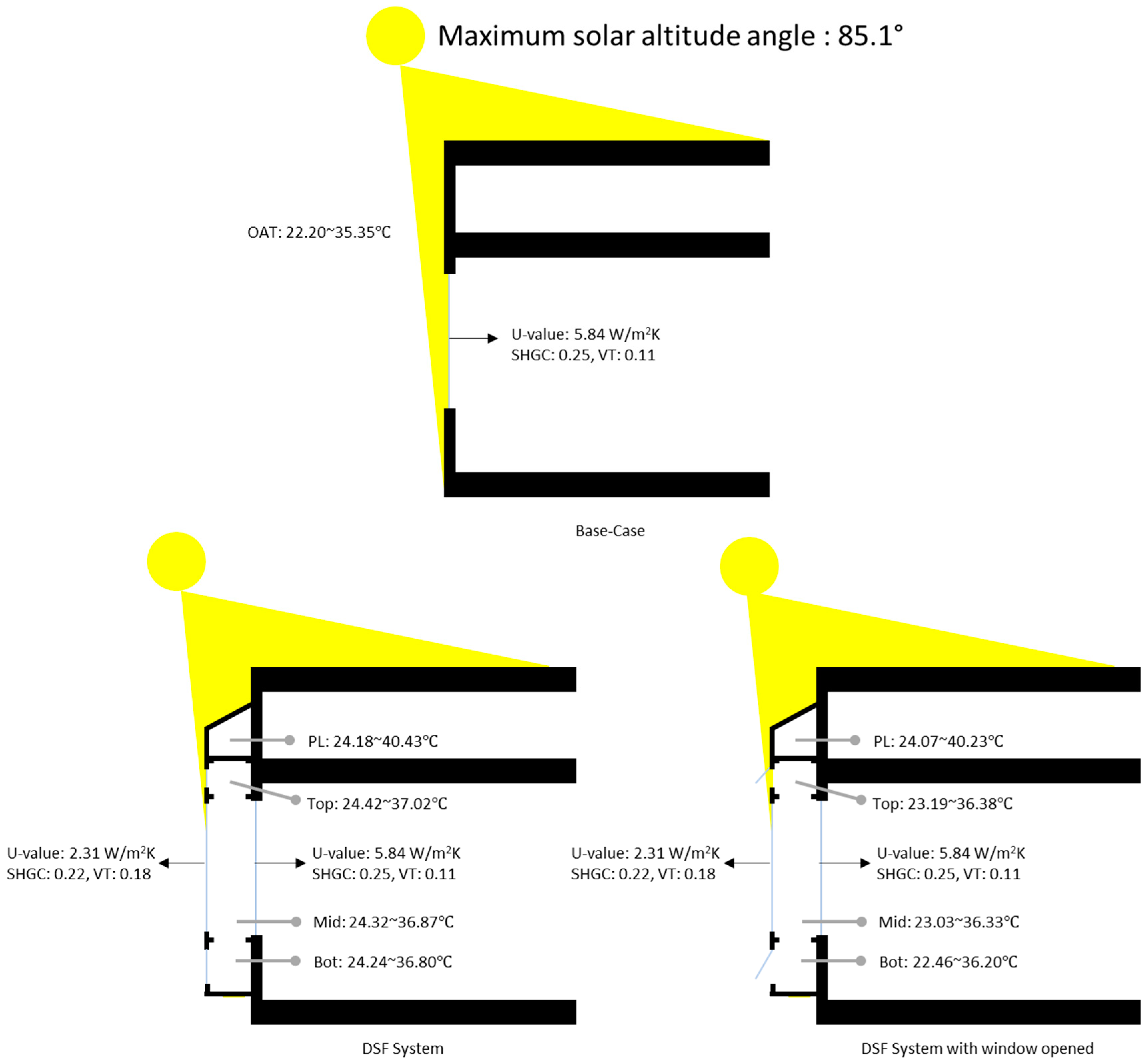
2.2. Simulation Model
2.3. Simulation Conditions
2.4. Three Simulation Cases
2.5. ANN Modeling
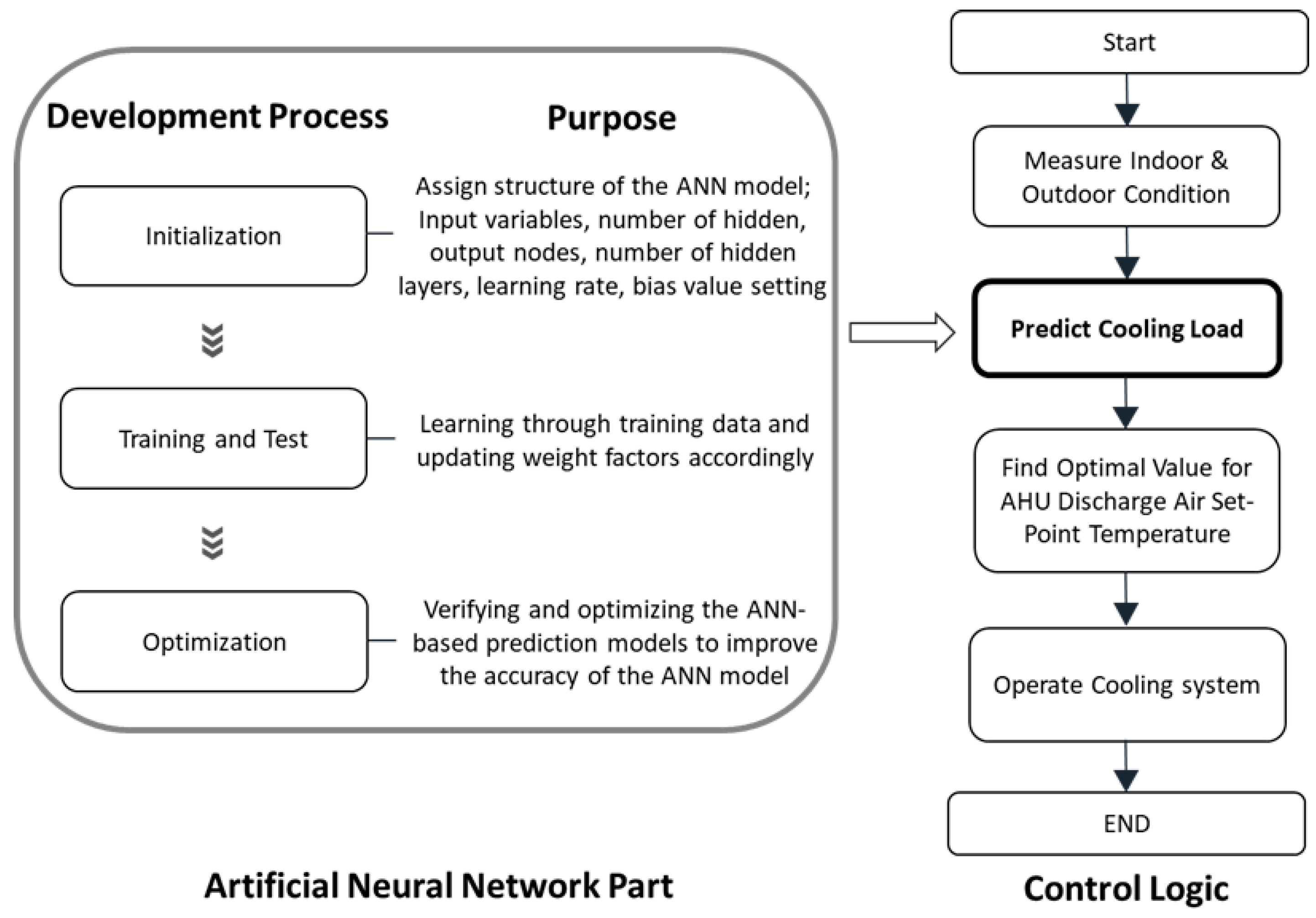
2.6. Development Process of the Predictive ANN Model
2.6.1. Subsubsection Initial ANN Model Development
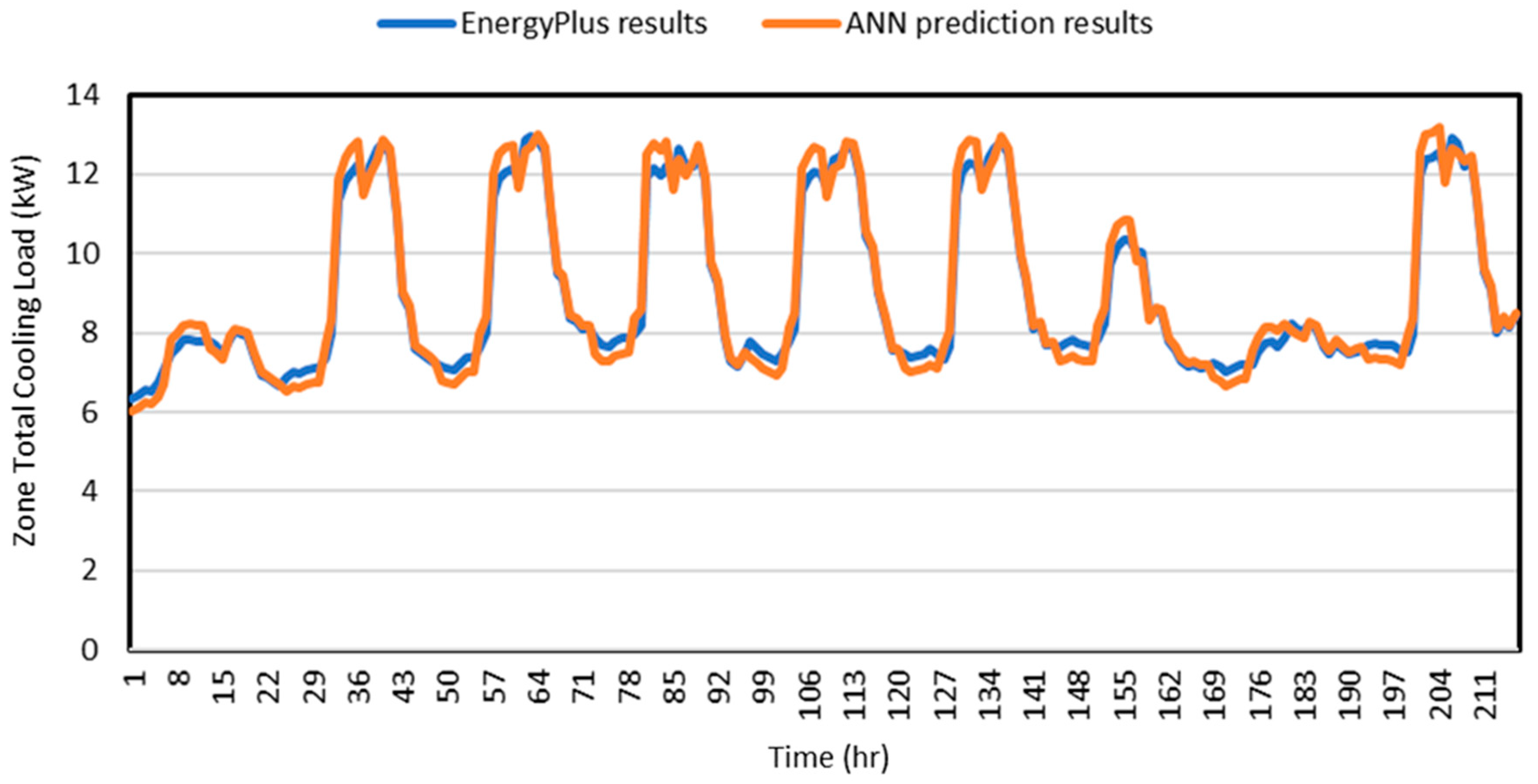
2.6.2. Subsubsection Initial ANN Model Development Optimized Performance Analysis of the ANN Model
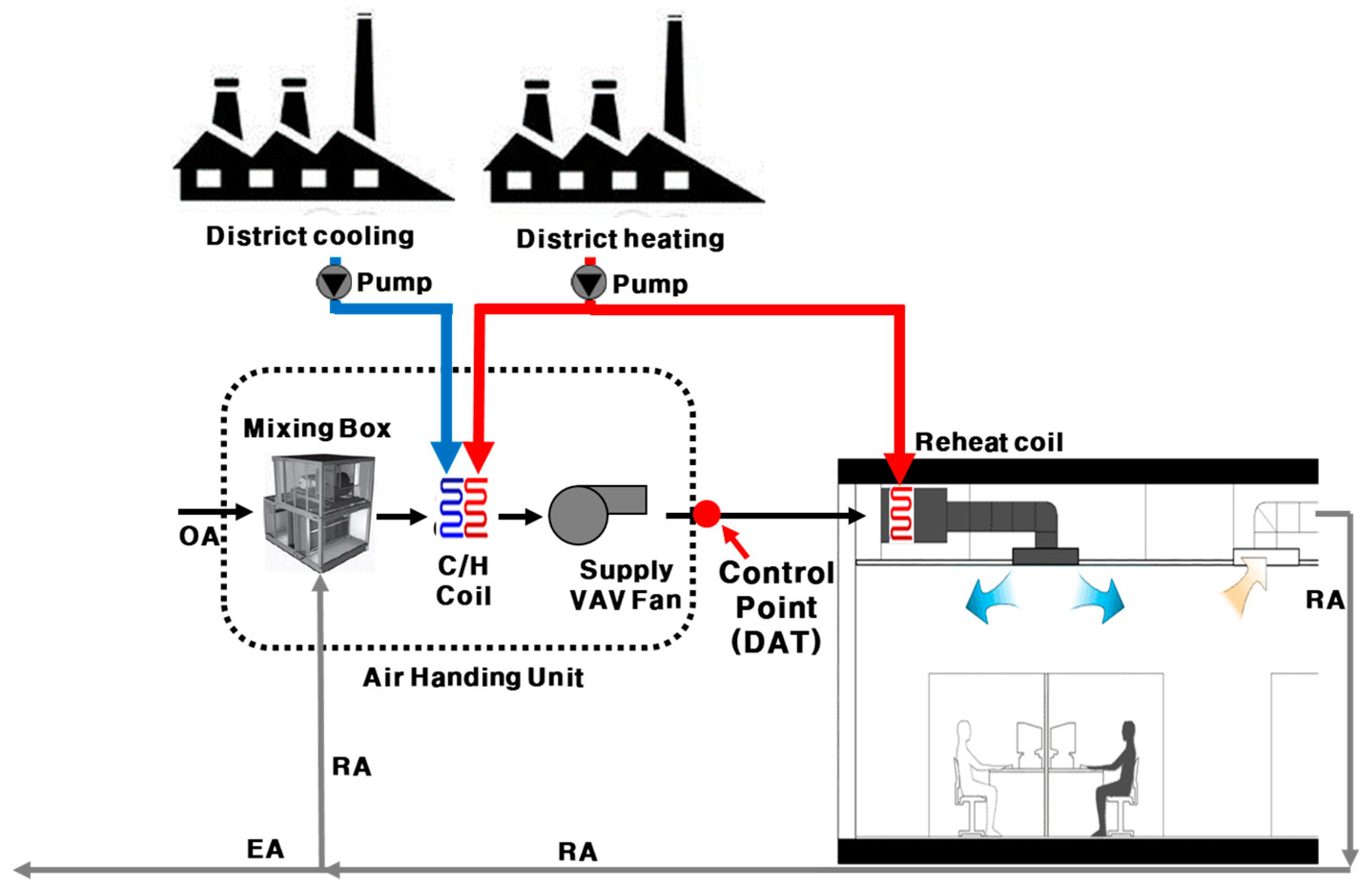
2.6.3. Initial ANN Model Development Optimized Performance Analysis of the ANN Model HVAC Control Strategy Based on the ANN Results
3. Results Analysis and Discussions
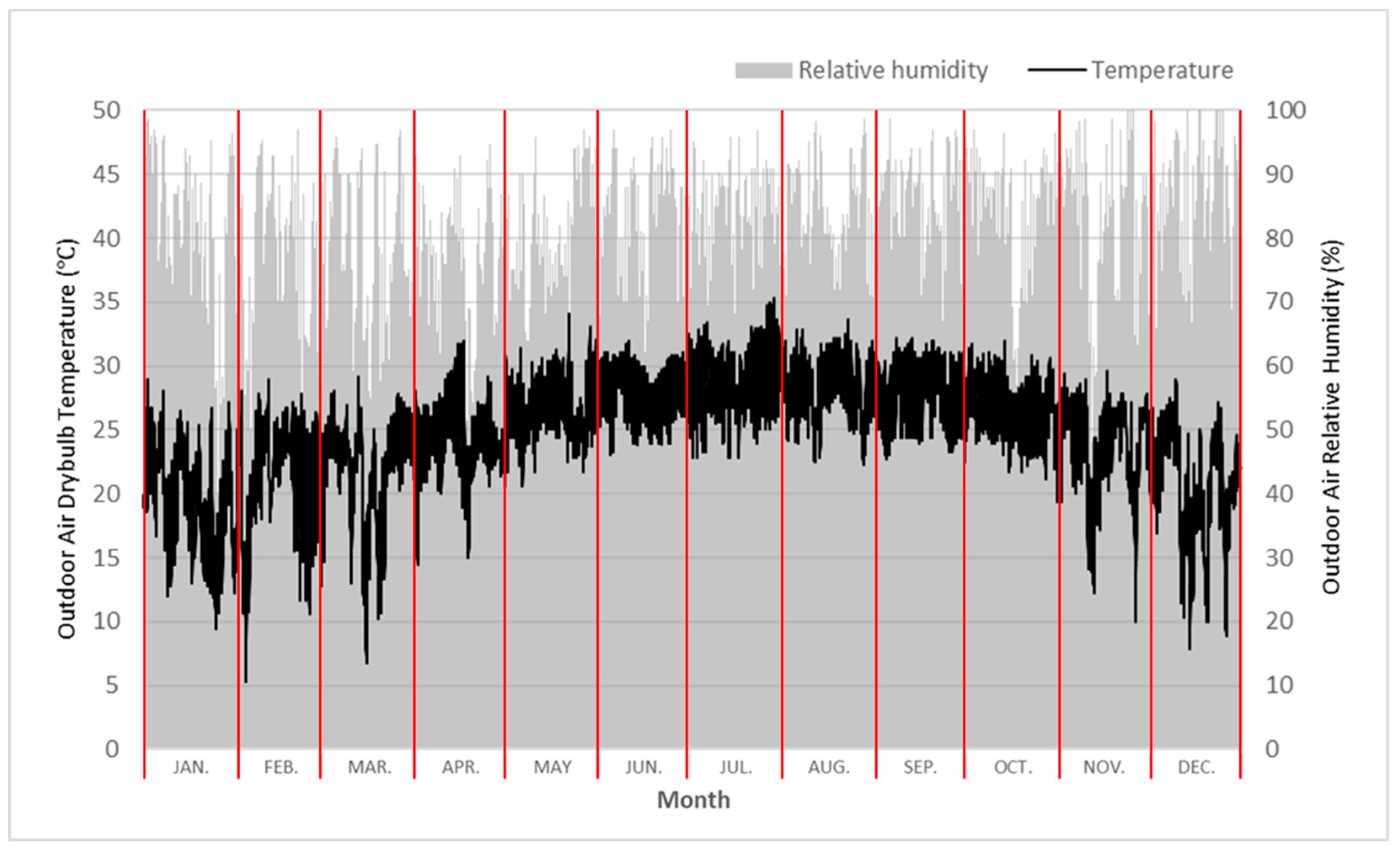
3.1. Weather Conditions
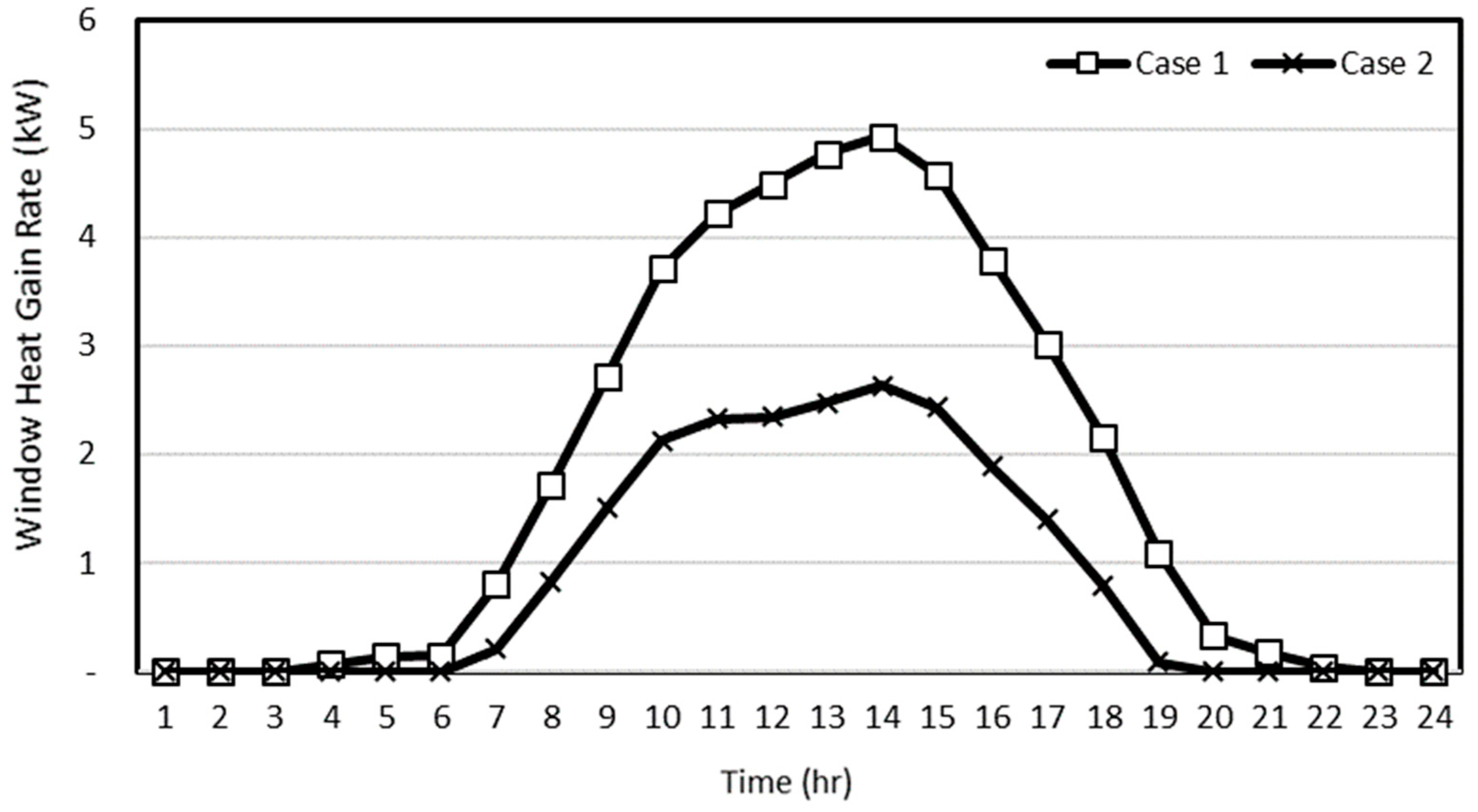
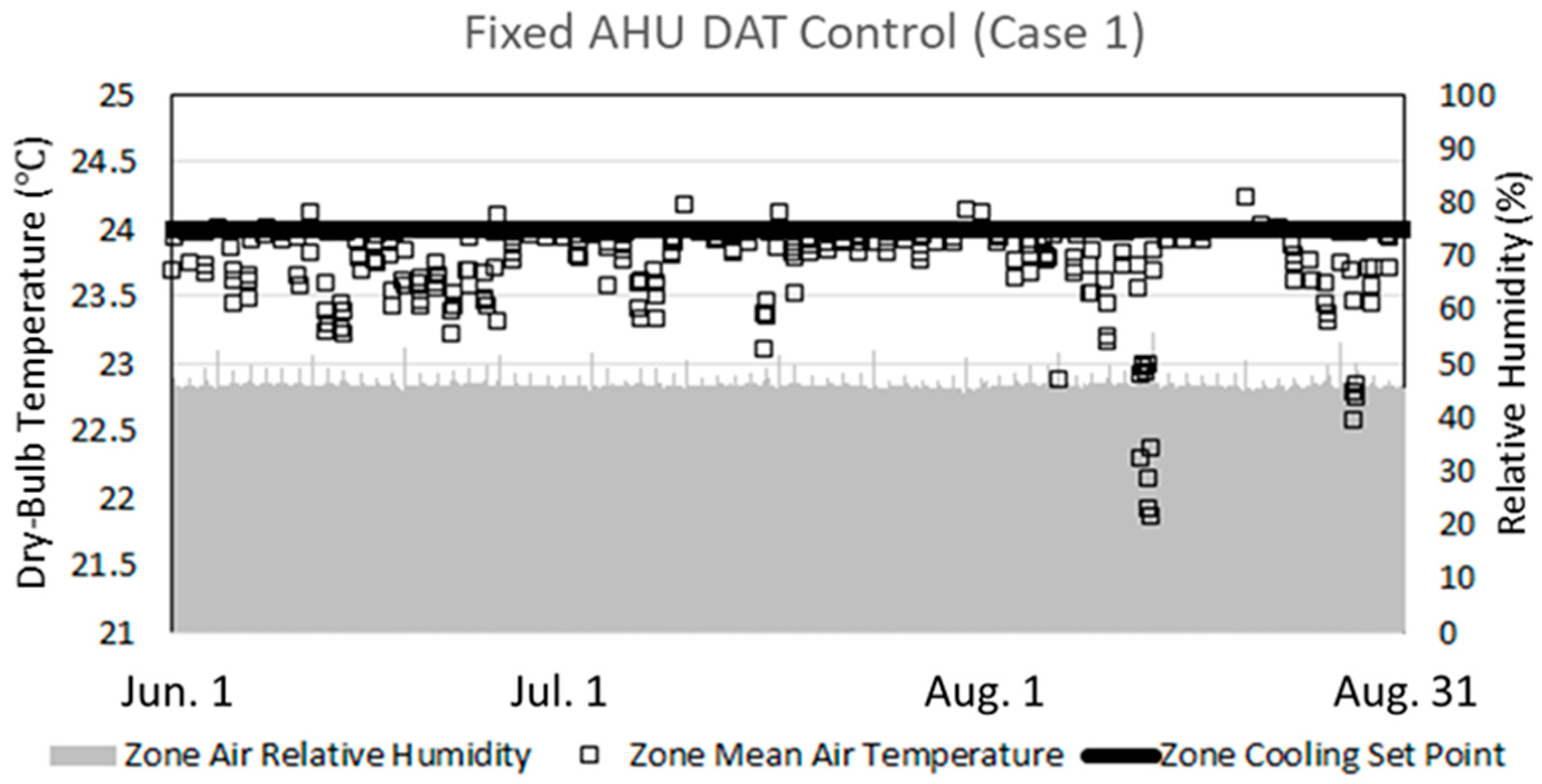
3.2. Analysis of the Summer Representative Day
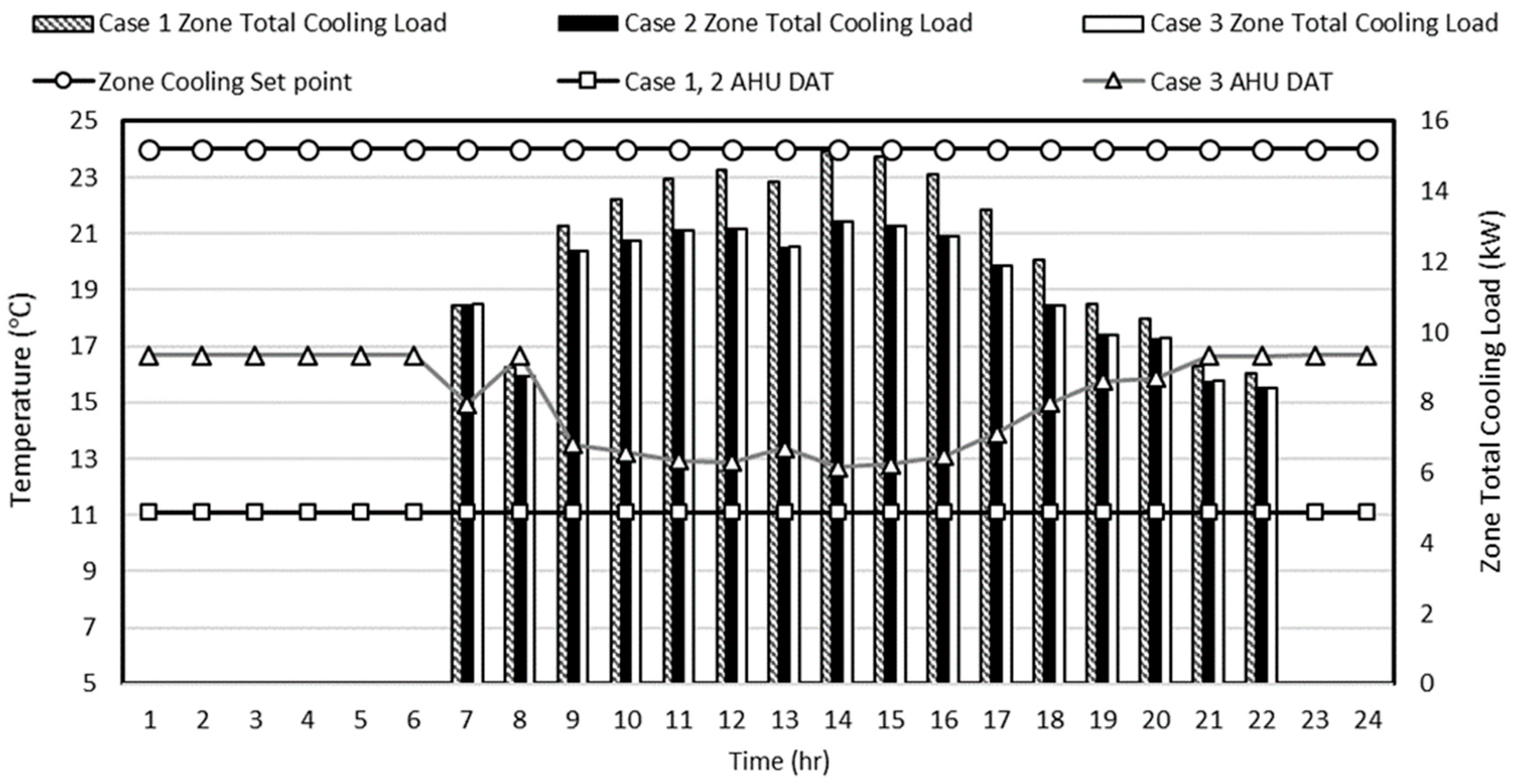
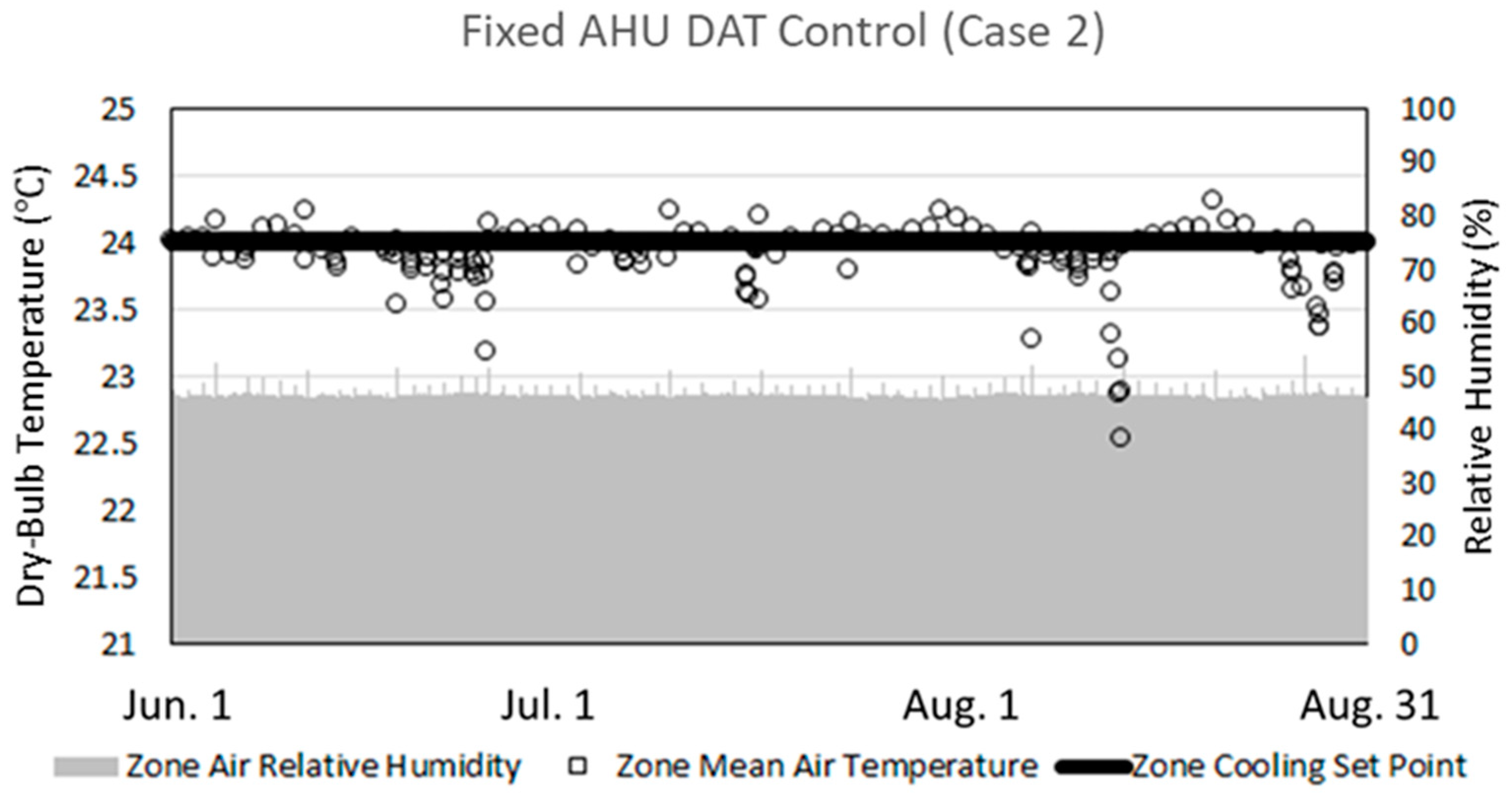
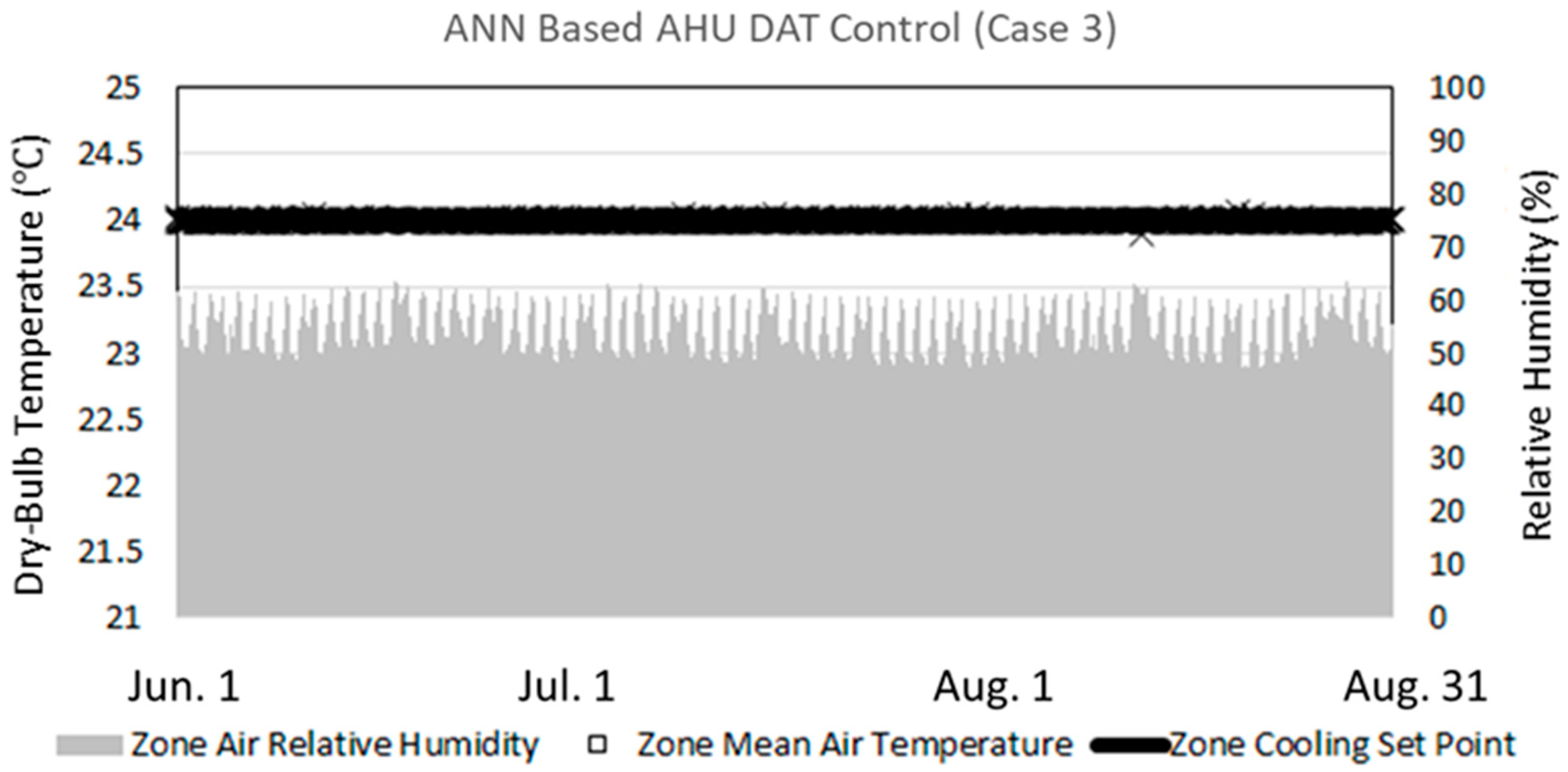
3.2.1. Comparison of AHU Discharge Air Temperature Pattern on the Summer Representative Day
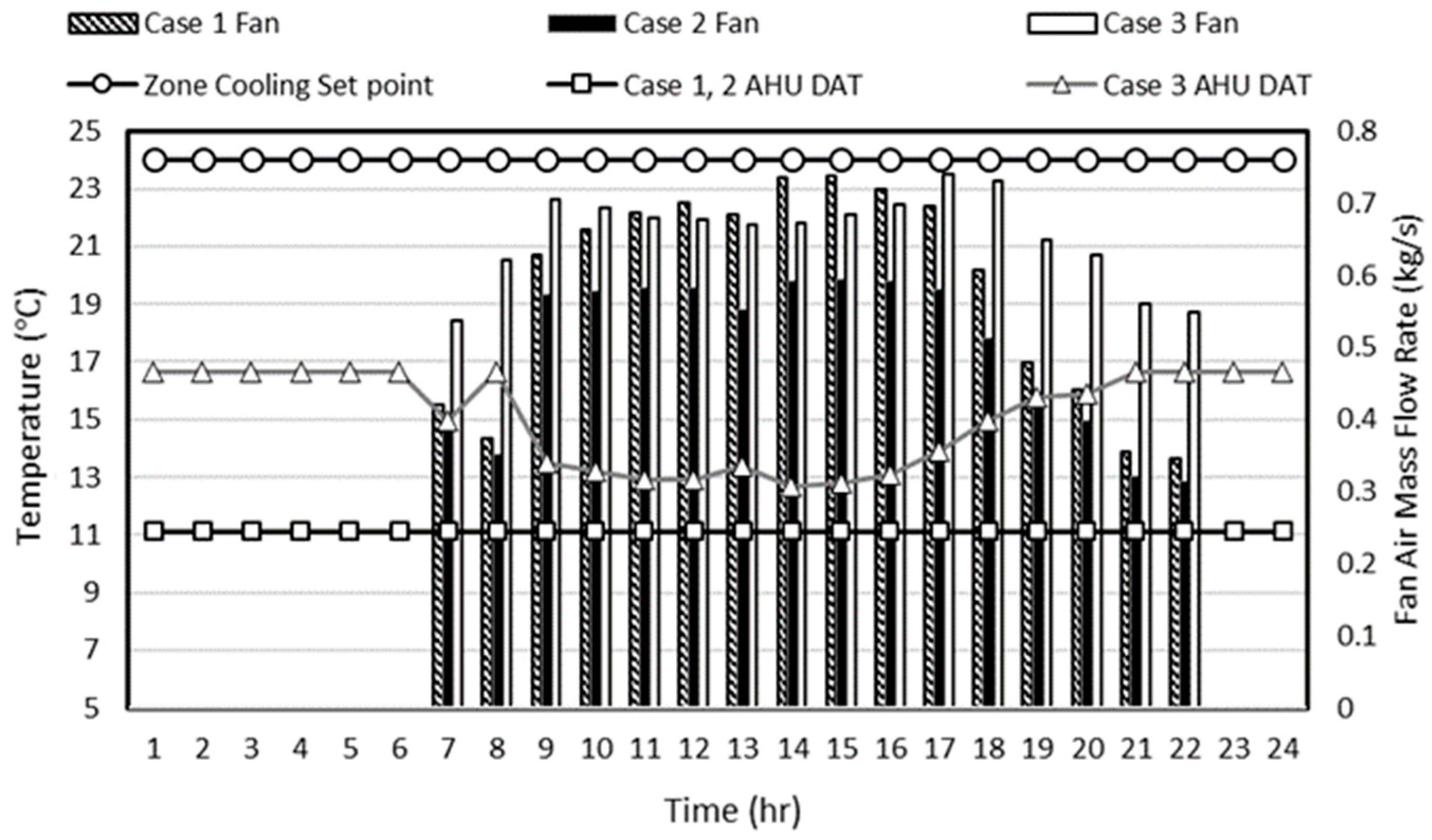
3.2.2. Comparison of the Fan Mass Flow Rate on the Summer Representative Day
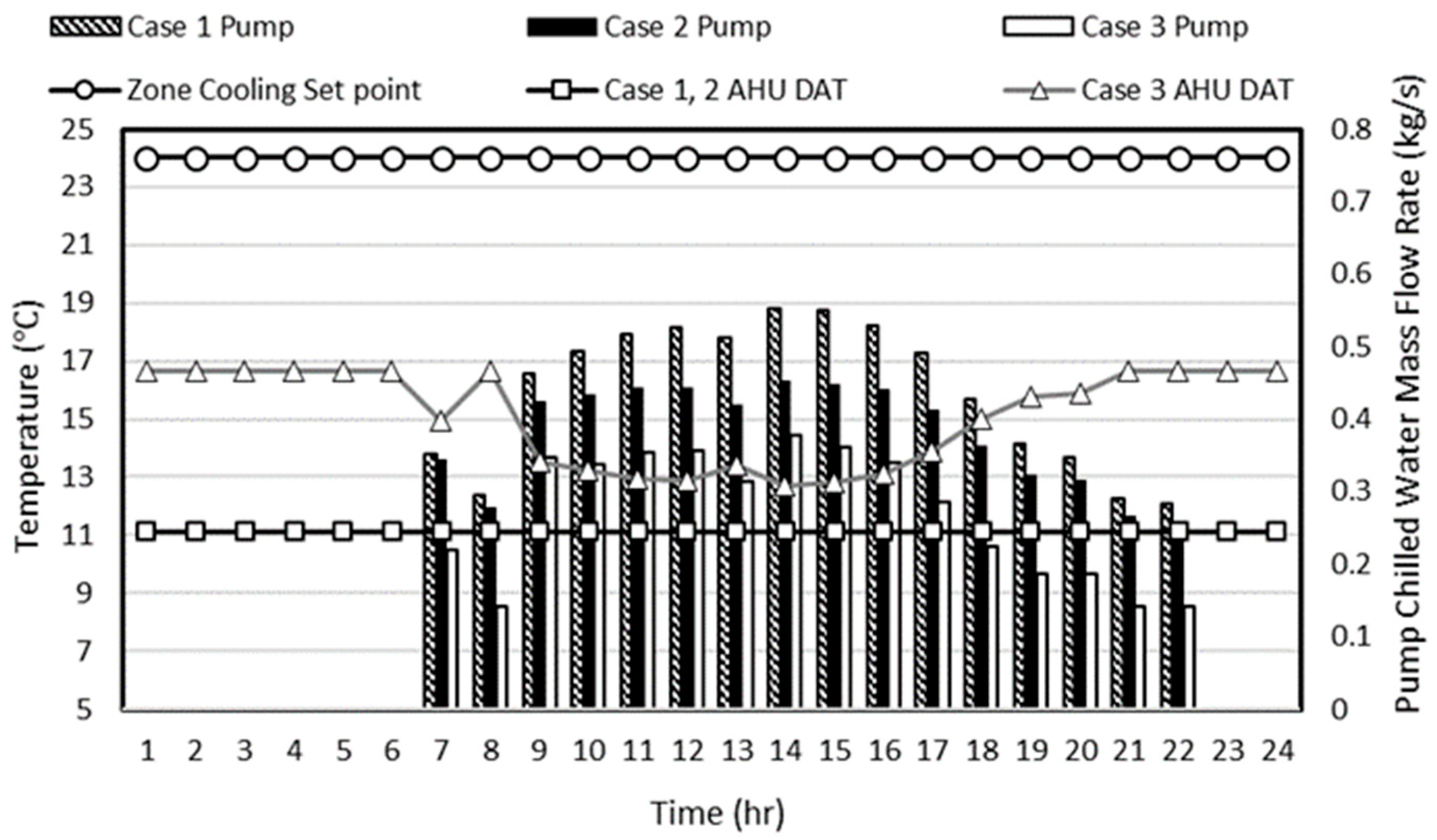
3.2.3. Comparison of the Pump Chilled Water (CHW) Mass Flow Rate on the Summer Representative Day
3.2.4. Comparison of the Cooling Energy Consumption on the Summer Representative Day
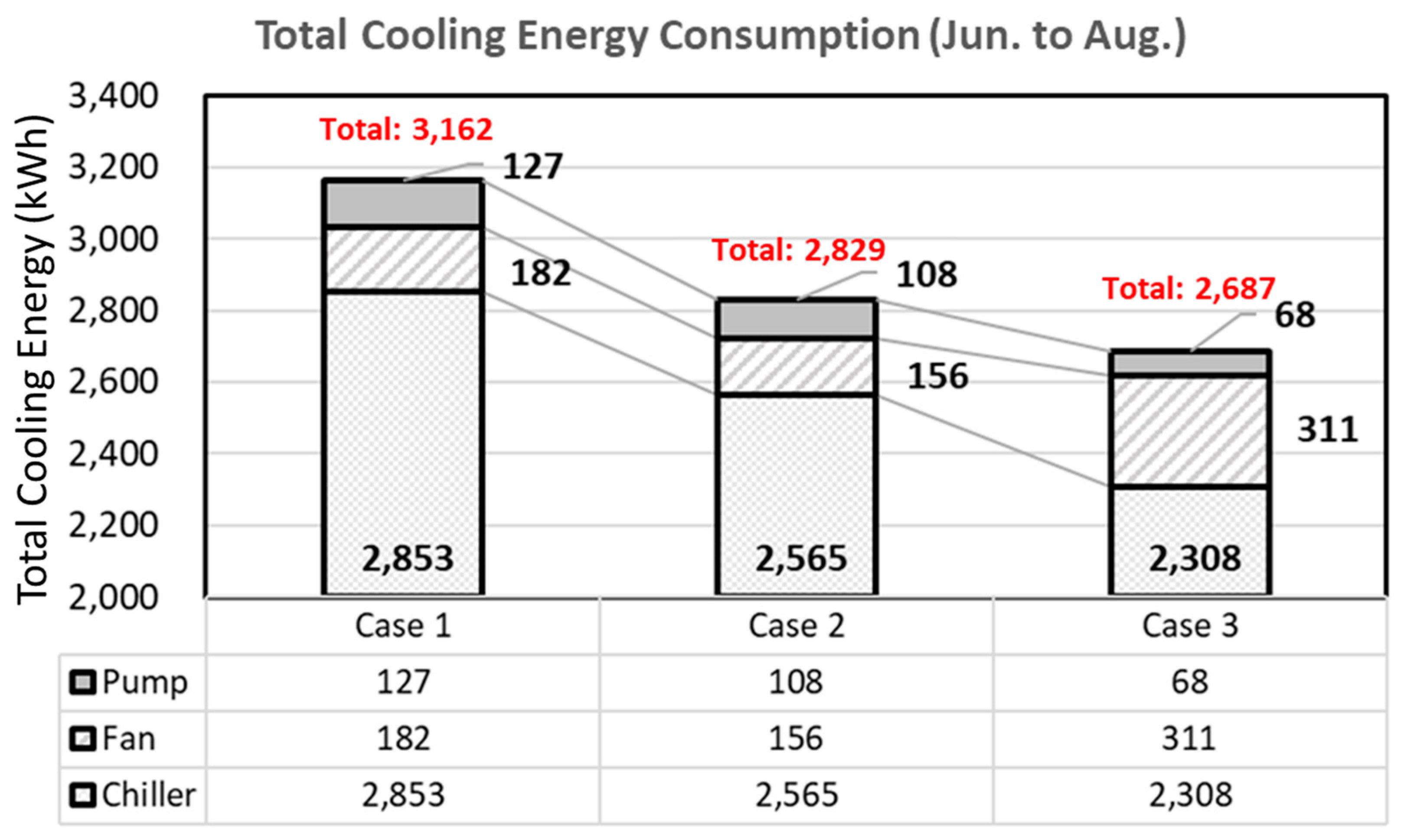
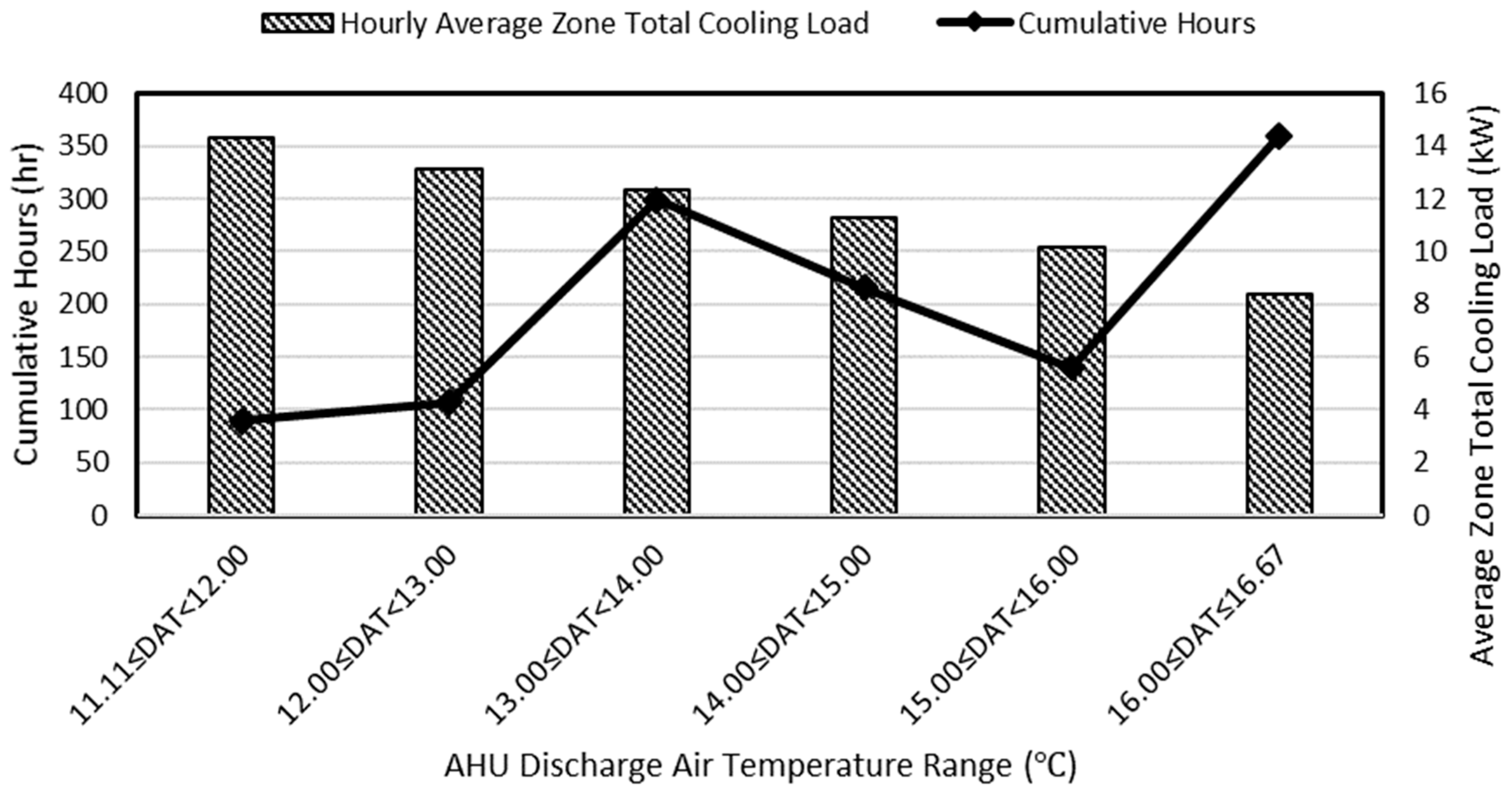
3.3. Analysis of Cooling Energy Consumption in the Summer Season
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, D.Y.; Seo, B.M.; Yoon, Y.B.; Hong, S.H.; Choi, J.M.; Lee, K.H. Heating energy performance and part load ratio characteristics of boiler staging in an office building. Front. Energy 2019, 13, 339–353. [Google Scholar] [CrossRef]
- U.S. Energy Information Administration (EIA)/Annual Energy Outlook. 2019. Available online: https://www.eia.gov/outlooks/aeo/ (accessed on 18 November 2019).
- Ghaffarianhoseini, A.; Ghaffarianhoseini, A.; Berardi, U.; Tookey, J.; Li, D.H.W.; Kariminia, S. Exploring the advantages and challenges of double-skin facades (DSFs). Renew. Sustain. Energy Rev. 2016, 60, 1052–1065. [Google Scholar] [CrossRef]
- Yoon, Y.B.; Seo, B.; Koh, B.B.; Cho, S. Performance analysis of a double-skin facade system installed at different floor levels of high-rise apartment building. J. Build. Eng. 2019, 26, 100900. [Google Scholar] [CrossRef]
- Joe, J.; Choi, W.; Kwak, Y.; Huh, J.H. Optimal design of a multi-story double skin facade. Energy Build. 2014, 76, 143–150. [Google Scholar] [CrossRef]
- Kim, D.; Cox, S.J.; Cho, H.; Yoon, J. Comparative investigation on building energy performance of double skin facade (DSF) with interior or exterior slat blinds. J. Build. Eng. 2018, 20, 411–423. [Google Scholar] [CrossRef]
- Shameri, M.A.; Alghoul, M.A.; Sopian, K.; Zain, M.F.M.; Elateb, O. Perspectives of double skin facade systems in buildings and energy saving. Renew. Sustain. Energy Rev. 2011, 15, 1468–1475. [Google Scholar] [CrossRef]
- Raji, B.; Tenpierik, M.J.; Dobbelsteen, A. An assessment of energy-saving solutions for the envelope design of high-rise buildings in temperate climates: A case study in the Netherlands. Energy Build. 2016, 124, 210–221. [Google Scholar] [CrossRef]
- Joe, J.; Choi, W.; Kwon, H.; Huh, J.H. Load characteristics and operation strategies of building integrated with multi-story double skin facade. Energy Build. 2013, 60, 185–198. [Google Scholar] [CrossRef]
- Choi, W.; Joe, J.; Kwak, Y.; Huh, J.H. Operation and control strategies for multi-storey double skin facades during the heating season. Energy Build. 2017, 49, 454–465. [Google Scholar] [CrossRef]
- Chan, A.L.S.; Chow, T.T.; Fong, K.F.; Lin, Z. Investigation on energy performance of double skin facade in Hong Kong. Energy Build. 2009, 41, 1135–1142. [Google Scholar] [CrossRef]
- Hamza, N. Double versus single skin facades in hot arid areas. Energy Build. 2008, 40, 240–248. [Google Scholar] [CrossRef]
- Souza, L.C.O.; Souza, H.A.; Rodrigues, E.F. Experimental and numerical analysis of a naturally ventilated double skin façade. Energy Build. 2018, 165, 328–339. [Google Scholar] [CrossRef]
- Zomorodian, Z.S.; Tahsildoost, M. Energy and carbon analysis of double skin façades in the hot and dry climate. J. Clean. Prod. 2018, 197, 85–96. [Google Scholar] [CrossRef]
- Gratia, E.; Herde, A.D. Are energy consumptions decreased with the addition of a double-skin? Energy Build. 2007, 39, 605–619. [Google Scholar] [CrossRef]
- Gelesz, A.; Reith, A. Climate-based performance evaluation of double skin façade by building energy modelling in Central Europe. In Proceedings of the 6th International Building Physics Conference (IBPC2015), Torino, Italy, 14–17 June 2015. [Google Scholar]
- Moon, J.W.; Lee, J.H.; Kim, S. Application of control logic for optimum indoor thermal environment in buildings with double skin envelope systems. Energy Build. 2014, 85, 59–71. [Google Scholar] [CrossRef]
- Moon, J.W.; Lee, J.H.; Yoon, Y.; Kim, S. Determining optimum control of double skin envelope for indoor thermal environment based on artificial neural network. Energy Build. 2014, 69, 175–183. [Google Scholar] [CrossRef]
- Moon, J.W.; Yoon, S.H.; Kim, S. Development of an artificial neural network model based thermal control logic for double skin envelopes in winter. Build. Environ. 2013, 61, 149–159. [Google Scholar] [CrossRef]
- Moon, J.W.; Part, J.C.; Kim, S. Development of control algorithms for optimal thermal environment of double skin envelope buildings in summer. Build. Environ. 2018, 144, 657–672. [Google Scholar] [CrossRef]
- Moon, J.W. Integrated control of the cooling system and surface openings using the artificial neural networks. Appl. Therm. Eng. 2015, 78, 150–161. [Google Scholar] [CrossRef]
- Moon, J.W.; Lee, J.H.; Chang, J.D.; Kim, S. Preliminary performance tests on artificial neural network models for opening strategies of double skin envelopes in winter. Energy Build. 2014, 75, 301–311. [Google Scholar] [CrossRef]
- Alberto, A.; Ramos, N.M.M.; Almeida, R.M.S.F. Parametric study of double-skin facades performance in mild climate countries. J. Build. Eng. 2017, 12, 87–98. [Google Scholar] [CrossRef]
- Lee, J.M.; Seo, B.M.; Hong, S.H.; Lee, K.H. Application of Artificial Neural Networks for Optimized AHU Discharge Air Temperature Set-point and Minimized Cooling Energy in VAV System. Appl. Therm. Eng. 2019, 153, 726–738. [Google Scholar] [CrossRef]
- Yeon, S.H.; Yu, B.; Seo, B.M.; Yoon, Y.B.; Lee, K.H. ANN Based Automatic Slat Angle Control of Venetian Blind for Minimized Total Load in an Office Building. Sol. Energy 2019, 180, 133–145. [Google Scholar] [CrossRef]
- Seo, B.; Yoon, Y.B.; Song, S.; Cho, S. ANN-based thermal load prediction approach for advanced controls in building energy systems. In Proceedings of the Conference for ARCC 2019 International Conference, Toronto, ON, Canada, 29 May–1 June 2019. [Google Scholar]
- The U.S. DOE. Getting Started. EnergyPlus Version 9.1.0 Documentation; The U.S. DOE: Washington, DC, USA, 2019.
- The U.S. DOE. EnergyPlus Engineering Reference. The Reference to EnergyPlus Calculations, Version 9.1; The U.S. DOE: Washington, DC, USA, 2019.
- Seo, B.M.; Lee, K.H. Detailed analysis on part load ratio characteristics and cooling energy saving of chiller staging in an office building. Energy Build. 2016, 119, 309–322. [Google Scholar] [CrossRef]
- Lutz, M.; Ascher, D. Learning Python, 5th ed.; O’Reilly: Sebastopol, CA, USA, 2013. [Google Scholar]
- The U.S. DOE. EnergyPlus Input Output Reference: The Encyclopedic Reference to EnergyPlus Input and Output, Version 9.1; The U.S. DOE: Washington, DC, USA, 2019.
- American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE). Handbook of Fundamentals; American Society of Heating, Refrigerating and Air-Conditioning Engineers Inc.: Atlanta, GA, USA, 2009; Volume 30329(404). [Google Scholar]
- Costola, D.; Etheridge, D.W. Unsteady natural ventilation at model scale-Flow reversal and discharge coefficients of a short stack and an orifice. Build. Environ. 2008, 43, 1491–1506. [Google Scholar] [CrossRef]
- Schulze, T.; Eicker, U. Controlled natural ventilation for energy efficient buildings. Energy Build. 2013, 56, 221–232. [Google Scholar] [CrossRef]
- Rashid, T. Make Your Own Neural Network. CreateSpace Independent Publishing Platform, 2016 Hargan, MR., ASHRAE Guideline 14-2002 Measurement of Energy and Demand Savings; American Society of Heating Refrigerating and Air-Conditioning Engineers Inc.: Atlanta, GA, USA, 2012. [Google Scholar]
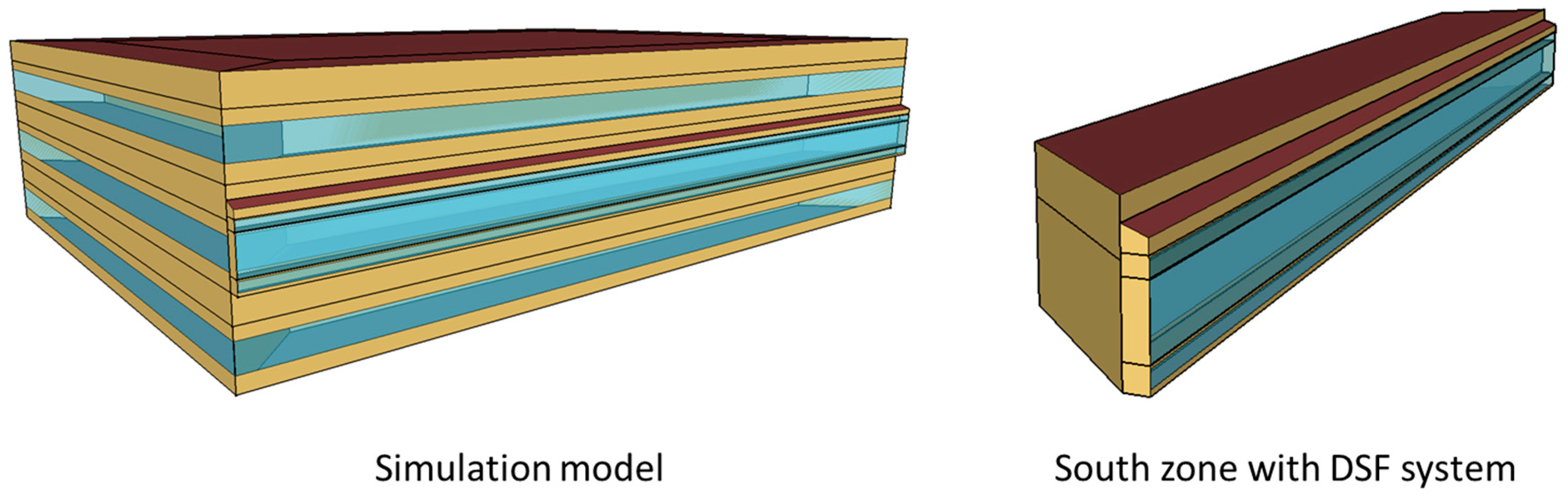




| Construction | U-Value (W/m2) | Visible Transmittance | Solar Heat Gain Coefficient | Reference |
|---|---|---|---|---|
| Exterior Wall | 0.79 | X | X | ASHRAE Standard 90.1-2004 (Climate Zone 1A) |
| Interior Wall | 5.68 | X | X | |
| Raised Floor | 1.74 | X | X | |
| Ceiling Slab | 1.88 | X | X | |
| Roof | 0.38 | X | X | |
| Exterior window for the building | 5.84 | 0.11 | 0.25 | |
| DSF Frame | 6.64 | X | X | [6] |
| Exterior window for the DSF system | 2.31 | 0.18 | 0.22 |
| Type | Input |
|---|---|
| People | 0.057 Person/m2 |
| Light | 11.840 W/m2 |
| Equipment | 10.333 W/m2 |
| Cooling set-point temperature | 24 °C |
| Division | Range | Initial Values |
|---|---|---|
| Number of Hidden Layers | 1–n | 1 |
| Number of Hidden Neurons | 1–n | 9 |
| Learning Rate | 0.01–1.00 | 0.2 |
| Epochs | 1–n | 300 |
| Division | Range | Optimize Values |
|---|---|---|
| Number of Hidden Layers | 1–n | 2 |
| Number of Hidden Neurons Layer 1 | 1–n | 11 |
| Number of Hidden Neurons Layer 2 | 1–n | 9 |
| Learning Rate | 0.01–1.00 | 0.1 |
| Epochs | 1–n | 800 |
| Case 1 | Case 2 | Case 3 | |
|---|---|---|---|
| CHW use (kWh/day) | 200.26 | 182.13 | 172.68 |
| Chiller (COP 5) electric (kWh/day) | 40.05 | 36.43 | 34.54 |
| Fan electric (kWh/day) | 2.65 | 2.34 | 3.13 |
| Pump electric (kWh/day) | 1.79 | 1.55 | 1.10 |
| Total cooling energy (Chiller + Fan + Pump) (kWh/day) | 44.49 | 40.32 | 38.77 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, B.; Yoon, Y.B.; Mun, J.H.; Cho, S. Application of Artificial Neural Network for the Optimum Control of HVAC Systems in Double-Skinned Office Buildings. Energies 2019, 12, 4754. https://doi.org/10.3390/en12244754
Seo B, Yoon YB, Mun JH, Cho S. Application of Artificial Neural Network for the Optimum Control of HVAC Systems in Double-Skinned Office Buildings. Energies. 2019; 12(24):4754. https://doi.org/10.3390/en12244754
Chicago/Turabian StyleSeo, Byeongmo, Yeo Beom Yoon, Jung Hyun Mun, and Soolyeon Cho. 2019. "Application of Artificial Neural Network for the Optimum Control of HVAC Systems in Double-Skinned Office Buildings" Energies 12, no. 24: 4754. https://doi.org/10.3390/en12244754
APA StyleSeo, B., Yoon, Y. B., Mun, J. H., & Cho, S. (2019). Application of Artificial Neural Network for the Optimum Control of HVAC Systems in Double-Skinned Office Buildings. Energies, 12(24), 4754. https://doi.org/10.3390/en12244754






