Fault Current Constraint Transmission Expansion Planning Based on the Inverse Matrix Modification Lemma and a Valid Inequality
Abstract
1. Introduction
2. Mathematical Formulation
2.1. Objective Function
2.2. Fault Current Constraints
2.2.1. Conventional Method for the Bus Impedance Update
2.2.2. Derivation of the Bus Impedance Update Equation Based on the IMML
2.3. Other Constraints
2.3.1. Power Flow Equation
2.3.2. Node Balance Equation
2.3.3. Limit on Generator Output
2.3.4. Transmission Limit
2.3.5. Bus Voltage Angel Limit
2.3.6. New Transmission Line Constraint
3. Solution Methods
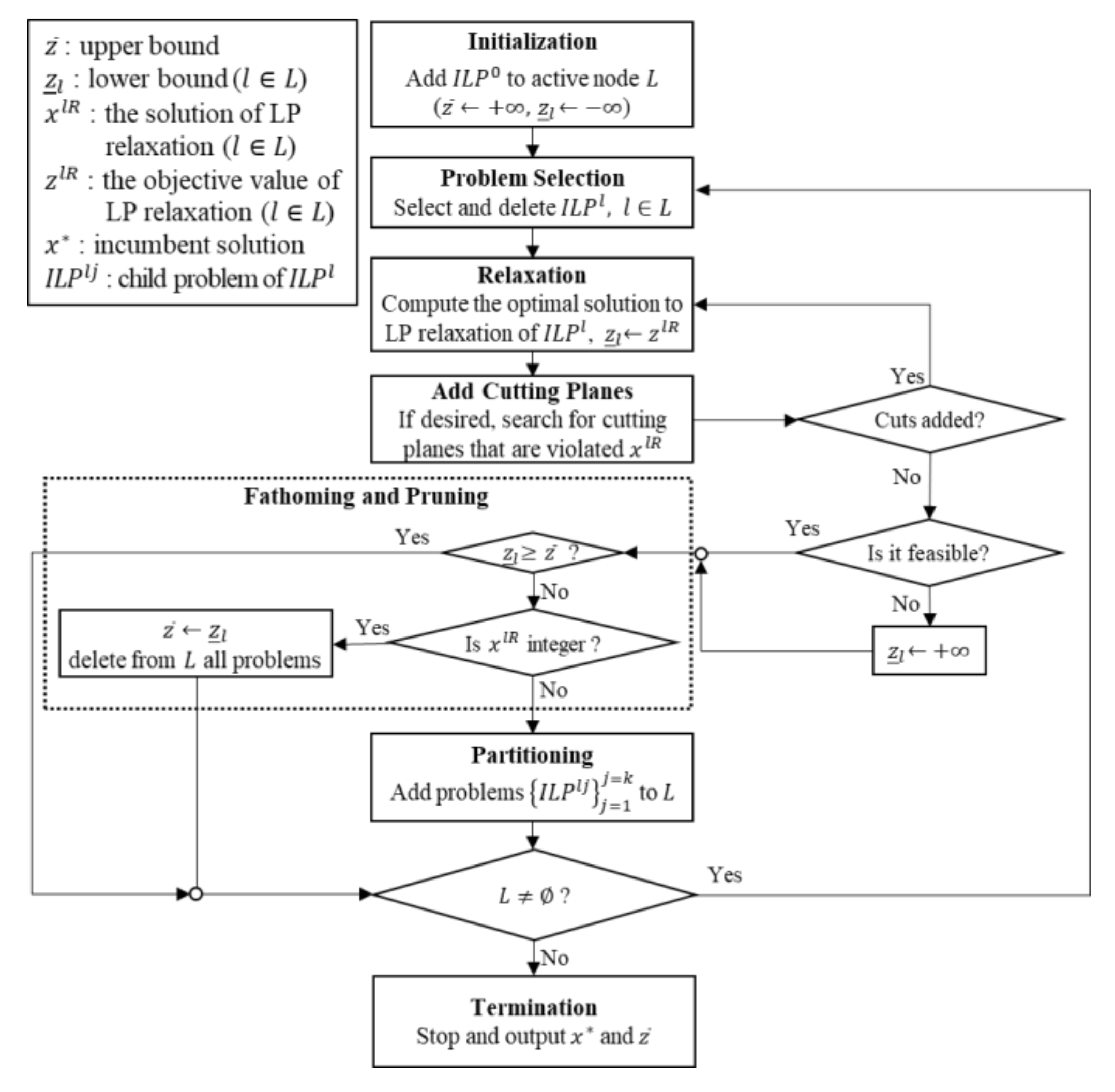
3.1. Branch and Cut(B&C) Algorithm
3.2. Valid Inequalities
4. Simulation Results
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Indices |
| : Index of years : Index of electricity load blocks : Index of buses : Sub-index of buses applying fault current constraint : Index of generators |
| Sets and Function |
| : Set of all planning years : Set of all buses : Set of buses connected to new line candidates : Set of buses to which fault current constraints are applied : Set of all generators : Set of generators connected to bus : Bus pair of new line candidates between bus and : Set of all electricity load blocks : Fuel cost of generator |
| Variables and Time-varying Parameters |
| : Bus admittance matrix in year : Bus impedance matrix in year : Active power output of generator of load block in year : Active power flow of existing line from bus to of load block in year : Active power flow of new line from bus to of load block in year : Binary variable for on/off status of generator at bus of load block in year : Binary variable for construction status of new transmission line at bus in year : Phase angle of bus of load block in year : Solution to the linear relaxation problem of B&C algorithm at bus in year |
| Fixed Parameters |
| : Maximum fault current at bus : Bus admittance matrix between bus and in base year : Bus impedance matrix between bus and in base year : Impedance of new line candidate between bus and : Construction cost of new line candidate between and : Life span of new line candidate between and : Time duration of load block : Discount rate : Coefficients of the cost function of generator : Active power demand at bus of load block in year , : Maximum/Minimum active power output of generator : Maximum active power transmission limit of existing line between bus and ,: Maximum/Minimum active power transmission limit of new line between bus and : Susceptance of transmission line between bus and : Susceptance of new line candidate between bus and , : Maximum/Minimum voltage angle at bus |
Appendix A. Parameters
| Branch | ID | R (p.u.) | X (p.u.) | Limit (MW) | Branch | ID | R (p.u.) | X (p.u.) | Limit (MW) |
|---|---|---|---|---|---|---|---|---|---|
| 101-102 | 1 | 0.003 | 0.014 | 175 | 201-202 | 1 | 0.003 | 0.014 | 175 |
| 101-103 | 1 | 0.055 | 0.211 | 175 | 201-203 | 1 | 0.055 | 0.211 | 175 |
| 101-105 | 1 | 0.022 | 0.085 | 175 | 201-205 | 1 | 0.022 | 0.085 | 175 |
| 102-104 | 1 | 0.033 | 0.127 | 175 | 202-204 | 1 | 0.033 | 0.127 | 175 |
| 102-106 | 1 | 0.050 | 0.192 | 175 | 202-206 | 1 | 0.050 | 0.192 | 175 |
| 103-109 | 1 | 0.031 | 0.119 | 175 | 203-209 | 1 | 0.031 | 0.119 | 175 |
| 104-109 | 1 | 0.027 | 0.104 | 175 | 204-209 | 1 | 0.027 | 0.104 | 175 |
| 105-110 | 1 | 0.023 | 0.088 | 175 | 205-210 | 1 | 0.023 | 0.088 | 175 |
| 106-110 | 1 | 0.014 | 0.061 | 175 | 206-210 | 1 | 0.014 | 0.061 | 175 |
| 107-108 | 1 | 0.016 | 0.061 | 175 | 207-208 | 1 | 0.016 | 0.061 | 175 |
| 108-109 | 1 | 0.043 | 0.165 | 175 | 208-209 | 1 | 0.043 | 0.165 | 175 |
| 108-110 | 1 | 0.043 | 0.165 | 175 | 208-210 | 1 | 0.043 | 0.165 | 175 |
| 111-113 | 1 | 0.006 | 0.048 | 500 | 211-213 | 1 | 0.006 | 0.048 | 500 |
| 111-114 | 1 | 0.005 | 0.042 | 500 | 211-214 | 1 | 0.005 | 0.042 | 500 |
| 112-113 | 1 | 0.006 | 0.048 | 500 | 212-213 | 1 | 0.006 | 0.048 | 500 |
| 112-123 | 1 | 0.012 | 0.097 | 500 | 212-223 | 1 | 0.012 | 0.097 | 500 |
| 113-123 | 1 | 0.011 | 0.087 | 500 | 213-223 | 1 | 0.011 | 0.087 | 500 |
| 114-116 | 1 | 0.005 | 0.059 | 500 | 214-216 | 1 | 0.005 | 0.059 | 500 |
| 115-121 | 1 | 0.006 | 0.049 | 500 | 215-221 | 1 | 0.006 | 0.049 | 500 |
| 115-124 | 1 | 0.007 | 0.052 | 500 | 215-224 | 1 | 0.007 | 0.052 | 500 |
| 116-117 | 1 | 0.003 | 0.026 | 500 | 216-217 | 1 | 0.003 | 0.026 | 500 |
| 116-119 | 1 | 0.003 | 0.023 | 500 | 216-219 | 1 | 0.003 | 0.023 | 500 |
| 117-118 | 1 | 0.002 | 0.014 | 500 | 217-218 | 1 | 0.002 | 0.014 | 500 |
| 117-122 | 1 | 0.014 | 0.105 | 500 | 217-222 | 1 | 0.014 | 0.105 | 500 |
| 118-121 | 1 | 0.003 | 0.026 | 500 | 218-221 | 1 | 0.003 | 0.026 | 500 |
| 119-120 | 1 | 0.005 | 0.040 | 500 | 219-220 | 1 | 0.005 | 0.040 | 500 |
| 120-123 | 1 | 0.003 | 0.022 | 500 | 220-223 | 1 | 0.003 | 0.022 | 500 |
| 107-203 | 1 | 0.042 | 0.161 | 175 |
| Branch | R (p.u.) | X (p.u.) | Limit (MW) | Tr | R (p.u.) | X (p.u.) | Limit (MW) |
|---|---|---|---|---|---|---|---|
| 103-124 | 0.002 | 0.09 | 400 | 203-224 | 0.002 | 0.09 | 400 |
| 109-111 | 0.002 | 0.09 | 400 | 209-211 | 0.002 | 0.09 | 400 |
| 109-112 | 0.002 | 0.09 | 400 | 209-212 | 0.002 | 0.09 | 400 |
| 110-111 | 0.002 | 0.09 | 400 | 210-211 | 0.002 | 0.09 | 400 |
| 110-112 | 0.002 | 0.09 | 400 | 210-212 | 0.002 | 0.09 | 400 |
| Branch | R (p.u.) | X (p.u.) | Limit (MW) | Investment Cost (Million $) | Life (year) |
|---|---|---|---|---|---|
| 102-201 | 0.090 | 0.346 | 175 | 90,000,000 | 30 |
| 106-204 | 0.072 | 0.276 | 175 | 72,000,000 | 30 |
| 107-203 | 0.042 | 0.161 | 175 | 42,000,000 | 30 |
| 107-108 | 0.016 | 0.061 | 175 | 16,000,000 | 30 |
| 112-224 | 0.011 | 0.089 | 500 | 120,000,000 | 30 |
| 113-215 | 0.010 | 0.075 | 500 | 78,000,000 | 30 |
| 113-217 | 0.042 | 0.161 | 175 | 42,000,000 | 30 |
| 115-116 | 0.002 | 0.017 | 500 | 18,000,000 | 30 |
| 115-121 | 0.006 | 0.049 | 500 | 51,000,000 | 30 |
| 116-117 | 0.003 | 0.026 | 500 | 27,000,000 | 30 |
| 118-121 | 0.003 | 0.026 | 500 | 27,000,000 | 30 |
| 119-120 | 0.005 | 0.040 | 500 | 41,250,000 | 30 |
| 120-123 | 0.003 | 0.022 | 500 | 22,500,000 | 30 |
| 121-122 | 0.009 | 0.068 | 500 | 70,500,000 | 30 |
| 122-218 | 0.009 | 0.068 | 500 | 76,500,000 | 30 |
| 123-217 | 0.010 | 0.074 | 500 | 76,500,000 | 30 |
| 203-209 | 0.031 | 0.119 | 175 | 31,000,000 | 30 |
| 207-208 | 0.016 | 0.061 | 175 | 16,000,000 | 30 |
| 215-216 | 0.002 | 0.017 | 500 | 18,000,000 | 30 |
| 215-221 | 0.006 | 0.049 | 500 | 51,000,000 | 30 |
| 218-221 | 0.003 | 0.026 | 500 | 27,000,000 | 30 |
| 219-220 | 0.005 | 0.040 | 500 | 41,250,000 | 30 |
| 220-223 | 0.003 | 0.022 | 500 | 22,500,000 | 30 |
| 221-222 | 0.009 | 0.068 | 500 | 70,500,000 | 30 |
| 211-224 | 0.006 | 0.046 | 500 | 49,500,000 | 30 |
| Bus ID | Pmax (MW) | Pmin (MW) | Bg ($/MWh) | Cg ($/h) | Xd″ (p.u) | Bus ID | Pmax (MW) | Pmin (MW) | Bg ($/MWh) | Cg ($/h) | Xd″ (p.u) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 101 | 192 | 154 | 52 | 1220 | 0.19 | 201 | 192 | 154 | 42 | 976 | 0.19 |
| 102 | 192 | 154 | 52 | 1220 | 0.19 | 202 | 192 | 154 | 42 | 976 | 0.19 |
| 107 | 300 | 70 | 78 | 13,152 | 0.13 | 207 | 300 | 70 | 62 | 10,521 | 0.13 |
| 113 | 591 | 352 | 4 | 281 | 0.06 | 213 | 591 | 352 | 3 | 225 | 0.06 |
| 115 | 215 | 152 | 71 | 9116 | 0.17 | 215 | 215 | 152 | 56 | 7293 | 0.17 |
| 116 | 155 | 44 | 113 | 7810 | 0.24 | 216 | 155 | 44 | 91 | 6278 | 0.24 |
| 118 | 400 | 244 | 20 | 3848 | 0.12 | 218 | 400 | 244 | 17 | 3078 | 0.12 |
| 121 | 400 | 244 | 24 | 3452 | 0.12 | 221 | 400 | 244 | 19 | 2762 | 0.12 |
| 122 | 300 | 122 | 129 | 2778 | 0.12 | 222 | 300 | 122 | 103 | 2222 | 0.12 |
| 123 | 660 | 562 | 5 | 947 | 0.06 | 223 | 660 | 562 | 4 | 758 | 0.06 |
| Bus ID | kV | Peak Load | Bus ID | kV | Peak Load | Bus ID | kV | Peak Load | Bus ID | kV | Peak Load |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 101 | 138 | 92 | 111 | 230 | 225 | 201 | 138 | 46 | 211 | 230 | 113 |
| 102 | 138 | 82 | 112 | 230 | 167 | 202 | 138 | 41 | 212 | 230 | 84 |
| 103 | 138 | 153 | 113 | 230 | 225 | 203 | 138 | 77 | 213 | 230 | 113 |
| 104 | 138 | 63 | 114 | 230 | 165 | 204 | 138 | 31 | 214 | 230 | 82 |
| 105 | 138 | 60 | 115 | 230 | 269 | 205 | 138 | 30 | 215 | 230 | 135 |
| 106 | 138 | 116 | 116 | 230 | 85 | 206 | 138 | 58 | 216 | 230 | 43 |
| 107 | 138 | 106 | 118 | 230 | 283 | 207 | 138 | 53 | 218 | 230 | 142 |
| 108 | 138 | 145 | 119 | 230 | 154 | 208 | 138 | 73 | 219 | 230 | 77 |
| 109 | 138 | 149 | 120 | 230 | 109 | 209 | 138 | 74 | 220 | 230 | 54 |
| 110 | 138 | 166 | 210 | 138 | 83 |
References
- Sarmiento, H.G.; Castellanos, R.; Pampin, G.; Tovar, C.; Naude, J. An example in controlling short circuit levels in a large metropolitan area. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting (IEEE Cat. No.03CH37491), Toronto, ON, Canada, 13–17 July 2003; Volume 2, pp. 589–594. [Google Scholar]
- Vovos, P.N.; Bialek, J.W. Direct incorporation of fault level constraints in optimal power flow as a tool for network capacity analysis. IEEE Trans. Power Syst. 2005, 20, 2125–2134. [Google Scholar] [CrossRef]
- Moon, G.; Wi, Y.; Lee, K.; Joo, S. Fault Current Constrained Decentralized Optimal Power Flow Incorporating Superconducting Fault Current Limiter (SFCL). IEEE Trans. Appl. Supercond. 2011, 21, 2157–2160. [Google Scholar] [CrossRef]
- Vovos, P.N.; Song, H.; Cho, K.; Kim, T. A network reconfiguration algorithm for the reduction of expected fault currents. In Proceedings of the 2013 IEEE Power Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Ngoc, P.T.; Singh, J.G. Short circuit current level reduction in power system by optimal placement of fault current limiter. Int. Trans. Electr. Energy Syst. 2017, 27, 2457. [Google Scholar] [CrossRef]
- Moon, G.; Lee, J.; Joo, S. Integrated Generation Capacity and Transmission Network Expansion Planning With Superconducting Fault Current Limiter (SFCL). IEEE Trans. Appl. Supercond. 2013, 23, 5000510. [Google Scholar] [CrossRef]
- Teimourzadeh, S.; Aminifar, F. MILP Formulation for Transmission Expansion Planning With Short-Circuit Level Constraints. IEEE Trans. Power Syst. 2016, 31, 3109–3118. [Google Scholar] [CrossRef]
- Gharibpour, H.; Aminifar, F.; Bashi, M.H. Short-circuit-constrained transmission expansion planning with bus splitting flexibility. IET Gener. Transm. Distrib. 2017, 12, 217–226. [Google Scholar] [CrossRef]
- Ghanaatian, M.; Lotfifard, S. Sparsity-Based Short-Circuit Analysis of Power Distribution Systems With Inverter Interfaced Distributed Generators. IEEE Trans. Power Syst. 2019, 34, 4857–4868. [Google Scholar] [CrossRef]
- Džafić, I.; Pal, B.C.; Gilles, M.; Henselmeyer, S. Generalized π Fortescue Equivalent Admittance Matrix Approach to Power Flow Solution. IEEE Trans. Power Syst. 2014, 29, 193–202. [Google Scholar] [CrossRef]
- Grainger, J.J.; Stevenson, W.D. Power System Analysis; Mcgrawhill: New York, NY, USA, 2003. [Google Scholar]
- Alsac, O.; Stott, B.; Tinney, W.F. Sparsity-Oriented Compensation Methods for Modified Network Solutions. IEEE Trans. Power Appar. Syst. 1983, 102, 1050–1060. [Google Scholar] [CrossRef]
- Glover, J.D.; Sarma, M.S.; Overbye, T.J. Power System Analysis and Design, 5th ed.; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- GAMS Solvers. Available online: https://www.gams.com/latest/docs/S_MAIN.html. (accessed on 17 January 2017).
- Gendreau, M.; Laporte, G.; Semet, F. A branch-and-cut algorithm for the undirected selective traveling salesman problem. Networks 1998, 32, 263–273. [Google Scholar] [CrossRef]
- Ostrowski, J.; Anjos, M.F.; Vannelli, A. Tight Mixed Integer Linear Programming Formulations for the Unit Commitment Problem. IEEE Trans. Power Syst. 2012, 27, 39–46. [Google Scholar] [CrossRef]
- Brimberg, J.; Hansen, P.; Lin, K.-W.; Mladenović, N.; Breton, M. An Oil Pipeline Design Problem. Oper. Res. 2003, 51, 228–239. [Google Scholar] [CrossRef]
- Mitchell, J.E. Branch-and-cut algorithms for combinatorial optimization problems. Handb. Appl. Optim. 2002, 1, 65–77. [Google Scholar]
- Grigg, C.; Wong, P.; Albrecht, P.; Allan, R.; Bhavaraju, M.; Billinton, R.; Li, W. The IEEE Reliability Test System-1996. A report prepared by the Reliability Test System Task Force of the Application of Probability Methods Subcommittee. IEEE Trans. Power Syst. 1999, 14, 1010–1020. [Google Scholar] [CrossRef]
- Rosenthal, R.E. GAMS-A User’s Guide; GAMS Develop. Corpor.: Washington, DC, USA, 2016. [Google Scholar]
- PSS®E Homepage. Available online: New.siemens.com/global/en/products/energy/services/transmission-distribution-smart-grid/consulting-and-planning/pss-software/pss-e.html (accessed on 20 March 2019).

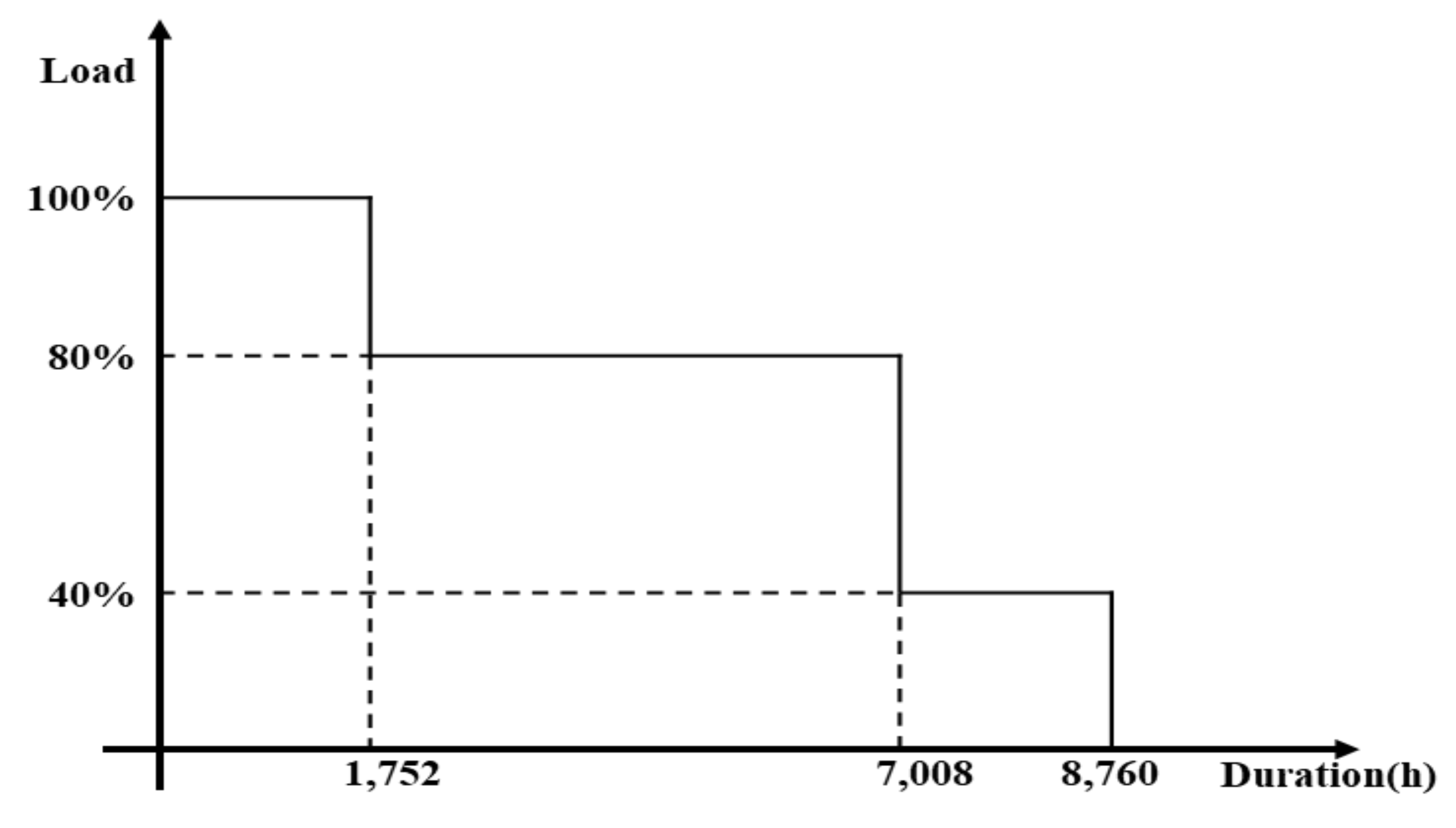


| Branch (From Bus-to Bus) | Line | Year 1 | Year 2 | Year 3 | Year 4 | Year 5 |
|---|---|---|---|---|---|---|
| 107-203 | 1 | ○ | ||||
| 107-203 | 2 | ○ | ||||
| 107-108 | 1 | ○ | ||||
| 113-215 | 1 | ○ | ||||
| 122-218 | 1 | ○ | ||||
| 203-209 | 1 | ○ | ||||
| 207-208 | 1 | ○ | ||||
| 215-216 | 1 | ○ |
| Branch (From Bus-to Bus) | Line | Year 1 | Year 2 | Year 3 | Year 4 | Year 5 |
|---|---|---|---|---|---|---|
| 102-201 | 1 | ○ | ||||
| 107-203 | 1 | ○ | ||||
| 107-203 | 2 | ○ | ||||
| 107-108 | 1 | ○ | ||||
| 107-108 | 2 | ○ | ||||
| 112-224 | 1 | ○ | ||||
| 211-224 | 1 | ○ |
| Branch (From Bus-to Bus) | Line | Year 1 | Year 2 | Year 3 | Year 4 | Year 5 |
|---|---|---|---|---|---|---|
| 102-201 | 1 | ○ | ||||
| 106-204 | 1 | ○ | ||||
| 106-204 | 2 | ○ | ||||
| 107-203 | 1 | ○ | ||||
| 112-224 | 2 | ○ | ||||
| 207-208 | 1 | ○ | ||||
| 211-224 | 1 | ○ |
| Bus Number | Case | Base | Year 1 | Year 2 | Year 3 | Year 4 | Year 5 |
|---|---|---|---|---|---|---|---|
| 113 | Case 1 | 8779 | 11,116 | 11,157 | 11,157 | 11,160 | 11,175 |
| Case 2 | 8779 | 9430 | 9430 | 9433 | 9433 | 9474 | |
| Case 3 | 8779 | 9385 | 9407 | 9407 | 9407 | 9522 | |
| 203 | Case 1 | 7254 | 8467 | 8556 | 8556 | 9145 | 10,231 |
| Case 2 | 7254 | 8957 | 8957 | 9533 | 9533 | 9622 | |
| Case 3 | 7254 | 8688 | 8719 | 8719 | 8719 | 8995 | |
| 209 | Case 1 | 9111 | 9372 | 9385 | 9385 | 9477 | 10,575 |
| Case 2 | 9111 | 9656 | 9656 | 9752 | 9752 | 9833 | |
| Case 3 | 9111 | 9795 | 9850 | 9850 | 9850 | 10,356 | |
| 215 | Case 1 | 5200 | 11,049 | 11,050 | 11,050 | 11,087 | 11,543 |
| Case 2 | 5200 | 6529 | 6529 | 6545 | 6545 | 6549 | |
| Case 3 | 5200 | 5960 | 5961 | 5961 | 5961 | 6540 | |
| 216 | Case 1 | 7670 | 11,151 | 11,152 | 11,152 | 11,180 | 11,772 |
| Case 2 | 7670 | 7859 | 7859 | 7868 | 7868 | 7875 | |
| Case 3 | 7670 | 7767 | 7773 | 7773 | 7773 | 7887 | |
| 218 | Case 1 | 8182 | 8753 | 8753 | 8753 | 8762 | 10,586 |
| Case 2 | 8182 | 8369 | 8369 | 8376 | 8376 | 8379 | |
| Case 3 | 8182 | 8369 | 8372 | 8372 | 8372 | 8382 |
| Case | Objective Value (Million $) | Computation Time (Seconds) |
|---|---|---|
| Case 1 | 2053 | 34 |
| Case 2 | 2100 | 267 |
| Case 3 | 2129 | 44 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Kim, H.; Kim, T.H.; Shin, H.; Kim, W. Fault Current Constraint Transmission Expansion Planning Based on the Inverse Matrix Modification Lemma and a Valid Inequality. Energies 2019, 12, 4769. https://doi.org/10.3390/en12244769
Lee S, Kim H, Kim TH, Shin H, Kim W. Fault Current Constraint Transmission Expansion Planning Based on the Inverse Matrix Modification Lemma and a Valid Inequality. Energies. 2019; 12(24):4769. https://doi.org/10.3390/en12244769
Chicago/Turabian StyleLee, Sungwoo, Hyoungtae Kim, Tae Hyun Kim, Hansol Shin, and Wook Kim. 2019. "Fault Current Constraint Transmission Expansion Planning Based on the Inverse Matrix Modification Lemma and a Valid Inequality" Energies 12, no. 24: 4769. https://doi.org/10.3390/en12244769
APA StyleLee, S., Kim, H., Kim, T. H., Shin, H., & Kim, W. (2019). Fault Current Constraint Transmission Expansion Planning Based on the Inverse Matrix Modification Lemma and a Valid Inequality. Energies, 12(24), 4769. https://doi.org/10.3390/en12244769






