An Ultrasonic Pulse-Echo Method to Detect Internal Defects in Epoxy Composite Insulation
Abstract
1. Introduction
2. Ultrasonic Pulse-Echo Method
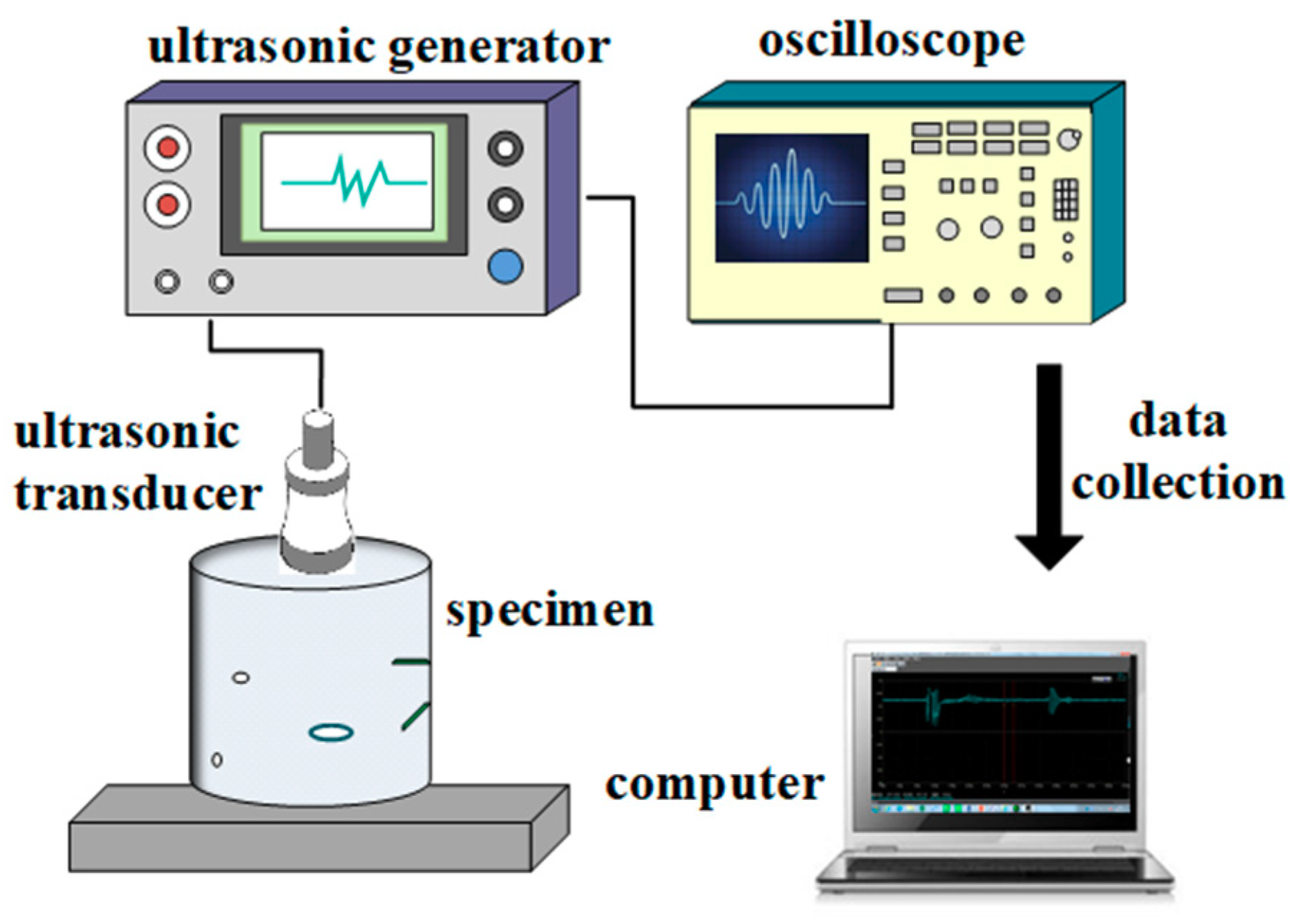
2.1. Ultrasound Testing System
2.1.1. Ultrasonic Generator
2.1.2. Transducer
2.2. Specimen
2.3. Detection Principle
3. Results and Discussion
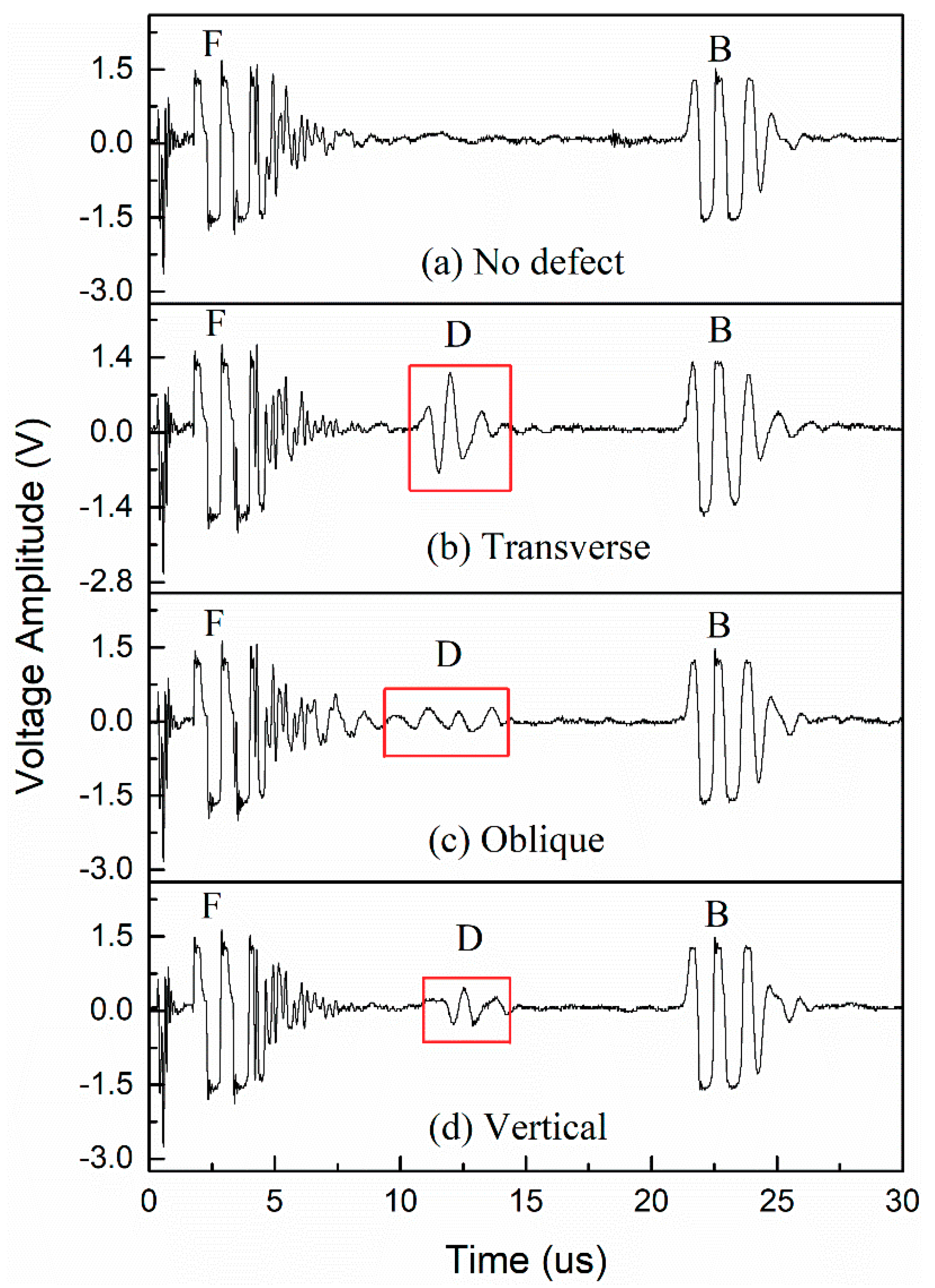
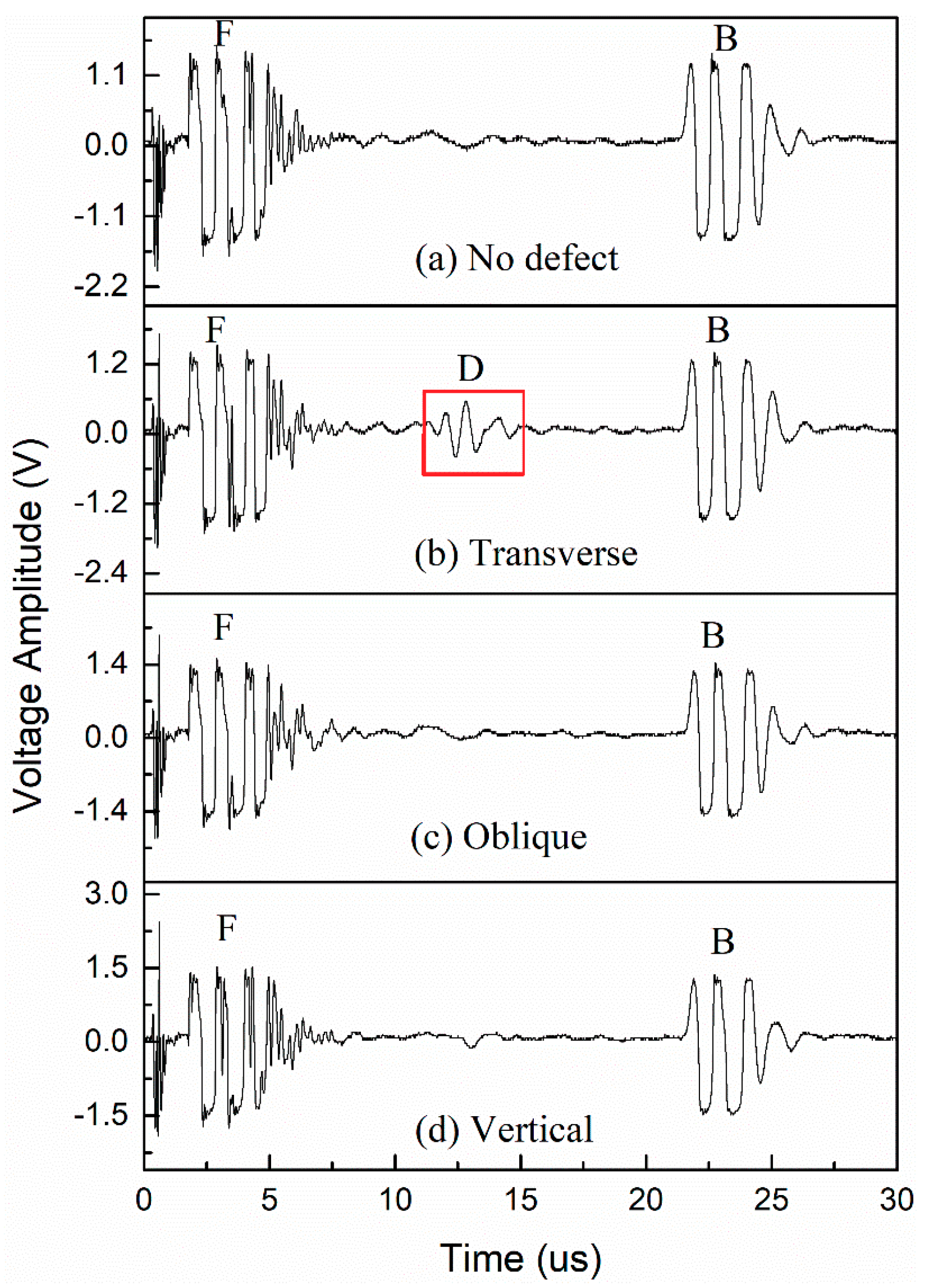
3.1. Void Detection
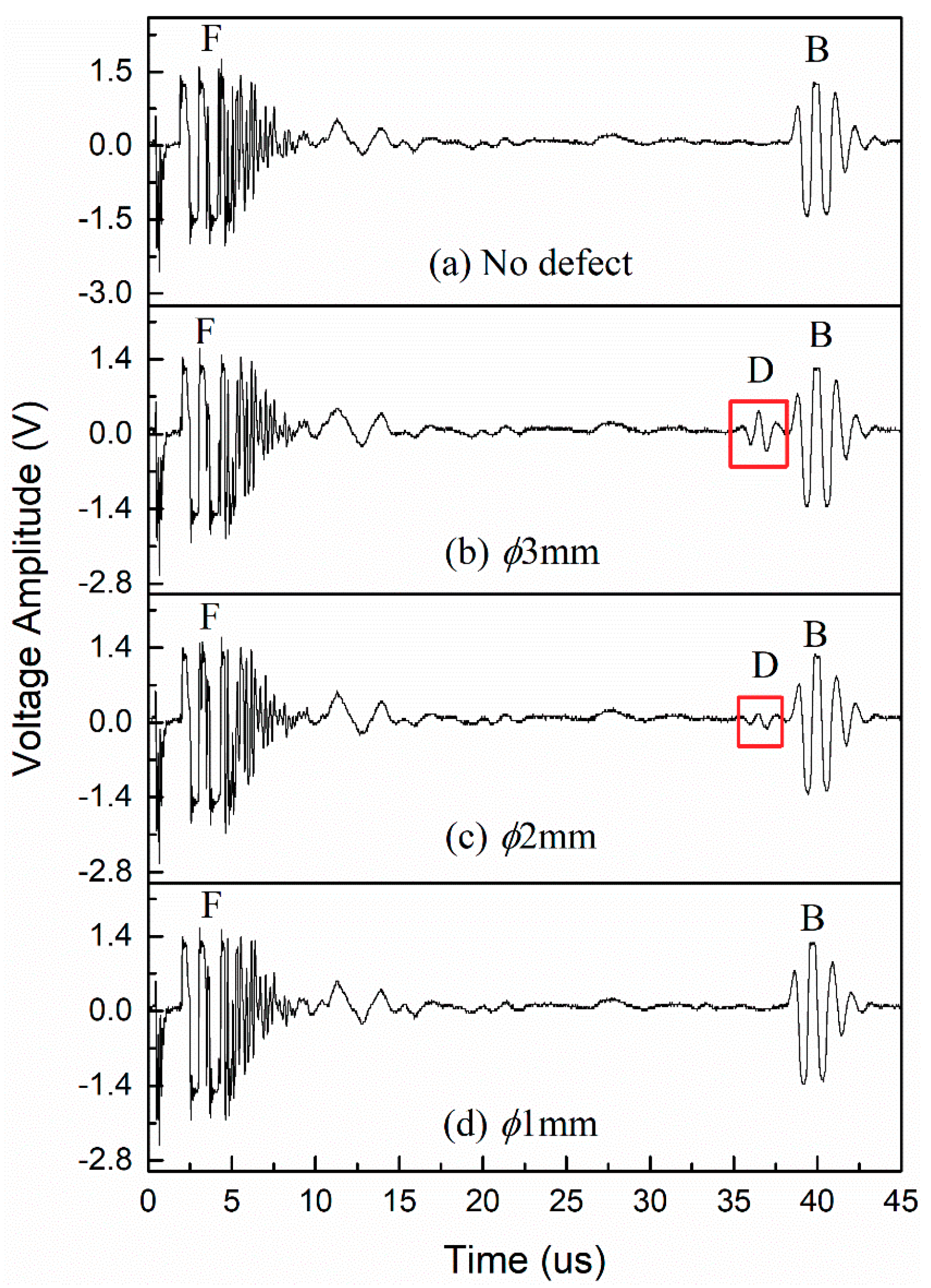
3.1.1. Voids of φ3 mm
3.1.2. Sensitivity of Detection
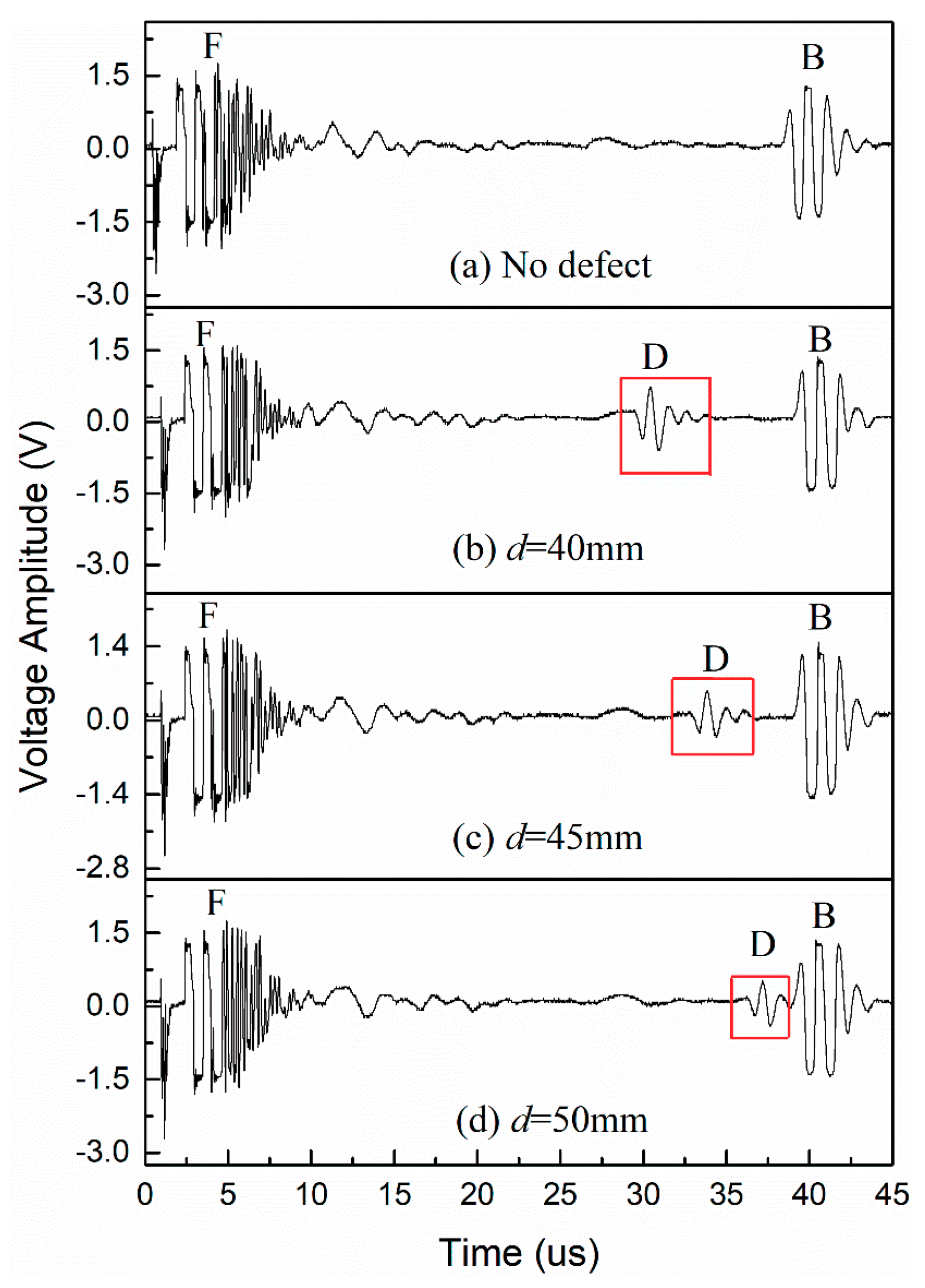
3.1.3. Depth of Detection
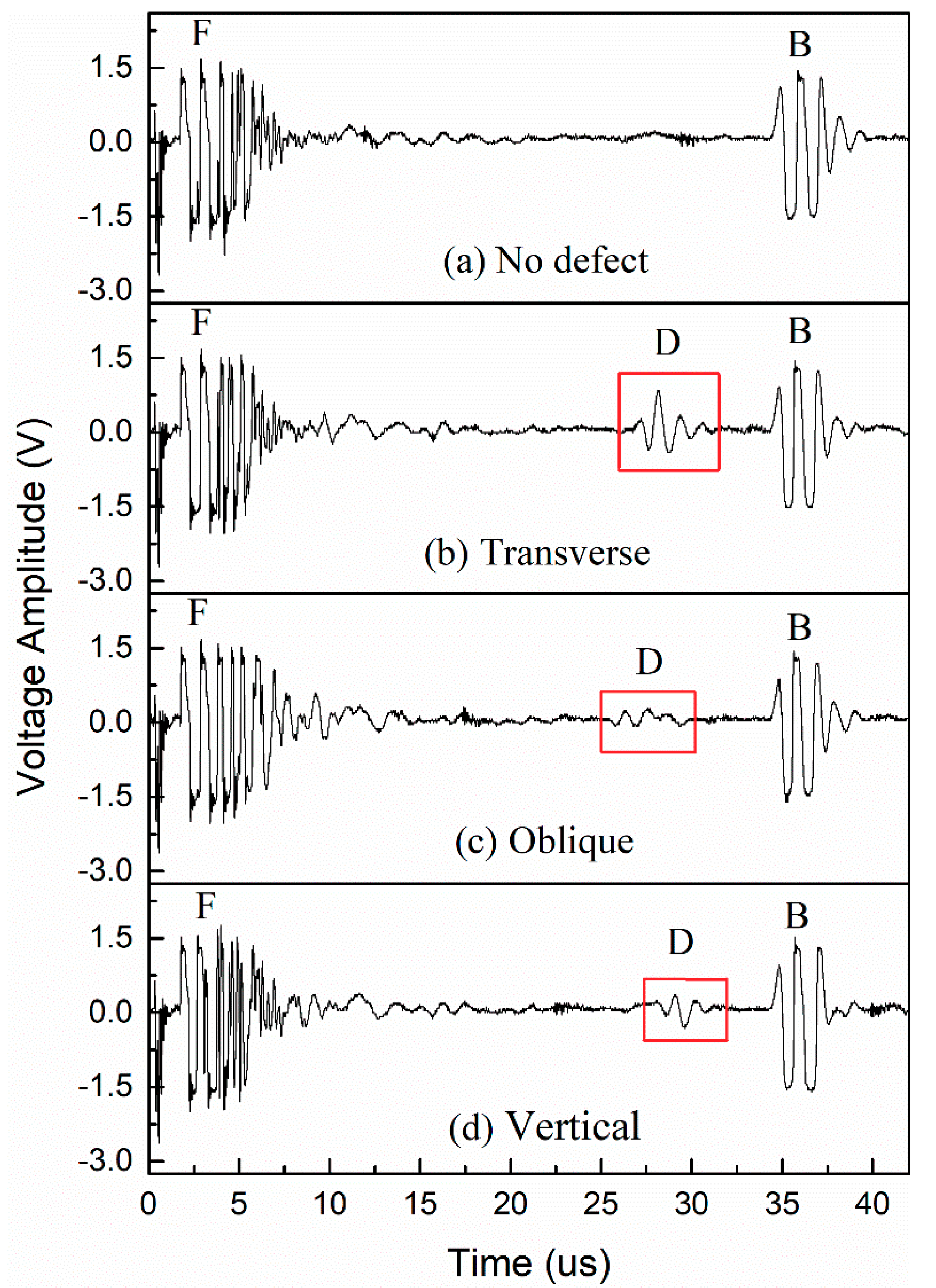
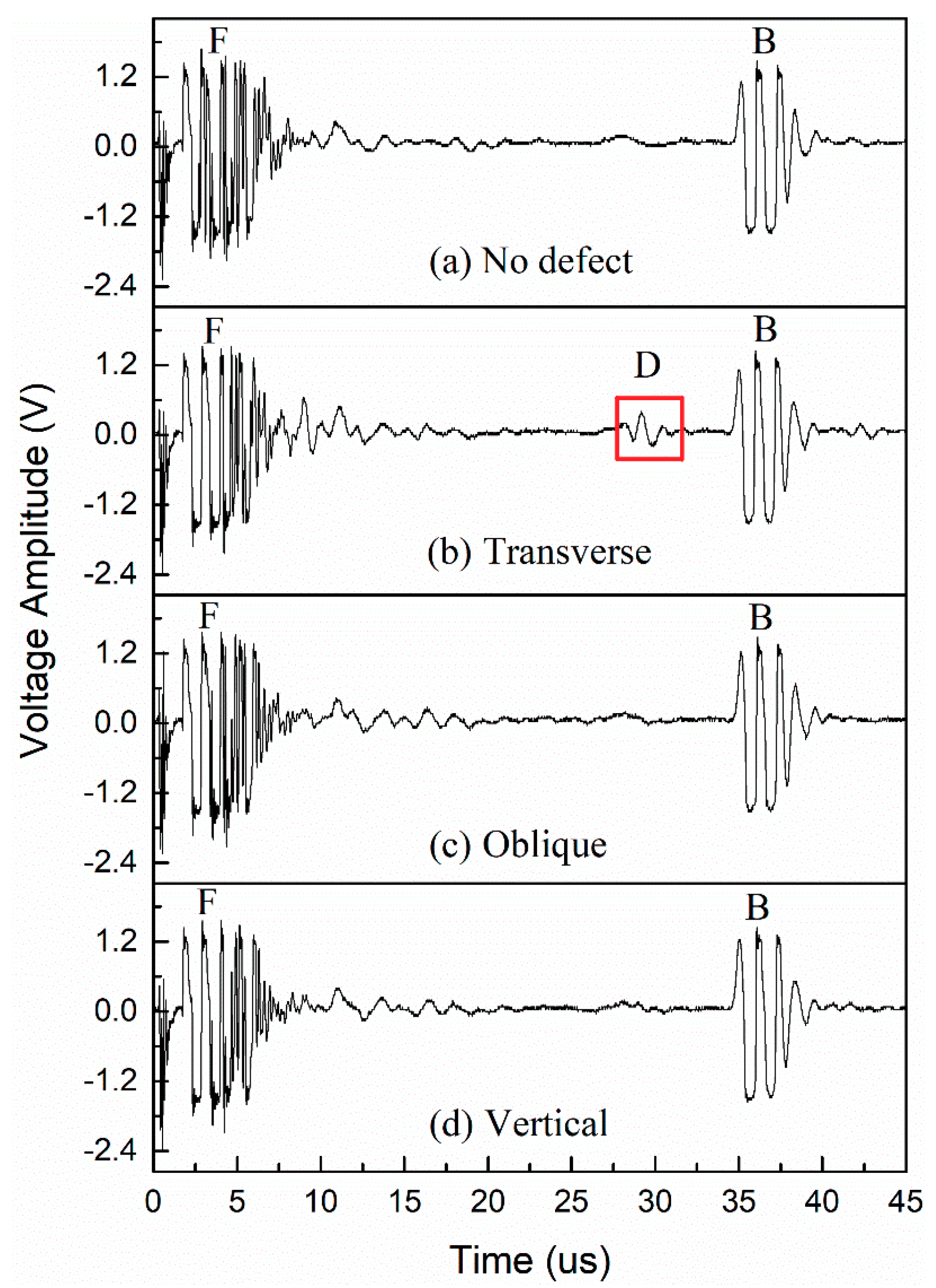
3.2. Crack Detection
3.2.1. Crack Orientations
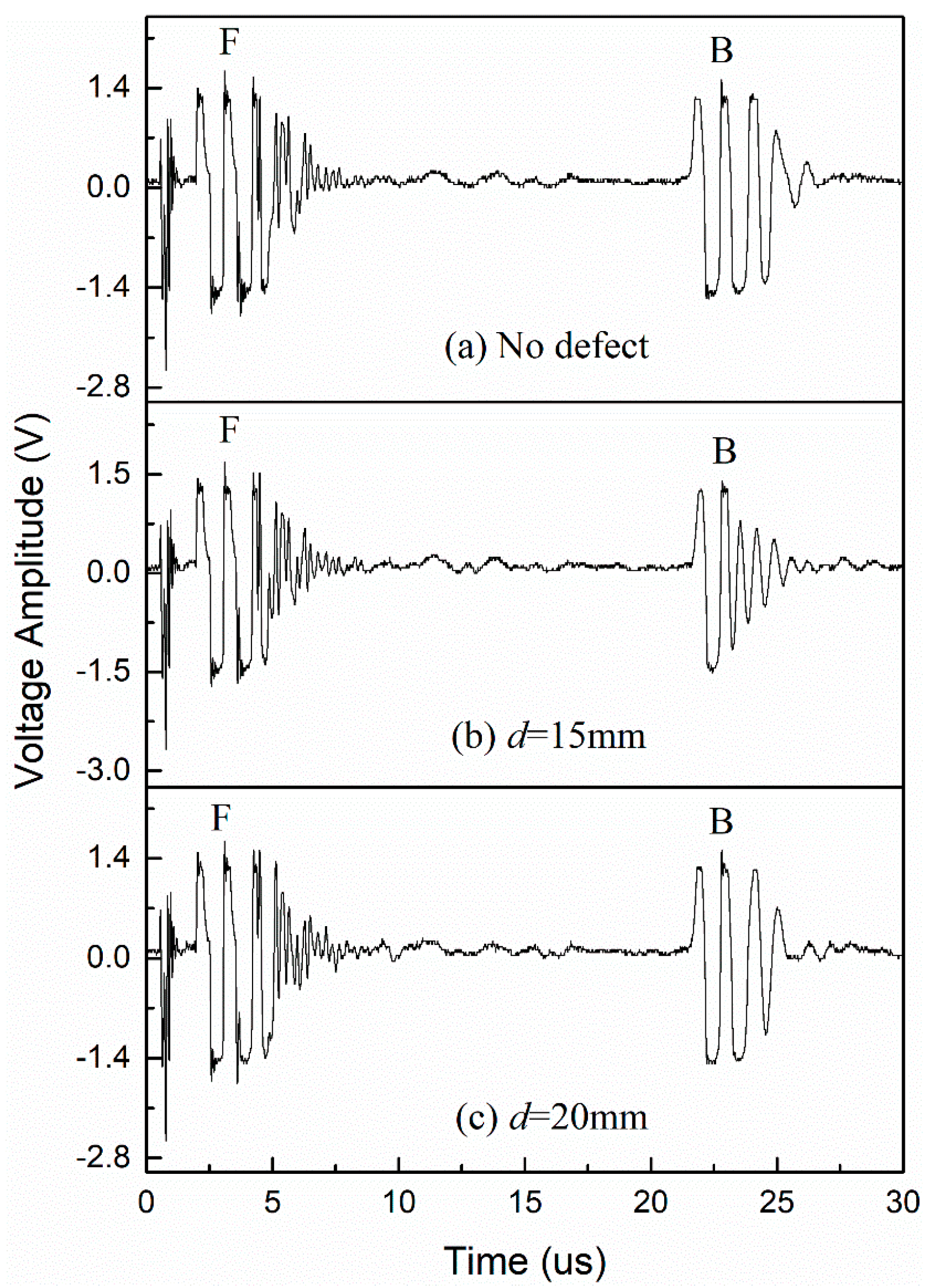
3.2.2. Sensitivity of Detection
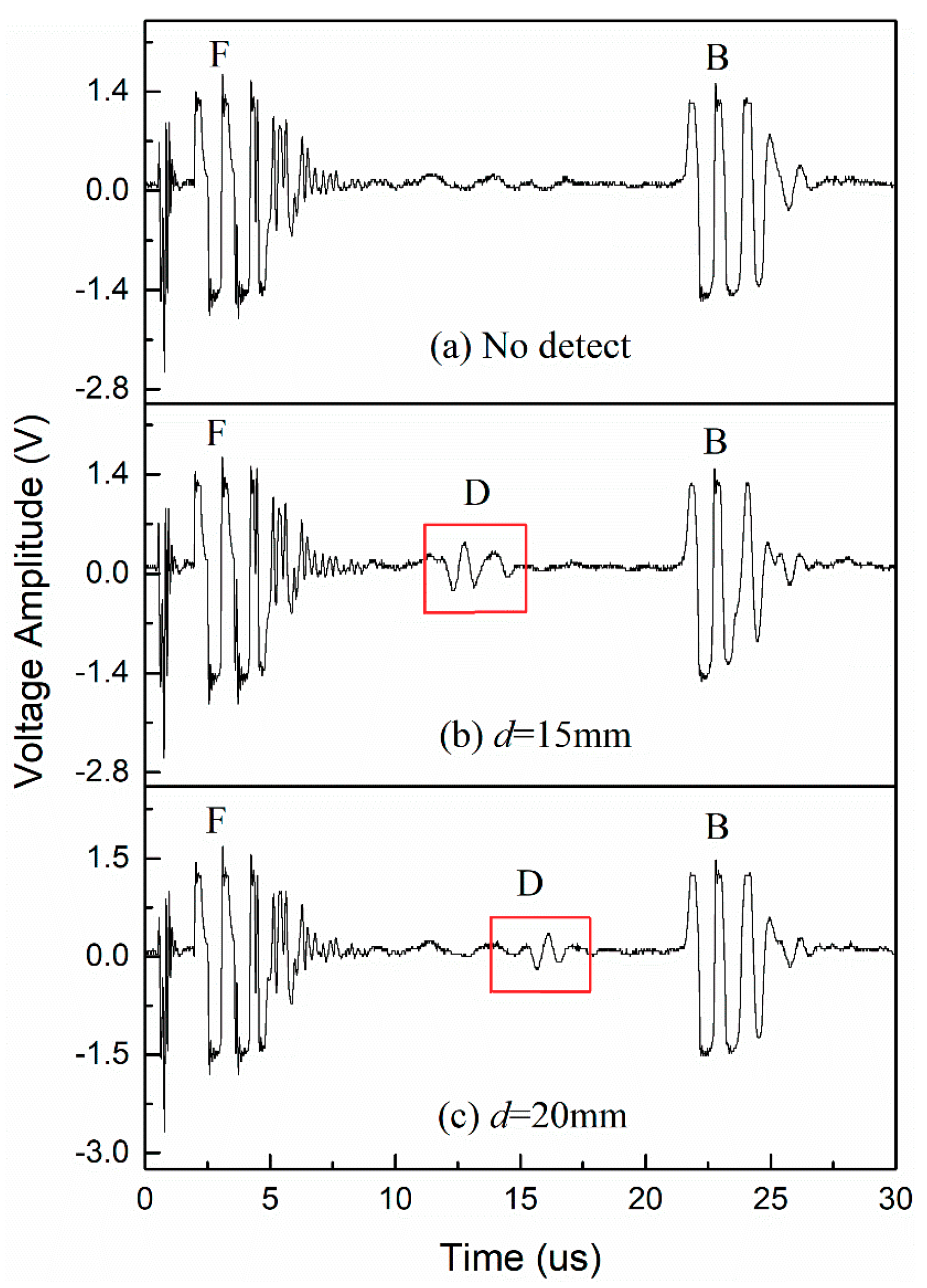
3.2.3. Depth of Detection
4. Partial Discharge Measurements and Ultrasonic Detection of Voids
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xie, J.; Chalmers, I.D. The influence of surface charge upon flashover of particle-contaminated insulators in under impulse-voltage conditions. J. Phys. D Appl. Phys. 1997, 30, 1055–1063. [Google Scholar]
- Tian, Y.; Fu, M.L. Investigation report on surface flashover failure mechanism of GIS basin insulators. In press.
- Yuan, W.Q. The study of crack discharge in ultra-high voltage basin-type insulator. Master’s Thesis, North China Electric Power University, BeiJing, China, 2014. [Google Scholar]
- China Standard NB/T42105. Basin Insulator for High-Voltage Alternating Current Gas-Insulated Metal-Enclosed Switchgear; Electric Power Press of China: Beijing, China, 2016. [Google Scholar]
- China Standard Q GDW11127. Specifications for Basin Insulators Used in 1100kV Gas-Insulated Metal-Enclosed Switchgear; Electric Power Press of China: Beijing, China, 2014. [Google Scholar]
- China Standard GB-Z24836. 1100kV Gas-Insulated Metal-Enclosed Switchgear; Electric Power Press of China: Beijing, China, 2009. [Google Scholar]
- China Standard DL/T555. Guide for Withstand Voltage and Insulated Test of Gas Insulated Metal-Enclosure Switchgear on Site; Electric Power Press of China: Beijing, China, 2004. [Google Scholar]
- Meijer, S.; Smit, J.J. UHF defect evaluation in gas insulated equipment. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 285–296. [Google Scholar] [CrossRef]
- Hoshihino, T.; Maruyama, S.; Ohtsuka, S.; Hikita, M.; Wada, J.; Okabe, S. Sensitivity comparison of disc- and loop-type sensors using the UHF method to detect partial discharges in GIS. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 910–916. [Google Scholar] [CrossRef]
- Xiong, J.; Yuan, W.; Ma, G.M.; Zhang, Q.; Zheng, S.S. Field Applications of Ultra High Frequency Techniques for Defect Detection in GIS. Sensors 2018, 18, 2425. [Google Scholar] [CrossRef] [PubMed]
- Zheng, W. The Experimental Study of Partial DischargeDetection Technology in GIS Equipments. Master’s Thesis, North China Electric Power University, BeiJing, China, 2012. [Google Scholar]
- Lundgaard, L.E.; Tangen, G.; Skyberg, B.; Faugstad, K. Acoustic diagnoses of GIS; field experience and development of expere system. IEEE Trans. Power Deliv. 1992, 7, 287–294. [Google Scholar] [CrossRef]
- Qi, B.; Li, C.R.; Hao, Z.; Geng, B.; Xu, D.; Liu, S.; Deng, C. Partial Discharge Detection for GIS: A Comparison between UHF and Acoustic Methods. In Proceedings of the 2010 IEEE International Symposium on Electrical Insulation, San Diego, CA, USA, 6–9 June 2010; Available online: https://ieeexplore.ieee.org/document/5549553 (accessed on 10 September 2019).
- Yoshida, M.; Kojima, H.; Hayakawa, N.; Endo, F.; Okubo, H. Evaluation of UHF method for partial discharge measurement by simultaneous observation of UHF signal and current pulse waveforms. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 425–431. [Google Scholar] [CrossRef]
- Kock, N.D.; Coric, B.; Pietsch, R. UHF PD detection in gas-insulator switchgear-suitability and sensitivity of the UHF method in comparison with the IEC 270 method. IEEE Electr. Insul. Mag. 1996, 12, 20–26. [Google Scholar] [CrossRef]
- Xu, H.Q.; Ma, J.P.; Wang, C.L.; Zheng, S.S.; Huang, X.C.; Liu, X.B. Study on Digital X-Ray Imaging Technology for Detecting Typical Defects in GIS Equipment. Power Syst. Technol. 2017, 41, 1967–1972. [Google Scholar]
- Tehlar, D.; Riechert, U.; Behrmann, G.; Schraudolph, M.; Herrmann, L.G.; Pancheshnyi, S. Pulsed X-ray induced partial discharge diagnostics for routine testing of solid GIS insulators. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 2173–2178. [Google Scholar] [CrossRef]
- Auckland, D.W.; Varlow, B.R.; Maloney, D. Ultrasonic detection of insulation degradation. IEE Proc. A Phys. Sci. Meas. Instrum. Manag. Educ. 1990, 137, 356–360. [Google Scholar] [CrossRef]
- Yuan, C.; Xie, C.Z.; Li, L.C.; Zhang, F.Z.; Gubanski, S.M. Ultrasonic phased array detection of internal defects in composite insulators. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 525–531. [Google Scholar] [CrossRef]
- Lee, Y.S.; Nelson, J.K.; Scarton, H.A.; Teng, D.; Azizi-Ghannad, S. An acoustic diagnostic technique for use with electric machine insulation. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 1186–1193. [Google Scholar] [CrossRef]
- Wisheart, M.; Richardson, M.O.W. Low velocity response of a complex geometry pultruded glass/polyester composite. J. Mater. Sci. 1999, 34, 1107–1116. [Google Scholar] [CrossRef]
- Aymerich, F.; Meili, S. Ultrasonic evaluation of matrix damage in impacted composite laminates. Compos. Part B Eng. 2000, 31, 1–6. [Google Scholar] [CrossRef]
- Mouritz, A.P.; Townsend, C.; Shah Khan, M.Z. Non-destructive detection of fatigue damage in thick composites by pulse-echo ultrasonics. Compos. Sci. Technol. 2000, 60, 23–32. [Google Scholar] [CrossRef]
- Hao, Y.P.; Wang, G.L.; Jia, Z.D.; Xie, H.K. Application of ultrasonic pulse-echo method to insu lation condition diagnosis for large generators. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 104–113. [Google Scholar]
- Hao, Y.P.; Xie, H.K.; Wang, G.L.; Jia, Z.D. Assessment of insulation condition of generator stator bars based on velocity of ultrasonic waves. IEEE Trans. Dielectr. Electr. Insul. 2003, 10, 539–547. [Google Scholar]
- Hao, Y.P.; Wang, G.L.; Xie, H.K. Ultrasonic nondestructive detection for defects in epoxy/mica insulation. In Proceedings of the 2001 International Symposium on Electrical Insulating Materials, Himeji, Japan, 22 November 2001; Available online: https://ieeexplore.ieee.org/document/973767 (accessed on 10 September 2019).
- Auckland, D.W.; Smith, C.D.; Varlow, B.R. Application of ultrasound to the NDT of solid insulation. IEE Proc. A Sci. Meas. Technol. 1994, 141, 20–24. [Google Scholar] [CrossRef]
- Armentrout, D.L.; Kumosa, M.; McQuarrie, T.S. Boron-Free Fibers for Prevention of Acid Induced Brittle Fracture of Composite Insulator GRP Rods. IEEE Trans. Power Deliv. 2003, 18, 684–693. [Google Scholar] [CrossRef]
- Liang, X.D.; Dai, J.J.; Zhou, Y.X.; Chen, Y.F. Ultrasonic detection on crack of frp rod in brittle fracture of composite insulators. Proc. CSEE 2005, 25, 110–114. [Google Scholar]
- Xie, C.Z.; Zhang, Y.; Hao, Y.P.; Yuan, X.J.; Wei, Q.H. Application of ultrasonic flaw detector to internal defects in composite insulators. High Volt. Eng. 2008, 35, 2464–2469. [Google Scholar]
- Chen, H.Y.; Li, L.; Xia, Z.W.; Li, C.L.; Liu, G.Q. Inspection of Internal Defects of Composite Insulators by Ultrasonic Phased Array Method Based on Flexible Coupling. High Voltage Eng. 2019, 45, 1274–1280. [Google Scholar]
- Shen, W.; Meng, Y.P.; Jian, Y.F. Study on ultrasonic spectral characteristics of internal defects in epoxy composite materials. Insul. Mater. 2015, 48, 55–60. [Google Scholar]
- Shen, W.; Meng, Y.P.; Jian, Y.F.; Yang, R.; Song, W.J. Study on ultrasonic detection for internal defects appearance of solid insulation materials. High Volt. Appar. 2016, 52, 145–151. [Google Scholar]
- Song, W.J.; Meng, Y.P.; Men, C.; Zhu, B.W.; Cheng, Y.H. Study on the ultrasonic detection method for internal defects of insulation pull rod in circuit breakers. In Proceedings of the 2016 International Conference on Condition Monitoring and Diagnosis (CMD), Xi’an, China, 25–28 September 2001; Available online: https://ieeexplore.ieee.org/document/7757898 (accessed on 10 September 2019).
- Zhu, T.Y.; Yang, D.W.; Ye, J.T. GIS basin insulator damage detection based active motivation. J. Tianjin Univ. Technol. 2017, 33, 39–43. [Google Scholar]
- Zheng, H.; Lin, S.Q. Ultrasonic Detection, 2nd ed.; China Labor and Social Security Publishing House: Beijing, China, 2008; pp. 57–61. [Google Scholar]
- Ueno, H.; Walter, P.; Cornelissen, C.; Schnettler, A. Resolution evaluation of ultrasonic diagnosis tools for electrical insulation devices and the detection of electrical trees. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 249–256. [Google Scholar] [CrossRef]
- Naous, W.; Yu, X.Y.; Naito, K.; Kagawa, Y. Morphology, tensile properties, and fracture toughness of epoxy/Al2O3 nanocomposites. J. Polym. Sci. Part B Polym. Phys. 2006, 44, 1466–1473. [Google Scholar] [CrossRef]
- Rohatgi, P.K.; Matsunaga, T.; Gupta, N. Compressive and ultrasonic properties of polyester/fly ash composites. J. Mater. Sci. 2009, 44, 1485–1493. [Google Scholar] [CrossRef]
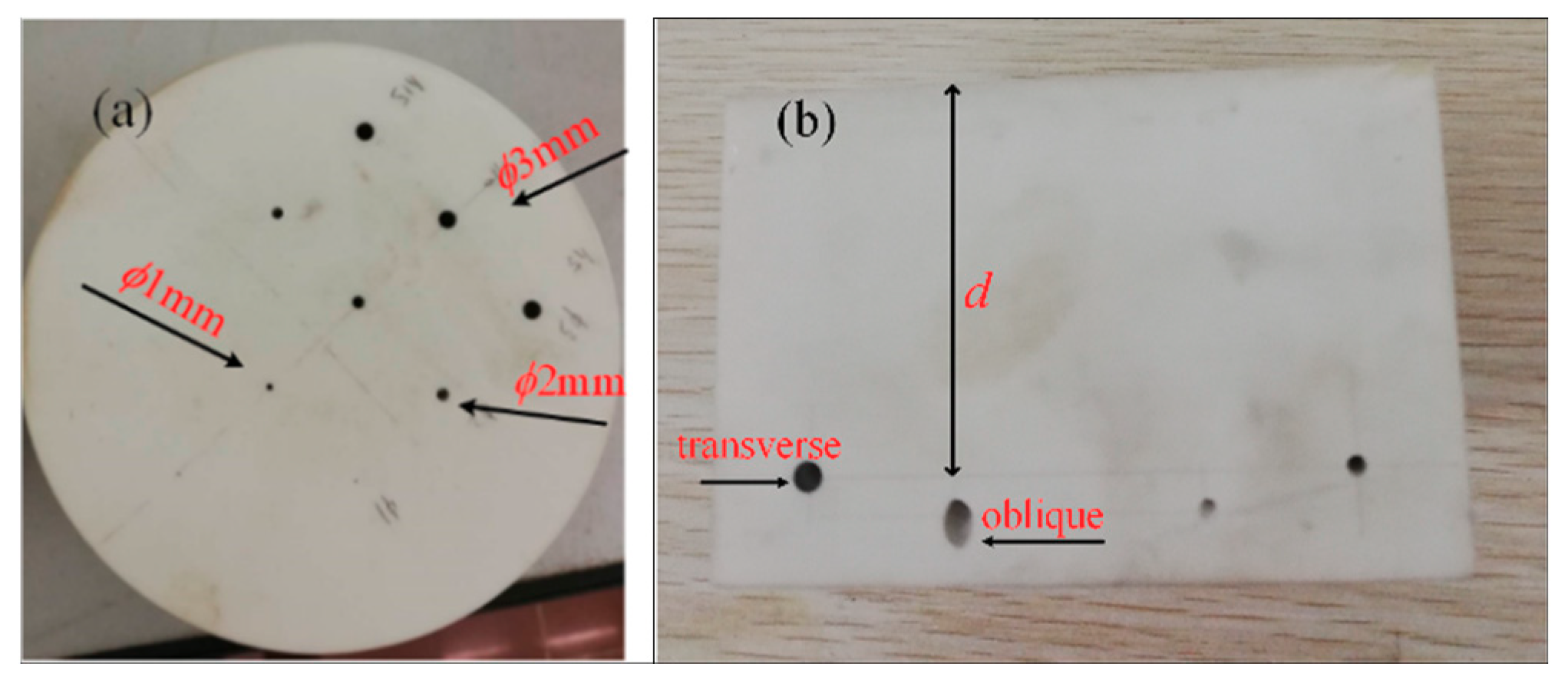
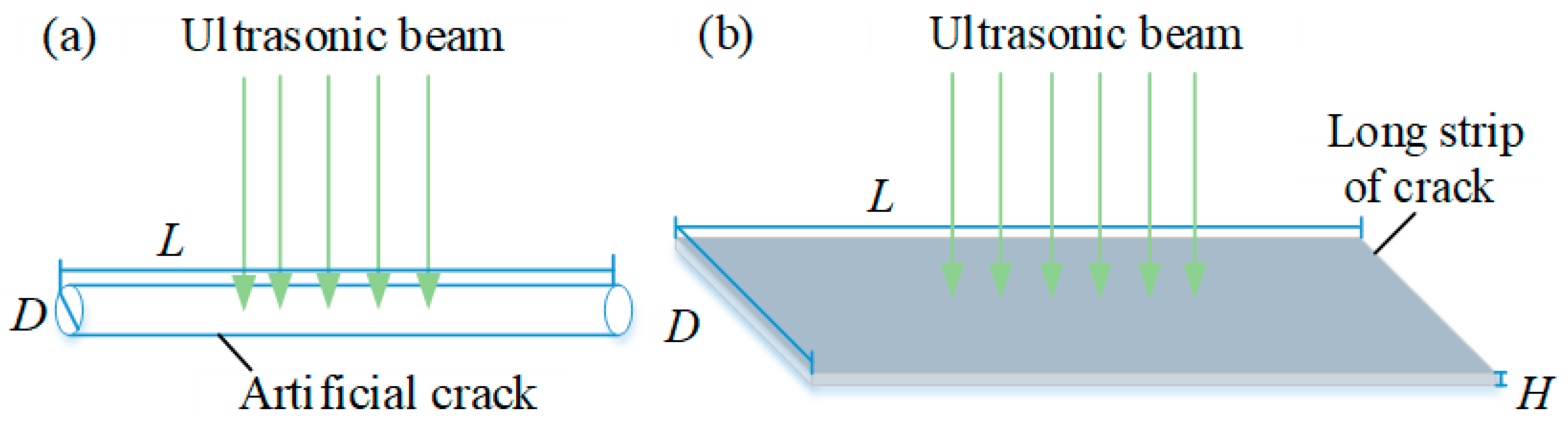
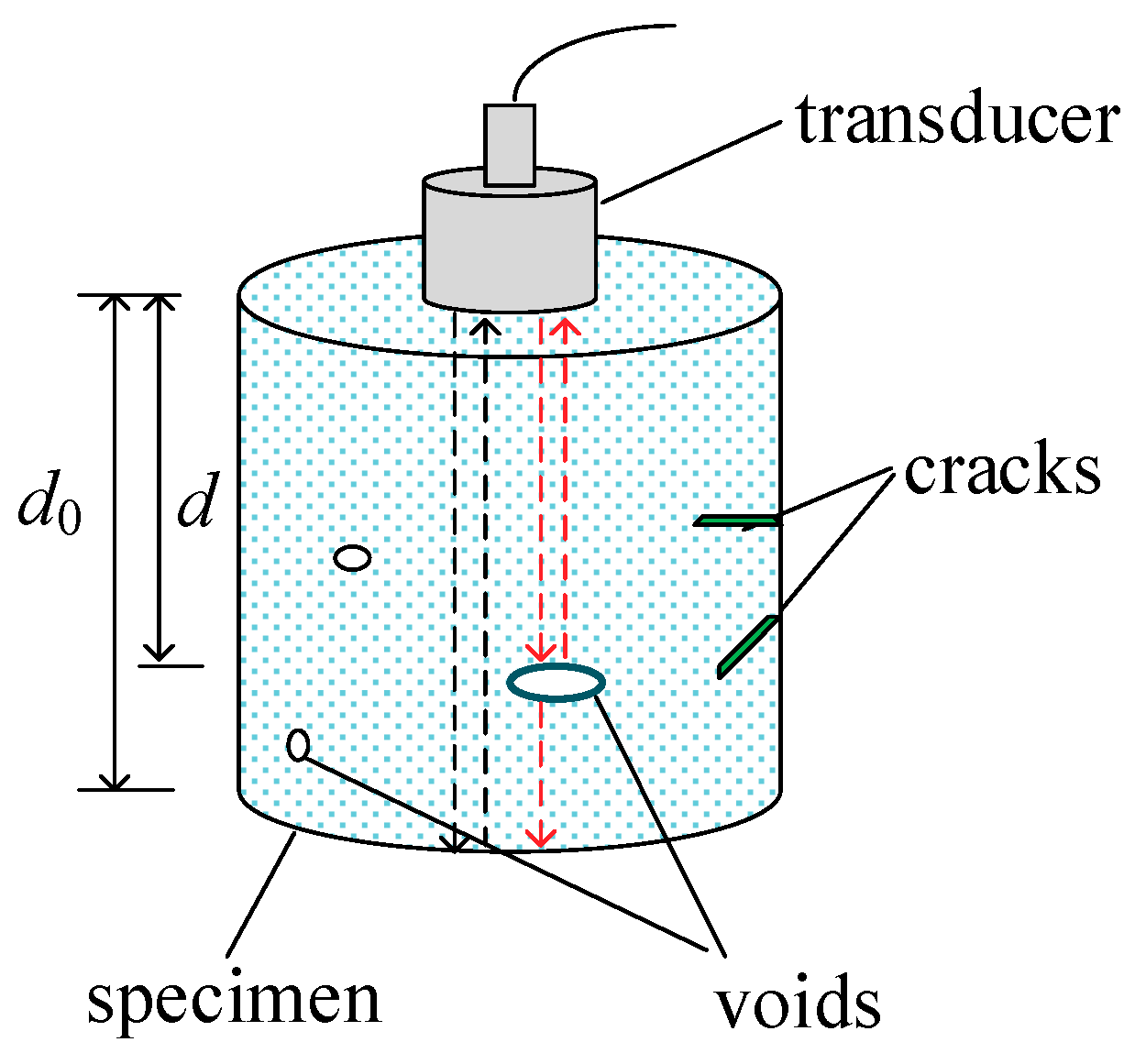

| Specimens | φ1 mm d/mm | φ2 mm d/mm | φ3 mm d/mm |
|---|---|---|---|
| A1 | - | 40 | 40 |
| 45 | 45 | 45 | |
| 50 | 50 | 50 | |
| A2 | 15 | 15 | - |
| 20 | 20 | - |
| Actual d/mm | t0/us | t1/us | t2/us | Calculated d/mm | d% | Ad/V |
|---|---|---|---|---|---|---|
| 40 | 3.13 | 39.88 | 29.66 | 39.70 | 0.75 | 0.75 |
| 45 | 3.13 | 39.88 | 33.07 | 44.81 | 0.42 | 0.52 |
| 50 | 3.08 | 39.93 | 36.47 | 49.84 | 0.32 | 0.48 |
| φ/mm | t0/us | t1/us | t2/us | Calculated d/mm | d% | Ad/V |
|---|---|---|---|---|---|---|
| 3 | 3.08 | 39.93 | 36.47 | 49.84 | 0.32 | 0.48 |
| 2 | 3.17 | 39.88 | 36.47 | 49.89 | 0.22 | 0.16 |
| Actual d/mm | t0/us | t1/us | t2/us | Calculated d/mm | d% | Ad/V |
|---|---|---|---|---|---|---|
| 15 | 3.08 | 22.81 | 12.81 | 14.79 | 1.40 | 0.44 |
| 20 | 3.08 | 22.76 | 16.14 | 19.91 | 0.45 | 0.32 |
| φ2 mm | t0/us | t1/us | t2/us | Calculated d/mm | d% | Ad/V |
|---|---|---|---|---|---|---|
| Transverse | 2.94 | 35.73 | 28.22 | 39.55 | 1.13 | 0.84 |
| Oblique | 2.94 | 35.73 | 27.57 | 37.56 | 6.10 | 0.24 |
| Vertical | 2.94 | 35.73 | 29.15 | 39.97 | 0.08 | 0.32 |
| φ2 mm | t0/us | t1/us | t2/us | Calculated d/mm | d% | Ad/V |
|---|---|---|---|---|---|---|
| Transverse | 2.89 | 22.53 | 11.99 | 14.90 | 0.67 | 0.80 |
| Oblique | 2.89 | 22.57 | 11.19 | 12.65 | 15.67 | 0.24 |
| Vertical | 2.89 | 22.43 | 12.59 | 14.89 | 0.73 | 0.28 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, F.; Hao, Y.; Zou, Z.; Zheng, Y.; He, W.; Yang, L.; Li, L. An Ultrasonic Pulse-Echo Method to Detect Internal Defects in Epoxy Composite Insulation. Energies 2019, 12, 4804. https://doi.org/10.3390/en12244804
Tian F, Hao Y, Zou Z, Zheng Y, He W, Yang L, Li L. An Ultrasonic Pulse-Echo Method to Detect Internal Defects in Epoxy Composite Insulation. Energies. 2019; 12(24):4804. https://doi.org/10.3390/en12244804
Chicago/Turabian StyleTian, Fangyuan, Yanpeng Hao, Zhouyiao Zou, Yao Zheng, Weiming He, Lin Yang, and Licheng Li. 2019. "An Ultrasonic Pulse-Echo Method to Detect Internal Defects in Epoxy Composite Insulation" Energies 12, no. 24: 4804. https://doi.org/10.3390/en12244804
APA StyleTian, F., Hao, Y., Zou, Z., Zheng, Y., He, W., Yang, L., & Li, L. (2019). An Ultrasonic Pulse-Echo Method to Detect Internal Defects in Epoxy Composite Insulation. Energies, 12(24), 4804. https://doi.org/10.3390/en12244804






