Reliability Evaluation of Micro-grids Containing PV System and Hydropower Plant
Abstract
1. Introduction
2. Reliability Models for Each Generation Type
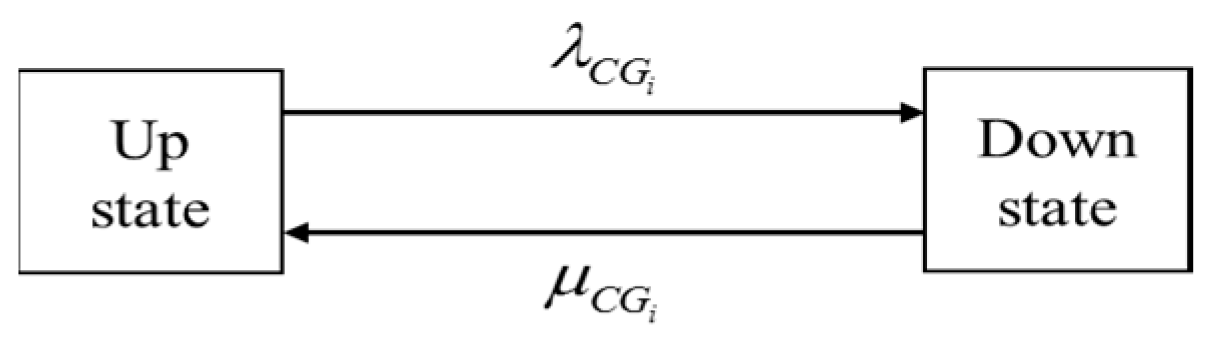
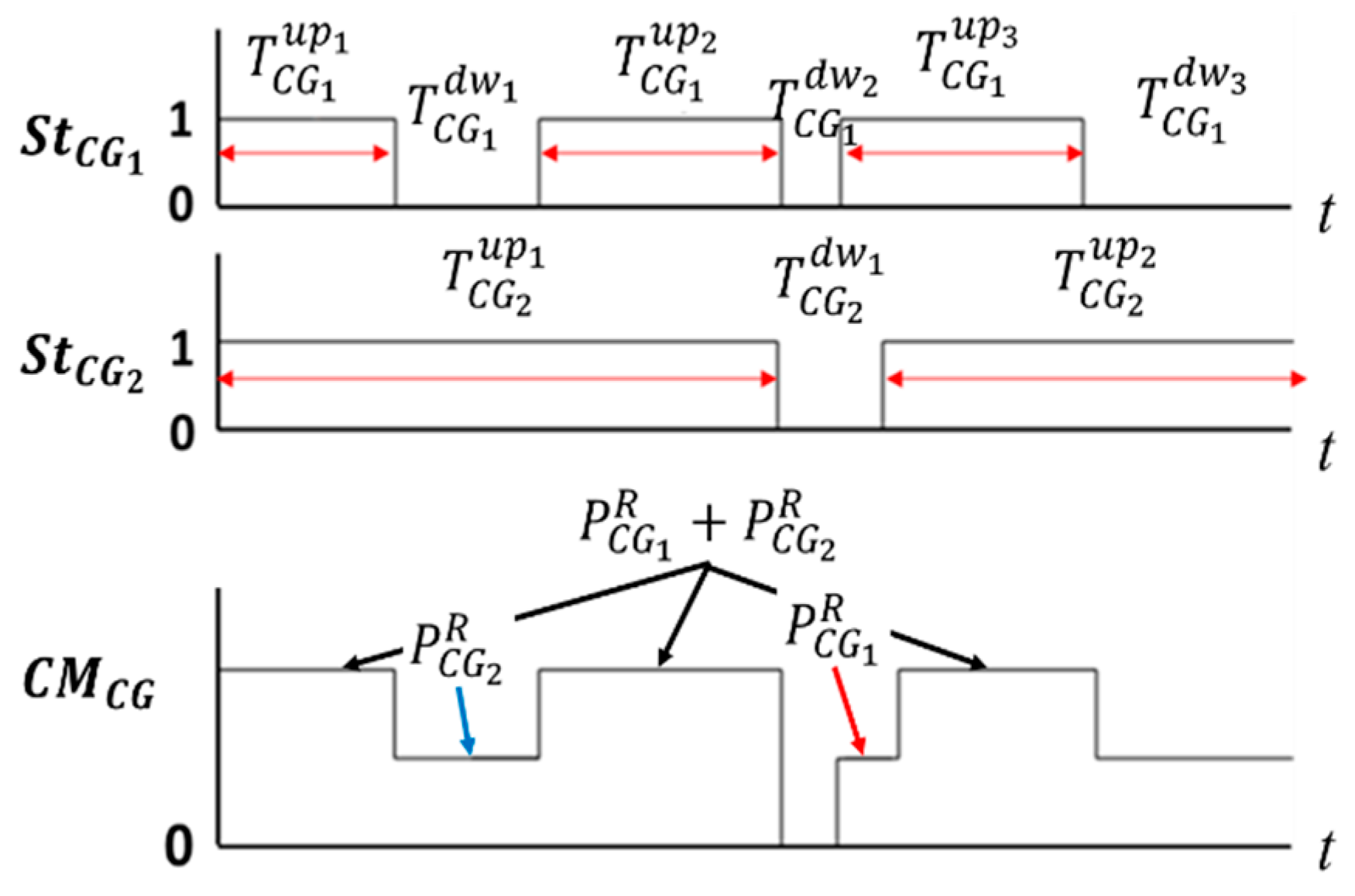
2.1. Conventional Generator Model
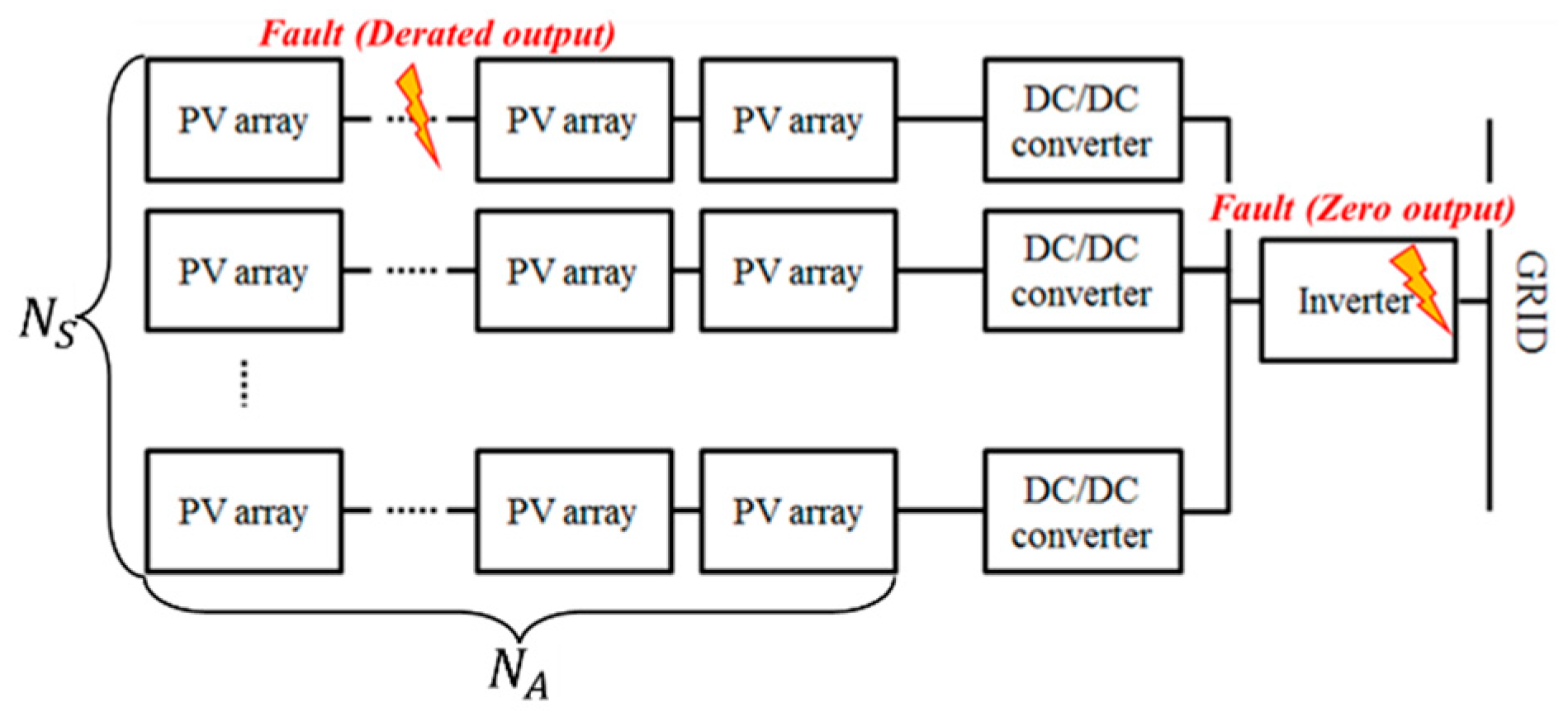
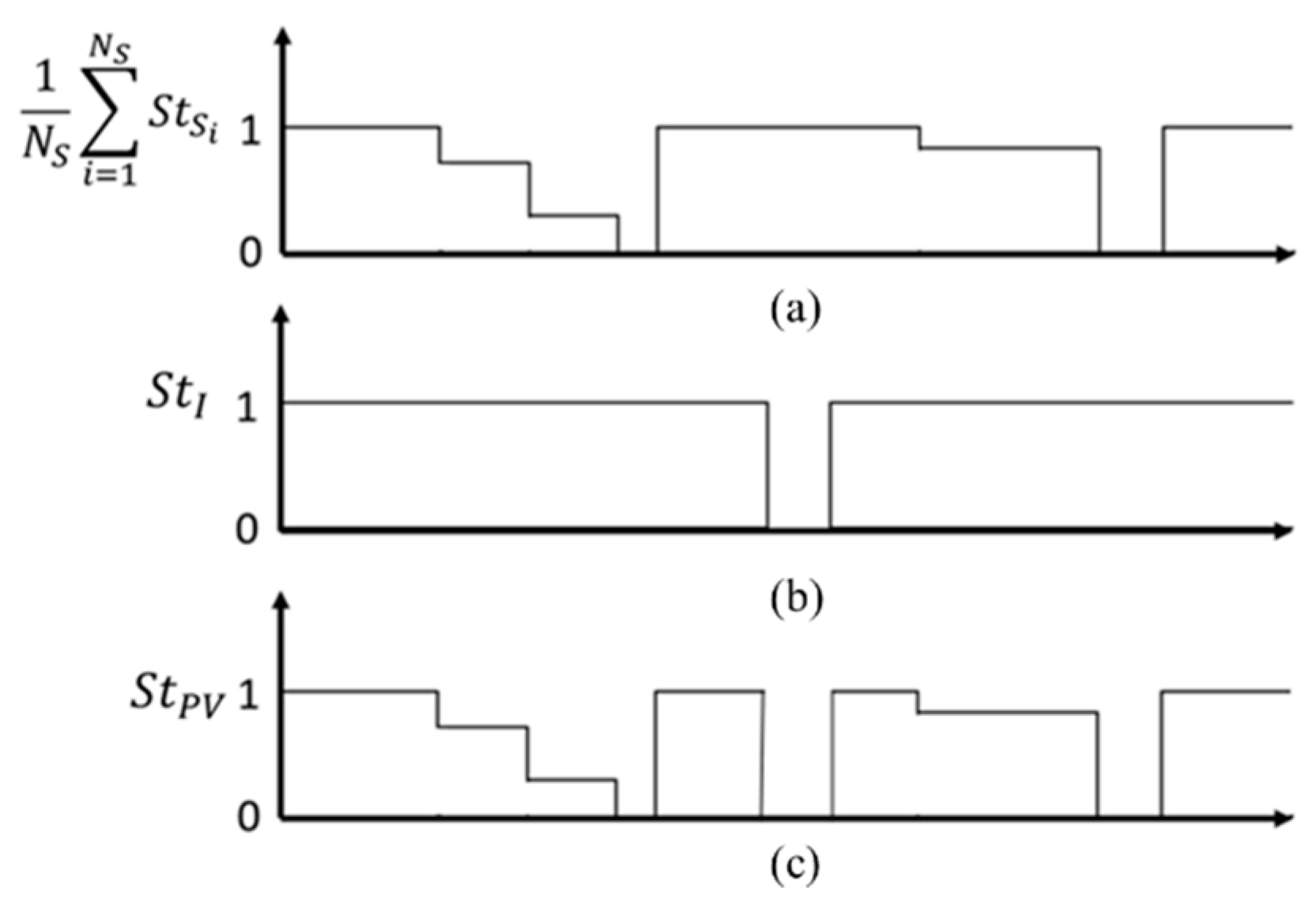
2.2. PV Generation Model
2.3. Hydropower Plant Model
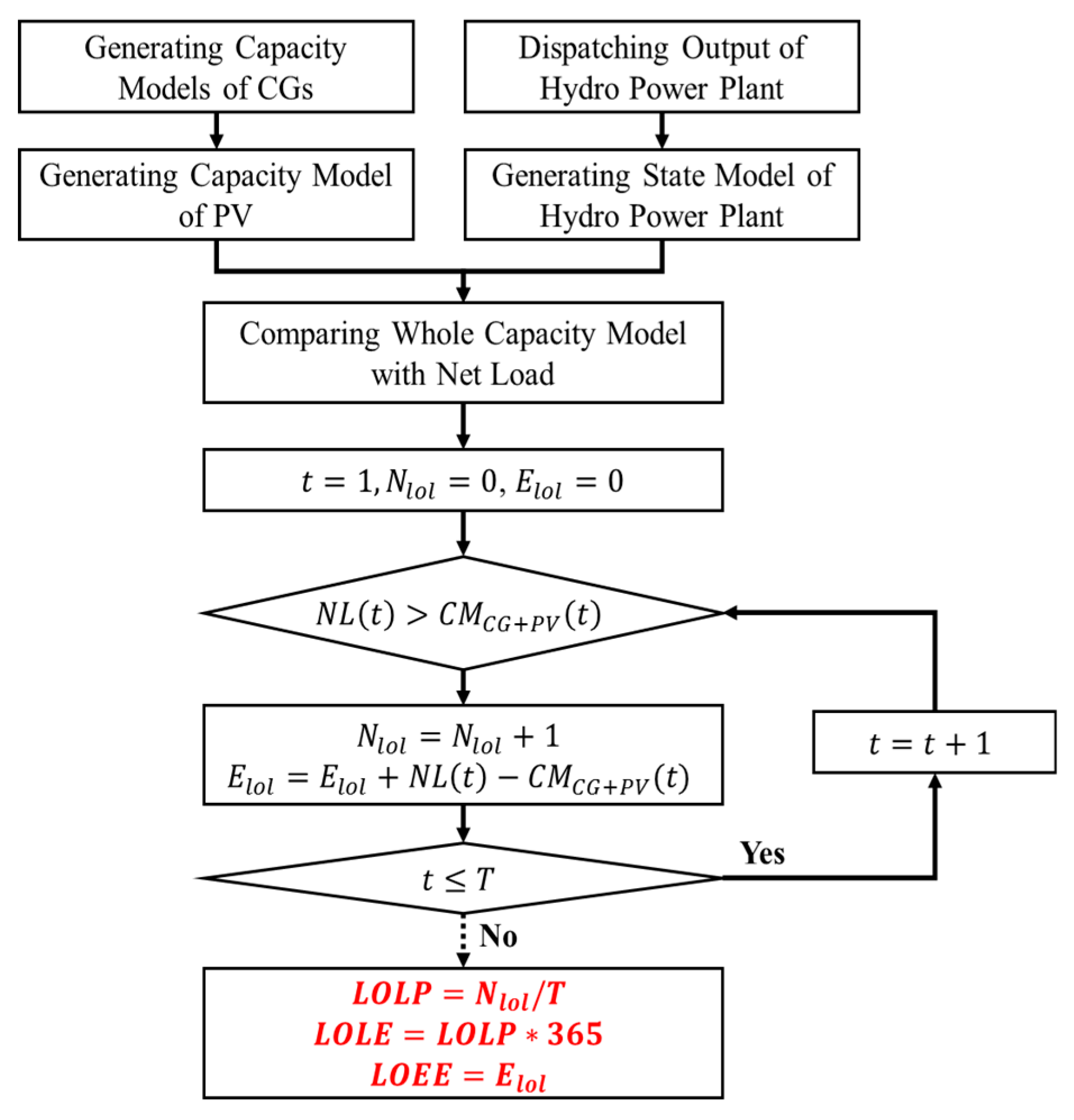
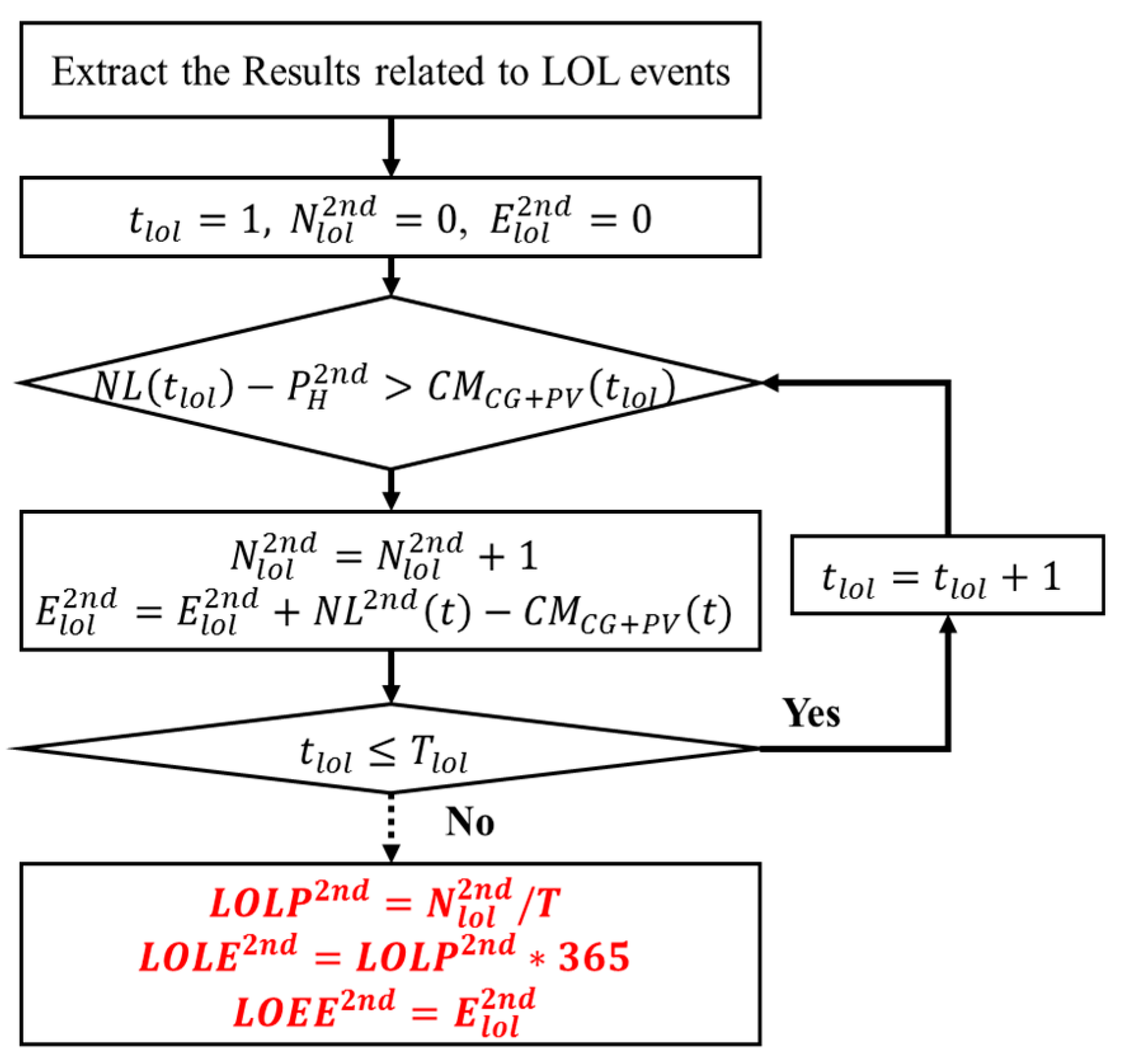
3. Methodology of Reliability Evaluation for the Microgrid Containing HPP
- 1st term: the amount of water in the reservoir that exceeds Vref at time t.
- 2nd term: the amount of water required to generate the rated power.
- 3rd term: the amount of water required to generate the power as much as the PNS.
- 4th term: the amount of water available when considering the remaining water after the present.
4. Case Study
4.1. Test System Data
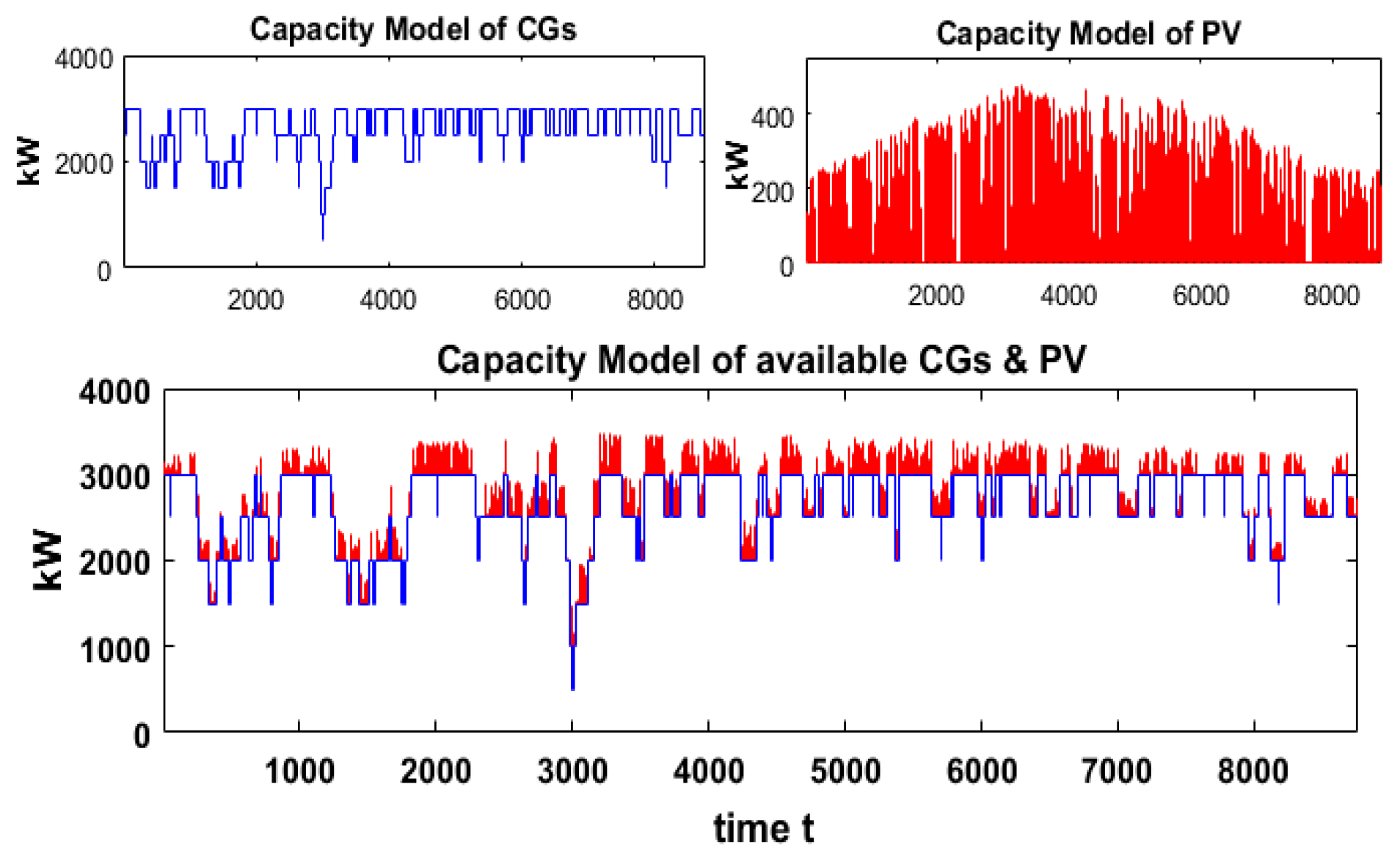
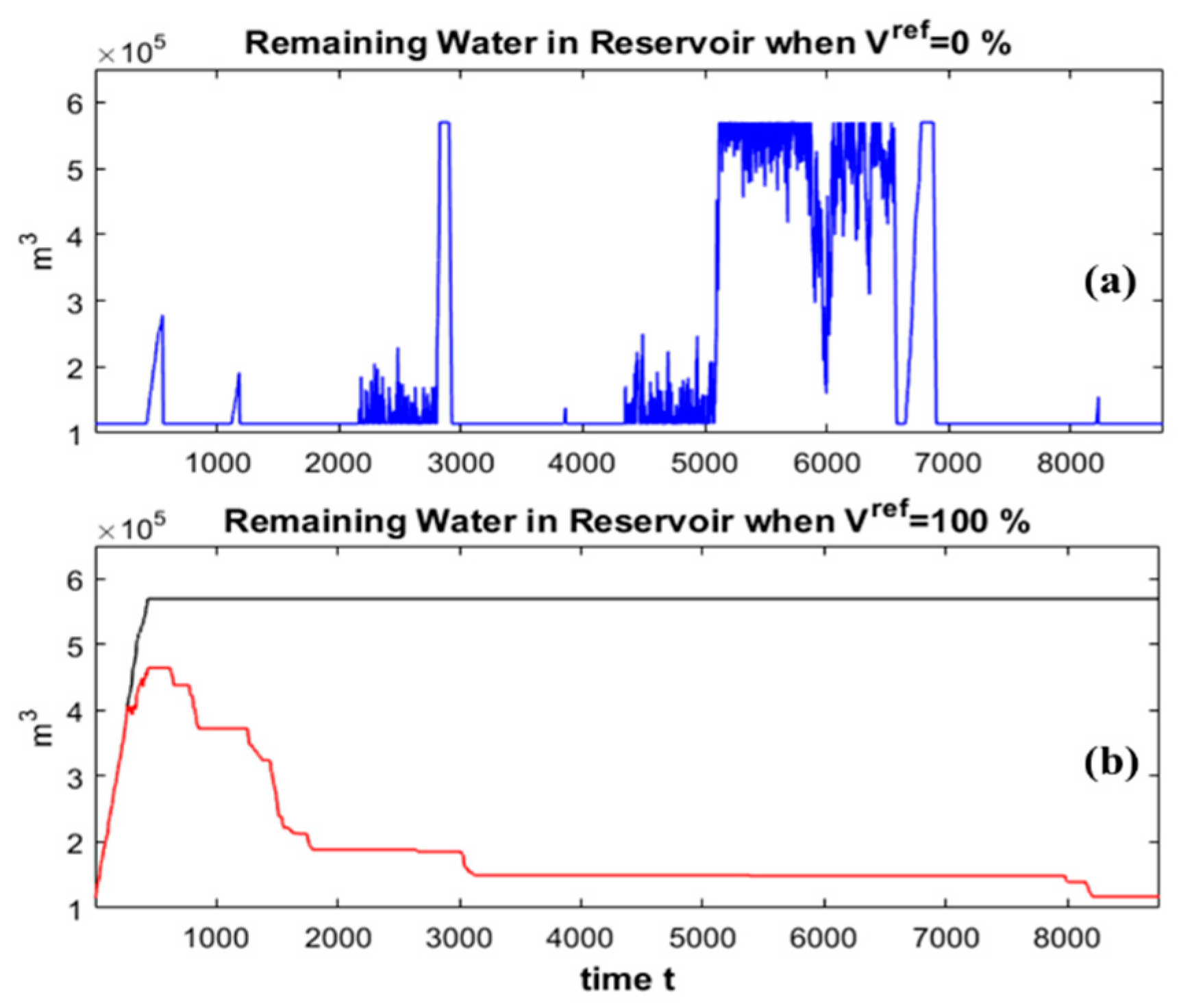
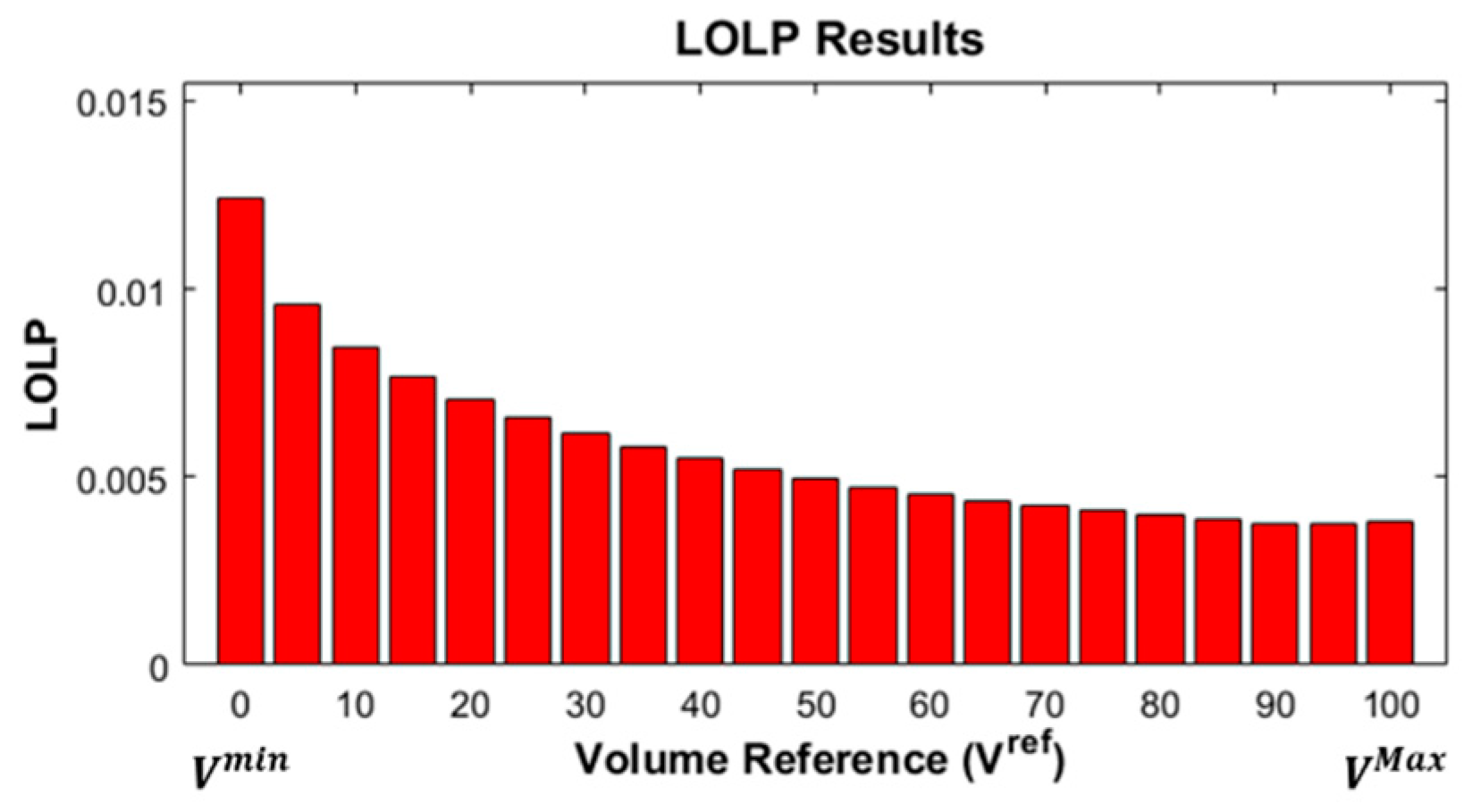
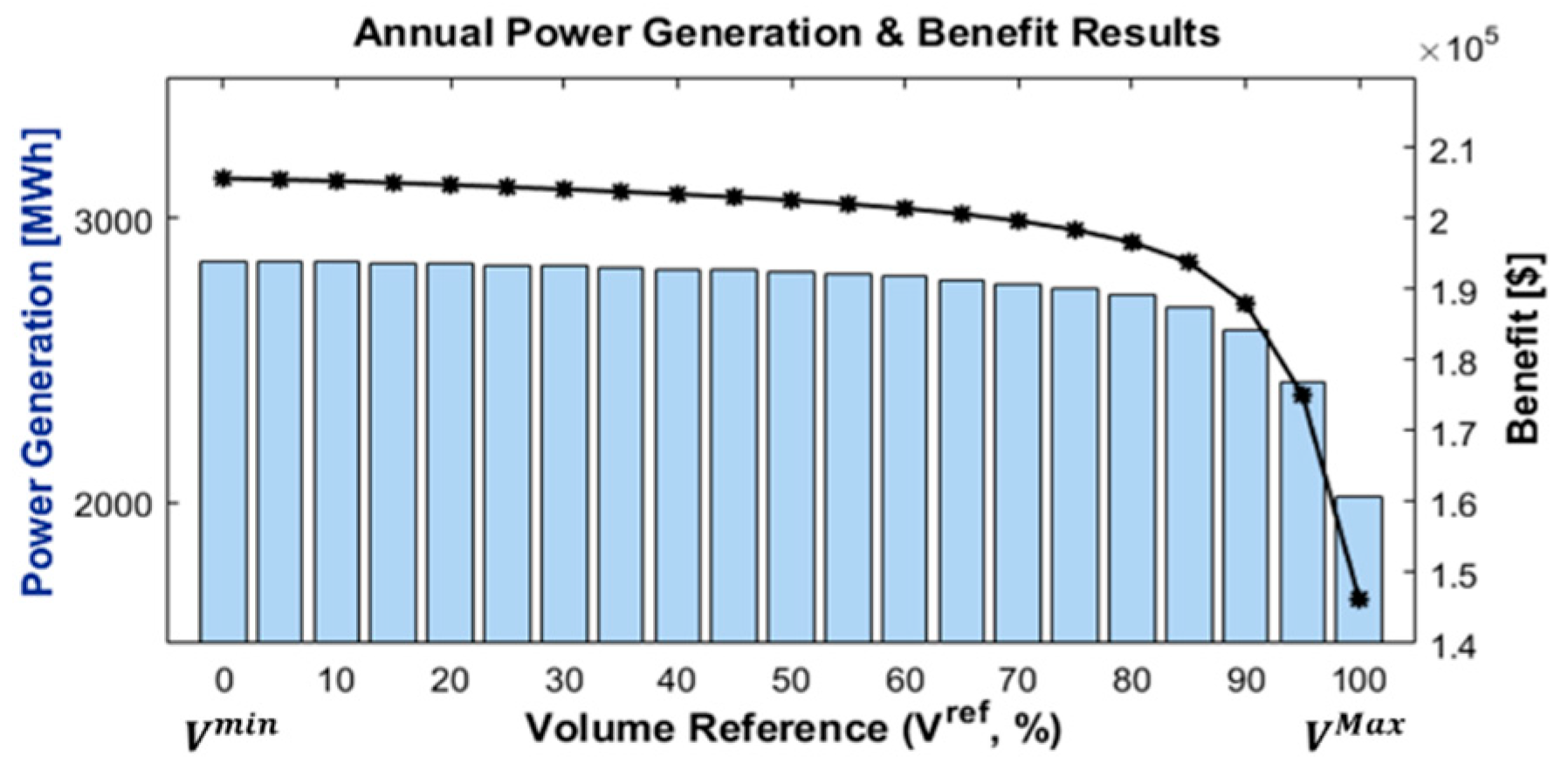
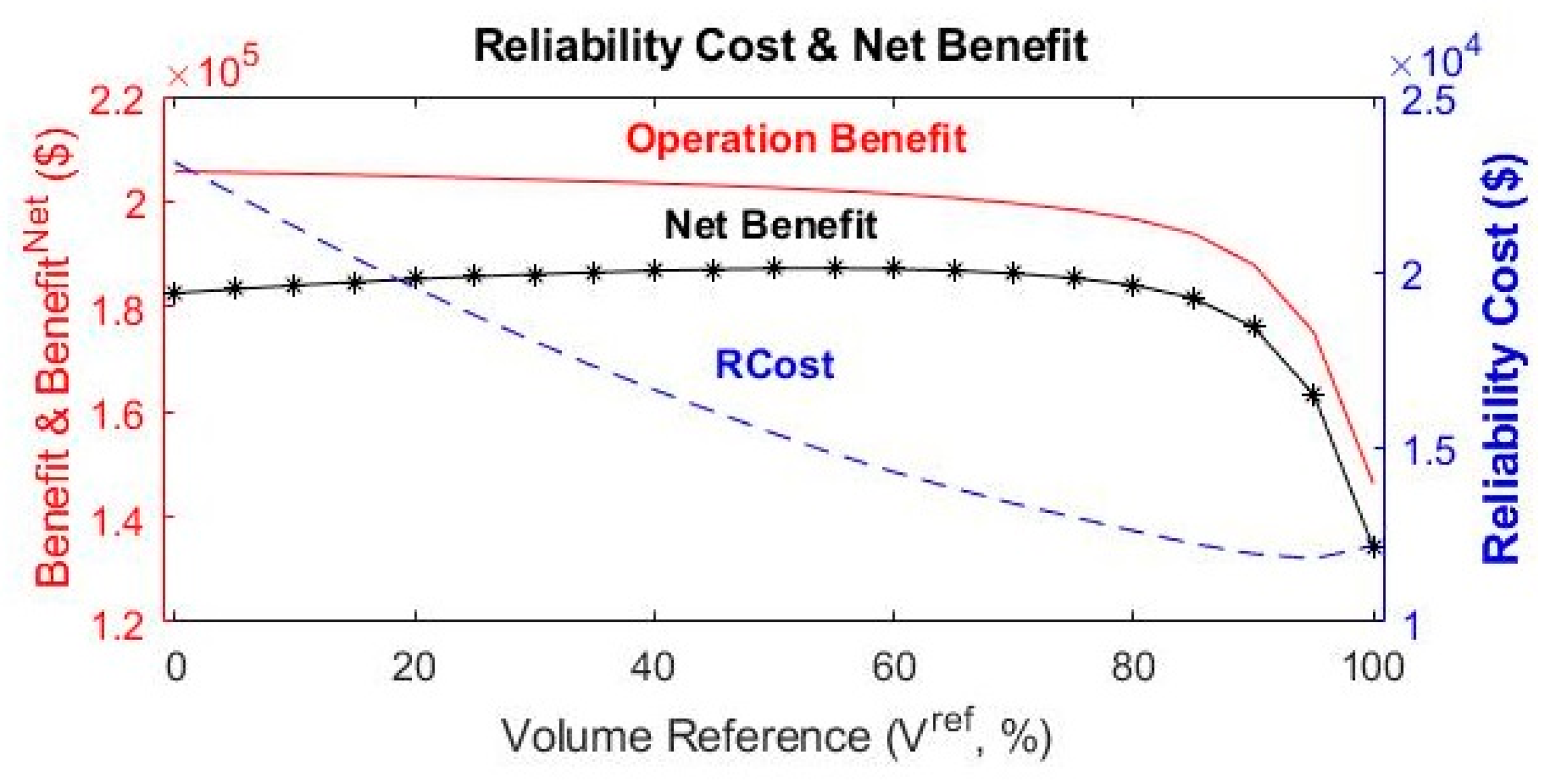
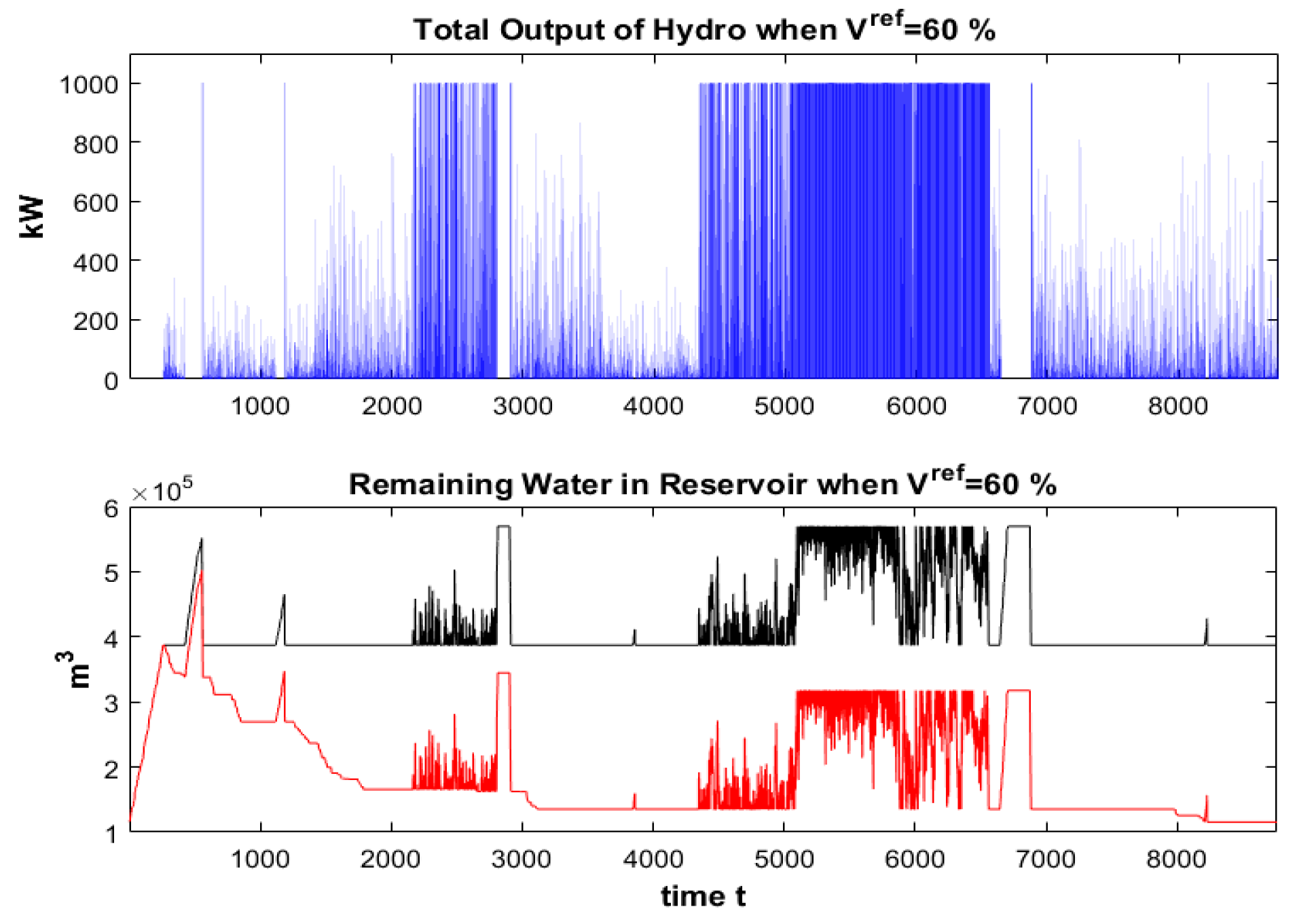
4.2. Simulation Result
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sacramento, E.M.; Carvalho, P.C.M.; de Araújo, J.C.; Riffel, D.B.; Corrêa, R.M.d.; Neto, J.S.P. Scenarios for use of floating photovoltaic plants in Brazilian reservoirs. IET Renew. Power Gen. 2015, 9, 1019–1024. [Google Scholar] [CrossRef]
- Teixeira, L.E.; Caux, J.; Beluco, A.; Bertoldo, I.; Louzada, J.A.S.; Eifler, R.C. Feasibility Study of a Hydro PV Hybrid System Operating at a Dam for Water Supply in Southern Brazil. J. Power Energy Eng. 2015, 3, 70–83. [Google Scholar] [CrossRef]
- Kougias, I.; Szabo, S.; Monforti-Ferrario, F.; Huld, T.; Bodis, K. A methodology for optimization of the complementarity between small-hydropower plants and solar PV systems. Renew. Energy 2016, 87, 1023–1030. [Google Scholar] [CrossRef]
- Lee, S.; Lee, N.; Choi, H.; Kim, J. Study on Analysis of Suitable Site for Development of Floating Photovoltaic System. J. Korean Inst. Illum. Electr. Instal. Eng. 2012, 26, 30–38. [Google Scholar]
- Bansal, A.K.; Kumar, R.; Gupta, R.A. Economic Analysis and Power Management of a Small Autonomous Hybrid Power System (SAHPS) Using Biogeography Based Optimization (BBO) Algorithm. IEEE Trans. Smart Grid 2013, 4, 638–648. [Google Scholar] [CrossRef]
- Jadoun, V.K.; Gupta, N.; Niazi, K.R.; Swarnkar, A. Enhanced Particle Swarm Optimization for Short-Term Non-Convex Economic Scheduling of Hydrothermal Energy Systems. J. Electr. Eng. Technol. 2015, 10, 1940–1949. [Google Scholar] [CrossRef]
- Bagena, B.; Huang, D.; Singh, C. A new analytical technique for incorporating base loaded energy limited hydro units in reliability evaluation. Electr. Power Syst. Res. 2016, 131, 218–223. [Google Scholar] [CrossRef]
- Billinton, R.; Li, W. Reliability Assessment of Electric Power Systems Using Monte Carlo Methods; Plenum Press: New York, NY, USA, 1994. [Google Scholar]
- Billinton, R.; Allan, R.N. Reliability Evaluation of Power Systems; Plenum Press: New York, NY, USA, 1996. [Google Scholar]
- D’Annunzio, C.; Santoso, S. Noniterative Method to Approximate the Effective Load Carrying Capability of a Wind Plant. IEEE Trans. Energy Convers. 2008, 23, 544–550. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, Y.; Xiao, W.; Li, W. Reliability Evaluation of Grid-Connected Photovoltaic Power Systems. IEEE Trans. Sustain. Energy 2012, 3, 379–389. [Google Scholar] [CrossRef]
- Karki, R.; Hu, P.; Billinton, R. Reliability Evaluation Considering Wind and Hydro Power Coordination. IEEE Trans. Power Syst. 2010, 25, 685–693. [Google Scholar] [CrossRef]
- Andalib-Bin-Karim, C.; Liang, X.; Chowdhury, H.A. Generation Reliability Assessment of Stand-alone Hybrid Power System—A Case Study. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Toronto, ON, Canada, 22–25 March 2017. [Google Scholar]
- Park, J.; Choi, J. Development of Methodology of New Effective Installed Reserve Rate considering Renewable Energy Generators. Trans. Korean Inst. Electr. Eng. 2010, 59, 26–32. [Google Scholar]



| Component | Configuration Data and Constraints |
|---|---|
| CGs | |
| PV | |
| Hydro |
| Component | Reliability Data | |||
|---|---|---|---|---|
| CGs | 0.0016 | 0.0167 | ||
| PV | 0.0033 | 0.0417 | ||
| 0.0024 | 0.0278 | |||
| Hydro | 0.0013 | 0.0139 | ||
| (%) | LOEE (MWh) | RCost ($) | BenefitH ($) | ($) |
|---|---|---|---|---|
| 0 (=Vmin) | 23.13 | 34,691.8 | 205,700.3 | 171,008.5 |
| 50 | 15.38 | 23,073.1 | 202,617.0 | 179,543.8 |
| 60 | 14.28 | 21,423.1 | 201,445.1 | 180,022.1 |
| 100 (=VMax) | 12.18 | 18,275.7 | 146,258.2 | 127,982.5 |
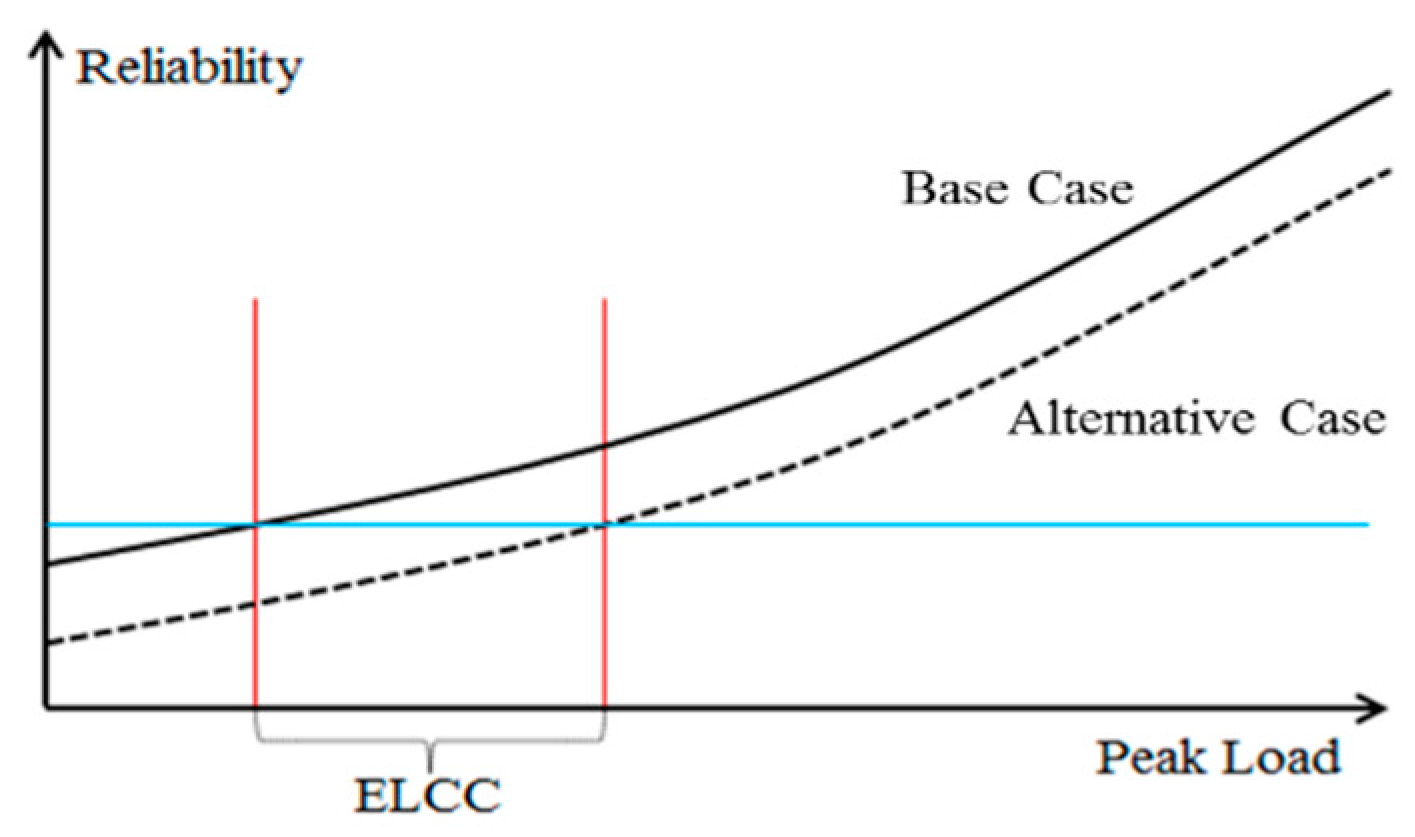
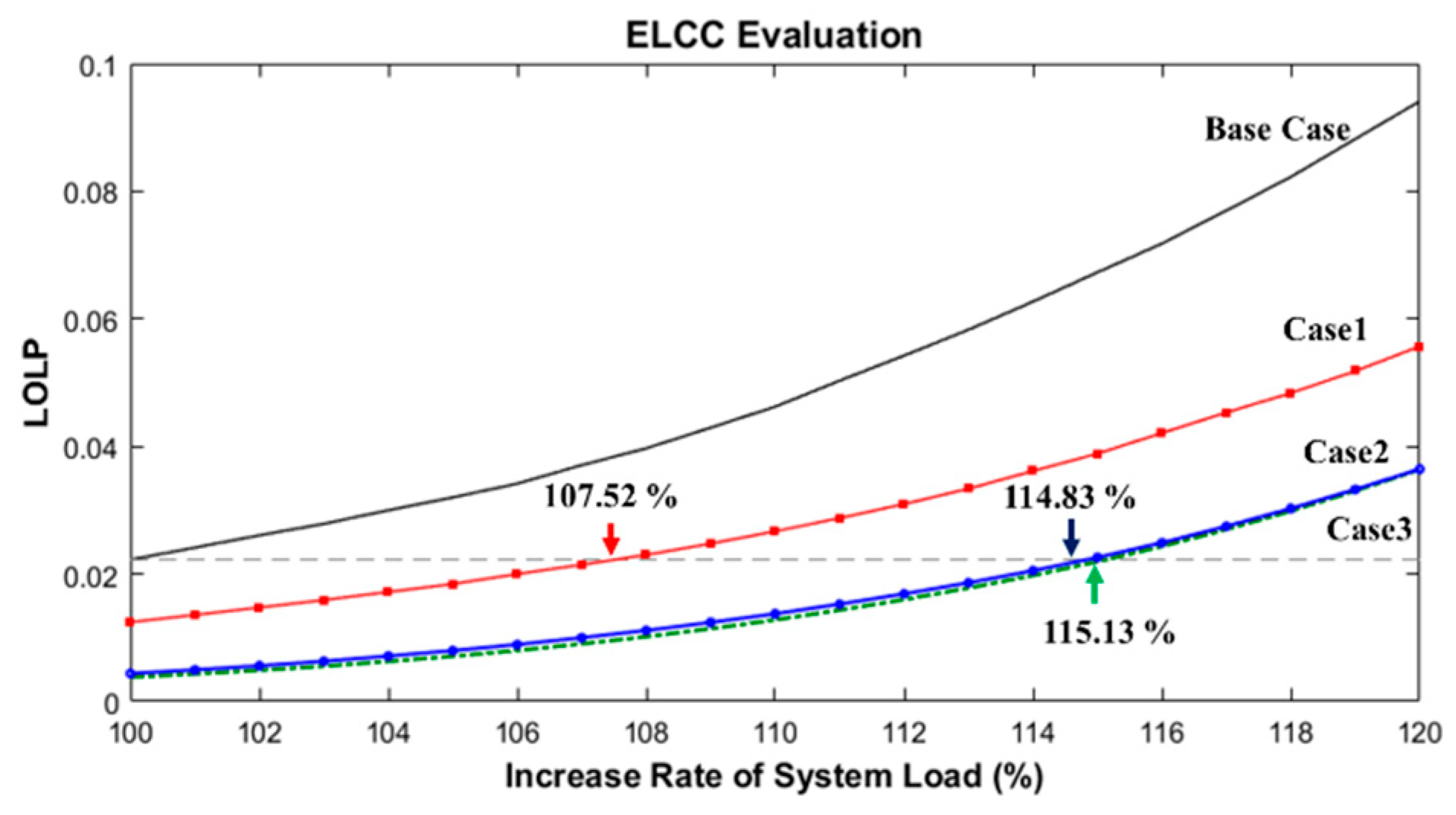
| Test Cases | Vref (%) | System Load (%, kW) | ELCC (kW) | |
|---|---|---|---|---|
| Base | - | 100 | 2500 | - |
| Case1 | 0 | 107.52 | 2687.90 | 187.90 |
| Case2 | 60 | 114.83 | 2870.77 | 370.77 |
| Case3 | 100 | 115.13 | 2878.34 | 378.34 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Na, M.-S.; Kim, J.-O. Reliability Evaluation of Micro-grids Containing PV System and Hydropower Plant. Energies 2019, 12, 343. https://doi.org/10.3390/en12030343
Na M-S, Kim J-O. Reliability Evaluation of Micro-grids Containing PV System and Hydropower Plant. Energies. 2019; 12(3):343. https://doi.org/10.3390/en12030343
Chicago/Turabian StyleNa, Moon-Su, and Jin-O Kim. 2019. "Reliability Evaluation of Micro-grids Containing PV System and Hydropower Plant" Energies 12, no. 3: 343. https://doi.org/10.3390/en12030343
APA StyleNa, M.-S., & Kim, J.-O. (2019). Reliability Evaluation of Micro-grids Containing PV System and Hydropower Plant. Energies, 12(3), 343. https://doi.org/10.3390/en12030343




