Testing the Efficiency of Electricity Markets Using a New Composite Measure Based on Nonlinear TS Tools

Abstract

In this paper we examine and compare the efficiency of four European electricity markets (NordPool, Italian, Spanish and Greek) of different microstructure and level of maturity, by testing the weak form of the Efficient Market Hypothesis (EMH). To quantify the level of efficiency deviation of each market from the ‘ideal’ or ‘benchmark market of random walk’, we have constructed a Composite Electricity Market Efficiency Index (EMEI), inspired by similar works on other energy commodities. The proposed index consists of linear and nonlinear components each one measuring a different feature or dimension of the market efficiency such as its complexity, fractality, entropy, long-term memory or correlation, all connected to the associated benchmark values of the Random Walk Process (RWP). The key findings are that overall, all examined electricity markets are inefficient in respect to the weak form of EMH and the less inefficient market, as measured by the EMEI is the NordPool, closely followed by the Spanish market, with the Italian being the third. The most inefficient market is the Greek one. These results are in accordance with the predominant view about the maturity of these markets. This study contributes significantly on improving the research framework in developing consistent and robust tools for efficiency measurement, while the proposed index can be a valuable tool in designing improved guidelines towards enhancing the efficiency of electricity markets.

1. Introduction

Electricity market systems are “governed” by interacting subsystems or mechanisms, operating across multiple spatial and temporal scales. One can consider the natural gas, CO₂, Brent oil, demand etc., as separate markets or systems, with their own underlying dynamics, that interact and determine the whole system’s (electricity market) marginal price, SMP. This wholesale price (or spot price), viewed as an output variable of an electricity market, exhibits most of the time, complex dynamic behavior, mainly due to “information” generated by the above mentioned multivariable interaction, as well as due to the “real-world” noise that contaminates the dynamics.

In this context, the analysis and “quantification” of the efficiency of a very complex market such as the electricity market is a challenging problem, which contains both deterministic (due to various seasonalities) and stochastic components. On the one hand, in the analysis of the deterministic component time series, Takens’ theorem (Takens, [1]; Eckmann et al. [2]) is the cornerstone of this analysis, stating that one does not have to observe all variables that affect the dynamics of the-usually-high-dimensional system in order to study and understand it. Instead, by observing a single factor one can “reconstruct” the full state or phase space of the dynamical system, having the “same” qualitative and quantitative features as the original phase space. Due to the fact that experimental or “real world” data are affected by dynamical noise, Takens’ approach is of limited use and is only applied to low dimensional dynamics (Theiler et al. [3]). On the other hand, the aim in the analysis of the stochastic component is the quantification of the statistical properties of the dynamical system, by using, for example, the diffusion process at both “macroscopic” and “microscopic” levels. In the former, the Fick’s law and the principle of mass conservation are used to derive the diffusion equation, while the theory of Brownian motion, which is based on random walk models and consists the Benchmark process on which the Efficient Market Hypothesis (EMH) is developed, is used to formulate the diffusion equation in the latter case. Both deterministic and stochastic approaches are used in analyzing time series since they complement each other and provide useful and augmented information that sheds light on the dynamics of “real-world” complex systems.

The purpose of this paper is to measure the efficiency of electricity markets based on the framework of EMH and Random Walk Process (RWP), by using a Composite Index, that is proposed and presented in this work. In particularly, we analyze the time series of wholesale electricity prices for a number of European electricity markets, using the aforementioned Composite Index. Moreover, by using this composite measure, our aim is to compare the degree of complexity of the spot price time series of the NordPool, Spanish, Italian and Greek electricity markets and therefore also to evaluate the complexity structure of these markets, with the ultimate objective of discriminating these markets in view of their degree of competitiveness by testing the weak form of EMH.

A naive approach in measuring the degree of regularity of a signal is the estimation of the dynamics of repetitive modes, however in this case a straightforward correspondence between regularity and complexity is not possible. As Grassberger “intuitively” states, “complexity” can be viewed as a “meaningful structural richness” which shows relatively higher regularity, a feature not exhibited by random processes [4]. Furthermore, there is a one-to-one relation between the degree of randomness and entropy-oriented measures such as the well-known Kolmogorov-Sinai (KS) entropy (Kolmogorov [5]; Sinai [6]) or entropy rate. In other words, uncorrelated random signals (white noise) have the highest values of entropy, are unpredictable but are not structurally “complex”, having globally very simple dynamics. Therefore, one should be very careful when analyzing electricity market time series, since entropy-based measures may lead to unreasonable outputs. For example, one could consider the case when electricity markets that are known to be less competitive, small size, immature, with a small number of participants display higher entropy, in comparison with other “more advanced” mature, competitive and larger in size markets. The “ideal” measure of complexity is one that assigns minimum values of entropy to both extreme signals, deterministic—predictable and pure extreme random (uncorrelated)—unpredictable ones (Yaneer [7]). However, no consensus exists so far on this problem.

Finding an “ideal” entropy-oriented measure for evaluating the complexity of the electricity market is not an easy task, due to the following assumptions that hold true for the “complex” dynamics of these markets:

(a)

An electricity market is “an alive” system which exchanges continuously information with its external environment, which in turn affects the interaction between its internal variables caused by the system’s effort to adapt continuously to its ever-changing environment. This is mathematically described as a stochastic dynamical high-dimensional system evolving on a manifold, the structure of which reflects the effects of the various forces (factors) that shape the dynamics of the system.

(b)

Electricity market systems operate across multiple spatial and temporal scales, since their fundamental endogenous and external (e.g., weather, macroeconomic factors, etc.) variables evolve on different spatial and time scales, thus their complexity is also multiscaled.

(c)

A number of various market malfunctions, internal structural frictions, external political and regulatory interventions etc., can have degrading results on the market’s ability in adapting to its external forces, therefore the information carried by its spot price is degraded, due to a “loss of complexity”, which is a generic feature of not efficient markets.

Therefore, in order to find a “good” and reliable complexity measure, we consider a composite measure of complexity, using in this way not only entropy-based measures but also other measures (linear and nonlinear) that complement each other. The idea of building a Composite Complexity or Efficiency measure came to our minds from the works of Kristoufek et al. [8], which however are limited on measuring the efficiency of commodity markets only.

The proposed composite Electricity Market Efficiency Index (EMEI) consists of five components or measures. Beginning with the information or entropy-based component of the proposed composite complexity measure, we utilize the Sample Entropy which is an extension of the Approximate Entropy (Pincus [9]; Richman et al. [10]). In order to take into consideration the previous mentioned dependence of entropy on various time scales, the concept of Multiscale Entropy, MSE, which has been developed by Costa et al. [11], is also examined as an extra tool of evaluating how the complexity of the analyzed electricity markets depends on time scales, and to further distinguish the markets based on the efficiency criterium. The EMEI additionally uses the nonlinear measures of Hurst Exponent (captures the long-term memory or dependence of a time series), the Fractal dimension (measures the local memory and the degree of roughness of time series) and the Herfindahl-Hirschman Index (HHI), which measures the degree of market concentration, developed in the field of Industrial Econometrics. It is worth mentioning that the HHI has been recently used in the literature as a nonlinear constraint in the traditional Optimal Power flow algorithm to capture market power possibilities in a dynamical approach (Sahni et al. [12]). All the above measures belong to the groups of Nonlinear Time Series tools and Econophysics. Finally, the linear measures of Variance Ratio Test (VRT) for testing the random walk hypothesis (RWH) against stationary alternatives, which are a tool of Financial Econometrics, are also incorporated in the EMEI. Overall, the EMEI is used to rank in a comprehensive way the degree of efficiency of each electricity market that is examined in this paper.

Furthermore, recently in the literature of commodity price volatility, evidence of leverage effects has been found in various energy markets. Chan and Grant [13] have found a significant negative leverage effect in crude oil spot markets. An extensive literature review in this area is provided in the work of Kristoufek [14] in which he connects the Hurst exponent with the standard leverage effect founded in crude oil and the inverse leverage effect observed in natural gas markets. Similarly, Baum, et al. [15], using high-frequency (intra-day) data (which provides an almost continuous observation of return series) on crude oil and natural gas, provide evidence for inverse leverage effect in natural gas market, showing that volatility becomes higher when energy returns increase. Nomikos and Andriosopoulos [16] have shown evidence for the presence of “leverage effect” in crude oil and heating oil and inverse leverage effect in other commodities by analyzing eight energy markets that trade futures contracts on NYMEX. An extensive literature review and a comprehensive study, using comparative microeconomic analysis, of the asymmetric volatility (leverage effect) in fourteen wholesale electricity markets in Europe, is provided by Erdogdu [17]. The search for leverage effect in the wholesale price volatility of the Greek market has also been carried out in the work of Papaioannou et al. [18], who have shown that there is no leverage effect in the Greek market compared to the other European electricity markets examined in their paper, in which the leverage or inverse leverage effect exist. In this frame, we “exploit” these results by linking it with the results on VR test, Hurst exponent, and entropy measures of market efficiency. As we show in this paper, the markets with higher efficiency levels exhibit leverage effects in the volatility of their wholesale price. Overall, the main contributions of this paper can be summarized as follows:

(1)

Papers presented currently in the literature usually focus on a single (or a few) efficiency measure(s) to test whether the specific, mainly commodity, markets are or are not efficient. However, the efficiency analysis of electricity markets, within the framework of EMH and RWH, to the best of our knowledge, has been almost ignored. In this context, we contribute by proposing a new Composite Index for measuring efficiency (which incorporates a number of linear and nonlinear measures that we considered to be the most powerful tools in better capturing the degree of complexity of the markets analyzed), by linking the inefficiency with complexity and finally by ranking the markets according to their value of EMEI, following the work of Kristoufek and Vosvrda [19].

(2)

One other key finding of this work is the linking (based on qualitatively analysis) of the concept of the volatility clustering with the leverage effect and the market efficiency measures.

(3)

Finally, based on the proposed composite EMEI a detailed and rigorous efficiency analysis is carried out for four European Electricity markets (NordPool, Italian, Spanish and Greek). This analysis provides a reliable complexity measure of the aforementioned markets and presents a comprehensive assessment of their efficiency.

The structure of this paper is as follows: Section 2 covers the literature review regarding the testing of the EMH on Spot electricity market as well as on other commodities, and the link between the various forms of EMH with the RWP and its prerequisite. Section 3 describes in brief the Greek, Italian, Iberian and NordPool wholesale electricity markets. In Section 4 we describe the methodology and provide a short theoretical analysis of the tools used in this paper, specifically the Hurst exponent, the VRT, entropy related measures, the fractal dimension and the HHI. Section 5 describes the analyzed dataset and showcases results of the considered metrics. Finally, Section 6 presents the proposed composite EMEI, followed by Conclusions in Section 7.

2. Testing the EMH on Spot Electricity Prices: Literature Review

According to Fama [20], an efficient market is a market in which prices always fully reflect available information (Efficient Market Hypothesis or EMH) and all available information is used in pricing securities, thus it is not possible to make economic profits through trading using the current accumulated information up to the moment of trading. Fama [20] also makes a distinction between different types of efficient markets, according to the concept of available information. The first type is the weak-form of EMH which assumed that historical price information is instantaneously incorporated into prices. The semi-strong form of EMH, the second type, assumes that all publicly available information is also impounded into prices. Finally, the third type, the strong-form of EMH requires also that apart from historical and publicly available information, private information is also reflected in the prices. However, as it is well accepted, market efficiency per se is not testable, so its estimation is only possible via using some asset pricing models. In 1991 Fama [21] revised his EMH by acknowledging that short-horizon returns (e.g., daily, weekly) can be predicted, a fact that refutes the strong form of EMH. The weaker forms of EMH are however still considered to present a rational approximation of market efficiency.

In the area of electricity markets, a number of research papers have tested the EMH as well as the price discovery processes of future or expected prices and futures prices. In the work of Higgs and Worthington [22] the EMH has been tested for the Australian Electricity Spot market for the period 1999–2001. They examined whether the Australian electricity prices follow a Random Walk. According to their results, only one of the five regional markets that consist the Australian National Electricity Market (ANEM), namely the Victorian base-load spot market verifies the weak form of EMH. Borenstein and Holland [23] present a different perspective of the efficiency of the electricity markets, by considering the presence of a share of customers on time-invariant pricing in these markets and the impact they have on them. The authors also provide evidence that any attempts to enhance investments via taxes or subsidies on electricity or capacity will probably fail, because interventions of this type generate new inefficiencies. Even though their work is not related directly to testing the EMH, it is worth of mentioning this work here since it provides information on how the structural characteristics of electricity market affect the whole price-retail price relationship and as a consequence the efficiency of the market. Shawky et al. [24], have investigated the daily spot and futures prices of NYMEX, and have found that they are broadly consistent with efficient markets. They used a GARCH model to estimate the minimum variance hedge ratios for electricity futures, and an EGARCH model to study the dynamics between spot and futures returns. Due to the unique stylized fact of electricity as a non-storable commodity they also found that electricity futures are significantly different than other standard commodities, regarding premium and hedge ratios.

The above mentioned works rely mainly on econometric models, namely co-integration for EMH testing, Vector Error Correction (VECM) for information transfer between futures and spot prices, and Impulse Response Functions (IRF) to study the market’s response to various shocks in the prices, as Shawky et al. [24] have shown. Arciniegas et al. [25] assess the mark of efficiency reached by the electricity markets in California, New York and PJM. According to their analysis and measures of efficiency (Unit root tests—ADF, Co-integration analysis, Vector Autoregressive—VAR model), PJM and California electricity markets are more efficient than the New York Market. Also, they found that as the maturity of these markets increase, their efficiency level goes up. Electricity market efficiency testing is the subject of the research of Lu et al. [26]. They propose a testing approach for electricity market efficiency assessment by calculating the correlation between fuel prices and electricity market prices. They applied their testing on the National Electricity market of Australia and concluded that because the returns on electricity markets are different for different market players, the expected return model or fair game model of Fama [20] cannot be applied directly for electricity market efficiency tests.

A new approach for measuring deviations from the efficient market state, taken from the nonlinear time series analysis tools, is the one proposed by Uritskaya and Apostolos [27]. This tool estimates a scale-dependent fractal exponent which characterizes correlations at different time scales. They apply this approach on the Alberta and Mid-Columbia (Mid-C) electricity markets as well as on AECO Alberta natural gas market, in order to compare the two commodities (the first two not-storable and the third storable). They found that price changes in all above markets are not efficient, due to the existence of serial (time) correlations in the returns. Furthermore, the correlation of electricity prices exhibit complex multiscale structure. Growitsch and Nepal [28] have assessed the overall efficiency of the German electricity wholesale market using cointegration analysis and error correction modelling. They showed that this market seems to be inefficient and not well functioning. Redl et al. [29], assessed the crucial impact parameters of forward electricity prices and the relationship between forward and future spot prices, in European Energy Exchange (EEX) and NordPool Power Exchange. In their work, the EMH is tested via examining the systematic bias between those two prices, called risk premium. This bias, not permitted under EMH, rely on the fact that futures (forward) prices under-or over-predict the spot prices. Serletis and Rosenberg [30] revisited the evidence for the weaker form of the EMH, in the US stock market. They used a new statistical physics approach, namely the Detrending Moving Average DMA introduced by Alessio et al. [31].

An efficiency analysis of the Nordic electricity futures market is presented in the work of Yang, et al. [32], where the market validity, price discovery function and the hedge function are calculated by using econometric models, such as Variance Ratio test for testing the weak-form of EMH, the Co-integration test of Johansen on futures and spot prices as well as the Hasbrouck Variance Decomposition to estimate the price discovery and hedge functions. They found that: (a) the Nordic electricity futures market satisfies the weak-form efficiency hypothesis, (b) the futures and spot prices are co-integrated and (c) the hedging can reduce the market risk to a certain extent, but a high basis risk still remains in this kind of market. Long-term memory in electricity prices (which refutes the EMH) is analyzed in Czech Electricity prices by Kristoufek et al. [33]. Due to the existence of seasonalities in the prices, they applied Detrended Fluctuation Analysis (DFA) approach. They found that electricity prices are non-stationary but strongly mean-reverting, which distinguishes them from other financial asset prices, a characteristic of the prices which is attributed to the non-storability of electricity. This work has influenced very much our present work, in which we used also multi-fractal DFA tool. Kristoufek and Vosvrda [8] have analyzed the market efficiency of 25 commodity futures (metals, energies, grains etc.), by using their recently proposed Efficiency Index, a composite index which consists of various (mainly) non-linear measures like Hurst Exponent, Fractal Dimension, Approximate Entropy. They found that the energy commodities (Crude Oil, Natural Gas) are the most efficient. They also discuss how the various aforementioned measures contribute separately to the total inefficiency. A very interesting result is also the nonstandard relationship between the fractal dimension and the Hurst Exponent, which was found to be positive indicating that local persistence (trending) is connected to global anti-persistence. The works of Kristoufek et al. [8,19] mentioned above, have both influenced the work described in this paper, in which we enrich the toolbox used in their work with other tools, in measuring the efficiency of the four aforementioned European electricity markets.

An investigation of the relation between technical analysis and market efficiency in energy markets is presented in the work of Lin et al., [34]. Their empirical results strongly indicate that data snooping, non-synchronous trading and transaction costs affect greatly the technical analysis and support the EMH in thirteen energy market indices they have analyzed. The deviation from the Random Walk process of the Alberta and Ontario electricity markets, is shown in the work of Uritskaya and Uritsky [35]. Using scale-depend DFA, spectral analysis and probability distribution analysis, they show that the markets exhibit strongly anti-persistent or mean reversion, a behavior of processes with Hurst exponent smaller than 0.5 which deviates from the exponent of an efficient market which is equal to 0.5. The mean reversion behavior suggests that the dynamics of these markets can be predicted based on historic records, a fact in complete opposition to the EMH.

More recently, Ballester et al. [36] have analyzed the relationship between prices from three different markets within the Spanish zone of MIBEL, futures, spot and over-the-counter (OTC) forward markets. Actually, they have tested the weak-form EMH of the aforementioned markets, but also they analyzed the semi-strong-form of EMH of the MIBEL futures market as well as the price discovery relationships between the price time series of the above markets. The tests for the weak-form EMH has shown that only for one contract of the futures market (1-quarter-ahead) the null hypothesis for random walk is not rejected, while for the rest of the examined series this null hypothesis of RW is rejected. In a very recent paper by Morales et al. [37] the level of efficiency and degree of integration is analyzed, for the markets ARXUK, NordPool and Phelix. The authors applied the ADF (Augmented Dickey-Fuller) and Variance Ratio tests for measuring the weak form of market efficiency, on daily observations covering the period 2004–2014, splitted into two subperiods, before and after 2009/72/EC directive. Their main findings highlight that these markets do not behave like random walk, therefore they are considered inefficient markets, not fulfilling the weak form of market efficiency. The results of the work above are very related and consistent with our results, in general, and for the NordPool in particular, since this market is also analyzed in our case. In

Table 1. The results of EMH testing on various commodities, a short literature review.

Reference	Commodity	EMH Result
Roll (1972) [38]	Commodity price index	Inefficient
Danthine (1977) [39]	Commodity price index	Disputes inefficiency
Gjoberg (1985) [40]	Oil spot prices	Inefficient
Panas (1991) [41]	Oil spot prices	Inefficient
Herbert and Kreil (1996) [42]	Natural gas spot and future	Inefficient
Tabak and Cajueiro (2007) [43]	Brent and WTI crude oil	Becoming more efficient over time
Alvarez-Ramirez et al. (2010) [44]	Crude oil	Inefficient
Wang and Liu (2010) [45]	WTI crude oil	Becomes more efficient over time
Wang et al. (2011) [46]	WTI crude oil spot and futures	Inefficient
Charles and Darne (2009) [47]	Brent and WTI	Brent-weak form efficient WTI-inefficient
Lee and Lee (2009) [48]	Coal, oil, gas and electricity	Inefficient
Lean et al. (2010) [49]	WTI crude oil spot and futures	No arbitrage
Narayan et al. (2010) [50]	Gold and oil spot and futures prices	Inefficient
Wang and Yang (2010) [51]	Crude oil, heating oil, natural gas high frequency data	Inefficient
Gebre-Mariam (2011) [52]	US natural gas spot and futures	Efficient only for contracts
Martina et al. (2011) [53]	WTI crude oil spot	Cycles in prices
Zunino et al. (2011) [54]	Commodity markets	Silver and cotton the most efficient
Wang et al. (2011) [46]	Gold market	More efficient over time
Kim et al. (2011a) [55]	Korean agricultural market	Leans toward inefficiency
Kim et al. (2011b) [56]	Stock and commodity markets	Markets are decoupled, oil and gold shows signs of inefficiency
Ortiz-Cruz et al. (2012) [57]	Daily WTI prices	Efficient

, we provide a literature review of the results of the EMH testing on a variety of commodities.

3. The Greek, Italian, Iberian and NordPool Wholesale Electricity Markets in Brief

In order to better assess the complexity of the four wholesale electricity markets under consideration, namely the Greek, the Italian, the Iberian and the Nordic one, and interpret more accurately the dynamics of their spot prices (SMP, PUN, SPELL and ELSPOT respectively) we must first examine the structure of their respective electricity markets and their different operational principles. All the aforementioned countries operate under the European Directives, which have deregulated the electricity sector, albeit at different levels of maturity. In brief the so-called Target Model for the electricity markets in Europe comprises of four different markets:

• Forward and future market
• Day-ahead (or spot) market
• Intra-day market
• Balancing market (For a detailed description for the current electricity market design in Europe we refer the interested reader to https://set.kuleuven.be/ei/factsheets)

The Nordic electricity market is the oldest and probably the most successful international power market. Norway was virtually the founding country by introducing first the electricity market competition with the Energy Act of June 1990 (Flatabo et al. [58]). The market was extended to include Sweden in 1996 and thus forming a common Norwegian-Swedish Exchange (Nord Pool). Finland, West Denmark, East Denmark were next to join in 1998, 1999 and 2000 respectively. In the years to follow Nord Pool has expanded to also include the Baltic region. At this point, the market covers four currencies, three synchronous areas and encompasses a wide range of technologies including hydro, nuclear, thermal, wind generation etc. (Energinet [59]). The Nordic power market design has remained fairly uninfluenced for the past two decades, while adapting to the inclusion of new zones over time. It possesses all the basic characteristics of an efficient market such as liquidity, transparency, growth and diversity. In fact, its’ underlying design has been proven so successful that is being used as a basis for the European Target Model.

Greece’s liberalized electricity market was established according to the European Directive 96/92/EC. Currently only Day-Ahead market is operational in Greece, which sets Greece as the less mature of the electricity markets analyzed in this study. The Greek electricity market (GEM) is currently in a transitional period, during which the market structure evolves towards its final design, namely the Target Model. The wholesale electricity market is a day ahead mandatory pool which is subject to inter-zonal transmission constraints, unit technical constraints, reserve requirements, the interconnection Net Transfer Capacities (NTCs) and in general all system constraints. More specifically, based on forecasted demand, generators’ offers, suppliers’ bids, power stations’ availabilities, unpriced or must-run production (e.g., hydro power mandatory generation, cogeneration and RES outputs), schedules for interconnection as well as a number of transmission systems’ and power stations’ technical constraints, an optimization process is followed in order to dispatch the power plant with the lower cost, both for energy and ancillary services.

The Italian wholesale electricity market, commonly called the Italian Power Exchange (IPEX), is run by the Gestore del Mercato Elettrico (GME), which consists of the following:

➢

The Spot Electricity Market (MPE) which includes:

• The Day-Ahead Market (MGP), where all market participants (producers, wholesalers, consumers) trade energy blocks for the next day.
• The Intra-Day Market (MI) where the initial schedules can be modified by the market participants.
• The Ancillary Services Market (MSD), which consists of the ex-ante MSD which is a scheduling substage of MSD and of the Balancing Market (MB).

➢

The Forward Electricity Market (MTE), which is the venue where market participants can sell/purchase future electricity supplies via forward electricity contracts.

➢

The platform for physical delivery of financial contracts concluded on Italian Derivatives Energy Exchange (IDEX) (CDE).

The Iberian wholesale electricity market, commonly called MIBEL is a joint wholesale electricity market which comprises Spain and Portugal. In order to implement an Iberian electricity market (MIBEL) between the Kingdom of Spain and the Republic of Portugal, an Iberian Market Operator business group was created, OMI-Polo Español S.A. (OMIE), which is subject to the rules and regulations governing Spain’s electricity sector. The spot market is composed of the intra-day market and the day-ahead market. The spot price is common for both countries, unless the interconnection capacity between Spain and Portugal exceeds a predetermined limit; in that case a market splitting mechanism is activated setting different spot prices for both countries. The system operator is responsible for the technical implementation of the daily schedules. After the gate closure, six intraday market sessions are held four hours ahead of the physical delivery. In that case market players can adjust their positions prior according to their forecasts (for a detailed analysis per country, we refer interested readers to: https://www.iea.org/countries/).

4. Methodology and the Proposed Composite Electricity Market Efficiency Index (EMEI)

The electricity market is a multidimensional system containing a lot of concepts regarding its efficiency (degree of competitiveness, complexity, long-term memory, etc.). Multidimensional concepts should be ideally measured by a composite index that can summarize complex multidimensional realities without losing information, because a single index cannot capture all the concepts contained (Saisana and Tarantole [60]).

Based on above information and the work of Kristoufek and Vosvrda [8], in order to assess the efficiency level of a market we propose the following Electricity Market Efficiency Index (EMEI) (the construction of this composite index is in compliance with rules of the OECD European Commission described in the related handbook (OECD-JRC EC Handbook, 2008, https://www.oecd.org/sdd/42495745.pdf), defined as:

$$EMEI=\sqrt{{\displaystyle \sum }_{i=1}^n{\left(\frac{{\widehat{M}}_i-M_i^{*}}{R_i}\right)}^2}$$

(1)

where $M_i$ is the ith component measure, ${\widehat{M}}_i$ is an estimate of the ith measure, $M_i^{*}$ is an expected value of the ith measure for the efficient market (based on the value of measure for Random Walk process) and $R_i$ is a range of the ith measure. The EMEI consists of five metrics that are illustrated in

Table 2. Summary of measures forming EMEI, symbols and expected values.

	$\mathbf{Measure}\mathbf{,}{\mathit{M}}_{\mathit{i}}$	Symbol	Expected Value for Efficient Market
			Symbol	Value
$M_1$	Hurst Exponent	H	$M_H^{*}$	0.5
$M_2$	Fractal Dimension	DF	$M_{DF}^{*}$	1.5
$M_3$	Sample Entropy	E	$M_E^{*}$	1 (rescaled)
$M_4$	Variance Ratio	VR	$V{R}^{*}$	1
$M_5$	Herfindahl-Hirschman Index	HHI	$HH{I}^{*}$	100

. Each metric features a different range of values, as the distance from the expected value for the efficient market hypothesis also differs. In order for all metrics to be accurately expressed in the context of the proposed composite EMEI, all considered indices need to be of the same range. To this end, the Hurst Exponent, the Fractal Dimension, the Sample Entropy and the Variance Ratio Test metrics along with the HHI Index have been rescaled to range between 0 and 1, by considering the ranges $R_{HE}=1$, $R_{FD}=1$, $R_{SE}=2.42$, $R_{VRT}=1$ and $R_{HHI}=10.000$ respectively. Therefore, due to this rescaling, the market that acquires the smallest EMEI value is the most efficient.

In the following sections we provide a short description of the individual metrics that comprise the proposed EMEI index. In most cases, such as the Hurst exponent and the fractal dimension, we applied different estimators and calculated the final result of each component as an average, a technique that provides more stable results.

4.1. Hurst Exponent

A long memory process is a process with a random component, where a past event has a decaying effect on future events. The mathematical definition of long memory processes is given in terms of autocorrelation. When a data set exhibits autocorrelation, a value $x_t$ at time $t$ is correlated with a value $x_{t-d}$ at time $t-d$ where $d$ is some time increment in the future. In a long memory process autocorrelation decays over time and the decay follows a power law, i.e.,:

$$p\left(k\right)=C{k}^{-\delta }$$

(2)

where $C$ is a constant and $p\left(k\right)$ is the autocorrelation function with lag time $k$. The Hurst exponent is related to the exponent $\delta$ by:

$$H=1-\frac{\delta }{2}$$

(3)

The Hurst component, which values belong in the interval $0\le H\le 1$, is equal to 0.5 for random walk time series, H < 0.5 for anticorrelated series, and H > 0.5 for positively correlated series. In the case of market prices time series, if the Hurst exponent $H>0.5$, then it reveals that the price process is correlated or that a price increase in the past is more likely to be followed by an additional increase than a price decrease. Hence, daily price movements are persistent and subject to trends. Thus, the deviation from random walk additionally provides interesting information on the volatility and risk inherent in electricity market.

In order to calculate the Hurst exponent we applied the following methods:

• The rescaled range (R/S) method, developed by Hurst (Hurst [61])
• The Generalized Hurst Exponent (GHE) and weighted GHE (Di Matteo [62]; Barabasi et al., [63])
• The Detrended Fluctuation Analysis (DFA), by Peng et al. [64]
• The Hurst estimation via Periodogram Regression (GPH), originally proposed by Geweke and Porter-Hudak [65]

We will briefly present two of the abovementioned methods, namely the DFA and the GPH.

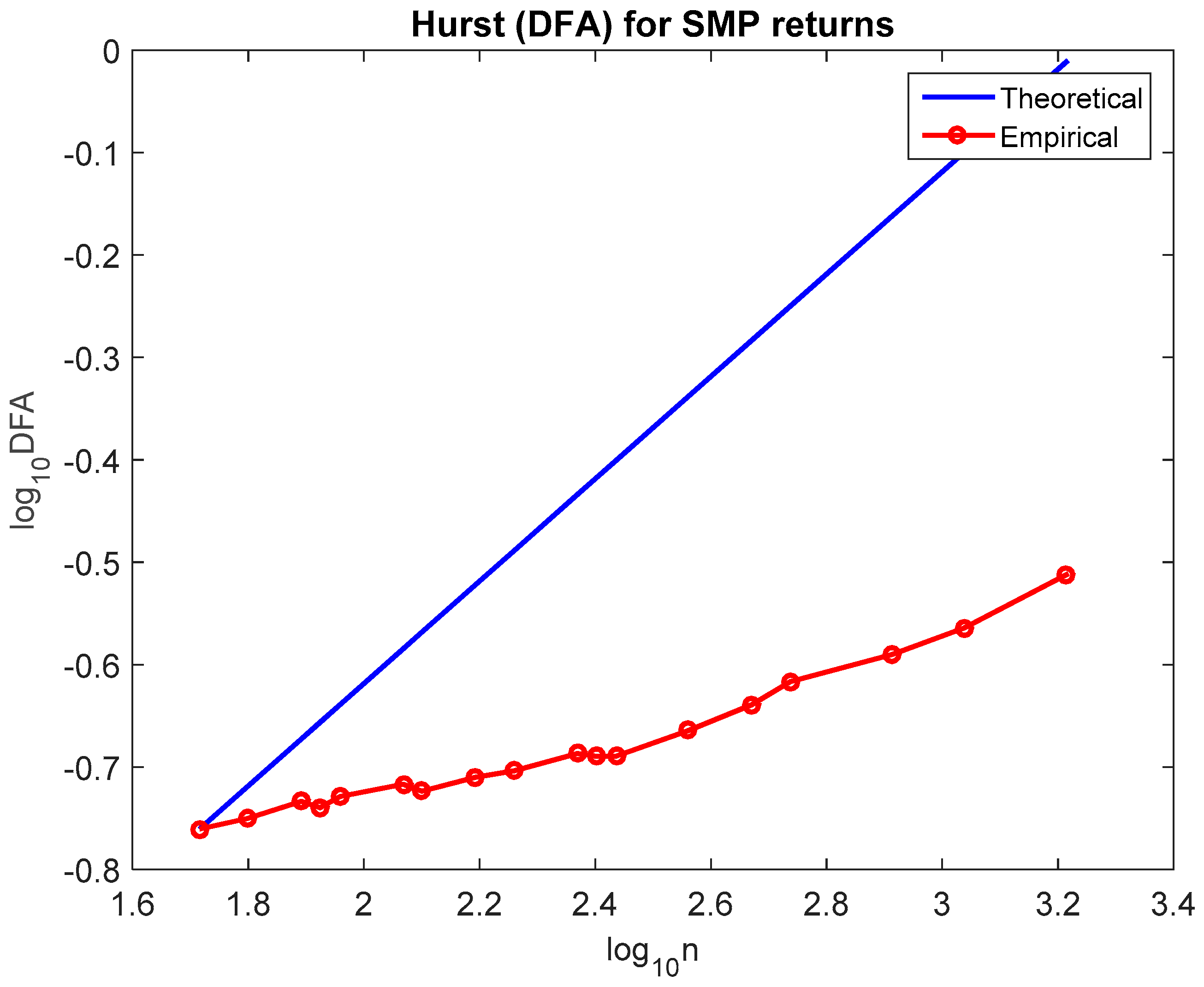
4.1.1. Detrended Fluctuation Analysis (DFA)

To estimate DFA we divide again a time series of length L into d subseries of length n. For each subseries then $k=1,\dots ,d$; (a) we create a cumulative time series $Y_{i,k}={{\displaystyle \sum }}_{j=1}^i{X}_{j,k}$ for $i=1,\dots ,n;$ where $X_{j,k}$ the j element of the k subseries (b) we fit a least squares line $\widetilde{Y_k\left(x\right)=a_{k}x+b_{k}to}\left\{Y_{1,k},\dots Y_{n,k}\right\}$ and finally (c) compute the RMS fluctuation (i.e., standard deviation), $F\left(k\right)$, of the integrated and detrended time series:

$$F\left(k\right)=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(Y_{i,k}-a_{k}i-b_k\right)}^2}$$

(4)

where $Y_{i,k}$ the cumulative series generated from $X_{j,k}$, $a_k$ and $b_k$ the coefficient of the fitted linear regression model, used to detrend the series.

The mean value of RMS fluctuation for all subseries of length $n$ is:

$$\underset{\_}{F}\left(n\right)=\frac{1}{d}{\displaystyle \sum }_{k=1}^{d}F\left(k\right)$$

(5)

As in the case of Hurst analysis, we plot on a double-logarithmic “paper” $\underset{\_}{F}\left(k\right)$ against $n$ and we get the power-law scaling $F\left(n\right)~c{n}^H$ where $H$ is the fractal DFA exponent. If the returns process is white noise then the slope is roughly $0.5$. If the slope is > 0.5 the process is persistent while for an anti-persistent process the slope is $<0.5$. For various processes, index $a$ takes the following values: $H<\frac{1}{2}$ (anti-correlated), $H\approx \frac{1}{2}$, (white noise, uncorrelated), $H>\frac{1}{2}$ (correlated), $H\approx 1(\frac{1}{f}-$ noise, pink noise), $H>1$ (non-stationary, unbounded) and $H\approx \frac{3}{2}$ (Brownian noise) (Weron [66]).

4.1.2. Hurst Estimation via Periodogram Regression (GPH)

This estimation procedure of the Hurst exponent begins with calculating the periodogram. Then a linear regression model is developed such as:

$$log\left\{I_L\left({\omega }_k\right)\right\}=\alpha -d{x}_t+{\epsilon }_k=a-dlog\left\{4si{n}^2{\left(\frac{{\omega }_k}{2}\right)}^2\right\}+{\epsilon }_k$$

(6)

at low frequencies ω_k, k = 1, 2, …, Κ ≤ [L/2], where ω_k the Fourier frequencies, $I_L$ the squared absolute value of the Fourier transform, L the length of the time series, a and d the coefficients of the linear regression and ${\epsilon }_k$ the error term. The least squares estimate of the slope yields the differencing parameter d, hence the Hurst exponent is given by the following formula:

$$H=0.5+\widehat{d}$$

(7)

The choice of k differs in the sense that some authors recommend Κ = [L^0.5], however other values have been also suggested; Κ = [L^0.45] or [L^0.2] ≤ Κ ≤ [L^0.5]. Parameter $\widehat{d}$ is calculated according to the formula:

$$\widehat{d}~N\left(d,\frac{{\pi }^2}{6{{\displaystyle \sum }}_{{\rm K}=1}^{{\rm K}}(x_t-{\underset{\_}{x)}}^2}\right)$$

(8)

where $x_t$ is the quantity in { } in Equation (6).

We now show the relations between indices $\beta$ (power spectral index), DFA index $\alpha$, index in decaying ACF $\delta$ (2), and the Hurst exponent $H$. Using Wiener-Khinchin theorem we have:

$$\begin{gathered} \delta =2-2\alpha \\ \beta =2\alpha -1 \\ \delta =1-\beta \end{gathered}$$

(9)

Therefore, $\alpha$ is connected to the slope of the power spectrum $\beta$, useful in describing the color noise by the following relation:

$$\alpha =\frac{\left(\beta +1\right)}{2}$$

(10)

For fractional Gaussian noise (FGN), $\beta \in \left[-1,1\right]$ therefore $\alpha =\left[0,1\right]$ and $\beta =2H-1$. For fractional Brownian motion (FBM), $\beta \in \left[1,3\right]$ so $\alpha =\left[1,2\right]$ and $\beta =2H+1$.

4.2. Variance Ratio Test (VRT)

4.2.1. Variance Ratio Test Methods

The standard method of testing the random walk hypothesis (RWH) is the outcome of the seminal work of Lo and MacKinlay [67,68] as well as Poterba and Summers [69]. The method has undergone a number of improved modifications and has been broadly applied for market efficiency testing (Serletis and Andreadis [70]). The purpose of the VRT is to test the RWH against stationary alternatives, by considering the fact that the increments of a random walk process have variance that is linear in all sampling intervals. Let $y_t$ is the time series under testing, and $y_t-y_{t-k}$ the k-period differences. Then the sample variance of this k-period return is k times the sample variance of one-period (k = 1) return, which is the first difference $y_t-y_{t-1}$ of the series. The Variance Ratio, VR, at lag k therefore is defined as the ratio between (1/$k$)th of the k-period return (or the kth difference) to the variance of the first difference or k = 1 period return. Therefore, the variance of a random walk process calculated at each separate lag interval $\mathrm{k}$ ($k$ = 2, 3, …, n) should be equal to one. The null hypothesis, H₀, of RW is that the time series $y_t$ or its return or first difference $x_t=y_t-y_{t-1}$ is an iid (independent and identically distributed) process, or that $y_t$ follows a Martingale difference sequence.

According to Wright [71], the VR statistics is written as:

$$VR\left(x;k\right)=\frac{\left\{{\left(T·k\right)}^{-1}{{\displaystyle \sum }}_{t=k}^T{\left(x_t+\dots +x_{t-k+1}-k\widehat{\mu }\right)}^2\right\}}{\left\{T^{-1}{{\displaystyle \sum }}_{t=1}^T{\left(x_t-\widehat{\mu }\right)}^2\right\}}$$

(11)

where $\widehat{\mu }=T^{-1}{{\displaystyle \sum }}_{t=1}^T{x}_t$ and $T$ the sample size. Thus if the asset’s return follows a RW, the expected value (VR) should be equal to unity for all horizons k. However, in the case that VR < 1 at long periods then there exist a negative serial correlation (anti-persistence or mean reversion) while when VR > 1 at long horizons a positive serial correlation (persistence or mean-aversion).

Under the assumption of conditional heteroskedasticity and by assuming that k is fixed for T→∞, Lo and MacKinlay [67] suggest the asymptotic distribution of $VR\left(x;k\right)$. More specifically, under the null hypothesis that $VR\left(k\right)=1$, the test statistic $M\left(x;k\right)$ is as follows:

$$M\left(x;k\right)=\frac{VR\left(x;k\right)-1}{{\Phi }^{*}{\left(k\right)}^{\frac{1}{2}}}$$

(12)

which follows asymptotically the standard normal distribution, where:

$${\Phi }^{*}\left(k\right)={\displaystyle \sum }_{j=1}^{k-1}{\left[\frac{2\left(k-j\right)}{k}\right]}^2\delta \left(j\right)$$

(13)

$$\delta \left(j\right)=\frac{\left\{{{\displaystyle \sum }}_{t=j+1}^T{\left(x_t-\widehat{\mu }\right)}^2{\left(x_{t-j}-\widehat{\mu }\right)}^2\right\}}{\left\{{\left[{{\displaystyle \sum }}_{t=1}^T{\left(x_t-\widehat{\mu }\right)}^2\right]}^2\right\}}$$

(14)

The standard VR test of Lo and MacKinlay has a well-known problem, due to its asymptotic approximations (Actually, the finite-sample null distribution of the test statistic is quite asymmetric and non-normal, and can give rise to serious size distortions or low power, producing misleading inferences. When the sample is not large enough to justify asymptotic approximation then the problem is intense (Cecchetti et al., [72]), and therefore may generate fault statistical inferences. By using ranks, Wright [71] proposed an alternative to the “traditional” asymptotic VR tests which has advantages over the conventional approach when the sample size is relatively small. In particular, the rank-based tests proposed by Wright display low size distortion under conditional heteroskedasticity.

In this paper we perform the VR tests at α = 5% significance level. The test is two-tailed, so the test rejects the random walk null hypothesis when the test statistic $M\left(x;k\right)$ is outside the critical value interval. Each tail outside of this interval has probability α/2.

4.2.2. Variance Ratio Test, Volatility Clustering and Leverage Effect

The Variance Ratio test applied here assumes, as previously mentioned, the existence of conditional heteroskedasticity in the electricity prices of a quite general form, including deterministic changes in the variance due, for example, to seasonal factors, which in electricity markets are the main deterministic driving forces causing the seasonal dynamic component in the wholesale prices. Therefore, the type of time volatility (heteroskedasticity) of the electricity prices of the examined markets, namely symmetric, asymmetric is expected to have an impact on VR test. In the symmetric case both negative and positive shocks in the returns have the same effect on volatility. So, there is no leverage effect. In the asymmetric case (Black [73]), negative innovations to returns tend to increase volatility more than positive innovations of the same magnitude. This is called leverage effect. When positive innovations to returns tend to increase volatility, this is called inverse leverage effect. Models designed to capture the asymmetric volatility behavior are extensions of the traditional GARCH model (Bollerslev [74]), namely the exponential GARCH (EGARCH) (Nelson [75]) and the GJR-GARCH (Glosten et al. [76]). In the case of electricity markets, positive disturbances (or positive shocks in returns) have a stronger impact on volatility than negative ones, as shown in Knittels and Roberts [77] for prices in California.

The link between the volatility clustering effects (of symmetric or asymmetric type) and the VR test, at daily or lower frequencies was first attempted by Andersen et al. [78], where the proposed improved tools where used in order to account for the importance of linking VR test and volatility clustering in returns. This link has motivated us in this work, to relate the result of the VR test with the existence of leverage effect (or volatility clustering effect) in the electricity market we analyzed. Even though this linking is not quantitatively “proved” in our work but only qualitatively supported, we consider this very useful and informative in shedding light in this still “hot” issue and leaves the quantitative empirical analysis an open question for future research.

4.3. Entropy-Oriented Complexity Measures

In this section we present a short description of the Entropy-Oriented Measures used in this study.

4.3.1. Sample Entropy

According to information theory, entropy is considered as an “uncertainty measure” of a given system. High entropy corresponds to no information flow, thus characterizing a system as random, while low entropy corresponds to deterministic systems. The approximate entropy ($ApEn$) (Pincus, 1991 [9]), which is bounded, is derived as following:

• Let u be a time series $u\left(1\right),u\left(2\right),\dots ,u\left(N\right),$ of N observations. Given a non-negative number $m,m\le {\rm N}$, we formulate $m$-blocks of subsequences $x\left(i\right)\equiv \left(u\left(i\right),u\left(i+1\right),\dots ,u\left(i+m-1\right)\right)$
• The distance between 2 blocks can be calculated as:

  $$d\left(x\left(i\right),x\left(j\right)\right)\equiv \left(\left|u\left(i+k-1\right)-u\left(j+k-1\right)\right|\right)$$

  (15)

  which gives the maximum point-wise distance.
• Given $r\in R$, for a given block $x\left(i\right)$, we calculate the percentage of blocks $x\left(j\right)$ with distance $<r$, which we call $C_i^m\left(r\right)$.
• Using the Heaviside $\Theta$ function, which counts how many times the distance exceeds the given threshold $r$, we define:

  $$C_i^m\left(r\right)=\frac{1}{N-m+1}{\displaystyle \sum }_{j=1}^{N-m+1}\Theta \left(r-d\left(x\left(i\right),x\left(j\right)\right)\right)$$

  (16)

  $${\Phi }^m\left(r\right)=\frac{1}{N-m+1}{\displaystyle \sum }_{i=1}^{N-m+1}log{C}_i^m\left(r\right)$$

  (17)

Finally, $ApEn$ is defined as:

$$ApEn\left(m,r,N\right)\left(u\right)={\Phi }^m\left(r\right)-{\Phi }^{m+1}\left(r\right),m\ge 0$$

(18)

$$ApEn\left(0,r,N\right)\left(u\right)=-{\Phi }^1\left(r\right)$$

(19)

• $ApEn\left(m,r,N\right)$ is always a well-defined function. From (16) when a percentage of the block is <1, the distance from itself $d\left(x_i,x_i\right)$ is always measurable. It follows that, $C_i^m\left(r\right)\ge 1$ and consequently the logarithm of $C_i^m\left(r\right)$ is always defined.
• The $ApEn$ measures the degree to which, different segments of the series follow similar patterns.

  $$-ApEn\left(m,r,N\right)\left(u\right)={\Phi }^{m+1}\left(r\right)-{\Phi }^m\left(r\right)$$

  $$=\frac{1}{N-m}{\displaystyle \sum }_{i=1}^{N-m}log{C}_i^{m+1}\left(r\right)-\frac{1}{N-m+1}{\displaystyle \sum }_{i=1}^{N-m+1}log{C}_i^m\left(r\right)$$

  $$\approx \frac{1}{N-m}{\displaystyle \sum }_{i=1}^{N-m}\left(log{C}_i^{m+1}\left(r\right)-log{C}_i^m\left(r\right)\right)$$

  $$=\frac{1}{N-m}{\displaystyle \sum }_{i=1}^{N-m}log\left(\frac{C_i^{m+1}\left(r\right)}{C_i^m\left(r\right)}\right)$$

  (20)

The last line in (20), is the average logarithm, for all m-blocks, of the conditional probability $\left|u\left(j+m\right)-u\left(i+m\right)\right|<r$ given $\left|u\left(j+k\right)-u\left(i+k\right)\right|<r$ for all $k=0,1,\dots ,m-1$, thus the approximate entropy estimates the logarithmic probability that sequences of patterns which are close for $m$ observations, will remain close. In this sense, the $ApEn$ measures persistence, correlation and regularity. Higher values indicate lower persistence and independence between the observations, while lower values of approximate entropy corresponds to higher persistence, autocorrelation and regularity. If $C_i^{m+1}\left(r\right)=C_i^m\left(r\right)$, the approximate entropy is 0, which corresponds to weak serial correlation.

Another useful form of the ApEn comes from (20), for $m=1$, so ApEn $\left(m=1,r,N\right)$ can be considered to be the expected log-likelihood value of two block that remain close to each other, when they are expanded by one data point. Assuming stationarity of the stochastic process, the number of steps in calculating ApEn $\left(m=1,r,N\right)$ is significantly reduced as follows:

$$\begin{array}{ll}ApEn\left(1,r,N\right)\left(u\right)& ={\Phi }^1-{\Phi }^2=\frac{1}{N-1}{\displaystyle {\displaystyle \sum }_{i=1}^{N-1}}log\left(\frac{C_i^2\left(r\right)}{C_i^1\left(r\right)}\right)\\ & =-E\left(log\left(\frac{C_i^2\left(r\right)}{C_i^1\left(r\right)}\right)\right),\left(=forN\to \infty \right)\end{array}$$

(21)

The threshold $r$ can be seen as the parameter which differentiates the measured distances (as stated by Takens), while the embedding dimension $m$ is the number of adjacent points. Thus $ApEn$ measures the degree of which different segment of the time series follow similar patterns. For a random process, $ApEn\to log\left(\frac{r}{\sqrt{3}}\right)$ for all $m$ (Pincus, 1991 [9]), while for a purely deterministic process $ApEn\to 0$. We can therefore rescale so that $0\le ApEn\le 1$, where 1 defines a purely random process which is the characteristic of an efficient market.

Now, we are ready to introduce the Sample Entropy (SaEn), which is a modification of the ApEn that has been recently proposed (Richman. et al. [10]), which has the advantage of being less dependent on the length of the time series and that exhibits relative consistency over a broader range of possible $r.m\mathrm{and}N$. On the base of K₂ entropy, Richman and Moorman defined the parameter:

$$SaEn\left(m,r\right)=\left(-log\frac{U^{m+1}\left(r\right)}{U^m\left(r\right)}\right)$$

(22)

which is estimated by the statistic:

$$SaEn\left(m,r,N\right)=-log\frac{U^{m+1}\left(r\right)}{U^m\left(r\right)},N\to \infty$$

(23)

The differences between the previously defined $C^{m+1}\left(r\right)$ and $U^{m+1}\left(r\right)$ (similarly between $C^m\left(r\right)$ and $U^m\left(r\right)$), are due to (a) defining the distance between two vectors as the maximum absolute difference between their components, (b) vectors are not compared to themselves and finally (c) for a time series of length N, only the first N-m vectors of length m, $U_m\left(i\right)$, are considered by taking care of defining also the vector $U_{m+1}\left(i\right)$ of length m+1, when $1\le i\le N-m$. SaEn is exactly equal to the negative of the natural logarithm of conditional probability that m data sequences that are very close in proximity will remain also close to each other when on more point is added to the sequence. A detail algorithm for calculating SaEn is given in Costa et al. [11]. Now let $n_i^m\left(r\right)$ represent the number of vectors $x_m\left(j\right)$ that are close to the vector $x_m\left(i\right)$ i.e., the number of vectors that satisfy $d\left(x\left(i\right),x\left(j\right)\right)\le r,$ where $d$ is the distance. Then we note that:

$$ApEn\left(m,r,N\right)\cong \frac{1}{N-m}{\displaystyle \sum }_{i=1}^{N-m}log\frac{n_i^m}{n_i^{m+1}}$$

(24)

and:

$$SaEn\left(m,r,N\right)=log\frac{{{\displaystyle \sum }}_{i=1}^{N-m}{n}_i^{\prime m}}{{{\displaystyle \sum }}_{i=1}^{N-m}{n}_i^{\prime m+1}}$$

(25)

where $n_i^{\prime m}$ differs from $n_i^m$ to the extent that for SaEn self-matches are not counted $\left(i\ne j\right)$ and $1\le i\le N-m$.

A smaller value of sample entropy indicates less level of complexity or more self-similarity in a data series. SaEn is largely independent of record length and display relative consistency under circumstances where ApEn does not (Richman et al. [10]). The ApEn approximates the Renyi entropy of order $q=1$ (corresponding to Shannon entropy) and SaEn the Renyi entropy for $q=2$. The SaEn has the advantage that it is unbiased estimator (Grassberger et al. [4]).

4.3.2. Multiscale Entropy (MSE) Approach

Let $\left\{x_1,\dots ,x_i,\dots ,x_n\right\}$ be an one dimensional discrete time series from which a consecutive coarse-grained time series $\left\{y^{\tau }\right\}$ is constructed, where $\tau$ is the scale factor. In order to do so, first the original time series is divided into non-overlapping windows of length $\tau$. Then, the average of data points inside each window is taken. Therefore, in general, the following equation gives each element of a coarse-grained time series:

$$y_j^{\left(\tau \right)}=\frac{1}{\tau }{\displaystyle \sum }_{i=\left(j-1\right)\tau +1}^{j\tau }{x}_i,1\le j\le \frac{N}{\tau }$$

(26)

For $\tau =1$, scale one, we obtain the original time series. Each coarse-grained time series has a length equal to that of the original time series divided by the scale factor. The final stage in the construction is the calculation of the sample entropy $S_E$ for each coarse-grained series plotted as a function of $\tau$. This process is called multiscale entropy (MSE) (Costa et al. [11]). In case we have a set of normalized time series (having the same variance for scale $\tau =1$), we can use MSE to compare their complexity, according to the following guidelines: (a) a time series A is considered more complex than B if for the majority of scales the entropy values of A are higher than B. (b) The original signal contains information only in the smallest scale when there is a monotonic decrease of the entropy values.

4.4. Fractal Dimension

The existence of a correlation structure and the global dependence property in a time series are reflected by its long-term memory behavior. Local memory in a time series, instead, which is a measure of its roughness, is captured by the fractal dimension. The degree of roughness or smoothness of a time series varies with time, and different parts of the series may have completely difference smoothness appearance. The fractal dimension component of the proposed in this work Electricity Market Efficiency Index (EMEI) is given by the estimators Hall-Wood and Genton (Gneiting et al. [79]), as well as the traditional Box-counting. Finally, we use the mean value of the three estimators, in a similar way as the Hurst exponent.

The Hall-Wood estimator (Hall and Wood [80]) is an improvement of the traditional box-counting procedure using scaling of absolute deviations between steps. Let $X\subset {ℝ}^d$ the graph of a time series. The generic box-count dimension is given by:

$$D_{BC}=\underset{\epsilon \to 0}{\lim }\frac{\log N\left(\epsilon \right)}{\log \left(\frac{1}{\epsilon }\right)}$$

(27)

where $N\left(\epsilon \right)$ denotes the smallest number of cubes of width $\epsilon$ in ${ℝ}^d$ which can cover $X$. The above box-count estimator uses the slope in an ordinary least squares regression fit of $\log N\left(\epsilon \right)$ on $\log \epsilon$. The Hall and Wood introduced a version of the above estimator that operates at the smallest observed scales and avoids the need for rules of thumb in implementing it. Actually, their proposed variant of the naïve $D_{BC}$ uses scale ${\epsilon }_l=\raisebox{1ex}{$l$}\!\left/ \!\raisebox{-1ex}{$n$}\right.$, where l an integer number and $n$ the sample size of the time series. Let $A\left(\epsilon \right)$ is the total area of the boxes at scale $\epsilon$ that intersect with the linearly interpolated time series graph. There are $N\left(\epsilon \right)$ such boxes, therefore $A\left(\epsilon \right)\propto N\left(\epsilon \right){\epsilon }^2$ which finally results to an alternative definition of $D_{BC}$, namely:

$$D_{BC}=2-\underset{\epsilon \to 0}{\lim }\frac{\log A\left(\epsilon \right)}{\log \left(\epsilon \right)}$$

(28)

At scale ${\epsilon }_l=\raisebox{1ex}{$l$}\!\left/ \!\raisebox{-1ex}{$n$}\right.$, where $l=1,2,\dots$, an estimator of $A\left(\raisebox{1ex}{$l$}\!\left/ \!\raisebox{-1ex}{$n$}\right.\right)$ is:

$$\widehat{A\left(\frac{l}{n}\right)}=\left[\frac{l}{n}\right]{\displaystyle \sum }_{i=1}^{\left[\frac{l}{n}\right]}\left|x_{i\left[\frac{l}{n}\right]}-x_{\left(i-1\right)\left[\frac{l}{n}\right]}\right|$$

(29)

where $\left[\raisebox{1ex}{$l$}\!\left/ \!\raisebox{-1ex}{$n$}\right.\right]$ denotes the integer part of $\raisebox{1ex}{$l$}\!\left/ \!\raisebox{-1ex}{$n$}\right.$. The quantity in (28) approximates $A\left(\raisebox{1ex}{$l$}\!\left/ \!\raisebox{-1ex}{$n$}\right.\right)$ with all features at scales less than $\raisebox{1ex}{$l$}\!\left/ \!\raisebox{-1ex}{$n$}\right.$ being ignored. Using the definition of fractal dimension, the estimator becomes:

$$\widehat{D_{HN}}=2-\frac{{{\displaystyle \sum }}_{l=1}^L{S}_l-\underset{\_}{S}log\left(\widehat{A\frac{l}{n}}\right)}{{{\displaystyle \sum }}_{l=1}^L{\left(S_l-\underset{\_}{S}\right)}^2}$$

(30)

where $L\ge 2,S_l=log\left(\frac{l}{n}\right)and\underset{\_}{S}=\frac{1}{L}{\displaystyle \sum }_{l=1}^L{S}_l$.

Using $L=2$ the potential bias is minimized, so the final estimate of the fractal dimension $\widehat{D_{HN}}$ is given by:

$$\widehat{D_{HN}}=2-\frac{log\widehat{A\left(\frac{2}{n}\right)}-log\widehat{A\left(\frac{1}{n}\right)}}{2log2}$$

(31)

Using the robust variogram of Genton (Genton [81]), Gneiting and Schlather [82] and Gneiting et al. [79], propose a moment estimator, based on the variogram, defined as:

$$\widehat{V_2\left(\frac{l}{n}\right)}=\frac{1}{2\left(n-l\right)}{\displaystyle \sum }_{i=l}^n{\left(x_{\frac{i}{n}}-x_{\frac{\left(i-l\right)l}{n}}\right)}^2$$

(32)

Thus, the estimator of Genton is given by:

$$\widehat{D_G}=2-\frac{log{{\displaystyle \sum }}_{l=1}^L\left(S_l-\underset{\_}{S}\right)log\left(\widehat{V_2\left(\frac{l}{n}\right)}\right)}{2{{\displaystyle \sum }}_{l=1}^L{\left(S_l-\underset{\_}{S}\right)}^2}$$

(33)

where $L\ge 2,S_l=log\frac{l}{n}and\underset{\_}{S}=\frac{1}{L}{{\displaystyle \sum }}_{l=1}^L{S}_l$.

For reducing the potential bias, Davies and Hall [83], Zhu and Stein [84] suggest $L=2$, thus the estimator $\widehat{D_G}$ is written:

$$\widehat{D_G}=2-\frac{log\widehat{V_2\left(\frac{2}{n}\right)}-log\widehat{V_2\left(\frac{1}{n}\right)}}{2log2}$$

(34)

As it is mentioned before, fractal dimension $D_F$ is a measure of roughness on ℝⁿ⁺¹ for n-dimensional series. For a random series, $D_F=1.5$. In real markets short-term phenomena cannot captured by its global behavior because these short-term episodes are quickly disappeared. However, these short-term dynamics change the degree of roughness of the time series, resulting in a deviation of $D_F$ from the random “benchmark” 1.5 of an efficient market. If a market is characterized by short-term trends (local persistence), then $D_F<1.5$, since the surface of time series becomes smoother. Instead, if the market is dominated by short-term bursts of volatility (volatility clusters), then the market is mean-reverting or local anti-persistence with $D_F>1.5$ since the time series is more coarsened. A combination of both behaviors can exist in a market.

4.5. The Herfindahl-Hirschman Index of Concentration (HHI)

Finally, we have utilized in this paper one of the most widely applied measure of market concentration called the Herfindahl-Hirschman Index of concentration, or HHI (Hirschman [85]; Herfindahl [86]). This Index belongs to a family of indices that also includes the Rosenbluth Index (Rosenbluth [87]) and the Entropy Index (Jacquemin [88]). The HHI has become an ingredient in constructing some more complex indices for particular types of markets such as an oligopolistic market (Cabral [89]). Depending on the firm size distribution, the simulation of HHI is based on three types of specifications, the arithmetic progression, the linear function and a group of non-linear specifications in which the firm size is a function of the firm rank. In this paper we consider the case that the firm market shares form a linear function, leaving the consideration of a nonlinear functional for a later research. The most recent application of HHI in Power Systems, to the best of the Authors’ knowledge, is the work of Sahni et al. [12]. They utilized the HHI within a probabilistic framework to arrive at a parametric trend indicating the possible market power in a given Power Market. We have taken advantage of the results of the paper of Sahni et al. [12] in order to examine the consistency of the HHI index results for the market efficiency with the results from the other measures.

The Index has been adopted in USA as a measure of market concentration (United States Department of Justice, link: http://www.justice.gov/atr/public/guidelines/hhi.html). If HHI = 10,000 (upper limit) the market is considered a monopoly, while for HHI > 5000 the market is over-concentrated, for H > 1800 concentrated, for 1000 < HHI < 1800 efficiently or moderately competitive and finally for HHI ≤ 1000 the market is low concentrated or competitive. The Index is calculated as follows:

$$HHI={\displaystyle \sum }_{i=1}^n{s}_i^2$$

(35)

where $s_i$ is the ith firm’s (or generator’s) percent or share of the market, or:

$$HH{I}_n=\mathrm{10,000}\times {\displaystyle \sum }_{i=1}^n{s}_i^2(\%)$$

(36)

If there is one participant or a monopoly in the industry, its market share is 100%. Its $s=100,\mathrm{and}HHI={100}^2=10000.$ If there are two equal-sized firms in the industry, then market share is one-half or 50% each, and $HHI={50}^2+{50}^2=5000$.

Perfect competition is represented by a large number of firms with small shares, as follows:

$$HHI={\displaystyle \sum }_{i=1}^n{s}_i=0$$

(37)

That is, the closer to zero expected competition, and the closer to 10,000, the more expected market power. Sometimes it is used to measure share, and then the measure falls between 0 and 1.

5. Data Description and Results

5.1. Overview of Time Series Data

We have collected data on the Italian, Greek, Iberian and NordPool electricity markets. The data consists of daily spot prices, spanning over the course of nine years, from January 2005 to December 2013. The daily prices were calculated as the average of the 24 hourly prices for each day. For the Italian market we have the hourly day-ahead system marginal price, so-called Prezzo Unico Nazionale, or PUN, publicly available on the Italian Power Exchange IPEX website (www.mercatoelettrico.org). For the Greek market the hourly spot, day-ahead System wide Marginal Price, SMP, is available at the official site of the Greek Independent Power Transmission Operator, IPTO, ADMIE S.A. (www.admie.gr). For the Spanish Market, the spot price, called daily Spanish Electricity (SPEL) base index, was extracted from the OMIP web page (www.omip.pt). For the Nord Pool we used the ELSPOT Day-ahead prices extracted from the site www.nordpoolgroup.com/Market-data1/Dayahead/.

5.2. Metrics Calculation

In this section, we calculate the different indicators, which are incorporated in the proposed EMEI and analyzed in Section 4, for the daily spot price time series of the four aforementioned countries.

5.2.1. The Hurst Exponent

We start by calculating the Hurst exponent estimations on the returns of the prices of each market. Calculations for the Hurst exponent based on Equation (5) of the DFA approach, R/S method, GHE technique and the mean value of the DFA approach and R/S method are shown in

Table 3. Estimation of Hurst Exponent for Electricity (SMP, PUN, SPEL, ELSPOT) and financial markets (Greece, Italy and Spain).

Time Series (Returns)	Hurst Exponent’s Estimation Method				Mean of 1st and 2nd Columns
	R/S (AL)	DFA	GHE
			H(1)	H(2)
A. Electricity Market
SMP	0.214	0.152	0.169	0.149	0.183
PUN	0.243	0.106	0.105	0.085	0.175
SPEL	0.343	0.238	0.174	0.164	0.291
ELSPOT	0.390	0.331	0.301	0.243	0.361
B. Financial Market
ASE	0.605	0.650	0.556	0.542	0.628
FTMIB	0.530	0.541	0.494	0.467	0.536

. For comparison purposes we provide also results of Hurst exponent estimations for the General Index of the financial markets of Greece (ASE) and Italy (FTMIB). It is apparent that all wholesale prices are generated by anti-persistent, mean-reverting processes far away from the Random Walk or Geometric Brownian Motion for which H = 0.5.

Indicatively, the results for the Greek market in the DFA approach are graphically represented in Figure 1. As it can be easily observed, the slope of the Hurst exponent line presented significantly deviates from the theoretical line with a slope of 0.5, hence according to the weak form of RWH it is characterized as inefficient. To further verify our results, Figure 2 depicts the power spectrum of SMP returns. One can easily determine the DFA index α from the power spectral index β. In particular, the Greek market has β = 1.30, while by adopting (10), the DFA index α for the Greek market is found to be 1.15. The derived indices suggest that the examined market is inefficient, a conclusion which is consistent with the other Hurst exponent estimations results.

5.2.2. Variance Test

Next we proceed in presenting the results of the VRT.

Table 4. Variance ratio tests for lags 2, 4, 8, 16 and 32 (for testing RW3 hypothesis).

Market	Statistics	Period (in Days) Used for Overlapping Return Horizons					Mean VR
		K = 2	K = 4	K = 8	K = 16	K = 32
SMP	VR(K)	0.689	0.433	0.244	0.145	0.084	0.319
	p Value	0.000	0.000	0.000	0.000	0.000
	Stat(M)	−11.978 ***	−12.286 ***	−10.94 ***	−8.653 ***	−6.648 ***
PUN	VR(K)	0.824	0.473	0.184	0.138	0.078	0.339
	p Value	0.000	0.000	0.000	0.000	0.000
	Stat(M)	−8.644 ***	−13.781 ***	−14.02 ***	−9.877 ***	−7.378 ***
SPEL	VR(K)	0.844	0.501	0.273	0.198	0.116	0.386
	p Value	0.000	0.000	0.000	0.000	0.000
	Stat(M)	−6.519 ***	−11.104 ***	−10.237 ***	−7.69 ***	−6.014 ***
NordPool (ELSPOT)	VR(K)	0.936	0.633	0.381	0.327	0.260	0.507
	p Value	0.1996	0.0001	0.000	0.0002	0.0008
	Stat(M)	−1.282	−3.850 ***	−4.457 ***	−3.737 ***	−3.34 ***
ASE (GREECE)	VR(K)	1.065	1.091	1.136	1.208	1.408	1.182
	p Value	0.0267	0.118	0.152	0.136	0.035
	Stat(M)	2.216 **	1.559	1.429	1.487	2.099 **
FTMIB (ITALY)	VR(K)	0.950	0.906	0.861	0.858	0.941	0.903
	p Value	0.063	0.070	0.098	0.255	0.738
	Stat(M)	−1.873 *	−1.810 *	−1.650 *	−1.138	−0.334

Notes: VR(K): Variance Ratio estimate. Stat(M): Test Statistic M in the text asymptomatically standard normal, and under the assumption of conditional heteroskedasticity. ***, **, * indicate significance at the 10, 5 and 1% respectively, according to the test p-value.

shows the results of VRT for testing the weak form of RW hypothesis for the four electricity markets, as well as for the financial markets of Greece and Italy. The VRT is calculated for lags k = 2 to k = 32 by adopting (11) and (12), while the final column contains the mean value of the tests. As we observe, the null hypothesis of RW process is rejected for all electricity markets, while for the financial markets the null hypothesis of RW is accepted as expected. A very interesting and consistent with the results given by Hurst exponent test, is that for all electricity markets it holds VR < 1 which indicates that the returns exhibit negative serial correlation or anti-persistence or mean reversion behavior. In opposite, all financial returns are very close to one, as it is expected.

5.2.3. Entropy Oriented Measures

Firstly, we proceed in presenting results regarding the estimation of the sample entropy based on Equation (25) for the price returns of all markets analyzed in this paper. The results are shown in

Table 5. Calculation of Sample Entropy for electricity markets compared with financial market.

Returns	Market	Sample Entropy (m = 2, r = 0.20 × SD)
SMP	Greek	1.83
PUN	Italian	1.80
SPEL	Spanish	1.76
ELSPOT	Nord Pool	1.69
Athens Stock Exchange (ASE)	(Greek)	2.14
FTMIB	(Italian)	2.21

. The larger the value of the entropy the closer to the random walk process is the price return process of each market.

In the sequel, in order to detect different volatility regimes in the time series of returns the SaEn as described by (25) is applied in a rolling framework. We use the improved and unbiased SaEn on a rolling base (with an annual window of 365 days), on the price returns of the all markets analyzed in this paper. It is noted, that the choice of selecting a rolling window of one year provides high resolution capabilities and enables the accurate representation of the Entropy metric.

Specifically, we start with the Nord Pool market. As presented in Figure 3, the Sample Entropy curve, reveals several ups and downs which correspond to higher uncertainty and lower complexity respectively. This practically means that the Nord Pool market presented both periods of higher efficiency and of lower complexity over the course of the considered years in our sample. Similarly, the Spanish electricity market displays also several ups and downs in the Sample Entropy curve. More specifically, after the year 2010 an abrupt decrease in rolling sample entropy is observed, while after the year 2013 a U shape of the rolling sample entropy captures completely the dynamics of the volatility in this period, up to early months of 2014 (Figure 4). Concerning the Greek and the Italian market, one can observe from Figure 5 and Figure 6 that there is an upward trend in the value of the Rolling SaEn for both the SMP and PUN. This can be explained by the fact that both countries, namely Greece and Italy, promote the liberalization and deregulation of their electricity markets which gradually increases the degree of the market structural complexity. However, a sag in the Rolling SaEn of SMP during the year 2006 can be observed in Figure 5, indicating that the market has become less complex in this period.

Additionally, the multiscale entropy over 30 scales, calculated based on equation (26), is shown in Figure 7 below together with a white noise and a 1/f flicker signal. As it can be seen, all series differ significantly from the white noise signal, Specifically, SMP, PUN and SPEL market prices form a cluster, with NordPool prices being closer to white noise. Based on the multiscale entropy analysis, we can conclude that the NordPool market is more efficient than the other markets, although qualitatively all the markets are considered to be inefficient and differ significantly from the white noise benchmark. Moreover, over total of 30 scales, the NordPool’s SaEn Curve is higher than the same curve of the other markets, for 22 scales, therefore the NordPool Spot price is considered to be the most complex time series, indicating the efficiency superiority of this market over the others (Costa et al. [11]).

5.2.4. Fractal Component

The fractal dimension is calculated based on expressions (28), (31) and (34) and their mean value is also computed. The results are presented in

Table 6. Fractal Dimension of wholesale prices calculated by three estimators.

Estimator of Fractal Dimension	SMP	PUN	SPEL	NordPool
Boxcount	1.666	1.649	1.572	1.412
Genton Estimator	1.679	1.469	1.578	1.324
Hall-Wood Estimator	1.698	1.544	1.578	1.447
Mean value	1.681	1.554	1.576	1.394

. We observe that a fractal dimension above 1.5 which indicates anti-persistence, is characteristic for SMP, PUN and SPEL returns, while for NordPool is below 1.5 which indicate local persistence. The market which is closer to the fractal dimension of 1.5 is the Italian one, showing the less degree of local inefficiency, followed by SPEL and NordPool. The most inefficient market, based on this measure, is the Greek market having a D_F with the largest deviation from 1.5. Another interesting characteristic is also that all markets exhibit higher complexity in small time scales.

5.2.5. Herfindahl-Hirschman Index

Table 7. Herfindahl-Hirschman Index (HHI) in Power Generation ‘’market’’ of the analyzed electricity markets for 2005–2013 as appeared in the National reports of Regulators sent to EC.

Year	HHI (Greek Market)	HHI (Italian Market)	HHI (Spanish Market)	HHI (NordPool-Mean Value)
2005	9409 (vhc *)	1900 (hc *)	2520 (hc *)	1781 (mc *)
2006	8905 (vhc *)	1643 (mc *)	2450 (hc *)
2007	8390 (vhc *)	1440 (mc *)	2325 (hc *)
2008	8390 (vhc *)	1380 (mc *)	1789 (mc *)
2009	8427 (vhc *)	1280 (mc *)	1403 (mc *)	1767 (mc *)
2010	6844 (vhc *)	1097 (mc *)	1262 (mc *)
2011	5746 (vhc *)	953 (d *)	1432 (mc *)	1524 (mc *)
2012	6983 (vhc *)	884 (d *)	1329 (mc *)	1432 (mc *)
2013	6553 (vhc *)	830 (d *)	1300 (mc *)	1382 (mc *)
MEAN VALUE (2005–2013)	7739 (vhc *)	1267 (mc *)	1757 (mc *)	1577 (mc *)

* Legend (according to European Commission 2014): vhc = very high concentration (HHI > 5000). hc = high concentration (1800 < HHI < 5000). mc = moderate concentration (1000 < HHI < 1800). d = deconcentration (HHI < 1000).

provides information on the “degree” of competition in the generation “market” of the electricity markets under consideration measured by the HHI index based on Equation (35). We observe that the Greek market for the entire period 2005–2013 is a very high concentrated market (HHI > 5000). The Italian market was a highly concentrated market (HHI > 1800) only in 2005 and moderately concentrated from 2006 to 2010 (1000 < HHI < 18,000) and a deconcentrated or competitive market from 2011 to 2013 (HHI < 1000), a significant improvement. The Spanish market was a highly concentrated market for 2005 to 2007 and moderately concentrated from 2008–2013, while the NordPool market is moderately concentrated for the whole period of examination. Thus, the least competitive market, according to this index, is the Greek market. Additionally, we can observe that concentration levels for Italy and Greece have decreased, but the Italian market at the start of the period of analysis 2005, was a medium concentration market, while the Greek market was close to the monopoly top limit. However, the Greek market, even with a very slow rate, gradually becomes less and less concentrated with the lowest HHI index value in 2011. However, it still remains a highly concentrated generation market. In the opposite direction, the Italian market decreased the level of concentration very fast and since 2007 went beyond the 1500 “threshold”.

6. The Proposed Composite Electricity Market Efficiency Index (EMEI)

One can easily conclude that it is difficult to evaluate the efficiency of an electricity market by examining separately the various metrics. On top of that, considering only one or even two indices could result in misleading results for the market efficiency evaluation. Therefore, there is a need for a composite metric that integrates effectively all the characteristics of the previously described measures which capture different aspects of the volatility dynamics. Furthermore, the proposed index also considers the important information regarding the market concentration.

For the reader convenience, in

Table 8. Values of the components of the proposed composite Efficiency Measure for Electricity Markets as well as for financial markets, for comparison.

Measure, Mi	Electricity Markets				Financial Markets
	SMP	PUN	SPEL	NordPool	ASE	FTMIB
Hurst Exponent (mean)	0.183	0.175	0.291	0.361	0.628	0.536
Fractal Dimension DF (mean)	1.681	1.554	1.576	1.394	1.353	1.427
Sample Entropy	1.830	1.800	1.760	1.690	2.140	2.210
VRT (mean)	0.319	0.339	0.386	0.507	1.182	0.903
HHI (mean of period considered)	7739	1267	1757	1577	-	-

we show the results of the estimated components of the proposed composite index, as calculated in the previous Section, for both electricity and financial markets for the purpose of comparison. Specifically, the Hurst Exponent value is calculated as the mean value of only the R/S and the DFA methods as seen in Table 3, without considering the values derived via the GHE approach which is generally less robust and more susceptible to noise. The mean value of the Fractal Dimension represents the average of all three estimators given in Table 6. Additionally, the sample entropy value is taken as presented in Table 5, while the mean value of the VRT metric is adopted as in the last column of Table 4. Finally, the average HHI metric value is calculated with respect to the time period considered.

Based on the measures in Table 8 and utilizing Equation (1) the composite EMEI for each market is calculated and displayed in Figure 8. Given the fact that lower values of this index are consistent with efficient markets, while higher values of it suggest market irregularities, it is evident that the NordPool market is found to be the most efficient. The Spanish market (SPEL) and the Italian market (PUN) follow close by in that order. On the other hand, the most noticeable difference is observed by examining the Greek market (SMP) in relation with the other three ones, where apparently, the Greek market is considered by far as the most inefficient.

Although the EMEI can adequately characterize the efficiency of each market, an important aspect of this classification is the level of contribution of every included metric in the composite index EMEI. Figure 9 displays this contribution for each market included in the analysis, by considering the complementary of every metric (which actually describes inefficiency as we obtained the deviation from one) and represented as a percentage. One can easily establish that the highly contributing metric is definitely the VRT for all markets. For the case of Greece due to the fact that it has a highly concentrated market, the HHI value also plays a significant part in the SMP efficiency characterization. Also, the Hurst Exponent seems to gain more significant value in the total percentage of inefficiency as the markets become less efficient with the exception of the Greek Market. According to Table 8, the Variance Ratio Test metrics indicate a certain rank in the efficiency as NordPool, SPEL, PUN and SMP in that specific order. This result could possibly be interpreted by the fact that NordPool market is characterized by inverse leverage effect, while the Spanish and Italian markets exhibit also the properties of leverage effect (Papaioannou et al. [18]; Gianfreda [90]). On the other hand, the Greek market shows no signs of leverage effect at all and is regarded as the least efficient one. However, the Fractal Dimension and the Sample Entropy measures indicate a different order in the market efficiency as the Italian market ranks as the most efficient one, followed by the Spanish and the NordPool and finally the Greek as the least efficient one. This fact actually showcases the significance of the proposed complex metric in the process of market efficiency evaluation, as each individual metric looks into the market efficiency from different perspective and presents certain unique characteristics, which are “summed up” and accurately represented by the EMEI. Another important remark that derives from the conducted study is that the inclusion of several indices in the composite EMEI metric leads to a robust and accurate EMH analysis. As one might expect, a consideration of only one or even two indices could be misleading in some cases of market efficiency estimation process. For example, by examining only the Sample Entropy, the SMP of the Greek market can be compared to the most efficient ones, like NordPool or SPEL markets, which of course is not the case in reality.

7. Conclusions

We have analyzed and measured the market efficiencies among four different electricity markets, of various maturity levels and structural organization, namely the emerging and “less” developed Greek electricity market, the well-developed Spanish and Italian markets and the most developed and well-establish NordPool market.

For the efficiency measurement a Composite Electricity Market Efficiency Index, that uses a variety of complementary measures, such as linear and nonlinear, is proposed. Based on the EMEI a detailed and rigorous efficiency analysis is carried out for the above mentioned wholesale electricity markets. This analysis effectively provides a reliable complexity measure of the aforementioned markets and presents a comprehensive assessment of their efficiency. The key findings of this work has shown that overall the four markets are inefficient based on the weak form of EMH and that the most efficient one, based on our new proposed EMEI efficiency index is the NordPool market, closely followed by the Spanish market, with the Italian being third. The least efficient market detected is the Greek market. Therefore, the introduced so far policies and guidelines, according to EU electricity Directives, to help power market to move closer to an efficient state of operation regarding price formation mechanism, have not fully achieved their goals. The level of deviation of the behavior of these markets from the weak form of EMH as measured by EMEI is an important finding since aspiring investors in these markets can assess each market’s inefficiency associated with the existence of predictability and its asymmetric information effects. So, EMEI quantifies, so to speak, the concerns of various market participants about the suitability of each market for investing opportunities. Therefore, we believe that our work can contribute toward designing better policies for enhancing electricity market efficiency, since by measuring more accurately the level of discrepancies of main constituents of efficiency from the weak form of EMH, these policies can be more effective in improving for example pricing transparency and level of liquidity, two characteristics that can be monitored by different constituents of the EMEI.

Another important finding is that that market’s idiosyncrasies play a vital role in their efficiency level. For example, in the Greek market there is currently no forward, intraday or separate balancing market operating. This results in an electricity market that is organized around a mandatory pool system with an ex post price settlement. Moreover, there are no possibilities for market interactions outside the pool and forward products trading. All these factors may have limited the efficiency of the Greek Market. In Italy on the other hand, there exists the MGP, MI, MSD and MTE which are complementary markets to each other, reinforcing in this way the liquidity of the market and also creating a more competitive market structure. This may explain why the Italian market is more efficient than the Greek one. In Spain, as mentioned before, the spot market is composed of the intra-day and day-ahead market and there is also the possibility to trade futures, options, swaps and forward contracts. This enhances the completeness of the market, while creating competitive advantages and more liquidity. These characteristics as expected result in EMEI with lower value that represent a more efficient market. Finally, the Nordic electricity market, which consists from a physical, financial and emission market, not only includes all the aforementioned characteristics but exhibits the features of liquidity, transparency, growth and diversity, as well. The latter features further increase the complexity of the market, therefore explaining why the Nordic electricity market is the most efficient market from all the four and why EMEI displays the lowest value.

The fact that EMEI “captures” the market idiosyncrasies pretty well, as the results have revealed, enhances the usefulness of this index in taking into consideration the uniqueness of each country’s electricity market in designing better policies, directives and guidelines, in order to enhance the efficiency of these markets. The moto “you cannot manage something that you can’t measure” it seems to fit well in this case. EMEI could be a very useful and strong measuring tool of the level of inefficiency of an electricity market.