Diesel Engine Valve Clearance Fault Diagnosis Based on Improved Variational Mode Decomposition and Bispectrum
Abstract
1. Introduction
2. Methodology
2.1. VMD
2.1.1. The Theory of the VMD Algorithm
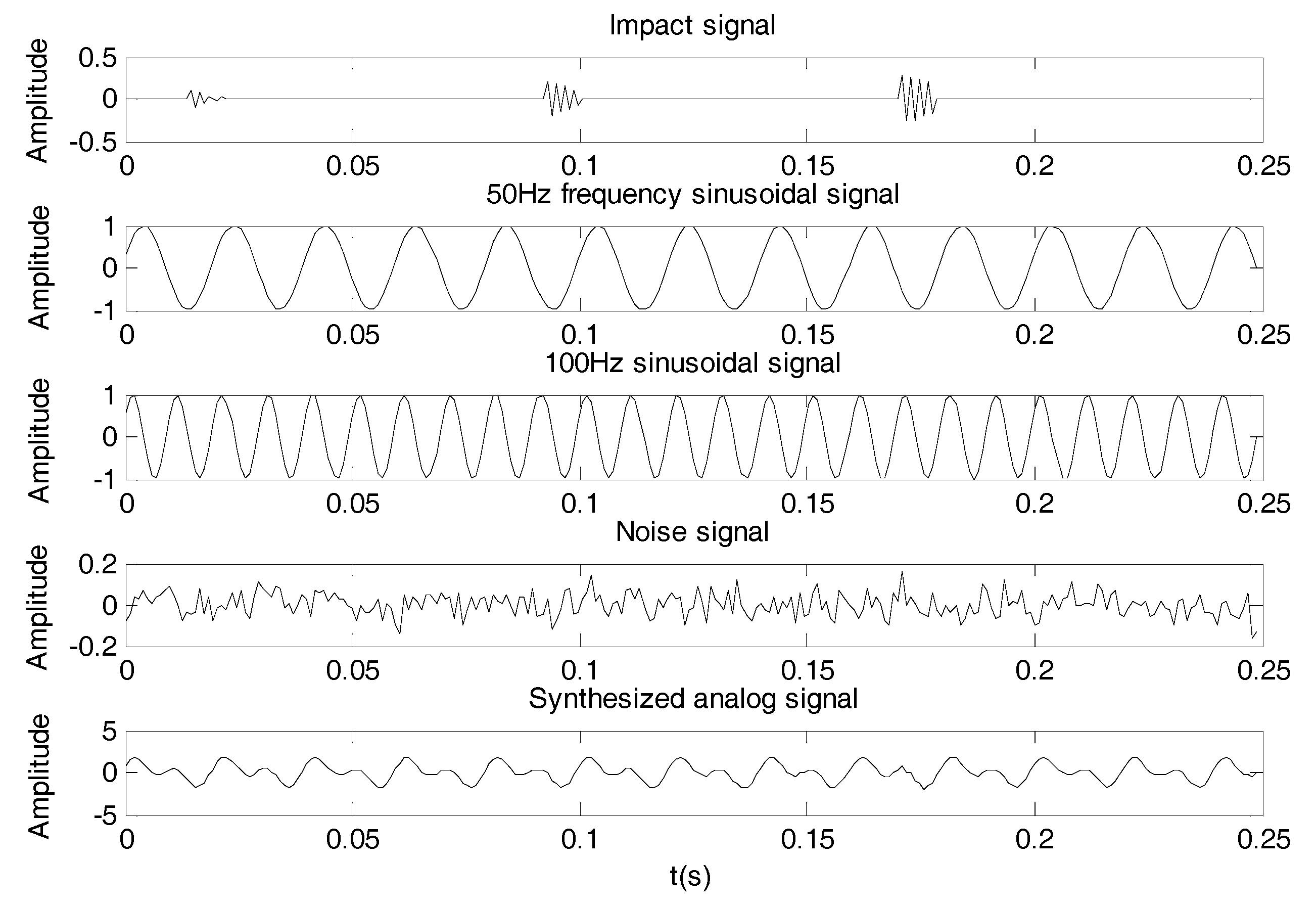
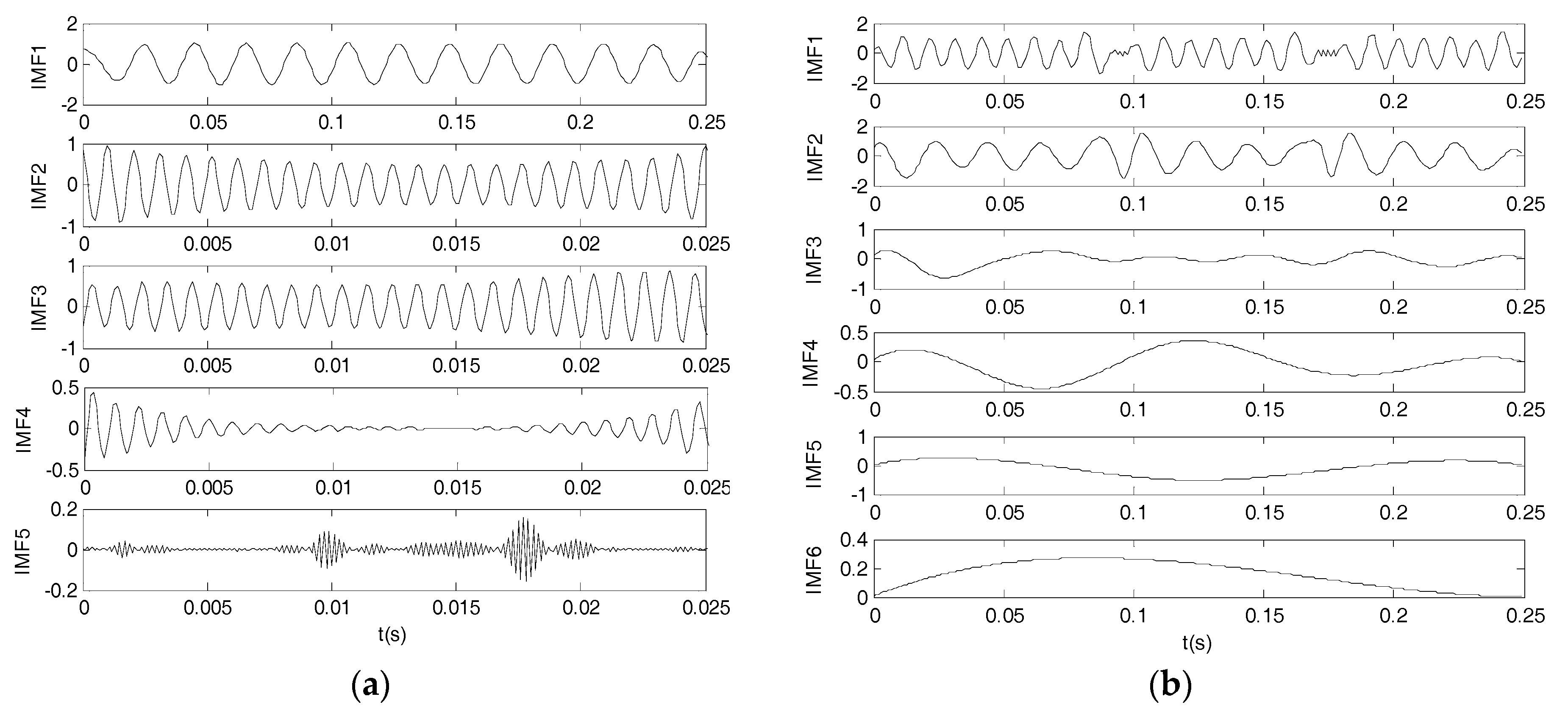
2.1.2. Verification of VMD Algorithm
2.2. Bispectrum
2.2.1. The Definition of Bispectrum
2.2.2. Bispectrum Calculation
2.2.3. Bispectrum Slice
3. Engine Test Program and Experimental Data Acquisition
4. Results
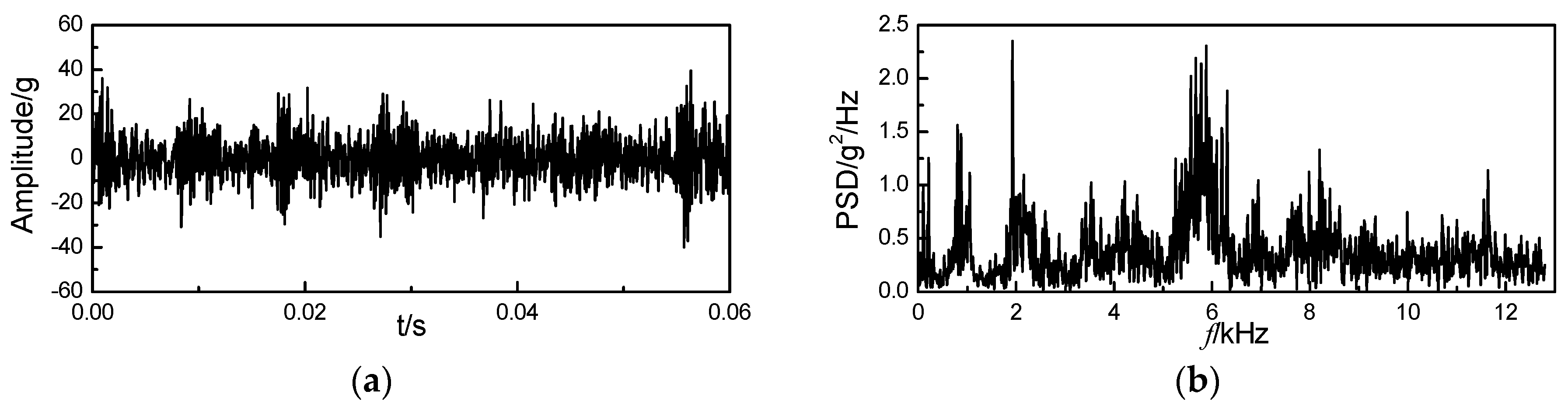
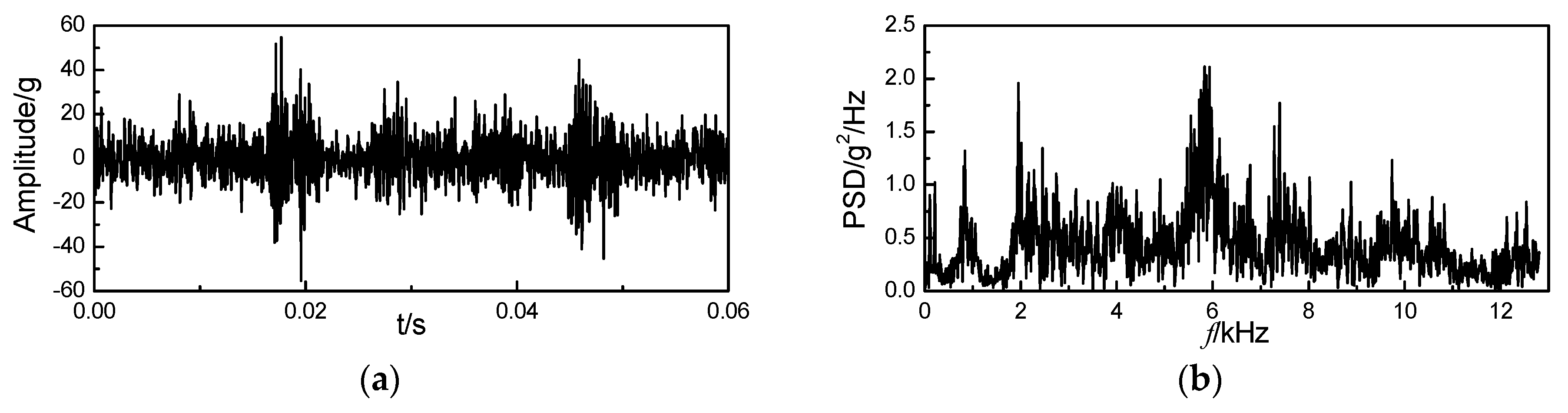
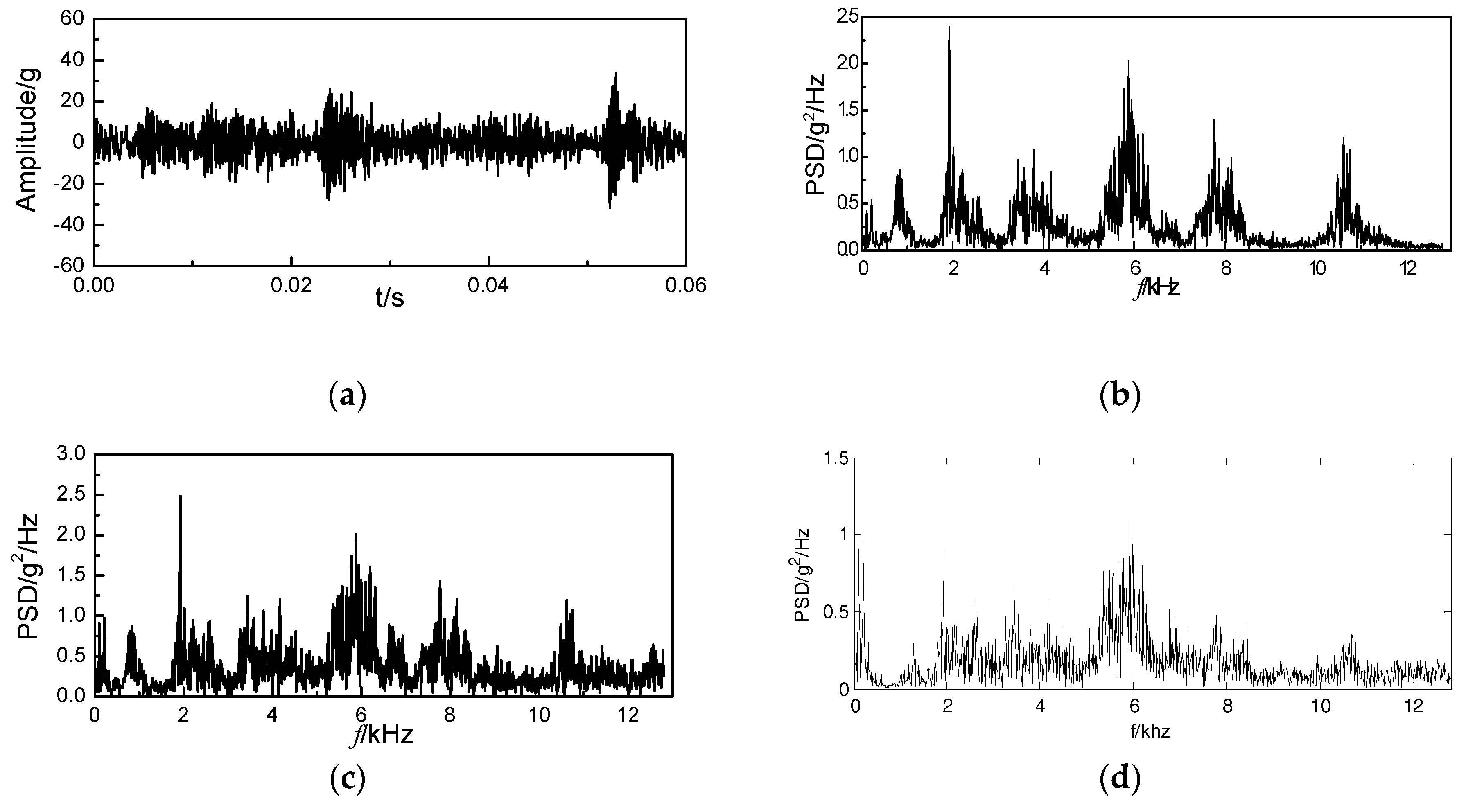
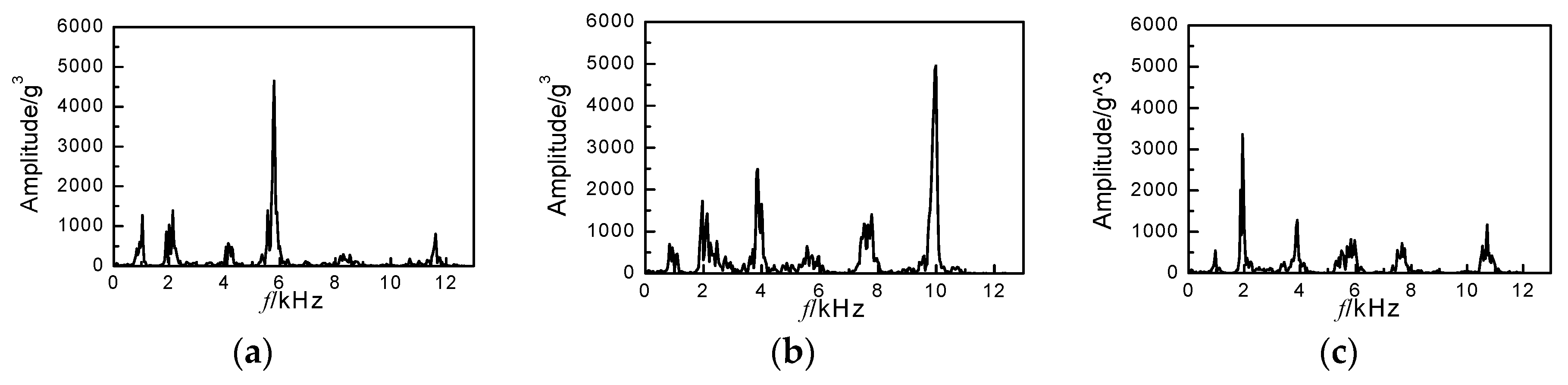
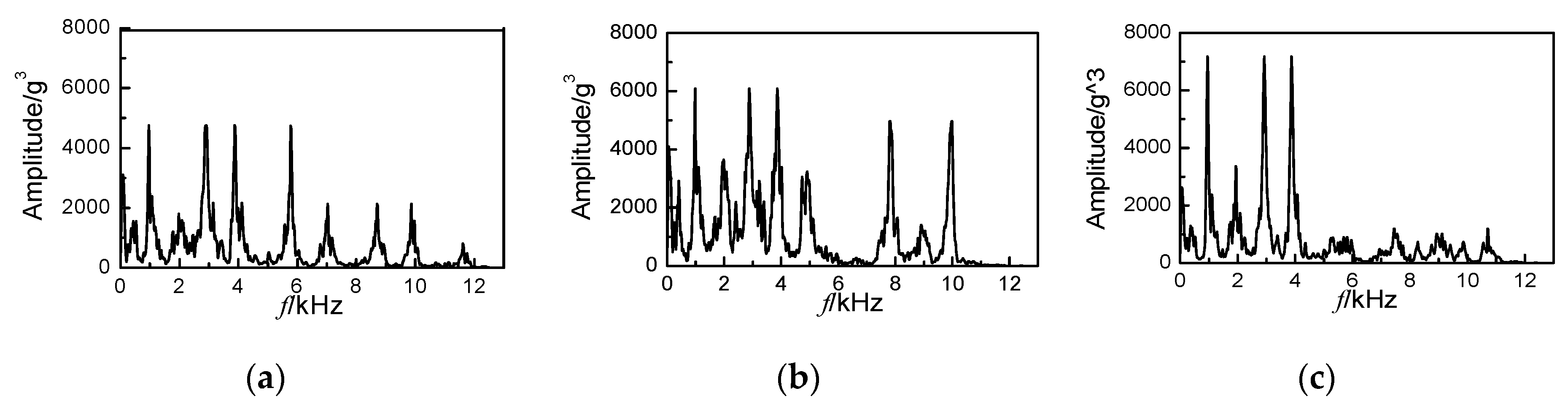
4.1. Signal Denoising by Improved VMD
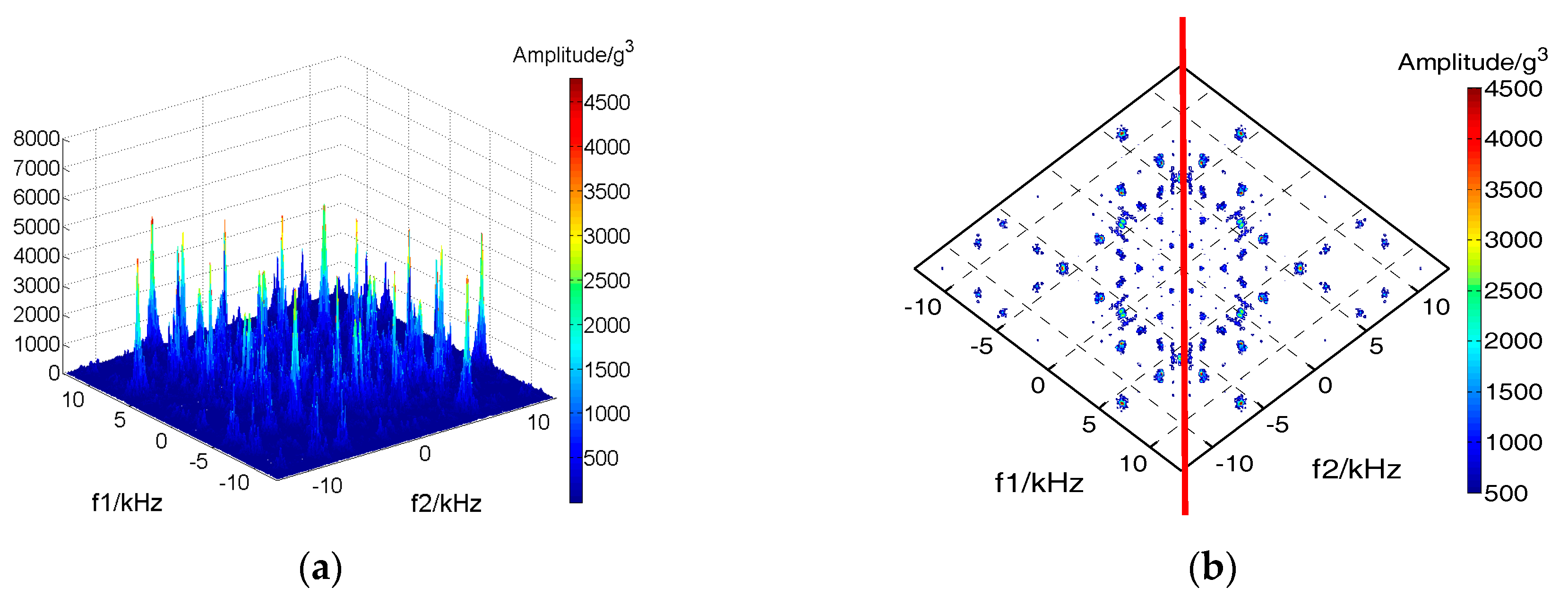
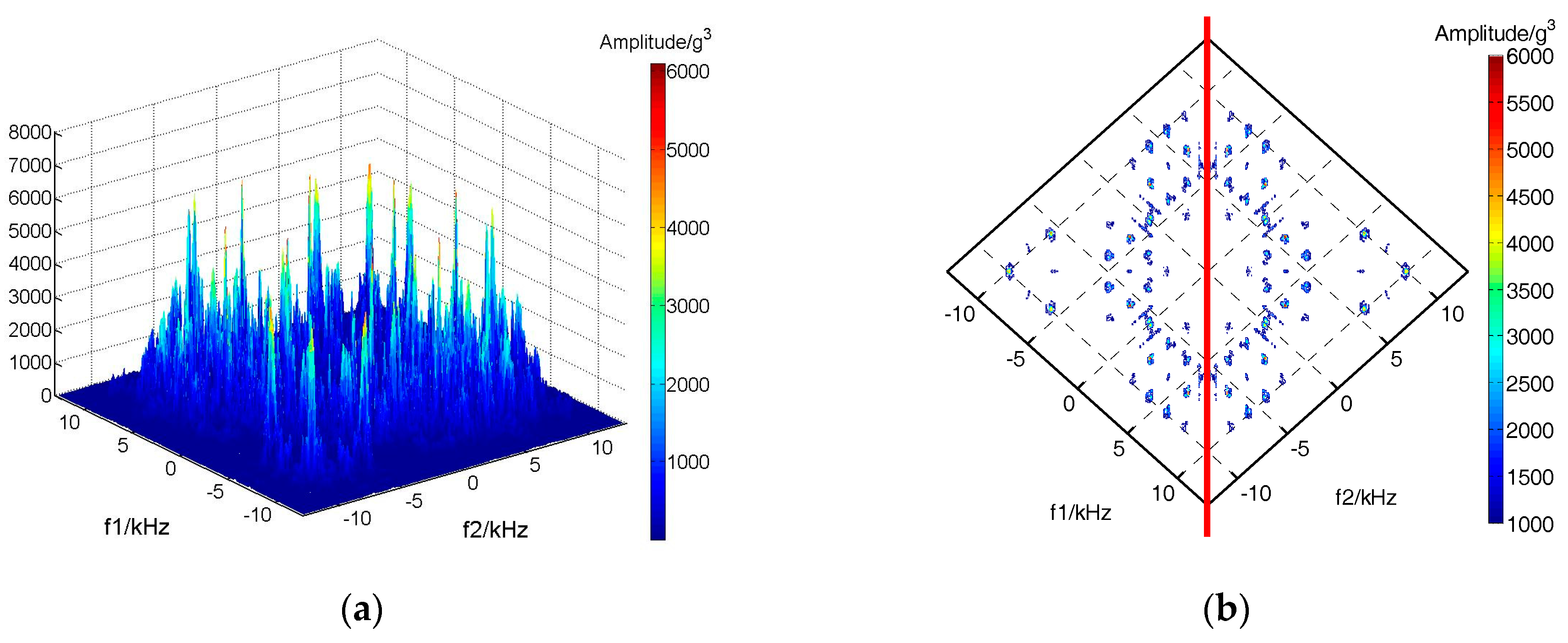
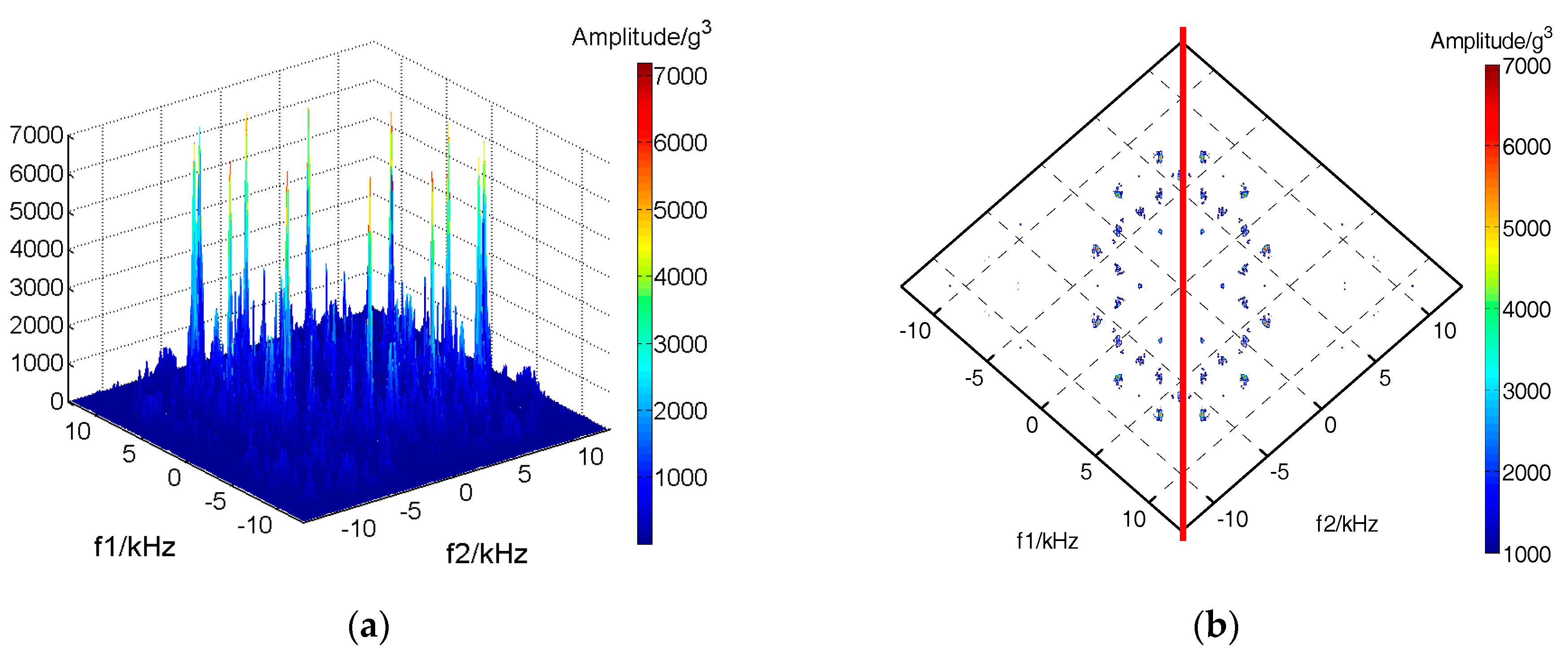
4.2. Fault Feature Extraction by Improved Bispectrum
5. Summary and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yu, L.; Junhong, Z.; Fengrong, B.; Lin, J.; Ma, W. A fault diagnosis approach for diesel engine valve train based on improved ITD and SDAG-RVM. Meas. Sci. Technol. 2015, 26, 025003. [Google Scholar] [CrossRef]
- Vulli, S.; Dunne, J.F.; Potenza, R.; Richardson, D.; King, P. Time-frequency analysis of single-point engine-block vibration measurements for multiple excitation-event identification. J. Sound Vib. 2009, 321, 1129–1143. [Google Scholar] [CrossRef]
- Wang, X.; Liu, C.; Bi, F.; Bi, X.; Shao, K. Fault diagnosis of diesel engine based on adaptive wavelet packets and EEMD-fractal dimension. Mech. Syst. Signal Process. 2013, 41, 581–597. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.; Ma, L. A fault diagnosis approach for diesel engines based on self-adaptive WVD, improved FCBF and PECOC-RVM. Neurocomputing 2016, 177, 600–611. [Google Scholar] [CrossRef]
- Antoni, J.; Daniere, J.; Guillet, F. Effective vibration analysis of IC engine using cyclostationarity Part I: A methodology for condition monitoring. J. Sound Vib. 2002, 257, 815–837. [Google Scholar] [CrossRef]
- Lin, J.; Qu, L. Feature extraction based on Morlet wavelet and its application for mechanical fault diagnosis. J. Sound Vib. 2000, 234, 135–148. [Google Scholar] [CrossRef]
- Cai, Y.; Li, A.; He, Y.; Wang, T.; Zhao, J. Application of wavelet packets and GA-BP algorithm in fault diagnosis for diesel valve gap abnormal fault. In Proceedings of the 2010 2nd International Conference on Advanced Computer Control, Shenyang, China, 27–29 March 2010. [Google Scholar]
- Deng, W.; Zhang, S.; Zhao, H.; Yang, X. A Novel Fault Diagnosis Method Based on Integrating Empirical Wavelet Transform and Fuzzy Entropy for Motor Bearing. IEEE Access 2018, 6, 35042–35056. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, L. Bearing fault diagnosis based on improved LMD. In Proceedings of the International Conference on Transportation, Mechanical, and Electrical Engineering, Changchun, China, 16–18 December 2012; pp. 2544–2547. [Google Scholar]
- Zhang, S.; Wang, Y.; He, S.; Jiang, Z. Bearing fault diagnosis based on variational mode decomposition and total variation denoising. Meas. Sci. Technol. 2016, 27, 075101. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, S.; Zhishen, L.I.; Fucai, L.I.; Yue, H.U. Application of New Denoising Method Based on VMD in Fault Feature Extraction. J. Vib. Meas. Diagn. 2018, 38, 11–19. [Google Scholar]
- Ma, Z.Q.; Liu, X.Y.; Zhang, J.J.; Wang, J. Application of VMD-ICA combined method in fault diagnosis of rolling bearings. J. Vib. Shock 2017, 36, 201–207. [Google Scholar]
- Mohanty, S.; Gupta, K.K.; Raju, K.S. Comparative study between VMD and EMD in bearing fault diagnosis. In Proceedings of the International Conference on Industrial & Information Systems, Gwalior, India, 15–17 December 2015. [Google Scholar]
- Zhang, J.; Liu, C.W.; Bi, F.R.; Bi, X.B.; Yang, X. Fault Feature Extraction of Diesel Engine Based on Bispectrum Image Fractal Dimension. Chin. J. Mech. Eng. 2018, 31, 216–226. [Google Scholar] [CrossRef]
- Gu, F.; Shao, Y.; Hu, N.; Fazenda, B.; Ball, A. Motor current signal analysis using a modified bispectrum for machine fault diagnosis. In Proceedings of the 2009 ICCAS-SICE, Fukuoka, Japan, 18–21 August 2009; pp. 4890–4895. [Google Scholar]
- Gu, F.; Shao, Y.; Hu, N.; Naid, A.; Ball, A.D. Electrical motor current signal analysis using a modified bispectrum for fault diagnosis of downstream mechanical equipment. Mech. Syst. Signal Process. 2011, 25, 360–372. [Google Scholar] [CrossRef]
- Shen, G.; Stephen, M.; Xu, Y.; Paul, W. Theoretical and experimental analysis of bispectrum of vibration signals for fault diagnosis of gears. Mech. Syst. Signal Process. 2014, 43, 76–89. [Google Scholar]
- Feng, F.; Si, A.; Zhang, H. Research on Fault Diagnosis of Diesel Engine Based on Bispectrum Analysis and Genetic Neural Network. Procedia Eng. 2011, 15, 2454–2458. [Google Scholar] [CrossRef]
- Liang, B.; Iwnicki, S.D.; Zhao, Y. Application of power spectrum, cepstrum, higher order spectrum and neural network analyses for induction motor fault diagnosis. Mech. Syst. Signal Process. 2013, 39, 342–360. [Google Scholar] [CrossRef]

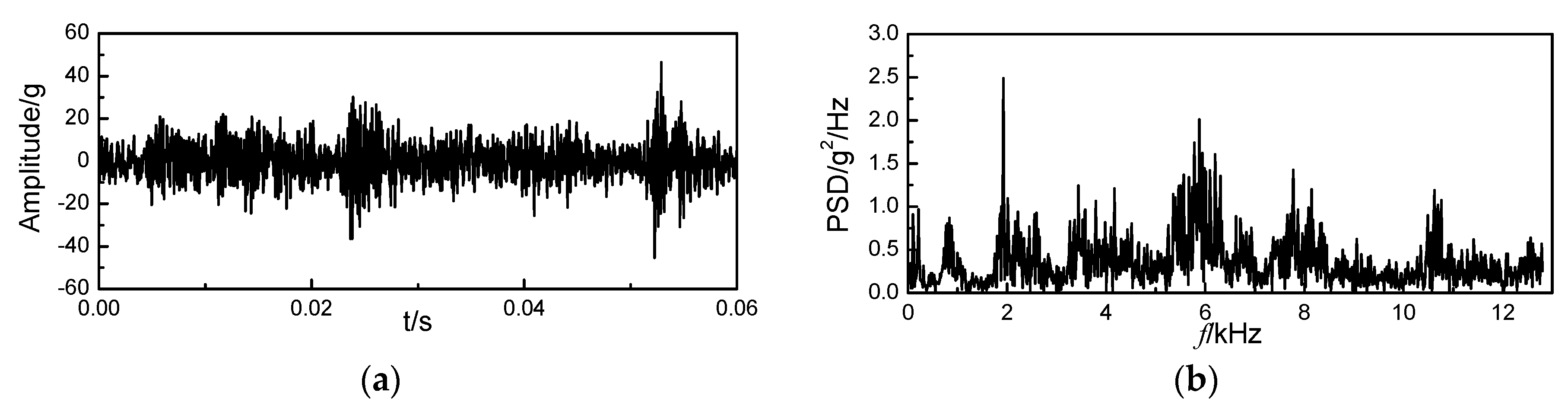
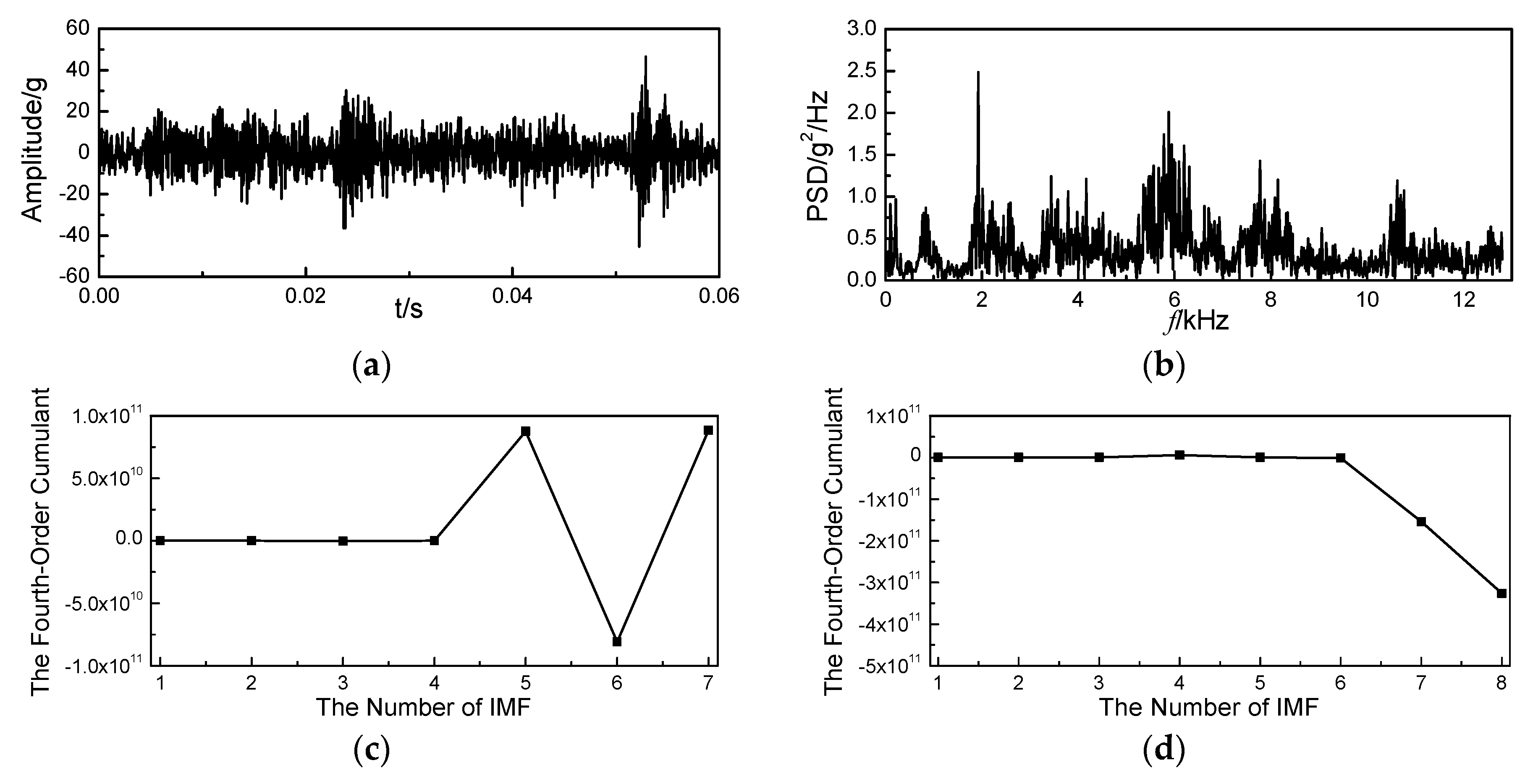
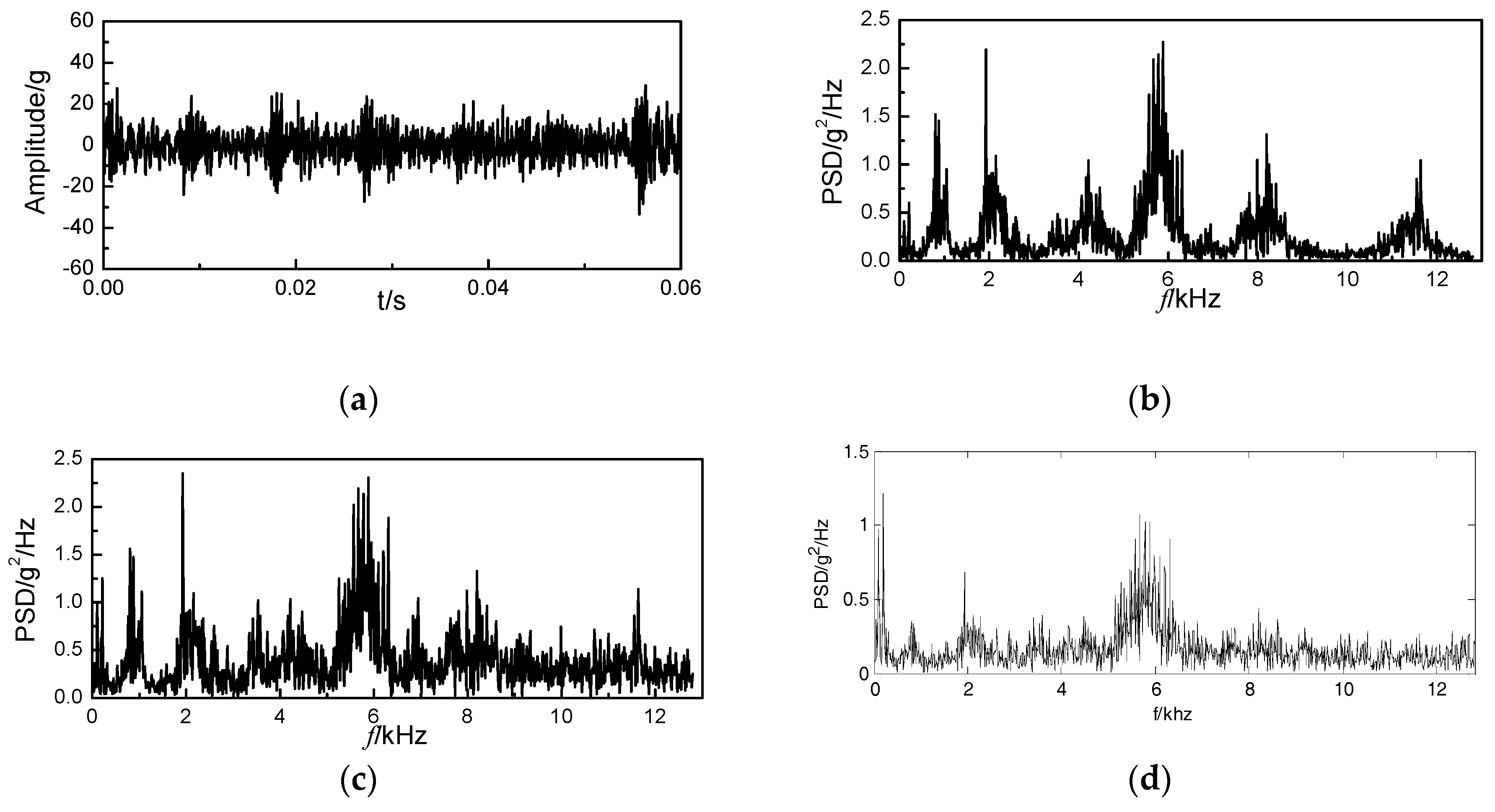
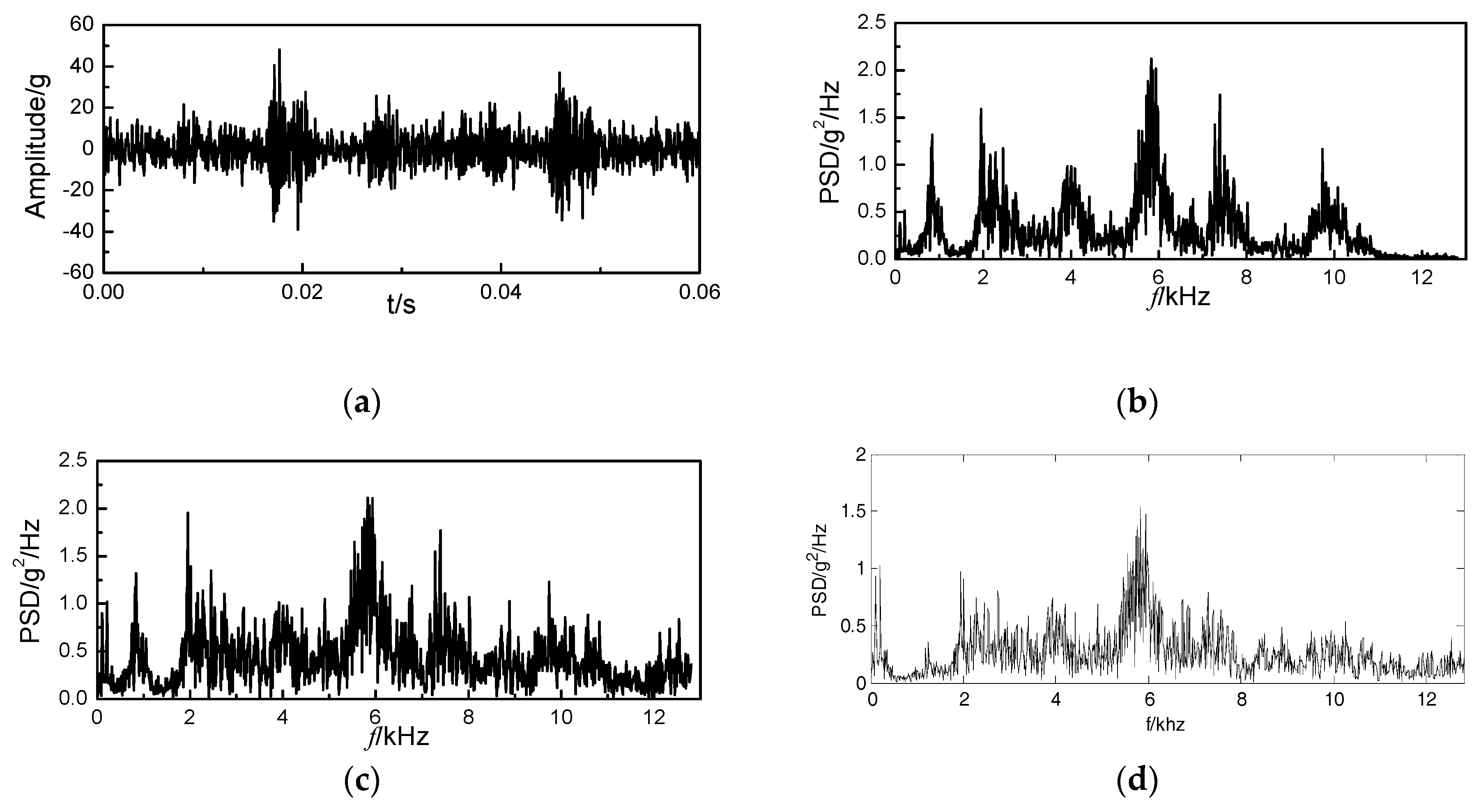

| Condition | Intake Valve Clearance (mm) | Exhaust Valve Clearance (mm) |
|---|---|---|
| Clearance small | 0.25 | 0.45 |
| Clearance normal | 0.3 | 0.5 |
| Clearance big | 0.35 | 0.55 |
| Decomposition Layer K | 5 | 6 | 7 | 8 |
|---|---|---|---|---|
| Fourth-order cumulant | 6.75 × 109 | 5.52 × 109 | 1.36 × 1010 | −5.9 × 1010 |
| Working Condition | Original Signal | VMD Reconstructed | Wavelet Denoising |
|---|---|---|---|
| Normal working condition | 109.77 | 69.64 | 43.55 |
| Big valve clearance | 80.73 | 50.93 | 20.33 |
| Small valve clearance | 91.39 | 57.96 | 18.03 |
| Working Condition | Diagonal Section | Diagonal Projection |
|---|---|---|
| Normal working condition | 1.00 | 0.00 |
| Big valve clearance | 0.90 | 1.00 |
| Small valve clearance | 0.00 | 0.29 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bi, X.; Cao, S.; Zhang, D. Diesel Engine Valve Clearance Fault Diagnosis Based on Improved Variational Mode Decomposition and Bispectrum. Energies 2019, 12, 661. https://doi.org/10.3390/en12040661
Bi X, Cao S, Zhang D. Diesel Engine Valve Clearance Fault Diagnosis Based on Improved Variational Mode Decomposition and Bispectrum. Energies. 2019; 12(4):661. https://doi.org/10.3390/en12040661
Chicago/Turabian StyleBi, Xiaoyang, Shuqian Cao, and Daming Zhang. 2019. "Diesel Engine Valve Clearance Fault Diagnosis Based on Improved Variational Mode Decomposition and Bispectrum" Energies 12, no. 4: 661. https://doi.org/10.3390/en12040661
APA StyleBi, X., Cao, S., & Zhang, D. (2019). Diesel Engine Valve Clearance Fault Diagnosis Based on Improved Variational Mode Decomposition and Bispectrum. Energies, 12(4), 661. https://doi.org/10.3390/en12040661





