Canonical Variate Residuals-Based Fault Diagnosis for Slowly Evolving Faults
Abstract
:1. Introduction
- The development of a new monitoring index based on statistics, , and . The combined index is seen to be more sensitive than and for slowly developing faults while still maintaining satisfactory missed detection rates.
- The development of a CVR-based contribution method for the monitoring of slowly evolving faults. To our best knowledge, it is the first time that it is the first time that CVR-based contribution has been derived and used for fault identification.
- The use of the proposed diagnostic method for incipient fault diagnosis using data captured from a CSTR simulation program and an operational industrial centrifugal compressor.
2. Methods
2.1. CVA-Based Diagnosis
2.1.1. CVA Revisited
2.1.2. and Indices
2.1.3. Index
2.1.4. Combined Index
2.2. CVA-Based Fault Identification
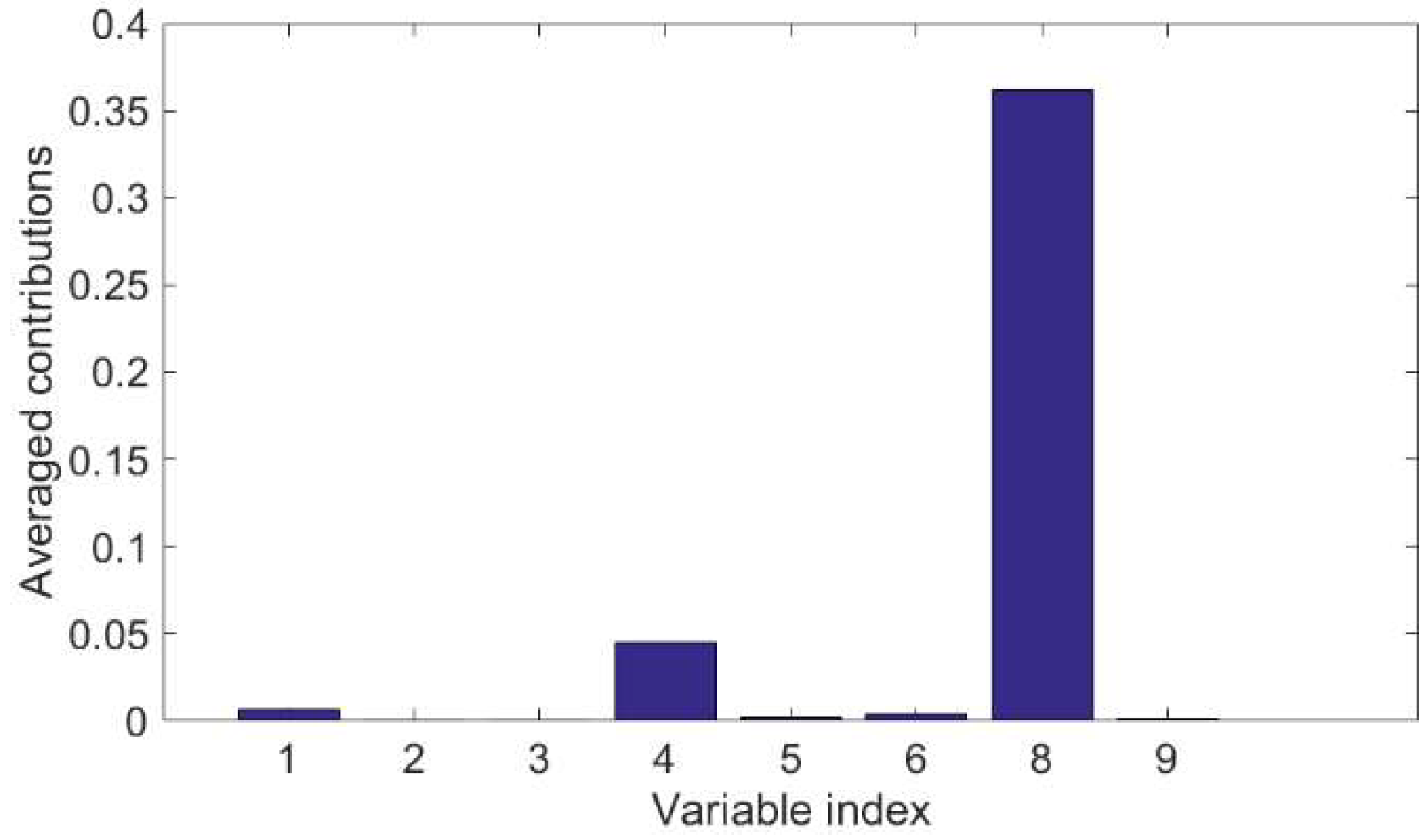
2.2.1. CVA-Based Contributions
3. Results
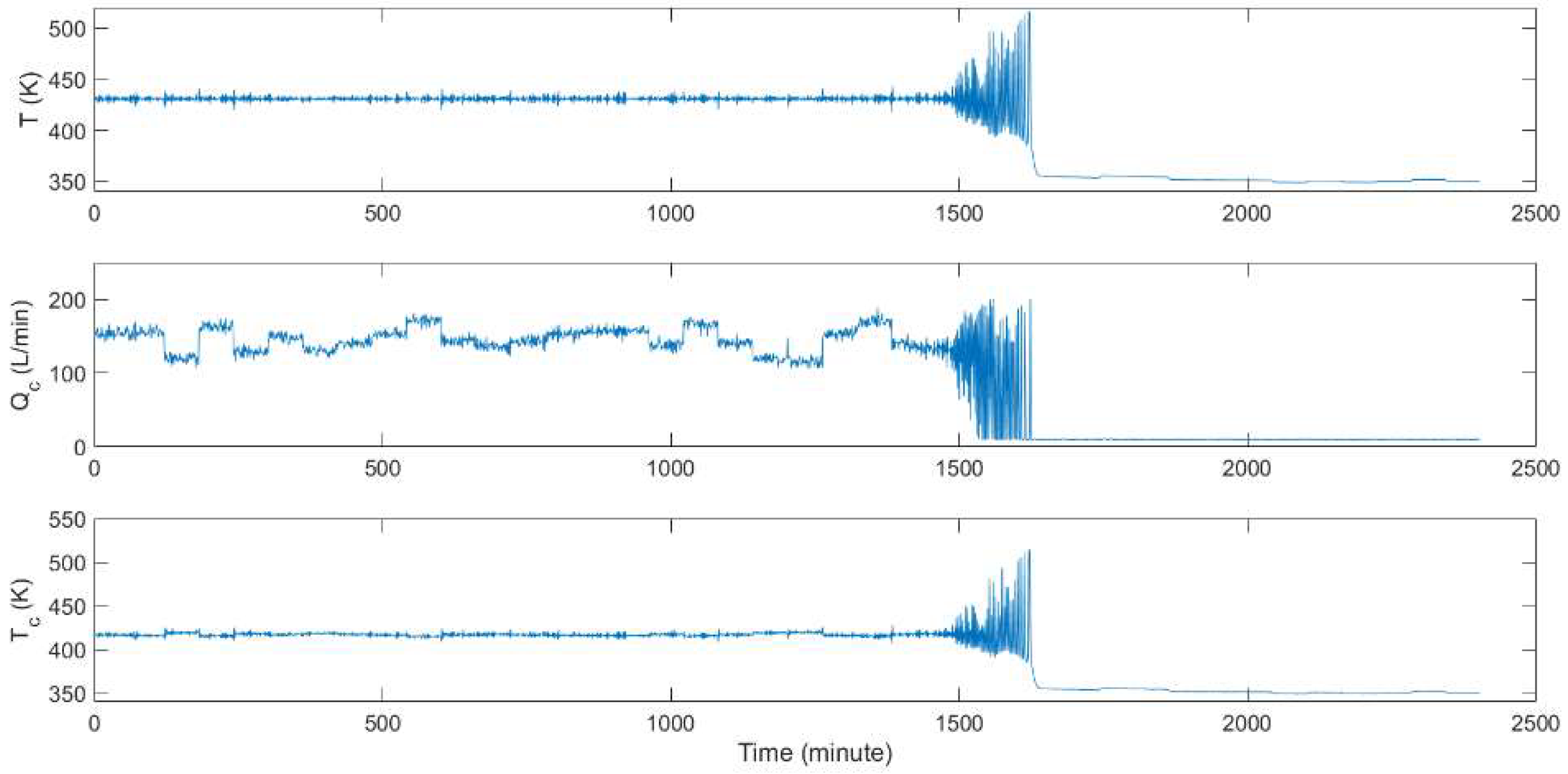
3.1. Fault Description
3.1.1. CSTR Fault Description
3.1.2. Compressor Fault Description
3.2. Fault Detection
3.2.1. CSTR Fault Detection
3.2.2. Compressor Fault Detection
3.3. Fault Identification
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, X.; Duan, F.; Mba, D.; Bennett, I. Multidimensional prognostics for rotating machinery: A review. Adv. Mech. Eng. 2017, 9, 1–20. [Google Scholar] [CrossRef]
- Zhao, R.; Wang, D.; Yan, R.; Mao, K.; Shen, F.; Wang, J. Machine Health Monitoring Using Local Feature-Based Gated Recurrent Unit Networks. IEEE Trans. Ind. Electron. 2018, 65, 1539–1548. [Google Scholar] [CrossRef]
- Wook, S.; Lee, C.; Lee, J.; Hyun, J.; Lee, I. Fault detection and identification of nonlinear processes based on kernel PCA. Chemom. Intell. Lab. Syst. 2005, 75, 55–67. [Google Scholar]
- Fan, J.; Wang, Y. Fault detection and diagnosis of non-linear non-Gaussian dynamic processes using kernel dynamic independent component analysis. Inf. Sci. 2014, 259, 369–379. [Google Scholar] [CrossRef]
- Li, X.; Duan, F.; Loukopoulos, P.; Bennett, I.; Mba, D. Canonical variable analysis and long short-term memory for fault diagnosis and performance estimation of a centrifugal compressor. Control Eng. Pract. 2018, 72, 177–191. [Google Scholar] [CrossRef]
- Li, W.; Qin, S.J. Consistent dynamic PCA based on errors-in-variables subspace identification. J. Process Control 2001, 11, 661–678. [Google Scholar] [CrossRef]
- Yin, S.; Zhu, X.; Member, S.; Kaynak, O. Improved PLS Focused on Key-Performance- Indicator-Related Fault Diagnosis. IEEE Trans. Ind. Electron. 2015, 62, 1651–1658. [Google Scholar] [CrossRef]
- Ruiz-cárcel, C.; Cao, Y.; Mba, D.; Lao, L.; Samuel, R.T. Statistical process monitoring of a multiphase flow facility. Control Eng. Pract. 2015, 42, 74–88. [Google Scholar] [CrossRef] [Green Version]
- Stefatos, G.; Hamza, A.B. Dynamic independent component analysis approach for fault detection and diagnosis. Expert Syst. Appl. 2010, 37, 8606–8617. [Google Scholar] [CrossRef]
- Jiang, Q.; Ding, S.X.; Wang, Y.; Yan, X. Data-Driven Distributed Local Fault Detection for Large-Scale Processes Based on the GA-Regularized Canonical Correlation Analysis. IEEE Trans. Ind. Electron. 2017, 64, 8148–8157. [Google Scholar] [CrossRef]
- Chen, Z.; Ding, S.X.; Peng, T.; Yang, C.; Gui, W. Fault Detection for Non-Gaussian Processes Using Generalized Canonical Correlation Analysis and Randomized Algorithms. IEEE Trans. Ind. Electron. 2018, 65, 1559–1567. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, K.; Ding, S.X.; Shardt, Y.A.W.; Hu, Z. Improved canonical correlation analysis-based fault detection methods for industrial processes. J. Process Control 2016, 41, 26–34. [Google Scholar] [CrossRef]
- Jiang, Q.; Gao, F.; Yi, H.; Yan, X. Multivariate Statistical Monitoring of Key Operation Units of Batch Processes Based on Time-Slice CCA. IEEE Trans. Control Syst. Technol. 2018, 99, 1–8. [Google Scholar] [CrossRef]
- Pilario, K.E.S.; Cao, Y. Canonical Variate Dissimilarity Analysis for Process Incipient Fault Detection. IEEE Trans. Ind. Inform. 2018, 14, 5308–5315. [Google Scholar] [CrossRef]
- Samuel, R.T.; Cao, Y. Kernel Canonical Variate Analysis for Nonlinear Dynamic Process Monitoring. IFAC-PapersOnLine 2015, 48, 605–610. [Google Scholar] [CrossRef]
- Alcala, C.F.; Qin, S.J. Reconstruction-based contribution for process monitoring. Automatica 2009, 45, 1593–1600. [Google Scholar] [CrossRef]
- Tan, R.; Cao, Y. Deviation Contribution Plots of Multivariate Statistics. IEEE Trans. Ind. Inform. 2019, 15, 833–841. [Google Scholar] [CrossRef]
- Zhu, X.; Braatz, R.D. Two-Dimensional Contribution Map for Fault Identification. IEEE Control Syst. Mag. 2014, 34, 72–77. [Google Scholar]
- Jiang, B.; Huang, D.; Zhu, X.; Yang, F.; Braatz, R.D. Canonical variate analysis-based contributions for fault identification. J. Process Control 2015, 26, 17–25. [Google Scholar] [CrossRef]
- Li, X.; Duan, F.; Mba, D.; Bennett, I. Combining Canonical Variate Analysis, Probability Approach and Support Vector Regression for Failure Time Prediction. J. Intell. Fuzzy Syst. 2018, 34, 746–752. [Google Scholar]
- Jiang, B.; Braatz, R.D. Fault detection of process correlation structure using canonical variate analysis-based correlation features. J. Process Control 2017, 58, 131–138. [Google Scholar] [CrossRef]
- Jiang, B.; Zhu, X.; Huang, D.; Paulson, J.A.; Braatz, R.D. A combined canonical variate analysis and Fisher discriminant analysis (CVA–FDA) approach for fault diagnosis. Comput. Chem. Eng. 2015, 77, 1–9. [Google Scholar] [CrossRef]
- Lu, Q.; Jiang, B.; Gopaluni, R.B.; Loewen, P.D.; Braatz, R.D. Locality preserving discriminative canonical variate analysis for fault diagnosis. Comput. Chem. Eng. 2018, 117, 309–319. [Google Scholar] [CrossRef]
- Odiowei, P.E.P.; Yi, C. Nonlinear Dynamic Process Monitoring Using Canonical Variate Analysis and Kernel Density Estimations. IEEE Trans. Ind. Inform. 2010, 6, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Hotelling, H. New Light on the Correlation Coefficient and its Transforms. J. R. Stat. Soc. Ser. B 1953, 15, 193–232. [Google Scholar] [CrossRef]
- Juricek, B.C.; Seborg, D.E.; Larimore, W.E. Fault Detection Using Canonical Variate Analysis. Ind. Eng. Chem. Res. 2004, 43, 458–474. [Google Scholar] [CrossRef]
- Flury, B.K.; Riedwyl, H. Standard distance in univariate and multivariate analysis. Am. Stat. 1986, 40, 249–251. [Google Scholar]
- Botev, B.Z.I.; Grotowski, J.F.; Kroese, D.P. Kernel density estimation via diffusion. Ann. Stat. 2010, 38, 2916–2957. [Google Scholar] [CrossRef] [Green Version]














| Fault ID | Fault Description | Decaying rate | Fault Type |
|---|---|---|---|
| 1 | Additive | ||
| 2 | Multiplicative | ||
| 3 | . | Multiplicative |
| Variable ID | Variable | Units |
|---|---|---|
| 1 | (noise-free) | mol/L |
| 2 | (noise-free) | K |
| 3 | (noise-free) | K |
| 4 | mol/L | |
| 5 | K | |
| 6 | mol/L | |
| 7 | K | |
| 8 | K | |
| 9 | K | |
| 10 | L/min |
| ID | Variable Name | ID | Variable Name |
|---|---|---|---|
| 1 | Stage 1 Suction Pressure | 12 | Stage 1–2 DE Radial Vibration Overall Y * |
| 2 | Stage 1 Discharge Pressure | 13 | Stage 1–2 NDE Radial Vibration Overall X * |
| 3 | Stage 1 Suction Temperature | 14 | Stage 1–2 NDE Radial Vibration Overall Y * |
| 4 | Stage 1 Discharge Temperature | 15 | Stage 1–2 Thrust Position Axial Probe 1 |
| 5 | Stage 2 Suction Pressure | 16 | Stage 1–2 Thrust Position Axial Probe 2 |
| 6 | Stage 2 Discharge Pressure | 17 | Stage 3 DE Radial Vibration Overall X * |
| 7 | Stage 2 Suction Temperature | 18 | Stage 3 DE Radial Vibration Overall Y * |
| 8 | Stage 2 Discharge Temperature | 19 | Stage 3 NDE Radial Vibration Overall X * |
| 9 | Stage 3 Suction Pressure | 20 | Stage 3 NDE Radial Vibration Overall Y * |
| 10 | Stage 3 Discharge Pressure | 21 | Stage 3 Thrust Position Axial Probe 1 |
| 11 | Stage 1–2 DE Radial Vibration Overall X * | 22 | Stage 3 Thrust Position Axial Probe 2 |
| Fault Type | ||||
|---|---|---|---|---|
| CSTR fault 1 | Detection time (min) | 1626 | 1619 | 1544 |
| Missed detection rate (%) | 8.75% | 9.04% | 6.5% | |
| CSTR fault 2 | Detection time (min) | 1882 | 1869 | 1841 |
| Missed detection rate (%) | 20.08% | 19.29% | 18.42% | |
| CSTR fault 3 | Detection time (min) | 1502 | 1502 | 1490 |
| Missed detection rate (%) | 4.37% | 4.17% | 4.04% | |
| Compressor | Detection time (min) | 1641 | 1976 | 1579 |
| Missed detection rate (%) | 2.82% | 19.37% | 0.55% |
| Fault Type | CSTR Fault 1 | CSTR Fault 2 | CSTR Fault 3 | Compressor |
|---|---|---|---|---|
| False alarm rate | 1.13% | 0.71% | 2.76% | 3.25% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Mba, D.; Diallo, D.; Delpha, C. Canonical Variate Residuals-Based Fault Diagnosis for Slowly Evolving Faults. Energies 2019, 12, 726. https://doi.org/10.3390/en12040726
Li X, Mba D, Diallo D, Delpha C. Canonical Variate Residuals-Based Fault Diagnosis for Slowly Evolving Faults. Energies. 2019; 12(4):726. https://doi.org/10.3390/en12040726
Chicago/Turabian StyleLi, Xiaochuan, David Mba, Demba Diallo, and Claude Delpha. 2019. "Canonical Variate Residuals-Based Fault Diagnosis for Slowly Evolving Faults" Energies 12, no. 4: 726. https://doi.org/10.3390/en12040726
APA StyleLi, X., Mba, D., Diallo, D., & Delpha, C. (2019). Canonical Variate Residuals-Based Fault Diagnosis for Slowly Evolving Faults. Energies, 12(4), 726. https://doi.org/10.3390/en12040726






