Experimental and Numerical Investigations on the Fluidized Heat Absorption inside Quartz Glass and Metal Tubes
Abstract
:1. Introduction
2. Experiments and Results
2.1. Experimental Apparatus
2.2. Uncertainty Analysis
2.3. Results and Discussions
3. Model Description
3.1. Physical Model and Assumptions
3.2. Governing Equations
3.3. Radiative Transfer
3.4. Heat Transfer Correlations
3.5. Initial Conditions and Boundary Conditions
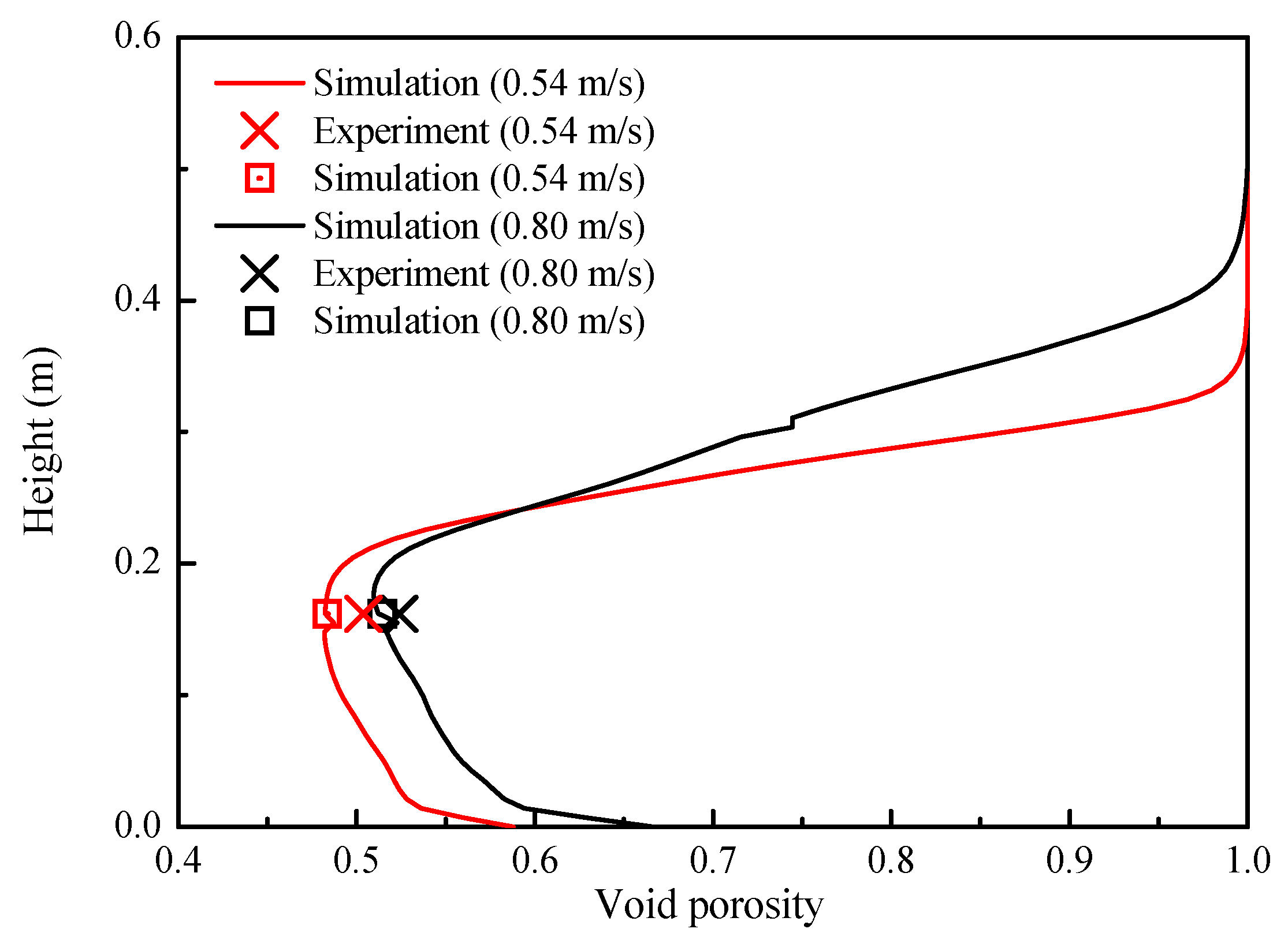
4. Model Validation on the Cold State
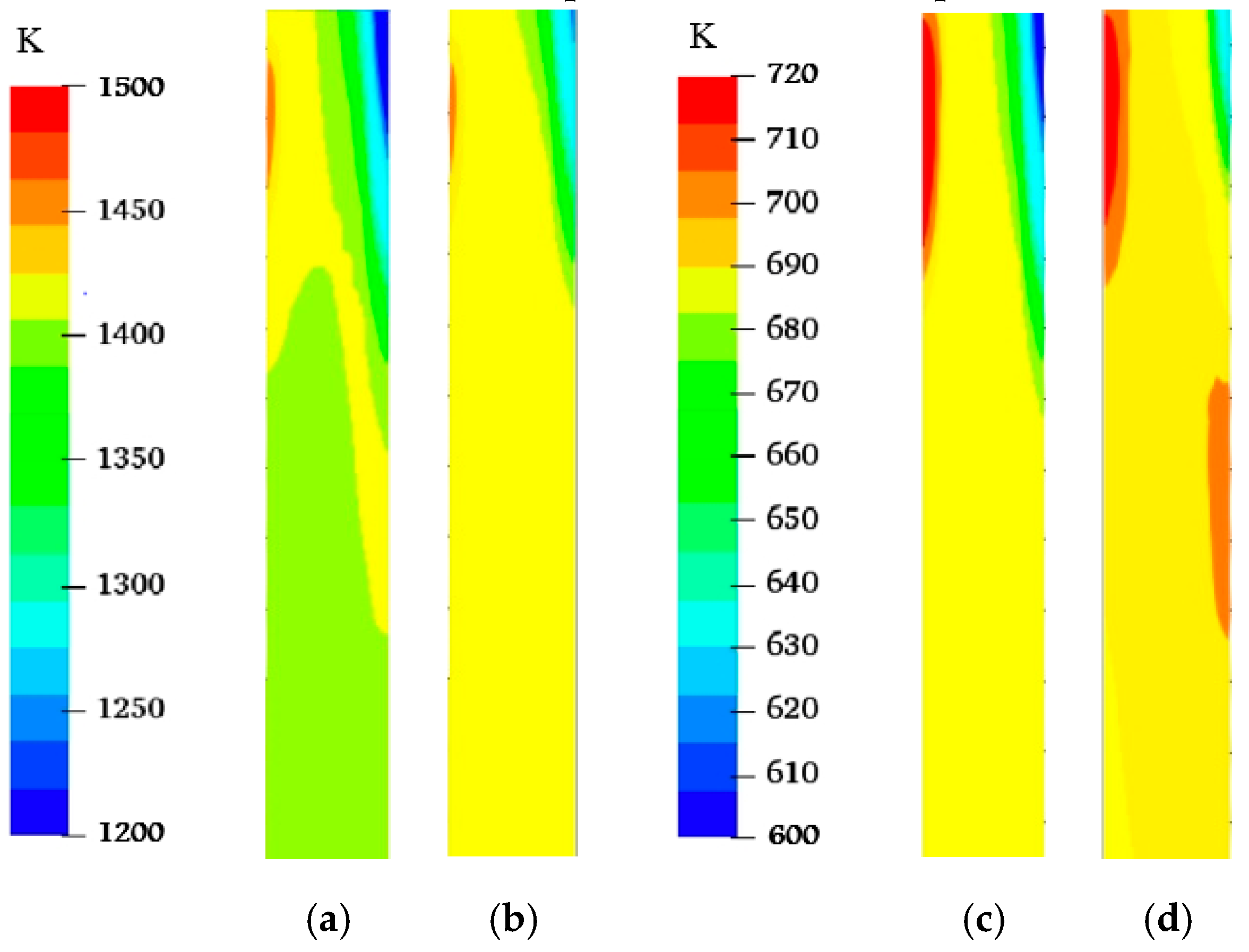
5. Model Validation on the Thermal State
6. Conclusions
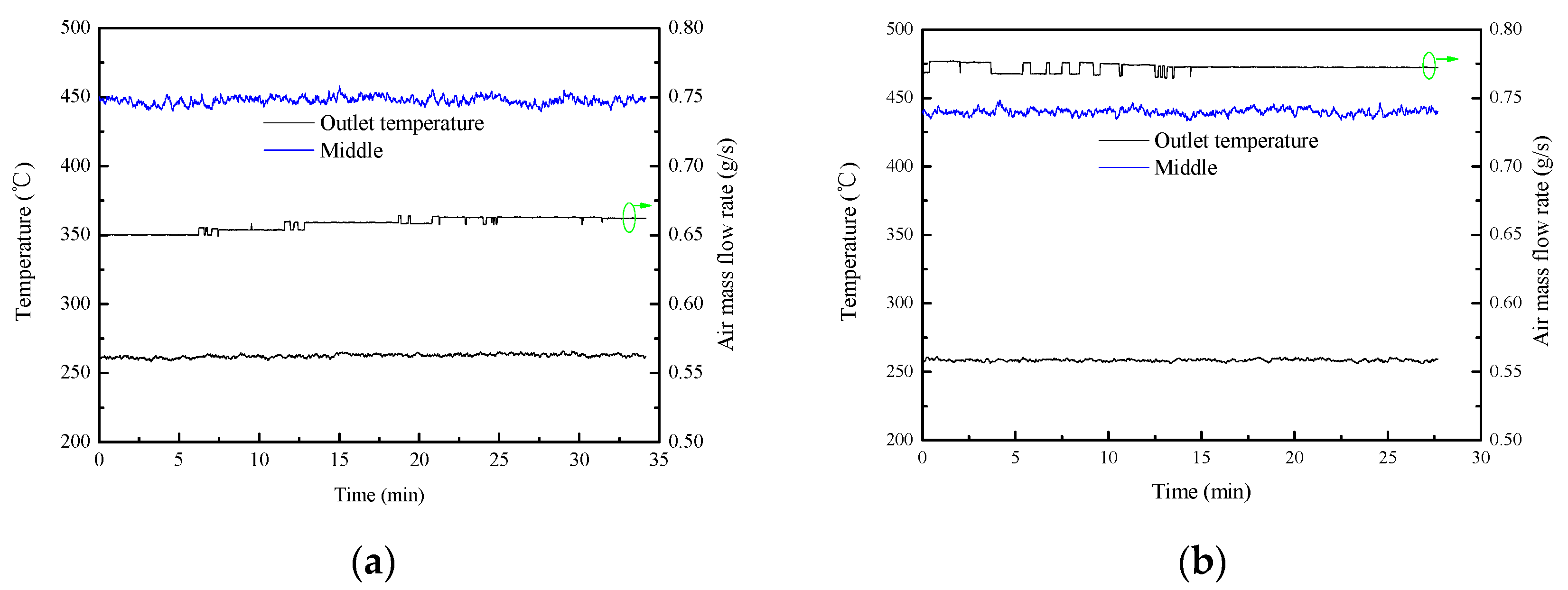
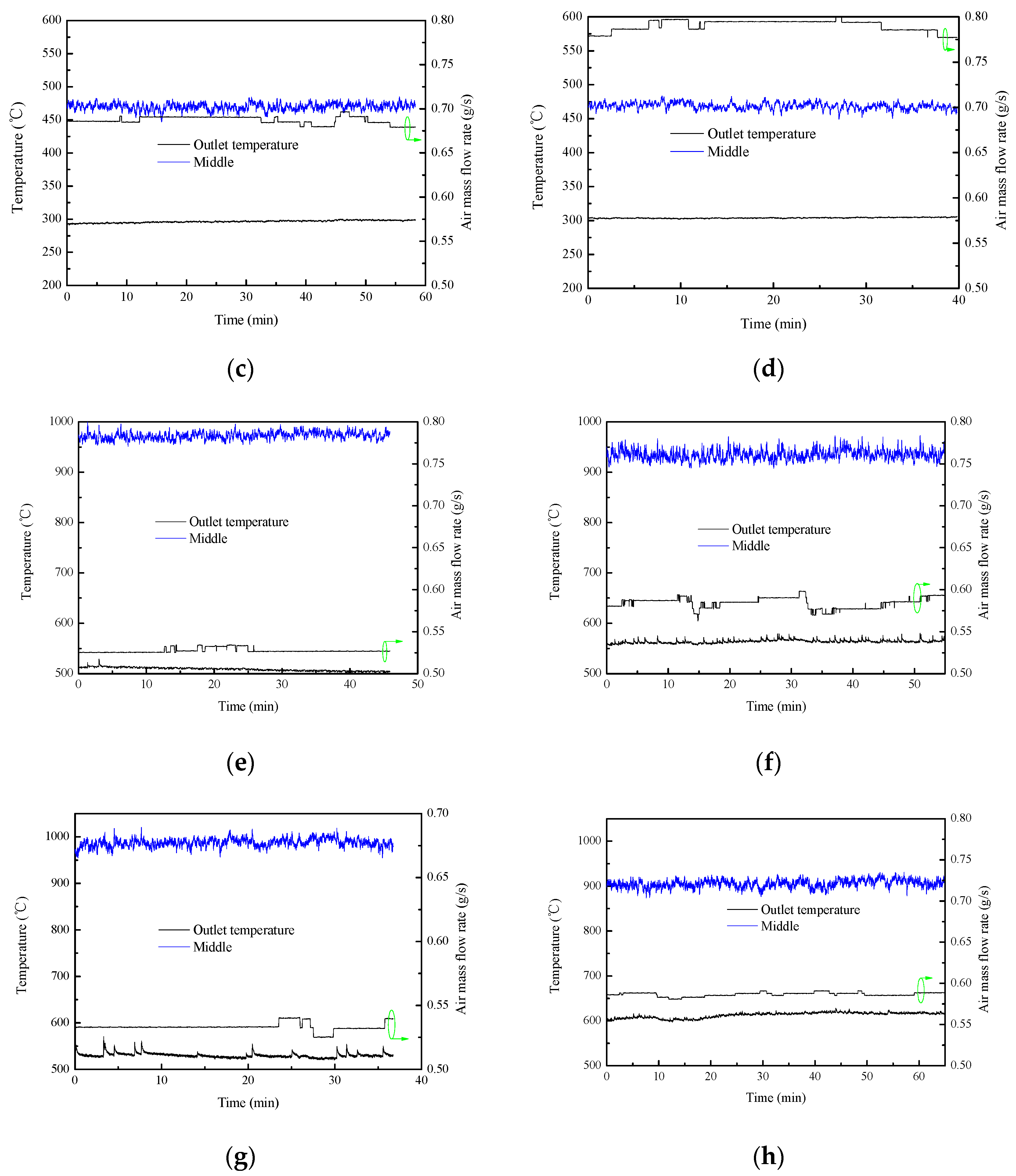
- Case 1–4 shows that an increase in the air mass flow rate leads to a lower outlet air temperature and a higher thermal efficiency (e.g., Case 1, 263 °C, 31.7% and Case 2, 258 °C, 36.3%) and increasing packed particle mass enhances the heat transfer (e.g., Case 1, 31.7% and Case 3, 33.1%).
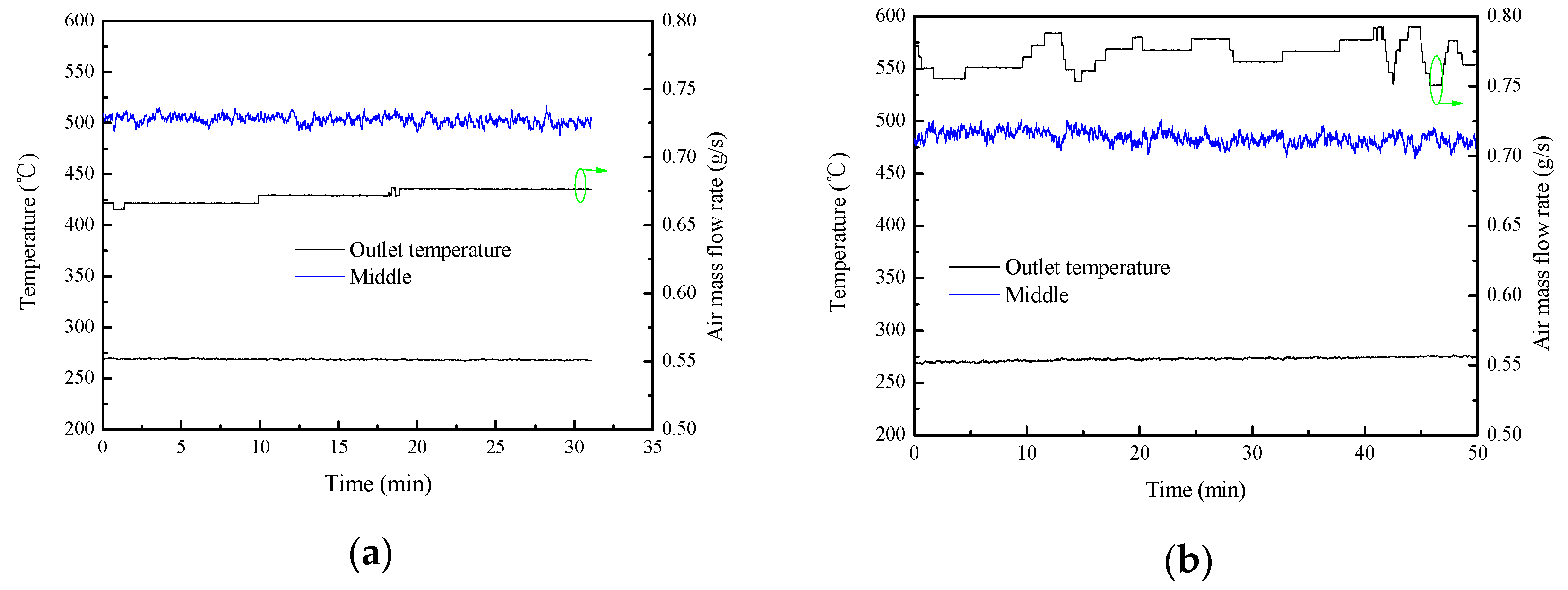
- Case 5–12 shows that increasing air mass flow rate improves the thermal efficiencies (e.g., Case 11, 21.9% and Case 12, 24.2%) and the heat transfer is enhanced by increasing the packed particle mass (e.g., Case 10, 22.9% and Case 12, 24.2%).
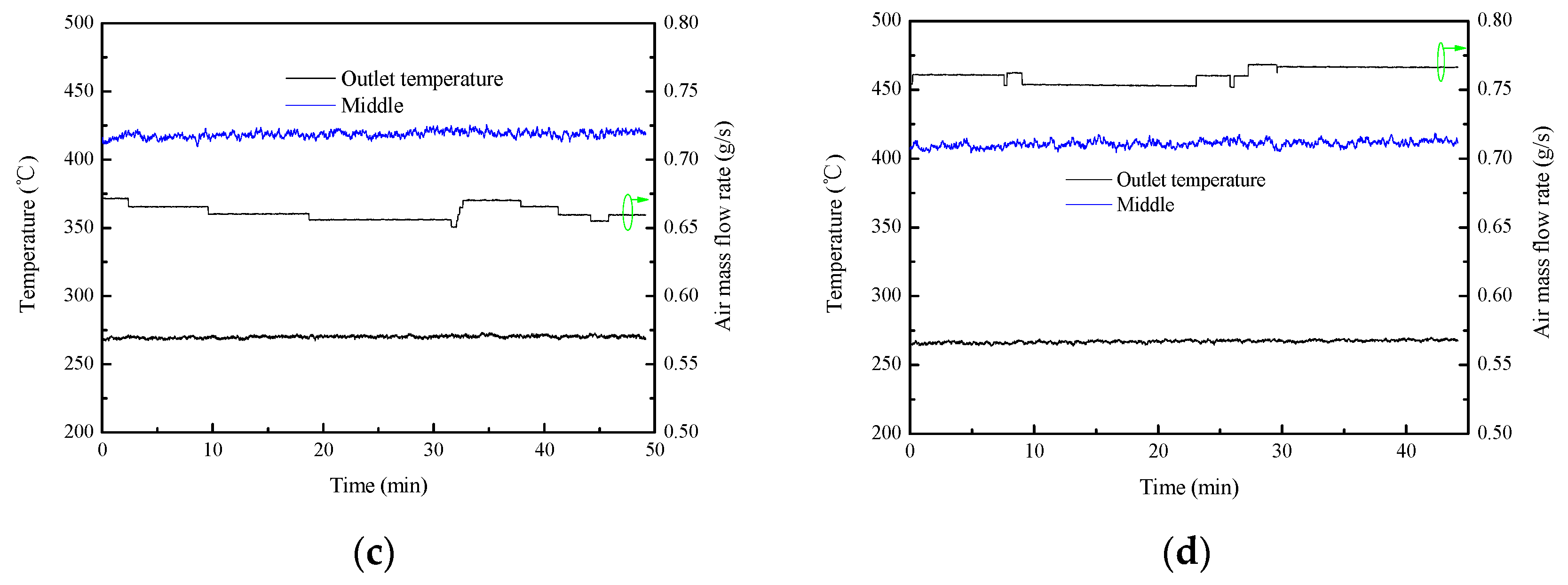
- The comparisons between Case 1–4 and Case 5–8 indicate that the fluidized heat absorption inside the quartz tube is better than that inside the metal tube (e.g., Case 4, 37.4% and Case 8, 44.6%). In addition, the outlet air temperature increases with the increase of the air mass flow rate inside the quartz glass tube (e.g., Case 7, 297 °C and Case 8, 304 °C), however, that decreases with the increase of the air mass flow rate inside the metal tube (e.g., Case 3, 270 °C and Case 4, 267 °C).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Coefficient |
| Ai | Area (m2) |
| B | Coefficient |
| cpg | Air specific heat (J/(kgK)) |
| cpg,in | Inlet air specific heat (J/(kgK)) |
| cpg,out | Outlet air specific heat (J/(kgK)) |
| cps | Solid specific heat (J/(kgK)) |
| dp | Particle size (m) |
| D1 | Internal diameter of the tube (m) |
| D2 | External diameter of the tube (m) |
| D3 | External diameter of tube insulation layer (m) |
| e | Restitution coefficient for the collision between particles |
| E | Coefficient |
| F | Coefficient |
| g | Gravitational acceleration (m/s2) |
| g0 | Radial distribution function |
| G | Incident radiation (W/m2) |
| h1 | Convective heat transfer coefficient on the inner wall of the receiver (W/(m2K)) |
| h2 | Convective heat transfer coefficient on the outer wall of the tube (W/(m2K)) |
| hw1 | Overall heat loss coefficient inside the receiver (W/(m2K)) |
| hw2 | Overall heat transfer coefficient for the tube (W/(m2K)) |
| i | Number |
| I | Unit stress tensor |
| Js | The dissipation of fluctuating energy (kg/(m3s)) |
| kg | Air thermal conductivity (W/(m•K)) |
| kg,eff | Air effective thermal conductivity (W/(m•K)) |
| kI | Thermal conductivity of the insulting material (W/(m•K)) |
| ks | Solid thermal conductivity (W/(m•K)) |
| ks,eff | Solid effective thermal conductivity (W/(m•K)) |
| kT | Thermal conductivity of the tube (W/(m•K)) |
| l | The height of the receiver cavity (m) |
| Air mass flow rate (kg/s) | |
| N | Number of the meshes along x axis |
| N1 | Number |
| Nugs | Nusselt number |
| NUM | Number of meshes exposed to the incident flux |
| pg | Air pressure (Pa) |
| ps | Solid pressure (Pa) |
| pr | Prandtl number |
| qair | Thermal energy absorbed inside the tube (kW) |
| qsolar | Incident solar flux (W/m2) |
| Qext | Extinction factor |
| Reg | Reynolds number |
| Rep | Reynolds number |
| Sg | Identity tensor |
| Ss | Identity tensor |
| Srad | Radiative source term (W/m3) |
| Ta | Ambient temperature (K) |
| Tg | Air temperature (K) |
| Tg,in | Inlet air temperature (K, = Ta) |
| Tg,out | Outlet air temperature(K) |
| Ts | Solid temperature (K) |
| vg | Air velocity (m/s) |
| vrs | Terminal solid velocity (m/s) |
| vs | Solid velocity (m/s) |
| x | Coordinate (m) |
| Symbols | |
| α | Constant |
| β | Extinction coefficient (1/m) |
| βgs | Interphase drag force (kg/(m3s)) |
| γgs | Gas-solid heat transfer coefficient (W/(m2K)) |
| Γ | Effective conductivity parameter |
| εs | Particle emissivity |
| εw | Wall emissivity |
| ζ | Transmittance |
| Function of restitution coefficient | |
| Thermal efficiency | |
| θs | Granular temperature (m2/s2) |
| κp,θ | Granular conductivity (kg/(m•s)) |
| μ | Dilute phase shear viscosity (Pa•s) |
| μg | Air viscosity (Pa•s) |
| μge | Air effective viscosity (Pa•s) |
| μs | Granular shear viscosity (Pa•s) |
| ξg | Void porosity |
| Π | Exchange term between solid and air |
| ρg | Air density (kg/m3) |
| ρs | Solid density (kg/m3) |
| σ | Stefan–Boltzmann constant (5.67×10-8 W/(m2K4)) |
| τ | Time (s) |
| τg | Air stress-strain tensor (Pa) |
| τs | Solid stress-strain tensor (Pa) |
| Scattering albedo |
References
- Kim, K.; Siegel, N.; Kolb, G.; Rangaswamy, V.; Moujaes, S.F. A study of solid particle flow characterization in solar particle receiver. Sol. Energy 2009, 83, 1784–1793. [Google Scholar] [CrossRef]
- Siegel, N.P.; Ho, C.K.; Khalsa, S.S.; Kolb, G.J. Development and Evaluation of a Prototype Solid Particle Receiver: On-Sun Testing and Model Validation. J. Sol. Energy Eng. 2010, 132, 021008. [Google Scholar] [CrossRef]
- Ho, C.K.; Christian, J.M.; Yellowhair, J.; Siegel, N.; Jeter, S.; Golob, M.; Abdel-Khalik, S.I.; Nguyen, C.; Al-Ansary, H. On-Sun testing of an advanced falling particle receiver system. AIP Conf. Proc. 2016, 1734, 030022. [Google Scholar]
- Lee, T.; Lim, S.; Shin, S.; Sadowski, D.L.; Abdel-Khalik, S.I.; Jeter, S.M.; Al-Ansary, H. Numerical simulation of particulate flow in interconnected porous media for central particle-heating receiver applications. Sol. Energy 2015, 113, 14–24. [Google Scholar] [CrossRef] [Green Version]
- Martinek, J.; Ma, Z. Granular flow and heat-transfer study in a near-blackbody enclosed particle receiver. J. Sol. Energy Eng. 2015, 137, 051008. [Google Scholar] [CrossRef]
- Morris, A.B.; Ma, Z.; Pannala, S.; Hrenya, C.M. Simulations of heat transfer to solid particles flowing through an array of heated tubes. Sol. Energy 2016, 130, 101–115. [Google Scholar] [CrossRef] [Green Version]
- Ketchem, T.C. Experimental and Numerical Analysis of Heat Transfer in a Particle-Based Concentrated Solar Power Receiver. Ph.D. Thesis, Colorado School of Mines, Golden, CO, USA, 2015. [Google Scholar]
- Bai, F.; Zhang, Y.; Zhang, X.; Wang, F.; Wang, Y.; Wang, Z. Thermal performance of a quartz tube solid particle air receiver. Energy Procedia 2014, 49, 284–294. [Google Scholar] [CrossRef]
- Wang, F.; Bai, F.; Wang, Z.; Zhang, X. Numerical simulation of quartz tube solid particle air receiver. Energy Procedia 2015, 69, 573–582. [Google Scholar] [CrossRef]
- Wang, F.; Bai, F.; Wang, T.; Li, Q.; Wang, Z. Experimental study of a single quartz tube solid particle air receiver. Sol. Energy 2016, 123, 185–205. [Google Scholar] [CrossRef]
- Flamant, G.; Gauthier, D.; Benoit, H.; Sans, J.L.; Boissière, B.; Ansart, R.; Hemati, M. A new heat transfer fluid for concentrating solar systems: Particle flow in tubes. Energy Procedia 2014, 49, 617–626. [Google Scholar] [CrossRef]
- Marti, J.; Haselbacher, A.; Steinfield, A. A numerical investigation of gas-particle suspensions as heat transfer media for high-temperature concentrated solar power. Int. J. Heat Mass Transf. 2015, 90, 1056–1070. [Google Scholar] [CrossRef]
- García-Triñanes, P.; Seville, J.; Boissière, B.; Ansart, R.; Leadbeater, T.; Parker, D. Hydrodynamics and particle motion in upward flowing dense particle suspensions: Application in solar receivers. Chem. Eng. Sci. 2016, 146, 346–356. [Google Scholar] [CrossRef] [Green Version]
- Benoit, H. Tubular Solar Receiver with Dense Particle Suspension Upward Flow. Ph.D. Thesis, Universite De Perpignan Via Domitia, Perpignan, France, 2015. [Google Scholar]
- Wu, W.; Trebing, D.; Amsbeck, L.; Buck, R.; Pitz-Paal, R. Prototype testing of a centrifugal particle receiver for high-temperature concentrating solar applications. J. Sol. Energy Eng. 2015, 137, 041011. [Google Scholar] [CrossRef]
- Urrutia, A.R.; Benoit, H.; Zambon, M.; Gauthier, D.; Flamant, G.; Mazza, G. Simulation of the behavior of a dense SiC particle suspension as an energy transporting vector using computational fluid dynamics (CFD). Chem. Eng. Res. Des. 2016, 106, 141–154. [Google Scholar] [CrossRef]
- Benoit, H.; Ansart, R.; García-Triñanes, P.; Gauthier, D.; Flamant, G.; Simonin, O. 3D numerical simulation of upflow bubbling fluidized bed in opaque tube under high flux solar heating. AIChE J. 2018, 64, 3857–3867. [Google Scholar] [CrossRef]
- Li, T.; Pannala, S.; Shahnam, M. Reprint of “CFD simulations of circulating fluidized bed risers, part II, evaluation of differences between 2D and 3D simulations. Powder Technol. 2014, 265, 13–22. [Google Scholar] [CrossRef]
- Peirano, E.; Delloume, V.; Leckner, B. Two- or three-dimensional simulations of turbulent gas –solid flows applied to fluidization. Chem. Eng. Sci. 2001, 56, 4787–4799. [Google Scholar] [CrossRef]
- Xie, N.; Battaglia, F.; Pannala, S. Effects of using two-versus three-dimensional computational modeling of fluidized beds: Part I, hydrodynamics. Powder Technol. 2008, 182, 1–13. [Google Scholar] [CrossRef]
- Xie, N.; Battaglia, F.; Pannala, S. Effects of using two-versus three-dimensional computational modeling of fluidized beds: Part II, budget analysis. Powder Technol. 2008, 182, 14–24. [Google Scholar] [CrossRef]
- Go´mez, L.C.; Milioli, F.E. Numerical study on the influence of various physical parameters over the gas- solid two-phase flow in the 2D riser of a circulating fluidized bed. Powder Technol. 2003, 132, 216–225. [Google Scholar] [CrossRef]
- Almuttahar, A.; Taghipour, F. Computational fluid dynamics of a circulating fluidized bed under various fluidization conditions. Chem. Eng. Sci. 2008, 63, 1696–1709. [Google Scholar] [CrossRef]
- Bakshi, A.; Altantzis, C.; Ghoniem, A.F. Towards accurate three-dimensional simulation of dense multi-phase flows using cylindrical coordinates. Powder Technol. 2014, 264, 242–255. [Google Scholar] [CrossRef] [Green Version]
- Syamlal, M.; Rogers, W.; O’Brien, T.J. MFIX Documentation: Theory Guide; National Energy Technology Laboratory: Morgantown, WV, USA, 1993.
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef] [Green Version]
- Wen, C.Y.; Yu, Y.H. Mechanics of fluidization. Chem. Eng. Prog. Symp. Ser. 1966, 62, 100–111. [Google Scholar]
- Blaszczuk, A.; Nowak, W. Bed-to-wall heat transfer coefficient in a supercritical CFB boiler at different bed particle sizes. Int. J. Heat Mass Transf. 2014, 79, 736–749. [Google Scholar] [CrossRef]
- Formisani, B.; Girimonte, R.; Mancuso, L. Analysis of the fluidization process of particle beds at high temperature. Chem. Eng. Sci. 1998, 53, 951–961. [Google Scholar] [CrossRef]
- Benyahia, S.; Syamlal, M.; O’Brien, T.J. Summary of MFIX Equations 2012-1; National Energy Technology Laboratory: Morgantown, WV, USA, 2012.
- Syamlal, M.; O’brien, T.J. Simulation of granular layer inversion in liquid fluidized beds. Int. J. Multiph. Flow 1988, 14, 473–481. [Google Scholar] [CrossRef]
- Modest, M.F. Radiative Heat Transfer, 2nd ed.; Academic Press: New York, NY, USA, 2003; pp. 465–580. [Google Scholar]
- Gunn, D.J. Transfer of heat or mass to particles in fixed and fluidized beds. Int. J. Heat Mass Transf. 1978, 21, 467–476. [Google Scholar] [CrossRef]
- Li, X.; Kong, W.; Wang, Z.; Chang, C.; Bai, F. Thermal model and thermodynamic performance of molten salt cavity receiver. Renew. Energy 2010, 35, 981–988. [Google Scholar] [CrossRef]
- Cengel, A. Heat Transfer: A Practical Approach, 2nd ed.; McGraw-Hill: New York, NY, USA, 2003; pp. 384–389. [Google Scholar]
- Zehner, P.; Schlunder, E.U. Warmeleitfahigkeit von Schuttungen bei Massigen Temperaturen. Chem. Ing. Tech. 1970, 42, 933–941. [Google Scholar] [CrossRef]
- Marti, J.; Roesle, M.; Steinfeld, A. Combined experimental numerical approach to determine radiation properties of particle suspensions. J. Heat Transf. 2014, 136, 092701. [Google Scholar] [CrossRef]
- Wang, P.; Vafai, K.; Liu, D.Y.; Xu, C. Analysis of collimated irradiation under local thermal non-equilibrium condition in a packed bed. Int. J. Heat Mass Transf. 2015, 80, 789–801. [Google Scholar] [CrossRef]
- Geldart, D. Types of gas fluidization. Powder Technol. 1973, 7, 285–292. [Google Scholar] [CrossRef]
- Makkawi, Y.T.; Wright, P.C.; Ocone, R. The effect of friction and inter-particle cohesive forces on the hydrodynamics of gas-solid flow: A comparative analysis of theoretical predictions and experiments. Powder Technol. 2006, 163, 69–79. [Google Scholar] [CrossRef]
- Li, T.; Zhang, Y.; Grace, J.R.; Bi, X. Numerical investigation of gas mixing in gas-solid fluidized beds. AIChE J. 2010, 56, 2280–2296. [Google Scholar] [CrossRef]
- Johnson, P.C.; Jackson, R. Frictional collisional constitutive relations for granular materials, with application to plane shearing. J. Fluid Mech. 1987, 176, 67–93. [Google Scholar] [CrossRef]
- Li, T.; Benyahia, S. Evaluation of wall boundary condition parameters for gas-solids fluidized bed simulations. AIChE J. 2013, 59, 3624–3632. [Google Scholar] [CrossRef]



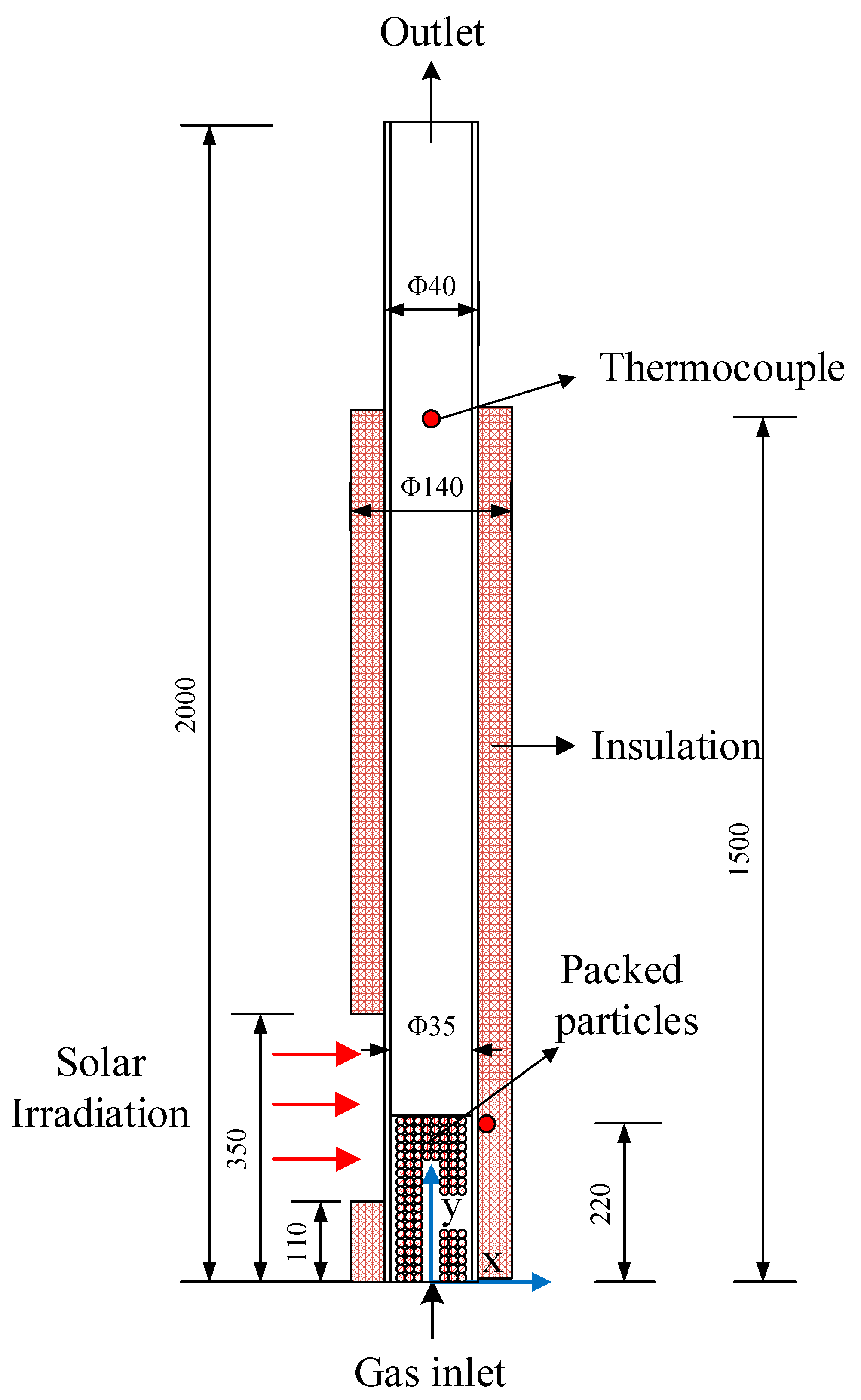


| Name | Specification | Quantity | Remark | Uncertainty |
|---|---|---|---|---|
| Air compressor | 1.2 MPa | 1 | 3 phase | / |
| Thermocouple | Type K | 6 | / | ±0.5% |
| Flow meter | Thermal mass flow meter | 1 | 0–41.9 Nm3/h | ±1% |
| Data acquisition | HP Agilent 34972A | 1 | 3M/60C | / |
| Air tank | / | 1 | 2 m3 | / |
| Buffer tank | / | 1 | 0.3 m3 | / |
| Case | 2.0 m Tube | Current (A) | Initial Packed Particle Mass (g) | Inlet Air Temperature (°C) | Outlet Air Temperature (°C) | Air Mass Flow Rate (g/s) | Thermal Efficiency (%) |
|---|---|---|---|---|---|---|---|
| 1 | Q235B | 50 | 160 | 24 | 263 | 0.66 | 31.7 |
| 2 | Q235B | 50 | 160 | 24 | 258 | 0.77 | 36.3 |
| 3 | Q235B | 50 | 240 | 23 | 270 | 0.66 | 33.1 |
| 4 | Q235B | 50 | 240 | 23 | 267 | 0.76 | 37.4 |
| 5 | Quartz | 50 | 160 | 23 | 269 | 0.67 | 33.7 |
| 6 | Quartz | 50 | 160 | 23 | 273 | 0.77 | 38.5 |
| 7 | Quartz | 50 | 240 | 21 | 297 | 0.69 | 38.5 |
| 8 | Quartz | 50 | 240 | 21 | 304 | 0.79 | 44.6 |
| 9 | Quartz | 100 | 160 | 27 | 509 | 0.53 | 17.5 |
| 10 | Quartz | 100 | 160 | 27 | 564 | 0.58 | 22.9 |
| 11 | Quartz | 100 | 240 | 25 | 530 | 0.53 | 21.9 |
| 12 | Quartz | 100 | 240 | 25 | 613 | 0.59 | 24.2 |
| Gas-phase Equations | |
| Continuity equation | |
| Momentum equation | |
| Energy equation | |
| Solid-phase Equations | |
| Continuity equation | |
| Momentum equation | |
| Energy equation | |
| Constitutive Equations | |
| Gas stress tensor | |
| Solid phase stress tensor | |
| Granular temperature | |
| Interphase drag model | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Wang, Z. Experimental and Numerical Investigations on the Fluidized Heat Absorption inside Quartz Glass and Metal Tubes. Energies 2019, 12, 806. https://doi.org/10.3390/en12050806
Zhang S, Wang Z. Experimental and Numerical Investigations on the Fluidized Heat Absorption inside Quartz Glass and Metal Tubes. Energies. 2019; 12(5):806. https://doi.org/10.3390/en12050806
Chicago/Turabian StyleZhang, Shengchun, and Zhifeng Wang. 2019. "Experimental and Numerical Investigations on the Fluidized Heat Absorption inside Quartz Glass and Metal Tubes" Energies 12, no. 5: 806. https://doi.org/10.3390/en12050806




