Research on a Faulty Line Selection Method Based on the Zero-Sequence Disturbance Power of Resonant Grounded Distribution Networks
Abstract
:1. Introduction
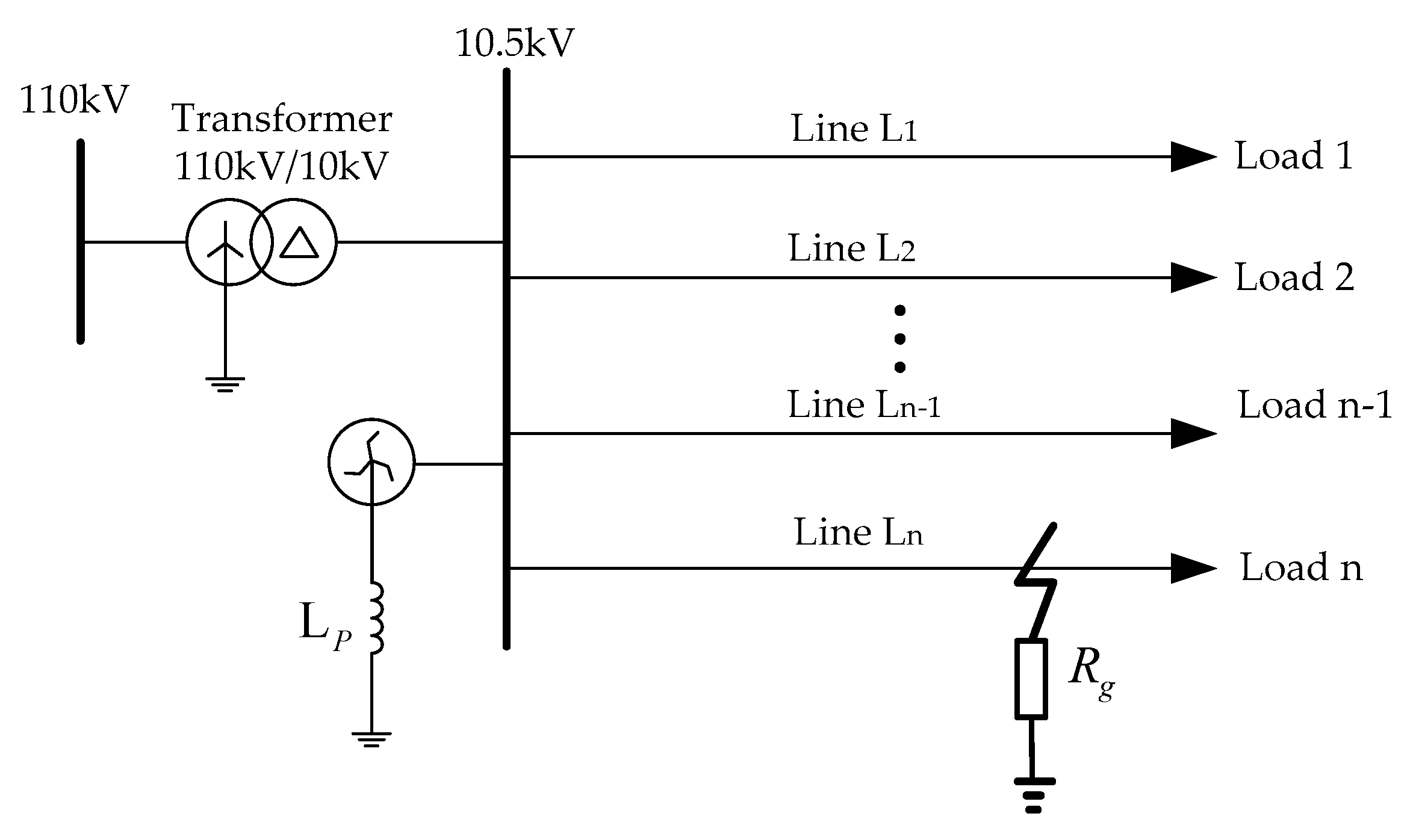
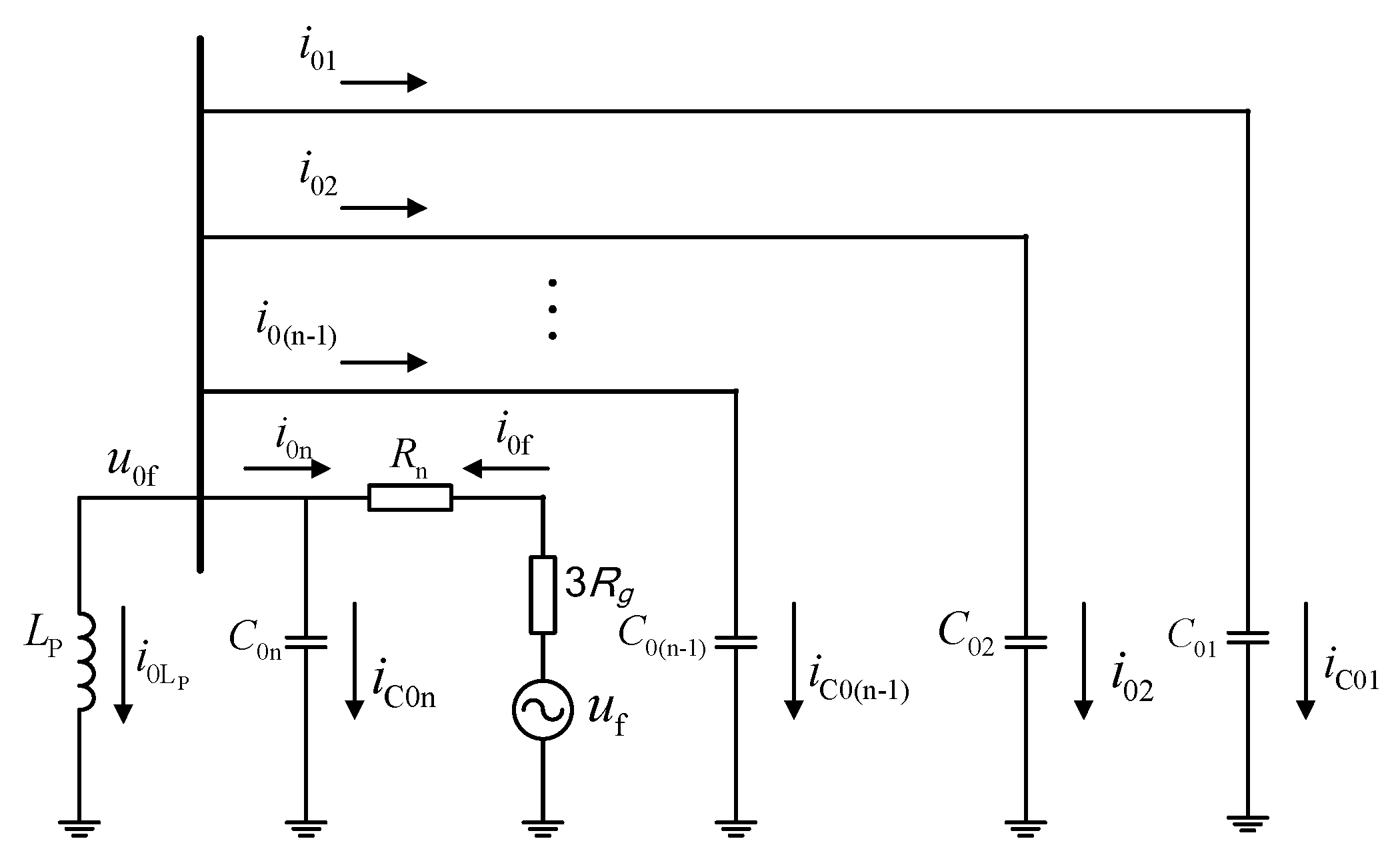
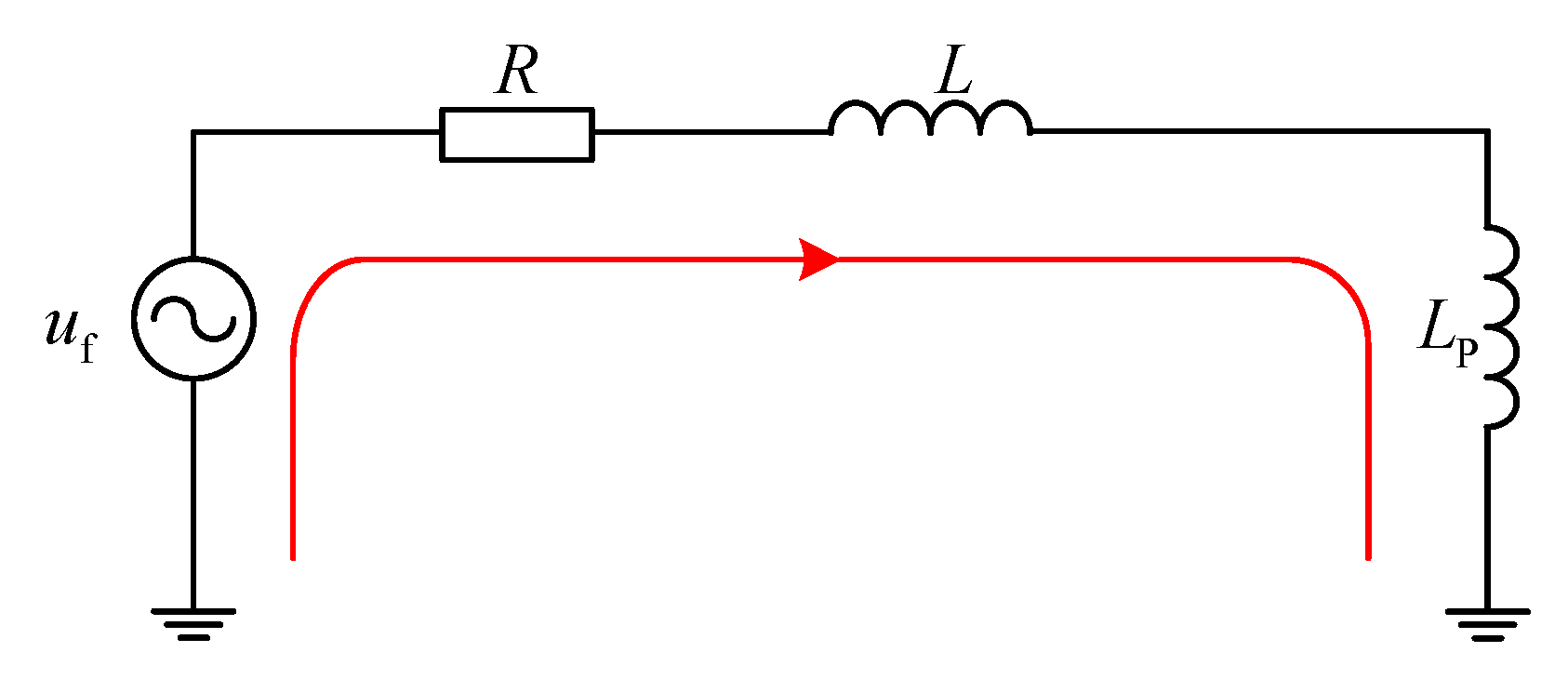
2. Characteristics of Transient Zero-sequence Current in RGDN
- is the equivalent source at the fault point, that is , where is the voltage amplitude of the fault phase, and is the fundamental angular frequency, and is the initial phase angle at the fault time;
- is the neutral point displacement voltage;
- is anti-arc coil branch current, is the zero-sequence current of each line; is the zero sequence capacitance of each line to ground ().
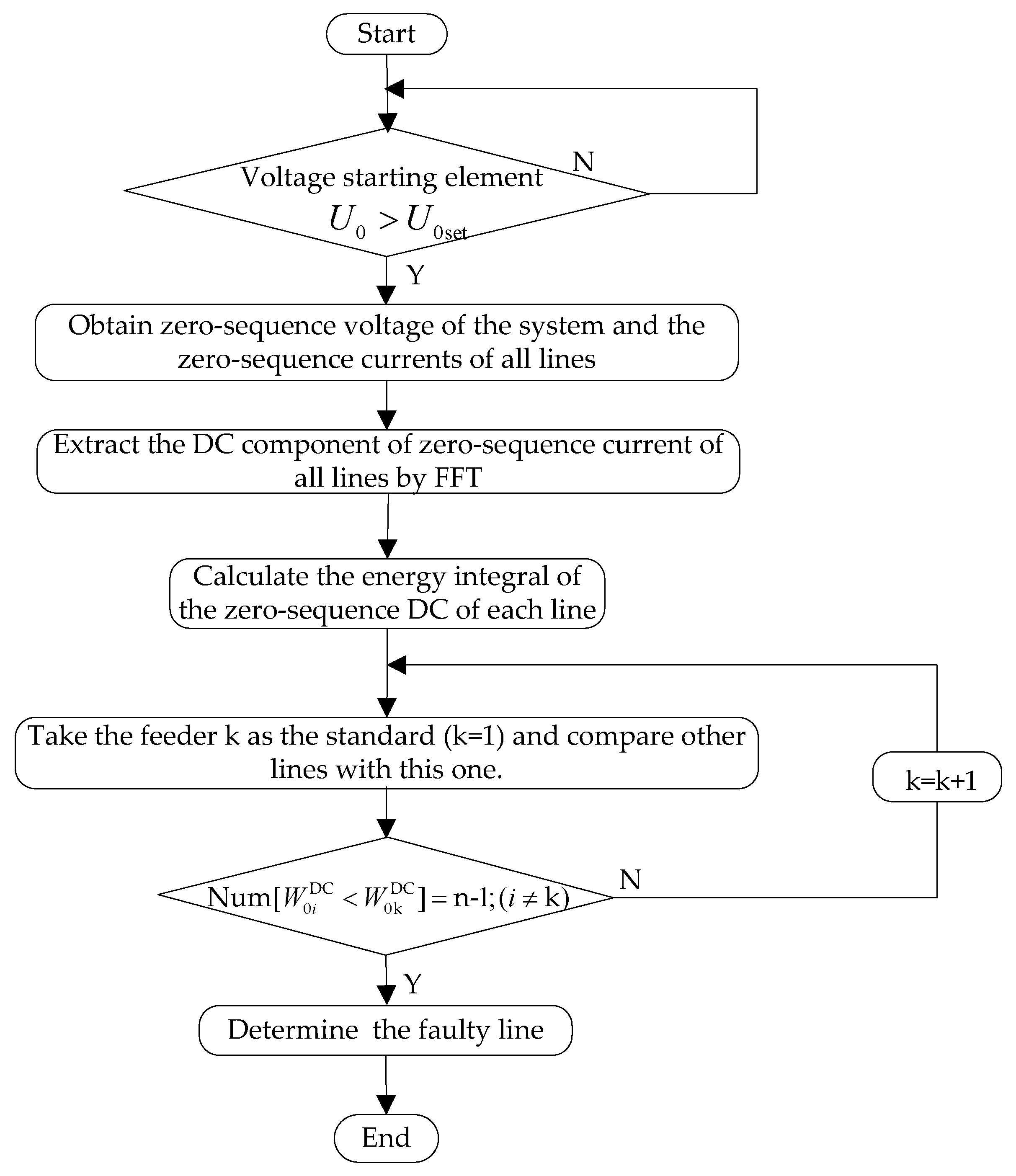
3. FLS Scheme Using Energy Integral of Zero-Sequence DC Component
- Step 1: Collect the bus terminal zero-sequence voltage in real time and judge whether that zero-voltage element exceeds the setting value, if not, return to continue; else, the system may occurred a SPG fault, perform the next step.
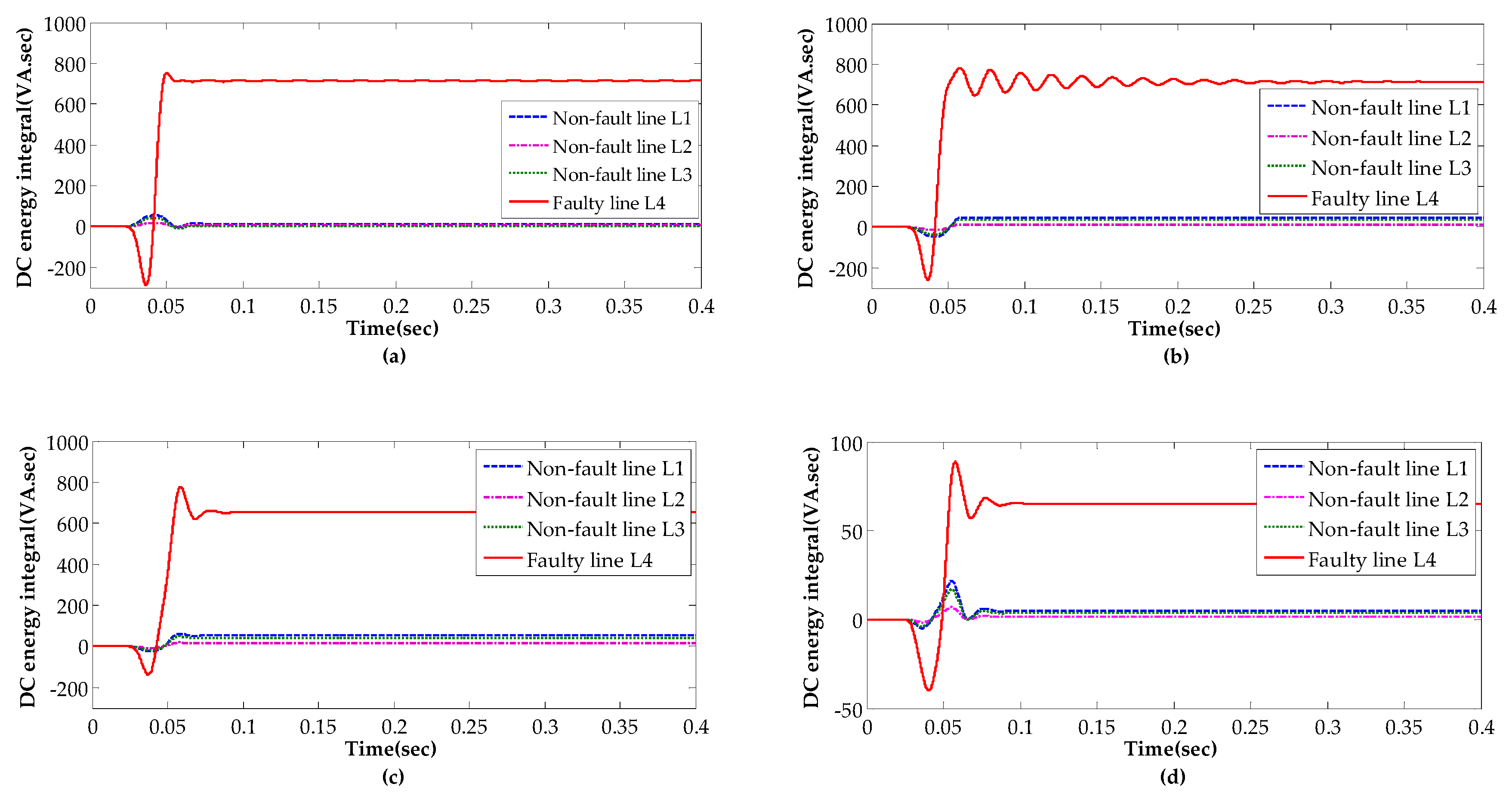
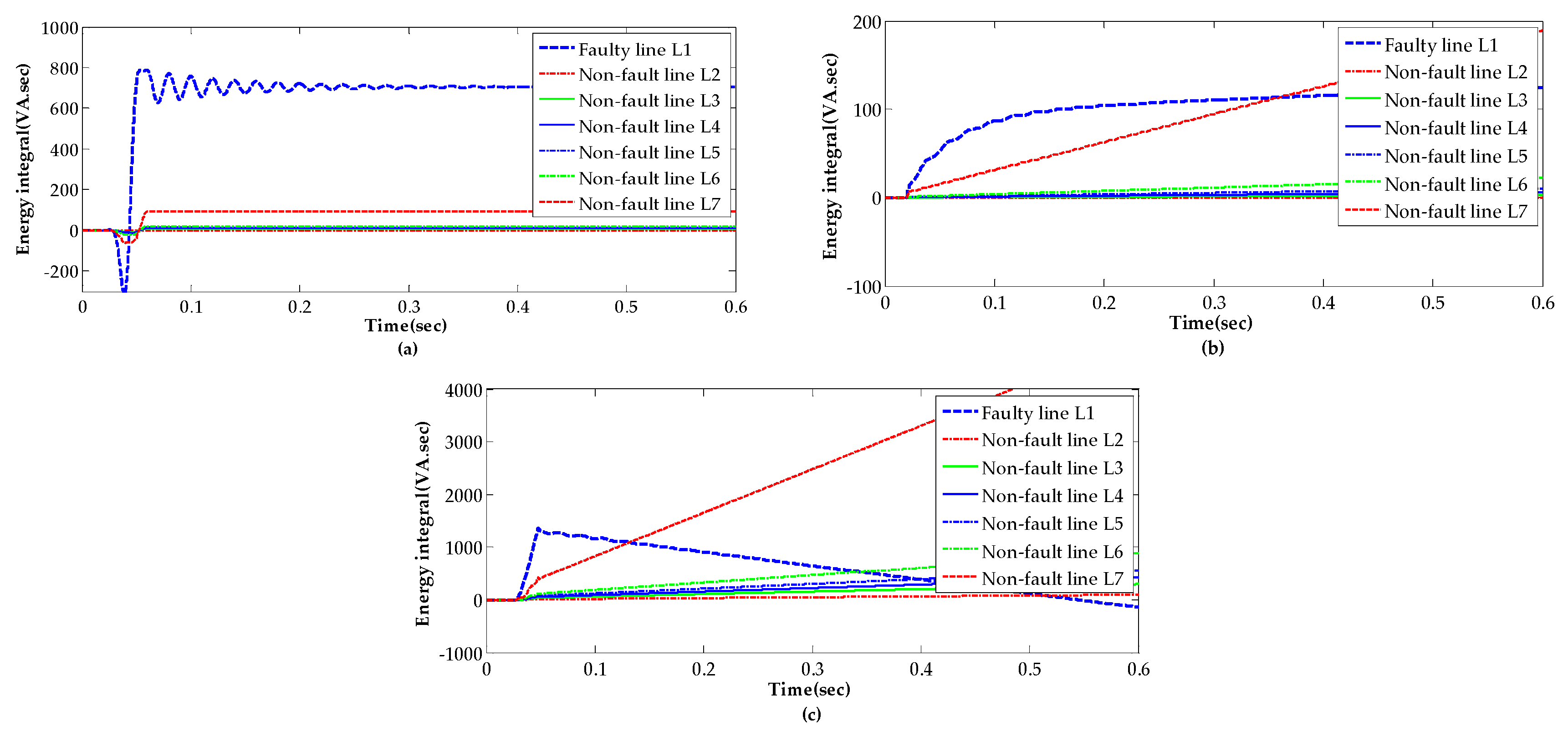
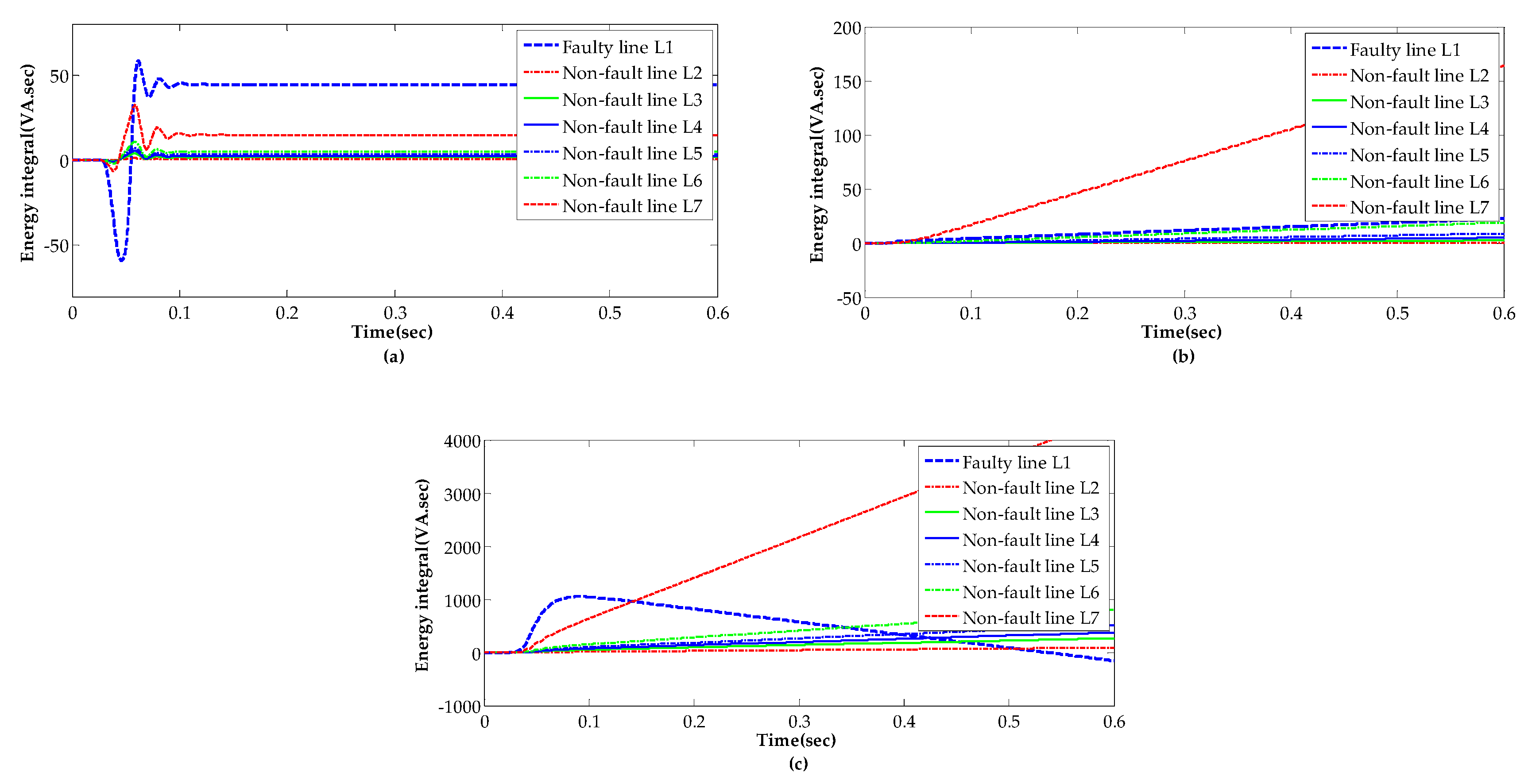
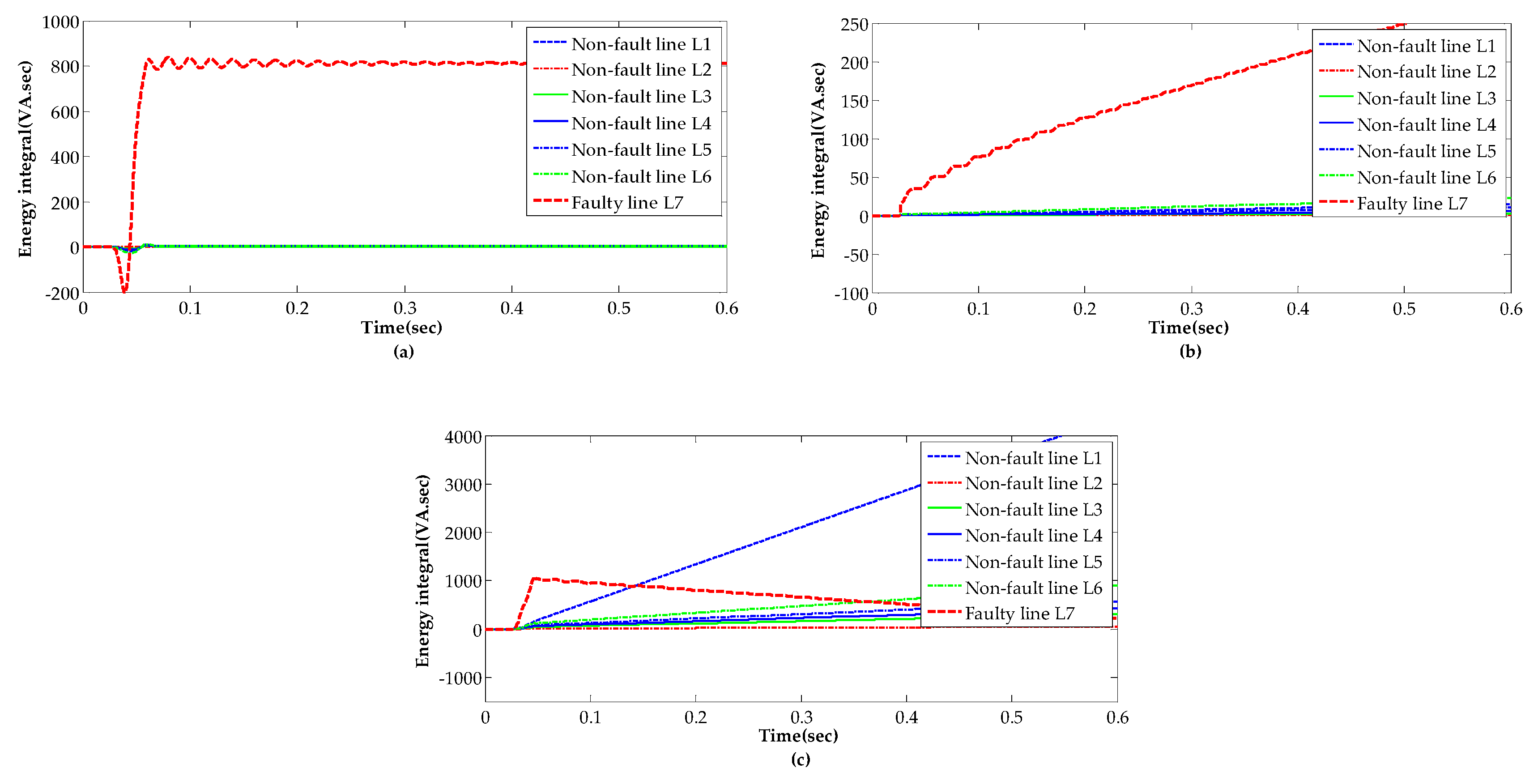
- Step 2: Obtain the zero-sequence currents of all lines and extract the DC component by fast Fourier transform (FFT), then calculate the energy integral of the zero-sequence DC current of each line.
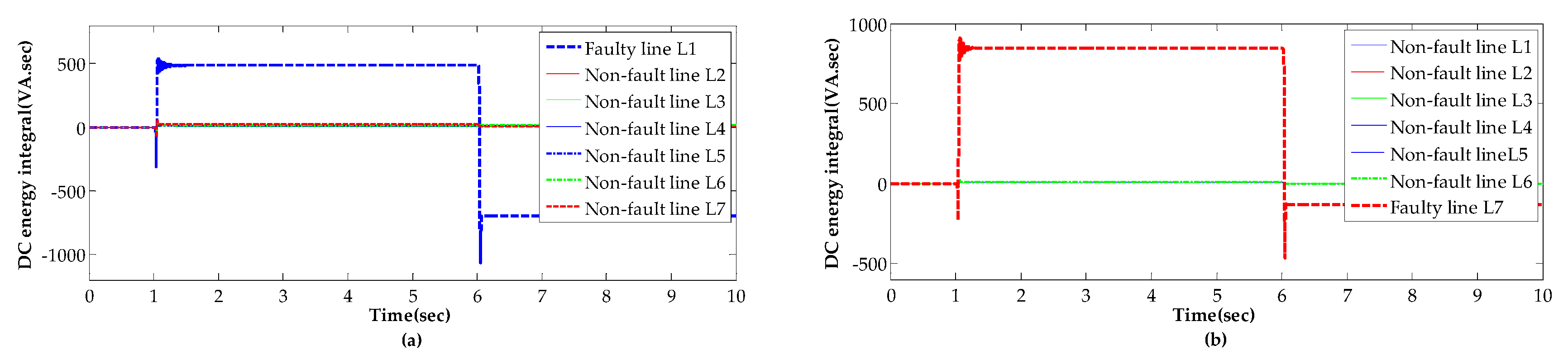
- Step 3: By comparing the DC energy of all lines one by one, the line with the largest energy integral is identified as the faulty line and the result feedback to fault processing system timely.
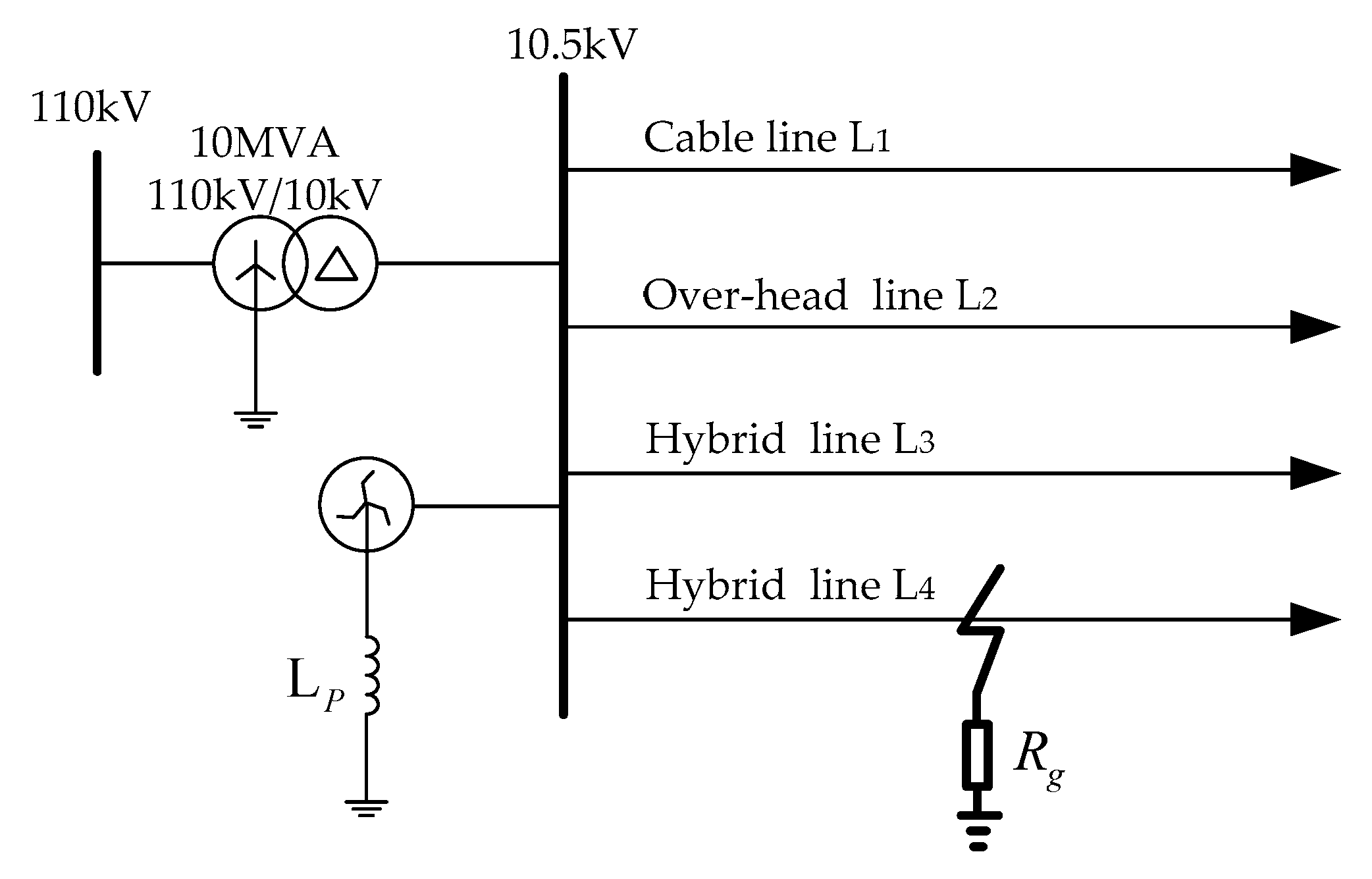
4. Simulation Study
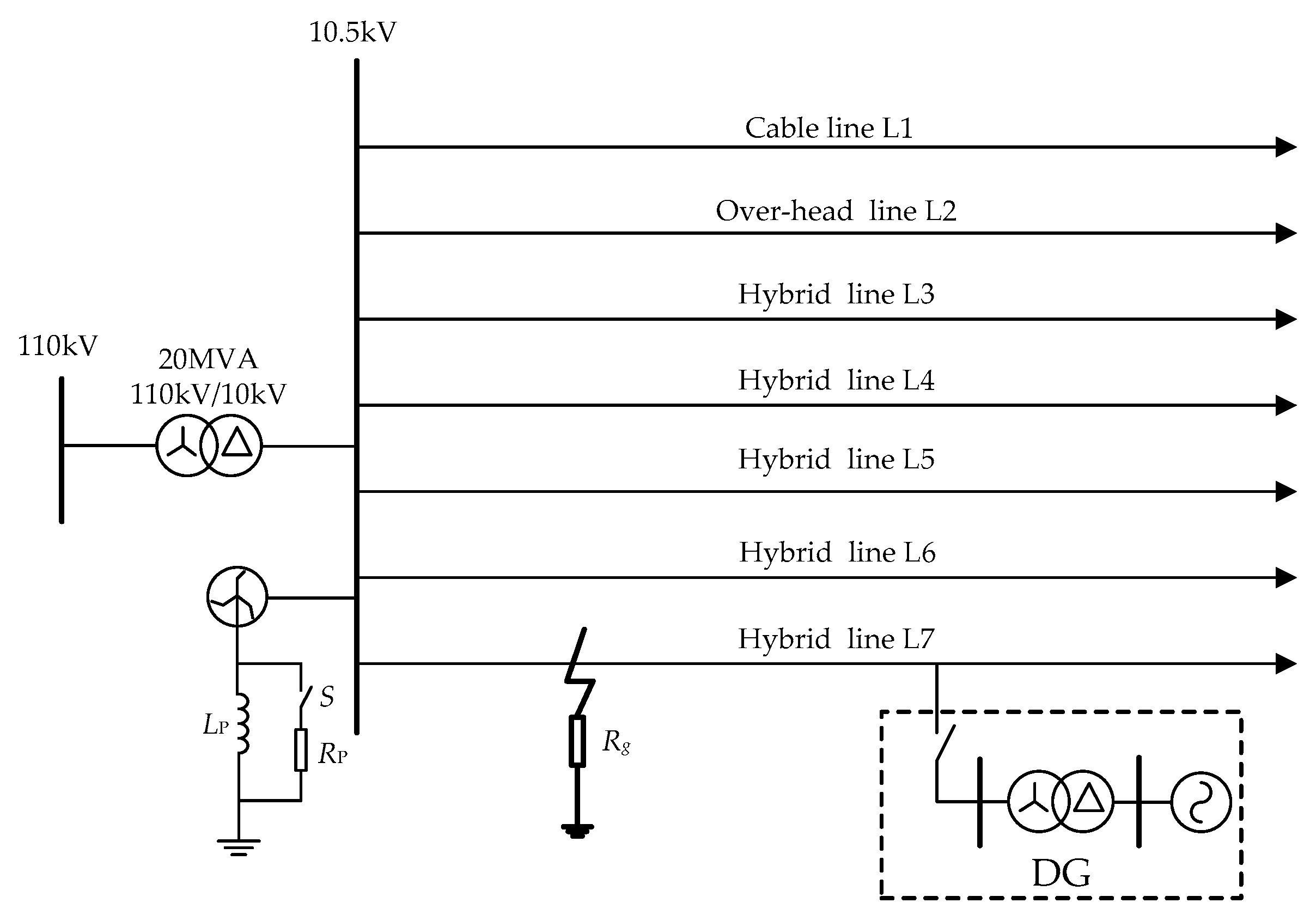
4.1. Simulation Modeling
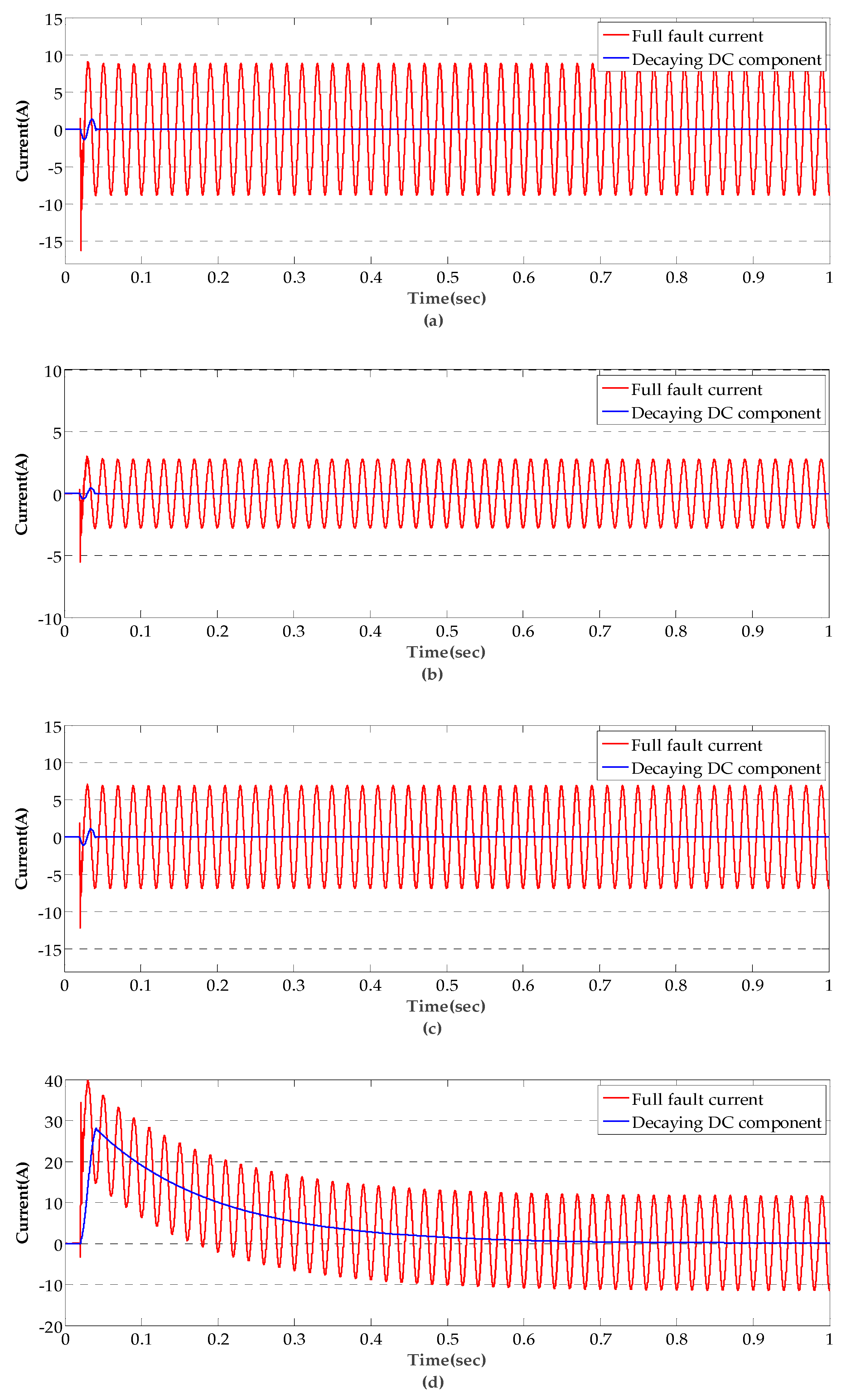
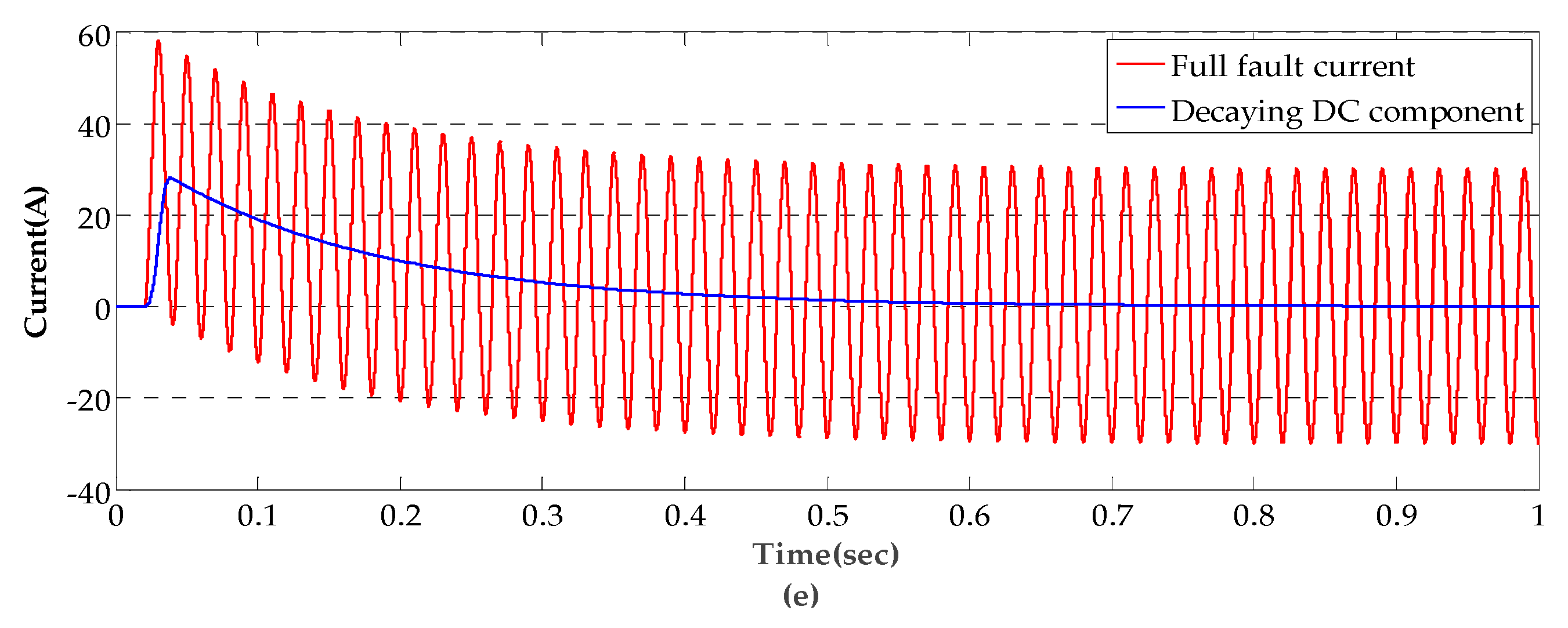
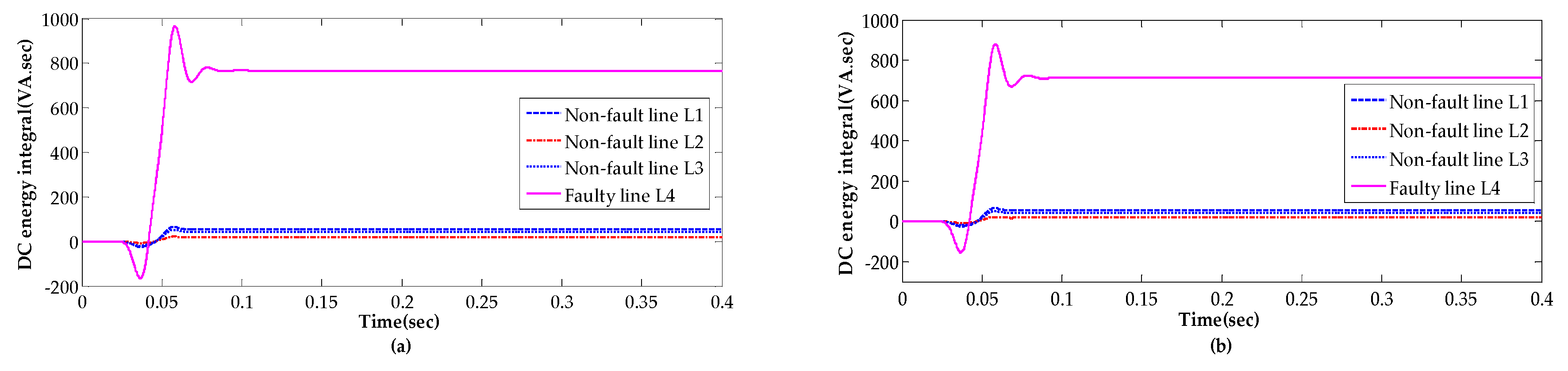
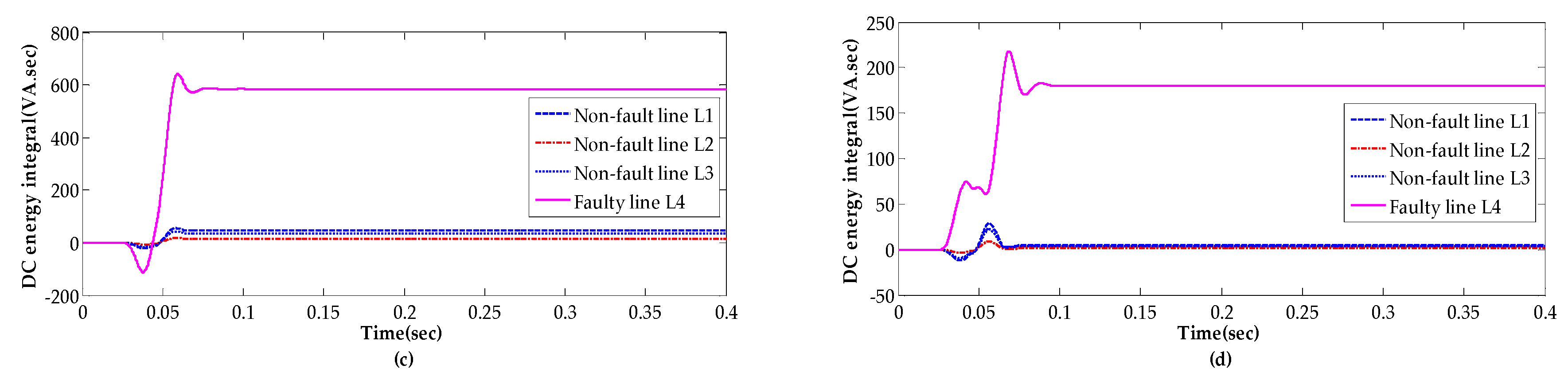
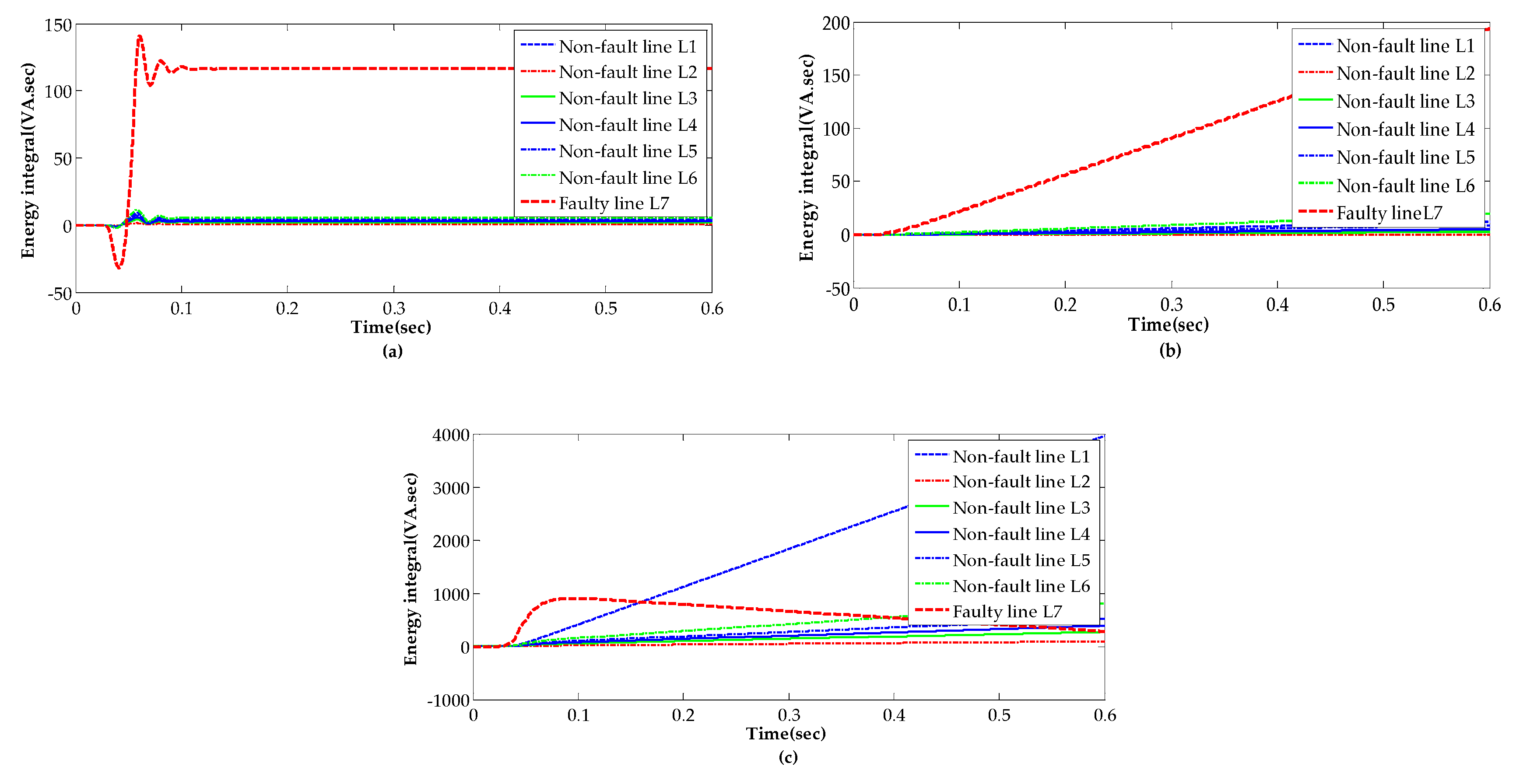
4.2. Performance Analysis
4.3. Analysis of Other Conditions
- the line L1 is a 5 km cable line;
- the line L2 is a 20 km over-head line;
- the line L3 is a hybrid of a 2 km cable line and a 15 km over-head line;
- the line L4 is a hybrid of a 3 km cable line and a 10 km over-head line;
- the line L5 is a hybrid of a 4 km cable line and a 12 km over-head line;
- the line L6 is a hybrid of a 6 km cable line and a 13 km over-head line;
- the line L7 is a hybrid of a 18 km cable line and a 5 km over-head line;
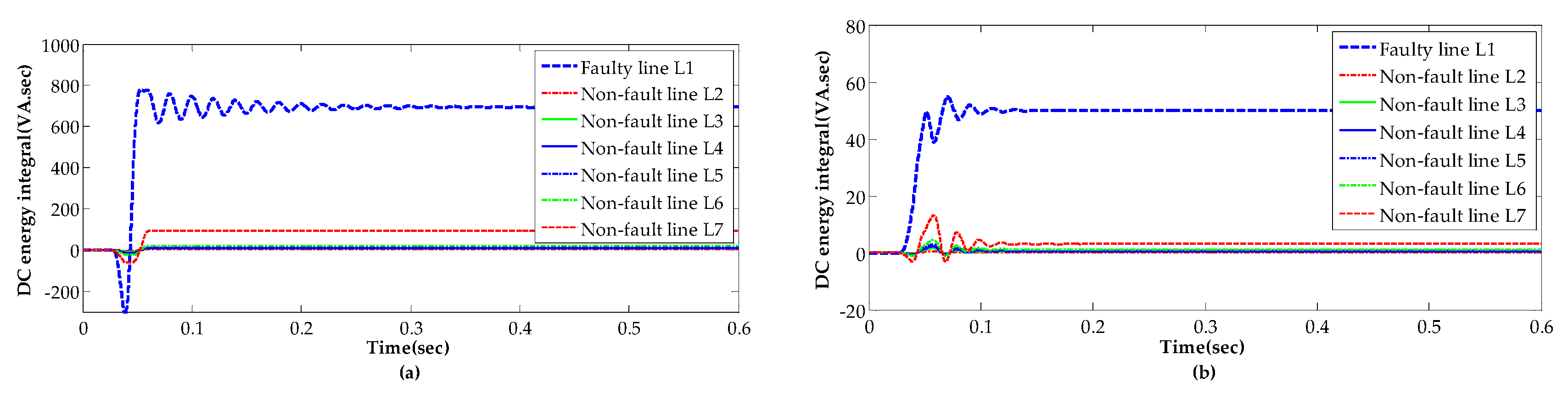
4.4. Comparison Analysis
5. Conclusions
- This paper analyzed in detail the characteristics of the currents in zero-sequence of the faulty line and the sound line. It found that the current consists of abundant decaying slowly DC component in the faulty line, but the DC component is weak and attenuated quickly in the sound line.
- Thus, a FLS scheme based on energy integral of DC component in zero-sequence is developed. The simulation under different conditions verified that the proposed FLS can detect the faulty line quickly and accurately.
- Moreover, the performance was assessed under various fault conditions, and a comparison study was made between the proposed method and other transient zero-sequence energy- based methods, indicating that the proposed method has better capability and adaptability than other transient zero-sequence energy methods, and it is more suitable for field application.
Author Contributions
Funding
Conflicts of Interest
References
- Chaari, O.; Bastard, P.; Meunier, M. Prony’s method: An effect tool for the analysis of earth fault currents in Petersen-coil-protected networks. IEEE Trans. Power Deliv. 1995, 3, 1234–1241. [Google Scholar] [CrossRef]
- Zhang, J.; He, Z.; Lin, S.; Zhang, Y.; Qian, Q. An ANFIS-based fault classification approach in power distribution system. Int. J. Electr. Power Energy Syst. 2013, 49, 243–252. [Google Scholar] [CrossRef]
- Sadeh, J.; Bakhshizadeh, E.; Kazemzadeh, R. A new fault location algorithm for radial distribution systems using modal analysis. Int. J. Electr. Power Energy Syst. 2013, 45, 271–278. [Google Scholar] [CrossRef]
- Guo, Z.; Yao, J.; Yang, S.; Zhang, H.; Mao, T.; Dong, T. A new method for non-unit protection of power transmission lines based on fault resistance and fault angle reduction. Int. J. Electr. Power Energy Syst. 2014, 55, 760–769. [Google Scholar] [CrossRef]
- Verho, P.; Nikander, A.; Jarventausta, P. Aspects on development of distribution network fault location and management. Proc. IEE Int. Conf. Dev. Power Syst. Protect. 2004, 2, 784–787. [Google Scholar]
- Xue, Y.; Li, J.; Xu, B. Transient equivalent circuit and transient analysis of single-phase earth fault in arc suppression coil grounded system. Electr. Power Autom. Equip. 2015, 35, 5703–5714. [Google Scholar]
- Su, J. Research of neutral grounding modes in power distribution network. Power Syst. Protect. Control 2013, 8, 141–148. [Google Scholar]
- Guo, M.; Gao, Y.; Yang, G. Faulty line detection based on transient waveform difference recognition for resonant earthed system. Electr. Power Autom. Equip. 2014, 5, 59–66. [Google Scholar]
- Guo, Q.; Wu, T. Survey of the methods to select faulty line in neutral point ineffectively grounded power system. Power Syst. Protec. Control 2010, 2, 146–152. [Google Scholar]
- Lin, X.; Sun, J.; Kuran, I.; Zhao, F.; Li, Z.; Li, X.; Yang, D. Zero-sequence compensated admittance based faulty feeder selection algorithm used for distribution network with neutral grounding through Peterson-coil. Electr. Power Energy Syst. 2014, 63, 747–752. [Google Scholar] [CrossRef]
- Zhang, H.; He, Z.; Zhang, J. Frequency spectrum characteristic analysis of single-phase grounding fault in resonant grounded systems. Autom. Electr. Power Syst. 2012, 6, 79–84. [Google Scholar]
- Song, J.; Li, Y.; Shi, Z.; Ma, L. A faulty line selection method for resonant earthed system with high accuracy. Power Syst. Protect. Control 2017, 6, 9–15. [Google Scholar]
- Han, X.L.; Wu, Q.H.; Li, M.S.; Zhang, L.L. Mathematical morphology-based single phase-to-ground fault feeder selector for a resonant grounded distribution system. IEEJ Trans. Electr. Electr. Eng. 2018, 13, 517–518. [Google Scholar] [CrossRef]
- Costa, F.; Souza, B.; Brito, N.; Silva, J. Real-Time Detection of transients induced by high-impedance faults based on the boundary wavelet transform. IEEE Trans. Indus. Appl. 2015, 6, 5312–5323. [Google Scholar] [CrossRef]
- Veerapandiyan, V.; Noor, I.; Rajeswari, R.; Muhammad, M.; Mariammal, T.; Mohammad, L. High impedance fault detection in medium voltage distribution network using discrete wavelet transform and adaptive neuro-fuzzy inference system. Energies 2018, 11, 3330. [Google Scholar] [CrossRef]
- Russell, B.; Benner, C. Arcing fault detection for distribution feeders: Security assessment in long term field trials. IEEE Trans. Power Deliv. 1995, 2, 676–683. [Google Scholar] [CrossRef]
- Benner, C.; Russell, B. Practical high-impedance fault detection on distribution feeders. IEEE Trans. Ind. Appl. 1997, 3, 635–640. [Google Scholar] [CrossRef]
- Wang, X.; Wei, Y.; Zeng, Z.; Hou, Y.; Gao, J.; Wei, X. Faulty line selection method of small current to ground system based on atomic sparse decomposition and extreme learning machine. J. Sens. 2015, 2015, 678120. [Google Scholar] [CrossRef]
- Cui, T.; Dong, X.; Bo, Z.; Juszczyk, A. Hilbert-transform-based transient intermittent earth fault detection in non-effectively grounded distribution systems. IEEE Trans. Power Deliv. 2011, 1, 143–151. [Google Scholar] [CrossRef]
- Wu, L.; Huang, C.; Huang, J.; Zheng, J. Fault line detection algorithm for resonant ground power distribution system by improving energy. Comput. Eng. Appl. 2013, 16, 248–251. [Google Scholar]
- Zhang, J.; Liu, H.; He, Z.; Wu, S. A novel fault line identification approach based on instantaneous energy function. Power Syst. Prot. Control 2012, 14, 1–9. [Google Scholar]
- Fang, Y.; Xue, Y.; Song, H.; Guan, Y.; Yang, F.; Xu, B. Transient energy analysis and faulty feeder identification method of high impedance fault in the resonant grounding system. Proc. Chim. Soc. Electr. Eng. 2018, 19, 5636–5645. [Google Scholar]
- Haghifam, M.; Sedighi, A.; Malik, O. Development of a fuzzy inference system based on genetic algorithm for high-impedance fault detection. IEE Gen. Trans. Distr. 2006, 3, 359–367. [Google Scholar] [CrossRef]
- Xu, Y.; Guo, M.; Chen, B.; Yang, G. Modeling and simulation analysis of arc in distribution network. Power Syst. Prot. Control 2015, 7, 57–64. [Google Scholar]
- Xue, Y.; Guo, L. Discussion about grounding mode of active distribution networks. Distrib. Util. 2015, 6, 6–11. [Google Scholar]
- Wang, F.; Cheng, H. Application of Arc Suppression Coil and Damping Resistance in Distribution Network. China Water Transp. 2016, 12, 141–143. [Google Scholar]
- Wang, W.; Zhou, J.; Ji, S.; Cao, T.; Zhang, J.; Ou, X.; Li, Y. Impact of Neutral Grounding Mode on Ferroesonance in 35 kV Power System. High Volt. App. 2010, 1, 93–96. [Google Scholar]
- Huang, Z.; Wei, L.; Li, G. Flexible grounding via arc-suppression coil and low resistance in parallel. Guang Dong Electr. Power 2014, 6, 64–67. [Google Scholar]

| Line Types | Sequence | Resistance (/km) | Inductance | Capacitance |
|---|---|---|---|---|
| Over-head line | positive-sequence | 0.1250 | 1.300 | 0.0096 |
| zero-sequence | 0.2750 | 4.600 | 0.0054 | |
| Cable line | positive-sequence | 0.2700 | 0.2250 | 0.3390 |
| zero-sequence | 2.7000 | 1.0190 | 0.2800 |
| Grounding Resistance (Ω) | Fault Position (km) | Fault Initial Phase Angle (°) | Non-Fault Line L1 | Non-Fault Line L2 | Non-Fault Line L3 | Fault Line L4 |
|---|---|---|---|---|---|---|
| 50 | 8 | 0 | 17.23% | 17.24% | 17.29% | 64.80% |
| 45 | 21.21% | 21.17% | 21.19% | 122.71% | ||
| 90 | 21.34% | 21.24% | 21.43% | 120.26% |
| Grounding Resistance (Ω) | Fault Position (km) | Fault Initial Phase Angle (°) | Non-Fault Line L1 | Non-Fault Line L2 | Non-Fault Line L3 | Fault Line L4 |
|---|---|---|---|---|---|---|
| 50 | 2 | 45 | 20.94% | 20.81% | 20.93% | 125.66% |
| 8 | 21.21% | 21.17% | 21.19% | 122.71% | ||
| 16 | 21.41% | 21.36% | 21.40% | 120.92% |
| Grounding Resistance (Ω) | Fault Position (km) | Fault Initial Phase Angle (°) | Non-Fault Line L1 | Non-Fault Line L2 | Non-Fault Line L3 | Fault Line L4 |
|---|---|---|---|---|---|---|
| 50 | 8 | 45 | 21.21% | 21.17% | 21.19% | 122.71% |
| 500 | 23.79% | 23.65% | 23.69% | 64.76% | ||
| 1000 | 25.18% | 25.07% | 25.13% | 58.40% |
| Fault Position (km) | Grounding Resistance (Ω) | Fault Initial Phase Angle (°) | DC Energy Integral (VA·s) | Detection Results | |||
|---|---|---|---|---|---|---|---|
| Non-Fault Line L1 | Non-Fault Line L2 | Non-Fault Line L3 | Faulty Line L4 | ||||
| 2 | 50 | 0 | 64.12 | 20.22 | 50.05 | 825.61 | √ |
| 5 | 64.13 | 20.23 | 50.06 | 825.63 | √ | ||
| 10 | 64.38 | 20.31 | 50.25 | 823.31 | √ | ||
| 20 | 65.28 | 20.54 | 50.96 | 799.92 | √ | ||
| 35 | 66.05 | 20.85 | 51.55 | 764.70 | √ | ||
| 50 | 64.85 | 20.54 | 50.59 | 693.55 | √ | ||
| 70 | 50.23 | 14.92 | 39.55 | 578.82 | √ | ||
| 90 | 21.12 | 5.95 | 17.22 | 137.22 | √ | ||
| Fault Position (km) | Grounding Resistance (Ω) | Fault Initial Phase Angle (°) | DC Energy Integral (VA·s) | Detection Results | |||
|---|---|---|---|---|---|---|---|
| Non-Fault Line L1 | Non-Fault Line L2 | Non-Fault Line L3 | Faulty Line L4 | ||||
| 0.1 | 50 | 45 | 65.29 | 20.60 | 50.98 | 699.96 | √ |
| 1 | 65.15 | 20.63 | 50.80 | 696.90 | √ | ||
| 2 | 64.85 | 20.54 | 50.60 | 693.53 | √ | ||
| 4 | 64.27 | 20.31 | 50.23 | 686.92 | √ | ||
| 7 | 63.56 | 20.00 | 49.65 | 677.29 | √ | ||
| 9 | 62.90 | 19.75 | 49.13 | 669.48 | √ | ||
| 13 | 61.67 | 19.34 | 48.07 | 656.17 | √ | ||
| 16 | 60.51 | 18.96 | 47.27 | 647.76 | √ | ||
| Fault Position (km) | Grounding Resistance (Ω) | Fault Initial Phase Angle (°) | DC Energy Integral (VA·s) | Detection Results | |||
|---|---|---|---|---|---|---|---|
| Non-Fault Line L1 | Non-Fault Line L2 | Non-Fault Line L3 | Faulty Line L4 | ||||
| 8 | 0.01 | 45 | 12.39 | 4.91 | 6.66 | 697.04 | √ |
| 5 | 9.80 | 2.47 | 9.42 | 694.30 | √ | ||
| 10 | 28.65 | 8.63 | 23.33 | 693.38 | √ | ||
| 20 | 49.77 | 15.48 | 39.18 | 690.36 | √ | ||
| 50 | 63.31 | 19.87 | 49.46 | 674.15 | √ | ||
| 100 | 52.72 | 16.64 | 41.19 | 635.15 | √ | ||
| 200 | 31.95 | 10.08 | 24.96 | 522.35 | √ | ||
| 500 | 18.79 | 5.93 | 14.74 | 251.01 | √ | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, W.; Bai, J.; Cheng, Y.; Zhang, Z.; Li, N. Research on a Faulty Line Selection Method Based on the Zero-Sequence Disturbance Power of Resonant Grounded Distribution Networks. Energies 2019, 12, 846. https://doi.org/10.3390/en12050846
Shao W, Bai J, Cheng Y, Zhang Z, Li N. Research on a Faulty Line Selection Method Based on the Zero-Sequence Disturbance Power of Resonant Grounded Distribution Networks. Energies. 2019; 12(5):846. https://doi.org/10.3390/en12050846
Chicago/Turabian StyleShao, Wenquan, Jie Bai, Yuan Cheng, Zhihua Zhang, and Ning Li. 2019. "Research on a Faulty Line Selection Method Based on the Zero-Sequence Disturbance Power of Resonant Grounded Distribution Networks" Energies 12, no. 5: 846. https://doi.org/10.3390/en12050846
APA StyleShao, W., Bai, J., Cheng, Y., Zhang, Z., & Li, N. (2019). Research on a Faulty Line Selection Method Based on the Zero-Sequence Disturbance Power of Resonant Grounded Distribution Networks. Energies, 12(5), 846. https://doi.org/10.3390/en12050846






