A Novel Filter Extracted Equivalent Control Based Fixed Frequency Sliding Mode Approach for Power Electronic Converters
Abstract
:1. Introduction
- Achieving precise voltage regulation in presence of unknown load disturbances and un-modeled dynamics of the system.
- Extraction of the actual equivalent control from the discontinuous function under sliding mode operation.
- Improvement in both the dynamic response and the robustness of the closed loop system in comparison with double integral sliding mode control.
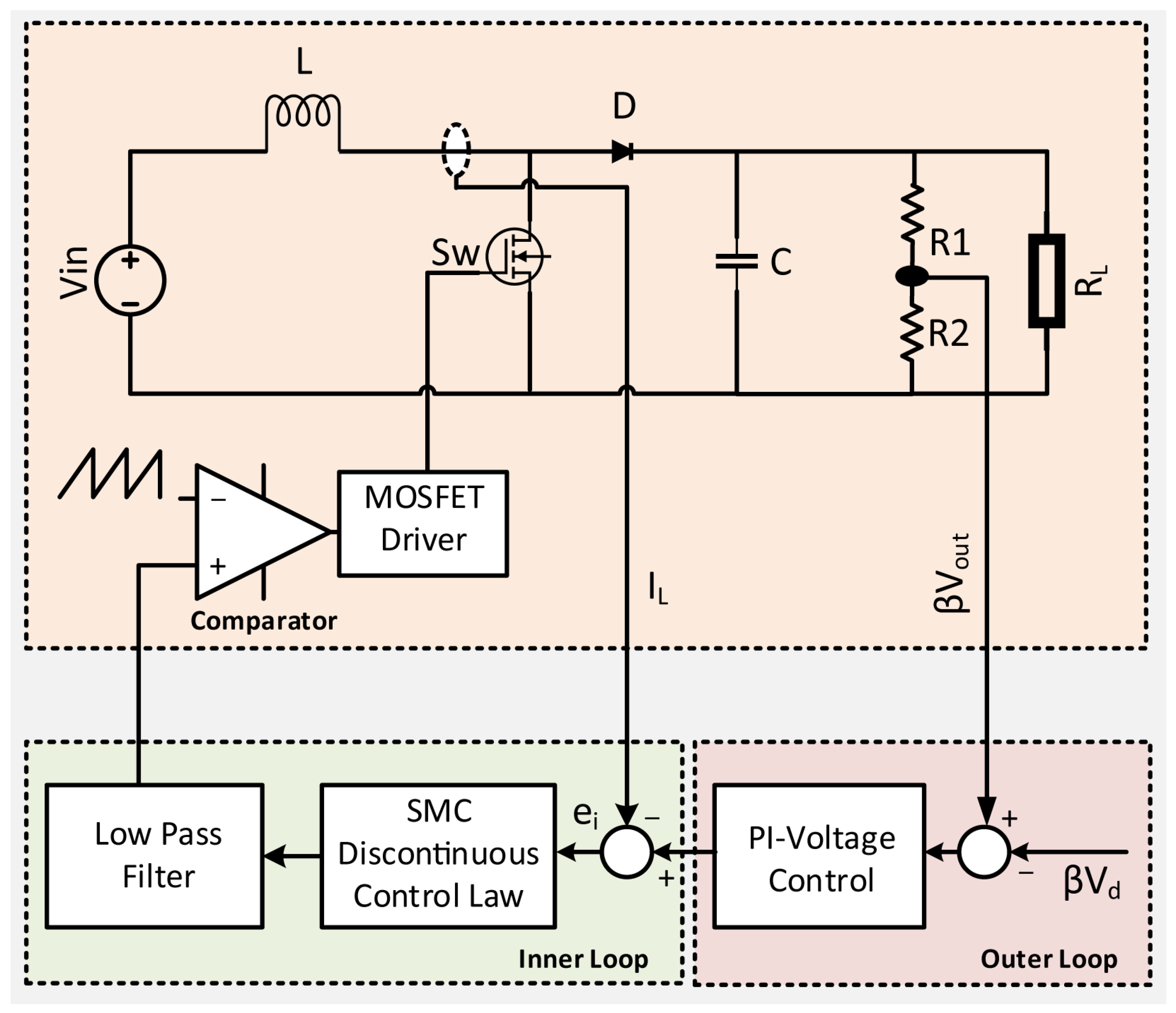
2. Proposed Technique
3. PWM-SMC with Double Integral Type Sliding Surface
Stability of Inner Loop
4. Experimental Results and Discussion
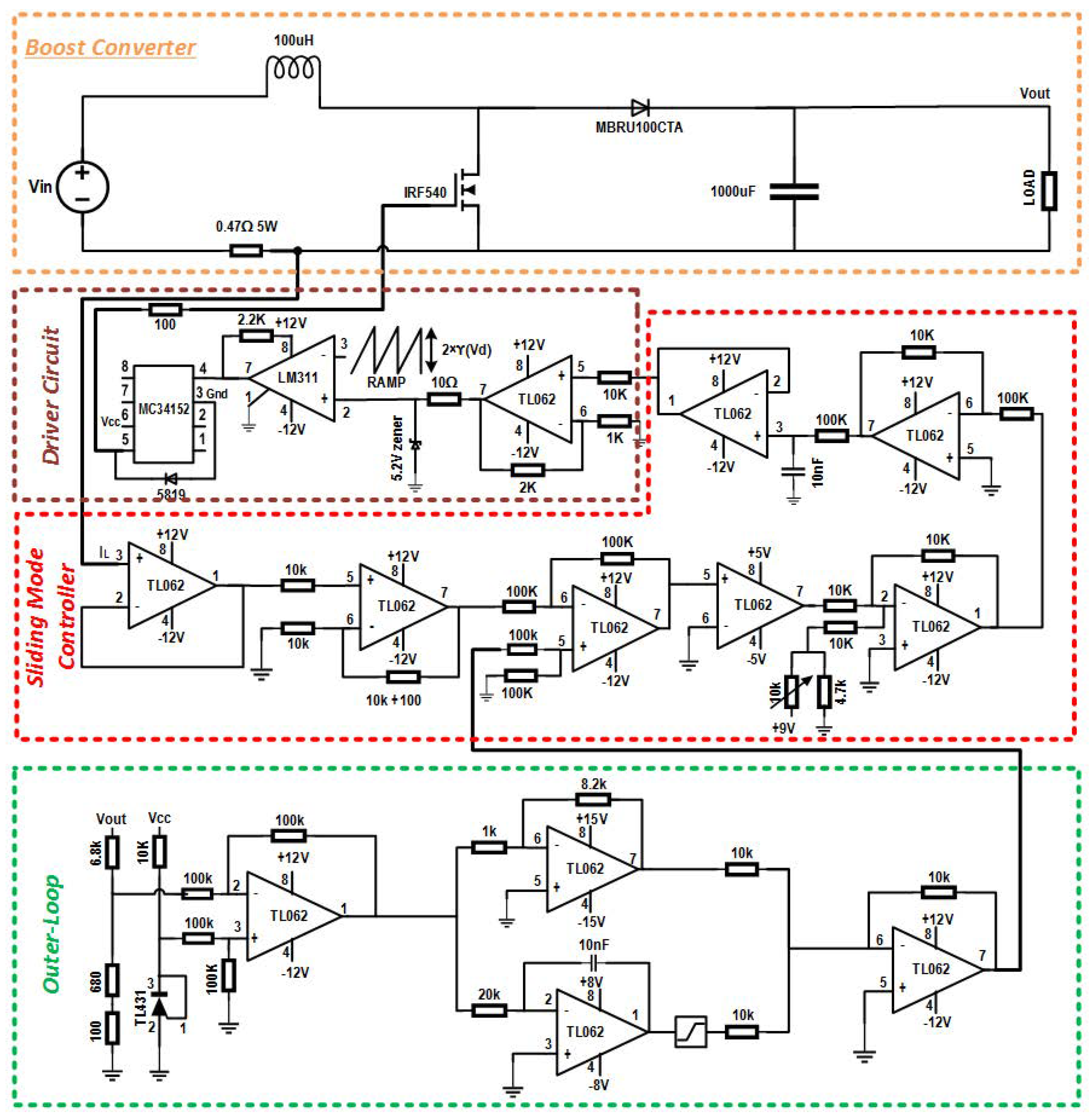
4.1. Experimental Setup
4.2. Steady State Error
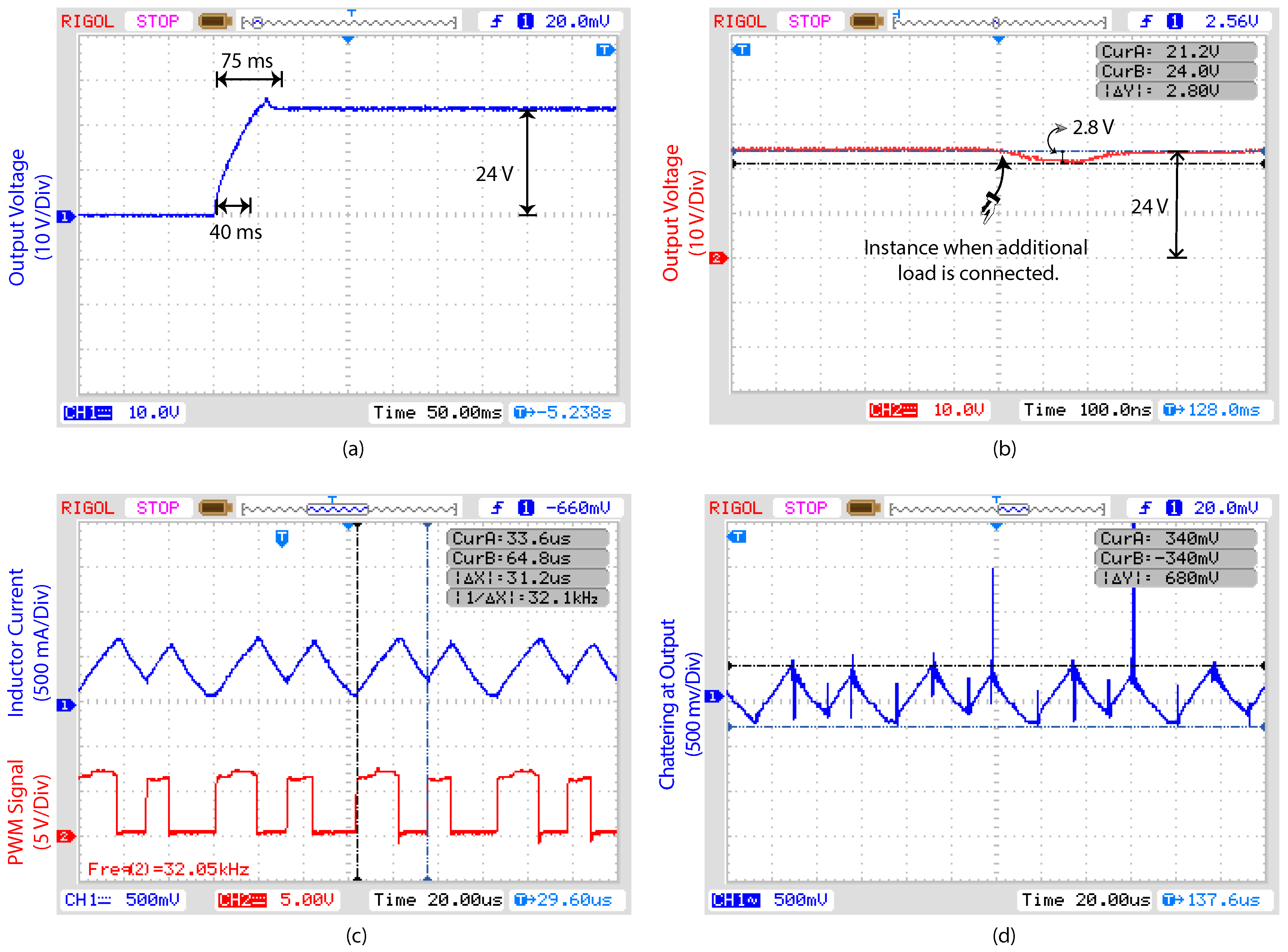
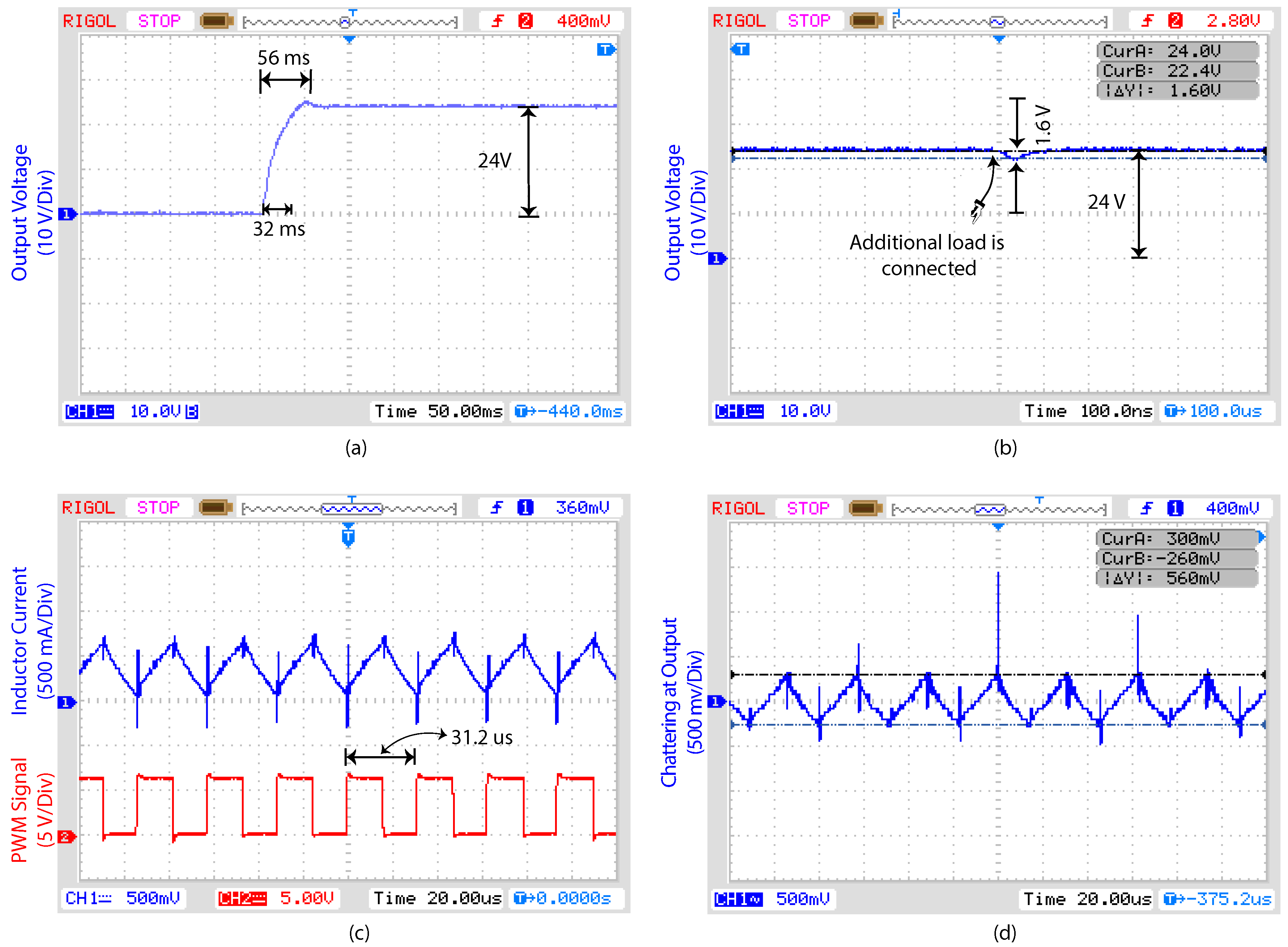
4.3. Transient Response
4.4. Robustness to Load Variations
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Pan, Y.; Yang, C.; Pan, L.; Yu, H. Integral Sliding Mode Control: Performance, Modification, and Improvement. IEEE Trans. Ind. Inform. 2018, 14, 3087–3096. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Hong, S.K. Fault-tolerant Control of Quadcopter UAVs Using Robust Adaptive Sliding Mode Approach. Energies 2019, 12, 95. [Google Scholar] [CrossRef]
- Mobayen, S. Chaos synchronization of uncertain chaotic systems using composite nonlinear feedback based integral sliding mode control. ISA Trans. 2018, 77, 100–111. [Google Scholar] [CrossRef] [PubMed]
- Utkin, V.; Guldner, J.; Shi, J. Sliding Mode Control in Electro-Mechanical Systems; CRC Press: Boca Raton, FL, USA, 2009; Volume 34. [Google Scholar]
- Du, H.; Chen, X.; Wen, G.; Yu, X.; Lu, J. Discrete-Time Fast Terminal Sliding Mode Control for Permanent Magnet Linear Motor. IEEE Trans. Ind. Electron. 2018, 65, 9916–9927. [Google Scholar] [CrossRef]
- Kali, Y.; Ayala, M.; Rodas, J.; Saad, M.; Doval-Gandoy, J.; Gregor, R.; Benjelloun, K. Current Control of a Six-Phase Induction Machine Drive Based on Discrete-Time Sliding Mode with Time Delay Estimation. Energies 2019, 12, 170. [Google Scholar] [CrossRef]
- Liu, J.; Vazquez, S.; Wu, L.; Marquez, A.; Gao, H.; Franquelo, L.G. Extended state observer-based sliding-mode control for three-phase power converters. IEEE Trans. Ind. Electron. 2017, 64, 22–31. [Google Scholar] [CrossRef]
- Riani, A.; Madani, T.; Benallegue, A.; Djouani, K. Adaptive integral terminal sliding mode control for upper-limb rehabilitation exoskeleton. Control Eng. Pract. 2018, 75, 108–117. [Google Scholar] [CrossRef]
- Delghavi, M.B.; Yazdani, A. Sliding-Mode Control of AC Voltages and Currents of Dispatchable Distributed Energy Resources in Master-Slave-Organized Inverter-Based Microgrids. IEEE Trans. Smart Grid 2019, 10, 980–991. [Google Scholar] [CrossRef]
- Merabet, A. Adaptive Sliding Mode Speed Control for Wind Energy Experimental System. Energies 2018, 11, 2238. [Google Scholar] [CrossRef]
- Benhalima, S.; Miloud, R.; Chandra, A. Real-Time Implementation of Robust Control Strategies Based on Sliding Mode Control for Standalone Microgrids Supplying Non-Linear Loads. Energies 2018, 11, 2590. [Google Scholar] [CrossRef]
- Wang, H.; Shi, L.; Man, Z.; Zheng, J.; Li, S.; Yu, M.; Jiang, C.; Kong, H.; Cao, Z. Continuous Fast Nonsingular Terminal Sliding Mode Control of Automotive Electronic Throttle Systems Using Finite-Time Exact Observer. IEEE Trans. Ind. Electron. 2018, 65, 7160–7172. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding mode control design principles and applications to electric drives. IEEE Trans. Ind. Electron. 1993, 40, 23–36. [Google Scholar] [CrossRef] [Green Version]
- Alsmadi, Y.M.; Utkin, V.; Haj-Ahmed, M.; Xu, L.; Abdelaziz, A.Y. Sliding-mode control of power converters: AC/DC converters & DC/AC inverters. Int. J. Control 2018, 91, 2573–2587. [Google Scholar]
- Venkataramanan, R. Sliding Mode Control of Power Converters. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1986. [Google Scholar]
- Carpita, M.; Marchesoni, M. Experimental study of a power conditioning system using sliding mode control. IEEE Trans. Power Electron. 1996, 11, 731–742. [Google Scholar] [CrossRef]
- González, J.A.; Barreiro, A.; Dormido, S.; Baños, A. Nonlinear adaptive sliding mode control with fast non-overshooting responses and chattering avoidance. J. Franklin Inst. 2017, 354, 2788–2815. [Google Scholar] [CrossRef]
- Abeywardana, D.B.W.; Hredzak, B.; Agelidis, V.G. A fixed-frequency sliding mode controller for a boost-inverter-based battery-supercapacitor hybrid energy storage system. IEEE Trans. Power Electron. 2017, 32, 668–680. [Google Scholar] [CrossRef]
- Mohanty, P.R.; Panda, A.K. Fixed-frequency sliding-mode control scheme based on current control manifold for improved dynamic performance of boost PFC converter. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 576–586. [Google Scholar] [CrossRef]
- Gao, M.; Wang, D.; Li, Y.; Yuan, T. Fixed frequency pulse-width modulation based integrated sliding mode controller for phase-shifted full-bridge converters. IEEE Access 2018, 6, 2181–2192. [Google Scholar] [CrossRef]
- Nguyen, V.; Huynh, H.; Kim, S.; Song, H. Active EMI Reduction Using Chaotic Modulation in a Buck Converter with Relaxed Output LC Filter. Electronics 2018, 7, 254. [Google Scholar] [CrossRef]
- Pareschi, F.; Rovatti, R.; Setti, G. EMI reduction via spread spectrum in DC/DC converters: State of the art, optimization, and tradeoffs. IEEE Access 2015, 3, 2857–2874. [Google Scholar] [CrossRef]
- Chiarelli, C.; Malesani, L.; Pirondini, S.; Tomasin, P. Single-phase, three-level, constant frequency current hysteresis control for UPS applications. In Proceedings of the Fifth European Conference on Power Electronics and Applications, Brighton, UK, 13–16 September 1993; pp. 180–185. [Google Scholar]
- Holmes, D.G.; Davoodnezhad, R.; McGrath, B.P. An improved three-phase variable-band hysteresis current regulator. IEEE Trans. Power Electron. 2013, 28, 441–450. [Google Scholar] [CrossRef]
- Guzman, R.; de Vicuna, L.G.; Morales, J.; Castilla, M.; Matas, J. Sliding-mode control for a three-phase unity power factor rectifier operating at fixed switching frequency. IEEE Trans. Power Electron. 2016, 31, 758–769. [Google Scholar] [CrossRef]
- Huerta, S.C.; Alou, P.; Oliver, J.Á.; Garcia, O.; Cobos, J.A.; Abou-Alfotouh, A.M. Nonlinear Control for DC–DC Converters Based on Hysteresis of the CrmOUT Current With a Frequency Loop to Operate at Constant Frequency. IEEE Trans. Ind. Electron. 2011, 58, 1036–1043. [Google Scholar] [CrossRef]
- Huerta, S.C.; Alou, P.; Garcia, O.; Oliver, J.A.; Prieto, R.; Cobos, J. Hysteretic mixed-signal controller for high-frequency DC-DC converters operating at constant switching frequency. IEEE Trans. Power Electron. 2012, 27, 2690–2696. [Google Scholar] [CrossRef]
- Yan, W.T.; Ho, C.N.M.; Chung, H.S.H.; Au, K.T. Fixed-frequency boundary control of buck converter with second-order switching surface. IEEE Trans. Power Electron. 2009, 24, 2193–2201. [Google Scholar] [CrossRef]
- Malesani, L.; Mattavelli, P.; Tomasin, P. Improved constant-frequency hysteresis current control of VSI inverters with simple feedforward bandwidth prediction. IEEE Trans. Ind. Appl. 1997, 33, 1194–1202. [Google Scholar] [CrossRef] [Green Version]
- Repecho, V.; Biel, D.; Olm, J.M.; Colet, E.F. Switching frequency regulation in sliding mode control by a hysteresis band controller. IEEE Trans. Power Electron. 2017, 32, 1557–1569. [Google Scholar] [CrossRef]
- Silva, J.F.; Paulo, S.S. Fixed frequency sliding mode modulator for current mode PWM inverters. In Proceedings of the 24th Annual IEEE Power Electronics Specialists Conference - PESC ’93, Seattle, WA, USA, 20–24 June 1993; pp. 623–629. [Google Scholar]
- Mattavelli, P.; Rossetto, L.; Spiazzi, G.; Tenti, P. General-purpose sliding-mode controller for DC/DC converter applications. In Proceedings of the 24th Annual IEEE Power Electronics Specialists Conference - PESC ’93, Seattle, WA, USA, 20–24 June 1993; pp. 609–615. [Google Scholar]
- Fossas, E.; Grinó, R.; Biel, D. Quasi-Sliding control based on pulse width modulation, zero averaged dynamics and the L2 norm. In Advances in Variable Structure Systems: Analysis, Integration and Applications; World Scientific: Singapore, 2000; pp. 335–344. [Google Scholar]
- Ramos, R.R.; Biel, D.; Fossas, E.; Guinjoan, F. A fixed-frequency quasi-sliding control algorithm: Application to power inverters design by means of FPGA implementation. IEEE Trans. Power Electron. 2003, 18, 344–355. [Google Scholar] [CrossRef]
- Ling, R.; Maksimovic, D.; Leyva, R. Second-order sliding-mode controlled synchronous buck DC–DC converter. IEEE Trans. Power Electron. 2016, 31, 2539–2549. [Google Scholar] [CrossRef]
- Ye, J.; Malysz, P.; Emadi, A. A fixed-switching-frequency integral sliding mode current controller for switched reluctance motor drives. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 381–394. [Google Scholar]
- Abrishamifar, A.; Ahmad, A.; Mohamadian, M. Fixed switching frequency sliding mode control for single-phase unipolar inverters. IEEE Trans. Power Electron. 2012, 27, 2507–2514. [Google Scholar] [CrossRef]
- Yasin, A.R.; Ashraf, M.; Bhatti, A.I. Fixed Frequency Sliding Mode Control of Power Converters for Improved Dynamic Response in DC Micro-Grids. Energies 2018, 11, 2799. [Google Scholar] [CrossRef]
- Zaman, H.; Zheng, X.; Wu, X.; Khan, S.; Ali, H. A Fixed-Frequency Sliding-Mode Controller for Fourth-Order Class-D Amplifier. Electronics 2018, 7, 261. [Google Scholar] [CrossRef]
- Tan, S.C.; Lai, Y.; Tse, C.K.; Cheung, M.K. A fixed-frequency pulsewidth modulation based quasi-sliding-mode controller for buck converters. IEEE Trans. Power Electron. 2005, 20, 1379–1392. [Google Scholar] [CrossRef]
- Yasin, A.R.; Ashraf, M.; Bhatti, A.I. Fixed frequency sliding mode control of renewable energy resources in DC micro grid. Asian J. Control 2019. [Google Scholar] [CrossRef]
- Jazi, H.N.; Goudarzian, A.; Pourbagher, R.; Derakhshandeh, S.Y. PI and PWM Sliding Mode Control of POESLL Converter. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2167–2177. [Google Scholar] [CrossRef]
- Al-Baidhani, H.; Kazimierczuk, M.K. PWM-based proportional-integral sliding-mode current control of DC-DC boost converter. In Proceedings of the 2018 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 8–9 February 2018; pp. 1–6. [Google Scholar]
- Pradhan, R.; Subudhi, B. Double integral sliding mode MPPT control of a photovoltaic system. IEEE Trans. Control Syst. Technol. 2016, 24, 285–292. [Google Scholar] [CrossRef]
- Tan, S.C.; Lai, Y.M.; Tse, C.K. Indirect Sliding Mode Control of Power Converters Via Double Integral Sliding Surface. IEEE Trans. Power Electron. 2008, 23, 600–611. [Google Scholar] [Green Version]
- Tan, S.C.; Lai, Y.M.; Chi, K.T. General design issues of sliding-mode controllers in DC–DC converters. IEEE Trans. Ind. Electron. 2008, 55, 1160–1174. [Google Scholar]
- Teodorescu, M.; Stanciu, D. Sliding coefficients estimation for fixed frequency sliding mode control of boost converter. In Proceedings of the 2015 9th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 7–9 May 2015; pp. 698–703. [Google Scholar]
- Wai, R.J.; Shih, L.C. Design of voltage tracking control for DC–DC boost converter via total sliding-mode technique. IEEE Trans. Ind. Electron. 2011, 58, 2502–2511. [Google Scholar] [CrossRef]
- Utkin, V.I.; Lee, H. The chattering analysis. In Proceedings of the 2006 IEEE 12th International Power Electronics and Motion Control Conference, Portoroz, Slovenia, 30 August–1 September 2006; pp. 2014–2019. [Google Scholar]
- Hu, Y.; Tan, C.; Broughton, J.; Roach, P.A.; Varga, L. Nonlinear dynamic simulation and control of large-scale reheating furnace operations using a zone method based model. Appl. Therm. Eng. 2018, 135, 41–53. [Google Scholar] [CrossRef]
- Kumar, Y.S.; Poddar, G. Medium-voltage vector control induction motor drive at zero frequency using modular multilevel converter. IEEE Trans. Ind. Electron. 2018, 65, 125–132. [Google Scholar] [CrossRef]
- Ghanaatian, M.; Lotfifard, S. Control of Flywheel Energy Storage Systems in the Presence of Uncertainties. IEEE Trans. Sustain. Energy 2019, 10, 36–45. [Google Scholar] [CrossRef]
- Sira-Ramirez, H. Sliding-mode control on slow manifolds of DC-to-DC power converters. Int. J. Control 1988, 47, 1323–1340. [Google Scholar] [CrossRef]
- Shabestari, P.; Gharehpetian, G.; Riahy, G.; Mortazavian, S. Voltage controllers for DC-DC boost converters in discontinuous current mode. In Proceedings of the 2015 International Energy and Sustainability Conference (IESC), Farmingdale, NY, USA, 12–13 November 2015; pp. 1–7. [Google Scholar]
- Alsmadi, Y.M.; Utkin, V.; Haj-ahmed, M.A.; Xu, L. Sliding mode control of power converters: DC/DC converters. Int. J. Control 2017. [Google Scholar] [CrossRef]
- Kokotovic, P.V.; O’Malley, R.E., Jr.; Sannuti, P. Singular perturbations and order reduction in control theory an overview. Automatica 1976, 12, 123–132. [Google Scholar] [CrossRef]
- Kokotović, P.V. Applications of singular perturbation techniques to control problems. SIAM Rev. 1984, 26, 501–550. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding Modes in Control and Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Morel, C.; Guignard, J.C.; Guillet, M. Sliding mode control of DC-to-DC power converters. In Proceedings of the 2002 9th International Conference on Electronics, Circuits and Systems, Dubrovnik, Croatia, 15–18 September 2002; Volume 3, pp. 971–974. [Google Scholar]
- Sira-Ramirez, H.J.; Ilic, M. A geometric approach to the feedback control of switch mode DC-to-DC power supplies. IEEE Trans. Circuits Syst. 1988, 35, 1291–1298. [Google Scholar] [CrossRef]

| Description | Symbol | Value |
|---|---|---|
| Input voltage | 12 V | |
| Desired output voltage | 24 V | |
| Capacitance | C | 1000 F |
| Capacitor ESR | 21 m | |
| Inductance of coil | L | 100 H |
| Resistance of coil | 0.18 | |
| Switching frequency | 32 kHz | |
| Load resistance | 15–100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasin, A.R.; Ashraf, M.; Bhatti, A.I. A Novel Filter Extracted Equivalent Control Based Fixed Frequency Sliding Mode Approach for Power Electronic Converters. Energies 2019, 12, 853. https://doi.org/10.3390/en12050853
Yasin AR, Ashraf M, Bhatti AI. A Novel Filter Extracted Equivalent Control Based Fixed Frequency Sliding Mode Approach for Power Electronic Converters. Energies. 2019; 12(5):853. https://doi.org/10.3390/en12050853
Chicago/Turabian StyleYasin, Abdul Rehman, Muhammad Ashraf, and Aamer Iqbal Bhatti. 2019. "A Novel Filter Extracted Equivalent Control Based Fixed Frequency Sliding Mode Approach for Power Electronic Converters" Energies 12, no. 5: 853. https://doi.org/10.3390/en12050853
APA StyleYasin, A. R., Ashraf, M., & Bhatti, A. I. (2019). A Novel Filter Extracted Equivalent Control Based Fixed Frequency Sliding Mode Approach for Power Electronic Converters. Energies, 12(5), 853. https://doi.org/10.3390/en12050853





