Performance Comparison of Mismatch Power Loss Minimization Techniques in Series-Parallel PV Array Configurations
Abstract
:1. Introduction
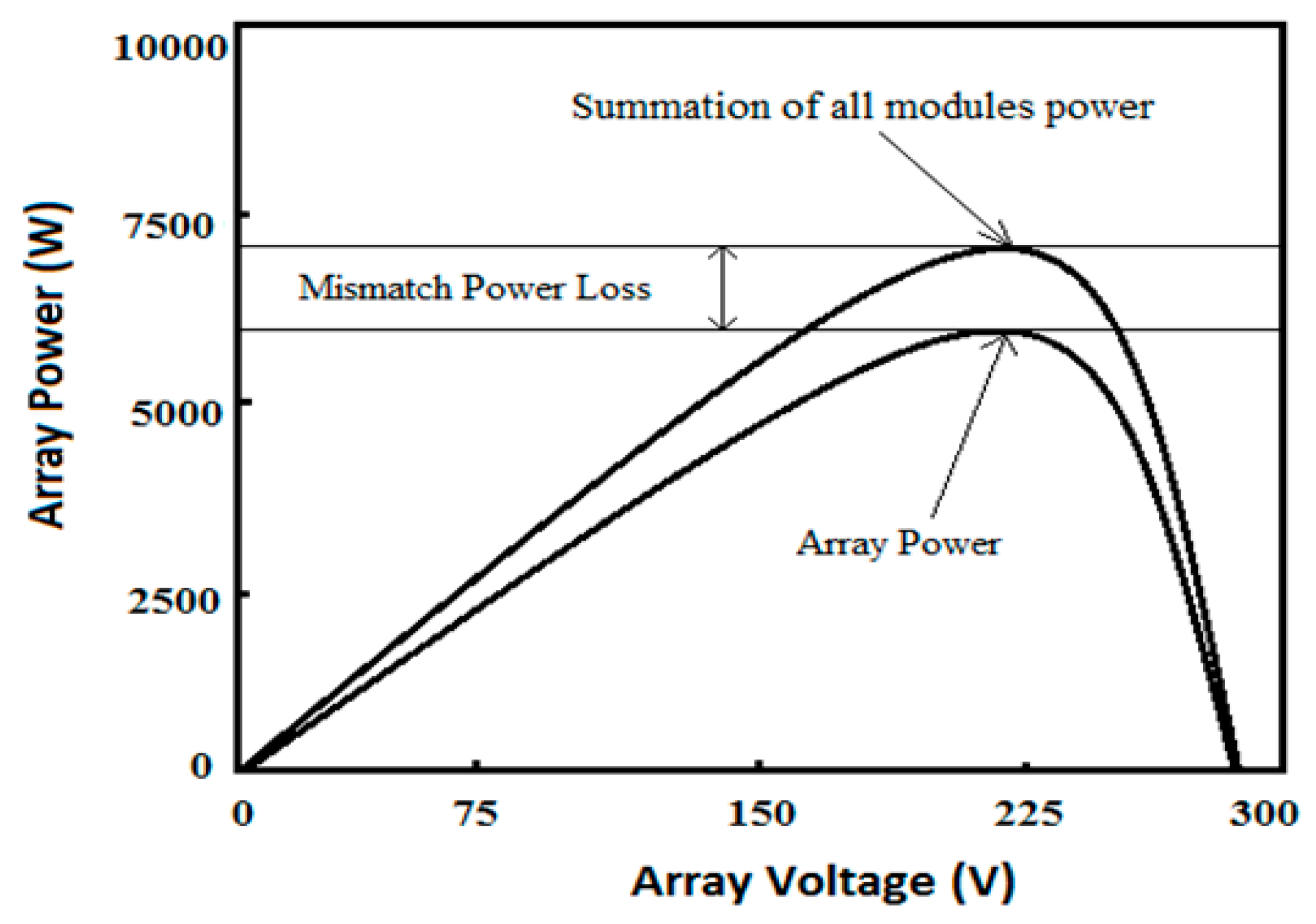
2. Mismatch Power Loss in PV Array
3. Mathematical Model of MML in SP Configuration
4. Simulation Work
4.1. Datasets of Three Different Arrays
4.2. Conventional Techniques of Module Arrangement
4.3. Proposed GA Technique for Module Arrangement
5. Simulation Result Analysis
5.1. Case Study on a 400 W PV Array
5.2. Case Study on 3400 W PV Array
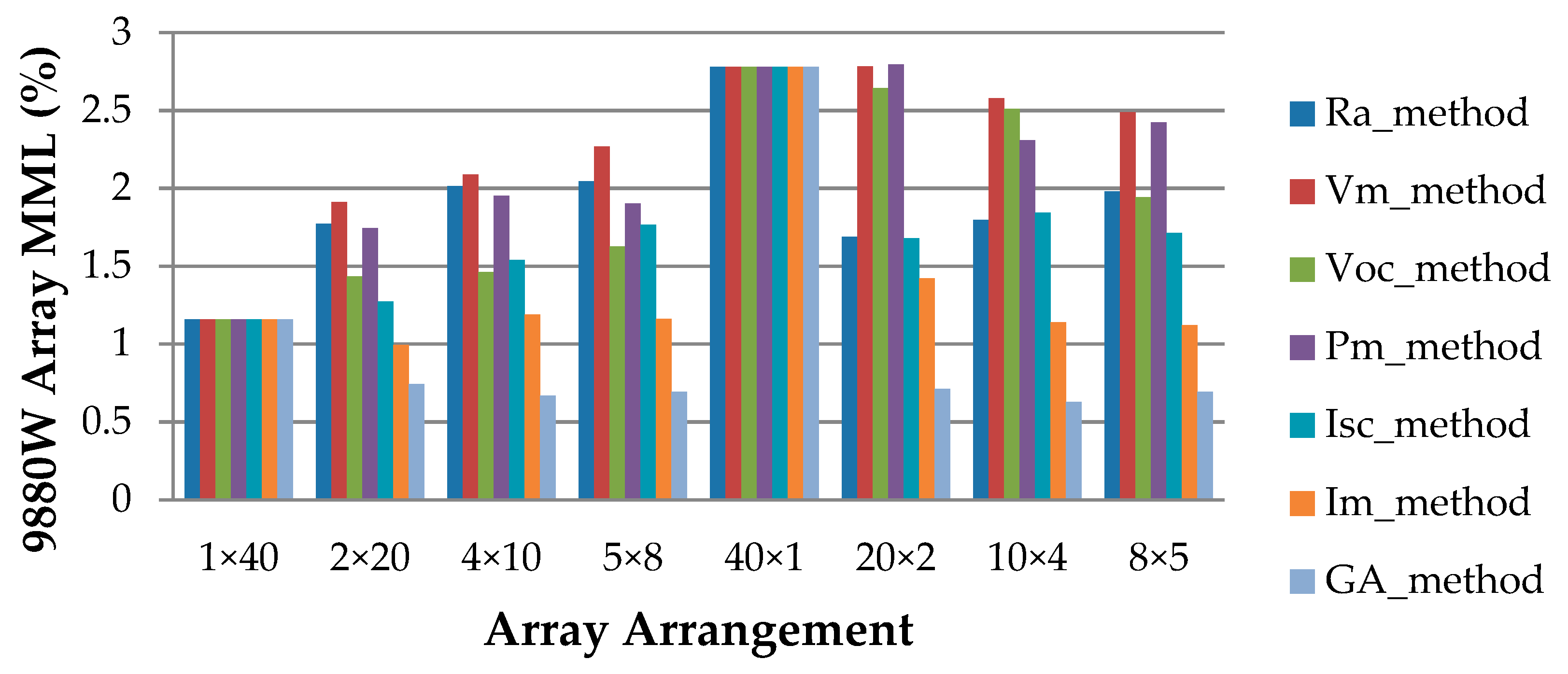
5.3. Case Study on 9880 W PV Array
5.4. Comparative Analysis of MML in 400 W, 3400 W, and 9880 W Systems
6. Experimental Validation
6.1. Experimental Setup
6.2. Experimental Measurement Procedure
6.3. Experimental Results
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Hu, Y.; Zhang, J.; Wu, J.; Cao, W.; Tian, G.Y.; Kirtley, J.L. Efficiency improvement of nonuniformly aged PV arrays. IEEE Trans. Power Electron. 2017, 32, 1124–1137. [Google Scholar] [CrossRef]
- Osório, G.J.; Shafie-khah, M.; Lujano-Rojas, J.M.; Catalão, J.P. Scheduling Model for Renewable Energy Sources Integration in an Insular Power System. Energies 2018, 11, 144. [Google Scholar] [CrossRef]
- Zhang, T.; Xie, L.; Li, Y.; Mallick, T.; Wei, Q.; Hao, X.; He, B. Experimental and Theoretical Research on Bending Behavior of Photovoltaic Panels with a Special Boundary Condition. Energies 2018, 11, 3435. [Google Scholar] [CrossRef]
- Ren, G.; Zhao, X.; Zhan, C.; Jin, H.; Zhou, A. Investigation of the Energy Performance of a Novel Modular Solar Building Envelope. Energies 2017, 10, 880. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, M.; Yang, H. A Review of the Energy Performance and Life-Cycle Assessment of Building-Integrated Photovoltaic (BIPV) Systems. Energies 2018, 11, 3157. [Google Scholar] [CrossRef]
- Lotfy, M.E.; Senjyu, T.; Farahat, M.A.-F.; Abdel-Gawad, A.F.; Matayoshi, H. A polar fuzzy control scheme for hybrid power system using vehicle-to-grid technique. Energies 2017, 10, 1083. [Google Scholar] [CrossRef]
- Subramani, G.; Ramachandaramurthy, V.K.; Padmanaban, S.; Mihet-Popa, L.; Blaabjerg, F.; Guerrero, J.M. Grid-tied photovoltaic and battery storage systems with Malaysian electricity tariff—A review on maximum demand shaving. Energies 2017, 10, 1884. [Google Scholar] [CrossRef]
- Su, M.; Luo, C.; Hou, X.; Yuan, W.; Liu, Z.; Han, H.; Guerrero, J.M. A Communication-Free Decentralized Control for Grid-Connected Cascaded PV Inverters. Energies 2018, 11, 1375. [Google Scholar] [CrossRef]
- Viinamäki, J.; Kuperman, A.; Suntio, T. Grid-forming-mode operation of boost-power-stage converter in PV-generator-interfacing applications. Energies 2017, 10, 1033. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Padmanaban, S.; Mihet-Popa, L.; Blaabjerg, F.; Azam, F. Maximum Power Point Tracking for Brushless DC Motor-Driven Photovoltaic Pumping Systems Using a Hybrid ANFIS-FLOWER Pollination Optimization Algorithm. Energies 2018, 11, 1067. [Google Scholar] [CrossRef]
- Jeong, D.-K.; Kim, H.-S.; Baek, J.-W.; Kim, H.-J.; Jung, J.-H. Autonomous Control Strategy of DC Microgrid for Islanding Mode Using Power Line Communication. Energies 2018, 11, 924. [Google Scholar] [CrossRef]
- Tubniyom, C.; Chatthaworn, R.; Suksri, A.; Wongwuttanasatian, T. Minimization of Losses in Solar Photovoltaic Modules by Reconfiguration under Various Patterns of Partial Shading. Energies 2019, 12, 24. [Google Scholar] [CrossRef]
- Gomez, A.; Sanchez, S.; Campoy-Quiles, M.; Abate, A. Topological distribution of reversible and non-reversible degradation in perovskite solar cells. Nano Energy 2018, 45, 94–100. [Google Scholar] [CrossRef]
- Udenze, P.; Hu, Y.; Wen, H.; Ye, X.; Ni, K. A Reconfiguration Method for Extracting Maximum Power from Non-Uniform Aging Solar Panels. Energies 2018, 11, 2743. [Google Scholar] [CrossRef]
- Kropp, T.; Schubert, M.; Werner, J.H. Quantitative Prediction of Power Loss for Damaged Photovoltaic Modules Using Electroluminescence. Energies 2018, 11, 1172. [Google Scholar] [CrossRef]
- Gasparin, F.P.; Bühler, A.J.; Rampinelli, G.A.; Krenzinger, A. Statistical analysis of I–V curve parameters from photovoltaic modules. Sol. Energy 2016, 131, 30–38. [Google Scholar] [CrossRef]
- Garrido-Alzar, C. Algorithm for extraction of solar cell parameters from I–V curve using double exponential model. Renew. Energy 1997, 10, 125–128. [Google Scholar] [CrossRef]
- Ciulla, G.; Brano, V.L.; Cellura, M.; Franzitta, V.; Milone, D. A finite difference model of a PV-PCM system. Energy Procedia 2012, 30, 198–206. [Google Scholar] [CrossRef]
- Franzitta, V.; Orioli, A.; Gangi, A.D. Assessment of the Usability and Accuracy of Two-Diode Models for Photovoltaic Modules. Energies 2017, 10, 564. [Google Scholar] [CrossRef]
- Franzitta, V.; Orioli, A.; Di Gangi, A. Assessment of the usability and accuracy of the simplified one-diode models for photovoltaic modules. Energies 2016, 9, 1019. [Google Scholar] [CrossRef]
- Babu, B.C.; Gurjar, S. A novel simplified two-diode model of photovoltaic (PV) module. IEEE J. Photovolt. 2014, 4, 1156–1161. [Google Scholar] [CrossRef]
- Bany, J.; Appelbaum, J.; Braunstein, A. The influence of parameter dispersion of electrical cells on the array power output. IEEE Trans. Electron. Devices 1977, 24, 1032–1040. [Google Scholar] [CrossRef]
- Gonzalez Montoya, D.; Bastidas-Rodriguez, J.D.; Trejos-Grisales, L.A.; Ramos-Paja, C.A.; Petrone, G.; Spagnuolo, G. A Procedure for Modeling Photovoltaic Arrays under Any Configuration and Shading Conditions. Energies 2018, 11, 767. [Google Scholar] [CrossRef]
- Ji, D.; Zhang, C.; Lv, M.; Ma, Y.; Guan, N. Photovoltaic Array Fault Detection by Automatic Reconfiguration. Energies 2017, 10, 699. [Google Scholar] [CrossRef]
- Serna-Garcés, S.I.; Bastidas-Rodríguez, J.D.; Ramos-Paja, C.A. Reconfiguration of Urban Photovoltaic Arrays Using Commercial Devices. Energies 2016, 9, 2. [Google Scholar] [CrossRef]
- Saha, H.; Bhattacharya, G.; Mukherjee, D. Mismatch losses in series combinations of silicon solar cell modules. Sol. Cells 1988, 25, 143–153. [Google Scholar] [CrossRef]
- Bishop, J. Computer simulation of the effects of electrical mismatches in photovoltaic cell interconnection circuits. Sol. Cells 1988, 25, 73–89. [Google Scholar] [CrossRef]
- Bucciarelli, L.L., Jr. Power loss in photovoltaic arrays due to mismatch in cell characteristics. Sol. Energy 1979, 23, 277–288. [Google Scholar] [CrossRef]
- Webber, J.; Riley, E. Mismatch loss reduction in photovoltaic arrays as a result of sorting photovoltaic modules by max-power parameters. ISRN Renew. Energy 2013, 2013, 327835. [Google Scholar] [CrossRef]
- Lorente, D.G.; Pedrazzi, S.; Zini, G.; Dalla Rosa, A.; Tartarini, P. Mismatch losses in PV power plants. Sol. Energy 2014, 100, 42–49. [Google Scholar] [CrossRef]
- Shirzadi, S.; Hizam, H.; Wahab, N.I.A. Mismatch losses minimization in photovoltaic arrays by arranging modules applying a genetic algorithm. Sol. Energy 2014, 108, 467–478. [Google Scholar] [CrossRef]
- Deshkar, S.N.; Dhale, S.B.; Mukherjee, J.S.; Babu, T.S.; Rajasekar, N. Solar PV array reconfiguration under partial shading conditions for maximum power extraction using genetic algorithm. Renew. Sustain. Energy Rev. 2015, 43, 102–110. [Google Scholar] [CrossRef]
- Rajan, N.A.; Shrikant, K.D.; Dhanalakshmi, B.; Rajasekar, N. Solar PV array reconfiguration using the concept of Standard deviation and Genetic Algorithm. Energy Procedia 2017, 117, 1062–1069. [Google Scholar] [CrossRef]
- Camarillo-Peñaranda, J.R.; Ramírez-Quiroz, F.A.; González-Montoya, D.; Bolaños-Martínez, F.; Ramos-Paja, C.A. Reconfiguration of photovoltaic arrays based on genetic algorithm. Revista Facultad de Ingeniería Universidad de Antioquia 2015, 75, 95–107. [Google Scholar] [CrossRef]
- Harrag, A.; Messalti, S. Adaptive GA-based reconfiguration of photovoltaic array combating partial shading conditions. Neural Comput. Appl. 2018, 30, 1145–1170. [Google Scholar] [CrossRef]
- Tazehkand, M.Z.; Fathi, S.H.; Eskandari, A.; Milimonfared, J. Optimal reconfiguration of PV modules in an array without any constraint on structure by the use of genetic algorithm. In Proceedings of the 2018 9th Annual Power Electronics, Drives Systems and Technologies Conference (PEDSTC), Tehran, Iran, 13–15 February 2018; pp. 145–150. [Google Scholar]
- Chen, P.-Y.; Chao, K.-H.; Liao, B.-J. Joint Operation between a PSO-Based Global MPP Tracker and a PV Module Array Configuration Strategy under Shaded or Malfunctioning Conditions. Energies 2018, 11, 2005. [Google Scholar] [CrossRef]
- Deline, C.; Marion, B.; Granata, J.; Gonzalez, S. A performance and economic analysis of distributed power electronics in photovoltaic systems. Contract 2011, 303, 275–3000. [Google Scholar]
- Teo, J.; Tan, R.; Mok, V.; Ramachandaramurthy, V.; Tan, C. Impact of Partial Shading on the PV Characteristics and the Maximum Power of a Photovoltaic String. Energies 2018, 11, 1860. [Google Scholar] [CrossRef]
- Seyedmahmoudian, M.; Mekhilef, S.; Rahmani, R.; Yusof, R.; Renani, E.T. Analytical modeling of partially shaded photovoltaic systems. Energies 2013, 6, 128–144. [Google Scholar] [CrossRef]
- Farh, H.; Othman, M.; Eltamaly, A.; Al-Saud, M. Maximum Power Extraction from a Partially Shaded PV System Using an Interleaved Boost Converter. Energies 2018, 11, 2543. [Google Scholar] [CrossRef]
- Babu, T.S.; Ram, J.P.; Dragičević, T.; Miyatake, M.; Blaabjerg, F.; Rajasekar, N. Particle swarm optimization based solar PV array reconfiguration of the maximum power extraction under partial shading conditions. IEEE Trans. Sustain. Energy 2018, 9, 74–85. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, X.; Ma, Y.; Liu, Y. Analysis of Dynamic Characteristic for Solar Arrays in Series and Global Maximum Power Point Tracking Based on Optimal Initial Value Incremental Conductance Strategy under Partially Shaded Conditions. Energies 2017, 10, 120. [Google Scholar] [CrossRef]
- Gutiérrez Galeano, A.; Bressan, M.; Jiménez Vargas, F.; Alonso, C. Shading Ratio Impact on Photovoltaic Modules and Correlation with Shading Patterns. Energies 2018, 11, 852. [Google Scholar] [CrossRef]
- Du, Y.; Yan, K.; Ren, Z.; Xiao, W. Designing localized MPPT for PV systems using fuzzy-weighted extreme learning machine. Energies 2018, 11, 2615. [Google Scholar] [CrossRef]
- Ramos-Paja, C.; Gonzalez Montoya, D.; Bastidas-Rodriguez, J. Sliding-Mode Control of Distributed Maximum Power Point Tracking Converters Featuring Overvoltage Protection. Energies 2018, 11, 2220. [Google Scholar] [CrossRef]
- Islam, H.; Mekhilef, S.; Shah, N.; Soon, T.; Seyedmahmousian, M.; Horan, B.; Stojcevski, A. Performance evaluation of maximum power point tracking approaches and photovoltaic systems. Energies 2018, 11, 365. [Google Scholar] [CrossRef]
- Hammami, M.; Grandi, G. A Single-Phase Multilevel PV Generation System with an Improved Ripple Correlation Control MPPT Algorithm. Energies 2017, 10, 2037. [Google Scholar] [CrossRef]
- Chang, L.-Y.; Chung, Y.-N.; Chao, K.-H.; Kao, J.-J. Smart Global Maximum Power Point Tracking Controller of Photovoltaic Module Arrays. Energies 2018, 11, 567. [Google Scholar] [CrossRef]
- Chao, K.-H.; Wu, M.-C. Global maximum power point tracking (MPPT) of a photovoltaic module array constructed through improved teaching-learning-based optimization. Energies 2016, 9, 986. [Google Scholar] [CrossRef]
- Pei, T.; Hao, X.; Gu, Q. A Novel Global Maximum Power Point Tracking Strategy Based on Modified Flower Pollination Algorithm for Photovoltaic Systems under Non-Uniform Irradiation and Temperature Conditions. Energies 2018, 11, 2708. [Google Scholar] [CrossRef]
- Koutroulis, E.; Blaabjerg, F. A new technique for tracking the global maximum power point of PV arrays operating under partial-shading conditions. IEEE J. Photovolt. 2012, 2, 184–190. [Google Scholar] [CrossRef]
- Spertino, F.; Akilimali, J.S. Are Manufacturing I–V Mismatch and Reverse Currents Key Factors in Large Photovoltaic Arrays? IEEE Trans. Ind. Electron. 2009, 56, 4520–4531. [Google Scholar] [CrossRef]
- Zilles, R.; Lorenzo, E. Statistical analysis of current voltage characteristics of PV modules. Int. J. Sol. Energy 1991, 9, 233–239. [Google Scholar] [CrossRef]
- Standard, I. 60904-1, Photovoltaic Devices, Part 1: Measurement of Photovoltaic Current-Voltage Characteristics; International Electrotechnical Commission: Geneva, Switzerland, 2006; Volume 2. [Google Scholar]
- Standard, I. 60891. Photovoltaic Devices. Procedures for Temperature and Irradiance Corrections to Measured IV Characteristics; International Electrotechnical Commission: Geneva, Switzerland, 2009. [Google Scholar]
- Sonnenenergie, D.G.F. Planning and Installing Photovoltaic Systems: A Guide for Installers, Architects and Engineers; Routledge: Abingdon-on-Thames, UK, 2013. [Google Scholar]
- Bakas, P.; Marinopoulos, A.; Stridh, B. Impact of PV module mismatch on the PV array energy yield and comparison of module, string and central MPPT. In Proceedings of the 2012 38th IEEE Photovoltaic Specialists Conference (PVSC), Austin, TX, USA, 3–8 June 2012; pp. 001393–001398. [Google Scholar]
- Kaushika, N.; Rai, A.K. An investigation of mismatch losses in solar photovoltaic cell networks. Energy 2007, 32, 755–759. [Google Scholar] [CrossRef]
- Bana, S.; Saini, R. Experimental investigation on power output of different photovoltaic array configurations under uniform and partial shading scenarios. Energy 2017, 127, 438–453. [Google Scholar] [CrossRef]












| PV Array Power | PV Module Power | PV Module No | Electrical Characteristics of PV Modules | ||||
|---|---|---|---|---|---|---|---|
| Voc (V) | Isc (A) | Pm (W) | Vm (V) | Im (A) | |||
| 400 W | 10 W | 1 | 10.464 | 1.309 | 10.118 | 8.569 | 1.181 |
| 2 | 10.396 | 1.295 | 10.032 | 8.570 | 1.171 | ||
| 3 | 10.454 | 1.307 | 10.150 | 8.588 | 1.182 | ||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||
| 40 | 10.453 | 1.320 | 10.238 | 8.630 | 1.186 | ||
| Average | 10.425 | 1.295 | 10.191 | 8.617 | 1.183 | ||
| SD | 0.116 | 0.020 | 0.194 | 0.123 | 0.013 | ||
| 3400 W | 85 W | 1 | 21.241 | 5.298 | 85.133 | 16.925 | 5.03 |
| 2 | 21.492 | 5.314 | 86.392 | 17.147 | 5.038 | ||
| 3 | 21.299 | 5.328 | 85.198 | 16.906 | 5.04 | ||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||
| 40 | 21.339 | 5.347 | 86.569 | 16.988 | 5.096 | ||
| Average | 21.382 | 5.354 | 86.035 | 16.995 | 5.063 | ||
| SD | 0.064 | 0.031 | 0.407 | 0.075 | 0.022 | ||
| 9880 W | 247 W | 1 | 40.556 | 7.516 | 249.606 | 34.62 | 7.21 |
| 2 | 40.599 | 7.512 | 245.324 | 33.858 | 7.246 | ||
| 3 | 40.665 | 7.545 | 247.991 | 33.788 | 7.34 | ||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ||
| 40 | 40.763 | 7.487 | 250.885 | 34.628 | 7.245 | ||
| Average | 40.538 | 7.544 | 247.107 | 34.094 | 7.248 | ||
| SD | 0.173 | 0.088 | 2.305 | 0.385 | 0.039 | ||
| Array Size | Array Output Power (W) by Using Different Techniques for 400 W LSS-SP Array | ||||||
|---|---|---|---|---|---|---|---|
| Ra_method | Vm_method | Voc_method | Pm_method | Isc_method | Im_method | GA_method | |
| 1 × 40 | 398.125 | 398.125 | 398.125 | 398.125 | 398.125 | 398.125 | 398.125 |
| 2 × 20 | 396.659 | 396.499 | 398.072 | 397.711 | 398.341 | 401.544 | 402.067 |
| 4 × 10 | 395.028 | 395.132 | 396.728 | 397.978 | 400.086 | 402.693 | 403.059 |
| 5 × 8 | 394.340 | 394.476 | 396.086 | 397.630 | 400.228 | 403.754 | 403.785 |
| Array Size | Array Output Power (W) by Using Different Techniques for 400 W LPB-SP Array | ||||||
|---|---|---|---|---|---|---|---|
| Ra_method | Vm_method | Voc_method | Pm_method | Isc_method | Im_method | GA_method | |
| 40 × 1 | 383.643 | 383.643 | 383.643 | 383.643 | 383.643 | 383.643 | 383.643 |
| 20 × 2 | 392.090 | 383.978 | 383.978 | 385.219 | 394.482 | 394.657 | 398.356 |
| 10 × 4 | 391.648 | 391.166 | 393.361 | 393.845 | 397.598 | 400.556 | 402.729 |
| 8 × 5 | 392.807 | 392.503 | 395.221 | 395.821 | 399.553 | 401.379 | 402.827 |
| Array Size | Array Output Power (W) by Using Different Techniques for 3400 W LSS-SP Array | ||||||
|---|---|---|---|---|---|---|---|
| Ra_method | Vm_method | Voc_method | Pm_method | Isc_method | Im_method | GA_method | |
| 1 × 40 | 3415.950 | 3415.950 | 3415.950 | 3415.950 | 3415.950 | 3415.950 | 3415.950 |
| 2 × 20 | 3405.038 | 3405.528 | 3409.419 | 3412.54 | 3418.861 | 3422.724 | 3424.072 |
| 4 × 10 | 3402.887 | 3401.572 | 3405.725 | 3412.003 | 3419.048 | 3425.178 | 3426.417 |
| 5 × 8 | 3403.273 | 3400.943 | 3405.158 | 3408.437 | 3414.527 | 3426.038 | 3427.430 |
| Array Size | Array Output Power (W) by Using Different Techniques for 3400 W LPB-SP Array | ||||||
|---|---|---|---|---|---|---|---|
| Ra_method | Vm_method | Voc_method | Pm_method | Isc_method | Im_method | GA_method | |
| 40 × 1 | 3407.484 | 3407.484 | 3407.484 | 3407.484 | 3407.484 | 3407.484 | 3407.484 |
| 20 × 2 | 3410.415 | 3405.485 | 3410.201 | 3406.900 | 3409.463 | 3414.522 | 3426.913 |
| 10 × 4 | 3407.268 | 3403.179 | 3406.017 | 3411.639 | 3412.906 | 3424.642 | 3425.935 |
| 8 × 5 | 3405.368 | 3401.627 | 3406.7 | 3408.674 | 3415.815 | 3425.138 | 3426.92 |
| Array Size | Array Output Power (W) by Using Different Techniques for the 9880 W LSS-SP Array | ||||||
|---|---|---|---|---|---|---|---|
| Ra_method | Vm_method | Voc_method | Pm_method | Isc_method | Im_method | GA_method | |
| 1 × 40 | 9769.912 | 9769.912 | 9769.912 | 9769.912 | 9769.912 | 9769.912 | 9769.912 |
| 2 × 20 | 9709.074 | 9695.554 | 9742.637 | 9712.042 | 9758.631 | 9786.046 | 9810.914 |
| 4 × 10 | 9685.239 | 9678.068 | 9740.016 | 9691.434 | 9732.185 | 9766.97 | 9818.371 |
| 5 × 8 | 9682.299 | 9660.148 | 9723.505 | 9696.234 | 9709.943 | 9769.702 | 9816.904 |
| Array Size | Array Output Power (W) by Using Different Techniques for the 9880 W LPB-SP Array | ||||||
|---|---|---|---|---|---|---|---|
| Ra_method | Vm_method | Voc_method | Pm_method | Isc_method | Im_method | GA_method | |
| 40 × 1 | 9609.63 | 9609.63 | 9609.63 | 9609.63 | 9609.63 | 9609.63 | 9609.63 |
| 20 × 2 | 9717.518 | 9609.245 | 9622.994 | 9608.048 | 9718.273 | 9743.883 | 9814.136 |
| 10 × 4 | 9706.703 | 9629.607 | 9636.243 | 9656.269 | 9702.061 | 9771.7 | 9822.291 |
| 8 × 5 | 9688.570 | 9638.369 | 9692.488 | 9644.886 | 9715.177 | 9773.501 | 9815.887 |
| Measurement | Range | Resolution | Accuracy |
|---|---|---|---|
| DC Voltage | 1–1000 V | 0.01 V/0.1 V/1 V | ±1% ± (1% of Voc ± 0.1 V) |
| DC Current | 0.1–12 A | 1 mA/10 mA | ±1% ± (1% of Isc ± 9 mA) |
| Irradiance | 0–2000 W/m2 | 1 W/m2 | ± 3 % ± 20 dgts |
| Temperature | −22–85 °C | 0.1 °C | ± 1 % ± 1 °C |
| Array Configuration | Array Size | 400 W Array Output Power Obtained by Experimental Work (W) | ||
|---|---|---|---|---|
| Ra_method | Im_method | GA_method | ||
| LSS-SP | 4 × 10 | 378.201 | 388.110 | 390.559 |
| 5 × 8 | 377.06 | 389.312 | 392.743 | |
| LPB-SP | 10 × 4 | 375.421 | 386.502 | 388.648 |
| 8 × 5 | 376.733 | 386.919 | 389.781 | |
| Array Configuration | Array Size | Recoverable Energy Obtained by Experimental Work | |
|---|---|---|---|
| %RE_Im | %RE_GA | ||
| LSS-SP | 4 × 10 | 2.620 | 3.267 |
| 5 × 8 | 3.249 | 4.159 | |
| LPB-SP | 10 × 4 | 2.951 | 3.523 |
| 8 × 5 | 2.703 | 3.463 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mansur, A.A.; Amin, M.R.; Islam, K.K. Performance Comparison of Mismatch Power Loss Minimization Techniques in Series-Parallel PV Array Configurations. Energies 2019, 12, 874. https://doi.org/10.3390/en12050874
Mansur AA, Amin MR, Islam KK. Performance Comparison of Mismatch Power Loss Minimization Techniques in Series-Parallel PV Array Configurations. Energies. 2019; 12(5):874. https://doi.org/10.3390/en12050874
Chicago/Turabian StyleMansur, Ahmed Al, Md. Ruhul Amin, and Kazi Khairul Islam. 2019. "Performance Comparison of Mismatch Power Loss Minimization Techniques in Series-Parallel PV Array Configurations" Energies 12, no. 5: 874. https://doi.org/10.3390/en12050874
APA StyleMansur, A. A., Amin, M. R., & Islam, K. K. (2019). Performance Comparison of Mismatch Power Loss Minimization Techniques in Series-Parallel PV Array Configurations. Energies, 12(5), 874. https://doi.org/10.3390/en12050874






