Liquid Water Transport in Porous Metal Foam Flow-Field Fuel Cells: A Two-Phase Numerical Modelling and Ex-Situ Experimental Study
Abstract
:1. Introduction
2. Experimental Methodology
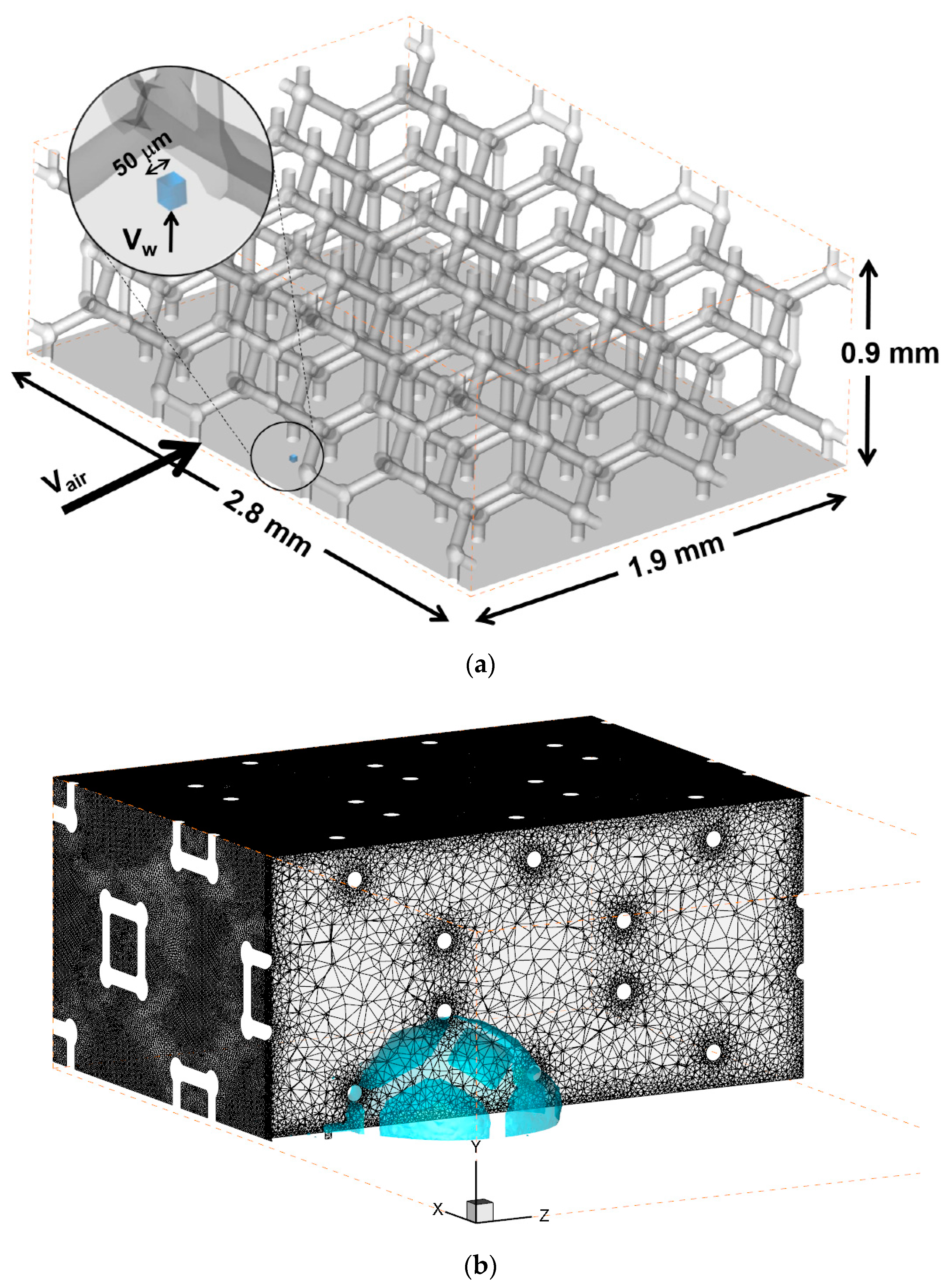
3. Numerical Model
4. Analysis and Discussion
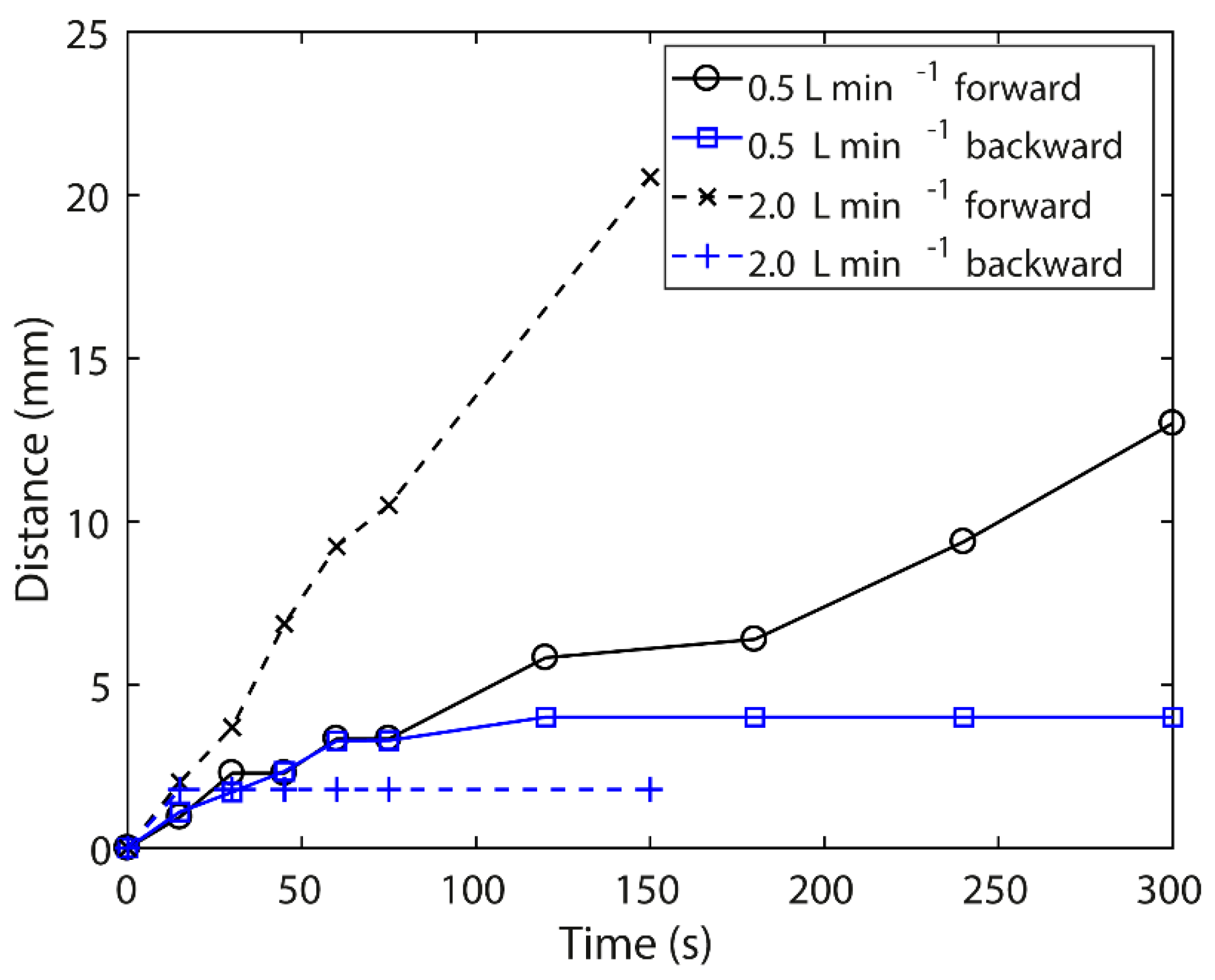
4.1. Experimental Results
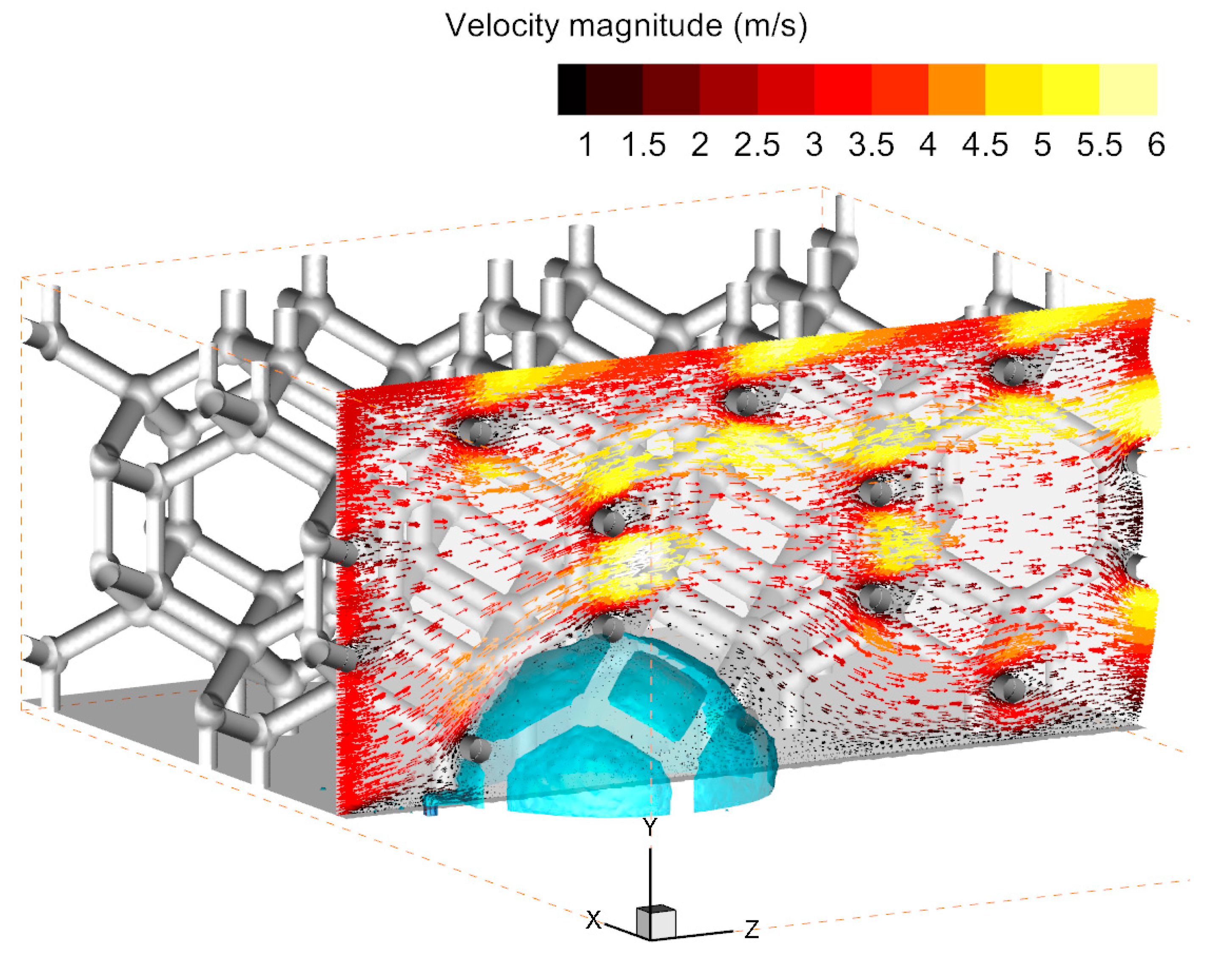
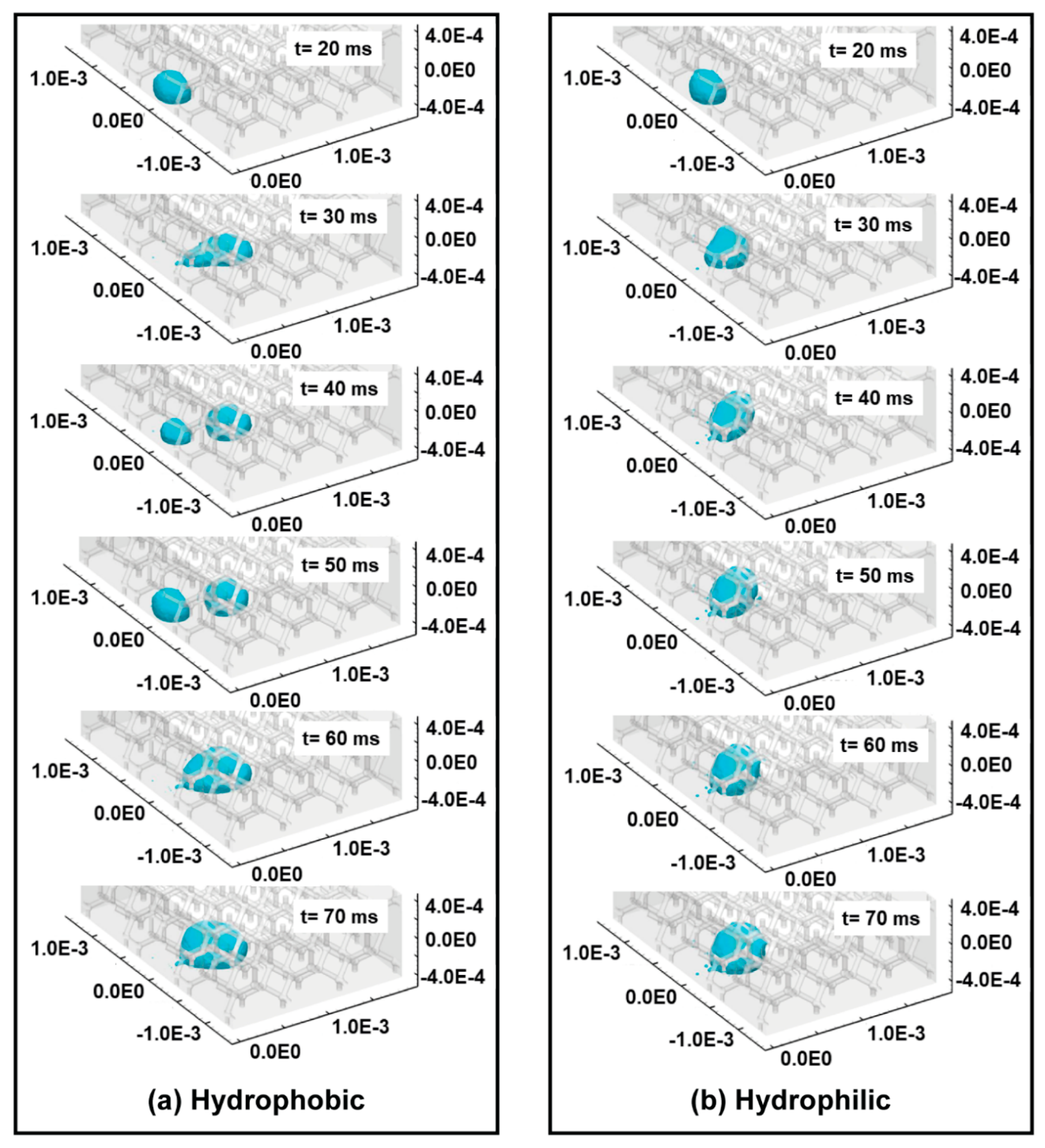
4.2. Numerical Study Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Larminie, J.; Dicks, A. Fuel Cell Systems Explained; Wiley Online Library: Hoboken, NJ, USA, 2003; ISBN 047084857X. [Google Scholar]
- Sasmito, A.P.; Kurnia, J.C.; Mujumdar, A.S. Numerical evaluation of various gas and coolant channel designs for high performance liquid-cooled proton exchange membrane fuel cell stacks. Energy 2012, 44, 278–291. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Q.; Shen, S.; Xiaohui, Y.; Zhu, F.; Cheng, X. The respective effect of under-rib convection and pressure drop of flow fields on the performance of PEM fuel cells. Nature 2017, 7, 1–9. [Google Scholar] [CrossRef]
- Song, M.; Kim, H.Y.; Kim, K. Effects of hydrophilic/hydrophobic properties of gas flow channels on liquid water transport in a serpentine polymer electrolyte membrane fuel cell. Int. J. Hydrogen Energy 2014, 39, 19714–19721. [Google Scholar] [CrossRef]
- Kim, H.Y.; Jeon, S.; Song, M.; Kim, K. Numerical simulations of water droplet dynamics in hydrogen fuel cell gas channel. J. Power Sources 2014, 246, 679–695. [Google Scholar] [CrossRef]
- Alrahmani, M.; Chen, R.; Ibrahim, S.; Patel, S. A Numerical Study on the Effects of Gas Channel Wettability in PEM Fuel Cells. ECS Trans. 2014, 48, 81–92. [Google Scholar] [CrossRef] [Green Version]
- Meyer, Q.; Ashton, S.; Jervis, R.; Finegan, D.P.; Boillat, P.; Cochet, M.; Curnick, O.; Reisch, T.; Adcock, P.; Shearing, P.R.; et al. The Hydro-electro-thermal Performance of Air-cooled, Open-cathode Polymer Electrolyte Fuel Cells: Combined Localised Current Density, Temperature and Water Mapping. Electrochim. Acta 2015, 180, 307–315. [Google Scholar] [CrossRef] [Green Version]
- Trogadas, P.; Cho, J.I.S.; Neville, T.P.; Marquis, J.; Wu, B.; Brett, D.J.L.; Coppens, M.-O. A lung-inspired approach to scalable and robust fuel cell design. Energy Environ. Sci. 2018, 11, 136–143. [Google Scholar] [CrossRef] [Green Version]
- Kariya, T.; Hirono, T.; Funakubo, H.; Shudo, T. Effects of the porous structures in the porous flow field type separators on fuel cell performances. Int. J. Hydrogen Energy 2014, 39, 15072–15080. [Google Scholar] [CrossRef]
- Yoshida, T.; Kojima, K. Toyota MIRAI Fuel Cell Vehicle and Progress Toward a Future Hydrogen Society. Interface Mag. 2015, 24, 45–49. [Google Scholar] [CrossRef] [Green Version]
- Murphy, O.J.; Cisar, A.; Clarke, E. Low-cost light weight high power density PEM fuel cell stack. Electrochim. Acta 1998, 43, 3829–3840. [Google Scholar] [CrossRef]
- Kumar, A.; Reddy, R.G. Materials and design development for bipolar/end plates in fuel cells. J. Power Sources 2004, 129, 62–67. [Google Scholar] [CrossRef]
- Tseng, C.-J.; Tsai, B.T.; Liu, Z.-S.; Cheng, T.-C.; Chang, W.-C.; Lo, S.-K. A PEM fuel cell with metal foam as flow distributor. Energy Convers. Manag. 2012, 62, 14–21. [Google Scholar] [CrossRef]
- Tsai, B.-T.; Tseng, C.-J.; Liu, Z.-S.; Wang, C.-H.; Lee, C.-I.; Yang, C.-C.; Lo, S.-K. Effects of flow field design on the performance of a PEM fuel cell with metal foam as the flow distributor. Int. J. Hydrogen Energy 2012, 37, 13060–13066. [Google Scholar] [CrossRef]
- Shin, D.K.; Yoo, J.H.; Kang, D.G.; Kim, M.S. Effect of Cell Size in Metal Foam Inserted to the Air Channel of Polymer Electrolyte Membrane Fuel Cell for High Performance. Renew. Energy 2017, 115, 663–675. [Google Scholar] [CrossRef]
- Tabe, Y.; Nasu, T.; Morioka, S.; Chikahisa, T. Performance characteristics and internal phenomena of polymer electrolyte membrane fuel cell with porous flow field. J. Power Sources 2013, 238, 21–28. [Google Scholar] [CrossRef] [Green Version]
- Lefebvre, L.-P.; Banhart, J.; Dunand, D.C. Porous metals and metallic foams: Current status and recent developments. Adv. Eng. Mater. 2008, 10, 775–787. [Google Scholar] [CrossRef]
- Kim, M.; Kim, C.; Sohn, Y. Application of Metal Foam as a Flow Field for PEM Fuel Cell Stack. Fuel Cells 2018, 18, 123–128. [Google Scholar] [CrossRef]
- Fly, A.; Butcher, D.; Meyer, Q.; Whiteley, M.; Spencer, A.; Kim, C.; Shearing, P.R.; Brett, D.J.L.; Chen, R. Characterisation of the diffusion properties of metal foam hybrid flow- fields for fuel cells using optical flow visualisation and X-ray computed tomography. J. Power Sources 2018, 395, 171–178. [Google Scholar] [CrossRef]
- Fly, A.; Meyer, Q.; Whiteley, M.; Iacoviello, F.; Neville, T.; Shearing, P.R.; Brett, D.J.L.; Kim, C.; Chen, R. X-ray tomography and modelling study on the mechanical behaviour and performance of metal foam flow-fields for polymer electrolyte fuel cells. Int. J. Hydrogen Energy 2019, 44, 7583–7595. [Google Scholar] [CrossRef]
- Calvo, S.; Beugre, D.; Crine, M.; Léonard, A.; Marchot, P.; Toye, D. Phase distribution measurements in metallic foam packing using X-ray radiography and micro-tomography. Chem. Eng. Process. Process Intensif. 2009, 48, 1030–1039. [Google Scholar] [CrossRef]
- Wallenstein, M.; Hafen, N.; Heinzmann, H.; Schug, S.; Arlt, W.; Kind, M.; Dietrich, B. Qualitative and quantitative insights into multiphase flow in ceramic sponges using X-ray computed tomography. Chem. Eng. Sci. 2015, 138, 118–127. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- ANSYS FLUENT 12.0 Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2009.







| Parameter | Foam A | Foam B |
|---|---|---|
| Thickness | 1.6 mm | 3.0 mm |
| Material | Nickel | Nickel |
| Pore size | 0.23 mm | 0.95 mm |
| Porosity | 97% | 95% |
| Foam | Air Flow Rate (Lmin−1) | Time for Liquid to Reach End of Sample (s) |
|---|---|---|
| Foam A | 0.5 | 630 |
| Foam A | 2.0 | 195 |
| Foam B | 0.5 | 1480 |
| Foam B | 2.0 | 1890 |
| Foam B (18.8 wt % PTFE) | 0.5 | 550 |
| Foam B (18.8 wt % PTFE) | 2.0 | 260 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fly, A.; Kim, K.; Gordon, J.; Butcher, D.; Chen, R. Liquid Water Transport in Porous Metal Foam Flow-Field Fuel Cells: A Two-Phase Numerical Modelling and Ex-Situ Experimental Study. Energies 2019, 12, 1186. https://doi.org/10.3390/en12071186
Fly A, Kim K, Gordon J, Butcher D, Chen R. Liquid Water Transport in Porous Metal Foam Flow-Field Fuel Cells: A Two-Phase Numerical Modelling and Ex-Situ Experimental Study. Energies. 2019; 12(7):1186. https://doi.org/10.3390/en12071186
Chicago/Turabian StyleFly, Ashley, Kyoungyoun Kim, John Gordon, Daniel Butcher, and Rui Chen. 2019. "Liquid Water Transport in Porous Metal Foam Flow-Field Fuel Cells: A Two-Phase Numerical Modelling and Ex-Situ Experimental Study" Energies 12, no. 7: 1186. https://doi.org/10.3390/en12071186
APA StyleFly, A., Kim, K., Gordon, J., Butcher, D., & Chen, R. (2019). Liquid Water Transport in Porous Metal Foam Flow-Field Fuel Cells: A Two-Phase Numerical Modelling and Ex-Situ Experimental Study. Energies, 12(7), 1186. https://doi.org/10.3390/en12071186







