A Fault Line Selection Method for DC Distribution Network Using Multiple Observers
Abstract
:1. Introduction
2. Basic Theory for Fault Line Selection
2.1. Time Reversal and Complex Conjugate
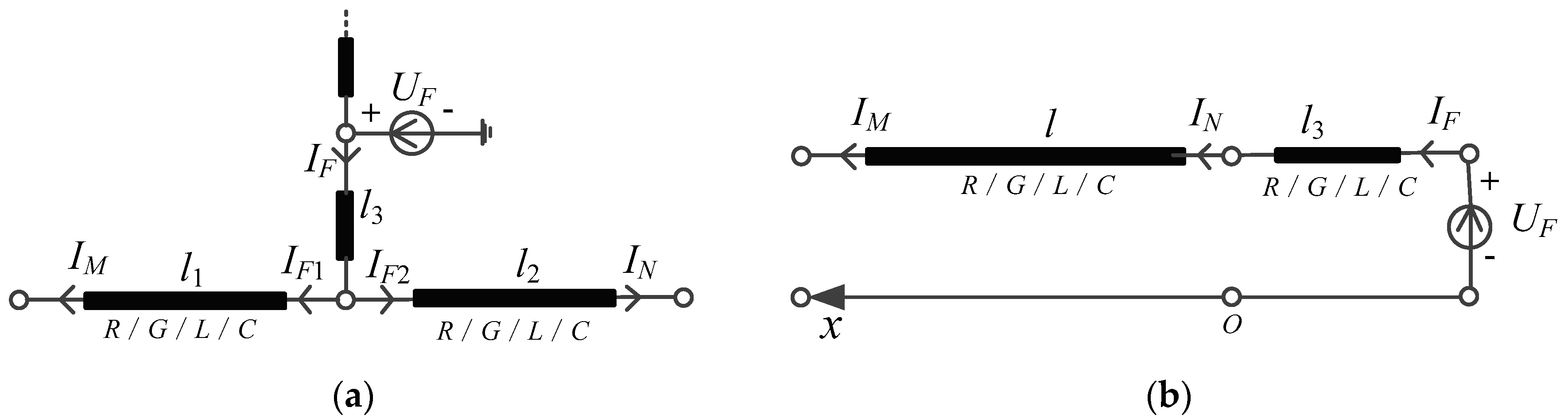
2.2. Locate Fault Using Two Internal Observers
- Because the lossless mirror line and its parameters are created subjectively, the phase coefficient () can be modified into from (7) to (11). The fault location result is simplified as .
- The initial forward current are extracted for locating faults, so , that causes in (11). Therefore, the fault location result is further simplified as .In fact, is not equal to due to the reflections of currents, so multiple local extremum may exist in formula (10). However, these local extrema are a superposition of the reflected currents, whose amplitude are smaller than the initial forward currents. Therefore, the global extremum exists where .
- The practical filtered current is a band signal whose frequency band is .Suppose achieves its peak at , for any , it can get the peak value at . Therefore, we can obtain (12):where, .
2.3. Locate Fault Using Two External Observers
2.4. Locate Fault Using Multiple Observers
2.5. Fault Line Selection with Variable Phase Coefficient
3. Fault Line Selection Algorithm
3.1. Basic Introduction for Wavelet Decompsition
3.2. Time-Domain Fault Line Selection Algorithm
4. Simulated Case Study
4.1. Simulation Model
4.2. Different Fault Types and Resistances
4.3. Different Wavelet Functions and Sampling Frequencies
4.4. Comparison With Tavelling-Wave-Based Method
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
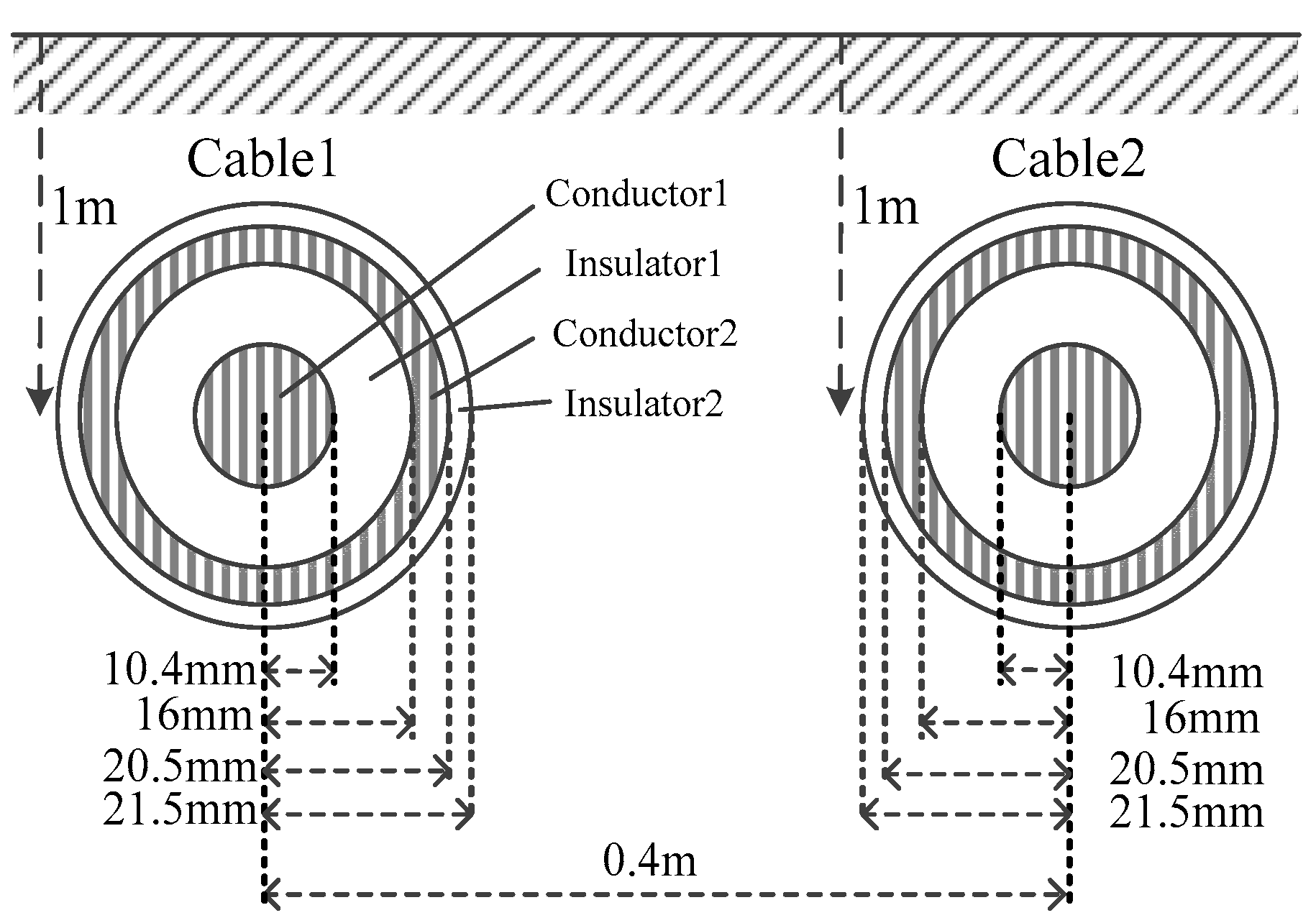
| Para. | Resistivity /(ohm × m) | Relative Permeability | Relative Permittivity | |
|---|---|---|---|---|
| Layout | ||||
| Conductor1 | 2.82 × 10−8 | 1.00 | ||
| Insulator1 | 1.00 | 4.10 | ||
| Conductor2 | 1.86 × 10−8 | 1.00 | ||
| Insulator2 | 1.00 | 2.30 | ||
| Ground | 100.00 | 1.00 | ||
Appendix B
| Wavelet. | Db4 | Coif4 | Rbio2.8 | Dmey | |
|---|---|---|---|---|---|
| Property | |||||
| Orthogonal | yes | yes | no | yes | |
| Biorthogonal | yes | yes | yes | yes | |
| Symmetry | far from | near from | |||
| Compact support | yes | yes | yes | yes | |
| Orthogonal | yes | yes | no | ||
References
- Huang, W. An Impedance Protection Scheme for Feeders of Active Distribution Networks. IEEE Trans. Power Deliv. 2014, 29, 1591–1602. [Google Scholar] [CrossRef]
- Ji, Y. Overall control scheme for VSC-based medium-voltage DC power distribution networks. IET Gener. Transm. Distrib. 2018, 12, 1438–1445. [Google Scholar] [CrossRef]
- Shamsi, P.; Fahimi, B. Stability Assessment of a DC Distribution Network in a Hybrid Micro-Grid Application. IEEE Trans. Smart Grid 2014, 5, 2527–2534. [Google Scholar] [CrossRef]
- Beerten, J.; Cole, S.; Belmans, R. Modeling of Multi-Terminal VSC HVDC Systems with Distributed DC Voltage Control. IEEE Trans. Power Syst. 2014, 29, 34–42. [Google Scholar] [CrossRef]
- Zhang, S.; Lin, S.; He, Z.; Lee, W. Ground fault location in radial distribution networks involving distributed voltage measurement. IET Gener. Transm. Distrib. 2018, 12, 987–996. [Google Scholar] [CrossRef]
- Majidi, M.; Arabali, A.; Etezadi-Amoli, M. Fault Location in Distribution Networks by Compressive Sensing. IEEE Trans. Power Deliv. 2015, 30, 1761–1769. [Google Scholar] [CrossRef]
- Shafiullah, M.; Abido, M.A.; Al-Hamouz, Z. Wavelet-based extreme learning machine for distribution grid fault location. IET Gener. Transm. Distrib. 2017, 11, 4256–4263. [Google Scholar] [CrossRef]
- Monadi, M.; Koch-Ciobotaru, C.; Luna, A.; Ignacio Candela, J.; Rodriguez, P. Multi-terminal medium voltage DC grids fault location and isolation. IET Gener. Transm. Distrib. 2016, 10, 3517–3528. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.; Fletcher, J.E.; O’Reilly, J. Multiterminal DC Wind Farm Collection Grid Internal Fault Analysis and Protection Design. IEEE Trans. Power Deliv. 2010, 25, 2308–2318. [Google Scholar] [CrossRef]
- De Kerf, K.; Srivastava, K.; Reza, M.; Bekaert, D.; Cole, S.; Van Hertem, D.; Belmans, R. Wavelet-based protection strategy for DC faults in multi-terminal VSC HVDC systems. IET Gener. Transm. Distrib. 2011, 5, 496–503. [Google Scholar] [CrossRef]
- Lianxiang, T.; Boon-Teck, O. Locating and Isolating DC Faults in Multi-Terminal DC Systems. IEEE Trans. Power Deliv. 2007, 22, 1877–1884. [Google Scholar] [CrossRef]
- Jin, Y.; Fletcher, J.E.; O’Reilly, J. Short-Circuit and Ground Fault Analyses and Location in VSC-Based DC Network Cables. IEEE Trans. Ind. Electron. 2012, 59, 3827–3837. [Google Scholar] [CrossRef] [Green Version]
- Azizi, S.; Sanaye-Pasand, M.; Abedini, M.; Hassani, A. A Traveling-Wave-Based Methodology for Wide-Area Fault Location in Multiterminal DC Systems. IEEE Trans. Power Deliv. 2014, 29, 2552–2560. [Google Scholar] [CrossRef]
- Nanayakkara, O.M.K.K.; Rajapakse, A.D.; Wachal, R. Traveling-Wave-Based Line Fault Location in Star-Connected Multiterminal HVDC Systems. IEEE Trans. Power Deliv. 2012, 27, 2286–2294. [Google Scholar] [CrossRef]
- Nanayakkara, O.M.K.K.; Rajapakse, A.D.; Wachal, R. Location of DC Line Faults in Conventional HVDC Systems With Segments of Cables and Overhead Lines Using Terminal Measurements. IEEE Trans. Power Deliv. 2012, 27, 279–288. [Google Scholar] [CrossRef]
- Zheng-you, H.; Kai, L.; Xiao-peng, L.; Sheng, L.; Jian-wei, Y.; Rui-kun, M. Natural Frequency-Based Line Fault Location in HVDC Lines. IEEE Trans. Power Deliv. 2014, 29, 851–859. [Google Scholar] [CrossRef]
- Jiale, S.; Shuping, G.; Guobing, S.; Zaibin, J.; Xiaoning, K. A Novel Fault-Location Method for HVDC Transmission Lines. IEEE Trans. Power Deliv. 2010, 25, 1203–1209. [Google Scholar] [CrossRef]
- Liang, Y.; Wang, G.; Li, H. Time-Domain Fault-Location Method on HVDC Transmission Lines Under Unsynchronized Two-End Measurement and Uncertain Line Parameters. IEEE Trans. Power Deliv. 2015, 30, 1031–1038. [Google Scholar] [CrossRef]
- Fink, M. Time reversal of ultrasonic fields. I. Basic principles. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1992, 39, 555–566. [Google Scholar] [CrossRef] [PubMed]
- Rachidi, F. On the Location of Lightning Discharges Using Time Reversal of Electromagnetic Fields. IEEE Trans. Electromagn. Compat. 2014, 56, 149–158. [Google Scholar]
- Razzaghi, R. An Efficient Method Based on the Electromagnetic Time Reversal to Locate Faults in Power Networks. IEEE Trans. Power Deliv. 2013, 28, 1663–1673. [Google Scholar] [CrossRef] [Green Version]
- Razzaghi, R.; Lugrin, G.; Rachidi, F.; Paolone, M. Assessment of the Influence of Losses on the Performance of the Electromagnetic Time Reversal Fault Location Method. IEEE Trans. Power Deliv. 2017, 32, 2303–2312. [Google Scholar] [CrossRef] [Green Version]
- Codino, A.; Wang, Z.; Razzaghi, R.; Paolone, M.; Rachidi, F. An Alternative Method for Locating Faults in Transmission Line Networks Based on Time Reversal. IEEE Trans. Electromagn. Compat. 2017, 59, 1601–1612. [Google Scholar] [CrossRef]
- Zhang, X.; Tai, N.; Wang, Y.; Liu, J. EMTR-based fault location for DC line in VSC-MTDC system using high-frequency currents. IET Gener. Transm. Distrib. 2017, 11, 2499–2507. [Google Scholar] [CrossRef]
- Dong, X.; Kong, W.; Cui, T. Fault Classification and Faulted-Phase Selection Based on the Initial Current Traveling Wave. IEEE Trans. Power Deliv. 2009, 24, 552–559. [Google Scholar] [CrossRef]
- Hong, Y.; Chang-Chian, P. Detection and correction of distorted current transformer current using wavelet transform and artificial intelligence. IET Gener. Transm. Distrib. 2008, 2, 566–575. [Google Scholar] [CrossRef]
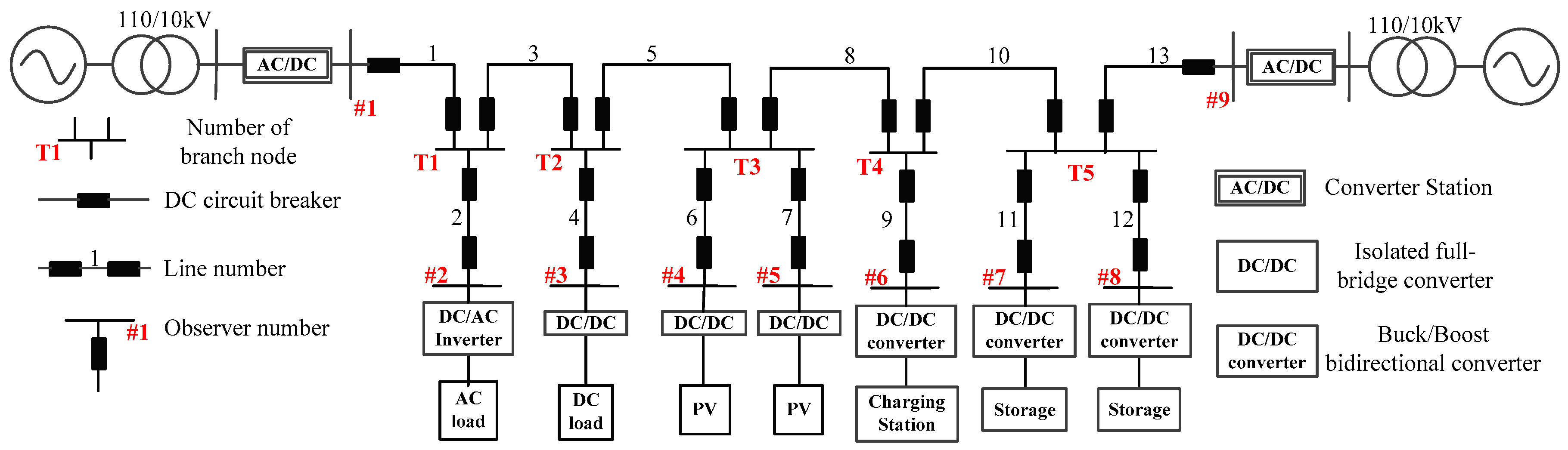

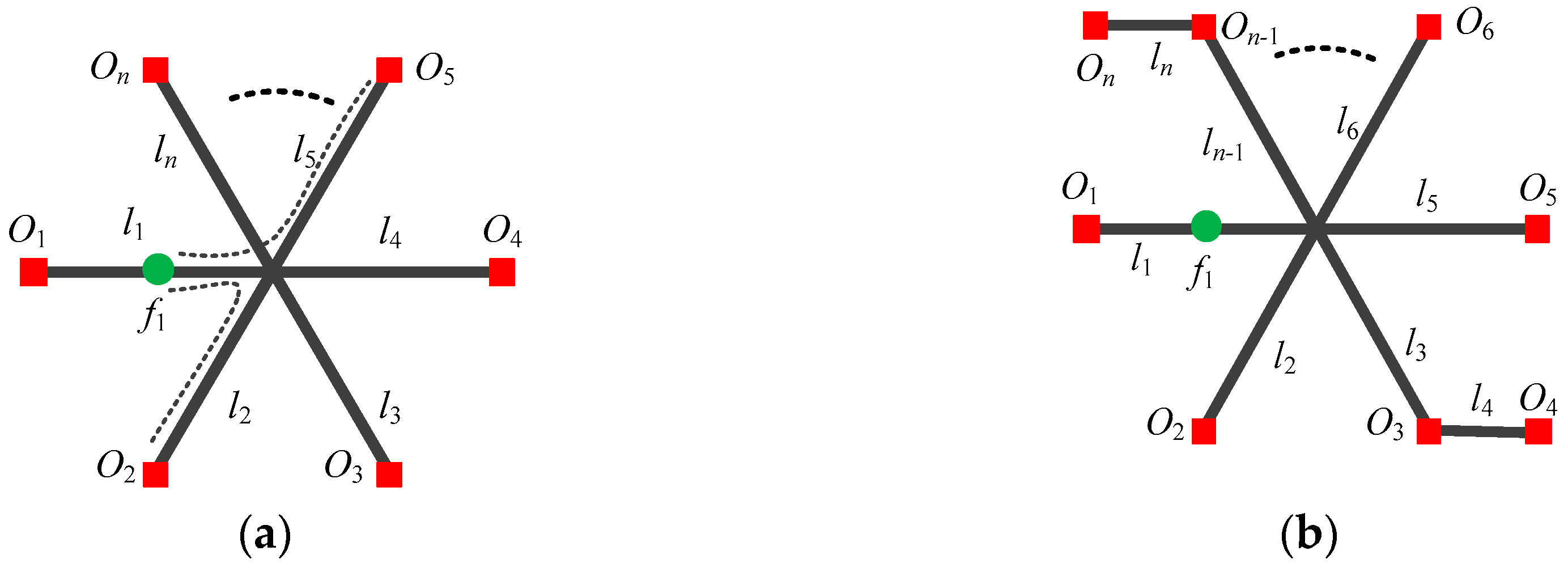



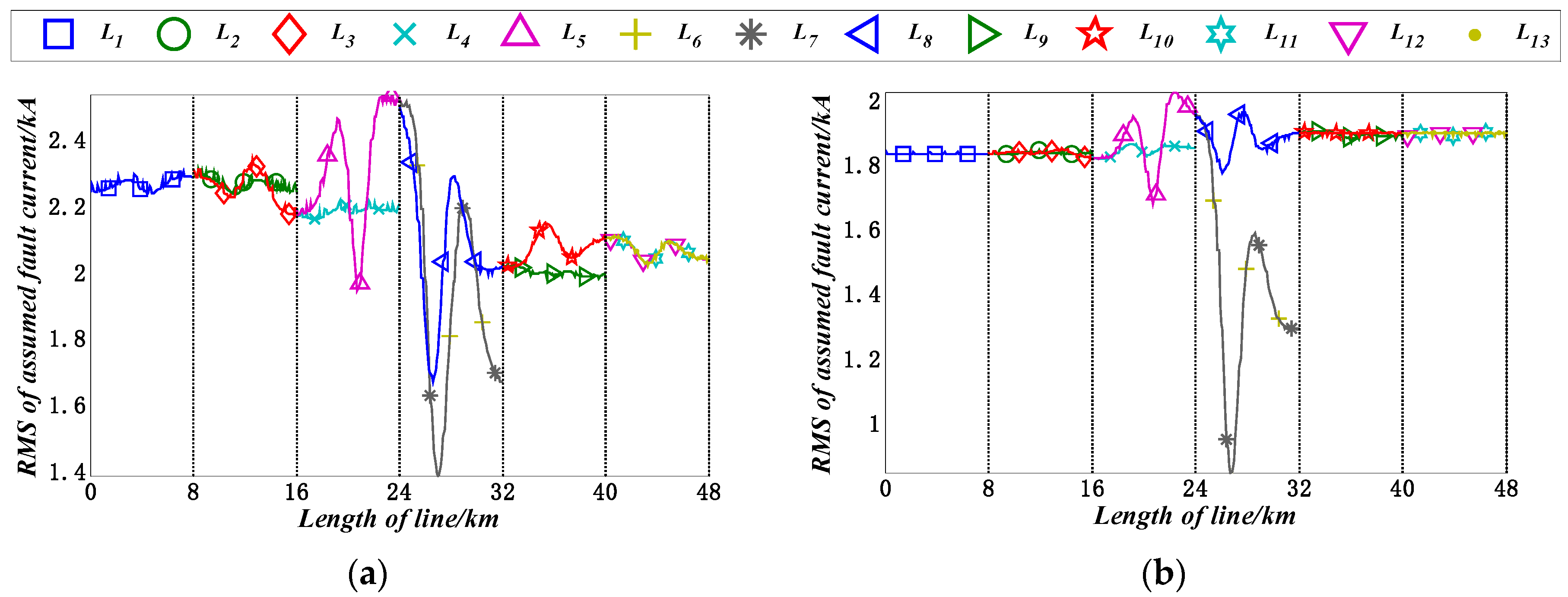
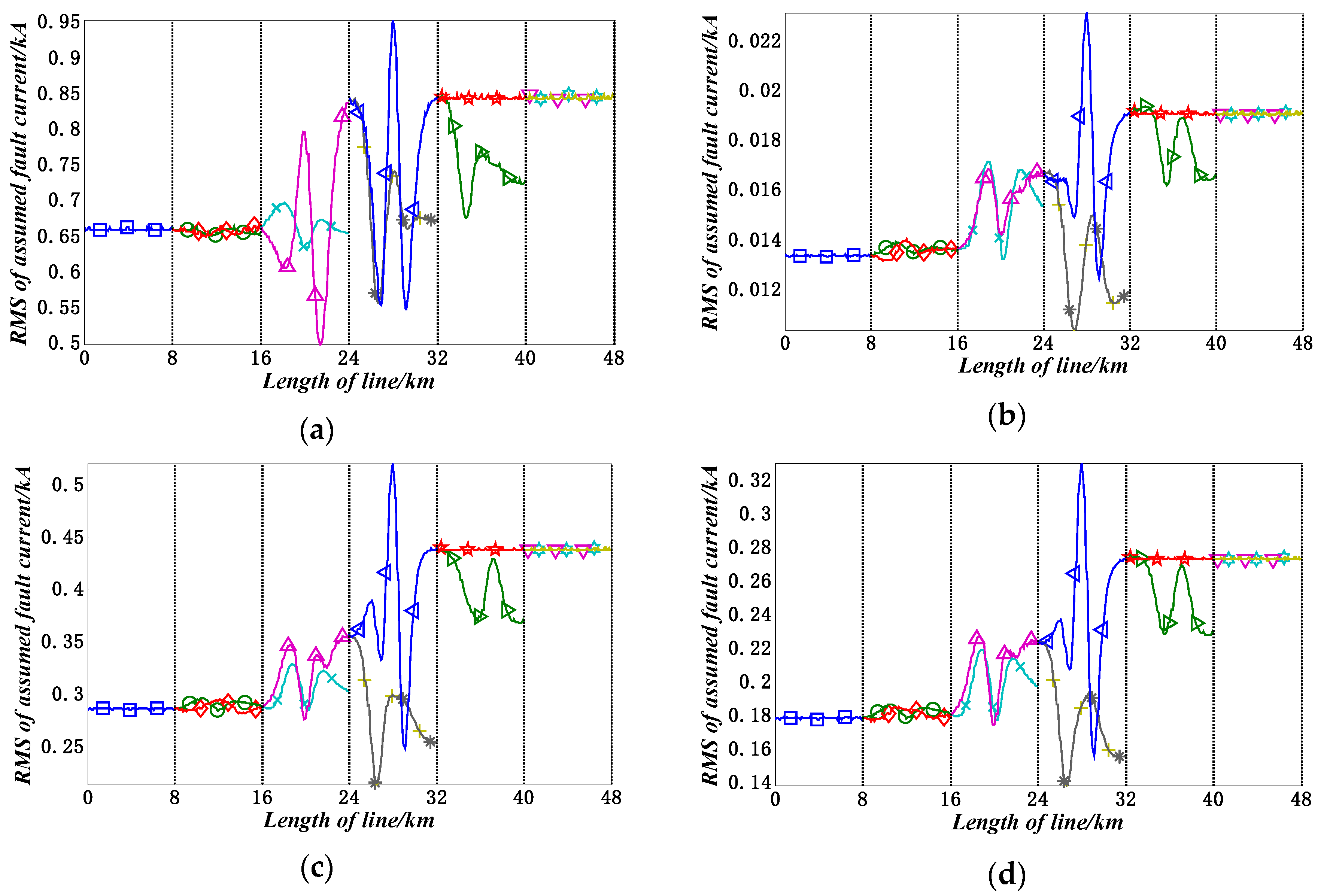

| Faulted Line | Observers | Faulted Line | Observers | Faulted Line | Observers |
|---|---|---|---|---|---|
| L1 | 1 2 3 | L6 | 3 4 5 6 | L11 | 6 7 8 9 |
| L2 | 1 2 3 | L7 | 3 4 5 6 | L12 | 6 7 8 |
| L3 | 1 2 3 4 | L8 | 3 4 5 6 7 | L13 | 6 7 8 9 |
| L4 | 2 3 4 | L9 | 4 6 7 | ||
| L5 | 2 3 4 5 6 | L10 | 4 6 7 8 9 |
| Fault Location/% | 2.50 | 50.00 | 97.50 | Branch Node | |
|---|---|---|---|---|---|
| Faulted Line | |||||
| L1 | 21.25 | 47.50 | 92.50 | 97.50 (T1) | |
| L2 | 6.25 | 51.25 | 78.75 | ||
| L3 | 10.00 | 50.00 | 85.00 | ||
| L4 | 6.25 | 47.50 | 77.50 | 5.00 (T2) | |
| L5 | 13.75 | 50.00 | 86.25 | ||
| L6 | 6.25 | 50.00 | 76.25 | ||
| L7 | 6.25 | 51.25 | 76.25 | ||
| L8 | 16.25 | 50.00 | 90.00 | 1.25 (T3) | |
| L9 | 6.25 | 48.75 | 77.50 | 1.25 (T4) | |
| L10 | 13.75 | 50.00 | 86.25 | 95.00 (T5) | |
| L11 | 76.25 | 51.25 | 76.25 | ||
| L12 | 76.25 | 51.25 | 76.25 | ||
| L13 | 6.25 | 51.25 | 78.75 | ||
| Mean-variance | 25.26 | 1.35 | 5.83 | ||
| Wavelet Function | Db4 | Coif4 | Rbio2.8 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fault Location/% | 2.50 | 50.00 | 97.50 | Branch Node | 2.50 | 50.00 | 97.50 | Branch Node | 2.50 | 50.00 | 97.50 | Branch Node | |
| Faulted Line | |||||||||||||
| L1 | 21.25 | 47.50 | 92.50 | 97.50 (T1) | 21.25 | 47.50 | 92.50 | 21.25 | 47.50 | 92.50 | 97.50 (T1) | ||
| L2 | 6.25 | 51.25 | 78.75 | 6.25 | 51.25 | 78.75 | 6.25 | 51.25 | 78.75 | ||||
| L3 | 21.25 | 50.00 | 76.25 | 37.50 | 50.00 | 61.25 | 1.25 (T1) | 37.50 | 50.00 | 61.25 | |||
| L4 | 6.25 | 47.50 | 78.75 | 5.00 (T2) | 6.25 | 47.50 | 77.50 | 30.00 (T2) | 6.25 | 63.75 | 78.75 | 5.00 (T2) | |
| L5 | 21.25 | 50.00 | 76.25 | 37.50 | 50.00 | 90.00 | 6.25 | 50.00 | 90.00 | ||||
| L6 | 6.25 | 50.00 | 76.25 | 1.25 (T3) | 6.25 | 50.00 | 76.25 | 6.25 | 51.25 | 76.25 | 1.25 (T3) | ||
| L7 | 6.25 | 51.25 | 76.25 | 6.25 | 51.25 | 76.25 | 6.25 | 51.25 | 76.25 | ||||
| L8 | 23.75 | 50.00 | 78.75 | 13.75 | 50.00 | 92.50 | 13.75 (T3) | 13.75 | 50.00 | 92.50 | |||
| L9 | 6.25 | 47.50 | 78.75 | 5.00 (T4) | 6.25 | 47.50 | 77.50 | 28.75 (T4) | 6.25 | 47.50 | 77.50 | 5.00 (T4) | |
| L10 | 23.75 | 50.00 | 76.25 | 38.75 | 50.00 | 62.50 | 86.25 (T5) | 38.75 | 50.00 | 23.75 | |||
| L11 | 40.00 | 51.25 | 76.25 | 1.25 (T5) | 76.25 | 51.25 | 76.25 | 76.25 | 51.25 | 76.25 | 1.25 (T5) | ||
| L12 | 40.00 | 51.25 | 76.25 | 76.25 | 51.25 | 76.25 | 76.25 | 51.25 | 76.25 | ||||
| L13 | 6.25 | 51.25 | 78.75 | 6.25 | 51.25 | 78.75 | 6.25 | 51.25 | 78.75 | ||||
| Mean-variance | 12.56 | 1.48 | 4.39 | 25.80 | 1.48 | 9.57 | 26.10 | 3.99 | 17.58 | ||||
| Wavelet Function | Db4 | Coif4 | Rbio2.8 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fault Location/% | 2.50 | 50.00 | 97.50 | Branch Node | 2.50 | 50.00 | 97.50 | Branch Node | 2.50 | 50.00 | 97.50 | Branch Node | |
| Faulted Line | |||||||||||||
| L1 | 15.00 | 51.25 | 88.75 | 17.50 | 50.00 | 83.75 | 23.750 | 51.250 | 92.500 | 97.50 (T1) | |||
| L2 | 10.00 | 47.50 | 85.00 | 15.00 | 48.75 | 81.25 | 13.750 | 47.500 | 76.250 | ||||
| L3 | 11.25 | 50.00 | 87.50 | 2.50 (T1) | 17.50 | 50.00 | 83.75 | 2.50 (T1) | 5.000 | 48.750 | 85.000 | ||
| L4 | 5.00 | 47.50 | 85.00 | 95.00 (T2) | 13.75 | 48.75 | 78.75 | 40.00 (T2) | 13.750 | 47.500 | 77.500 | 11.25 (T2) | |
| L5 | 11.25 | 50.00 | 87.50 | 15.00 | 50.00 | 83.75 | 13.750 | 50.000 | 85.000 | ||||
| L6 | 10.00 | 47.50 | 85.00 | 15.00 | 48.75 | 80.00 | 13.750 | 46.250 | 75.000 | 1.25 (T3) | |||
| L7 | 10.00 | 48.75 | 85.00 | 15.00 | 48.75 | 80.00 | 13.750 | 46.250 | 75.000 | ||||
| L8 | 15.00 | 50.00 | 73.75 | 5.00 (T3) | 17.50 | 50.00 | 83.75 | 10.00 (T3) | 13.750 | 50.000 | 92.500 | ||
| L9 | 5.00 | 47.50 | 83.75 | 13.75 | 48.75 | 78.75 | 30.00 (T4) | 13.750 | 47.500 | 77.500 | |||
| L10 | 11.25 | 50.00 | 87.50 | 2.50 (T4) | 17.50 | 50.00 | 82.50 | 92.50 (T5) | 16.250 | 51.250 | 90.000 | 10.00 (T4) | |
| L11 | 10.00 | 48.75 | 85.00 | 95.00 (T5) | 16.25 | 48.75 | 80.00 | 6.250 | 45.000 | 72.500 | 1.25 (T5) | ||
| L12 | 10.00 | 48.75 | 85.00 | 16.25 | 48.75 | 80.00 | 6.250 | 45.000 | 71.250 | ||||
| L13 | 10.00 | 47.50 | 85.00 | 15.00 | 48.75 | 80.00 | 6.250 | 46.250 | 75.000 | ||||
| Mean-variance | 2.94 | 1.30 | 3.66 | 1.40 | 0.63 | 1.98 | 5.200 | 2.188 | 7.610 | ||||
| Oj | O2 | O3 | O4 | O5 | O6 | O7 | O8 | O9 | |
|---|---|---|---|---|---|---|---|---|---|
| Oi | |||||||||
| O1 | L1 | L4 | L5 | L5 | L5 | L3 | L3 | L3 | |
| O2 | L4 | L5 | L5 | L5 | L3 | L3 | L3 | ||
| O3 | L5 | L5 | L5 | L4 | L4 | L4 | |||
| O4 | L6 | L6 | × | × | × | ||||
| O5 | L7 | × | × | × | |||||
| O6 | × | × | × | ||||||
| O7 | L11 | L11 | |||||||
| O8 | L12 | ||||||||
| Fault Location/% | 2.50 | 50.00 | 97.50 | Branch Node | |
|---|---|---|---|---|---|
| Faulted Line | |||||
| L1 | L1 | L1 | L1 | L1 | |
| L2 | L2 | L2 | L2 | ||
| L3 | L3 | L3 | L3 | ||
| L4 | L4 | L4 | L3 | L4 | |
| L5 | L5 | L5 | L5 | L6 | |
| L6 | L6 | L6 | L8 | ||
| L7 | L7 | L7 | L8 | ||
| L8 | L8 | L8 | L8 | ||
| L9 | L9 | L9 | L10 | L9 | |
| L10 | L10 | L10 | L10 | ||
| L11 | L11 | L11 | L10 | L11 | |
| L12 | L12 | L12 | L10 | ||
| L13 | L13 | L13 | L13 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Tai, N.; Wu, P.; Zheng, X.; Huang, W. A Fault Line Selection Method for DC Distribution Network Using Multiple Observers. Energies 2019, 12, 1245. https://doi.org/10.3390/en12071245
Zhang X, Tai N, Wu P, Zheng X, Huang W. A Fault Line Selection Method for DC Distribution Network Using Multiple Observers. Energies. 2019; 12(7):1245. https://doi.org/10.3390/en12071245
Chicago/Turabian StyleZhang, Xipeng, Nengling Tai, Pan Wu, Xiaodong Zheng, and Wentao Huang. 2019. "A Fault Line Selection Method for DC Distribution Network Using Multiple Observers" Energies 12, no. 7: 1245. https://doi.org/10.3390/en12071245
APA StyleZhang, X., Tai, N., Wu, P., Zheng, X., & Huang, W. (2019). A Fault Line Selection Method for DC Distribution Network Using Multiple Observers. Energies, 12(7), 1245. https://doi.org/10.3390/en12071245






