NOx Reduction in Diesel-Hydrogen Engines Using Different Strategies of Ammonia Injection
Abstract
:1. Introduction
2. Materials and Methods
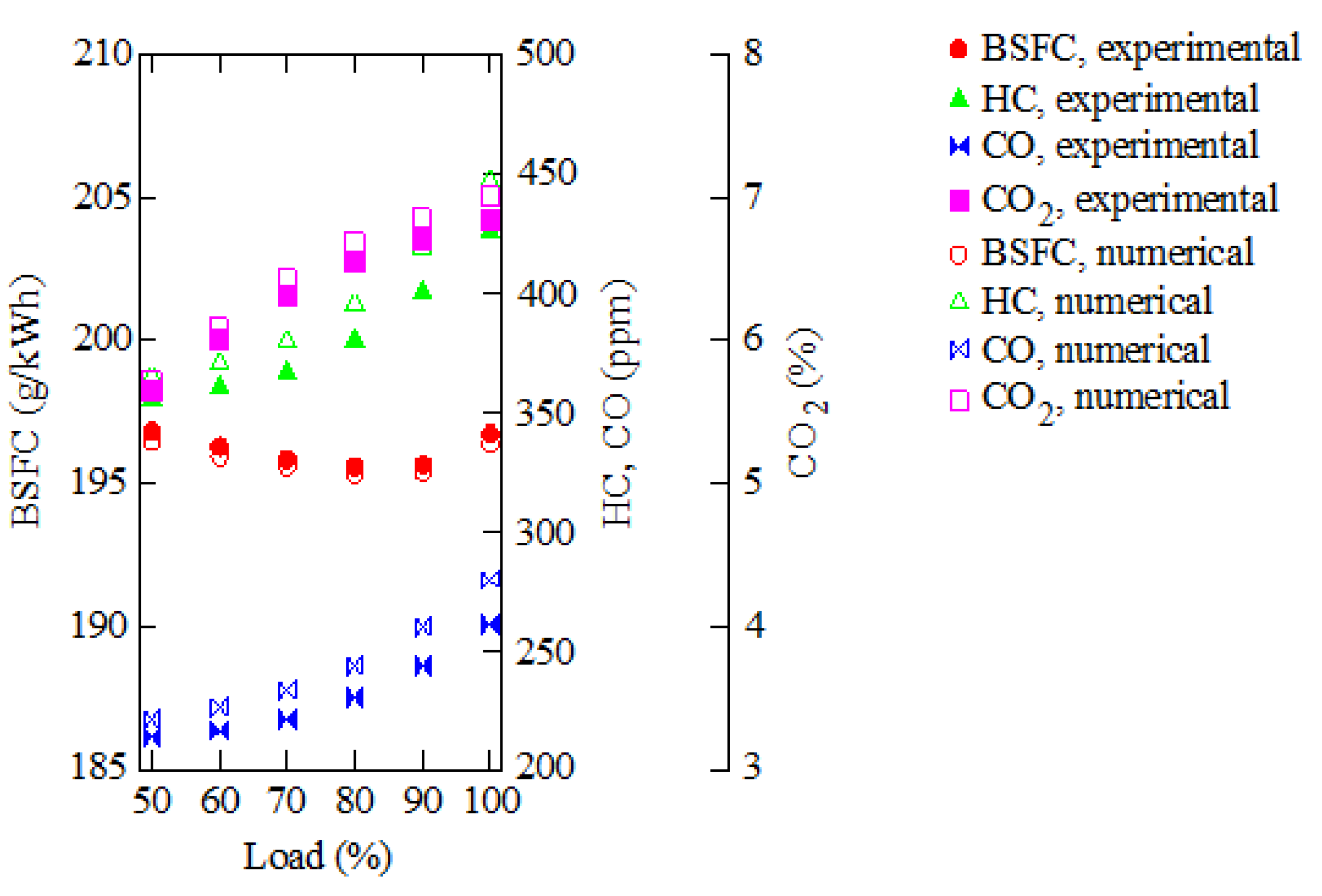
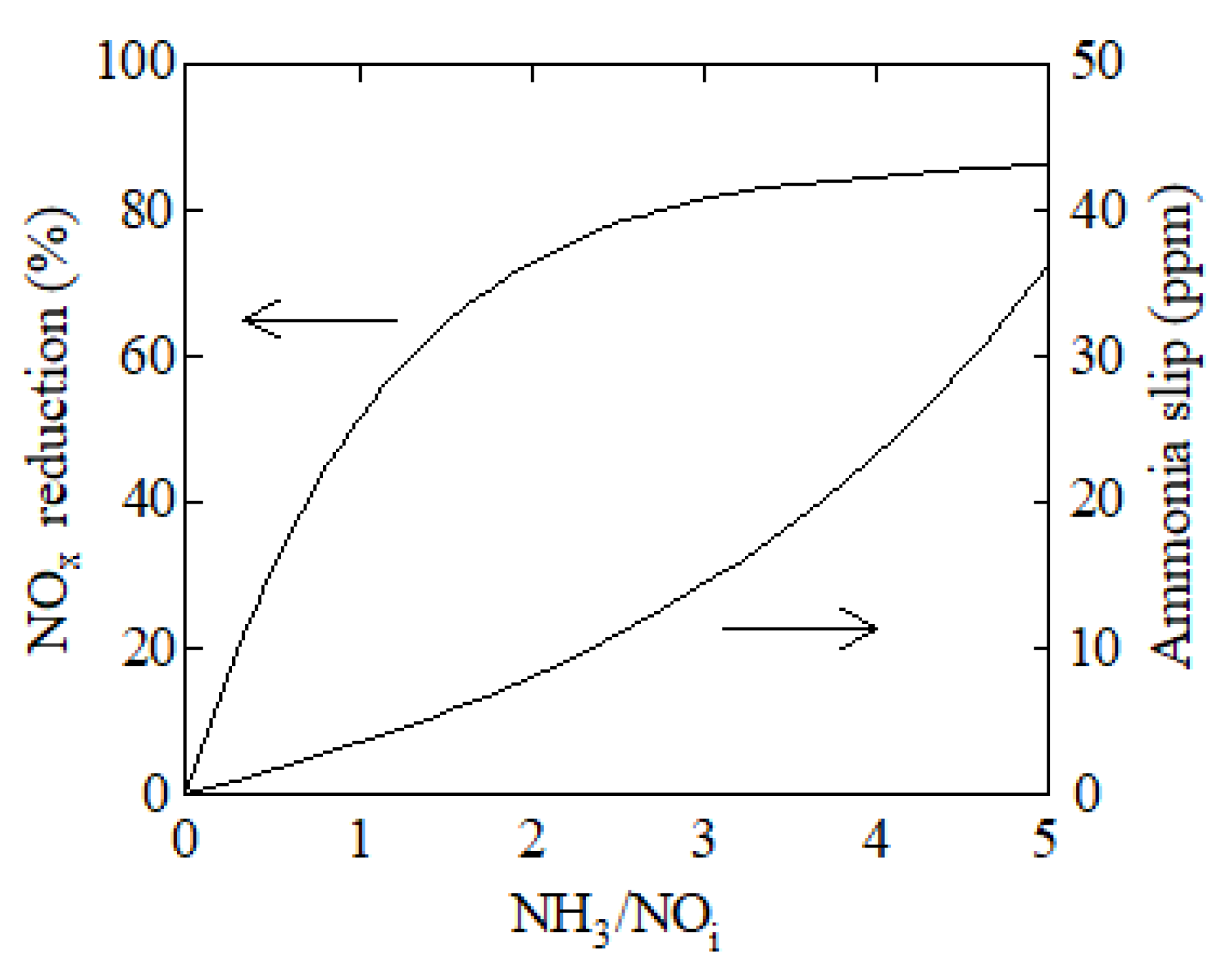
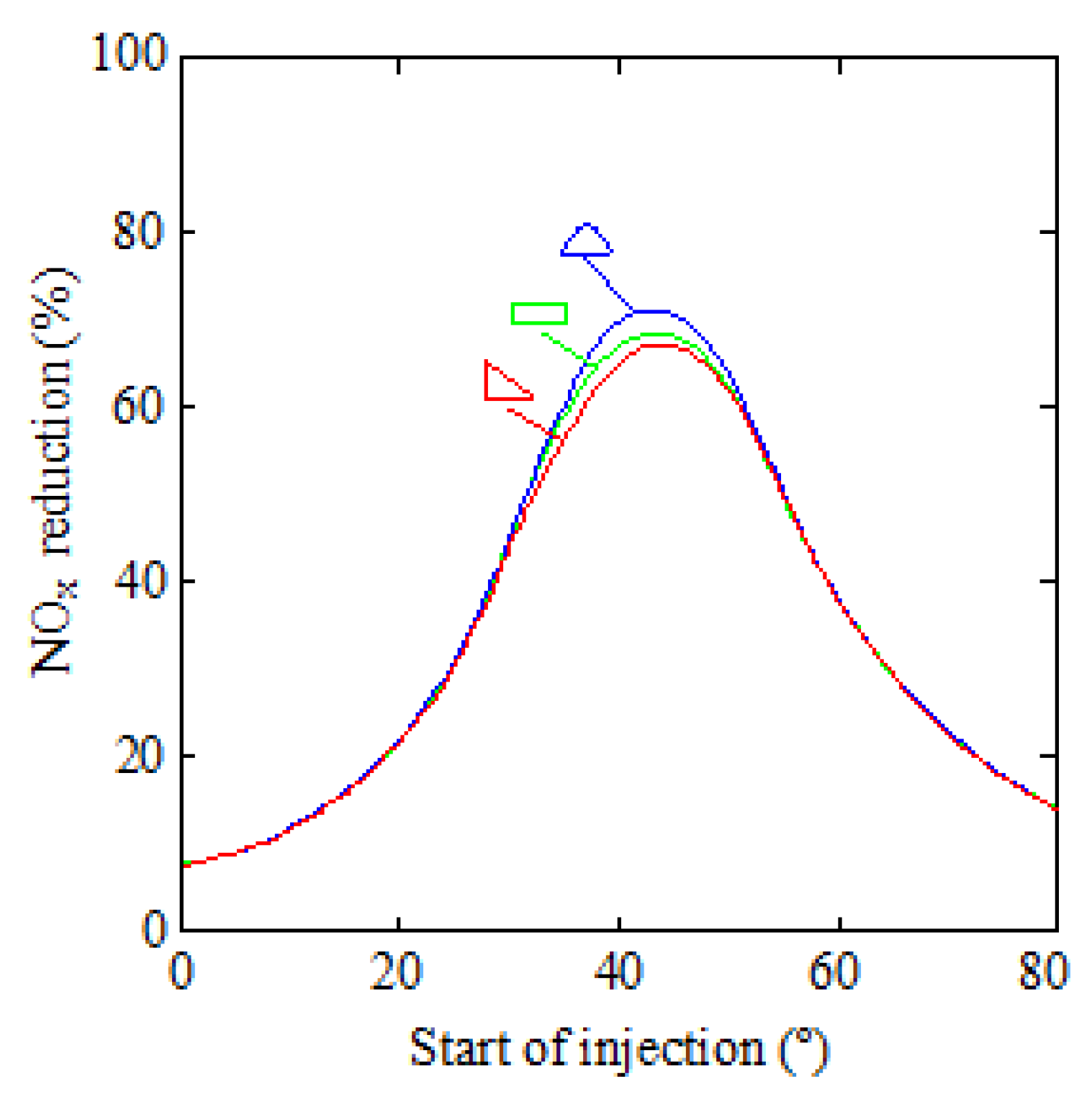
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Reaction | A (cm3/mol s) | b | E0 (K) | |
|---|---|---|---|---|
| 1 | N2 + O ↔ NO + N | 1.800∙1014 | 0 | 38370 |
| 2 | N + O2 ↔ NO + O | 1.800∙1010 | 1 | 4680 |
| 3 | N + OH ↔ NO + H | 7.100∙1013 | 0 | 450 |
Appendix B
| Reaction | A (cm3/mol s) | b | E0 (K) | |
|---|---|---|---|---|
| 1 | N2 + O ↔ NO + N | 1.800∙1014 | 0.0 | 38370 |
| 2 | N + O2 ↔ NO + O | 1.800∙1010 | 1.0 | 4680 |
| 3 | N + OH ↔ NO + H | 7.100∙1013 | 0.0 | 450 |
| 4 | N2O + O ↔ 2NO | 6.900∙1013 | 0.0 | 13400 |
| 5 | N2O + O ↔ N2 + O2 | 1.000∙1014 | 0.0 | 14200 |
| 6 | N2O + H ↔ N2 + OH | 7.587∙1013 | 0.0 | 7600 |
| 7 | N2O + N2 ↔ 2N2 + O | 6.918∙1023 | –2.5 | 32170 |
| 8 | N2O + N ↔ NO + N2 | 1.000∙1013 | 0.0 | 10000 |
| 9 | N2O + NO ↔ NO2 + N2 | 1.000∙1014 | 0.0 | 25000 |
| 10 | N2O + O2 ↔ NO + NO2 | 6.000∙1014 | –1.5 | 4985 |
| 11 | NO2 + O ↔ NO + O2 | 1.000∙1013 | 0.0 | 300 |
| 12 | NO2 + H ↔ NO + OH | 3.467∙1014 | 0.00 | 740 |
| 13 | NO2 + NO2 ↔ 2NO + O2 | 1.995∙1012 | 0.00 | 13500 |
| 14 | NO2 + N ↔ O + N2O | 5.012∙1012 | 0.0 | 0 |
| 15 | NO + HO2 ↔ NO2 + OH | 2.089∙1012 | 0.0 | –240 |
| 16 | NO + N2 + O2 ↔ N2O + NO2 | 2.300∙1014 | 0.0 | 18000 |
| 17 | N2 + O2 ↔ 2NO | 2.730∙1013 | 0.0 | 53800 |
| 18 | NO + O2 ↔ N + O3 | 2.700∙1014 | –1.0 | 63140 |
| 19 | NO2 + O ↔ N + O3 | 3.700∙1014 | –0.5 | 40280 |
| 20 | NO + O3 ↔ O + NO3 | 6.000∙1014 | –1.5 | 8000 |
| 21 | N2 + HO2 ↔ NO + HNO | 5.925∙1010 | 0.5 | 21550 |
| 22 | N + OH ↔ NH + O | 1.290∙1014 | 0.0 | 2165 |
| 23 | N + H2 ↔ NH + H | 1.320∙1015 | 0.0 | 11230 |
| 24 | N + H2O ↔ NH + OH | 3.590∙1015 | 0.0 | 18430 |
| 25 | NH + OH ↔ NO + H2 | 1.600∙1012 | 0.56 | 755 |
| 26 | NH + O ↔ NO + H | 5.000∙1011 | 0.5 | 0.0 |
| 27 | NH + OH ↔ HNO + H | 6.440∙1011 | 0.0 | 1460 |
| 28 | NH + O2 ↔ HNO + O | 4.380∙1012 | 0.0 | 6546 |
| 29 | HNO ↔ H + NO | 1.900∙1016 | 0.0 | 25179 |
| 30 | HNO + OH ↔ NO + H2O | 2.100∙1012 | 0.5 | 0 |
| 31 | HNO + H ↔ NO + H2 | 1.400∙1013 | 0.0 | 1510 |
| 32 | HNO + O ↔ NO + OH | 5.000∙1011 | 0.5 | 0 |
| 33 | NH + NO ↔ N2O + H | 2.240∙1013 | 0.0 | 10600 |
| 34 | N2O + NH ↔ N2 + HNO | 1.995∙1012 | 0.0 | 3000 |
| 35 | NO2 + NH ↔ HNO + NO | 1.000∙1011 | 0.5 | 2000 |
| 36 | N + H2O ↔ NH + OH | 1.000∙1013 | 0.0 | 1000 |
| 37 | N + HO2 ↔ NH + O2 | 1.000∙1013 | 0.0 | 1000 |
| 38 | NO + HO2 ↔ HNO + O | 1.900∙1011 | 0.0 | 1000 |
| 39 | HNO + NO ↔ N2O + OH | 6.140∙1012 | 0.0 | 17100 |
| 40 | HNO + N ↔ NO + NH | 1.000∙1013 | 0.0 | 1000 |
| 41 | HNO + HNO ↔ 2NO + H2 | 2.000∙1010 | 0.5 | 2230 |
| 42 | NH + N ↔ N2 + H | 6.310∙1011 | 0.5 | 0 |
| 43 | NH + N2 ↔ N + H + N2 | 3.160∙1021 | –2.0 | 42000 |
References
- Seddiek, I.S.; Elgohary, M.M.; Ammar, N.R. The hydrogen-fuelled internal combustion engines for marine applications with a case study. Brodogradnja 2015, 66, 23–38. [Google Scholar]
- Lamas, M.I.; Rodríguez, C.G.; Rodríguez, J.D.; Telmo, J. Internal modifications to reduce pollutant emissions from marine engines. A numerical approach. J. Nav. Archit. Mar. Eng. 2013, 5, 493–501. [Google Scholar] [CrossRef]
- Seddiek, I.S.; Elgohary, M.M. Eco-friendly selection of ship emissions reduction strategies with emphasis on SOx and NOx emissions. Int. J. Nav. Arch. Ocean Eng. 2014, 6, 737–748. [Google Scholar] [CrossRef]
- Ovaska, T.; Niemi, S.; Sirvio, K.; Nilson, O.; Portin, K.; Asplund, T. Effects of alternative marine diesel fuels on the exhaust particle size distributions of an off-road diesel engine. Appl. Therm. Eng. 2019, 150, 1168–1176. [Google Scholar] [CrossRef]
- Abdulwahid, A.A.; Sigu, R.; Brown, R.J. Underground diesel exhaust wet scrubbers: Current status and future prospects. Energies 2018, 11, 3006. [Google Scholar] [CrossRef]
- Frigo, S.; Gentili, R. Analysis of the behavior of a 4-stroke SI engine fuelled with ammonia and hydrogen. Int. J. Hydrogen Energy 2013, 38, 1607–1615. [Google Scholar] [CrossRef]
- Reyes-Ramírez, I.; Martínez-Boggio, S.D.; Curto-Risso, P.L.; Medina, A.; Calvo Hernández, A.; Guzmán-Vargas, L. Symbolic analysis of the cycle-to-cycle variability of a gasoline–hydrogen fueled spark engine model. Energies 2018, 11, 968. [Google Scholar] [CrossRef]
- Barrios, C.C.; Domínguez-Sáez, A.; Hormigo, D. Influence of hydrogen addition on combustion characteristics and particle number and size distribution emissions of a TDI diesel engine. Fuel 2017, 199, 162–168. [Google Scholar] [CrossRef]
- Li, Y.; Chen, H.; Zhang, X.; Tan, C.; Ding, Y. Renewable energy carriers: Hydrogen or liquid air/nitrogen? Appl. Therm. Eng. 2010, 30, 1985–1990. [Google Scholar] [CrossRef]
- Wang, W.; Herreros, J.M.; Tsolakis, A.; York, A.P.E. Ammonia as hydrogen carrier for transportation; investigation of the ammonia exhaust gas fuel reforming. Int. J. Hydrogen Energy 2013, 38, 9907–9917. [Google Scholar] [CrossRef]
- Cervantes-Bobadilla, M.; Escobar-Jiménez, R.F.; Gómez-Aguilar, J.F.; García-Morales, J.; Olivares-Peregrino, V.H. Experimental study on the performance of controllers for the hydrogen gas production demanded by an internal combustion engine. Energies 2018, 11, 2157. [Google Scholar] [CrossRef]
- Boretti, A. Novel dual fuel diesel-ammonia combustion system in advanced TDI engines. Int. J. Hydrogen Energy 2017, 42, 7071–7076. [Google Scholar] [CrossRef]
- Comotti, M.; Frigo, S. Hydrogen generation system for ammonia-hydrogen fuelled internal combustion engines. Int. J. Hydrogen Energy 2015, 40, 10673–10686. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, J.H.; Park, J.H.; Kwon, O.C. Studies on properties of laminar premixed hydrogen-added ammonia/air flames for hydrogen production. Int. J. Hydrogen Energy 2010, 35, 1054–1064. [Google Scholar] [CrossRef]
- Ryu, K.; Zacharakis-Jutz, G.E.; Kong, S.C. Performance enhancement of ammonia-fueled engine by using dissociation catalyst for hydrogen generation. Int. J. Hydrogen Energy 2014, 39, 2390–2398. [Google Scholar] [CrossRef]
- Boretti, A.A. Novel heavy duty engine concept for operation dual fuel H2-NH3. Int. J. Hydrogen Energy 2012, 37, 7869–7876. [Google Scholar] [CrossRef]
- Sahin, Z.; Akcanca, I.Z.; Durgun, O. Experimental investigation of the effects of ammonia solution (NH3OH) on engine performance and exhaust emissions of a small diesel engine. Fuel 2018, 214, 330–341. [Google Scholar] [CrossRef]
- Reiter, A.J.; Kong, S.C. Combustion and emissions characteristics of compression-ignition engine using dual ammonia-diesel fuel. Fuel 2011, 90, 87–97. [Google Scholar] [CrossRef]
- Gill, S.S.; Chatha, G.S.; Tsolakis, A.; Golunski, S.E.; York, A.P.E. Assessing the effects of partially decarbonizing a diesel engine by co-fuelling with dissociated ammonia. Int. J. Hydrogen Energy 2012, 37, 6074–6083. [Google Scholar] [CrossRef]
- Nishi, M.; Kanehara, M.; Lida, N. Assessment for innovative combustion on HCCI engine by controlling EGR ratio and engine speed. Appl. Therm. Eng. 2016, 99, 42–60. [Google Scholar] [CrossRef]
- Wu, H.W.; Hsu, T.T.; He, J.Y.; Fan, C.M. optimal performance and emissions of diesel/hydrogen-rich gas engine varying intake air temperature and EGR ratio. Appl. Therm. Eng. 2017, 124, 381–392. [Google Scholar] [CrossRef]
- di Sarli, V. Stability and emissions of a lean pre-mixed combustor with rich catalytic/lean-burn pilot. Int. J. Chem. React. Eng. 2014, 12, 77–89. [Google Scholar] [CrossRef]
- Lamas, M.I.; Rodríguez, C.G.; Aas, H.P. Computational fluid dynamics analysis of NOx and other pollutants in the MAN B&W 7S50MC marine engine and effect of EGR and water addition. Int. J. Marit. Eng. 2013, 155, A81–A88. [Google Scholar]
- Finesso, R.; Hardy, T.; Mancarella, A.; Marello, O.; Mittica, A.; Spessa, E. Real-time simulation of torque and nitrogen oxide emissions in a 11.0 L heavy-duty diesel engine for model-based combustion control. Energies 2019, 12, 460. [Google Scholar] [CrossRef]
- Jasminska, N.; Brestovic, T.; Puskar, M.; Grega, R.; Rajzinger, J.; Korba, J. Evaluation of hydrogen storage capacities on individual adsorbents. Meas. J. Int. Meas. Confed. 2014, 56, 219–230. [Google Scholar] [CrossRef]
- Lamas, M.I.; Rodríguez, J.d.; Castro-Santos, L.; Carral, L.M. Effect of multiple injection strategies on emissions and performance in the Wartsila 6L 46 marine engine. A numerical approach. J. Clean. Prod. 2019, 206, 1–10. [Google Scholar] [CrossRef]
- Park, C.; Park, W.; Kim, Y.; Choi, Y.; Lim, B. Effect of valve timing and excess air ratio on torque in hydrogen-fueled internal combustion engine for UAV. Energies 2019, 12, 771. [Google Scholar] [CrossRef]
- Miyamoto, N.; Ogawa, H.; Wang, J.; Shudo, T. Yamazaki K. Diesel NOx reduction with ammonium deoxidizing agents directly injected into the cylinder. Int. J. Veh. Des. 1995, 16, 71–79. [Google Scholar] [CrossRef]
- Larbi, N.; Bessrour, J. Measurement and simulation of pollutant emissions from marine diesel combustion engine and their reduction by ammonia injection. Adv. Mech. Eng. 2010, 41, 898–906. [Google Scholar] [CrossRef]
- Lamas, M.I.; Rodriguez, C.G.; Rodriguez, J.D.; Telmo, J. Computational fluid dynamics of NOx reduction by ammonia injection in the MAN B&W 7S50MC marine engine. Int. J. Marit. Eng. 2014, 156, A213–A220. [Google Scholar] [CrossRef]
- Bosse, T.K. High Temperature Gas Dynamics, 1st ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2004. [Google Scholar]
- Lamas, M.I.; Rodríguez, C.G. CFD analysis of the scavenging process in the MAN B&W 7S50MC two-stroke diesel marine engine. J. Ship Res. 2012, 56, 154–161. [Google Scholar] [CrossRef]
- Ricart, L.M.; Xin, J.; Bower, G.R.; Reitz, R.D. In-Cylinder Measurement and Modeling of Liquid Fuel Spray Penetration in a Heavy-Duty Diesel Engine; SAE 971591; SAE International: Warrendale, PA, USA, 1997. [Google Scholar]
- Dukowicz, J.K. Quasi-Steady Droplet Change in the Presence of Convection; LA7997-MS; Informal Report Los Alamos Scientific Laboratory: Los Alamos, NM, USA, 1979. [Google Scholar]
- Miller, J.A.; Glarborg, P. Modeling the formation of N2O and NO2 in the thermal DeNOx process. Springer Ser. Chem. Phys. 1996, 61, 318–333. [Google Scholar]
- Lamas, M.; Rodriguez, C.G. Numerical model to analyze NOx reduction by ammonia injection in diesel-hydrogen engines. Int. J. Hydrogen Energy 2017, 42, 26132–26141. [Google Scholar] [CrossRef]
- Zeldovich, Y.B.; Sadovnikov, D.A.; Kamenetskii, F. Oxidation of Nitrogen in Combustion; Institute of Chemical Physics: Moscow-Leningrad, Russia, 1947. [Google Scholar]
- Lavoie, G.A.; Heywood, J.B.; Keck, J.C. Experimental and theoretical investigation of nitric oxide formation in internal combustion engines. Combust. Sci. Technol. 1970, 1, 313–326. [Google Scholar] [CrossRef]
- Woodyard, D. Pounder’s Marine Diesel Engines and Gas Turbines, 8th ed.; Elsevier: Oxford, UK, 2004; ISBN 9780080943619. [Google Scholar]
- Mellor, A.M. Skeletal Mechanism for NOx Chemistry in Diesel Engines; SAE Tech Pap 981450; SAE International: Warrendale, PA, USA, 1998. [Google Scholar]
- Zabetta, E.C.; Kilpinen, P.; Hupa, M.; Stähl, K.; Leppälahti, J.; Cannon, M.; Nieminen, J. Kinetic modeling study on the potential of staged combustion in gas turbines for the reduction of nitrogen oxide emissions from biomass IGCC plants. Energy Fuels 2000, 14, 751–761. [Google Scholar] [CrossRef]
- Yang, H.; Krishnan, S.R.; Srinivasan, K.K.; Midkiff, K.C. Modeling of NOx emissions using a super-extended Zeldovich mechanism. In Proceedings of the ICEF03 2003 Fall Technical Conference of the ASME Internal Combustion Engine Division, Erie, PA, USA, 7–10 September 2003. [Google Scholar]
- Lamas, M.I.; Rodríguez, C.G. Numerical model to study the combustion process and emissions in the Wärtsilä 6L 46 four-stroke marine engine. Pol. Marit. Res. 2013, 20, 61–66. [Google Scholar] [CrossRef]
- Ra, Y.; Reitz, R. A reduced chemical kinetic model for IC engine combustion simulations with primary reference fuels. Combust. Flame 2008, 155, 713–738. [Google Scholar] [CrossRef]


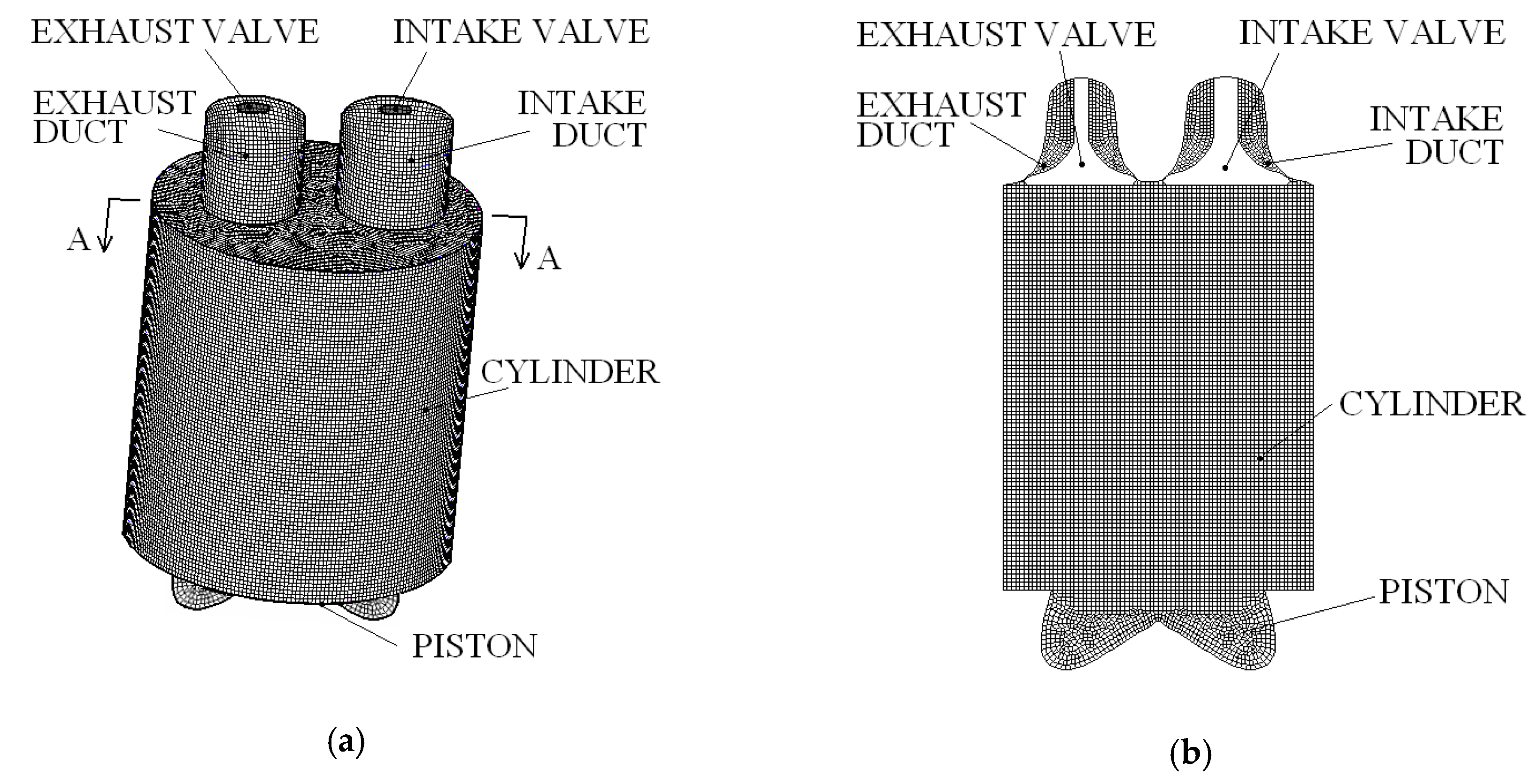



| Parameter | Value |
|---|---|
| Power (kW) | 320 |
| Speed (rpm) | 1500 |
| Number of cylinders | 10 |
| Cylinder displacement volume (cm3) | 18,270 |
| Bore (mm) | 128 |
| Stroke (mm) | 142 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamas, M.I.; Rodriguez, C.G. NOx Reduction in Diesel-Hydrogen Engines Using Different Strategies of Ammonia Injection. Energies 2019, 12, 1255. https://doi.org/10.3390/en12071255
Lamas MI, Rodriguez CG. NOx Reduction in Diesel-Hydrogen Engines Using Different Strategies of Ammonia Injection. Energies. 2019; 12(7):1255. https://doi.org/10.3390/en12071255
Chicago/Turabian StyleLamas, M. I., and C. G. Rodriguez. 2019. "NOx Reduction in Diesel-Hydrogen Engines Using Different Strategies of Ammonia Injection" Energies 12, no. 7: 1255. https://doi.org/10.3390/en12071255
APA StyleLamas, M. I., & Rodriguez, C. G. (2019). NOx Reduction in Diesel-Hydrogen Engines Using Different Strategies of Ammonia Injection. Energies, 12(7), 1255. https://doi.org/10.3390/en12071255






