Advanced Adaptive Fault Diagnosis and Tolerant Control for Robot Manipulators

Abstract

In this paper, an adaptive Takagi–Sugeno (T–S) fuzzy sliding mode extended autoregressive exogenous input (ARX)–Laguerre proportional integral (PI) observer is proposed. The proposed T–S fuzzy sliding mode extended-state ARX–Laguerre PI observer adaptively improves the reliability, robustness, estimation accuracy, and convergence of fault detection, estimation, and identification. For fault-tolerant control in the presence of uncertainties and unknown conditions, an adaptive fuzzy sliding mode estimation technique is introduced. The sliding surface slope gain is significant to improve the system’s stability, but the sliding mode technique increases high-frequency oscillation (chattering), which reduces the precision of the fault diagnosis and tolerant control. A fuzzy procedure using a sliding surface and actual output position as inputs can adaptively tune the sliding surface slope gain of the sliding mode fault-tolerant control technique. The proposed robust adaptive T–S fuzzy sliding mode estimation extended-state ARX–Laguerre PI observer was verified with six degrees of freedom (DOF) programmable universal manipulation arm (PUMA) 560 robot manipulator, proving qualified efficiency in detecting, isolating, identifying, and tolerant control for faults inherent in sensors and actuators. Experimental results showed that the proposed technique improves the reliability of the fault detection, estimation, identification, and tolerant control.

1. Introduction

Robot manipulators are often used in various industries, such as packaging and automotive manufacturing. A robot manipulator’s dynamic behavior is entirely nonlinear, coupled, and time-variant, which causes several challenges in fault detection, estimation, identification, and tolerant control. Heavy-duty cycles, overloading, poor installation, and operator errors can be caused by various defects: Sensor faults, actuator failures, and plant faults [1,2,3].

Several types of fault diagnosis and fault-tolerant control algorithms have been developed for robot manipulators. These methods are divided into four main classes: (a) Signal-based, (b) model-reference, (c) knowledge-based, and (d) hybrid techniques [4,5,6]. All methods for fault diagnosis have specific advantages and challenges. Signal-based fault diagnosis extracts the main features from output signals. Because of the presence of disturbances, the performance of this method is degraded. Knowledge-based fault diagnosis is highly dependent on the historical data used for training, which incur high computational costs for real-time data. The model-reference method identifies faults using a small dataset, but it requires an accurate system model [7]. Hybrid fault detection, estimation, and identification techniques use a combination of high-performance methods to design a stable and reliable technology [8]. In this paper, an intelligent model-reference (hybrid) technique is proposed for fault detection, estimation, and identification.

The core of this study was observer-based fault detection, estimation, and identification. System modeling was divided into two principal techniques: (a) Physical-based system modeling, which uses a disassembled robot manipulator to extract the Lagrange mathematical formulation, and (b) signal-based system identification, which uses various identification techniques. To address the challenges posed by the complexities and disturbance problems of physical-based system modeling, we used a signal-based system identification technique based on the autoregressive exogenous input (ARX)–Laguerre technique [9,10,11].

Various observer-based techniques have been used for fault detection, estimation, and identification, and they are divided into two main groups: (a) Linear-based observers and (b) nonlinear-based observers [10]. Proportional integral (PI) observers are linear and have been used in different systems for fault diagnosis, but they are ineffective in the presence of uncertainties and disturbances [12]. To address those issues, nonlinear observers (e.g., adaptive, sliding mode, feedback linearization, and fuzzy) have been introduced [10,13,14,15]. Feedback linearization observers are stable; however, they are not adequately robust [14]. Sliding mode observers are robust and stable, but chattering is the main drawback of this technique for fault diagnosis in the presence of uncertainties [10]. The fuzzy logic observer has an acceptable state estimation and works in uncertain conditions; however, reliability is the main drawback of this technique [15]. Among the available options, hybrid methods provide the most suitable techniques for fault detection, evaluation, and identification in a robot manipulator.

Linear and nonlinear fault-tolerant control algorithms are the main techniques for reducing or eliminating the effects of faults in robot manipulators. Coupling effects and an increase in the gear ratio are the main drawbacks of linear fault-tolerant control algorithms [16]. Model-reference fault-tolerant algorithms, knowledge-based techniques, and hybrid fault-tolerant control methods are the main techniques used in robot manipulators [16,17]. Model-based and knowledge-based fault-tolerant control algorithms have several advantages, such as system knowledge, stability, robustness, and reliability, but they face a big challenge in the unlimited level of a faulty signal [17]. Hybrid fault-tolerant algorithms are used to address that issue [18,19]. The sliding mode technique can be an excellent candidate for a robust fault-tolerant control algorithm, but it must address the challenge of chattering. Various techniques have been proposed to attenuate chattering [16,17,18,19]. An adaptive fuzzy sliding mode estimation fault-tolerant control algorithm is suitable for reducing chattering and the effects of faults in robot manipulators.

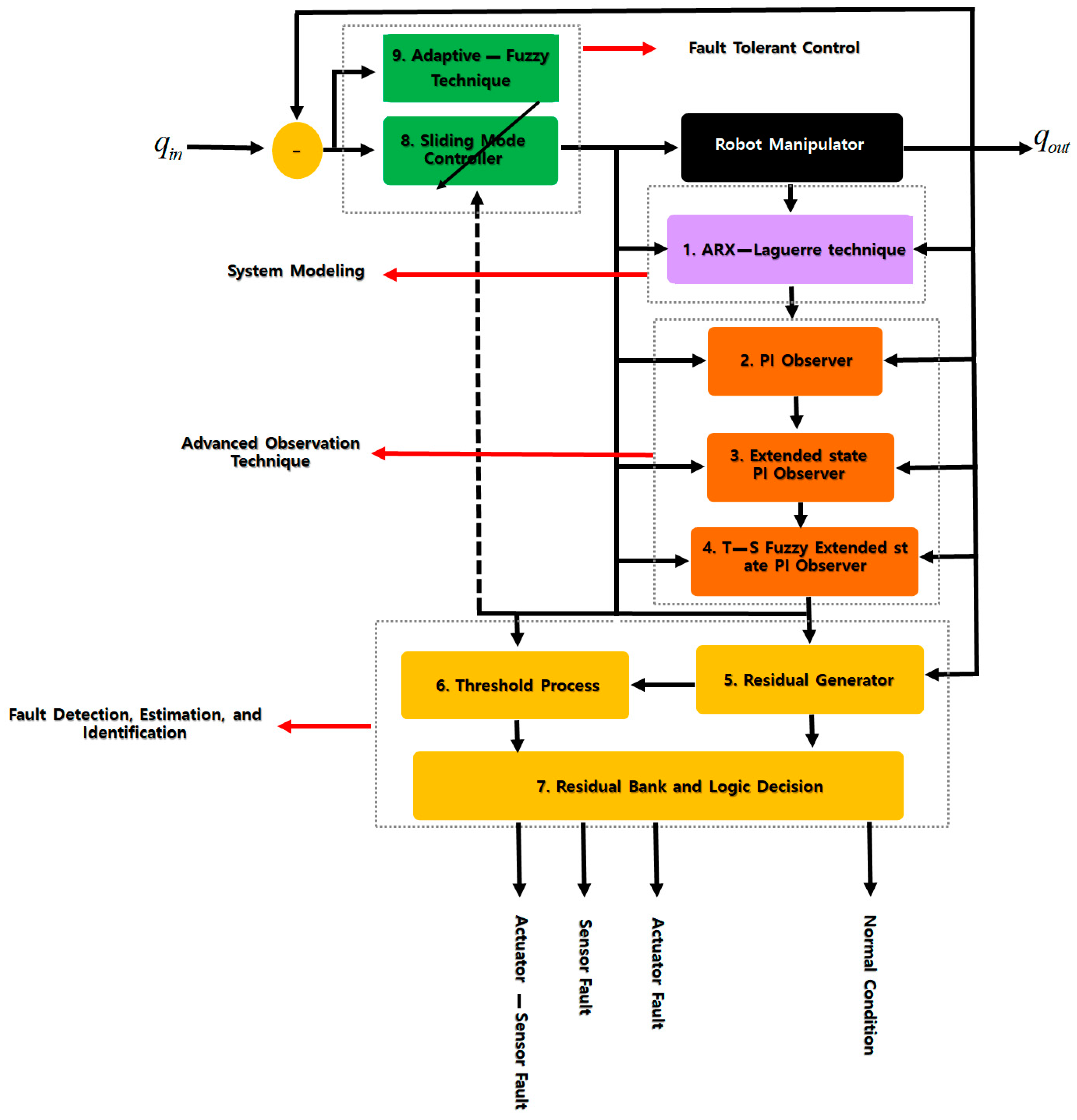
As shown in Figure 1, the proposed adaptive sliding mode Takagi–Sugeno (T–S) fuzzy extended-state ARX–Laguerre PI observer consists of four main steps: (a) System modeling, (b) the advanced observation technique, (c) decision part for fault diagnosis, and (d) fault-tolerant algorithm. The ARX–Laguerre technique (block 1) is used for system modeling. The advanced observation algorithm is divided into three main steps: (a) The ARX–Laguerre PI observer, (b) sliding mode extended-state ARX–Laguerre PI observer, and (c) T–S fuzzy sliding mode extended-state ARX–Laguerre PI observer. The ARX–Laguerre PI observer (block 2) is used for system estimation based on the PI observation technique. While the ARX–Laguerre PI observer is easy to implement, the main drawback of this technique is robustness and fault estimation accuracy. To address the robustness issue, a sliding mode extended algorithm (block 3) is introduced. The sliding mode extended algorithm improves robustness, but chattering is the main drawback of this algorithm in an uncertain condition. To improve the fault estimation accuracy, a T–S fuzzy algorithm (block 4) is used. The fuzzy algorithm was designed using the PI technique to reduce fault estimation error. The decision part has three main units: (a) Residual generation, (b) threshold generation, and (c) residual bank and logic decision. In the residual generation part (block 5), the residual signals in different conditions are calculated. The threshold unit (block 6) is used to find the best threshold value for fault detection and identification. Based on blocks 5 and 6, the residual bank and logic decision (block 7) is used for fault detection and identification. After fault diagnosis, the fault-tolerant control is designed using the following three steps: (a) Sliding mode control algorithm, (b) observer-estimation technique, and (c) fuzzy adaptive algorithm. The sliding mode control algorithm (block 8) is a robust and stable technique in certain and uncertain conditions. To increase the performance of this algorithm in an uncertain condition, the observation estimation (block 8) is used. The proposed T–S fuzzy extended ARX–Laguerre PI observer is used to improve fault estimation accuracy for the sliding mode fault-tolerant algorithm. To solve the chattering problem in a faulty condition, a fuzzy-based algorithm is used for online tuning of the sliding surface slope coefficient in the proposed observer estimation sliding mode technique (block 9). The proposed approach of this paper makes the following contributions: (a) It increases the robustness of the ARX–Laguerre PI observer by using a sliding mode extended algorithm, (b) reduces chattering and improves the accuracy of fault modeling (estimation) for the extended-state ARX–Laguerre PI observer by using the T–S fuzzy technique, (c) reduces the fault effect in the T–S fuzzy extended ARX–Laguerre PI observer by using the classical sliding mode fault-tolerant control, (d) increases the performance of classical sliding mode controller in unlimited uncertain (faulty) condition by using the proposed T–S fuzzy extended-state ARX–Laguerre PI observer, and (e) tunes the sliding surface (switching gain) for chattering attenuation in the observer estimation sliding mode fault-tolerant control by using the fuzzy adaptive technique.

The rest of this paper is organized as follows. In Section 2, the robot manipulator is modeled using the ARX–Laguerre procedure. The proposed robust adaptive fuzzy sliding mode extended ARX–Laguerre PI observer for robot manipulator fault detection, estimation, identification, and tolerant control is presented in Section 3. In the first step of that process, a PI observer is built using the ARX–Laguerre technique; in the second step, the extended-state sliding mode algorithm is added to the ARX–Laguerre PI observer to improve its reliability and robustness; in the third step, a T–S fuzzy–based estimator is applied to the robust ARX–Laguerre extended-state PI observer to improve its estimation accuracy and convergence. In Section 4, a sliding mode control technique is designed for fault-tolerant control. To improve the fault-tolerant control algorithm and reduce the chattering, an adaptive fuzzy algorithm is applied to the sliding mode technique. In Section 5, the fault detection, estimation, identification, and tolerant control of the proposed algorithm are analyzed using a programmable universal manipulation arm (PUMA) robot manipulator. Conclusions are provided in Section 6.

2. Robot Manipulator Modeling

A PUMA robot manipulator is a six degrees of freedom (DOF), serial linked, highly nonlinear, time-varying, and strong coupling effects system. The dynamic formulation for a robot manipulator is described below [1]:

$$\Gamma =A(q)[\ddot{q}]+W(q,\dot{q})+G(q)+\Psi ,$$

(1)

where $\Gamma ,A(q),W(q,\dot{q}),G(q),[q],[\dot{q}],[\ddot{q}]$ and $\Psi$ are an $n\times 1$ torque vector, time variant $n\times n$ inertial matrix, time variant velocity matrix, time variant $n\times 1$ gravity vector, position vector, velocity vector, acceleration vector, and robot manipulator’s faults and uncertainties, respectively. Based on Equation (1), the joint position is introduced as follows [1]:

$${\displaystyle \iint [\ddot{q}]}={\displaystyle \iint A{(q)}^{-1}\times (\Gamma -W(q,\dot{q})-G(q))+\Psi }.$$

(2)

Using Equations (1) and (2), the state–space equation for the robot manipulator is calculated [10]:

$$\{\begin{array}{l}{X}_{q,\Gamma }(k+1)=A{(q)}^{-1}(X_{q,\Gamma }).U_{\Gamma }(k)+\omega (X_{q,\Gamma })+\Psi (k)\\ Y_q(k+1)={(\kappa )}^T{X}_{q,\Gamma }\end{array},$$

(3)

where $\omega (X_{q,\Gamma })=(W(q,\dot{q})+G(q))$. The robot manipulator’s dynamic behavior in a theoretical or practical application might vary, which increases the challenge of fault diagnosis and tolerant control. To address that issue, the ARX–Laguerre system estimation method is used. As shown in Figure 1, block 1 shows the ARX–Laguerre technique for system modeling and estimation. The ARX–Laguerre method for robot manipulator modeling is defined as [10]:

$$q(k)={\displaystyle \sum _0^{i_q}{\alpha }_{n,q}}({\displaystyle \sum _{j=1}^{\infty }{\ell }_q\ast q(k))}.{\chi }_{n,q}(k)+{\displaystyle \sum _0^{i_{\Gamma }}{\alpha }_{n,\Gamma }}({\displaystyle \sum _{j=1}^{\infty }{\ell }_{\Gamma }\ast \Gamma (k))}.{\chi }_{n,\Gamma }(k),$$

(4)

where $q(k),({\alpha }_{n,q}\&{\alpha }_{n,\Gamma }),(i_q,i_{\Gamma }),({\ell }_q,{\ell }_{\Gamma }),\ast ,\Gamma (k),{\chi }_{n,q}(k)$, and ${\chi }_{n,\Gamma }(k)$ are the output joint variable (position), the Fourier coefficients, robot manipulator’s order, Laguerre orthonormal functions, convolution product, input signal (torque), filter position output, and filter position input, respectively.

Using Equation (4), the state–space robot manipulator modeling based on the ARX–Laguerre technique is generated as follows:

$$\{\begin{array}{l}{X}_{q,\Gamma }(k+1)=[{\alpha }_{q,\Gamma }{X}_{q,\Gamma }(k)+{\alpha }_q{Y}_q(k)+{\alpha }_{\Gamma }{U}_{\Gamma }(k)]+\Psi (k)\\ Y_q(k+1)={(\kappa )}^T{X}_{q,\Gamma }(k)\end{array},$$

(5)

where $X_{q,\Gamma }(k),({\alpha }_{q,\Gamma },{\alpha }_q,{\alpha }_{\Gamma }),Y_q(k),U_{\Gamma }(k),\Psi (k)$, and ${(\kappa )}^T$ are the state–function of the robot manipulator, (state, output, and input) coefficients, position output, torque input, robot manipulator faults and uncertainties, and Fourier coefficient, respectively. Figure 2 illustrates the estimation accuracy for the healthy condition based on the ARX–Laguerre technique. For the healthy state in Figure 2, the sensitivity of the position estimation is exceptionally high, and the error rate is close to zero (less than 0.05°).

3. Proposed Method for Fault Estimation, Detection, and Identification

In Figure 1, the proposed T–S fuzzy extended-state ARX–Laguerre PI observer for fault detection, estimation, and identification comprises six significant steps: ARX–Laguerre PI observer (block 2), sliding mode extended-state ARX–Laguerre PI observer (block 3) to improve the robustness of the ARX–Laguerre PI observer, estimation evaluator technique (block 4) that uses the T–S fuzzy technique to improve the fault estimation accuracy and reduce the chattering in the extended-state ARX–Laguerre PI observer, residual signal generator (block 5), threshold value calculation (block 6) based on the sliding mode algorithm, and fault detection and identification decision unit (block 7). Using the robot manipulator estimation based on the ARX–Laguerre technique presented in the previous Section, the ARX–Laguerre PI observer, block 2, for the robot manipulator is proposed as follows:

$$\{\begin{array}{l}{\widehat{X}}_{q,\Gamma (PI)}(k+1)=[{\alpha }_{q,\Gamma }{\widehat{X}}_{q,\Gamma (PI)}(k)+{\alpha }_q{\widehat{Y}}_{q(PI)}(k)+{\alpha }_{\Gamma }{U}_{\Gamma }(k)]+{\widehat{\Psi }}_{PI}(k)+{\alpha }_p(Y_q(k)-{\widehat{Y}}_{q(PI)}(k))\\ {\widehat{Y}}_{q(PI)}(k)={(\kappa )}^T{\widehat{X}}_{q,\Gamma (PI)}(k)\\ {\widehat{\Psi }}_{PI}(k+1)=\widehat{\Psi }(k)+{\alpha }_i(Y_q(k)-{\widehat{Y}}_{q(PI)}(k))\end{array}$$

(6)

where ${\widehat{X}}_{q,\Gamma (PI)}(k),{\widehat{Y}}_{q(PI)}(k),{\widehat{\Psi }}_{PI}(k)$, and $({\alpha }_p,{\alpha }_i)$ are the PI observation-based state function, the PI observation-based position output, the PI observation-based faults and uncertainties estimation, and the PI observer (proportional and integral) coefficients, respectively. Figure 3 illustrates the effectiveness of the PI observer for fault estimation in the first link of the robot manipulator. As shown in Figure 3, the error in the faulty signal estimation of the PI observer is not good enough for accurate fault estimation and identification.

In the next step, an extended-state sliding mode algorithm is used to modify the fault estimation, reliability, and robustness of the ARX–Laguerre PI observer, as represented in the following equation:

$$\{\begin{array}{l}{\widehat{X}}_{q,\Gamma (ESO)}(k+1)=[{\alpha }_{q,\Gamma }{\widehat{X}}_{q,\Gamma (ESO)}(k)+{\alpha }_q{\widehat{Y}}_{q(ESO)}(k)+{\alpha }_{\Gamma }{U}_{\Gamma }(k)]+{\widehat{\Psi }}_{ESO}(k)+{\alpha }_p(Y_q(k)-{\widehat{Y}}_{q(ESO)}(k))\\ {\widehat{Y}}_q(k)={(\kappa )}^T{\widehat{X}}_{q,\Gamma (ESO)}(k)\\ {\widehat{\Psi }}_{ESO}(k)={\widehat{\Psi }}_{PI}(k)+{\widehat{\Psi }}_{SM}(k)\\ {\widehat{\Psi }}_{SM}(k+1)={\alpha }_{SM}{\Vert (Y_q(k)-{\widehat{Y}}_{q(ESO)}(k))\Vert }^{0.5}\mathrm{sgn}(Y_q(k)-{\widehat{Y}}_{q(ESO)}(k))-\widehat{\gamma }\\ \widehat{\dot{\gamma }}=-{\alpha }_{S{M}_0}\times \mathrm{sgn}(Y_q(k)-{\widehat{Y}}_{q(ESO)}(k))\end{array},$$

(7)

where ${\widehat{X}}_{q,\Gamma (ESO)}(k),{\widehat{Y}}_{q(ESO)}(k),{\widehat{\Psi }}_{ESO}(k),{\widehat{\Psi }}_{SM},\gamma (k)$, and $({\alpha }_{S{M}_0},{\alpha }_{SM})$ are sliding mode extended observation-based state estimation, the sliding mode extended observation-based position output, the sliding mode extended observation-based faults and uncertainties estimation, the sliding mode faults and uncertainties estimation technique, and the sliding mode extended observation-based coefficients, respectively. Figure 4 demonstrates the fault estimation efficiency of the sliding mode extended-state ARX–Laguerre PI observer for the first link of the robot manipulator error and improves the convergence of fault estimation. The T–S fuzzy definition is represented as follows [15]:

$$\mathrm{IF}{r}_a(k)\mathrm{is}T{H}_i\mathrm{and}{r}_s(k)\mathrm{is}T{H}_j\mathrm{THEN}{\widehat{\Psi }}_{fuzzy}(k+1)={\widehat{\Psi }}_{fuzzy}(k)+{\alpha }_F(Y_q(k)-{\widehat{Y}}_q(k)),$$

(8)

where $r_a(k),r_s(k),(T{H}_i,T{H}_j),{\widehat{\Psi }}_{fuzzy}(k)$, and ${\alpha }_F$ are the residual signal for the actuator fault, residual signal for the sensor fault, threshold values for the actuator and sensor faults, T–S fuzzy faults and uncertainties estimation signal, and fuzzy coefficient, respectively. The proposed T–S fuzzy algorithm for fault estimation is represented as follows:

$${\widehat{\Psi }}_{fuzzy}:\{\begin{array}{l}\mathrm{IF}{r}_a(k)\mathrm{is}T{H}_a\mathrm{and}{r}_s(k)\cong 0\mathrm{THEN}{\widehat{\Psi }}_{fuzzy}(k+1)={\widehat{\Psi }}_{fuzzy}(k)+{\alpha }_{F_1}(Y_q(k)-{\widehat{Y}}_q(k))\\ \mathrm{IF}{r}_a(k)\cong 0\mathrm{and}{r}_s(k)\mathrm{is}T{H}_s\mathrm{THEN}{\widehat{\Psi }}_{fuzzy}(k+1)={\widehat{\Psi }}_{fuzzy}(k)+{\alpha }_{F_2}(Y_q(k)-{\widehat{Y}}_q(k))\\ \mathrm{IF}{r}_a(k)\mathrm{is}T{H}_a\mathrm{and}{r}_s(k)\mathrm{is}T{H}_s\mathrm{THEN}{\widehat{\Psi }}_{fuzzy}(k+1)={\widehat{\Psi }}_{fuzzy}(k)+{\alpha }_{F_3}(Y_q(k)-{\widehat{Y}}_q(k))\end{array},$$

(9)

where $({\alpha }_{F_1},{\alpha }_{F_2},{\alpha }_{F_3}),T{H}_a$ and $T{H}_s$ are fuzzy logic coefficients for three different conditions (actuator fault, sensor fault, and actuator-sensor fault), actuator threshold, and sensor threshold, respectively:

As shown in Figure 4, the performance of the extended-state ARX–Laguerre PI observer is more robust than that of the original ARX–Laguerre PI observer with a lower estimation error. After improving the signal estimation, reliability, and robustness of ARX–Laguerre PI observer via the sliding mode extended-state algorithm, the next block enhances the flexibility and accuracy of the fault estimation in an unknown condition. The T–S fuzzy algorithm is a powerful tool to reduce the error and improve the convergence of fault estimation. Three different membership functions are defined for T–S fuzzy fault estimation, as shown in Figure 5. Therefore, based on Equations (7) and (9), the T–S fuzzy sliding mode extended-state ARX–Laguerre PI observer is proposed by the following equations:

$$\{\begin{array}{l}{\widehat{X}}_{q,\Gamma (prop)}(k+1)=[{\alpha }_{q,\Gamma }{\widehat{X}}_{q,\Gamma (prop)}(k)+{\alpha }_q{\widehat{Y}}_{q(prop)}(k)+{\alpha }_{\Gamma }{U}_{\Gamma }(k)]+\\ {\widehat{\Psi }}_{prop}(k)+{\alpha }_p(Y_q(k)-{\widehat{Y}}_{q(prop)}(k))\\ {\widehat{Y}}_{q(prop)}(k)={(\kappa )}^T{\widehat{X}}_{q,\Gamma (prop)}(k)\\ {\widehat{\Psi }}_{prop}(k)={\widehat{\Psi }}_{ESO}(k)+{\widehat{\Psi }}_{fuzzy}\\ {\widehat{\Psi }}_{fuzzy}:\mathrm{IF}{r}_a(k)\mathrm{is}T{H}_i\mathrm{and}{r}_s(k)\mathrm{is}T{H}_j\mathrm{THEN}{\widehat{\Psi }}_{fuzzy}(k+1)={\widehat{\partial }}_{fuzzy}(k)+{\alpha }_F(Y_q(k)-{\widehat{Y}}_q(k))\end{array}.$$

(10)

Here, ${\widehat{X}}_{q,\Gamma (prop)}(k),{\widehat{Y}}_{q(prop)}(k)$, and ${\widehat{\Psi }}_{prop}(k)$ are the proposed observation-based state estimation, observation-based position output, and observation-based faults and uncertainties estimation, respectively. Therefore, the faults and uncertainties estimation signal $({\widehat{\Psi }}_{prop})$ has three main parts: Integral term, sliding mode term, and fuzzy logic part. Figure 6 illustrates the power of fault estimation based on the proposed T–S fuzzy extended-state ARX–Laguerre PI observer. As shown in Figure 6, the error rate in the faulty signal estimation of the proposed T–S fuzzy extended-state ARX–Laguerre PI observer is lower than in the previous iterations (Figure 3 and Figure 4). Therefore, ${\widehat{Y}}_q$ is represented by Equation (10). After procurement the stability, the state space estimation of ${\widehat{Y}}_q$ converges to $Y_q$, the estimation error converges to zero and ${\alpha }_{SM}{\Vert (Y_q(k)-{\widehat{Y}}_q(k))\Vert }^{0.5}\mathrm{sgn}(Y_q(k)-{\widehat{Y}}_q(k))=0$ [14]. The Lyapunov function of the proposed procedure is defined as follows:

$$V(x)=2{\alpha }_i\left|Y_q(k)-{\widehat{Y}}_q(k)\right|+0.5{\widehat{\Psi }}^2+{\alpha }_{SM}{\left|(Y_q(k)-{\widehat{Y}}_q(k))\right|}^{0.5}\mathrm{sgn}(Y_q(k)-{\widehat{Y}}_q(k))-{\widehat{\Psi }}^2.$$

(11)

The derivative of the Lyapunov is represented in Equation (12):

$$\begin{array}{l}\dot{V}(x)=\frac{1}{{\left|(Y_q(k)-{\widehat{Y}}_q(k))\right|}^{0.5}}\left[\begin{array}{cc}{(Y_q(k)-{\widehat{Y}}_q(k))}^{0.5}\mathrm{sgn}(Y_q(k)-{\widehat{Y}}_q(k))& \widehat{\Psi }\end{array}\right]\\ \frac{{\alpha }_{SM}}{2}\left[\begin{array}{cc}{\alpha }_{SM}{}^2& -{\alpha }_{SM}\\ -{\alpha }_{SM}& 1\end{array}\right]\left[\begin{array}{c}{(Y_q(k)-{\widehat{Y}}_q(k))}^{0.5}\mathrm{sgn}(Y_q(k)-{\widehat{Y}}_q(k))\\ \widehat{\Psi }\end{array}\right]\\ +\frac{\Delta \Psi }{{\left|(Y_q(k)-{\widehat{Y}}_q(k))\right|}^{0.5}}\left[\begin{array}{cc}\frac{{\alpha }_{SM}{}^2}{2}& \frac{-{\alpha }_{SM}}{2}\end{array}\right]\left[\begin{array}{c}{(Y_q(k)-{\widehat{Y}}_q(k))}^{0.5}\mathrm{sgn}(Y_q(k)-{\widehat{Y}}_q(k))\\ \widehat{\Psi }\end{array}\right]\end{array}$$

(12)

Here, $\Delta \Psi$ is the error of faults and uncertainty estimation. Based on Reference [20], if $\frac{{\alpha }_{SM}}{2}\left[\begin{array}{cc}{\alpha }_{SM}{}^2-({\alpha }_{SM})\Delta \Psi & -{\alpha }_{SM}\\ -({\alpha }_{SM}+2\Delta \psi & 1\end{array}\right]>0$; thus, $\dot{V}<0$. Therefore, the fault estimation using the proposed algorithm can be converged to zero in the finite time. The residual signal is generated by the following equation:

$$r=Y_q(k)-{\widehat{Y}}_{q(prop)}(k).$$

(13)

The next step of the proposed algorithm is the threshold process. Various techniques have been used previously, but we employed the sliding mode algorithm [10]. The following definition represents the threshold process based on the sliding-mode algorithm:

$$\{\begin{array}{l}T{H}_a={\alpha }_a[\mathrm{sgn}({\lambda }_a\times r_a+{\displaystyle \sum r_a)]}\\ T{H}_s={\alpha }_s[\mathrm{sgn}({\lambda }_s\times r_s+{\displaystyle \sum r_s)]}\end{array},$$

(14)

where $T{H}_a,T{H}_s,({\alpha }_a,{\alpha }_s,{\lambda }_a,{\lambda }_s),r_a$, and $r_s$ are the actuator fault threshold value, sensor fault threshold value, coefficients of the sliding mode algorithm for threshold value calculation, actuator fault residual signal, and sensor fault residual signal, respectively.

The last block in Figure 1 for fault detection, estimation, and identification is the logical decision. The main positive point in this study is an accurate fault estimation technique based on the T–S fuzzy sliding mode extended-state ARX–Laguerre PI observer. Based on Equation (10), the proposed faults and uncertainties estimation technique is represented by the following equation:

$${\widehat{\Psi }}_{prop}(k)={\widehat{\Psi }}_{ESO}(k)+{\widehat{\Psi }}_{fuzzy},$$

(15)

where:

$$\{\begin{array}{l}{\widehat{\Psi }}_{ESO}(k)={\widehat{\Psi }}_{PI}(k)+{\widehat{\Psi }}_{SM}(k)\\ {\widehat{\Psi }}_{PI}(k+1)=\widehat{\Psi }(k)+{\alpha }_i(Y_q(k)-{\widehat{Y}}_q(k))\\ {\widehat{\Psi }}_{SM}(k+1)={\alpha }_{SM}{\Vert (Y_q(k)-{\widehat{Y}}_{q(ESO)}(k))\Vert }^{0.5}\mathrm{sgn}(Y_q(k)-{\widehat{Y}}_{q(ESO)}(k))-\widehat{\gamma }\\ \widehat{\dot{\gamma }}=-{\alpha }_{S{M}_0}\times \mathrm{sgn}(Y_q(k)-{\widehat{Y}}_{q(ESO)}(k))\\ {\widehat{\Psi }}_{fuzzy}:\mathrm{IF}{r}_a(k)\mathrm{is}T{H}_i\mathrm{and}{r}_s(k)\mathrm{is}T{H}_j\mathrm{THEN}{\widehat{\Psi }}_{fuzzy}(k+1)={\widehat{\partial }}_{fuzzy}(k)+{\alpha }_F(Y_q(k)-{\widehat{Y}}_q(k))\end{array}$$

(16)

As shown in Figure 6, the error in the signal estimation with the proposed algorithm is close to zero. Based on Equations (13) and (14), the following algorithm is introduced for fault detection in the robot manipulator:

$$\begin{array}{l}\mathrm{Normal}\mathrm{Condition}:(r_a(k)<T{H}_a\&r_s(k)<T{H}_s)\\ \mathrm{Faulty}\mathrm{Condition}:(r_a(k)\ge T{H}_a\&/\mathrm{or}{r}_s(k)\ge T{H}_s)\end{array}$$

(17)

Fault identification is the third step in making a logical decision. In this research, we considered three types of faults: (a) Actuator faults, (b) sensor faults, and (c) actuator–sensor faults. To identify them, the following techniques are introduced:

$$\begin{array}{l}\mathrm{Actuator}\mathrm{Faulty}\mathrm{Condition}:(r_a(k)\ge T{H}_a\&r_s(k)<T{H}_s)\\ \mathrm{Sensor}\mathrm{Faulty}\mathrm{Condition}:(r_a(k)<T{H}_a\&r_s(k)\ge T{H}_s)\\ \mathrm{Sensor}+\mathrm{Actuator}\mathrm{Faulty}\mathrm{Condition}:(r_a(k)\ge T{H}_a\&r_s(k)\ge T{H}_s)\end{array}$$

(18)

The threshold value formulation is extracted from Equation (14). Sliding mode is a robust algorithm that can be used to design a robust controller and observer. In this study, we used this technique to calculate threshold values [10]. In the first step, the residual signal is calculated based on Equation (13). In the second step, the sliding surface $(S_a={\lambda }_a{r}_a+{\displaystyle \sum r_a}\mathrm{or}{S}_s={\lambda }_s{r}_s+{\displaystyle \sum r_s})$ is calculated to find the robust surface for each condition. We use an integral term of sliding surface to calculate the threshold value based on a steady-state residual signal. The residual signal and threshold values for various conditions (normal, actuator fault, sensor fault, and actuator–sensor fault) are completely different. In the third step, the switching function is used to find the maximum and minimum signal value $(\pm \mathrm{Threshold}\mathrm{Value})$ for each condition and improve the robustness. In the last step, threshold values are calculated. Thus, based on these threshold values, we can drive the decision logic part for fault detection and identification. Figure 7 illustrates the effect of incorrect threshold values for fault detection in normal and actuator fault conditions. Based on Figure 7a, the uncertainties and disturbances in normal condition are detected as faults and send an incorrect fault alarm to the fault-tolerant controller. In Figure 7b, based on the threshold value, the proposed method cannot detect the faulty signal.

4. Proposed Method for Fault-Tolerant Control

In this Section, we describe the design for a robust, fault-tolerant controller. The fuzzy adaptive sliding mode controller with variable estimation is a robust fault-tolerant control algorithm. The first step is designing the sliding mode controller. The equation for conventional sliding mode fault-tolerant control is as follows [16]:

$$\{\begin{array}{l}{U}_{CSM}=U_a+U_b\\ U_a=-A(X_{q,\Gamma })\times {\alpha }_{SM}\times \mathrm{sgn}([{\lambda }_{SM}\times r]+\dot{r})\\ U_b=A(X_{q,\Gamma })\times ({\ddot{X}}_d-{\lambda }_{SM}({\widehat{X}}_{q,\Gamma }-{\dot{X}}_d)-\omega ({\widehat{X}}_{q,\Gamma }))\\ S=[{\lambda }_{SM}\times r]+\dot{r}\to \dot{S}=\ddot{r}+[{\lambda }_{SM}\times \dot{r}]\to A{(X_{q,\Gamma })}^{-1}{U}_{\Gamma }+\omega (X_{q,\Gamma })\\ +\Psi -{\ddot{X}}_d+{\lambda }_{SM}(X_{q,\Gamma }-{\dot{X}}_d)\end{array},$$

(19)

where $U_{CSM},U_a,U_b,X_d,S,\dot{S}$, and ${\lambda }_{SM}$ are the output signal of the sliding mode algorithm, the switching part of the sliding mode algorithm to compensate for unknown conditions, the model-equivalent part of the sliding mode control law, the desired state, the sliding surface, the derivative of the sliding surface, and the sliding slope coefficient, respectively. The Lyapunov function and the derivative of the Lyapunov function for conventional sliding mode fault-tolerant control are presented in Equations (20) and (21), respectively:

$$V(x)=\frac{1}{2}{S}^{T}A(X_{q,\Gamma })S=\frac{1}{2}{({\lambda }_{SM}r+\dot{r})}^{T}A(X_{q,\Gamma })({\lambda }_{SM}r+\dot{r}),$$

(20)

$$\dot{V}(x)=({\lambda }_{SM}r+\dot{r})(\Psi -{\alpha }_{SM}\mathrm{sgn}({\lambda }_{SM}r+\dot{r}))-{({\lambda }_{SM}r+\dot{r})}^T{K}_{\beta }({\lambda }_{SM}r+\dot{r}).$$

(21)

Here, $K_{\beta }$ is a constant. As shown in Equations (20) and (21), if ${\alpha }_{SM}\ge T{H}_i$, $\dot{V}<0$, and the derivative of the Lyapunov function converges to zero in a finite time [16].

$$({\lambda }_{SM}r+\dot{r})(\Psi -{\alpha }_{SM}\mathrm{sgn}({\lambda }_{SM}r+\dot{r}))\le 0,$$

(22)

$$({\lambda }_{SM}r+\dot{r})(\psi -{\alpha }_{SM}\mathrm{sgn}({\lambda }_{SM}r+\dot{r}))-{({\lambda }_{SM}r+\dot{r})}^T{K}_{\beta }({\lambda }_{SM}r+\dot{r})\le -{({\lambda }_{SM}r+\dot{r})}^T{K}_{\beta }({\lambda }_{SM}r+\dot{r})<0.$$

(23)

Thus, the conventional sliding mode fault-tolerant control is robust and stable, but the chattering phenomenon and the system’s performance in faulty conditions remain problematic. Therefore, we introduce a sliding mode estimation fault-tolerant control. Its main positive point is that it can estimate the unmeasured variable $(X_{q,\Gamma })$ by observation. The formulation of the sliding mode estimation fault-tolerant control is represented as:

$$\{\begin{array}{l}{U}_{ESMC}=U_a+U_b+U_C\\ U_a=-A(X_{q,\Gamma })\times {\alpha }_{S{M}_2}\times \mathrm{sgn}([{\lambda }_{SM}\times r]+\dot{r})\\ U_b=A(X_{q,\Gamma })\times ({\ddot{X}}_d-{\lambda }_{SM}({\widehat{X}}_{q,\Gamma }-{\dot{X}}_d)-\omega ({\widehat{X}}_{q,\Gamma }))\\ U_C=A(X_{q,\Gamma })\times {\widehat{\Psi }}_{prop}\\ S=[{\lambda }_{SM}\times r]+\dot{r}\to \dot{S}=\ddot{r}+[{\lambda }_{SM}\times \dot{r}]\to A{(X_{q,\Gamma })}^{-1}(U_a+U_b+U_C)+\omega (X_{q,\Gamma })\\ +\Psi -{\ddot{X}}_d+{\lambda }_{SM}(X_{q,\Gamma }-{\dot{X}}_d)=A{(X_{q,\Gamma })}^{-1}\times [-A(X_{q,\Gamma })\times {\alpha }_{S{M}_2}\times \mathrm{sgn}([{\lambda }_{SM}\times r]+\dot{r})]-\\ {\widehat{\Psi }}_{prop}+\Psi =-{\alpha }_{S{M}_2}\times \mathrm{sgn}([{\lambda }_{SM}\times r]+\dot{r})+\Psi -{\widehat{\Psi }}_{prop}\end{array}$$

(24)

where $U_{ESMC},{\alpha }_{S{M}_2}$, and $U_C$ are the output signal of the sliding mode estimation fault-tolerant algorithm, sliding surface slope in sliding mode estimation controller, and the observer estimation part, respectively. The Lyapunov and the derivation of Lyapunov function are defined by the following formulation:

$$V(x)=\frac{1}{2}{S}^{T}A(X_{q,\Gamma })S,$$

(25)

$$\dot{V}(x)=S(\Psi -{\alpha }_{S{M}_2}\mathrm{sgn}(S))-S^T{K}_{\beta -2}S.$$

(26)

If the normal threshold value with respect to the uncertainties and disturbances is defined by $(\mathsf{\Upsilon }),$ for ${\alpha }_{S{M}_2}\ge \mathsf{\Upsilon }$, we have:

$$S(\Psi -{\alpha }_{S{M}_2}\mathrm{sgn}(S))\le 0.$$

(27)

Based on Equation (27):

$$S(\Psi -{\alpha }_{S{M}_2}\mathrm{sgn}(S))-S^T{K}_{\beta -2}S\le -S^T{K}_{\beta -2}S<0.$$

(28)

Based on Equation (28), $\dot{V}<0$, and the derivative of the Lyapunov function converges to zero in a finite time [16]. Based on Equations (25) and (26), the uncertainties and disturbances in normal and abnormal condition can be bounded by:

$$\{\begin{array}{l}{(\Psi -\widehat{\Psi })}_{normal}=\mathsf{\Upsilon }\le (T{H}_a\mathrm{or}T{H}_s)\\ {(\Psi -\widehat{\Psi })}_{faulty}>(T{H}_a\mathrm{or}T{H}_s)\end{array}.$$

(29)

Here, $\mathsf{\Upsilon }$ and ${\Psi }_{normal}$ are the normal threshold value and the uncertainties in a normal condition. Based on Equations (19), (24), and (29), $\mathsf{\Upsilon }\le {\Psi }_{normal}<(T{H}_a\mathrm{or}T{H}_s)$, and thus, ${\alpha }_{S{M}_2}<{\alpha }_{SM}$, and the chattering generated by the sliding mode estimation fault-tolerant control is meaningfully reduced compared to the conventional sliding mode fault-tolerant control. To improve the performance of the sliding-mode estimation fault-tolerant control, a fuzzy adaptive technique is proposed. Since the fault varies with respect to various conditions and is difficult to predict, calculating the minimum switching gain $({\alpha }_{S{M}_2})$ is very difficult. Increasing the value of the switching gain increases the chattering phenomenon. If the switching gain varies with the condition of the robot manipulator, chattering could be reduced. On the other hand, modeling a fault is very complicated; therefore, a fuzzy algorithm is designed for online tuning of the switching gain. Beginning from Equation (24), the adaptive fuzzy sliding mode estimation fault-tolerant control can be written as:

$$\{\begin{array}{l}{U}_{ESMC-online}=U_{a(online)}+U_b+U_C\\ U_{a(online)}=-A(X_{q,\Gamma })\times {\alpha }_{S{M}_{2-online}}\times \mathrm{sgn}([{\lambda }_{SM}\times r]+\dot{r})\\ U_b=A(X_{q,\Gamma })\times ({\ddot{X}}_d-{\lambda }_{SM}({\widehat{X}}_{q,\Gamma }-{\dot{X}}_d)-\omega ({\widehat{X}}_{q,\Gamma }))\\ U_C=A(X_{q,\Gamma })\times {\widehat{\Psi }}_{prop}\end{array}.$$

(30)

Here, $U_{ESMC-online},U_{a(online)}$, and ${\alpha }_{S{M}_{2-online}}$ are the output signal of the proposed fault-tolerant algorithm, the online tuning switching part of the proposed algorithm, and the auto-tuned sliding slope coefficient, respectively. The ${\alpha }_{S{M}_{2-online}}$ is a coefficient determined by the designed fuzzy technique as follows:

$${\alpha }_{S{M}_{2-online}}={\alpha }_{S{M}_2}\times {\alpha }_{online}.$$

(31)

The position output is designed as a fuzzy input, and the sliding surface is designed as the second input of the fuzzy algorithm. The fuzzy rule-base is defined as:

$$\mathrm{IF}{q}_m{\mathrm{is}\mathrm{F}}_q^m\mathrm{and}{S}_m{\mathrm{is}\mathrm{F}}_S^m\mathrm{THEN}{\alpha }_{online}\mathrm{is}{G}^m.$$

(32)

If the fuzzifier of the fuzzy set is a singleton, and the defuzzification technique is a center average, the fuzzy set is defined as:

$$\begin{array}{cc}{\alpha }_{online}=\frac{{\displaystyle \sum _1^N{X}_{\alpha }\mu F_s^m(S_m)\mu F_q^m(S_q)}}{{\displaystyle \sum _1^N\mu F_s^m(S_m)\mu F_q^m(S_q)}},& X_{\alpha }=\max \mu G^m({\alpha }_{online})\end{array},$$

(33)

where $(q_m,S_m),(F_q^m,F_s^m,G^m)$, and ${\alpha }_{online}$ are the fuzzy inputs, fuzzy sets, and fuzzy output, respectively. Therefore, if the fault-tolerant controller is designed as shown in Equation (24) with the adaptive gain tuning technique given in Equation (30) and the online switching gains as determined in Equation (33), the fault-tolerant controller is stable [21]. For the first fuzzy input $(q)$ in the interval $[\begin{array}{cc}-100,& 100\end{array}]$, the fuzzy membership functions are designed based on the Gaussian type, and the fuzzy sets are defined as negative big (NB), negative medium (NM), negative small (NS), zero (Z), positive small (PS), positive medium (PM), and positive big (PB). For the second fuzzy input $(S)$ in the interval $[\begin{array}{cc}-1,& 1\end{array}]$, the fuzzy membership functions are designed based on the Gaussian type, and the fuzzy sets are again NB, NM, NS, Z, PS, PM, and PB. For the fuzzy output $({\alpha }_{online})$ in the interval $[\begin{array}{cc}0,& 3\end{array}]$, the fuzzy membership functions are designed based on the Gaussian type and the fuzzy sets are PS, PM, and PB. The fuzzy rule table is given in

Table 1. Fuzzy rule table for the adaptive fuzzy sliding mode estimation algorithm.

Joint position (q)	Sliding Surface (S)
		NB	NM	NS	Z	PS	PM	PB
	NB	PB	PB	PB	PB	PM	PS	PS
	NM	PB	PB	PB	PM	PM	PS	PS
	NS	PB	PB	PB	PM	PS	PS	PS
	Z	PB	PB	PM	PS	PS	PS	PS
	PS	PM	PS	PS	PS	PM	PB	PB
	PM	PS	PS	PM	PM	PB	PB	PB
	PB	PS	PS	PM	PB	PB	PB	PB

.

Algorithm 1 illustrates the adaptive T–S fuzzy sliding mode extended-state ARX–Laguerre PI observer for fault detection, estimation, identification, and tolerant control of a robot manipulator. Figure 8 illustrates the proposed method as a block diagram for fault diagnosis and fault-tolerant control.

5. Results and Analysis

For fault detection, estimation, and identification, the effectiveness of the proposed T–S fuzzy extended-state ARX–Laguerre PI observer, sliding-mode extended-state ARX–Laguerre PI observer, and ARX–Laguerre PI observer were evaluated using a 6-DOF PUMA robot arm. The same robot arm was used to test the effectiveness of the proposed fuzzy adaptive sliding mode estimation algorithm, sliding mode estimation technique, and classical sliding mode procedure for fault-tolerant control. The dynamic of the 6-DOF PUMA robot manipulator was modeled in Reference [1]. The desired signals are defined based on the cubic polynomials of the third order function and are written using the following equations:

$$\{\begin{array}{l}q(t)=a_0+a_{1}t+a_2{t}^2+a_3{t}^3\\ \dot{q}(t)=a_1+2a_{2}t+3a_3{t}^2\\ \ddot{q}(t)=2a_2+6a_{3}t\end{array},$$

(34)

where the parameters $(a_0,a_1,a_2,a_3)$ can be calculated as follows:

$$\{\begin{array}{l}{a}_0=q_0\\ a_1=0\\ a_2=\frac{3}{t_f{}^2}(q_f-q_0)\\ a_3=\frac{2}{t_f{}^3}(q_f-q_0)\end{array}.$$

(35)

Here, $(q_0)$ is the initial position, $(q_f)$ is the final position, and $(t_f)$ is the ending time. To examine the proposed algorithm performance, two different cases are defined. In this study, we define $(q_0)$ and $(q_f)$ for all joints using the following values:

$$\begin{array}{l}{q}_{0_1}=30°,q_{f_1}=180°;q_{0_2}=120°,q_{f_2}=30°;q_{0_3}=30°,q_{f_3}=330°;\\ q_{0_4}=120°,q_{f_4}=-50°;q_{0_5}=50°,q_{f_5}=280°;q_{0_6}=180°,q_{f_6}=16°\end{array}$$

(36)

Algorithm 1. Adaptive T–S fuzzy sliding mode extended-state ARX–Laguerre PI observer for fault detection, estimation, identification, and tolerant control of a robot manipulator.
1:	Perform system modeling based on the ARX–Laguerre technique (4), (5)
2:	Run the ARX–Laguerre PI observer (6)
3:	Run the sliding mode extended-state ARX–Laguerre PI observer (7)
4:	Run the T–S fuzzy extended-state ARX–Laguerre PI observer (10)
5:	Run the residual generator (13)
6:	Run the threshold value based on the sliding mode technique (14)
7:	Run the proposed method for accurate fault estimation (15), (16)
8:	Run the decision logic for fault detection (17)
9:	Run the decision logic for fault identification (18)
10:	Run the sliding mode control for the fault-tolerant control algorithm (19)
11:	Run the sliding mode estimation technique to modify the fault tolerance (24)
12:	Run the adaptive fuzzy sliding mode estimation technique for fault tolerance (30)

5.1. Fault Estimation, Detection, and Identification

To examine the fault detection, fault estimation, and fault identification power of the proposed observer technique, the healthy condition, faulty actuator condition, defective sensor condition, and faulty actuator–sensor condition are tested in this step. Figure 9 demonstrates the robot’s joint and torque signals in the normal state. The residual signals for joint positions and torque in the healthy condition are shown in Figure 10.

As shown in Figure 10 and based on Equation (14), the actuator and sensor fault threshold values are defined in the intervals $[\begin{array}{cc}-1°& 1°\end{array}]$ and $[\begin{array}{cc}-2(N.M)& 2(N.M)\end{array}]$, respectively. The actuator fault for the PUMA robot manipulator is defined using the following equation:

$$({\Psi }_a)°=\{\begin{array}{l}1.5,0.1(s)\le t\le 0.25(s)\\ 0,\mathrm{Otherwise}\end{array}.$$

(37)

Figure 11 illustrates the fault estimation error based on the proposed T–S fuzzy extended-state ARX–Laguerre PI observer method, the sliding mode extended-state ARX–Laguerre PI observer technique, and the ARX–Laguerre PI observer procedure. As shown in Figure 11, the fault estimation error performance of the proposed algorithm is close to zero, but with the ARX–Laguerre PI observer, the average estimation error is about $1°$. Figure 12 demonstrates the effect of actuator faults in the joint position and torque residual signals.

The T–S fuzzy extended-state ARX–Laguerre PI observer is proposed for fault detection and identification in this part, and it detects the actuator fault in all joints. The sensor fault in the PUMA robot manipulator is defined using the following equation:

$$({\Psi }_s)=\{\begin{array}{l}5,0.1\le t\le 0.25\\ 0,\mathrm{Otherwise}\end{array}.$$

(38)

Figure 13 illustrates the effect of sensor faults in the joint position and torque residual signals.

The proposed T–S fuzzy extended-state ARX–Laguerre PI observer is used for fault detection and identification in this part, and it detects the sensor fault in all links. The actuator–sensor fault for the PUMA robot manipulator is defined using the following equation:

$$({\Psi }_a)°=\{\begin{array}{l}1.5,0.1\le t\le 0.25\\ 0,\mathrm{Otherwise}\end{array},({\Psi }_s)=\{\begin{array}{l}5,0.1\le t\le 0.25\\ 0,\mathrm{Otherwise}\end{array}.$$

(39)

Figure 14 shows the effect of actuator–sensor faults on the joint position and torque residual signals. The proposed T–S fuzzy extended-state ARX–Laguerre PI observer is used for actuator–sensor fault detection, estimation, and identification, and it detected the actuator and sensor faults in all links.

5.2. Fault-Tolerant Control

After detecting, estimating, and identifying the actuator and sensor faults using the proposed T–S fuzzy sliding mode extended-state ARX–Laguerre PI observer algorithm, we evaluated the performance of the proposed fuzzy adaptive sliding mode estimation algorithm, the sliding mode estimation algorithm, and the classical sliding mode procedure for fault-tolerant control using a 6-DOF PUMA robot arm. Figure 15 illustrates the trajectory and power of the proposed fault-tolerant algorithm, sliding mode estimation algorithm, and classical sliding mode algorithm for fault attenuation. As shown in Figure 15, the power of fault attenuation in the proposed technique is better than that in the sliding mode estimation and conventional sliding mode methods. Figure 16 shows the power of three types of fault-tolerant controllers, such as the proposed algorithm, sliding mode estimation method, and classical sliding mode technique, for fault attenuation in a faulty robot manipulator. As shown in Figure 15 and Figure 16, the adaptive fuzzy sliding mode estimation technique is the best to mitigate the level of the fault.

6. Conclusions

This paper explored fault detection, estimation, identification, and tolerant control using the proposed adaptive fuzzy sliding mode estimation extended-state ARX–Laguerre PI observer algorithm for a robot manipulator. First, the system’s dynamic was modeled and estimated based on the robust ARX–Laguerre technique. Second, for fault detection, estimation, and identification, an ARX–Laguerre PI observer was designed. To improve the reliability, robustness, and signal estimation of the ARX–Laguerre PI observer, the third step considered a sliding mode extended-state observer. Despite enhancing the robustness and reliability of the method, the accuracy of its faulty signal estimation still needed to be improved. Therefore, in the fourth step, the T–S fuzzy algorithm was used to improve the estimation accuracy of the sliding mode extended-state ARX–Laguerre PI observer. As shown in the results, the proposed algorithm is a reliable technique for fault detection, estimation, and identification. Because of its reliability and robustness, the sliding mode algorithm technique was introduced as the main algorithm for fault-tolerant control of a robot manipulator. To improve the power of fault attenuation, the estimated fault calculated by the proposed T–S fuzzy sliding mode extended-state observer in the previous step was applied to the classical sliding mode technique. As demonstrated in the results, the power of fault attenuation in the sliding mode estimation algorithm was better than that in the conventional sliding mode algorithm. In addition, the fuzzy adaptive sliding mode estimation fault-tolerant control algorithm was designed to reduce chattering and improve fault attenuation. The effectiveness of the proposed algorithm for fault diagnosis and fault-tolerant control was tested using a PUMA robot manipulator. The results and analysis demonstrated that the proposed algorithm estimates and identifies defects and attenuates the defects and chattering in the presence of uncertainty and disturbance. In the future, a higher-order intelligent extended-state sliding mode controller-observer will be designed for fault estimation-based fault diagnosis and tolerant control.