3.1.2. Setting the Fluent Solver
ANSYS 17.0 was used to generate the simplified 2D CFD model. There is no doubt that in simulation calculations, the accuracy of 2D simulation results is worse than that of 3D simulations. However, considering the hugeness of the DH network system, there is a high demand for simulation cost both in terms of calculation time and computational intensity. Therefore, the system was subjected to simulation. In order to obtain a high-quality mesh, a structural mesh was generated in the 2D CAD model, which can easily realize the boundary fitting of the region and is suitable for calculation of fluid and surface stress concentration. Structured meshes generate slower than unstructured meshes, but the number of structured meshes is much smaller than that of unstructured meshes, which can reduce computational intensiveness. The maximum mesh size was defined as 30 mm. In order to ensure the accuracy of the model, it was intended to increase the density of the mesh at the tee junction of the pipe. A partial view of the mesh from the heat source to the first elbow (see the red dotted ellipse area in
Figure 1) is shown in
Figure 2. The total number of meshes in the calculation domain is 252,7918.
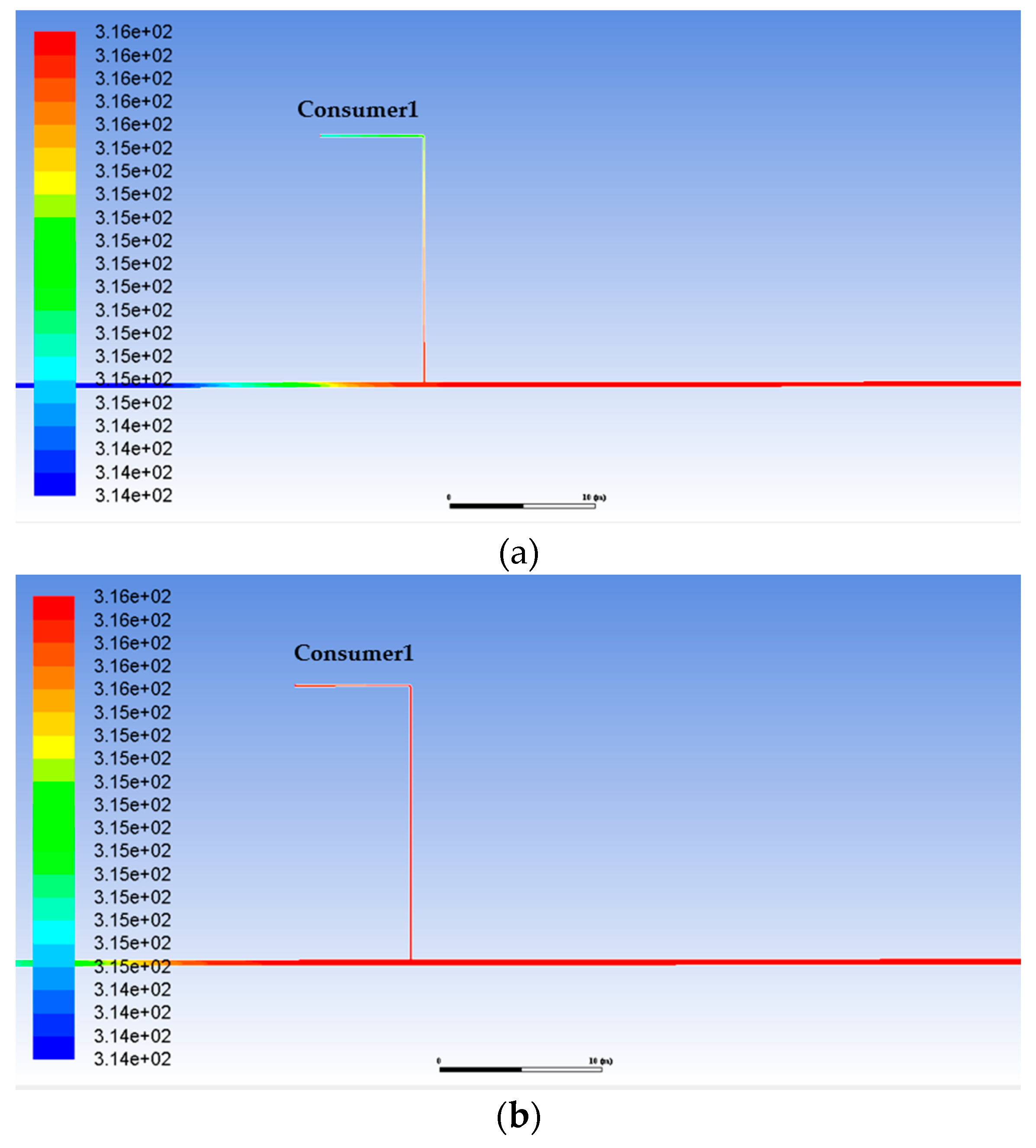
In order to prove the reasonableness and accuracy of the number of grids, the model needs to be verified for grid independent. The temperature and velocity contours comparisons from the heat source to the first elbow in five conditions of 1, 2, 2.5, 4 and 6 million are shown in
Figure 3.
The test results of grid independence are shown in
Figure 4. As can be seen from the grid independence results, when the number of grids reaches 2.5 million, the temperature and velocity changes will not be obvious. The computational cost and intensity are affected by the number of grids, and the computational cost increases as the number of grids increases. It is reasonable to have a grid number of 2.5 million.
In a large DH networks system, the temperature change of the supply water of the heat source takes a period of time to affect the heat consumers. This is the time delay due to changes in the water supply temperature. The Fluent solver was set up as a combination of steady-state calculations and transient calculations. The steady-state calculation makes the temperature in the DH network reach a certain value, and then the transient calculation was performed based on the steady state calculation to prove the influence of the water supply temperature change on the time delay of the DH network. The energy model was activated and the standard k-ε model equation was used as the turbulence model. Compared with the RNG model suitable for rotating flow calculation, the standard k-ε model is more suitable for solving the problem in this case. The turbulence governing equation is shown below:
where
is the production term of turbulent energy
k caused by average velocity gradient,
is the production term of turbulent energy
k caused by buoyancy,
represents the contribution of pulsation expansion in compressible turbulence, For incompressible fluids,
= 0.
,
,
,
and
are empirical constants,
,
,
,
and
,
is fluid density,
k is turbulent kinetic energy,
is turbulent kinetic energy dissipation rate,
u is fluid relative velocity,
is fluid dynamic viscosity.
The SIMPLE algorithm was used as the pressure-velocity coupling method. The pressure discrete difference format uses the standard discrete difference format. For solving the flow problem, the other variables use the 1
st upwind style. The 1
st upwind is less accurate than the 2
nd upwind, but it can make the steady-state calculation easier to converge, especially for this case. In order to improve the calculation accuracy, the 1
st upwind convergence under steady-state conditions was used as the initial condition for the 2
nd upwind transient calculation. The results of the comparison of the velocity and temperature profiles from the heat source to the first elbow are shown in
Figure 5 when the momentum, turbulent model, and energy were discretized in 2
nd order upward and 1
st, respectively. The results show that it is reasonable to use the 1
st upwind for steady-state calculations. The under-relaxation factors of pressure, density, momentum, turbulent kinetic energy, and energy were 0.3, 1, 0.7, 0.8 and 0.8, respectively. All of the given time steps are iteratively solved in a separate manner until the convergence condition was met. Two control monitors of the iterative process were defined to check convergence: a monitor for the residuals of the iterative process for the equations solved and the surface monitor of the outlet velocity. When the residual decreases at a value of 10
-5, the simulation process was considered to be convergent. However, the oscillation occurs when the residual is calculated to be below 10
-3. At this point, the surface monitor of the outlet velocity shows that the outlet velocity at this time remains constant, so the calculation is considered to have reached convergence. The Fluent 17.0 solver was calculated at steady state and the number of iterations is 4000. Another major step in CFD modeling was the establishment of boundary conditions. In the CFD model, the heat source and the heat consumers were defined as a velocity-inlet and pressure-outlet, respectively. The parameters of the boundary conditions were obtained from the measurements. Moreover, the wall of the pipe in the model was defined as an adiabatic wall to ignore the heat loss in the radial direction of the pipe.
After the steady state calculation converges, the temperature of the flow field in the model at this time reached the input temperature of the pipe velocity-inlet. Meanwhile, the Fluent 17.0 solver was subjected to transient calculations based on the steady-state simulation, with the temperature input of the velocity-inlet being changed. The second-order upwind space discretization algorithm was used for transient algorithms. Compared to first-order algorithms, second-order algorithms can achieve the best results because they can significantly reduce interpolation errors and false-value diffusion [
21,
22]. The time step size of the transient solver was set to 1s and the total time of the simulation was set to 4000 s. The maximum iterations were 20. The automatically save time for Fluent transient calculation was set to be automatically saved every 10 s. The temperature at each outlet of the DH network will vary with the input temperature of the velocity-inlet. The automatically saved Fluent data was read and analyzed the change of the temperature of the whole DH network system, which the time of the automatically saved Fluent data corresponding to each outlet temperature reaching the inlet temperature setting value to determine the time delay from the heat source to each consumer due to the temperature variation. By this method, the time delay of each heat consumer caused by the change in the water supply temperature of the heat source can be determined.
3.1.3. Boundary Conditions of the CFD Model
Boundary conditions need to be defined as part of the CFD model. In this case, the inlet and outlet of the model were set as the velocity-inlet and pressure-outlet, respectively. Parameters such as temperature and flow rate were obtained through experimental measurements and used as input parameters to define the boundary conditions.
Temperature and flow measurements were performed at the supply pipe for the heat source and each heat consumer. The average of the supply water temperature and flow rate at the heat source were set as the inlet temperature and the inlet flow rate. The probe of the temperature recorder was installed on the water supply pipe at the heat source, and the water supply temperature was measured every 10 minutes. Similarly, the ultrasonic flowmeter was used to measure the flow rate of the water supply pipeline at the heat source every 10 minutes. The measured water supply temperature and flow rate at the heat source were shown in
Figure 6. The average flow rate and water supply temperature at the heat source is 1.04 m/s and 39.2℃, which were used as a boundary condition for calculating the steady-state velocity-inlet of the CFD model. In the process of transient calculation, the velocity-inlet temperature was defined as 40.9℃ (The maximum temperature value on test day). In the CFD model, each consumer building heating entry was considered as an outlet, and the boundary condition of the outlet was defined as pressure-outlet. However, in an actual DH network system, the consumer building heating entry is not an outlet that is in communication with the atmosphere but rather has a pressure sufficient to provide hot water to the most unfavorable end of the building. This means that the pressure at the pressure-outlet cannot be set to 0 Pa. The outlet pressure can be obtained by reading the pressure gauge at the consumer building heating entry. A relative pressure of 0.4 MPa was defined as the input parameter of the pressure-outlet. The input parameters of the CFD model boundary conditions are shown in
Table 2.