1. Introduction
Compared with plastic IGBT modules, press-pack IGBT modules adopt the idea of the flat-packaged structure once applied to the gate turn-off thyristors (GTOs) or integrated gate commutated thyristors (IGCTs) [
1], which contain no bonding wires. Thus, the potential failure mechanisms affecting plastic IGBT modules, such as bonding wire lift-off or solder joint fatigue, are eliminated [
2]. On the other hand, the press-pack IGBT modules combine the properties of the double-sided cooling and multi-chip parallel package, which enable them to conduct higher current and propagate more heat. The features of press-pack IGBT modules allow them to be excellent candidates in the application of voltage-source-converter based high-voltage-direct-current (VSC-HVDC) transmission technology, which has been playing an increasingly important role in shaping the future of the electric industry [
3]. As the main kind of VSC-HVDC, modular-multilevel-converter-based HVDC (MMC-HVDC) technology has several significant advantages, such as enabling the integration of renewable energy sources, independent regulation of active and reactive powers, and power supply capabilities for passive networks [
4,
5]. As one of the significant components of MMC-HVDC systems, the reliability of press-pack IGBT modules for long-term operation is the key issue. According to [
6], the most common failure mode for press-pack IGBTs is the fretting damage out of coefficient-thermal-expansion (CTE) mismatch because of the high temperature variation. Therefore, it is urgent to accurately determine the thermal stress of press-pack IGBTs.
The precise evaluation of the thermal performance for IGBTs is required by the comprehensive IGBT thermal models. Nowadays, the thermal network models derived by the resistor-capacitor (RC) thermal networks are the most widely used in the thermal analysis of power modules. The RC thermal networks are based on a discretization of the heat diffusion equations. They are utilized to calculate the temperature of network nodes over the devices, packages, and heatsinks in analogy with the calculation of currents and voltages in the electrical networks. The thermal network also interacts with the electrical networks through the electro-thermal models of the IGBTs with instantaneous power dissipation and boundary conditions [
7,
8,
9,
10]. Hence the thermal network models are preferred due to the advances of accurate and computationally efficient calculation methods which are easy to be integrated into the electric circuit simulators to evaluate the steady-state and dynamic thermal stress in a long-term dynamic process.
However, it is challenging to carry out the precise junction temperature evaluation for the press-pack IGBT modules because of the physical and operational factors of press-pack devices. The physical factors are related to the press-packaging structure which can be divided into round type press-pack and StakPak [
11,
12]. Inside the modules, the semiconductor chips are close to each other and the thermal coupling effect among adjacent chips is rather serious, leading to an uneven temperature distribution among chips [
13,
14]. To calculate the actual junction temperature, the conventional lumped RC thermal impedance network should be reconstructed to take the multi-chip thermal coupling effect into account. Besides, due to the asymmetric double-sided package design of StakPak press-pack IGBTs, the thermal resistance from the junction to collector case and one the from the junction to emitter case have great differences from each other, which results in the unbalanced thermal dissipation and place more sophisticated demands on the thermal management of press-pack IGBT modules. Consequently, a better understanding of IGBT modules based on the StakPak packaging style is required.
For multi-chip IGBT modules, a 3D lumped RC thermal network model, which develops a thermal coupling impedance to represent the thermal coupling effect among the adjacent chips and critical layer, was proposed in [
15,
16]. The self-heating thermal impedances and thermal coupling impedances are combined together to form a matrix thermal network. This approach is employed in plastic IGBT modules loaded with the three-phase two-level DC-AC voltage source converter. The temperature calculated from the 3D thermal model shows good agreement with the experimental measurements. An analytical thermal model with the thermal impedance matrix using the Foster network representation is provided in [
17]. It is applied for the real-time junction temperature estimation of the plastic IGBT modules used in motor drives. The comparison between the modeling results and measurements is satisfactory in terms of accuracy and computational speed. In case of the distinction between the thermal impedance of junction to the two cooling sides of press-pack IGBT modules, the experimental analysis is introduced in [
18,
19] to measure the junction-to-case thermal resistance of round type press-pack IGBTs, but the measurement principle is applied with the double-sided cooling regardless of the differences inside the internal press-pack IGBT structures. Therefore, to achieve an accurate junction temperature monitoring tool and balanced thermal management, the thermal coupling effect among the paralleled chips and differences of thermal impedance between the junction to the two contact plates should be explored when modeling the temperature swing and heat distribution map of the press-pack IGBT modules.
This paper is organized as follows: In
Section 2, the structure of StakPak IGBT modules is shown and the internal configuration and chip layout within the submodule of a StakPak module are analyzed in detail. In
Section 3, the differences of thermal impedances between the chip junction to the disparate cooling plates are figured out and the impacts of imbalanced thermal distribution of the press-pack IGBT module are discussed. A 3D thermal network model is described and the elements of the thermal network are extracted by the finite element method (FEM), which is then validated by comparing with the parameters form device manufacturer in
Section 4. In
Section 5, the presented model is utilized to calculate the junction temperature of the target IGBT module under the operating conditions in an MMC-HVDC power converter and compared with the measured results. Finally,
Section 6 draws the conclusions.
2. Structure of Press-Pack IGBT Modules
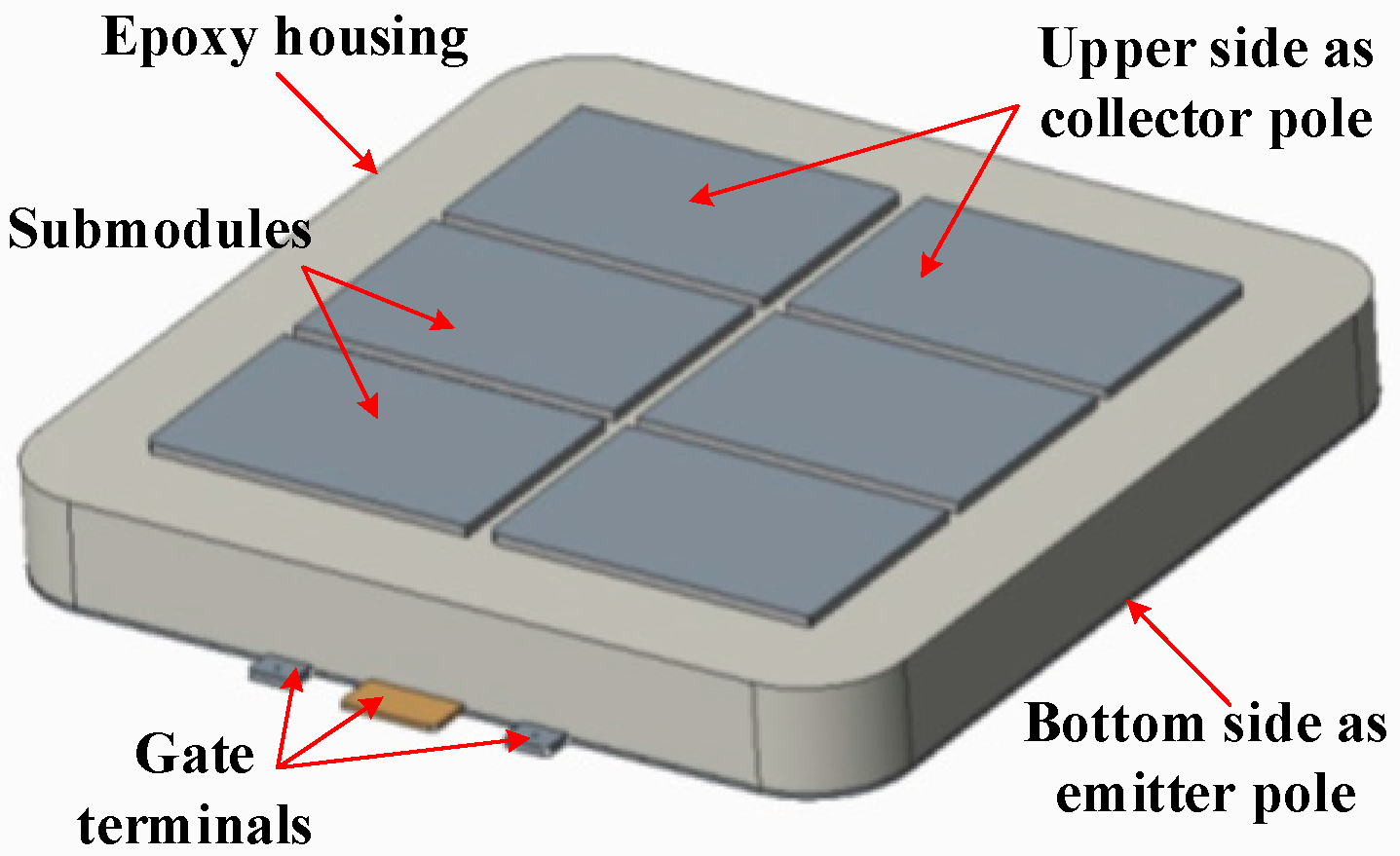
To elucidate the thermal performance for IGBT modules, the press-pack structure of power devices needs to be analyzed in detail. Without loss of generality, the StakPak press-pack IGBT rated at 4.5 kV and 3 kA (5SNA 3000K452300, ABB, Zurich, Switzerland) is chosen as the target device. The appearance of the target device as given by the Creo is shown in
Figure 1 [
20]. From the external point of view, the StakPak IGBT module looks like a flat cuboid. It consists of six identical submodules in parallel with insulated epoxy housing surrounding them. The upper side of the press-pack IGBT modules which is made up of contact faces of the submodules in
Figure 1 acts as the collector pole and the bottom side with only one whole face acts as the emitter pole. The gate terminals are placed at the front edge of the target module, which includes a connecting interface and two screw holes for mounting the gate driver.
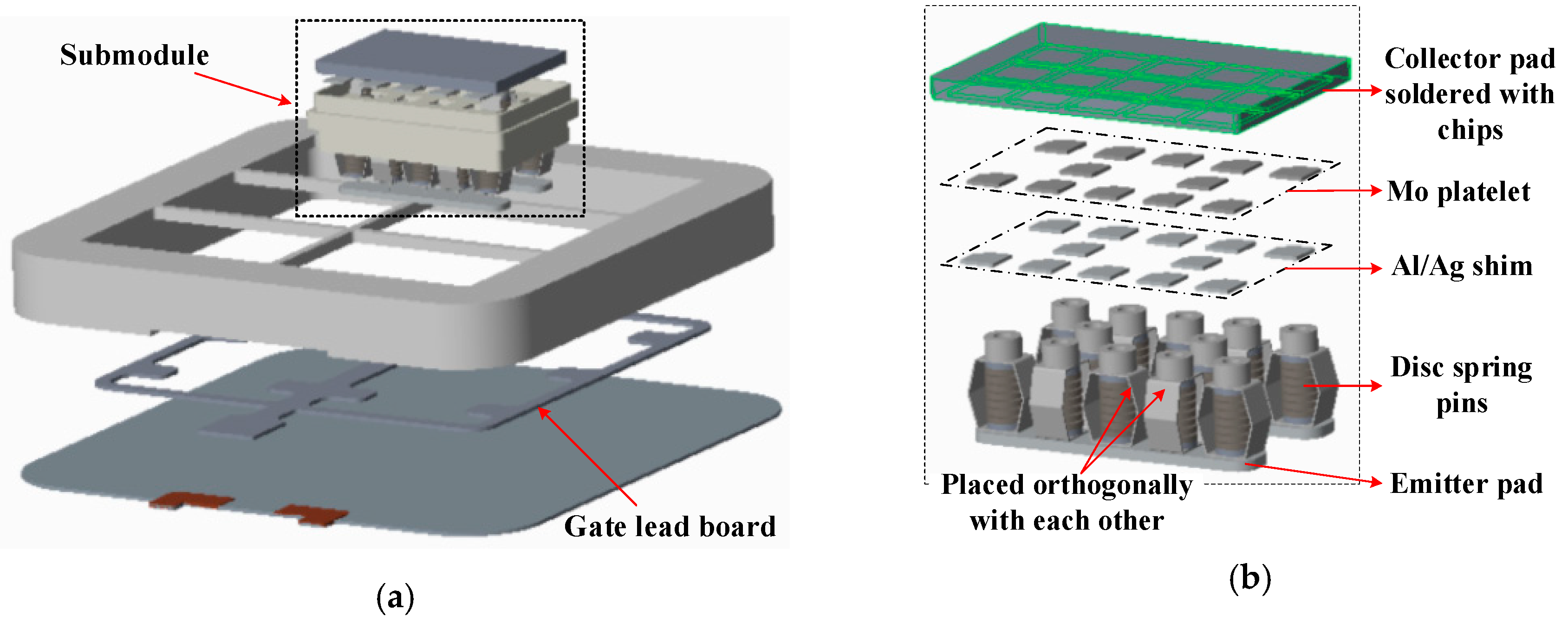
More in detail, the 3D model of StakPak press-pack IGBT is developed and the exploded graph which presents the internal profile of the IGBT module is displayed in
Figure 2a. Thanks to the parallel and symmetrical configuration of submodules inside press-pack IGBT module shown in
Figure 1, it is appropriate and time-saving to choose only one submodule in the dotted box to analyze the detailed profile shown in
Figure 2b. The types of materials within the submodule are identified according to the information given by the IGBT module manufacturer. Since the epoxy housing frame is a kind of neat (unfilled) epoxy and provides a thermal conductivity of about 0.2 W/m·K. Meanwhile, and the typical thermal conductivity values of metals fall in the range of 50~300 W/m·K, it can be neglected when establishing the 3D model of press-pack IGBT since it is electrically and thermally isolated.
The highlighted part of the press-pack submodule in
Figure 2b is the collector pad where the semiconductor chips are attached by soldering. The detailed layout of IGBT and free-wheeling diode (FWD) chips is configured, where the dimensions of and the distances between the chips are measured and displayed in
Figure 3.
There are eight IGBT chips (marked as T), four FWD chips (marked as D) and two gate pads (marked as G) placed on the collector pad of the press-pack submodule in total. The IGBT chips share the same size as the FWD chips. Meanwhile, the gate pad at the left or right edge is linked up to four IGBT chips through silver wire. Since the distance between IGBT chips at the same edge and the gate pad is almost the same, it can be assumed that all four of the IGBT chips in parallel switch simultaneously as one group. Thus, the current sharing among the paralleled chips is balanced and the electrical stress of each chip is supposed to be equal. Based on the structural information analyzed above, the cross-sectional view of the internal structure of the submodule for press-pack IGBT device can be sketched as in
Figure 4 to illustrate the heat flux and distribution of the target IGBT module.
Two pads located on the upper plate or bottom plate play the role of conductive electrodes (i.e., collector and emitter poles), providing both the electrical and thermal paths for the semiconductor chips. Molybdenum plates of nearly the same size of IGBT chips or FWD chips directly soldered on the collector pad are placed in the middle of silicon chips and disc spring pins, which ensures the uniform distribution of the mounting force. Besides a silver or aluminum shim platelet is between the silicon chip and the Mo plate [
12]. A semiconductor chip, an Al/Ag platelet and Mo plate form a chip assembly-like sandwiched structure. If the chip fails to short-circuit, the shim plate functions as a failure path to conduct the whole load current and then sufficiently high energy melts the platelet and forms a stable alloy with silicon [
12].
Inside the press-pack IGBTs, the external clamping force is mounted to maintain the thermal contact of all layers and the part outside the disc spring pins acts as the conductive path connecting the collector pole and the emitter pole. It is assumed that every layer which conducts current is pressured tightly and connected without relative displacement and the silicon oil filling inside the module has small thermal conductivity and spread no heat, which confirms that all heat dissipates vertically from junction areas of the active chips to the cooling plates of both sides. As shown in
Figure 2b, any two adjacent conductive paths outside the disc spring pins are placed orthogonally with each other, therefore it can be assumed that the layout of disc spring pins negligibly influences the thermal distribution vertically. The thermal conductivity of different packaging materials inside the studied press-pack IGBT module is obtained in [
21,
22] and listed in
Table 1.
3. Impact of Press-Pack IGBT Double-Sided Structure on Thermal Distribution
As shown in
Figure 4, the press-pack IGBT submodule consists of parallel chip assemblies which are made up of several press-contact layers. Among those, the single IGBT chip assembly is shown in
Figure 5. A temperature rise could be produced due to the self-heating of the active chip and the transient thermal impedance is gained. It is defined as
Zth_jc as:
where
Tj(
t) and
Tc(
t) are the temperatures of points located in the junction and case of the IGBT module, while Δ
Tjc is the temperature gap between the junction and case,
Ploss is the power loss of the heating chip itself. The transient thermal impedance
Zth_jc of the single chip assembly can be expressed as a lumped Foster-based RC thermal network model [
23,
24] based on thermal resistance
Rth and thermal capacitance
Cth of each layer.
It can be seen from
Figure 5 that the studied press-pack IGBT module features a double-sided cooling structure. Under double-sided cooling conditions, the heatsinks which are clamped on the surface of the heating press-pack module to achieve an effective cooling system act as both conducting and cooling components. A mechanical press-pack IGBT stack designed according to [
25] configured as half bridge topology is shown in
Figure 6a and the cooling channel inside the heatsink shown in
Figure 6b is designed to allow the coolant to flow to the center first and then go out to the outlet. Through the cooling channel the heat is absorbed and the temperature spread on the heatsink surface is minimized as cold and hot water flows very close to each other.
To reduce the volume of the cooling pump, the cooling channels of heatsinks pressed together are often in series and thus lead to almost the same heat dissipation capability for every heatsink. In the cooling design for high power plastic IGBT modules, the heat dissipation parameters of heatsinks can be set as the same because plastic modules dissipate the heat by only one cooling side. However, the path of heat flow from press-pack chip junction to the collector cooling plate is shorter than that from the chip to the emitter cooling plate, which results in the difference of heat release between the two heatsinks pressed at the surface of press-pack IGBT module.
The equivalent thermal impedance of the single press-pack IGBT chip under double-sided cooling conditions is presented in
Figure 7. The thermal parameters
Zth_jcc and
Zth_jce represent the thermal impedance from the chip junction to the collector surface and emitter surface.
TCc and
TCe is the case temperature of the collector case and emitter case.
Zth_hc or
Zth_he represents the thermal impedance of related heatsinks on either cooling side and they are supposed to have a very high heat transfer coefficient and very low thermal resistance in the boundary of the baseplate and the heatsink. Assume that the cooling conditions are kept the same (
TCc=
TCe) and thermal impedance
Zth_jc from the junction of the semiconductor chip to the IGBT’s case is equal to
Zth_jcc||
Zth_jce.
To extract the thermal parameters of the press-pack IGBT module, the eight IGBT chips belonging to one submodule displayed in
Figure 3 are picked out. As mentioned before, because the layout of chips and press-contact components is horizontally symmetrical, the analysis of thermal performance is concentrated on the chips of 1/2 unit (i.e., T1~T4) within the press-pack submodule in
Figure 3. And since the conductive paths outside the disc springs are placed orthogonally, the paralleled coupling effects among conductive paths can be left out.
5. Model Verification
In this section, the target press-pack IGBT module is employed in the electrical type test setup of modular-multilevel-converter based high-voltage-direct-current (MMC-HVDC) [
26] and the schematic diagram of the converter is shown in
Figure 12a. Due to the unbalanced thermal distribution analyzed in
Section 4, the unbalanced power loss distribution of the press-pack IGBT module in the MMC-HVDC power stack is considered and the thermal stress should be evaluated to ensure the reliable operation of MMC-HVDC system. Thus, the electrical type test setup of the MMC valves is established in
Figure 12b and the valves under the test are made up of six full-bridge submodules (FBSMs) and the auxiliary valve is made up of three half-bridge submodules (HBSMs). The operation parameters of the test setup are listed in
Table 4. The switching frequency listed in
Table 4 is set to be about 150 Hz which is the same as that in [
26].
To obtain the power loss of MMC converters, the MMC converter model configured as
Figure 12a is built in Matlab and it is implemented with the strategy of nearest-level-modulation [
27,
28]. The power loss of IGBT module consists of IGBT’s power loss and free-wheeling diode’s (FWD’s) power loss. The IGBT’s power loss
PT is made up of IGBT’s conduction loss
PTcon and switching loss
PTsw while FWD’s loss includes FWD’s conduction loss
PDcon and reverse recovery loss
PDrr, of which the conduction loss is expressed as Equation (9) [
29]:
In Equation (9)
UCE and
IC denote the collector-emitter voltage drop and the collector current of IGBT when it is on conduction stage, and
RT and
UCE0 mean the forward conduction resistance and the latch-up voltage of target IGBT which can be extracted from the curve of the on-state characteristics in [
20]. Likewise,
UD and
ID are the forward voltage drop and the conduction current of FWD, and
RD and
UD0 represent the FWD’s conduction resistance and the latch-up voltage.
The switching loss of IGBT and FWD is shown in Equation (10) [
29], where
UDC stands for the DC-link voltage while
Ts and
Tm denote the switching period and modulation period.
ETsw and
Err are switching energy and reverse recovery energy of IGBT and FWD, respectively. The coefficients
μ1~
μ6 are temperature-dependent parameters which can be obtained by fitting curves of
Esw-
IC or
Err-
IC from [
20]. Since
μ1~
μ6 are temperature-dependent, the temperature coefficients
ρT and
ρD are used to calculate the loss accurately under different temperature.
ρT and
ρD can be gotten by the interpolation method where
Tj means junction temperature of IGBT module.
ETsw1 and
ETsw2 refer to the switching energy of IGBT under 125 °C and 25 °C, respectively. Similarly,
Err1 and
Err2 are used to represent the reverse recovery energy of FWD under 125 °C and 25 °C. All of the energy parameters are available in the manufacturer’s datasheet:
In this way, the data and parameters related to the module’s power loss from [
20] are added to the simulation model. Based on the simulation model, the power losses’ calculation procedure is presented in
Figure 13, and the results of power losses for the press-pack IGBT modules are listed in
Table 5.
The total loss of average power losses in the IGBT modules is calculated as 17.42 kW. To validate the simulation results, the total average power loss of the FBSM should be acquired and the waveforms of the MMC valve under the required test parameters in
Table 4 is measured in
Figure 14.
The power loss of MMC valves is usually measured by means of a power analyzer. However, due to the high power rating of MMC type test setup, the cost of a proprietary power analyzer is unaffordable. Thus, the method of liquid calorimetry is developed and utilized to measure the average power loss of a single MMC-FBSM.
Since the heatsinks of the press-pack stack in
Figure 6 are designed with water cooling structure, liquid calorimetry can be applied in the press-pack stack to measure the quantity of heat absorbed by the coolant. Thanks to the compact packaging assembly of the mechanical press-pack stack, the heat dissipation of power devices is almost absorbed by the heatsinks and the heat is calculated as Equation (11):
where
H is the heat absorbed by coolant and Δ
t is the temperature difference between the inlet and outlet of the heatsink. The volume flow rate is symbolized as
Q, while
C and
ρ mean the specific heat capacity and density of the coolant. To measure the temperature difference Δ
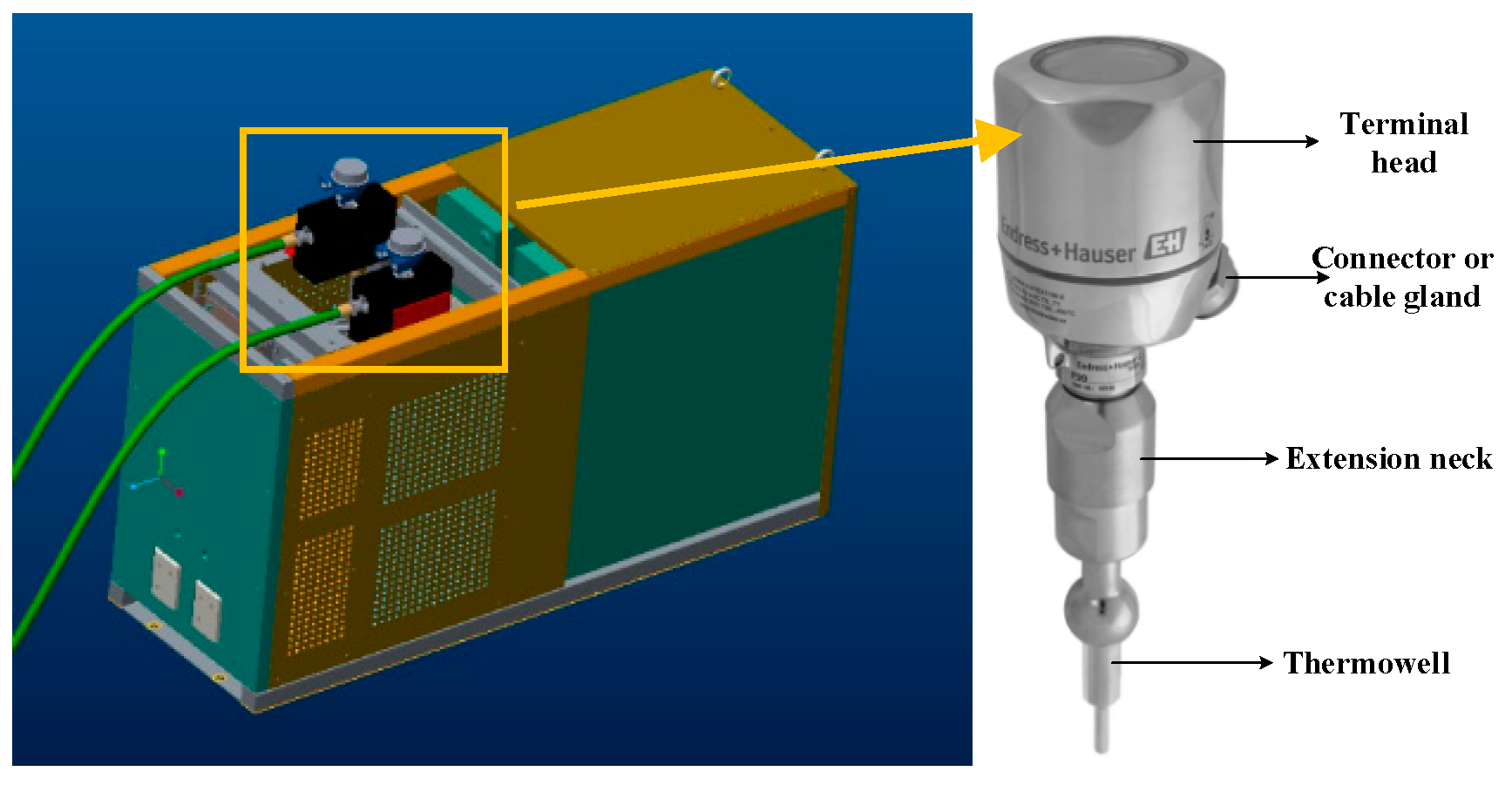
t, an iTHERM TM411 thermometer [
30] is placed at the inlet and outlet of the heatsink and the configuration of the thermometer is shown in
Figure 15.
Based on the thermometer and the cooling system, the average power loss of the single MMC-full-bridge-submodule (MMC-FBSM) can be obtained. The specific heat capacity and density of the coolant are 4200 J/(kg·K) and 1000 kg/m
3. The volumetric flow rate of the cooling system is set to be 16.8 L/min. The temperature difference between the inlet and outlet measured by the thermometers is listed in
Table 6.
The error between the simulation results and the measurement is around 5%, hence the calorimetry method usefulness is verified and thee average power loss distribution listed in
Table 5 can be applied in the analysis for the thermal behavior of the press-pack IGBT modules.
According to the loss distribution analysis of the press-pack IGBT module under double-sided cooling conditions which indicates that 88% of the module’s power loss is dissipated through the collector pad and the rest flows to the emitter pad, the loss distribution for the MMC-FBSM is calculated as illustrated in
Figure 16. The heatsink H1 undertakes the part of power loss dissipated from the emitter side of IGBT2, while the heat stress for H2 is made up of the power loss from the emitter side of IGBT1 and collector side of IGBT2. The power loss of heatsink H1 and H5 is almost the same. And H2 and H4 share nearly the same thermal stress as well. The heatsink in the middle of the stack undertakes the most power loss which absorbs the part of power loss from the collector side of IGBT1 and IGBT3.
To verify the validation of the proposed thermal model in
Section 4, the junction temperature of the critical points in the collector side of IGBT chip T2 in
Figure 3 is calculated via the proposed matrix thermal model and the lumped RC thermal model of which the parameters are dependent on
Table 3. The power loss injected to the proposed matrix thermal model is the distributed loss on the collector side of the press-pack IGBT while the loss as the input of traditional lumped RC model is the whole loss of the press-pack IGBT. The type of test setup in
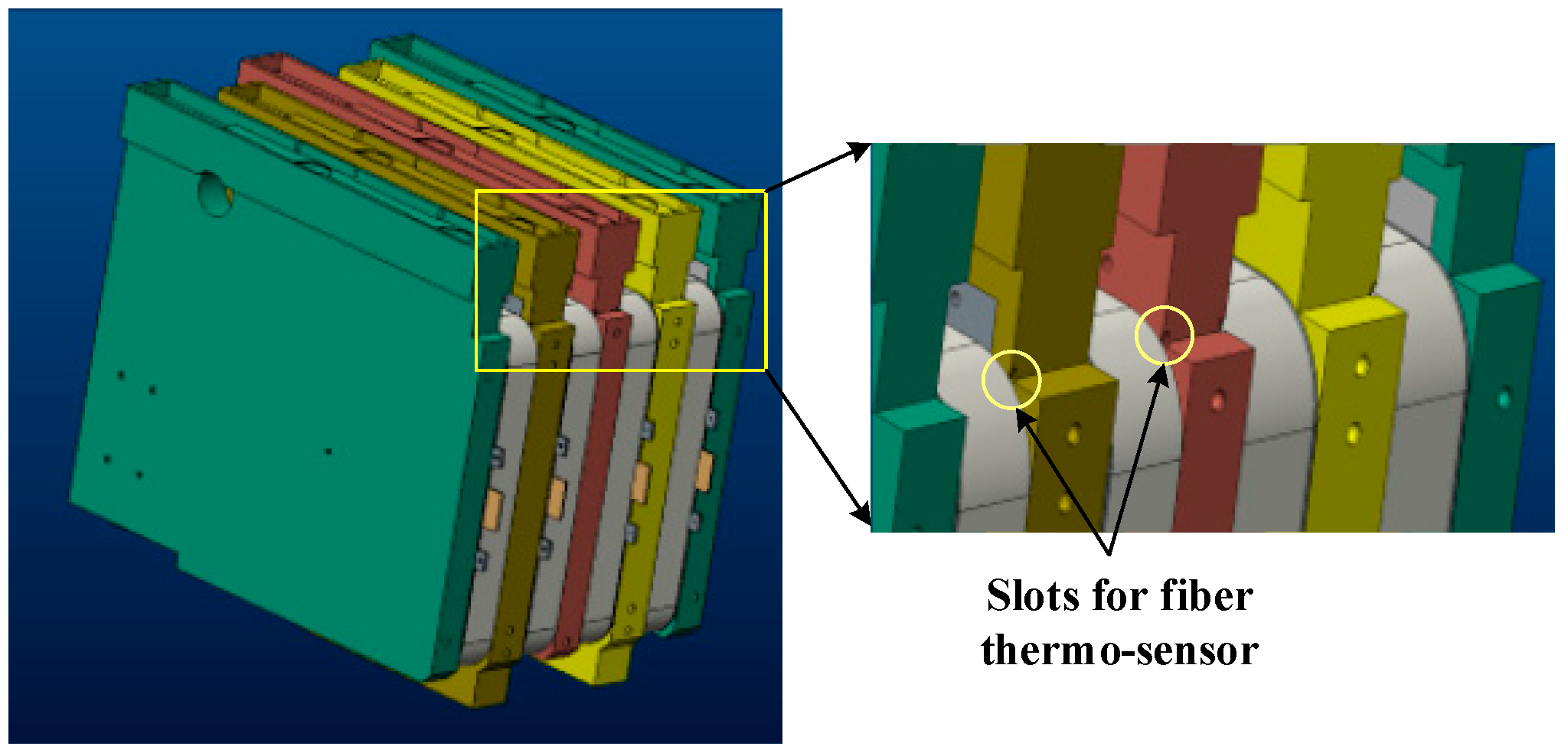
Figure 12 is employed, where the instant junction temperature is measured by optic fiber thermosensors. The optic fiber temperature sensor’s resolution is 0.1 °C which is enough to ensure the accuracy of the measurements. It is placed clinging to the press-pack IGBT’s submodule through the slot in the heatsink shown in
Figure 17. Through the slot, the fiber can be placed right at the chip whose coupling effect is the most obvious. The test setup with the optic fiber thermosensors is displayed in
Figure 18.
With the fiber thermosensors shown in
Figure 19, the simulated junction temperature swings using the proposed model and the traditional lumped RC model of which the parameters supported by the manufacturer are presented in
Figure 20 and
Figure 21, respectively.
The results are compared with the test measurements. The temperature of the IGBT module is measured every 2 minutes, and before it reaches the steady state the temperature is recorded about every 10 seconds. The measurement value of the collector’s temperature is marked with a triangle. The fitting curves are compared with the simulation curve.
Figure 20 displays the comparison between measurement results and model calculation for the junction temperature of IGBT1 which is marked by
Tj1, meanwhile, the comparison for the junction temperature of IGBT2 which is denoted as
Tj2 is shown in
Figure 21. The junction temperature curves gotten by proposed method and conventional method in
Figure 20 fall to range of 60.5 °C~63.4 °C and 59 °C~61.2 °C, while in
Figure 21 the curves fall to range of 61.6 °C~64.5 °C and 60 °C~62.3 °C. From the two figures it can be observed that the gap between the average simulation results of the proposed thermal model and the measurements is about 1.5 °C in
Tj1 and 1.0 °C in
Tj2, respectively, but the difference between the average simulation results of traditional thermal model and the measurements is about 3.4 °C in
Tj1 and 3.6 °C in
Tj2, respectively. The junction temperature of
Tj1 is about 0.5 °C lower than
Tj2 which corresponds to the higher power loss of
Tj2. The error between the measurements and the simulation results of the proposed thermal model is less than 2.1% while that between the measurements and the simulation results of traditional thermal model is about 5.5%. The differences between experimental results and calculation results by conventional and proposed methods are displayed in
Figure 22.
It can be verified that the matrix thermal model of the press-pack IGBT module under double-sided cooling conditions more closely fits the practical thermal behavior of the target module than the traditional RC model. The error between the proposed model and the traditional model will increase if the power loss generated by the IGBT module increases, and the thermal distribution could be more unbalanced if the operating conditions change. The proposed thermal model has considered the multi-chip thermal coupling effect and the thermal distribution between the two cooling plates inside the press-pack IGBT module. It does not only allow the accurate evaluation of the junction temperature of the press-pack IGBT module, but also helps to improve the cooling capability of the heat exchanger and reconstruct the thermal management in high power converter systems such as the MMC-HVDC system based on press-pack IGBT modules.