Shales Leaching Modelling for Prediction of Flowback Fluid Composition

Abstract

The object of the paper is the prediction of flowback fluid composition at a laboratory scale, for which a new approach is described. The authors define leaching as a flowback fluid generation related to the shale processing. In the first step shale rock was characterized using X-ray fluorescence spectroscopy, X-ray diffractometry and laboratory analysis. It was proven that shale rock samples taken from the selected sections of horizontal well are heterogeneous. Therefore, the need to carry a wide range of investigations for highly diversified samples occurred. A series of leaching tests have been conducted. The extracts were analyzed after leaching to determine Total Organic Carbon and selected elements. For the results analysis significant parameters were chosen, and regression equations describing the influence of rocks and fracturing fluid parameters on the flowback fluid composition were proposed. Obtained models are described by high values of determination coefficients with confidence coefficients above 0.99 and a relatively low standard deviation. It was proven that the proposed approach regarding shale leaching can be properly described using shale models at a laboratory scale, however scaling up requires further investigations.

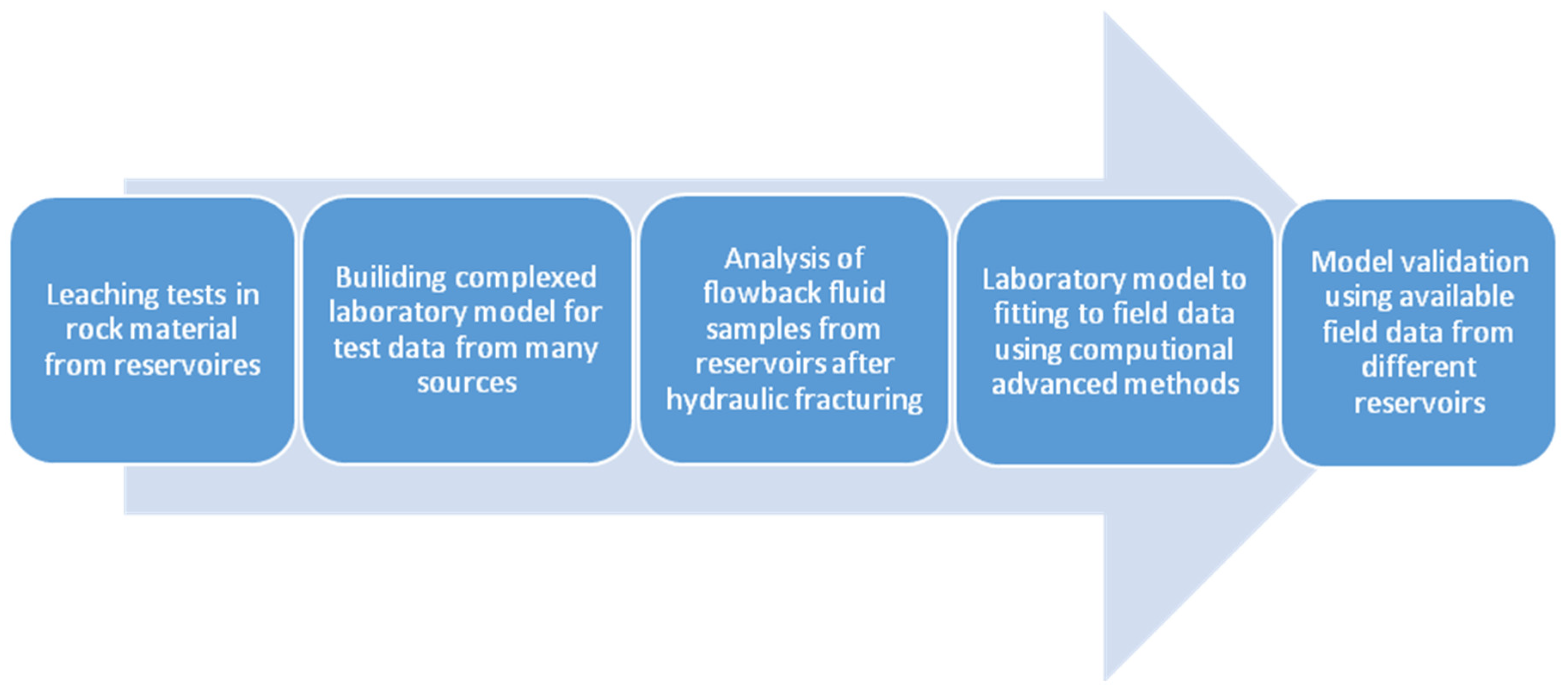
1. Introduction

Shales are fine-grained, fissile and the most common sedimentary rocks found in the Earth’s crust, composed of clay and other minerals, especially quartz and calcite, as well as organic matter [1]. Shales with proper mature organic matter have gas potential and represent unconventional gas reservoirs. The division into conventional and unconventional reservoirs is associated primarily with the permeability of the reservoir. Conventional reservoirs have a permeability above 0.1 mD, while unconventional reservoirs are below 0.1 mD, and for gas-bearing shales, even below 0.001 mD [2]. The differences in the construction of the reservoir (containing gas in the interstitial space) of a conventional and unconventional shale type are presented in Figure 1. The yellow area represents the gas field space whereas grey/white areas represent rock.

High heterogeneity regarding mineralogical structure, elemental composition and reservoir parameters are typical for shale formations. Individual properties may differ substantially even within individual formations [3,4,5]. Clear differences in the properties of the deposit occur on a scale of several hundreds to even a few meters [6,7]. The high heterogeneity of the deposit makes all of the well operations diverse and dependent on the given formation. Therefore, a number of deposit stimulation technologies have been developed [8,9].

In the shale rock gas-filled spaces are not interconnected, and the permeability is very low. To ensure gas flow, it is necessary to create a grid of fractures. For this purpose, stimulation of the reservoir is needed, wherein the hydraulic fracturing is the main technology currently applied [10,11]. Hydraulic fracturing consists of using a fracturing fluid pumped under pressure in the range of 700–1200 bar for gas or/and oil-bearing formations. The amount of water needed for fracturing is usually between 10–25 thousand cubic meters and depends on the length of the horizontal part of the borehole. The fracturing pressure must be higher than the tensile strength of the rock, but it cannot exceed the strength parameters of the piping, as it is limited by the power of the pumps. The purpose of the fracturing fluid is primarily to create as much contact surface of the deposit with the well by creating a network of gaps, and to prevent the fractures from closing after fracturing [12]. Fracturing fluids usually consist of at least 90% water containing a proppant as well as other additives [13]. Proppant is a small grain material added to the fracturing fluid in order to prevent the fractures from closing after pressure reduction resulting from hydraulic crushing of rocks [14]. Other additives, which are typically introduced at a level of about 0.5% (v/v), are used to modify the properties of the fluid to enable better penetration of the formation and provide compatibility between the fluid and reservoir [12,15].

After the fracturing is completed, 10–50% of the fluid returns automatically or by stimulation to the surface. The returning stream is called flowback fluid. In extreme cases, the flowback fluid does not return to the surface at all, or returns in larger quantities. The rest of the fluid remains in the reservoir [16]. Flowback fluid differs significantly from the fracturing fluid, as it contains suspended fine rocks as a result of the leaching process, reservoir water, drilling muds, and also various chemical substances, such as dissolved solids (e.g., chlorides, sulfates, etc., measured as total dissolved solids or TDS), suspended solid particles (TSS), bacteria, metals (e.g., calcium, magnesium, barium, strontium), iron compounds, aromatic hydrocarbons, carbon dioxide, hydrogen sulphide and other components [17].

Average results of fracturing and post-treatment fluid analysis from the Marcellus Shale basin in the United States are presented in

Table 1. Comparison of concentrations of the most important components in fracturing fluid and flowback fluid from the Marcellus Shale [18].

Component	Fracturing Fluid		Flowback Fluid
	Range of Concentrations (ppm)	Median Concentration (ppm)	Range of Concentrations (ppm)	Median Concentration (ppm)
Na+	25.70–6190	67.8	10700–65100	18000
Ca2+	6.70–2990	32.9	1440–23500	4950
Mg2+	1.20–235	6.7	135–1550	559
Fe2+	0.00–14.3	1.2	10.8–180	39
Ba2+	0.06–87.1	0.4	21.4–13900	686
Cl−	4.10–3000	42.3	26400–148000	41850
HCO3−	<1.00–188	49.9	29.8–162	74.4
NH4+	0.58–441	5.9	15–242	82.4

. The results of the concentrations of the ingredients may vary by a factor of several dozen with the concentrations of the fracturing fluid [18].

Although the fracturing fluid is environmentally friendly, flowback fluid should be treated as an environmental threat due to its composition. It can have adverse effects on the environment, and hence requires purifying and/or disposal. Flowback fluid, treated as a mining waste, can be transported to another drilling plant, and also be transferred to companies dealing with the disposal of mining waste. However usually it is transferred to a sewage treatment plant or another installation that neutralizes waste [19,20]. Due to the high variability of the flowback fluid and the difficulties of its composition estimation, models and tools that help in its prediction are desirable.

Flowback fluid analysis is being widely used in shale gas recovery modelling. There are many models describing propagation of shale fracture to assess possible production of shale gas [21,22,23,24,25,26]. Some attempts to describe flowback fluid production mechanisms are reported [27,28,29,30] and several methods to develop volume control are described [31,32]. Unfortunately, there are not many investigations dedicated to the prediction of the composition of fracturing flowback fluid and hardly any tools to limit the migration of chosen chemical compounds from the reservoir to the fluid. Methods focused on computer programs, supported by precipitation tests [33], statistics of reservoir data [34] or statistics of fracturing wells in chosen basin of gas bearing shales can be specified. However evaluation is not possible because the proposed tools are often unavailable and not described enough to test them due to the unnormalized character of the data [35]. Nevertheless very useful information can be found on the basis of Total Organic Carbon (TOC) regarding salt migration into flowback fluid streams [33]. Also ionic strength and the influence of ion interactions exhibit a crucial role [35]. Due to the unnormalized character of the data presented in the literature, the models are often non-comparable. The most interesting modeling approaches are presented below.

A promising model was presented by Gdanski et al. [35]. The model allows one to predict the amount and composition of the flowback fluid. A two-dimensional numerical modelling was used, taking into account the physics of fracturing fluid flow and flowback fluid and chemical interactions in the borehole. Leaching of sodium, potassium, chlorides, sulphates, carbonates and boron were considered in the model. The model provides separate data for post-treatment fluids and reservoir waters. Based on the adjustment of the fluid production rate, it is also possible to estimate certain properties of the reservoir, such as relative permeability and capillary pressure. However, it should be noted that the author based his model on a commercial simulator [36], that is unfortunately commonly unavailable and therefore, impossible to evaluate. In addition, the conducted considerations concerned on small-scale fracturing in a vertical hole with accurate characteristics. Such a large amount of data cannot be obtained for full-scale horizontal wells with diversified fluids, therefore, the model is unapplicable for the conditions presented by other types of wells.

Another model was developed by the Barbot team [33,34]. It concerned the fracturing of wells in the Devonian shale in the north-eastern United States. An analysis of 160 flowback fluids was used to build a model for the prediction of the quantity and composition of the flowback fluids in the American Marcellus basin. Models for the concentration prediction of sodium, calcium, magnesium, barium, strontium, bromides and chlorides were developed. The performed tests may be applicable during the management of the flowback fluid on this deposit. Despite the authors’ conclusions, analysis of only 160 flowback fluid samples cannot give enough data for modelling with no proper relation to shale rock properties. This type of model can be built at the advanced stage of shale gas extraction only for very specific areas and it is impossible to extend it for other reservoirs.

A much more advanced model was presented by Balashov [37] In addition to analyzing a larger amount of data, Balashov et. al. included considerations regarding the diffusion model based on shale rock. A numerical model was created and calibrated using field data from a specific area. In the conclusions, the author claimed that well-fitting numerical models were obtained, unfortunately we cannot verify this, as the model itself has not been sufficiently presented.

Unfortunately, the approaches presented in the literature are completely different and there is a lack of available data to evaluate and compare them. Therefore, an idea to create a new type of model for flowback fluid composition prediction was proposed and presented in this paper. The authors will make an attempt to contribute to the understanding of leaching method development.

A new approach to modeling flowback fluid composition prediction has been proposed. Research was carried out to describe the mechanism of flowback fluid production and composition generated during leaching of shale rock by fracturing fluid. The process was considered in a state of equilibrium due to the long residence time of fracturing fluid in the reservoir. Leaching course depends mainly on physical parameters like the heterogeneity of solids, size of particles, porosity, permeability and temperature of the process as well as pH, conductivity, total organic carbon (abr. TOC), time complexed reactions, redox potential and biological activity [38]. For shale leaching applying complexed fracturing fluids, a model complexity limiting approach needs to be applied. It was proposed to find a model based on rock properties which cannot be modified. Statistically significant parameters for leaching were identified as follows: pH, temperature, TOC and ionic strength [39,40,41], and the mentioned paramaters can be modified by changing the fracturing fluid composition. To make the model applicable, shale rock particles from drilling mud logging were prepared and used. Application of drill cuttings from mud logging can cause problems with sample preparation [42]. Nevertheless, at the same time, cross-sectional material from the fracturing process with no need for much expensive coring may come in handy. The proposed approach will allow other scientific groups and laboratories to evaluate the presented data and extend the presented considerations using samples from other different shale gas reservoirs. An overall conceptualization of data generation and processing is presented in Figure 2.

2. Materials and Methods

2.1. Shale Sample Acquisition

Samples of drill cuttings for further research were obtained from bentonite drilling mud. The samples come from the Baltic basin, in the Pomeranian area (Pomeranian voivodeship, Poland), from a depth of about 4.250 meters, taken along the entire length of the horizontal section (120 meters each).

2.2. Shale Sample Preparation

In order to remove the mud from the surface of the cuttings, cleaning of the tested material was carried out. For this purpose, the shale sample was sprinkled with a stream of water, next different sieves were used (sieve sizes: 2.362, 0.18, 0.088 mm). Samples were separated until the mud was completely removed. According to Carugo et al.’s [43] recommendations, a 2.362–0.18 mm size fraction was selected for further investigations. The higher fraction represents cuttings that could move from other parts of the well, or come from a damaged well walls, smaller drill cuttings were too small to perform further research due to their properties. After cleaning and sieving, the samples were dried at 40 °C for 24 h. The dried samples were ground in a vibratory ball mill to achieve a grain size below 0.088 mm, and then reduced by a flattened pile.

2.3. Shale Samples Analysis

Mineralogical characterization was realized using X-ray Diffraction (XRD) using a Miniflex 600 X-Ray diffractometer (Rigaku, Neu-Isenburg, Germany). The semi-quantitative mineral composition was calculated using Rietveld method, dedicated to rocks with high concentration of clay minerals. Elemental analysis was performed using an X-Ray fluorescence (XRF) spectrometer (S8 TIGER Wavelength Dispersive X-ray Fluorescence WDXRF, Bruker, Billerica, MA., USA). Total organic carbon was analyzed using a CHNS elemental analyzer (Flash, 2000; Thermo, Waltham, UK).

2.4. Preparation of Model Fracturing Fluids

In order to prepare model fracturing fluids, acetate (pH = 5), dihydrogen phosphate (pH = 7) and ammonium (pH = 9) buffers with appropriate acid-base ratios were used. The prepared fluid was buffered at 0.002 M. It results from the analysis of the components of fracturing fluids used in Polish deposits. Also, ionic strength and total organic carbon range is a result of calculations based on the compositions of these fracturing fluids. The ionic strength was controlled by the addition of potassium chloride and the organic carbon content added as propylene glycol.

2.5. Leaching Tests

Leaching tests were carried out according to OECD 106: Adsorption - Desorption method [42] using 10 g of a shale sample per 100 mL of “model fracturing fluid” (MFF) which is a laboratory composed model fluid to conduct leaching tests. Liquid/solid phase separation was preformed via centrifugation at 4000 rpm, vacuum filtration and final separation with 0.45 μm pore size polypropylene membranes. Leaching tests were conducted according to parameters presented in

Table 2. Parameters of “model fracturing fluids” (MFF) for leaching tests of shale samples.

No.	MFF	t (°C)	pH	IS (mol/L)	TOC (g/L)
		X1	X2	X3	X4
1	P1	60	9	0.51	0.06
2	P2	60	9	0.03	4.06
3	P3	60	5	0.51	4.06
4	P4	60	5	0.03	0.06
5	P5	80	9	0.51	4060
6	P6	80	9	0.03	0.06
7	P7	80	5	0.51	0.06
8	P8	80	5	0.03	4.06
9	P9	80	7	0.51	4.06
10	P10	60	7	0.03	0.06
11	P11	80	9	0.51	2.06
12	P12	60	5	0.03	2.06
13	P13	70	7	0.27	2.06
14	P13	70	7	0.27	2.06
15	P13	70	7	0.27	2.06

t—temperature of the experiment equal to assumed wellbore conditions, pH—pH of the MFF, IS—ionic strength of the MFF, TOC—total organic carbon of MFF.

which contains a summarized plan listing the following variables: temperature, pH, ionic strength and TOC.

For each of 10 rock samples 15 tests were performed—13 different fluids and two repetitions for fluid P13 (for the statistical approach) which is the average value of the range of the analyzed variables. The range of temperatures chosen for leaching tests is based on field data from service companies in Poland (i.e. BNK Petroleum, Camarillo, CA, USA) and corresponds with real temperatures in the depth of fractured horizontal sections of the well from Polish reservoirs with the highest gas production potential. Unfortunately, the tests presented are destructive to the core samples. Therefore, it is highly recommended to use shale cuttings which are cheaper and more available in comparison with core samples. Leachate compositions was analyzed by ICP-OES using an iCAP 6500 Duo spectrometer (Thermo, Waltham, UK). Data analysis and other calculations were performed using the RStudio Desktop (v. 1.0.143) software. Laboratory data obtained during analyses of liquids after leaching were grouped and entered into the program as descriptive variables. Temperature, ionic strength, pH, TOC and possible interactions between them as well as the results of rock analysis were variables. Then RStudio Desktop tools were used to compare different possible models, allowing the selection of the best one. A multistep linear regression was used to obtain the presented models. Only the models for which the coefficient of determination (abr. R²) was above 0.85 were taken into consideration, the probability value for all describing variables was below 0.05 (variable values are not random), so the confidence level was always above 0.95 (note: R² coefficients are calculated for obtained model equations not for the residual analysis diagrams). In the next step only those equations for which all separate levels of confidence for every separate parameter were above 0.95 were considered. Then the model with the highest determination coefficient was chosen for further analysis. For chosen model the standard deviation was always the lowest taking into account considered models and its value justifies the correctness of application of R² as a crucial parameter to choose the most adequate model. The residual analysis showed a sufficient number of describing variables (small inclination angle to the abscissa) and there was no correlation between residuals and described variables (Pearson between −0.5 and 0.5). The Pearson coefficients were calculated for the correlation between elements concentrations in leachates and the residuals of the model. The residuals were calculated as the difference between laboratory and model data values. The model was selected basing on the comparison of the standard model error, the determination coefficient, the level of significance and the number of parameters relevant to the correct description of the model. Other parameters presented in the next section were calculated using statistical and mathematical methods implemented in RStudio software [43].

3. Results and Discussion

Results of elemental and mineralogical analysis are presented in

Table 3. Results of elemental analysis of shale samples (A1 ÷ A10) using the XRF method.

No. of Sample	Element Concentration in the Shale Sample (CS) (ppm)									Aw (m2/g)	TOCS (%)
	B	Ba	Li	Mg	Mo	Rb	Si	Sr	Ca
A1	4050	821	139	18240	10	3372	247285	401	116287	15.17	2.11
A2	3988	593	149	14820	95	3570	278445	175	35020	16.15	0.84
A3	3325	708	97	19570	82	2542	229900	605	179117	12.77	2.41
A4	3637	967	112	15960	9	3469	241965	179	131634	10.24	2.43
A5	3467	1208	110	17670	97	2578	262200	178	114948	10.67	2.72
A6	3694	774	115	23560	97	3369	262105	262	100013	14.05	1.40
A7	3361	1119	88	26695	82	3280	248045	212	123188	14.61	1.61
A8	3918	1455	122	20805	106	3068	273505	178	68804	9.72	4.40
A9	3425	1395	120	19665	100	2777	277400	154	58916	13.29	1.81
A10	3513	842	119	18335	105	3358	282150	140	59019	12.62	1.77

Aw—internal area of shale sample, TOC_S—Total organic carbon in shale sample, B, Ba, Li, etc.—symbols of the indicated elements, CS_X—element X concentration in shale sample.

and

Table 4. Results of mineralogical analysis of shale samples (A1 ÷ A10) using the XRD method.

No. of Sample	Group of Minerals (%)
	G1	G2	G3	G4	G5
A1	21.50	11.95	9.13	15.24	42.19
A2	25.25	3.66	0.08	10.74	60.28
A3	18.10	37.19	0.12	20.83	23.75
A4	28.14	25.49	0.25	18.47	27.64
A5	25.94	27.60	0.12	23.84	22.50
A6	29.33	43.72	1.85	6.16	18.94
A7	19.61	46.83	0.24	8.82	24.50
A8	32.52	24.94	0.12	5.98	36.44
A9	46.16	20.36	0.88	9.31	23.29
A10	25.56	21.96	0.12	9.22	43.15

G1—sum of quartz, plagioclase (albite) and potassium feldspar (microcline, orthoclase), G2—sum of calcite and dolomite content, G3—sum of barite and pyrite content, G4—sum of chlorite, illite, montmorillonite and kaolinite content, G5—sum content of muscovite, biotite, paragonite and glauconite.

. In Table 3, only elements which provided data for creating models are presented.

A detailed mineralogical analysis is attached in the Appendix A (

Table A1. Detailed results of XRD analysis of shales samples.

No. Shale Sample	Mineral (%)
	Quarz	Alb	Micr	Ort	Calc	Dol	Pir	Bar	Chl	Ill	Mon	Kao	Mus	Bio	Par	Gla
A1	15.89	2.93	1.58	1.10	9.38	2.56	6.70	2.43	4.75	1.10	0.00	9.38	38.29	0.36	2.56	0.98
A2	21.58	1.83	1.10	0.74	2.93	0.74	0.00	0.08	7.19	0.74	0.00	2.81	57.48	1.58	0.61	0.61
A3	12.74	2.07	2.68	0.61	28.67	8.53	0.00	0.12	3.77	0.48	10.73	5.85	18.64	2.93	1.83	0.36
A4	19.58	3.10	5.08	0.37	21.52	3.97	0.00	0.25	7.81	8.80	0.00	1.86	2.61	22.81	1.11	1.11
A5	23.73	0.98	0.86	0.37	22.81	4.80	0.00	0.12	9.34	2.83	0.12	11.55	19.17	0.62	0.86	1.85
A6	22.57	3.44	2.59	0.74	13.05	30.67	1.73	0.12	4.06	1.73	0.00	0.37	13.29	0.24	3.32	2.09
A7	13.60	2.70	3.19	0.12	12.86	33.97	0.12	0.12	5.03	3.19	0.24	0.36	17.27	4.53	0.50	2.20
A8	25.66	4.16	2.08	0.62	8.44	16.50	0.00	0.12	4.88	0.74	0.00	0.36	33.76	0.48	1.72	0.48
A9	34.97	6.67	3.52	1.00	9.17	11.19	0.76	0.12	5.04	2.13	0.00	2.13	5.53	3.77	1.51	12.47
A10	21.81	2.18	1.09	0.48	9.82	12.13	0.12	0.00	7.52	0.48	0.00	1.21	41.45	0.36	0.97	0.36

Alb—albite, Micr—microclase, Ort—orthoclase, Calc—calcite, Dol—dolomite, Pir—pyrite, Bar-barite, Chl—chlorite, Ill—illite, Mon—montmorillonite, Kao—kalonite, Mus—muscovite, Bio—biotite, Par—paragonite, Gla—glaukonite

). The shale samples were tested for organic carbon content. When analyzing the results in Table 4, it can be assumed that the section of the well from which the A8 sample was taken is the most promising in terms of hydrocarbon production. Also, the TOC content for samples A1, A3, A4 and A5, which is above 2%, theoretically indicates that the hydrocarbon content in the test rock is sufficient for gas operation. However, this fact cannot be unambiguously conducted because no thermal maturity studies of organic matter have been carried out.

The analysis of the results of the mineralogical composition proves that the mineral structure of the rocks forming the gas-bearing slate form shows high heterogeneity in the single well’s circle. The distance between successive sections was only 120 meters, and the composition of the rocks from each of them is completely different, even for neighboring sections. During hydraulic fracturing, the operator should pay attention to the need to use different fracturing fluid compositions and parameters to obtain an effective gas flow. The big advantage of such a heterogeneity of the deposit in relation to the proposed model is the wide scope of the model’s application. The disadvantage is the poor estimation of impurities in the flowback fluid.

The content of minerals from the smectites group (montmorillonite) for samples A3 and A5 and A7 (Table A1 in the Appendix A) is respectively 10.73%, 0.12% and 0.24%, while for the remainder it is equal to 0%. This result means that the formation is heterogeneous on the scale of a single well. Most sections should be slightly susceptible to water. The content of carbonate minerals (which include calcite and dolomite) for the tested samples is in the range of 3.7–46.8%. Such a large variation indicates that the tested samples differ significantly in reactivity, which will certainly have an impact on the conducted leaching tests. The amount of quartz from the analyzed cuttings ranges from 13.6% to 35%. It can be deduced that in individual sections of the borehole, the formation will exhibit varied mechanical properties (diversification of brittleness). The content of other minerals is also very diverse, so the leaching process may proceed with different leaching efficiency for different rocks using the same model fracturing (leaching) fluids.

Differences in specific surface (which is actually the open surface as a result of grinding samples in vibratory mills) probably occur mainly due to differences in hardness and cleavage of the rock and random factors. The reference to the open area is necessary for the quantitative mathematical description of the model to be reliable. In selected cases, the surface may be negligible when the content of the component available through the open surface exceeds the solubility of this component in the fracturing fluid of a given composition and temperature.

The results of elemental analysis of leaching fluids and derived, as equations, models that describe correlation between concentrations of chosen elements (c_B, c_Ba, etc.) and variables. Residual analysis (difference between measured and calculated values) and maximum and minimum values calculated for the part of the model that can be influenced by controllable parameters of the fracturing fluid (c’_min (60), c’_min (80), c’_max (60), c’_max (80)) are presented in

Table 5. Results of leaching samples A1 to A10 rocks using fluids P1 to P13 for Boron (B).

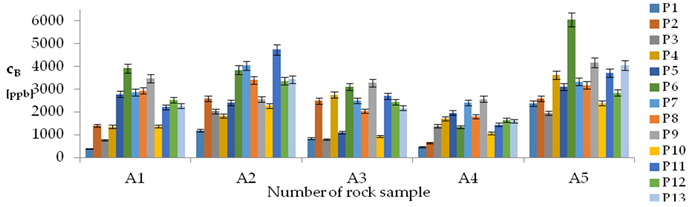
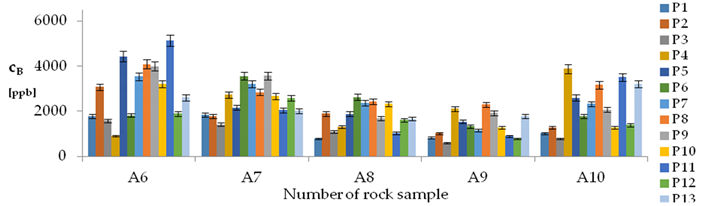
B concentration in samples after leaching of A1 to A10 rocks using fluids P1 to P13
Model
cB = −5155 + 35.6t − 549.7TOC − 74.7(TOC)2 − 341.7pH × IS + 25.5pH × TOC + 21.5t × IS + 9.3t × TOC − 211.6G1− 115.4G2 − 60.2G4 − 183.9G5 + 2.4CSB − 81CSMo + 0.06CSSi ± [286.4] c’B = −35.6t − 549.7TOC − 74.7 (TOC)2 − 341.7pH × IS + 25.5pH × TOC + 21.5t × IS + 9.3t × TOC
R2	0.90	Residual analysis
p	<0.000001
a	0.0888
α = arctan (a)	5.1°
Pearson	0.30
cmin (t = 60 °C)	1238 ppb
cmax (t = 60 °C)	1967 ppb
cmin (t = 80 °C)	2181 ppb
cmax (t = 80 °C)	3159 ppb

c_B—concentration of boron in leachates; r_A-residual in residual analysis; a—directional coefficient; arctan-arcus tangent which is equal to angle between regression line in residual analysis and 0x axis; Pearson-Pearson correlation coefficient for r_A and c_B; c’_min(t = 60 °C); c’_min(t = 80 °C); c’_max(t = 60 °C); c’_max(t = 80 °C)—explained before Table 5; CS_B, CS_Mo, CS_Si- B, Mo, Si concentrations in shale sample.

,

Table 6. Results of leaching samples A1 to A10 rocks using fluids P1 to P13 for Barium (Ba).

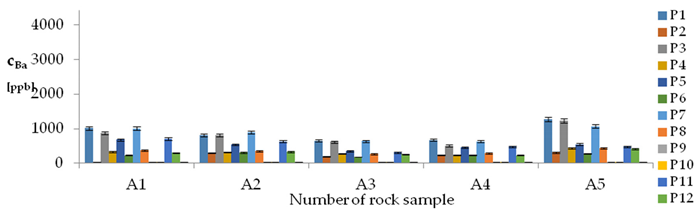
Ba concentrations in samples after leaching of A1 to A10 rocks using fluids P1 to P13
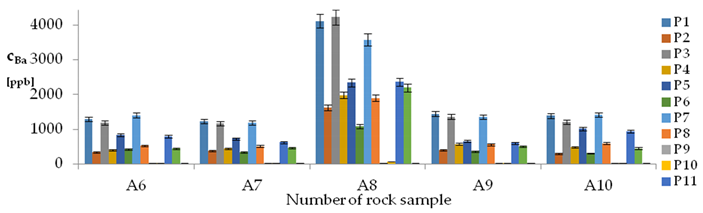Model
cBa = 1664 – 1792pH + 122pH2 + 43.8TOC2 + 157.7pH × IS − 3.14t × TOC − 48.73G2 − 118.41G3 − 271Aw − 0.44CSBa+ 34.44CSLi + 0.276CSMg + 0.00071CSCa ± [168] c’Ba = −1792pH + 122pH2 + 43.8TOC2 + 157.7pH × IS − 3.14t × TOC
R2	0.90	Residual analysis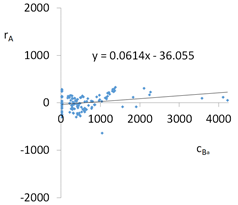
p	<0.000001
a	0.061
α = arctan (a)	3.5°
Pearson	0.28
c’min (t = 60 °C)	−6741
c’max (t = 60 °C)	−5524
c’min (t = 80 °C)	−6898
c’max (t = 80 °C)	−5527

c_Ba—concentration of barium in leachates; r_A—residual; a—directional coefficient, arctan-arcus tangent; Pearson-Pearson correlation coefficient for r_A and c_B; c’_min(t = 60 °C); c’_min(t = 80 °C); c’_max(t = 60 °C); c’_max(t = 80 °C)—explained before Table 5; CS_Ba, CS_Li, CS_Mg, CS_Ca-Ba, Li, Mg, Ca concentrations in shale sample.

,

Table 7. Results of leaching samples A1 to A10 rocks using fluids P1 to P13 for Strontium (Sr).

Sr concentration in samples after leaching of A1 to A10 rocks using fluids P1 to P13
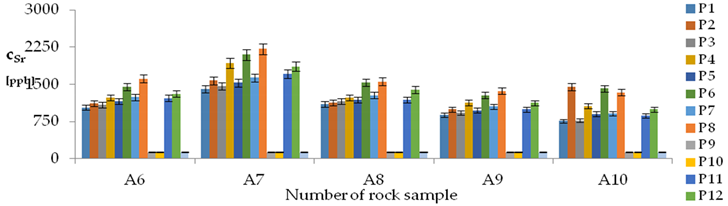Model
cSr = 11995 − 4001pH + 273.6pH2 + 12.1TOC2 + 2.2pH × t − 4.8pH × TOC − 7t × IS − 72.4IS × TOC + 40.2G2 + 25.6G5 + 129.1Aw + 1.11CSBa − 0.1CSMg − 0.005CSSi + 1.5CSSr ± [134.6] c’Sr = −4001pH + 273.6pH2 + 12.1TOC2 + 2.2pH × t − 4.8pH × TOC − 7t × IS − 72.4IS × TOC
R2	0.95	Residual analysis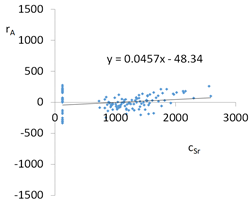
p	<0.000001
a	0.046
α = arctan (a)	2.6°
Pearson	0.24
c’min (t = 60 °C)	−13910 ppb
c’max (t = 60 °C)	−12700 ppb
c’min (t = 80 °C)	−13670 ppb
c’max (t = 80 °C)	−12310 ppb

c_Sr—concentration of strontium in leachates; r_A—residual; a-directional coefficient; arctan-arcus tangent; Pearson-Pearson correlation coefficient for r_A and c_B; c’_min(t = 60 °C); c’_min(t = 80 °C); c’_max (t = 60 °C); c’_max(t = 80 °C)—explained before Table 5; CS_Ba, CS_Li, CS_Mg, CS_Ca—Ba, Li, Mg, Ca concentrations in shale sample.

,

Table 8. Results of leaching samples A1 to A10 rocks using fluids P1 to P13 for Molybdenum (Mo).

Mo concentrations in samples after leaching of A1 to A10 rocks using fluids P1 to P13
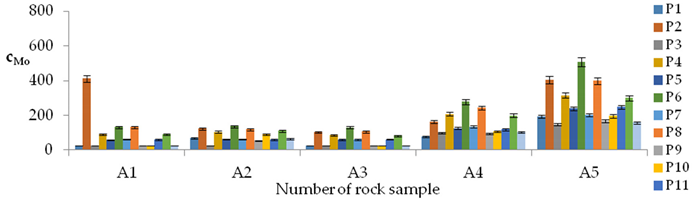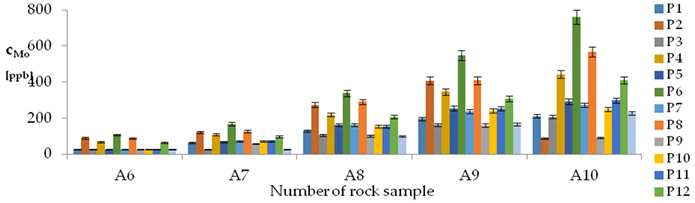Model
cMo = −1002.7 + 37.82t − 15576IS + 207.9TOC + 17.68pH2 − 4.05pH × t + 145.83pH × IS − 3.59t × TOC + 166.94IS × TOC + 3.82G4 + 2.41G5 − 0.38CSB + 10.19CSMo − 0.22CSSr ± [32.7] c’Mo = 37.82t − 15576IS + 207.9TOC + 17.68pH2 − 4.05pH × t + 145.83pH × IS − 3.59t × TOC + 166.94IS × TOC
R2	0.91	Residual analysis
p	<0.000001
a	0.069
α = arctan (a)	4.0°
Pearson	0.29
c’min (t = 60 °C)	1069
c’max (t = 60 °C)	1695
c’min (t = 80 °C)	1342
c’max (t = 80 °C)	1431

c_Mo-concentration of molybdenum in leachates; r_A—residual; a-directional coefficient; arctan-arcus tangent; Pearson-Pearson correlation coefficient for r_A and c_B; c’_min(t = 60 °C); c’_min(t = 80 °C); c’_max(t = 60 °C); c’_max(t =80 °C)—explained before Table 5; CS_B, CS_Mo, CS_Sr—Ba, Mo, Sr concentrations in shale sample.

,

Table 9. Results of leaching samples A1 to A10 rocks using fluids P1 to P13 for Rubidium (Rb).

Rb concentrations in samples after leaching of A1 to A10 rocks using fluids P1 to P13
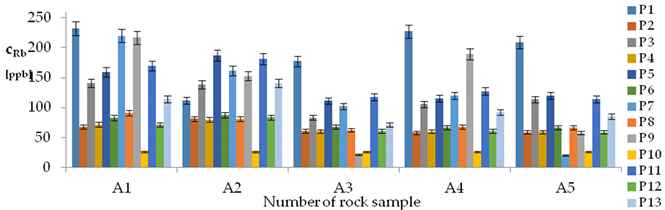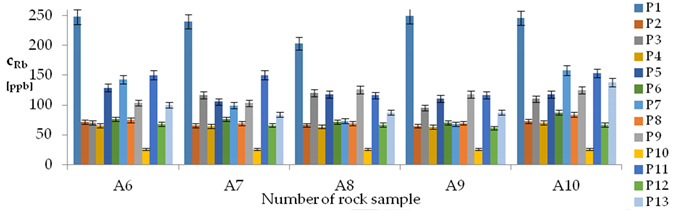Model
cRb = −77.42 + 1.05t + 462.79 IS + 27.92 pH × IS − 6.49t × IS − 21.88IS × TOC − 0.42G2 + 0.024CSRb ± [18.71] c’Rb = 1.05t + 462.79IS + 27.92pH × IS − 6.49t × IS − 21.88IS × TOC
R2	0.86	Residual analysis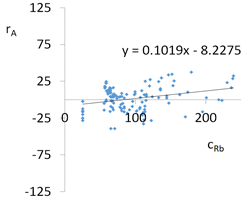
p	<0.000001
a	0.102
α = arctan (a)	5.8°
Pearson	0.31
c’min (t = 60 °C)	125.9
c’max (t = 60 °C)	227.5
c’min (t = 80 °C)	80.6
c’max (t = 80 °C)	182.2

c_Rb-concentration of rubidium in leachates; r_A—residual; a-directional coefficient; arctan-arcus tangent; Pearson-Pearson correlation coefficient for r_A and c_B; c’_min(t = 60 °C); c’_min(t = 80 °C); c’_max(t = 60 °C); c’_max(t = 80 °C)—explained before Table 5; CS_Rb,–Rb concentrations in shale sample.

,

Table 10. Results of leaching samples A1 to A10 rocks using fluids P1 to P13 for Lithium (Li).

Li concentrations in samples after leaching of A1 to A10 rocks using fluids P1 to P13
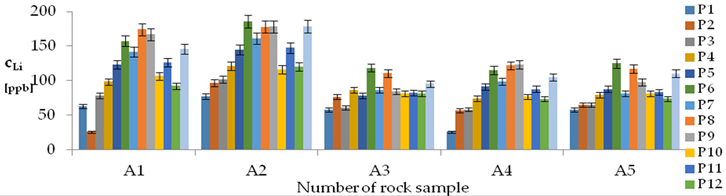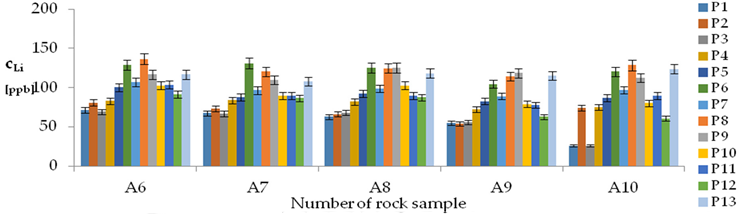Model
cLi = 500.56 + 78.85pH + 150.00IS − 7.51pH2 + 0.38pH × t − 2.50t × IS − 3.53IS × TOC − 3.03G1 + 1.23G4 − 1.73G5 + 0.41CSLi − 0.0019CSSi + 0.08CSSr − 0.0018CSCa ± [10.66] c’Li = 78.85pH + 150.00IS − 7.51pH2 + 0.38pH × t − 2.50t × IS − 3.53IS × TOC
R2	0.88	Residual analysis
p	<0.000001
a	0.082
α = arctan (a)	4.7
Pearson	0.27
c’min (t = 60 °C)	298.8
c’max (t = 60 °C)	343.6
c’min (t = 80 °C)	341.6
c’max (t = 80 °C)	371.4

c_Li-concentration of lithium in leachates; r_A—residual; a-directional coefficient; arctan-arcus tangent; Pearson-Pearson correlation coefficient for r_A and c_B; c’_min(t = 60 °C); c’_min(t = 80 °C); c’_max(t = 60 °C); c’_max(t = 80 °C)—explained before Table 5; CS_Li, CS_Si, CS_Sr, CS_Ca –Li, Si, Sr, Ca concentrations in shale sample.

,

Table 11. Results of leaching samples A1 to A10 rocks using fluids P1 to P13 for Calcium (Ca).

Ca concentrations in samples after leaching of A1 to A10 rocks using fluids P1 to P13
Model
cCa = 1000(3749.56 − 553.95pH − 52.84t + 799.88IS − 83TOC + 39.86TOC2 + 7.84pH × t − 322.63IS × TOC − 1.12G2 − 0.05CSBa − 0.09CSSr + 0.000553CSCa ± [27.07]) c’Ca = 1000(−553.95pH − 52.84t + 799.88IS − 83TOC + 39.86TOC2 + 7.84pH × t − 322.63IS × TOC)
R2	0.90	Residual analysis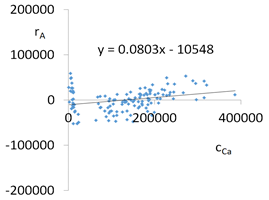
p	<0.000001
a	0.080
α = arctan (a)	4.6°
Pearson	0.29
c’min (t = 60 °C)	−3897280
c’max (t = 60 °C)	−3527670
c’min (t = 80 °C)	−3836130
c’max (t = 80 °C)	−3172780

c_Ca—concentration of calcium in leachates; r_A—residual; a-directional coefficient; arctan-arcus tangent; Pearson-Pearson correlation coefficient for r_A and c_B; c’_min(t = 60 °C); c’_min(t = 80 °C); c’_max(t = 60 °C); c’_max(t = 80 °C)—explained before Table 5; CS_Ba, CS_Ca, CS_Sr-Ba, Ca, Sr concentrations in shale sample.

,

Table 12. Results of leaching samples A1 to A10 rocks using fluids P1 to P13 for Magnesium (Mg).

Mg concentrations in samples after leaching of A1 to A10 rocks using fluids P1 to P13
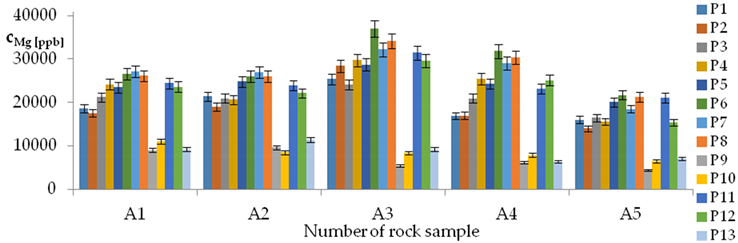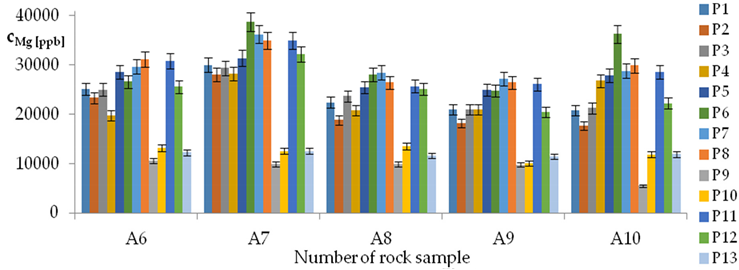Model
cMg = −16117 − 8518pH + 1756.39t − 21296IS + 35845TOC + 3511.7TOC2 + 30118pH × IS − 726.9t × TOC − 294G2 − 775G3 − 459Aw − 8.2CSBa + 1.6009CSMg − 0.1145CSSi ± [2311] cMg = −8518pH + 1756.39t − 21296IS + 35845TOC + 3511.7TOC2 + 30118pH × IS − 726.9t × TOC
R2	0.92	Residual analysis
p	<0.000001
a	0.079
α = arctan (a)	4.5°
Pearson	0.28
c’min (t = 60 °C)	26676
c’max (t = 60 °C)	57888
c’min (t = 80 °C)	30668
c’max (t = 80 °C)	92144

c_Mg—concentration of magnesium in leachates; r_A—residual; a-directional coefficient; arctan-arcus tangent; Pearson-Pearson correlation coefficient for r_A and c_B; c’_min(t = 60 °C); c’_min(t = 80 °C); c’_max(t = 60 °C); c’_max(t = 80 °C)—explained before Table 5; CS_Ba, CS_Mg, CS_Si-Ba, Mg, Si concentrations in shale sample.

and

Table 13. Results of leaching samples A1 to A10 rocks using fluids P1 to P13 for Silicon (Si).

Si concentrations in samples after leaching of A1 to A10 rocks using fluids P1 to P13
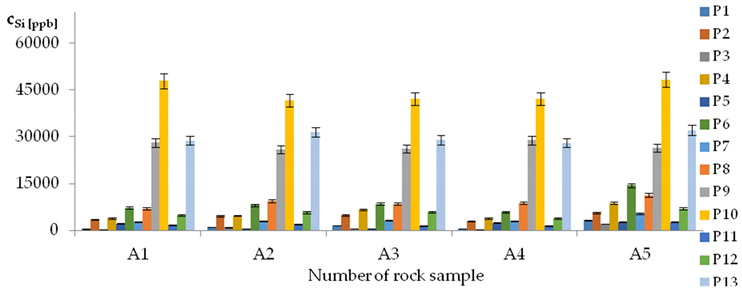Model
cSi = −298621 + 9229pH − 35067IS − 6556pH2 + 457TOC2 − 338pH × TOC + 324t × IS − 151.6G1 − 68G5 + 0.0555CSSi ± [2312] cSi = 92297pH − 35067IS − 6556pH2 + 457TOC2 − 338pH × TOC + 324t × IS
R2	0.96	Residual analysis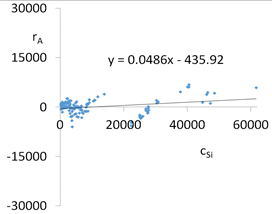
p	<0.000001
a	0.049
α = arctan (a)	2.8°
Pearson	0.30
c’min (t = 60 °C)	286589
c’max (t = 60 °C)	316728
c’min (t = 80 °C)	289889
c’max (t = 80 °C)	320028

c_Si—concentration of silicon in leachates; r_A-residual; a—directional coefficient; arctan-arcus tangent; Pearson-Pearson correlation coefficient for r_A and c_B; c’_min(t = 60 °C); c’_min(t = 80 °C); c’_max(t = 60 °C); c’_max(t = 80 °C)—explained before Table 5; CS_B, CS_Mo, CS_Sr –Ba, Mo, Sr concentrations in shale sample.

. Composition of shales and temperature in the borehole are parameters of a particular well, therefore, we can change: IS, TOC and pH (by changing the fracturing fluid composition) so c’_B, is a part of the whole c equation which can be manipulated and is used to calculate the possible range of changeability of the model by fracturing fluid parameter manipulations. The values of c’_min and c’_max were calculated for two extreme temperature values. It was calculated that the minimum and maximum values for all models are equal to 60 or 80 °C (minimum and maximum temperature). The differences between these values are presented in

Table 14. Possible range of selected elements decreased in flowback fluid.

Model	Concentration Operating Range (ppb)		Analysed Concentration Range in MFF (ppb)
	60 °C	80 °C	min	max
B	729	978	371	6044
Ba	1217	1371	25	4219
Sr	1210	1360	125	2687
Mo	626	89	25	760
Rb	101.6	101.6	25	249
Li	44.8	29.8	25	186
Ca	369608	663354	130	417450
Mg	31212	61476	4316	38782
Si	30139	30139	250	64153

. These results indicate how much the concentration of the element in the flowback fluid can be reduced by proper control of the parameters of the fracturing fluid according to the developed models. Due to the statistical nature of the model, in some cases lowering the concentration could give a negative value. This should be taken into account when using and possibly implementing the model using a computer tool. Model fracturing fluids are characterized in Table 14.

To derive general equations, the entire available data set for fluid variables as well as rocks was analyzed. Nine general equations describing the shale rock leaching with model fracturing fluids were obtained. For all equations, the determination coefficient values are in the range from 0.86 to 0.96. This means that the presented model matches are of high significance.

It was assumed that correctly performed regression allows to obtain a graph of residues from real values in the form of points approximately arranged on both sides of a straight line parallel to the abscissa, which represents the actual values. As an approximation, a straight line with the inclination angle of less than 22.5° was drawn, since the position of the points on both sides of the line inclined to abscissa at an angle of 45° means that a sufficient number of variables were not included in the description of the model.

Pearson correlation coefficients between laboratory data and residuals (difference between laboratory and model data) were lower than 0.5 (and higher than 0.5), which means that residuals are poorly correlated with the result. Residual analysis gives information that the applied variables describe the model in the tested range well enough and sufficiently. Moreover, no correlation occurrence between residuals and measured values means that there are probably no methodological errors.

For the obtained models it was calculated that appropriate control of the fracturing fluid parameters can significantly reduce the amount of leached contaminants (Table 14). The maximum value of possible changes in fixed temperature was named Concentration Operating Range (abr. COR). Concentration range (min/max) in MFF (min/max) are given as minimum and maximum values of components concentrations in analysed fluids after leaching tests. For boron, the possibility of lowering the concentration in flowback fluid is over 10 to almost 15% at 80 °C, while for lithium it is from 16 to 24% and for barium over 25%. Considerably greater COR was calculated for strontium, rubidium and silica, about 50%, for calcium and magnesium, so it is theoretically possible to select the parameters of the fluid giving no leaching of a given element. The biggest dependence on temperature was observed for molybdenum where at 60 °C the concentration could be increased by about 10% whereas at 80 °C by 80%. This is a direct argument that such a model development approach is justified and has a potential for practical use. Similar research needs to be continued and more advanced models should be developed according to scheme presented in Figure 3. Such models using data from many different reservoirs, evaluated and improved using field data, could have important impact on designing the flowback treatment technologies immediately after drilling. However using only fast and easy procedures of rock analysis is crucial for this approach.

4. Conclusions

The results of mineralogical and elemental analysis as well as the determination of organic carbon in the studied shale rock samples from various sections of the horizontal section of the exploration well, indicate high heterogeneity of the deposit at a macroscopic scale. A high divergence in the composition made it possible to make a model with a wide range of applications. Unfortunately, in the shale systems, a high heterogeneity of the mineral and elemental composition along the created fractures may occur. This can strongly limit the presented and other models and always has to be considered before its application as a developed industry tool. Nevertheless, using cross-sectional samples from whole fractured parts of the wellbore deliver the most technical/economical possible approximations of the shale composition in a chosen part of the reservoir.

For the model, fracturing fluid-shale rock, mathematical relationships based on T, ionic strength, TOC, pH of fracturing fluid and elemental composition, mineralogical composition, and surface area of shale rock were derived. This approach allows one to predict the concentration of selected metals in a wide range of variables. Nine equations were obtained, the coefficient of determination over 0.85 was obtained for the whole set with confidence level above 0.99. For chosen model the standard deviation was always the lowest among other taken into consideration and its value justifies the correctness of application of R² as a crucial parameter to choose most adequate model. Residual analysis gives information that applied variables describes the model in the tested range well enough. Moreover, no correlation between residuals and measured values means that there are probably no methodological errors. Selected parameters of the model fracturing fluid and rock properties are sufficient to predict the composition of the flowback fluid in the laboratory system. In the next research other shale rock samples should be tested and data from analysis of flowback fluid for attempts to develop industrial version of the model need to be carried.

Unfortunately, a comparison with other models in the literature is not possible due to unnormalized character off the data and a lack of model description from other sources. However, the presented paper may become a significant contribution in the modelling development approach in the shales leaching systems. Test results can be a good basis for developing a commercial tool for predicting the treatment fluid at the design stage of hydraulic fracturing.