Controllability Evaluation of EV Charging Infrastructure Transformed from Gas Stations in Distribution Networks with Renewables
Abstract
:1. Introduction
- The mapping relation between gas stations and EV charging stations is proposed to estimate the distribution of EV charging load in the power network, by using the online accessible data from E-map and service website of the facilities. These features render the proposed charging station model more realistic and accurate than the existing models, in which mobility statistics for vehicles in a certain area is adopted in the charging load computation.
- A novel operational model of EV charging stations is formulated by using membership function between EVs and parking places and queuing theory. The arrival and parking behavior of EVs are captured from the online data and used for estimating the 24-hour electric power demand. So far, there is no reported work that examines how the operation of an EV charging station can be modeled as a function of input parameters and control variables integrated into the optimal dispatch of the power system. In the proposed modeling of EV charging stations, the parameters and boundaries of control variables are calculated for the reliability constrained optimal dispatch of the distribution network.
- The optimal control of EV charging stations is devised under the typical V2G control framework, where the EV aggregator performs as the intermediate controller for EVs at each charging station. The optimal dispatch problem is composed of both EV charging station configuration and EV charging power regulation. The optimal setting of the EV charging station and the optimal charging plan of each individual EV are given by the optimal dispatch. A two-stage hybrid algorithm is developed to reduce the complexity of the optimization that evaluates the controllability of the charging stations in the oil-to-electricity transformation.
2. Modeling of EV Charging Stations Transformed from Gas Stations
2.1. Oil-To-Electricity Transformation with Membership Function between EVs and Parking Lots
2.2. Operation of EV Charging Stations Based on Queuing Theory and Accessible E-Map Database
2.3. Parameter Configuration of EV Charging Facilities
2.4. Mathematical Formulation of EV Charging Load and Controllable EV Charging Variables
3. Coordinated Integration of EV Charging Stations into the Electric Distribution Grid
3.1. Objective Function of the Optimal Control Strategy
3.2. Constraints of EV Charging Optimization
4. Two-Stage Hybrid Optimization Algorithm
4.1. Solution Procedure for Optimal Integration of EV Charging Stations into the Power Grid
4.2. Two-Stage Hybrid Optimization Algorithm
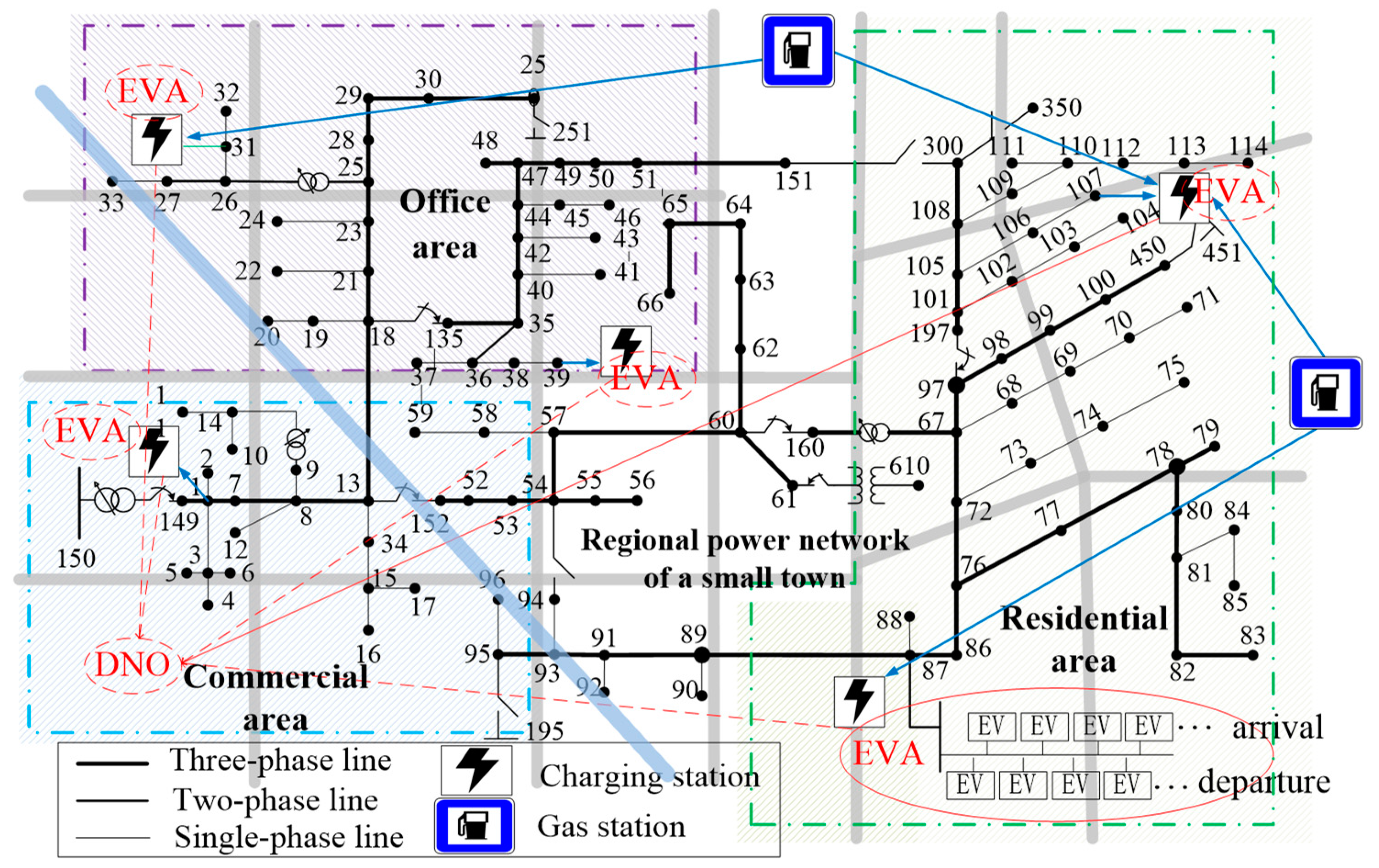
5. Simulation Results of the EV Charging Station in Oil-To-Electricity Transformation
5.1. Case Study
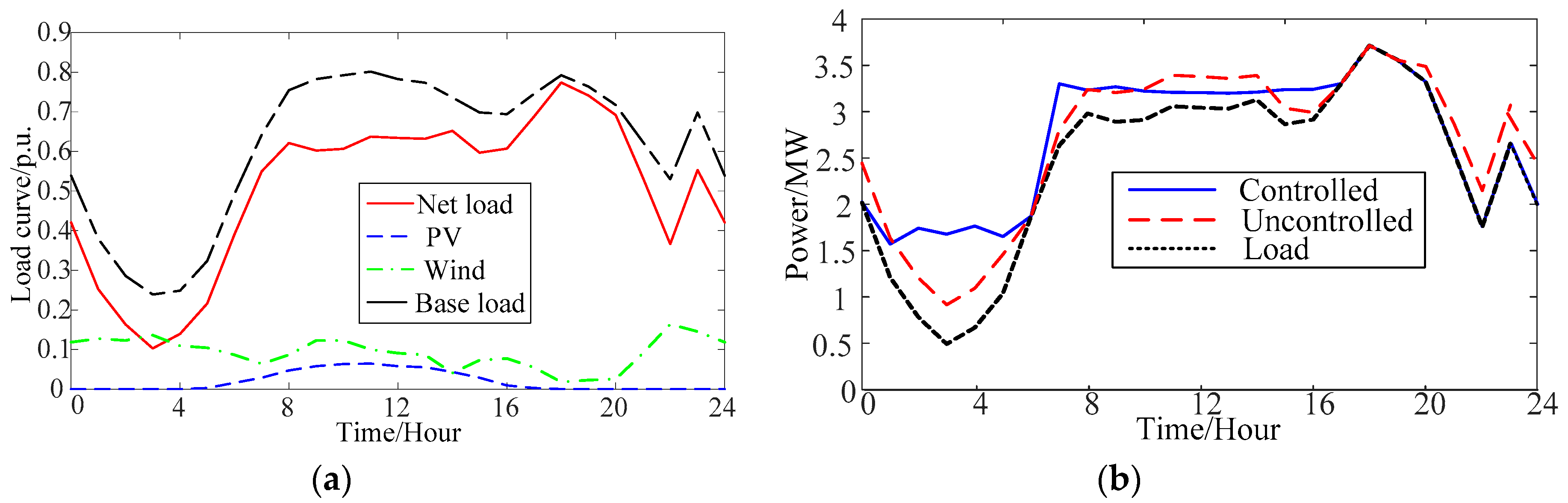
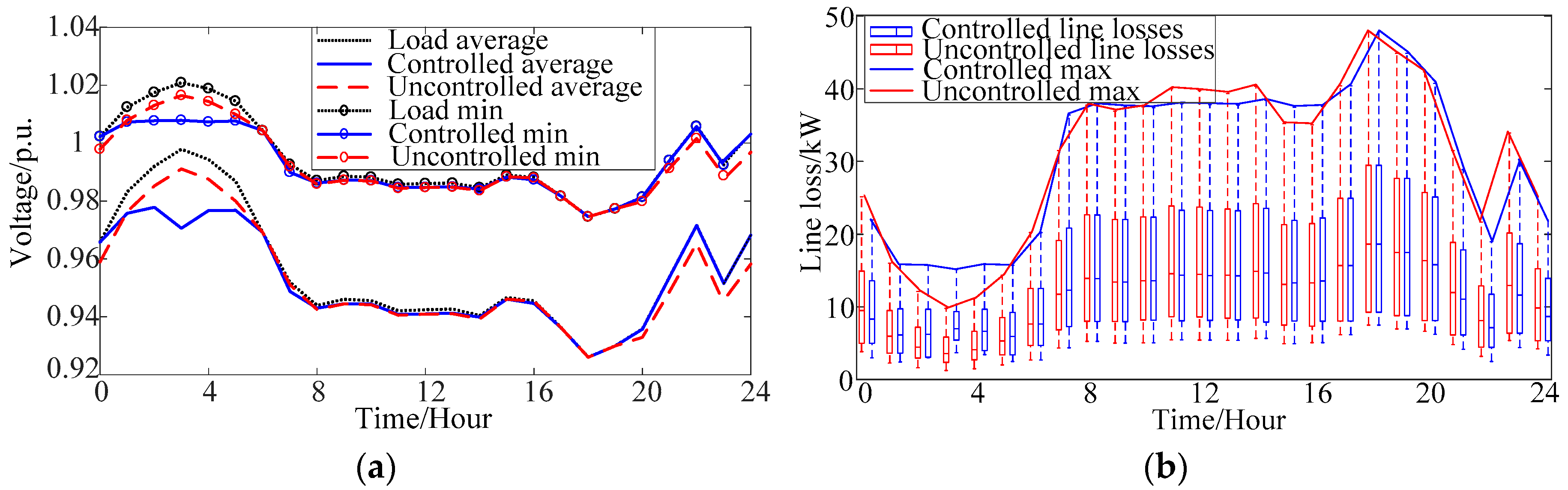
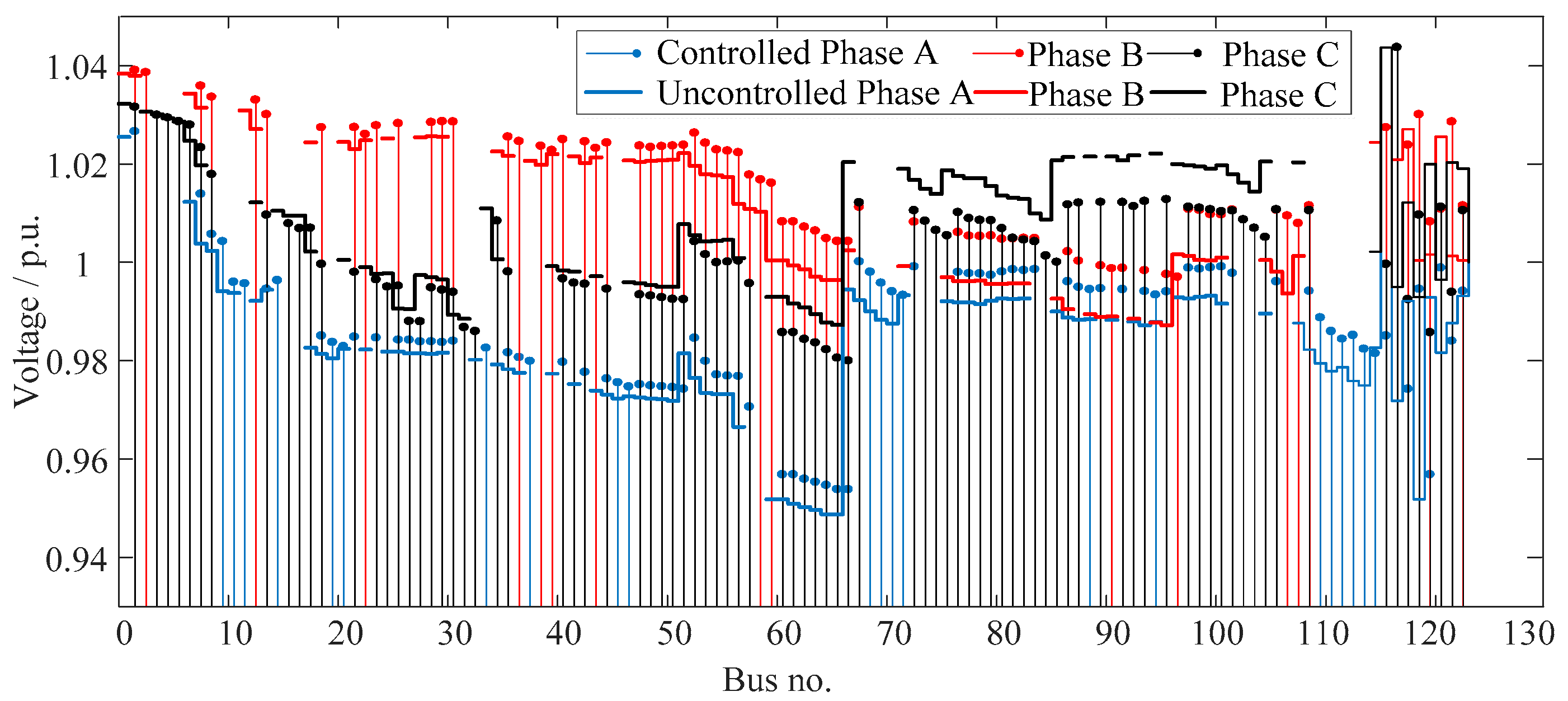
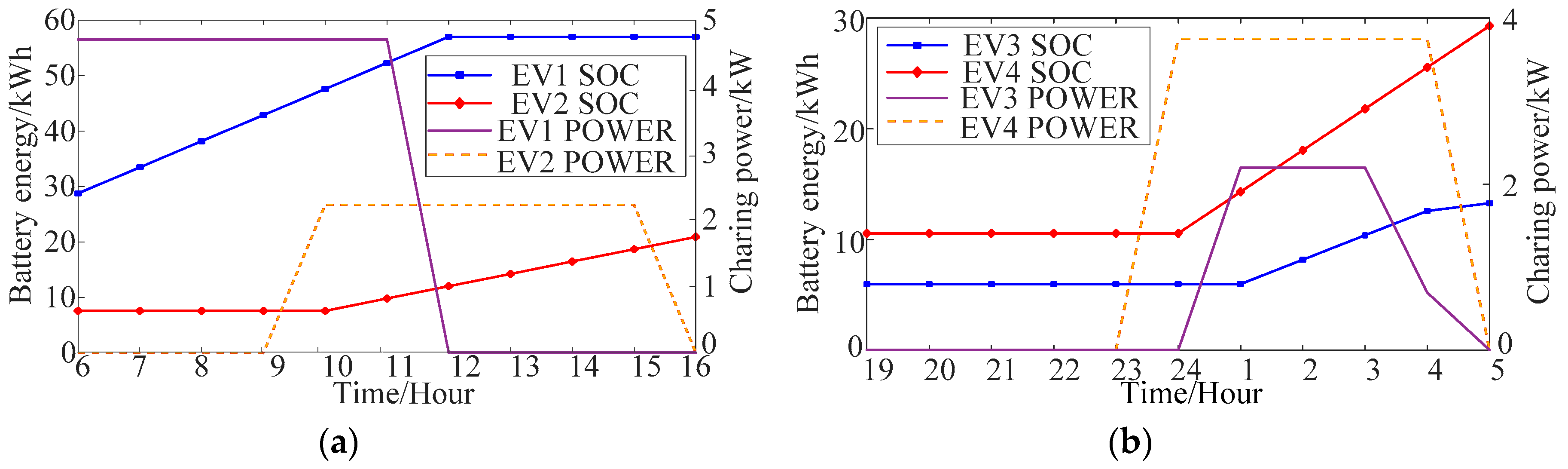
5.2. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Detailed Modeling of Parking Lots Based on Queuing Theory
References
- Tang, W.; Bi, S.; Zhang, Y.J. Online charging scheduling algorithms of electric vehicles in smart grid: An overview. IEEE Commun. Mag. 2016, 54, 76–83. [Google Scholar] [CrossRef]
- Bloomberg New Energy Finance. Electric Vehicle Outlook 2017. July 2017. Available online: https://data.bloomberglp.com/bnef/ (accessed on 10 March 2019).
- Farid, A.M. A hybrid dynamic system model for multimodal transportation electrification. IEEE Trans. Control Syst. Technol. 2017, 25, 940–951. [Google Scholar] [CrossRef]
- Farzin, H.; Moeini-Aghtaie, M.; Fotuhi-Firuzabad, M. Reliability studies of distribution systems integrated with electric vehicles under battery-exchange mode. IEEE Trans. Power Deliv. 2016, 31, 2473–2482. [Google Scholar] [CrossRef]
- Ying, Z.M.; Wu, X.; Yang, W. Carbon emission benefit accounting of Hangzhou bus oil-to-electricity project. Acta Ecol. Sin. 2018, 38, 6452–6464. [Google Scholar]
- Krishna, K.M.; Pandey, N.K.; Thimmalapura, S. Break-even analysis and economic viability of powertrain electrification—An analytical approach. In Proceedings of the IEEE Transportation Electrification Conference, Pune, India, 13–15 December 2017. [Google Scholar]
- Shaaban, M.F.; Atwa, Y.M.; El-Saadany, E.F. PEVs modeling and impacts mitigation in distribution networks. IEEE Trans. Power Syst. 2013, 28, 1122–1131. [Google Scholar] [CrossRef]
- Shojaabadi, S.; Abapour, S.; Abapour, M. Optimal planning of plut-in hybrid electric vehicle charging station in distribution network considering demand response programs and uncertainties. IET Gener. Trans. Distrib. 2016, 10, 3330–33340. [Google Scholar] [CrossRef]
- Gong, Q.; Midlam-Mohler, S.; Serra, E.; Marano, V. PEV charging control for a parking lot based on queuing theory. In Proceedings of the American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 1124–1129. [Google Scholar]
- Chukwu, U.C.; Mahajan, S.M. V2G parking lot with PV rooftop for capacity enhancement of a distribution system. IEEE Trans. Sustain. Energy 2014, 5, 119–127. [Google Scholar] [CrossRef]
- Bae, S.; Kwasinski, A. Spatial and temporal model of electric vehicle charging demand. IEEE Trans. Smart Grid 2012, 3, 3394–3403. [Google Scholar]
- Albarbi, W.; Bhattacharya, K. Electric vehicle charging facility as a smart energy microhub. IEEE Trans. Sustain. Energy 2017, 8, 616–628. [Google Scholar]
- Ko, K.S.; Han, S.; Sung, D.K. Performance-Based settlement of frequency regulation for electric vehicle aggregators. IEEE Trans. Smart Grid 2018, 9, 866–875. [Google Scholar] [CrossRef]
- Wenzel, G.; Negrete-Pincetic, M.; Olivares, D.E. Real-Time charging strategies for an electric vehicle aggregator to provide ancillary services. IEEE Trans. Smart Grid 2018, 9, 5141–5151. [Google Scholar] [CrossRef]
- Vagropoulos, S.I.; Balaskas, G.A.; Bakirtzis, A.G. An investigation of plug-In electric vehicle charging impact on power systems scheduling and energy costs. IEEE Trans. Power Syst. 2017, 32, 1902–1912. [Google Scholar] [CrossRef]
- DeForest, N.; MacDonald, J.S.; Black, D.R. Day ahead optimization of an electric vehicle fleet providing ancillary services in the Los Angeles Air Force Base vehicle-to-grid demonstration. Appl. Energy 2018, 210, 987–1001. [Google Scholar] [CrossRef]
- Bessa, R.J.; Matos, M.A. Optimization models for EV aggregator participation in a manual reserve market. IEEE Trans. Power Syst. 2013, 28, 3085–3095. [Google Scholar] [CrossRef]
- Wei, W.; Liu, F.; Mei, S. Charging strategies of EV aggregator under renewable generation and congestion: A normalized Nash equilibrium approach. IEEE Trans. Smart Grid 2016, 7, 1630–1641. [Google Scholar] [CrossRef]
- Shafie-khah, M.; Heydarian-Forushani, E.; Golshan, M.E.H. Optimal trading of plug-in electric vehicle aggregation agents in a market environment for sustainability. Appl. Energy 2016, 162, 601–612. [Google Scholar] [CrossRef]
- Ko, K.S.; Sung, D.K. The effect of EV aggregators with time-varying delays on the stability of a load frequency control system. IEEE Trans. Power Syst. 2018, 33, 669–680. [Google Scholar] [CrossRef]
- Li, W.J.; Tan, X.; Sun, B. Optimal power dispatch of a centralised electric vehicle battery charging station with renewables. IET Commun. 2018, 12, 579–585. [Google Scholar]
- Perez-Diaz, A.; Gerding, E.; McGroarty, F. Coordination and payment mechanisms for electric vehicle aggregators. Appl. Energy 2018, 212, 185–195. [Google Scholar] [CrossRef]
- Floch, C.L.; Kara, E.C.; Moura, S. PDE modeling and control of electric vehicle fleets for ancillary services: A discrete charging case. IEEE Trans. Smart Grid 2018, 9, 573–581. [Google Scholar] [CrossRef]
- Liu, Z.; Wen, F.; Ledwich, G. Optimal planning of electric-vehicle changing stations in distribution systems. IEEE Trans. Power Deliv. 2013, 28, 102–110. [Google Scholar] [CrossRef]
- Mosadeghy, M.; Yan, R.; Saha, T.K. A time-dependent approach to evaluate capacity value of wind and solar PV generation. IEEE Trans. Sustain. Energy 2016, 7, 129–138. [Google Scholar] [CrossRef]




| EV Type | Charging Power (kW) | Battery Capacity (kWh) | Target Stage of Charge (SOC) (%) | No. of EVs | Distance per Charge (km) | |
|---|---|---|---|---|---|---|
| Fast Charging | I: Tesla Model X | 13 | 60 | 90–95 | 60 | 355 |
| II: BMW i3 | 44 | 22 | 90–95 | 60 | 160 | |
| Slow Charging | III: Chevrolet VOLT | 2.2 | 13.2 | 90–95 | 150 | 80 |
| IV: Changan EADO | 3.75 | 30 | 90–95 | 150 | 200 |
| Bus no./ Type of Parking | Phase | Power Level of Charging Station | Ratio of Charging Station Capacities | EV Types | Ratio of EV Types (%) |
|---|---|---|---|---|---|
| 1/Complex | A | Fast + Slow charging | 33% | I/II/III/IV | 14/14/36/36 |
| 31/Office | C | Fast charging | 13% | I/II | 50/50 |
| 39/Office | B | Fast charging | 38% | I/II | 50/50 |
| 87/Home | B | Slow charging | 6% | III/IV | 50/50 |
| 107/Home | B | Slow charging | 10% | III/IV | 50/50 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, S.; Wu, J.; Xu, B. Controllability Evaluation of EV Charging Infrastructure Transformed from Gas Stations in Distribution Networks with Renewables. Energies 2019, 12, 1577. https://doi.org/10.3390/en12081577
Gao S, Wu J, Xu B. Controllability Evaluation of EV Charging Infrastructure Transformed from Gas Stations in Distribution Networks with Renewables. Energies. 2019; 12(8):1577. https://doi.org/10.3390/en12081577
Chicago/Turabian StyleGao, Shuang, Jianzhong Wu, and Bin Xu. 2019. "Controllability Evaluation of EV Charging Infrastructure Transformed from Gas Stations in Distribution Networks with Renewables" Energies 12, no. 8: 1577. https://doi.org/10.3390/en12081577
APA StyleGao, S., Wu, J., & Xu, B. (2019). Controllability Evaluation of EV Charging Infrastructure Transformed from Gas Stations in Distribution Networks with Renewables. Energies, 12(8), 1577. https://doi.org/10.3390/en12081577




