Real-Time Implementation of a Super Twisting Algorithm for PEM Fuel Cell Power System

Abstract

Proton exchange membrane fuel cell (PEMFC) topology is becoming one of the most reliable and promising alternative resource of energy for a wide range of applications. However, efficiency improvement and lifespan extension are needed to overcome the limited market of fuel cell technologies. In this paper, an efficient approach based on a super-twising algorithm (STA) is proposed for the PEMFC system. The control objective is to lengthen the fuel cell lifetime by improving its power quality, as well as to keep the system operating at an optimal and efficient power point. The algorithm adjusts the PEMFC operating point to the optimum power by tuning the duty cycle of the boost converter. The closed-loop system includes the Heliocentris hy-Expert^TM PEMFC, DC–DC boost converter, DSPACE DS1104, dedicated PC, and a programmable electronic load. The practical implementation of the proposed STA on a hardware setup is performed using a dSPACE real-time digital control platform. The data acquisition and the control system are conducted together with the dSPACE 1104 controller board. To demonstrate the performance of the proposed algorithm, experimental results are compared with 1-order sliding mode control (SMC) under different load resistance. The obtained results demonstrate the validity of the proposed control scheme by ensuring at least 72% of the maximum power produced by PEMFC. In addition, it is proven that the STA ensures all the fundamental properties of the 1-order SMC, as well as providing chattering reduction of 91%, which will ameliorate as a consequence the fuel cell lifetime.

1. Introduction

At present, the entire world is becoming aware of the problems derived from traditional energies such as fossil fuels and non-renewable energies which have destructive environmental impacts. On the other hand, the ever-increasing energy demand and rising crude oil prices, as well as predictable expiration of fossil fuels reserves, have also caused high ambitions toward renewable and sustainable energy resources. In this context, renewable energy sources (RES) such as wind and solar are considered as suitable and viable alternative options to generate electrical power [1,2,3,4,5]. However, despite the environmental friendly features of these energies, their dependency on the weather conditions is still a considerable obstacle. Thus, the solar energy is lower in winter months and cloudy days below, as it is only available during the daytime. On the other hand, the wind energy is only available when the wind blows.

Due to its low amount of contamination, its abundance on the Earth’s surface, as well as its high volatility and efficiency, hydrogen has been chosen as the most suitable alternative fuel to traditional fossil fuels. It could replace fossil fuels in the automotive sector (with properly modification in the motor), or also could be used with oxygen in fuel cells to produce electricity. Thereby, proton exchange membrane fuel cells (PEMFCs), which have hydrogen as fuel, are considered as some of the most reliable and promising energy conversion devices. They can provide a continuous power supply throughout all seasons as long as fuel is provided. Moreover, unlike internal combustion engines, fuel cells are not combusted, the energy instead is produced through a chemical reaction. This results in several benefits such as high efficiency, low maintenance, and quiet operation. Thus, for the same quantity of fuel, fuel cells can extract 90% more efficient power than traditional gasoline. Fuel cells are also very simple in maintenance since they have no moving parts in their construction. In addition, the absence of mechanical parts in their composition allows them to operate silently. PEMFCs have many advantages not only when compared with traditional fossil fuels, but also even when compared with other types of cells. They are characterized by their low operating temperature, fast electrochemical reaction (quick start up), low cost, which is a very important point, long cycle life and their high power density [6,7,8]. Therefore, PEMFCs are ideally suited for a wide range of applications, such as stationary, automotive, and portable power supplies. However, despite the sundry features of the PEMFCs, cost reduction and efficiency improvement are needed to overcome the limited market of fuel cells’ technologies [9,10]. The high cost of PEMFCs may have been the fundamental hindrance in the past, but with the development of technology, this may have not been the case. Therefore, it is necessary to overcome other specific barriers such as: low efficiency with output ripple current, low output voltage that decreases as the load current increases and limited overload capability. To overcome these specific challenges, power converters with a control strategy are usually required to step up and regulate the output voltage to provide an appropriate DC power source that may be used for various applications [11,12,13,14,15].

To date, over 800 different topologies of DC–DC converters have been developed [16]. The advantages and disadvantages of each topology are discussed in [16,17,18]. They can be used to transform the power with boosting or bucking the output voltage, which is controlled by the pulse width modulation (PWM) switching technique. Due to their higher efficiency in comparison with other converters’ topologies, buck, boost and back boost converters have been chosen as the most commonly used in a wide range of applications. These converters are characterized by a few component counts, which results in a reduction in the conduction losses. In this work, due to the low voltage of the PEMFCs, a DC–DC boost converter is used to step-up and regulate the generated DC voltage. In addition, in order to improve and optimise the dynamic response and efficiency of the overall system, a reliable digital controller that ensures stability is used to control the PWM generator, which feeds the DC–DC converter [9,11].

During the last few decades, many control strategies are proposed for PEM fuel cell power systems. Traditional controllers such as proportional-integral (PI) and proportional-integral derivative (PID) control are widely used in the literature. Thus, Choe [19] used PID control for a DC–DC boost converter with a fuel cell dynamic model. Andujar [20] used a small signal model with a linearized PEMFC model for controlling the DC–DC converter, given that the parameters of the controller should be changed for any variation in the operating conditions. Authors of [21] used a PI control to keep the PEMFC working in an efficient power point. In [22], Habib developed a genetic algorithm (GA) based on a linear quadratic regulator (LQR) to regulate the PEMFC terminal voltage. Obtained results show that chattering reduction of 84% could be achieved using the proposed algorithm. However, the linear control of DC–DC converter is not suitable for PEMFC application. To overcome this issue, many robust control approaches have been developed to cope with nonlinearity and ensure stability. In [23], Huang demonstrated experimentally that the efficiency of the fuel cell can be improved from $14.67\%$ when using a conventional PID controller to $37\%$ when using a fuzzy controller. However, some oscillations are accrued in the electrical characteristics, which may cause serious life-shortening and severe cell deterioration. In [24], chattering reduction of $70.93$% is achieved using an advanced variable step-size fuzzy logic control (FLC). Kim [25] and Samosir [26] used a dynamic evolution control (DEC) to achieve an accurate duty cycle control for energy storage in a hybrid fuel cell system. A comprehensive study of SMC implementation in a PEMFC power system is addressed in [27]. The control process is performed using first order SMC, which applied to a DC–DC buck converter in order to ensure low and stable output voltage. Several platforms of the $H\infty$ controller for the PEMFC are investigated in [28]. Wang concluded that an efficiency improvement of $1.4$% and a reduction of 93% in the root-mean-square error (RMSE) of the PEMFC voltage could be obtained. In addition, he concluded that this controller can be implemented on different modules without any modification taking into account that the resulting controller is only optimal in the predefined cost function and its performance in other aspects is not guaranteed. Rezazadeh [29] designed an adaptive inverse controller, known as radial basis function neural network (RBFNN), for the PEMFC system. This control scheme did not require any parameter identification of the system, which means that the needed experimental data for the control design can be reduced. In [30], to obtain an accurate controller, feedback linearization control applied to a PEMFC power system was optimized via a non-dominated sorting genetic algorithm II (NSGA-II). The optimization process was performed on the linear gains of the designed controller. Recently, authors of [31] have developed a super-twisting algorithm (STA) in order to optimize the produced power of the PEMFC. According to their results, the simplicity of the control scheme, robustness and high accuracy can be highlighted even with the presence of model uncertainties and large load variations. However, despite the good results obtained in [29,30,31] for PEMFC improvement, only simulation studies have been presented.

This paper is focused on validation of a previous study which was presented in [31]. The main aim of this work is to validate the performance of the STA applied to a DC–DC boost converter in order to keep the PEMFC operating at an efficient power point. This last aim is currently the least studied aspect of control of fuel cells, but also one of its most important issues. Therefore, in order to address this issue, a hardware system is realized with a FC50 fuel cell stack, DC–DC boost converter, and dSPACE real-time digital control platform. The data acquisition and the control system are conducted all around the dSPACE 1104 controller board environment.

This work has been organized as follows: the PEMFC model has been reviewed in Section 2. In Section 3, the power electronic interface has been presented. A description of the experimental system has been described in Section 4. Section 5 presents the experimental results obtained with a FC50 fuel cell stack. Finally, some conclusions have been pointed out in Section 6.

2. PEMFC Modeling and Analysis

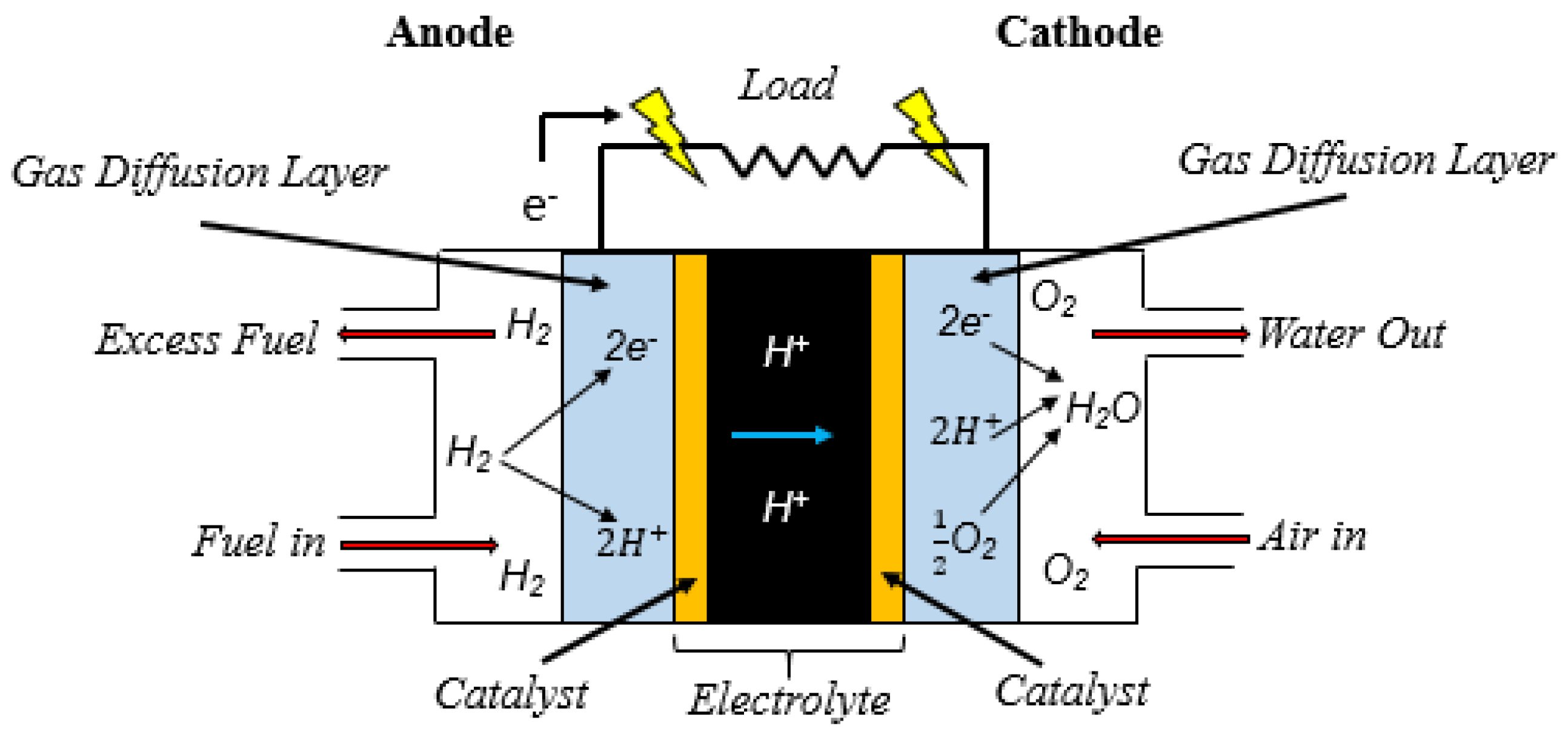
A PEMFC is used as a power supply source for a fuel cell power system. It is an electrochemical device that combines chemical energy to produce electricity, as well as water and heat as its by-product. A PEMFC uses air or pure oxygen ($O_2$) as the oxidant and hydrogen ($H_2$) as the fuel gas. Figure 1 shows a schematic diagram of the PEMFC, which consists of an electrolyte membrane placed between two electrodes (anode and cathode) that are coated with the platinum catalyst [32,33,34]. The electrolyte membrane plays a key role; it allows only the appropriate ions ($H^{+}$) to flow between the anode and cathode. The $H_2$ gas, extracted using a reformer from the hydrocarbon fuel ($C_n{H}_{2n+2}$), is supplied at the anode. Air, a source of $O_2$, is supplied at the cathode. At the anode, in the presence of platinum catalyst, $H_2$ is ionized into positively charged hydrogen ions ($H^{+}$) and negatively charged electrons ($e^{-}$). Then, $H^{+}$ move towards the cathode through the electrolyte membrane, while $e^{-}$ flow to the cathode via the external circuit to provide electricity along the way. At the cathode, the $O_2$ reacts with $H^{+}$ and $e^{-}$ to produce water and heat [35,36]. The electrochemical reactions occurring in the anode and cathode, as well as the overall electrochemical reaction of the PEMFC, are respectively described in Equations (1)–(3) [37]:

$$\begin{array}{ccccc}\hfill \begin{array}{c}\hfill H_2\end{array}& ⟹& 2H^{+}\hfill & +& 2e^{-},\end{array}$$

(1)

$$\begin{array}{ccccccc}\hfill \begin{array}{c}\hfill 2H^{+}\end{array}& +& \frac{1}{2}{O}_2\hfill & +& 2e^{-}& ⟹& H_{2}O,\end{array}$$

(2)

$$\begin{array}{ccccccc}\hfill \begin{array}{c}\hfill H_2\end{array}& +& \frac{1}{2}{O}_2\hfill & ⟹& H_{2}O& +& \mathrm{Energy}.\end{array}$$

(3)

The energy obtained by Equation (3) is called the enthalpy of formation $△H=-285.84$ kJ$·$mol${}^{-1}$, which referred to the higher heating value (HHV) when the water is in liquid form. It can be divided into thermal energy, represented by specific entropy $△S$ kJ$·$mol${}^{-1}$$·$K${}^{-1}$, multiplied by the thermodynamic system temperature T, and the Gibbs free energy $△G$ kJ$·$mol${}^{-1}$, which represents the work made by the movement of electrons in the external circuit. Therefore, the total energy as given in [38] is:

$$△H=△G+T·△S.$$

(4)

The electric work $△G$ is defined by the electric charge Q across the open circuit fuel cell voltage E, where Q can be calculated by multiplying the number of electrons n participating in the reaction with the Faraday constant F, which represents the electric charge of one mole of electrons ($F=96485$ C$·$mol${}^{-1}$):

$$△G=-Q·E=-2·F·E.$$

(5)

The values of $△H$, $△G$, and $△S$ are negative due to the exothermic of the reaction (gives energy). Therefore, the potential given by the PEMFC can be calculated as:

$$E=-\frac{△H-T·△S}{2·F}.$$

(6)

$△G$ also depends on the reactants. Therefore, their values can be calculated using the following expression:

$$△G=△G^0-RT[ln\left(P_{H2}\right)+\frac{1}{2}ln\left(P_{O2}\right)],$$

(7)

where $R=8.3143$ J$·$mol${}^{-1}$$·$K${}^{-1}$, $△G^0$ is the change in $△G$ at the standard state pressure (1 $atm$), and $P_{O2}$ and $P_{H2}$ represents, respectively, the oxygen and hydrogen partial pressures. Therefore, the PEMFC potential is expressed as:

$$E=-\frac{\Delta G^0}{2F}+\frac{RT}{2F}[ln\left(P_{H2}\right)+\frac{1}{2}ln\left(P_{O2}\right)].$$

(8)

The term $\frac{△G^0}{2·F}$ varies with temperature and differs from $1.229$ (its value at standard state) according to the following expression:

$$-\frac{\Delta G}{2F}=1.229+(T-298)\left(\frac{\Delta S^0}{2F}\right).$$

(9)

By applying the standard thermodynamical relations, which were developed in [39], Equation (8) can be written as:

$$E=1.229-0.85·{10}^{-3}(T-298)+4.3·{10}^{-5}\times T[ln\left(P_{H2}\right)+\frac{1}{2}ln\left(P_{O2}\right)].$$

(10)

This potential gives a value of about $1.2$ V for a cell operating at about 25 ${}^{\circ }$C. However, when a fuel cell is made and put to use, it is found that its voltage is often less than the theoretical value. Figure 2 shows the difference between the actual operating voltage and the “no loss” value (ideal voltage) of a typical single cell. The key points to notice about this graph are as follows: an important voltage drop at low currents, the voltage then decreases slowly and more linearly, and finally another important and sharp voltage drop at high currents. This voltage difference is a result of some losses including polarization and interconnection losses between cells. However, according to Larminie [39], the main losses that occur in a fuel cell are activation, ohmic, and concentration polarization losses. The activation losses $V_{act}$ are important at low currents and they occur due to the sluggishness of the reactions. The ohmic losses $V_{ohm}$ occur due to the resistances of the electrolyte and the electrodes which respectively hinder the transport of $H^{+}$ and $e^{-}$. The concentration losses $V_{conc}$ occur due to the fluctuation in concentration of reactants. The behavior of each polarization loss is clearly described in Figure 2, and their relationship with current density are respectively expressed in Equations (11)–(13):

$$V_{act}={\xi }_1+{\xi }_2·T+{\xi }_3·T·ln\left(C_{O2}\right)+{\xi }_4·T·ln\left(I\right),$$

(11)

$$V_{ohm}=I·(R_m+R_c),$$

(12)

$$V_{con}=-B\times ln(1-\frac{J}{J_{max}}),$$

(13)

where ${\xi }_1$, ${\xi }_2$, ${\xi }_3$, ${\xi }_4$, $C_{O2}$, $R_m$, $R_c$, B and $J_{max}$ are developed and calculated in [31].

Additionally, the fuel cell potential varies with fuel crossover and internal currents due to the waste of fuel and electron conduction through the electrolyte. However, these internal currents and fuel losses are very small and their effects are usually negligible. Therefore, according to [31], the voltage generated by a simple fuel cell can be expressed as:

$$V_{fc}=E-V_{act}-V_{ohm}-V_{con}.$$

(14)

The nominal voltage of an individual cell ($V_{fc}$) is approximately in the range of 0.8 and 1 volts. Therefore, in order to get a high potential, multiple unit cells (n) are stacked and connected in a series form. These n series cells will together produce the total voltage of the stack, which is called $V_{stack}$. By using the above equations, the model of the PEMFC stack unit can be introduced as Figure 3.

3. Power Electronic Interface

3.1. DC–DC Boost Converter

Taking into account the characteristics of the voltage curve presented in Figure 2, the unregulated output voltage can not be directly linked to the DC bus. Therefore, the application of a DC–DC power electronic converter circuit is mandatory in order to get an applicable voltage for end user applications. Among the DC–DC power electronic converters, the efficiency of the conventional boost converter is always greater than the other converter topologies due to its reduced component count and its simplicity in control. Basically, a boost converter consists of an inductor (L) for energy storage, a switching element (S), a capacitor (C) to reduce the ripple and a diode (D) to isolate the output stage when the switch is on. The choice of the components (inductor, capacitor) value is very important to decrease the ripple generation. It should be noted that, at large inductance, the start-up time could be slightly boosted, while at small inductance, higher levels of current could be reached before the switch turns off [40]. By varying the duty cycle $d_c$, the switching element change its state between $“on”$ and $“off”$ to finally obtain the desired regulated voltage. During the $“on”$ state of the switching element, the input current flows through the inductor L and switch S. Hence, electrical energy is stored in the inductor, and then the capacitor supplies current to the load and the diode with a reverse bias. When the switch is open, $“off”$ state, the stored energy is transferred to the load and capacitor C through the diode D [41]. The boost converter has two fundamentally different modes of operation, continuous-conduction-mode (CCM) and discontinuous-conduction-mode (DCM). In the CCM, the current in the energy transfer inductor is always greater than zero throughout the switching period, whereas it falls to zero after each switching cycle when in DCM. Furthermore, in DCM, the voltage is influenced by the duty ratio of the switching element and by the load which results more complicity in the DC analysis of the converter. Therefore, in this work, the boost converter and its control are designed based on CCM. The closed loop system including the PEMFC, the DC–DC boost converter, the load, and the controller is shown in Figure 4.

The boost converter state-space representation is expressed in Equation (15):

$$\left\{\begin{array}{c}\dot{x}=\left[\begin{array}{cc}0& \frac{d_c-1}{L}\\ \frac{1-d_c}{C}& -\frac{1}{RC}\end{array}\right]x+\left[\begin{array}{c}\frac{1}{L}\\ 0\end{array}\right]V_{stack},\hfill \\ y=\left[\begin{array}{cc}0& 1\end{array}\right]x,\hfill \end{array}\right.$$

(15)

where $x=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$, $x_1=I$: converter input current, and $x_2=V_{out}$: converter output voltage.

3.2. Super-Twisting Algorithm STA

Super-twisting algorithm (STA) is one of the most powerful 2-order continuous SMC, which ensures all fundamental properties of its traditional 1-order together with chattering reduction [42]. In other words, it is not only robust against system uncertainties and external disturbances, but also has the ability to track the system with high accuracy. It was proposed in 1993 by Professor Levant for systems with a relative degree equal to 1 [43]. Unlike other 2-order SMC algorithms, STA requires only the knowledge of the sliding variable and it does not need any information about its time derivative. This leads to make it a relatively straightforward control law, and, therefore, it is one of the most preferable algorithms for a wide range of applications. In this work, the STA has been applied to drive the converter with the purpose of keeping the PEMFC operating at an efficient power point. The control solution, as shown in Figure 4, directly tackles the stack current through a STA to generate the control signal $u\left(t\right)$ for the switch S after treating the sliding mode surface $s\left(x\right)$ (namely, the error between the reference current $I_{ref}$ and the measured inductor current I). Since STA belongs to the 2-order sliding mode approach, therefore the control signal $u\left(t\right)$ can be written as:

$$u=u_{equ}+u_d.$$

(16)

The equivalent control $u_{equ}$ is a continuous function proposed by slotine in [44]. The main purpose of this function is to ensure that the system reaches the sliding surface $(s=0)$. $u_{equ}$ was developed to drive the system without considering its uncertainties and external disturbance, and it can be obtained by zeroing $\dot{s}$ ($\dot{s}=0$). The switching control $u_d$ is a discontinuous function which contains the switching element. The main purpose of this function is to ensure the convergence of the overall system by keeping it moving onto the sliding surface. Moreover, it guarantees the robustness against uncertainties and external disturbances. In this work, $u_d$ is designed based on STA as given in Equation (17) [45]. It is composed of two parts: a discontinuous part $u_1$ and a continuous part $u_2$:

$$u_d=u_1+u_2,$$

(17)

$$u_1=-\lambda ·{\left|S\right|}^{1/2}·sign\left(s\right),$$

(18)

$${\dot{u}}_2=-\gamma ·sign\left(s\right),$$

(19)

where $\lambda$ and $\gamma$ are designed parameters. They can be obtained using the sufficient conditions that are required to ensure the convergence:

$$\left\{\begin{array}{c}\gamma >\frac{\Phi }{{\Gamma }_m},\hfill \\ \lambda >\sqrt{\frac{2}{{\Gamma }_m^2}.\frac{{({\Gamma }_m.\gamma +\Phi )}^2}{({\Gamma }_m.\gamma -\Phi )}}.\hfill \end{array}\right.$$

(20)

Accordingly, the overall command law of the STA can be obtained as given in Equation (19). On the other hand, the implementation of this command law in MATLAB/Simulink^TM is clearly presented in Figure 5:

$$u=\frac{V_{out}-V_{stack}}{L}-\lambda {\left|S\right|}^{0.5}sign\left(S\right)-\int \gamma ·sign\left(S\right)dt.$$

(21)

Trajectories on the 2-sliding plane are characterized by bending around the origin. Thus, as shown in Figure 6, they perform an infinite number of rotations while converging to the origin.

4. Description of the Experimental System

The experimental study presented in this section was developed at the laboratory of Automatic Control and System Engineering (ACSE)/Universidad del Pais Vasco–Euskal Herriko Uniberstsitatea (UPV/EHU). The schematic view of the overall experimental test bench system is shown in Figure 7. The test bench consists of five main parts: a Heliocentris hy-Expert^TM PEMFC Instructor system, a dedicated PC, a DC–DC boost converter, a DSPACE DS1104, and a programmable electronic load.

The technical specifications of the PEMFC Instructor system are enlisted in

Table 1. Fuel cell stack technical data.

General		Electrical
Type	PEM fuel cell stack, 10 cells	Rated voltage	5.0 VDC
Cooling	Air	Rated current	8.0 A
Fuel	Hydrogen	Rated power output	40 W
Design	Open cathode	Maximum current	10 A
W × D × H	120 × 103 × 135 mm	Maximum power output	50 W
Weight	1.15 kg	No-load voltage	9.0 VDC
$H_2$ Flow Meter		$H_2$ Connection Kit 15 bar
Measuring range	10–1000 sml/min	Inletpressure	1–15 bar
Precision	0.8% of measured value plus	Outlet pressure	0.6 bar
	0.2% of full-scale value
Thermal		$H_2$ Connection Kit 200 bar
Operating Temp.	15–50 ${}^{\circ }\mathrm{C}$	Inlet pressure	200 bar
Max.start temp.	45 ${}^{\circ }\mathrm{C}$	Outlet pressure	1–15 bar
Fuel		$H_2$ Detector
$H_2$ purity	5.0 (99.999 %)	Sensor type	Hydrogen 4%
$H_2$ input pressure	0.4–8 bar (5.8–11.6 psig)	Measuring principle	3-electrode sensor
$H_2$ consumption	Max. 700 sml/min (at 0 C, 1013 bar)	Standard range	0.00–4.00%

. The used PEMFC is comprised of a stack of 10 identical cells assembled together. Each fabricated cell has an effective membrane area of 25 cm${}^2$, a thickness equal to $175·{10}^{{}^{-6}}$ cm, and with platinum loadings of $0.3$ mg$·$Pt/cm${}^2$. According to the manufacturer’s specifications, the rated output power of the stack is about 40 W for a rated current of 8 A, and a rated voltage of 5 V. The PEMFC operating voltage ranges from 9 V (no load) to 5 V (Full load). At its maximum current condition, where $I_{max}=10$ A, the stack can deliver up to 50 W. The PEMFC operates in a temperature range between 15 ${}^{\circ }\mathrm{C}$ and 50 ${}^{\circ }\mathrm{C}$. It is fed directly by pure “dead-end-mode” hydrogen ($99.999$ vol%) and air (oxygen) without prior humidification. Therefore, a pressure regulator is required to feed the PEMFC with the exact rate of hydrogen that is being consumed. Using the $H_2$ Connection Kits $[1-15]/0.6$ bar (Manometers Ashcraft), hydrogen can be supplied from the supply tank into the PEMFC at around $0.6$ bar (maximum pressure at which the PEMFC could operate). The hydrogen supply tank used in this work is Lithiumhydride Cylinder Ovonics (LCO), Model: $25G25OB/25G555B$ (Heliocentris). The dimensions of this LCO are $64\times 305$ mm, and it could store $2.391$ kg of hydrogen. In order to refill the cylinder, a $H_2$ Connection Kits $200/[1-15]$ bar is used to supply the hydrogen from the refill tank at approximately 10 bar. The flow rate of hydrogen into the PEMFC is measured using the Bronkhorst Gas Flow Meter (BGFM). This latter operates in a measuring range of [10–1000] sml/min and with a precision of $0.8$% of measured value. The required oxygen that will be used in the electrochemical reactions is supplied to the PEMFC as air. Thus, using the cooling fans which are attached to the stack, air is streamed into the cells at atmospheric pressure. The cooling fans not only serve to provide air for the electrochemical reactions, but they also serve to regulate the PEMFC operating temperature through the convective cooling. Therefore, they result in a reduction in controlling the airflow rate and the stack temperature independently. In addition, the implementation of the oxygen cylinder in such systems can be avoided. The speed of the cooling fans can be either controlled manually by the operator or automatically by an internal controller. If the fan’s control software is adjusted in the position “AUTO” mode, the fans will be controlled automatically according to the PEMFC stack power. In other words, the controller sets the desired fan speed in order to ensure sufficient cooling at all times. Hence, an increase in the PEMFC stack power leads to an increase in the airflow rate (the greater the amount of air is needed for cooling and for the reaction), and so on increasing the fan speed. Additionally, the “AUTO” mode provides enough air in the cathode side in order to decrease as much as possible the mass transport limitations which will result in a reduction in the concentration loss. It should be noted that the airflow used for the convective cooling is significantly more than that used for the electrochemical reactions. Therefore, for systems such as the Heliocentris hy-Expert^TM PEMFC Instructor system, excess airflow is extremely important. On the other hand, if the fan’s control software is adjusted in a position other than “AUTO” mode, the fans will be controlled directly by the user. Hence, the fans can be operated manually by selecting the percentage of the speed that can be in a range between 0% and 100% of the maximum fan speed. According to the technical specifications provided by the Heliocentris hy-Expert^TM instructor, at full speed (100%) of $13,000$ rpm, each fan could pump around 276 L/min of airflow. Therefore, the two fans pump around 552 L/min as a maximum amount of airflow that could be supplied to the PEMFC.

A proprietary hy-Expert^TM controller board is used for real-time control of the PEMFC system. The controller board represents the distribution center for all data among the PEMFC’s complementary instruments including the fans, the $H_2$ flow meter, the temperature sensor, and the software. It has been developed to provide simple operation, ensure the safety of the PEMFC, as well as to protect the stack from over-loads and short circuits. In addition, it allows to supervise and control the PEMFC system through a dedicated PC using monitoring software provided by Heliocentris. Using an integrated RS232 interface, the software allows for initializing/closing the communications, recording and filing of all the data from the PEMFC auxiliaries and sending power commands during the test, as well as enabling the visualization of all of the operating parameters. Thus, parameters such as the electrical characteristics of the PEMFC (voltage (V) and current (A)), operating temperature (${}^{\circ }\mathrm{C}$), $H_2$ flow rate (L/min), and fan power (%) can be recorded and graphically drawn on the software interactive screen.

The DC–DC boost converter used in the test bench was manufactured by TEP-192-Research Group/University of Huelva, Spain. Detailed information about the utilized boost converter is enlisted in

Table 2. Technical specifications of the DC–DC boost converter.

Parameter	Description
Schottky diode	2xMURF1560 GT, 0.4 V, 10 A, 600 V, 15 A/150 ${}^{\circ }\mathrm{C}$
Capacitance $C_0$ and $C_1$	2xTK Series, 1500 $\mathsf{\mu }$$\mathrm{F}$ and 3000 $\mathsf{\mu }$$\mathrm{F}$
Inductance L	6xPCV-2-564-08 $560/6$ $\mathsf{\mu }$H, 7 A, 42 m$\Omega$
I GBT	1xHGT40N60B3, 600 V, 40 A, 1.5 V, 150 ${}^{\circ }\mathrm{C}$
Switching frequency	20 KHz
Maximum input/output voltage	$V_{in}max$ = 60 V, $V_{out}max$ = 200 V
Maximum input/output current	$I_{in}max$ = 20 A, $I_{out}max$ = 20 A

. It allows the operator to control the PEMFC system via its metal-oxide-semiconductor field-effect transistor (MOSFET) switching input (20 kHz) which comes directly from the PWM card of the dSpace. In addition, it is equipped with four sensors: two sensors are used to measure the input and output current, and the others are used to measure the input and output voltage. These sensors are calibrated in order to obtain analog signals between 0 and $\pm 10$ V as accepted by the analog-to-digital converter (ADC) block of the dSpace. In addition, low pass filters were utilized in the measuring units in order to remove the undesired high-frequency noise.

The dSpace used in this work is DS1104 real-time controller board. It has a MPC8240 processor (PowerPC $603e$ core; 250 MHz CPU), 64-bit floating-point processor, internal cache of 32 MB SDRAM Global memories, slave DSP subsystem DSP/TMS320F240 from Texas Instruments Company (Texas, TIC, United States), 8 MB Flash memories, 8 ADC channels, eight digital-to-analog converter (DAC) channels, and five timer interrupts. The dSpace is a powerful tool that is able to modify the controller parameters in real time, as well as to monitor the real processes while operating an experiment. Accordingly, using its Real-Time Interface (RTI), it enables the linkage between the hardware system and the MATLAB/Simulink software (R2015a-MATLAB/Simulink 8.5, MathWorks). In detail, the obtained signals from the sensors are linked to the dSpace via the ADC block and accordingly, they will be read by MATLAB/Simulink using the communication library element $DS1104ADC-CX$. In this work, four channels are used to read the signals from the ADC: $DS1104ADC-C5$ is configured to read $V_{stack}$, $DS1104ADC-C6$ is configured to read $I_{stack}$, $DS1104ADC-C7$ is configured to read $V_{out}$, $DS1104ADC-C8$ is configured to read $I_{out}$. 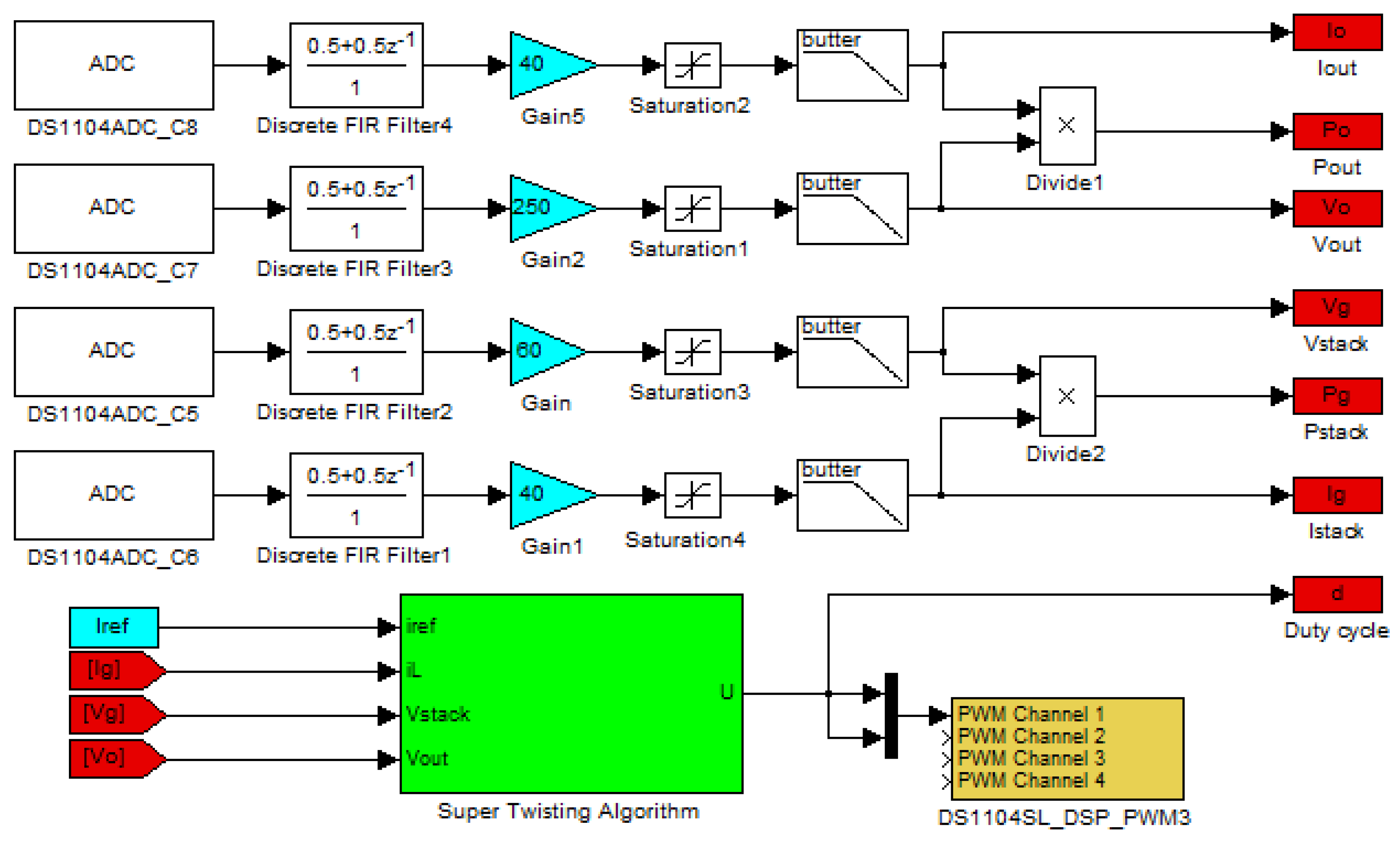As shown in Figure 8, the RTI allows the operator to design and implement a digital controller simply by drawing the needed block diagrams (available in the library) on the graphical interface of MATLAB/Simulink.

By compiling the model, the RTI generates and downloads a specific real-time C code for the dSPACE. The standard PWM pulses will be generated using the PWM library block $DS1104SL-DSP-PWM$ and then they will be linked to the MOSFET of the boost converter via the digital-to-analog converter (DAC) block. Meanwhile, the signals came from the channels will be sent to the MATLAB base workspace using “$To$$workspace$” block. The evolution of each signal will be screened online in the PC using “Controldesk” monitoring software which read the signals data from the workspace.

The system is connected with a BK-Precision-1788B programmable single-output DC power supply, which provides a programmable electronic load with a resistance in the range of $0.1$– 1000 $\Omega$. The load being made by the Fotronic Corporation Company (Washington, DC, USA), and it has an operating range between 0 W and 120 W, with a maximum input voltage of 115 V/47 Hz. It can be programmed through PV-1785B-1788 software.

5. Results and Discussion

The characteristics of Heliocentris hy-Expert^TM PEMFC 50 Instructor system are obtained by connecting the PEMFC stack directly to the load. To clarify the process, load current ($I_{out}$) is increased from $0.1$ to 4.6 A in steps of 0.5 A for each 10 s. In addition, in order to get precise points, steps of 0.1 A are used at the beginning and at the end of the measurements. The current $I_{out}$ and voltage $V_{out}$ are measured via the laboratory measuring instrument “DT9205A” to validate the theoretical work which presented in [31]. It is important to know that, during the last four years, many tests have been done on the PEMFC stack which occurred a degradation in the cells. This latter caused a decreasing in the fuel cell performances. However, since the main aim of this work is to validate the performance of the STA, a decreasing in the efficiency of the fuel cell will not be a big issue. The experimental polarization curves Current–Voltage (I–V) and Current–Power (I–P) for sundry operating temperatures are presented in Figure 9.

The open circuit voltage of the PEM fuel cell stack is in the range of 8–10 V. The drop voltage at the beginning and end of the curves shown in this figure are due to activation and concentration losses, respectively. Actually, the latter does not appear very well due to the integrated controller board which closes the system in order to protect the stack from the damage. The voltage drop in the middle of the curves (which is approximately linear) is due to the ohmic loss in the fuel cell. The polarization curves shown in Figure 9 indicate that the PEMFC stack performance is ameliorated with rising temperature from 20 to 38 ${}^{\circ }\mathrm{C}$, and diminished for higher temperatures (T > 45 ${}^{\circ }\mathrm{C}$). In other words, for a given current $I_{out}$, it is apparent that, by increasing the operating temperature, the PEMFC shows better performance. In terms of measured voltage and power, the performance improvement of the PEMFC stack between 20 and 38 ${}^{\circ }\mathrm{C}$ can be explained by the augmentation in the membrane conductivity, as well as to the increased exchange current density at higher degrees of temperature, which diminishes the activation losses. However, if the operating temperature is high enough, the membrane conductivity decreases as a consequence of the lack in relative humidity in the electrolyte membrane. Therefore, a diminution in the stack voltage is observed when T > 45 ${}^{\circ }\mathrm{C}$. In comparison with the theoretical description which is given in [31], it is clear that the efficiency of the real PEMFC is lower than the estimated theoretical efficiency. In addition, it is noticeable that the influence of temperature variations is greater than what is obtained in the theoretical work. This is due to the variations in some parameters that are used as constants in the theoretical model. However, practical results that are shown in Figure 9 validate that the efficiency of the fuel cell can be ameliorated by increasing its temperature. Additionally, it is obvious that the output power is improved by rising the current $I_{out}$ from 0.1 A to 4.6 A and the obtained curves have the same trends with the simulation results.

Usually, in fuel cell systems, the control processes are used to keep the system functioning at the maximum power point (MPP). However, in accordance with the obtained I–V and I–P characteristics which were presented in Figure 9, it is noticeable that attaining the MPP could be an intractable task. This is due to the safety system which turns off the fuel cell when its power is close to the MPP. Hence, although the safety system protects the stack from the damage, it also makes its operation very sensitive around the MPP. For this reason, an operation zone as presented in Figure 10 is established to provide at least 72% of the maximum power produced by the fuel cell. In fact, the MPP could be in the range of 2–8 W more than the operation zone. This range is used taking into account the controllers’ behavior (chattering phenomenon, overshoots when load changing) in order to guarantee the continuation of the fuel cell operating process.

In order to find out the performance of super twisting algorithm (STA) and its features over traditional 1-order SMC, load variation from 20 $\Omega$ to 50 $\Omega$ is applied at t = 25 s and from 50 $\Omega$ to 20 $\Omega$ is applied at t = 45 s. The controllers’ coefficients used in this work are enlisted in

Table 3. Controllers’ coefficients.

Sliding Mode Controller	Super-Twisting Algorithm
$\kappa$ = 0.01	$\lambda$ = 0.01, $\gamma$ = 0.1

.

Figure 11, Figure 12, Figure 13 and Figure 14 show respectively the duty cycle signal, the PEMFC output signals (voltage, current, and power), and finally the boost converter output signals (voltage, current, and power). These figures show the behaviour of the SMC and STA to track and maintain the system functioning at the efficient operation zone. In general, both of the controllers show global stability and satisfactory tracking results so as to keep the system at the operation zone. However, it is clearly shown that the STA has a high capability to decrease the chattering effect that occurs by the SMC. Consequently, these figures validate the results obtained in the previous simulations that were presented in [31]. On the other hand, Figure 11, Figure 12, Figure 13 and Figure 14 also show the behaviour of the SMC and STA when they are confronted by load variations at t = 25 s and t = 45 s.

The duty cycle signals generated by the controllers are shown in Figure 11.

As can be seen from this figure, the controllers effectively control the duty cycle so as to obtain constant current with fast response time and no drift. It is important to note that, in comparison with the previous simulation work, some noises occurred in the obtained experimental signals. However, this is resulting from the effect of time-delay in the control signal, as well as the parasite signals which came from hardware components.

The fuel cell output voltage and current signals are shown in Figure 12. This last illustrates the behavior of the SMC and STA when experiencing load variations at t = 25 s and t = 45 s. According to this figure, it is clear that both of the controllers manifest high robustness even when large load variations is accrued (30 $\Omega$). Thus, by varying the load resistance from 20 $\Omega$ to 50 $\Omega$ and from 50 $\Omega$ to 20 $\Omega$, the SMC manifests an overshoot and undershoot voltage of 0.6 V and 0.9 V, as well as an undershoot and overshoot current of 1.2 A and 2.6 A, respectively. For the same variations, the STA manifests an overshoot and undershoot voltage of 0.9 V and 1.6 V as well as an undershoot and overshoot current of 1.8 A and 3.9 A, respectively. Therefore, despite the large load variations, only small overshoots are accrued. In addition, these overshoots only appear for a short period of time (response time ≤ 1 s), and they swiftly converge to the steady-state value. Figure 12 also shows that, using SMC, the fuel cell output DC voltage oscillations can reach about $12\%$ while the oscillations of the output current is over $35\%$. These oscillations introduce small deviations from the operating point and especially they may even cause irreversible damage to the fuel cell. On the other side, the fuel cell output DC voltage oscillations using STA is only about $0.26\%$ and the oscillations of the output current is less than $7\%$. Therefore, compared to the SMC, high accuracy, robustness, and good dynamic behavior are obtained even with large load variations.

The fuel cell output power trajectories are presented in Figure 13. According to these trajectories, it is obvious that the operation zone is attained with swift speed and stability of the closed-loop system. On the other hand, it is clearly shown that the chattering phenomenon is almost eliminated by using the STA. Indeed, the chattering magnitude using the SMC varies approximately from 20.5 W to 27 W, while it only varies from 23.3 W to 23.9 W using the STA. Accordingly, it is proven that the proposed STA has succeeded at reducing about 91% of the chattering effect, which will improve, as a consequence, the fuel cell lifetime.

The behaviour of the output voltage, current, and power of the DC–DC boost converter under load variations are presented in Figure 14. According to this figure, it is clear that, despite the heavy loading conditions, the STA manifests gradual and smooth movement to the desired voltage at which the system will work in the operation zone. Moreover, high performances such as low response time (less than 1 s), robustness, great precision, as well as excellent dynamic behavior are achieved.

Based on the results obtained in this section, it is clearly manifested that this experimental work shows the same results with that obtained in the previous simulation work. Accordingly, the capability of the STA to reduce the chattering effect, while attaining high performances, is clearly proven.

6. Conclusions

A 50-W PEMFC Instructor system feeding load resistance through a step-up DC–DC power converter has been experimentally studied in this work. The hardware system components, including the fuel cell with its auxiliaries, the power converter, the control system and the data acquisition, have been installed and conducted together with the dSPACE 1104 controller board. The control algorithms have been designed in MATLAB/Simulink environment and connected to the dSPACE-card using the DS1104 linkage blocks.

The temperature effect on the PEMFC performance has been studied. The obtained I-V and I-P characteristics of the PEMFC for different operating temperatures proves that the PEMFC performance is improved by increasing its operating temperature from 20 to 38 ${}^{\circ }\mathrm{C}$. Alternatively, the fuel cell performance worsens at higher temperatures as the electrolyte membranes can be dried.

Therefore, in order to bring the system to an efficient power point, an operation zone is established to provide at least 72% of the maximum power produced by the fuel cell. Successful implementation of SMC and STA in an actual fuel cell has experimentally demonstrated the effectiveness of these control solutions to bring the system to the operation zone. However, high performances such as low response time, robustness, great precision, simple implementation, as well as excellent dynamic behavior, are attained using the proposed STA. Therefore, it is proven that the STA ensures all the fundamental properties of its traditional 1-order SMC, in addition to providing chattering reduction of 91%, which will ameliorate, as a consequence, the fuel cell lifetime.

Since the calculation of an optimal operation zone is significantly important for systems such as Heliocentris hy-Expert^TM PEMFC, this paper paves the way for further advanced research on this topic.