Optimization of the Energy Consumption of a Carbon Capture and Sequestration Related Carbon Dioxide Compression Processes
Abstract
:1. Introduction
2. Method
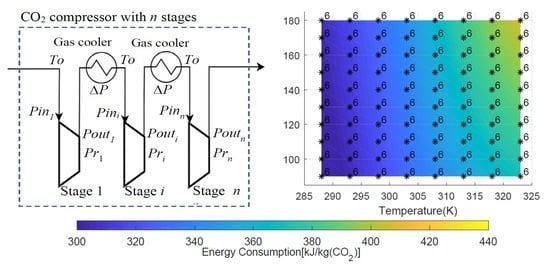
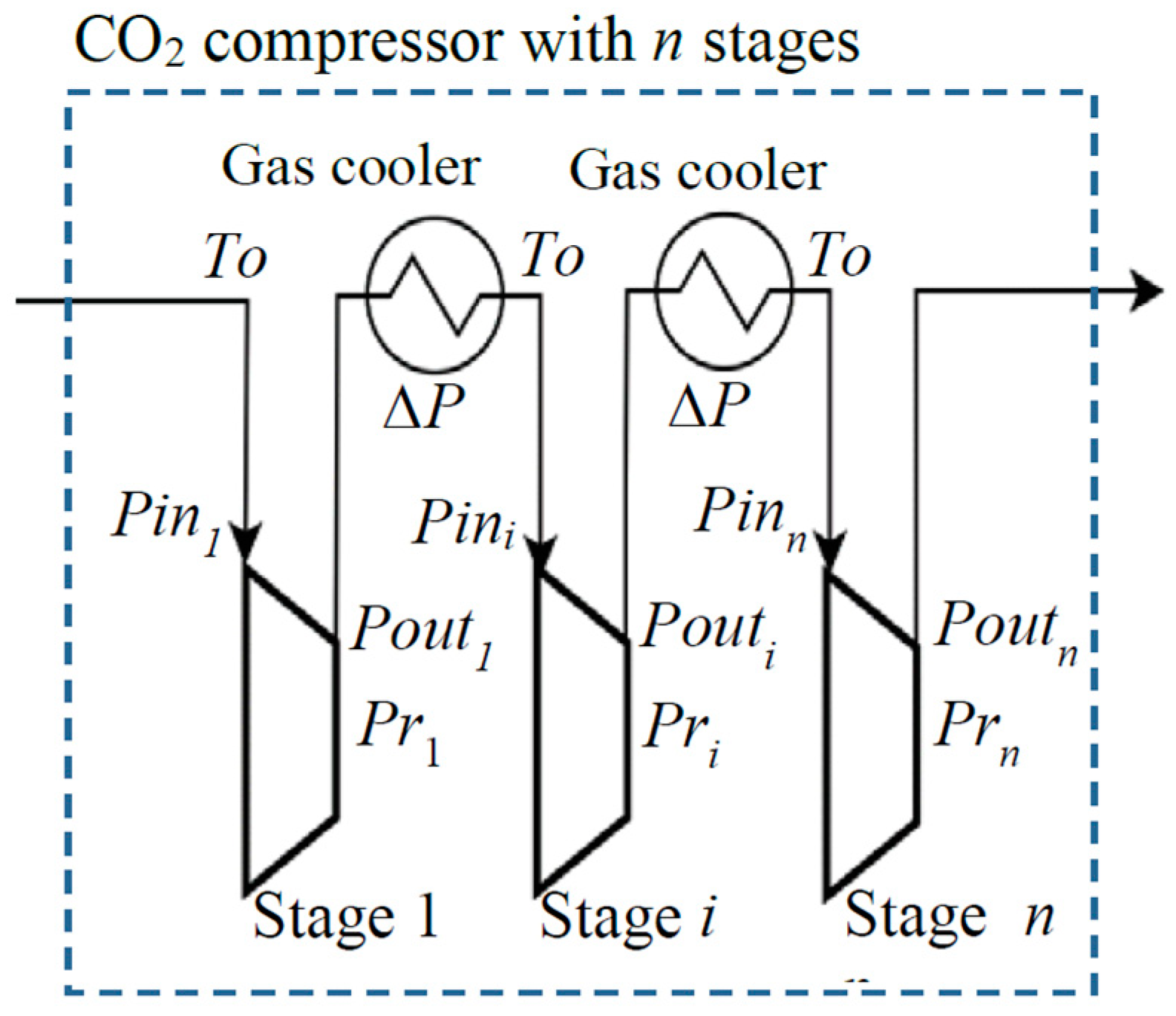
2.1. Compressor Modeling
2.2. Study Parameters
2.2.1. Post-Combustion Capture
2.2.2. Pre-Combustion Capture
2.2.3. Oxyfuel Capture
2.3. Optimization of Compressor Energy Consumption
2.3.1. Variables, Initial Guesses, and Constraints
2.3.2. Objective Function
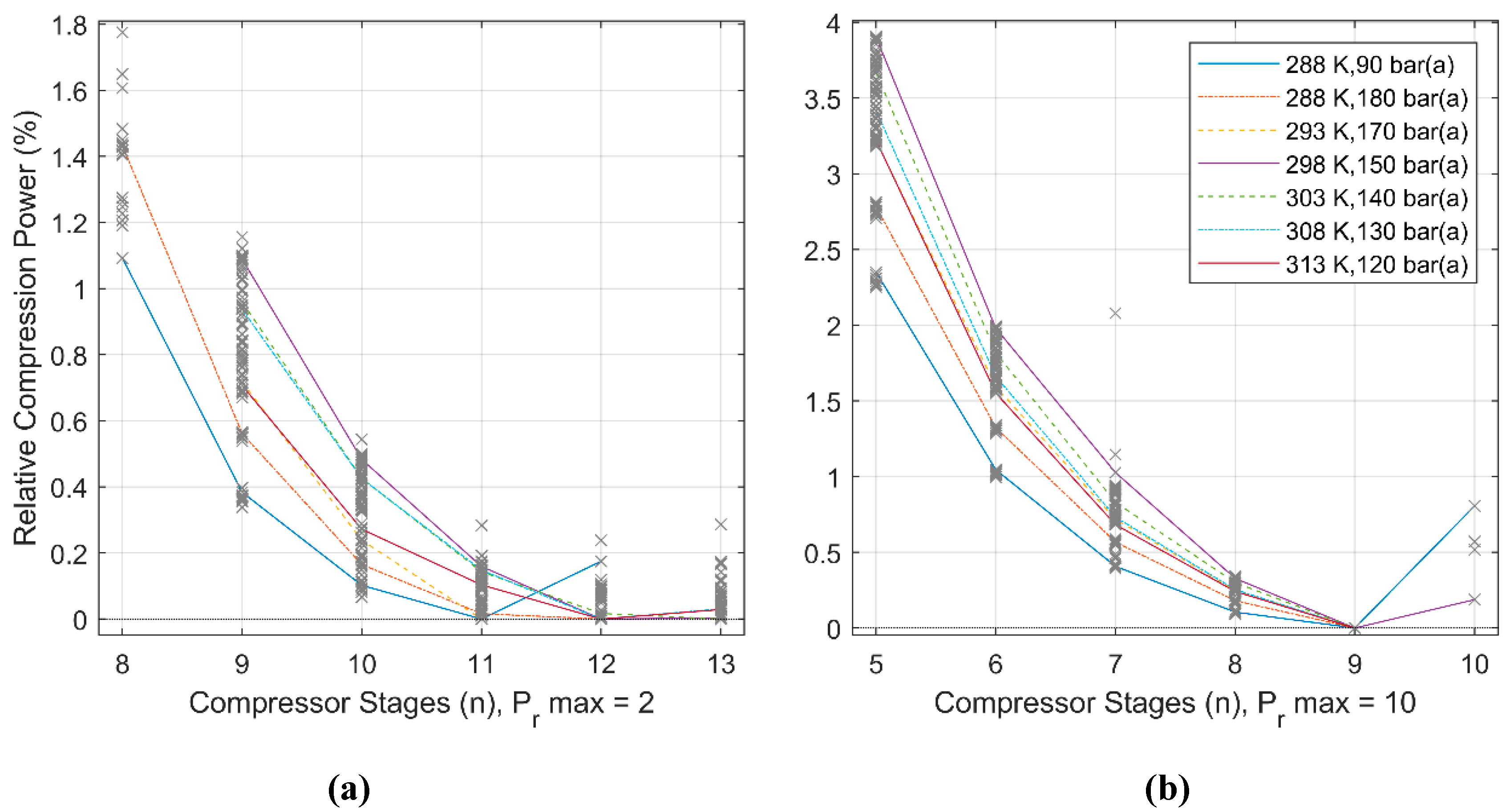
2.4. Identifying the Optimum Number of Compression Stages
3. Results and Discussion
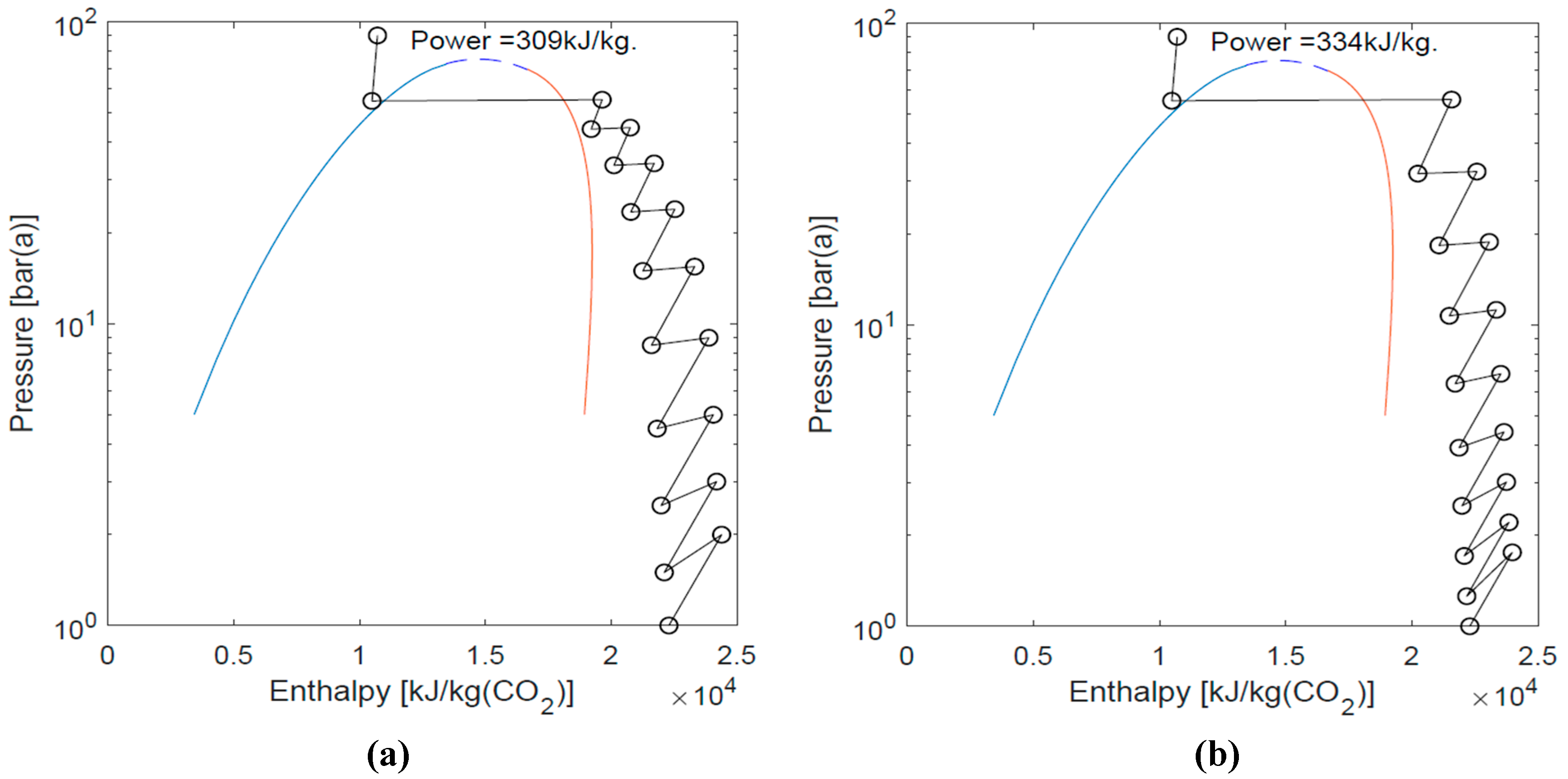
3.1. The Benefits of Optimization
3.2. Consistency Checking and Optimum Stages
3.3. Variation of Energy Consumption with Cooling Temperature and Pressure
3.4. Constrained vs. Unconstrained Cases
4. Discussion
5. Conclusions
Nomenclature
| Enthalpy at the inlet to stage i | |
| Enthalpy at the outlet if stage i (isentropic basis) | |
| n | Number of compressor stages |
| Crycondenbar pressure | |
| Dew point pressure | |
| Inlet pressure pressure for stage i | |
| Outlet pressure pressure for stage i | |
| Pressure ratio for stage i | |
| ∆P | Aftercooler pressure drop |
| Entropy for stage i | |
| To | Aftercooler outlet temperature |
| Wc | Energy used in compression |
| Gas composition stage i | |
| Isentropic efficiency |
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Lucquiaud, M.; Liang, X.; Errey, O.; Chalmers, H.; Gibbins, J. Addressing technology uncertainties in power plants with post-combustion capture. Energy Procedia 2013, 37, 2359–2368. [Google Scholar] [CrossRef]
- Jordal, K.; Aspelund, A. Gas conditioning—The interface between CO2 capture and transport. Int. J. Greenh. Gas Control. 2007, 1, 343–354. [Google Scholar]
- Dittmer, R.; Strube, R. Integrally-geared compressors as state-of-the-art technology. Carbon Capture J. 2015, 47, 15–18. [Google Scholar]
- Habel, R.; Wacker, C. Innovative and proven CO2 compression technology for CCS and EOR. Carbon Capture J. 2009, 11, 15–18. [Google Scholar]
- Irlam, L. Global Costs of Carbon Capture and Storage, 2017 Update; Global CCS Institute: Docklands, Australia, 2017. [Google Scholar]
- Romeo, L.M.; Bolea, I.; Lara, Y.; Escosa, J.M. Optimization of intercooling compression in CO2 capture systems. Appl. Therm. Eng. 2009, 29, 1744–1751. [Google Scholar] [CrossRef]
- Luo, X.; Wang, M.; Chen, J. Heat integration of natural gas combined cycle power plant integrated with post-combustion CO2 capture and compression. Fuel 2015, 151, 110–117. [Google Scholar] [CrossRef]
- Posch, S.; Haider, M. Optimization of CO2 compression and purification units (CO2CPU) for CCS power plants. Fuel 2012, 101, 254–263. [Google Scholar] [CrossRef]
- Font-Palma, C.; Errey, O.; Corden, C.; Chalmers, H.; Lucquiaud, M.; Sanchez Del Rio, M.; Jackson, S.; Medcalf, D.; Livesey, B.; Gibbins, J.; et al. Integrated oxyfuel power plant with improved CO2 separation and compression technology for EOR application. Process. Saf. Environ. Prot. 2016, 103, 455–465. [Google Scholar] [CrossRef]
- Alabdulkarem, A.; Hwang, Y.; Radermacher, R. Development of CO2 liquefaction cycles for CO2 sequestration. Appl. Therm. Eng. 2012, 33, 144–156. [Google Scholar] [CrossRef]
- Harkina, T.; Hoadley, A.; Hooper, B. A comparison of the Process Integration of Shockwave CO2 compression with conventional turbo machinery into PCC power station design. Energy Procedia 2011, 4, 1339–1346. [Google Scholar] [CrossRef]
- Pei, P.; Barse, K.; Gil, A.J.; Nasah, J. Waste heat recovery in CO2 compression. Int. J. Greenh. Gas Control. 2014, 30, 86–96. [Google Scholar] [CrossRef]
- Calado, M. Modeling and design synthesis of a CCS compression train system via MINLP optimization. Instituto Superior Técnico, Universidade de Lisboa. 2012. Available online: https://fenix.tecnico.ulisboa.pt/downloadFile/395144614662/ExtendedAbstract_MarioCalado_12Outubro2012.pdf (accessed on 26 April 2019).
- Jackson, S.; Brodal, E. A comparison of the energy consumption for CO2 compression process alternatives. Available online: https://iopscience.iop.org/article/10.1088/1755-1315/167/1/012031/pdf (accessed on 26 April 2019).
- Pipitone, G.; Bolland, O. Power generation with CO2 capture: Technology for CO2 purification. Int. J. Greenh. Gas Control. 2009, 3, 528–534. [Google Scholar] [CrossRef]
- Amrollahi, Z.; Ystad, P.A.M.; Ertesvåg, I.S.; Bolland, O. Optimized process configurations of post-combustion CO2 capture for natural-gas-fired power plant—Power plant efficiency analysis. Int. J. Greenh. Gas Control. 2012, 8, 1–11. [Google Scholar] [CrossRef]
- D.N.V. Recommended Practice, DNV-RP-J202, Design and Operation of CO2 Pipelines. DNV, 2010. Available online: https://rules.dnvgl.com/docs/pdf/DNV/codes/docs/2010-04/RP-J202.pdf (accessed on 26 April 2019).
- Eickhoff, C.; Neele, F.; Hammer, M.; DiBiagio, M.; Hofstee, C.; Koenen, M.; Fischer, S.; Isaenko, A.; Brown, A.; Kovacs, T. IMPACTS: Economic Trade-offs for CO2 Impurity Specification. Energy Procedia 2014, 63, 7379–7388. [Google Scholar] [CrossRef]
- Damen, K.; Troost, M.v.; Faaij, A.; Turkenburg, W. A comparison of electricity and hydrogen production systems with CO2 capture and storage. Part A: Review and selection of promising conversion and capture technologies. Prog. Energy Combust. Sci. 2006, 32, 215–246. [Google Scholar] [CrossRef]
- IEA Greenhouse Gas R&D Programme. Techno-Economic Evaluation of SMR Based Standalone (Merchant) Hydrogen Plant with CCS. 2017. Available online: https://ieaghg.org/exco_docs/2017-02.pdf (accessed on 26 April 2019).
- Tanaka, Y.; Sawada, Y.; Tanase, D.; Tanaka, J.; Shiomi, S.; Kasukawa, T. Tomakomai CCS Demonstration Project of Japan, CO2 Injection in Process. Energy Procedia 2017, 114, 5836–5846. [Google Scholar] [CrossRef]
- Alhajaj, A.; Mac Dowell, N.; Shah, N. A techno-economic analysis of post-combustion CO2 capture and compression applied to a combined cycle gas turbine: Part I. A parametric study of the key technical performance indicators. Int. J. Greenh. Gas Control. 2016, 44, 26–41. [Google Scholar] [CrossRef]


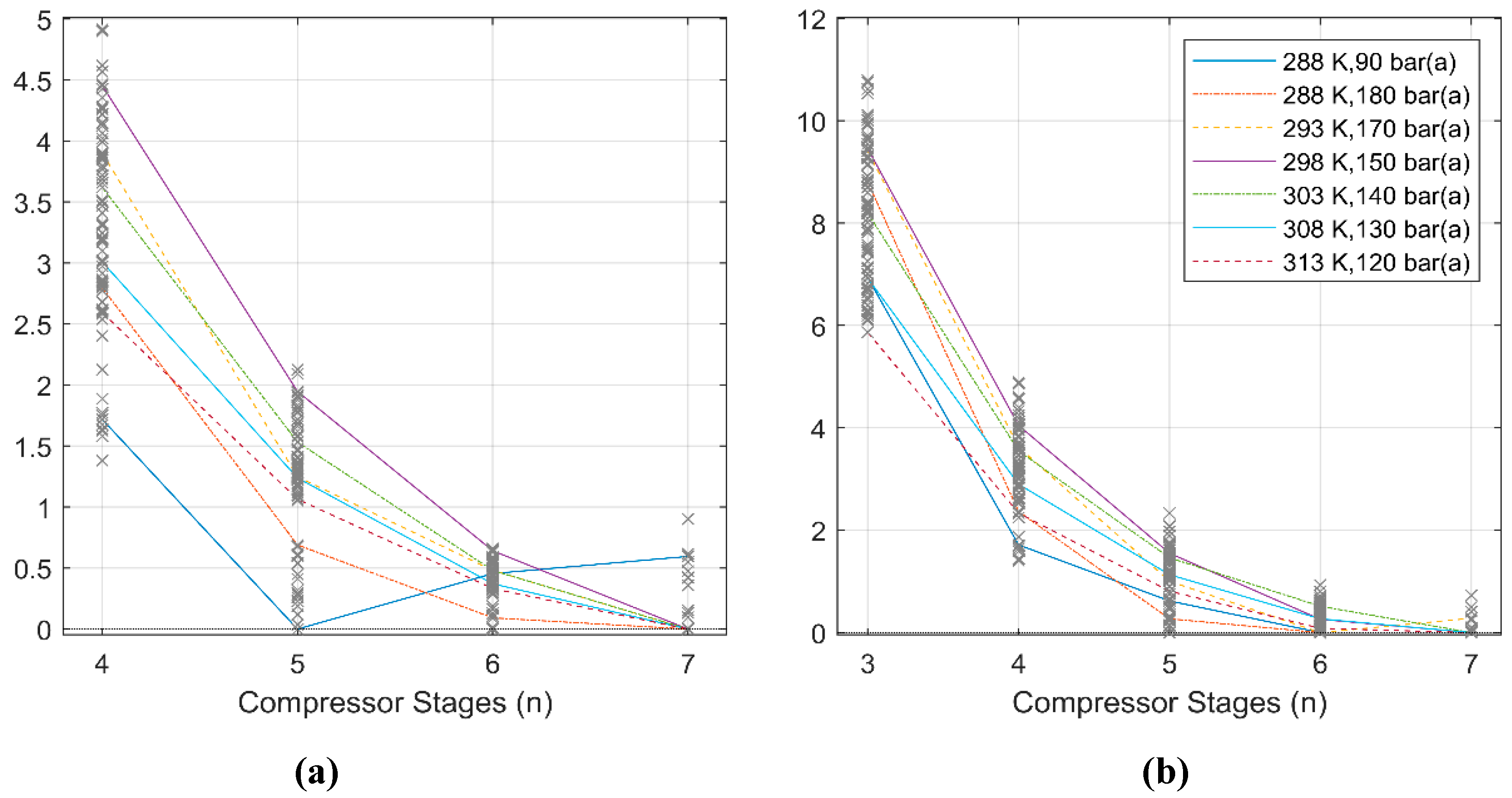

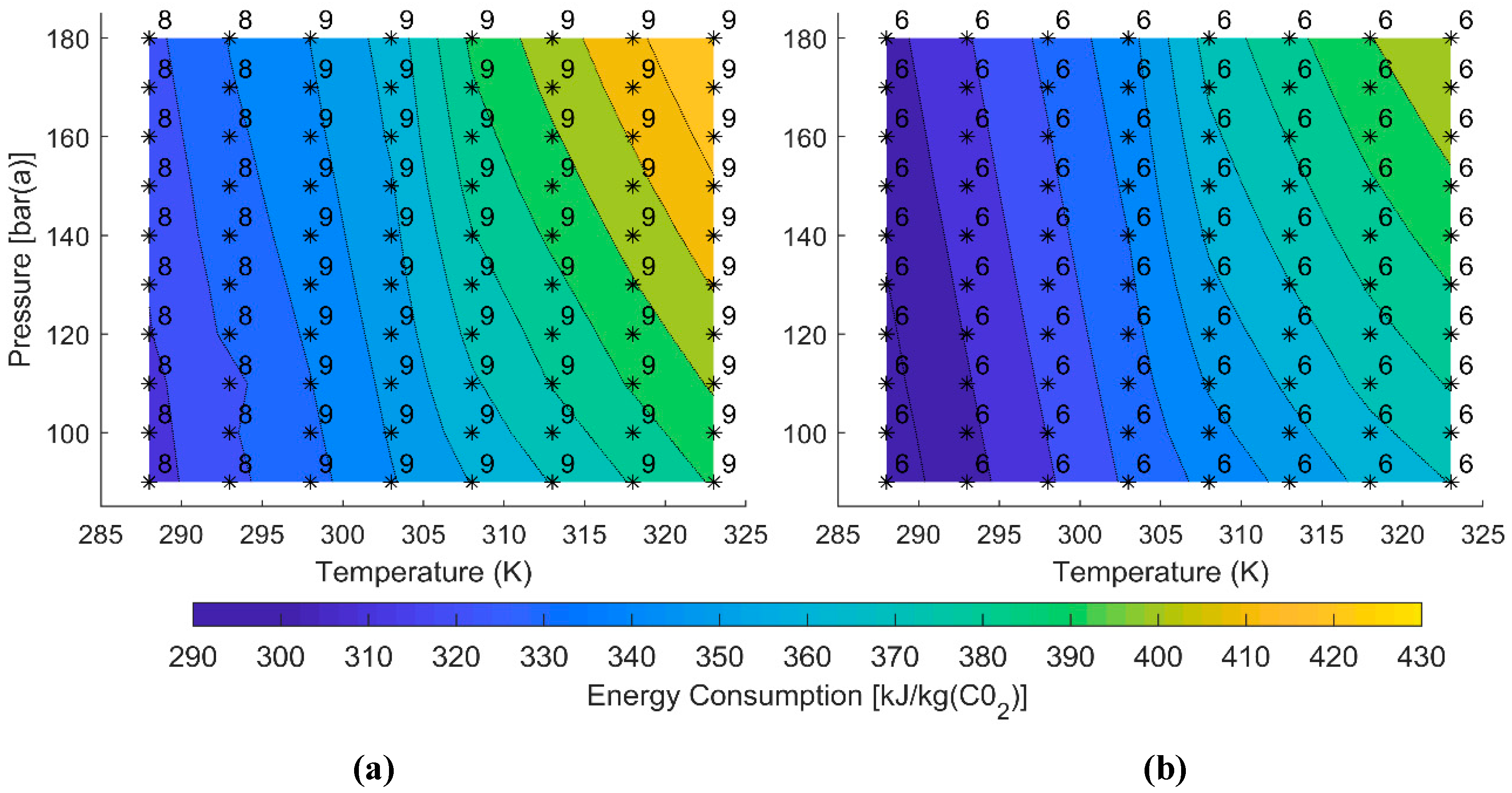
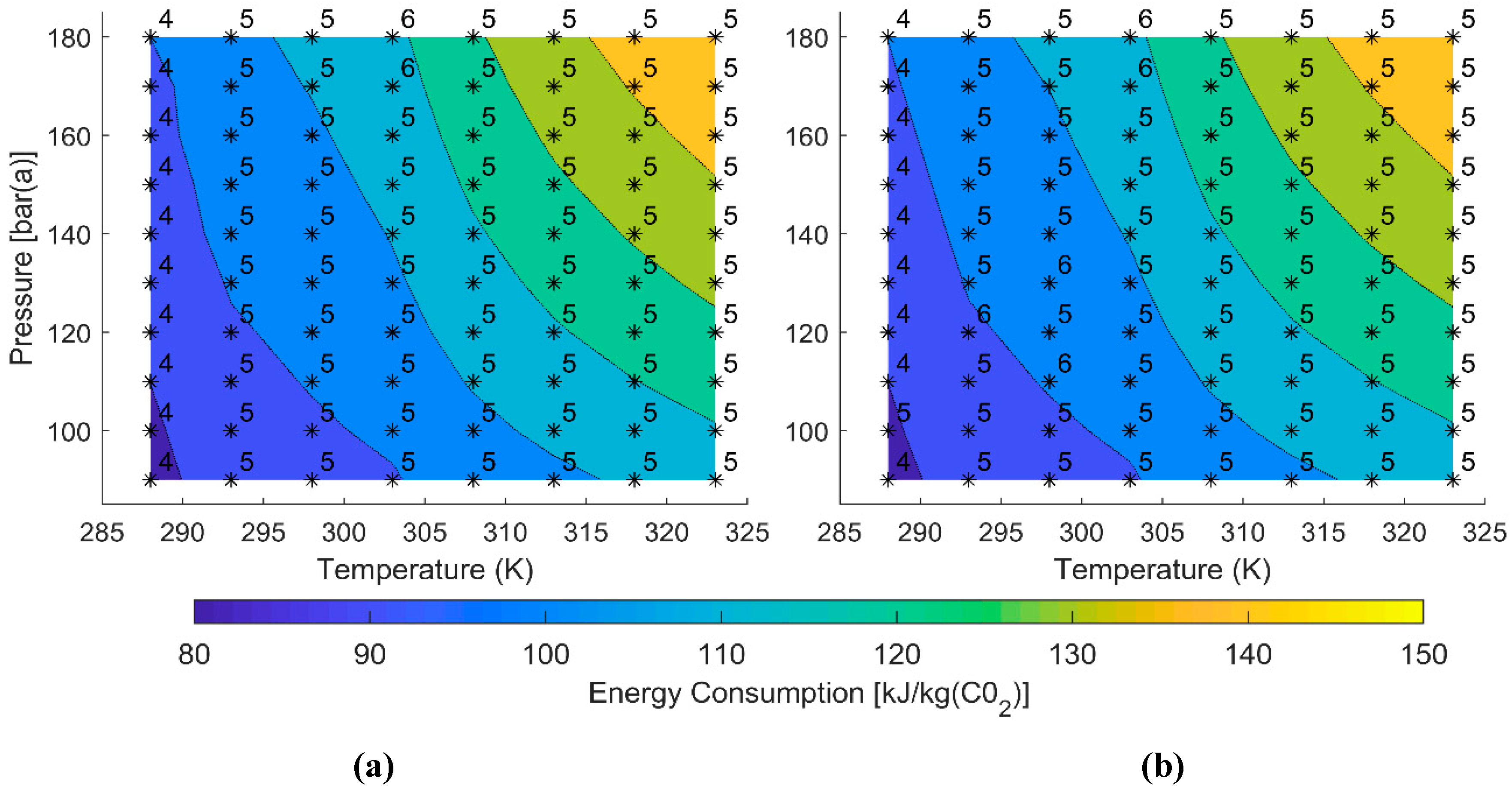

| Parameter | Constrained Cases | Unconstrained Cases |
|---|---|---|
| Pressure Ratio, | <2 | <10 |
| Efficiency, | 85% | |
| Stage pressure drop, | 0.5 bar | |
| Final stage inlet pressure, | Minimum of + 5 bar and, + 5 bar | |
| Parameter | Post | Pre | Oxyfuel |
|---|---|---|---|
| Cooling temperature, | 288 K to 323 K | 288 K to 323 K | 288 K to 323 K |
| Discharge pressure, | 90 bar(a) to 180 bar(a) | 90 bar(a) to 180 bar(a) | 90 bar(a) to 180 bar(a) |
| Inlet pressure, | 1.01 bar(a) | 1.01 bar(a) | 16.5 bar(a) |
| Dry stream composition | CO2 99.99 mole% N2 0.01 mole% | CO2 99.5 mole% CH4 0.5 mole% | CO2 96.16 mole% N2 2.45 mole% Ar 0.96 mole% O2 0.43 mole% |
| Parameter | Post const. | Post u.con. | Pre const. | Pre u.con. | Oxy const. | Oxy u.con. |
|---|---|---|---|---|---|---|
| Energy, Wc [kJ/kg(CO2)] | 292 to 406 | 312 to 425 | 316 to 431 | 294 to 140 | 87 to 150 | 87 to 150 |
| Stages, n (-) | 8 to 9 | 6 | 8 to 9 | 6 | 4 to 5 | 4 to 6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jackson, S.; Brodal, E. Optimization of the Energy Consumption of a Carbon Capture and Sequestration Related Carbon Dioxide Compression Processes. Energies 2019, 12, 1603. https://doi.org/10.3390/en12091603
Jackson S, Brodal E. Optimization of the Energy Consumption of a Carbon Capture and Sequestration Related Carbon Dioxide Compression Processes. Energies. 2019; 12(9):1603. https://doi.org/10.3390/en12091603
Chicago/Turabian StyleJackson, Steven, and Eivind Brodal. 2019. "Optimization of the Energy Consumption of a Carbon Capture and Sequestration Related Carbon Dioxide Compression Processes" Energies 12, no. 9: 1603. https://doi.org/10.3390/en12091603
APA StyleJackson, S., & Brodal, E. (2019). Optimization of the Energy Consumption of a Carbon Capture and Sequestration Related Carbon Dioxide Compression Processes. Energies, 12(9), 1603. https://doi.org/10.3390/en12091603