Optimal Re-Dispatching of Cascaded Hydropower Plants Using Quadratic Programming and Chance-Constrained Programming
Abstract
:1. Introduction
- A combination of QP and CC programming for the minimization of HPP re-dispatching is proposed in this paper. The aim of re-dispatching is to avoid congestion in the transmission network caused by uncertain WPP production.
- The meshed transmission network and uncertainty in wind speed forecast are taken into consideration using the concept of PTDFs, together with CC programming.
- Verification of the proposed optimization methodology was carried out using a model of a real-life transmission system, as well as a real-life cascaded hydropower system.
2. Problem Formulation
2.1. General Description of the Problem
2.2. Modeling of the Hydropower Plants
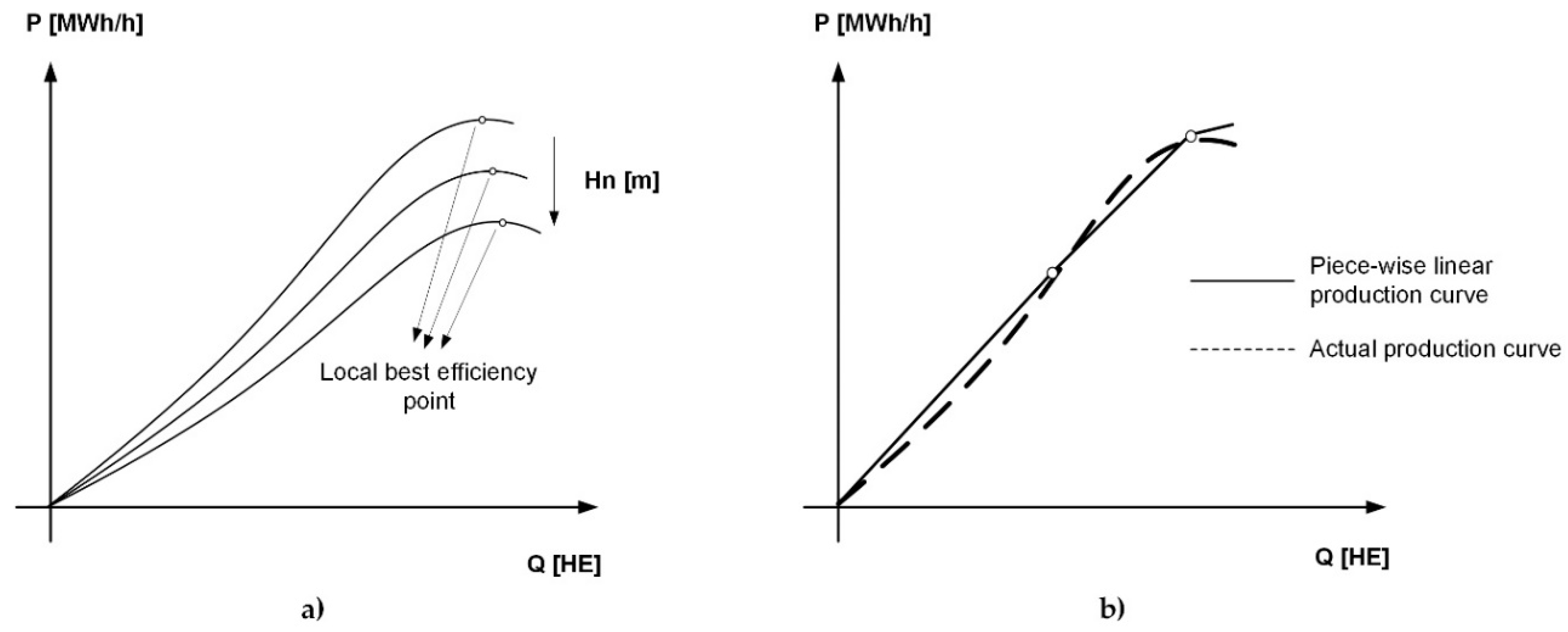
- When the reservoir of the HPP is large (seasonal reservoir), then discharge of water through the HPP turbine for one day is very small compared to the total volume of water in the reservoir; therefore, the head does not change significantly in one day. This is the situation with HPP1 and HPP2 in our case study.
- When the reservoir of the HPP is located in one place (up a hill) and a water turbine is located in another place (in a valley), the total head can be very large (even a few hundred meters). The reservoir and the turbine are connected with long penstock, which constitutes most of the head. Such a hydropower plant type is called a diversion. Since the water level in the reservoirs is just a small portion of the total head, its variability cannot significantly change the total head. This is the situation with HPP4 in our case study.
2.3. Modeling of the Wind Power Plants
2.4. Modeling of the Power Flows in the Transmission Network
3. Proposed Optimization Methodology
3.1. Description of the Proposed Methodology
- Technical data of the HPPs—the number of production units in every HPP and discharge characteristics of every production unit.
- Data from the day previous to the optimization period—reservoir levels at the end of the previous day (this is the starting point for the reservoir level in the optimization period), and discharge from the last few hours of the previous day (these data are necessary due to the time delay of water).
- Hydrological data—reservoir limits (minimum water limit of the reservoir, as well as maximal water limit of the reservoir), the time delay of water from the upstream reservoir to the downstream reservoir, and the desired level of water in the reservoirs at the end of the optimization period.
- Forecast of local water inflow to the river and reservoirs, the forecast of day-ahead electricity market price, and the forecast of the average market price for the next optimization period (future market price).
- Day-ahead dispatch plan of all HPPs (discharge or production plan for every hour in the optimization period).
- Day-ahead reservoir management plan (the levels of water in reservoirs at the end of every hour of the optimization period).
- All the output data from the first optimization stage.
- Forecasted wind speed for every hour of the optimization period, together with the error of the forecast.
- Available transfer capacities (ATCs) of the transmission lines that are congested.
- PTDFs for the congested transmission lines and HPPs.
- Changed dispatched plan of the HPPs (changed discharge plan) and changed reservoir management plan for the optimization period.
3.2. First Optimization Stage—Mixed-Integer Linear Programming
- HPP owner is a price taker (they cannot influence the electricity market price). The day-ahead electricity market price is forecasted and forecast uncertainty is neglected.
- Production costs (fuel costs and maintenance costs) of HPP are neglected.
- The discharge characteristics of every production unit are modeled using a piece-wise linear model, as explained in Section 2.2.
- Modeling of the forbidden zone in the discharge characteristic is enabled using an integer variable, as explained in Section 2.2.
- The optimization period is one day with the optimization step of one hour.
3.2.1. Objective Function
3.2.2. Optimization Constraints
3.3. Second Optimization Stage—Mixed-Integer Quadratic Programming and Chance-Constrained Programming
- The dispatch characteristic of the HPP is linearized with only one linear segment around the operating point, obtained in the first optimization stage. It is expected that the operating point of the HPP will be slightly changed due to re-dispatching.
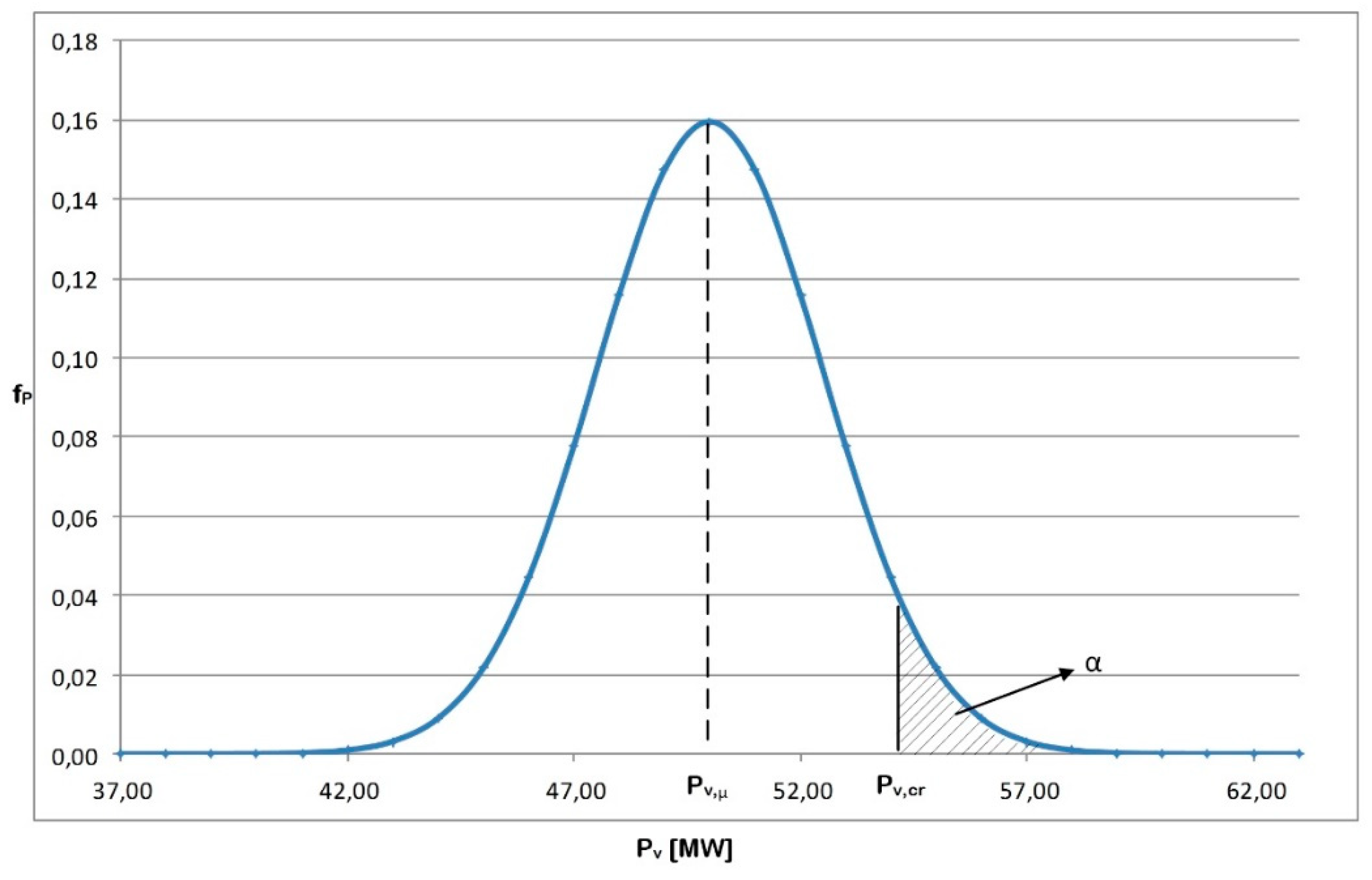
- The production of the WPPs is modeled based on the forecasted value and associated uncertainty of the forecast. The uncertainty of the forecast is not a constant value, but it increases as the time between the moment of forecasts and the moment that is forecasted increases. The assumed probability distribution of the uncertainty of WPP production forecasts is a normal or Gaussian distribution.
- The optimization period is the same as in the first optimization stage—one day with the optimization step of one hour. The optimization step can be changed easily.
3.3.1. Objective Function
3.3.2. Optimization Constraints
4. Case Study
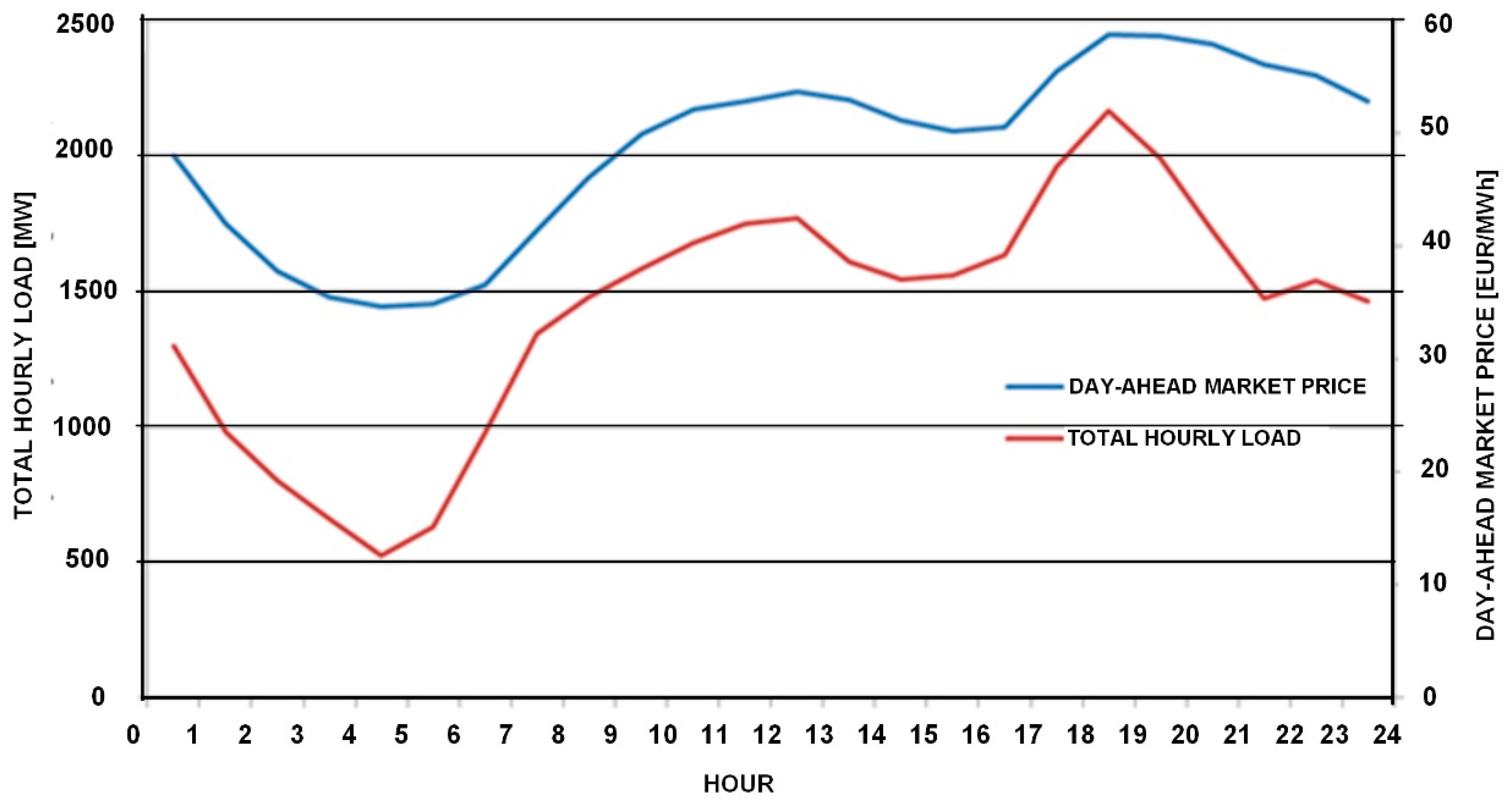
4.1. Input Data
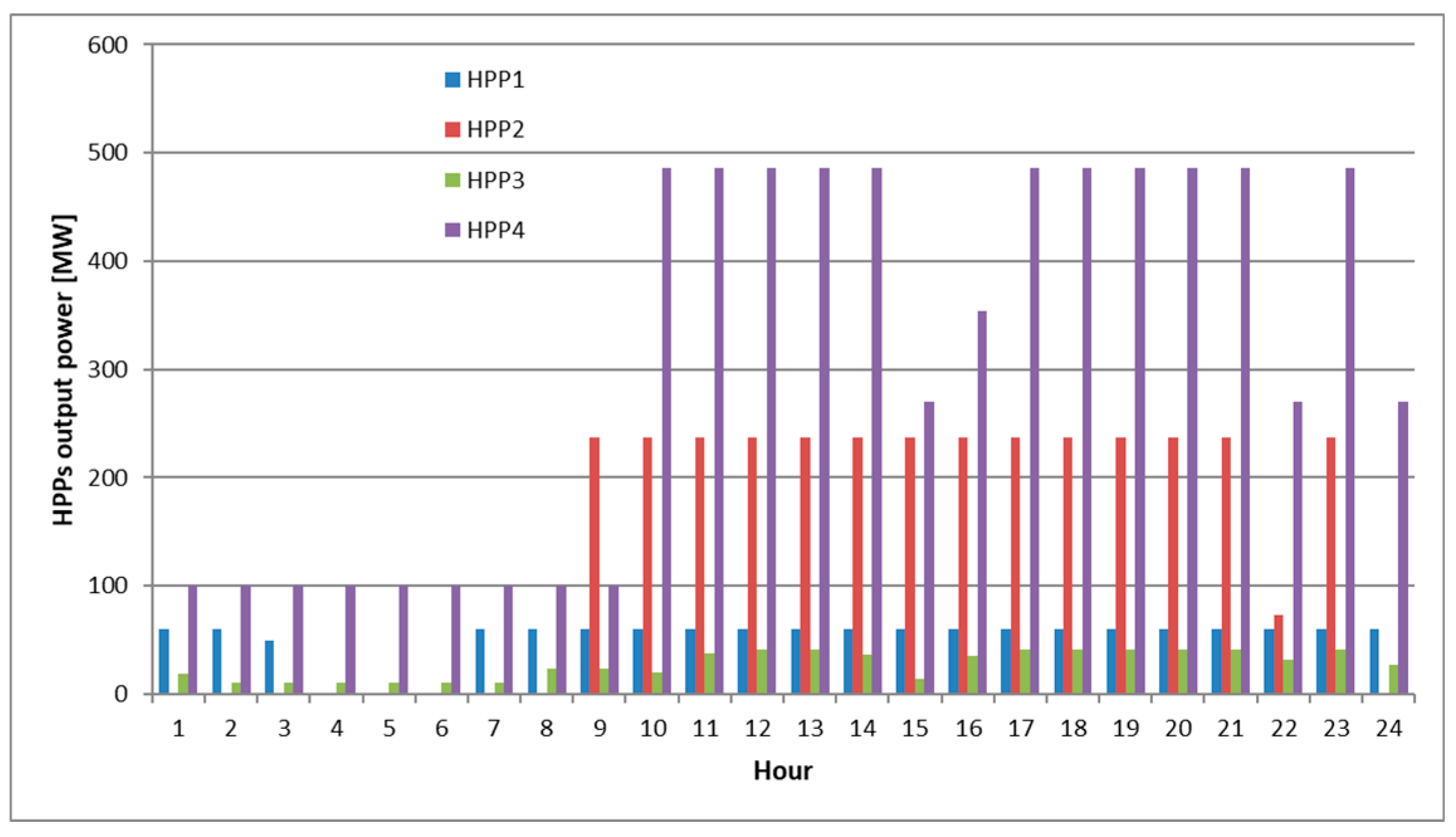
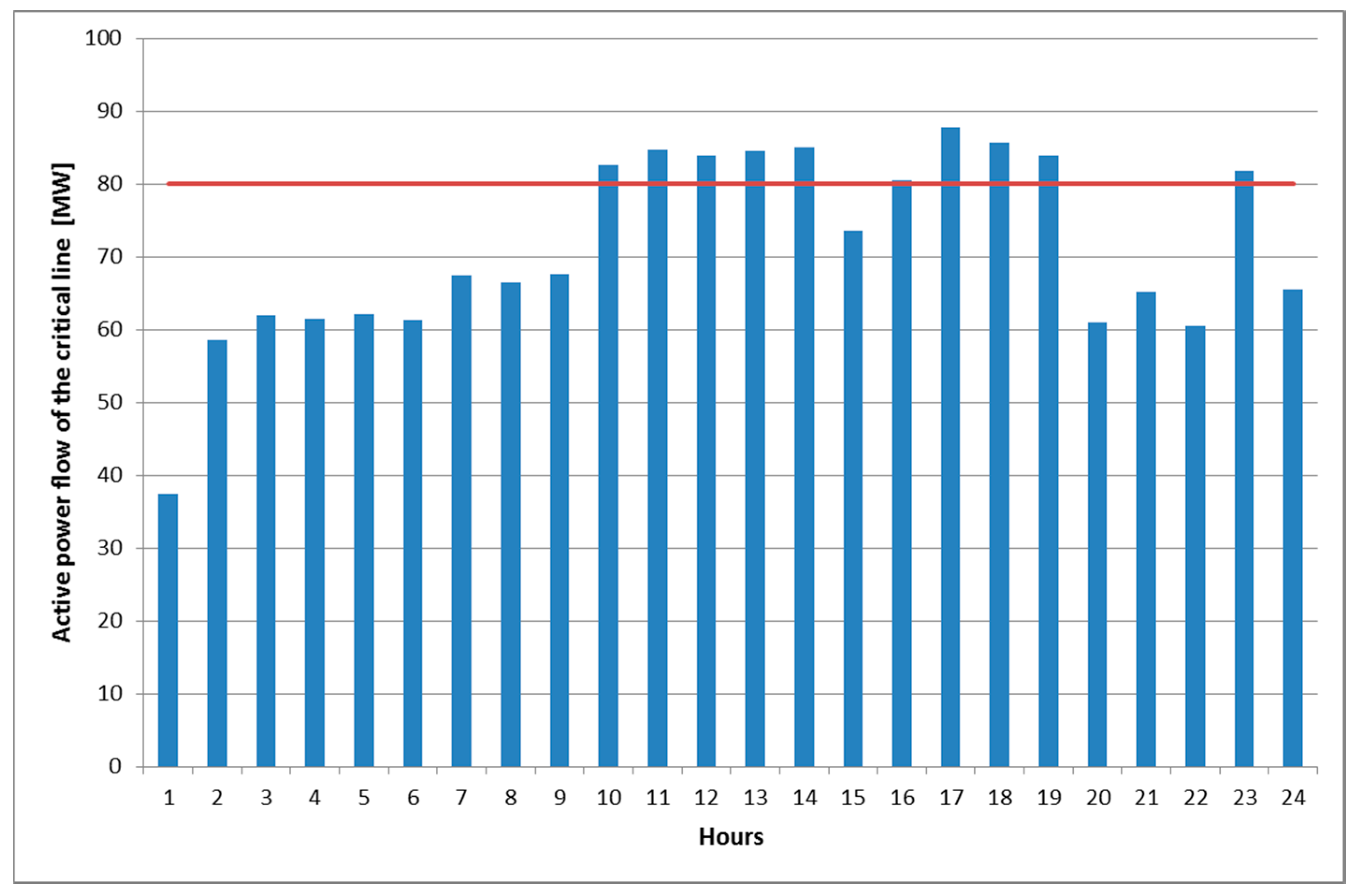
4.2. Results of the First Optimization Stage
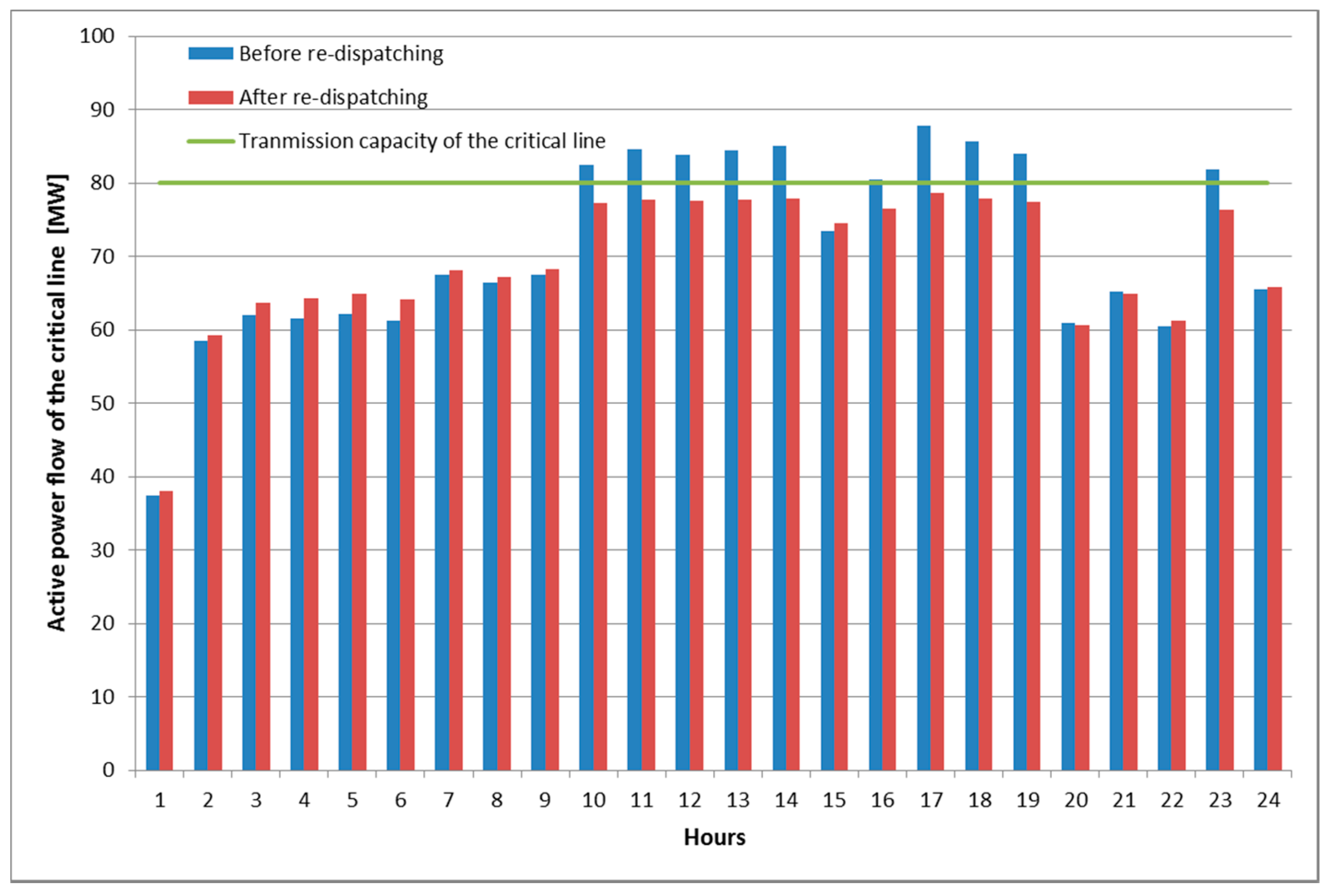
4.3. Results of the Second Optimization Stage
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Indices: | |
| i | Index of the HPP, i = 1, …, ni, where ni is the total number of HPPs. |
| t | Discrete time interval in the optimization period (hours, t = 1, …, 24). |
| a | Index of production unit (water turbine and generator) in the HPP, a = 1, …, nai, where nai is the total number of production units in the HPP i. |
| j | Index of the linear segment in the discharge characteristic of the production unit, j = 1, …, njai, where njai is the total number of linear segments in the discharge characteristic of the production unit a in the HPP i. |
| v | Index of the WPP, v = 1, …, nv, where nv is the total number of WPPs. |
| Parameters: | |
| Maximal discharge of the linear segment j in the discharge characteristic of production unit a in HPP i. The unit is HE. | |
| Minimal discharge of production unit a in HPP i. The unit is HE. | |
| Maximal discharge through production unit a in HPP i. The unit is HE. | |
| Production equivalent of the linear segment j in the discharge characteristic of production unit a in HPP i. The unit is MWh/HEh. | |
| Production equivalent that describes a minimum discharge segment of production unit a in HPP i. The unit is MWh/HEh. | |
| Production equivalent of HPP i that is used for calculation of HPP production in the future optimization period (next day). The unit is MWh/HEh. | |
| Production equivalent of the discharge characteristic around the operating point obtained in the first optimization stage of the production unit a in the HPP i. The unit is MWh/HEh. | |
| Maximal reservoir volume of HPP i. The unit is HE. | |
| Minimal reservoir volume of HPP i. The unit is HE. | |
| Minimum amount of water that can remain in the reservoir of HPP i in the last hour of the optimization period. This value is slightly smaller than the V(i, t = 24) obtained in the first optimization stage. The unit is HE. | |
| The maximum amount of water that can remain in the reservoir of the HPP i in the last hour of the optimization period. This value is slightly higher than the V(i, t = 24) obtained in the first optimization stage. The unit is HE. | |
| Minimal amount of water that needs to be discharged from the reservoir i during the optimization period. This value is determined by the medium-term reservoir management plan. The unit is HE. | |
| The maximal amount of water that can be discharged from the reservoir i during the optimization period. This value is determined by the medium-term reservoir management plan. The unit is HE. | |
| The local inflow of water in the reservoir i in the hour t. The unit is HE. | |
| Forecasted day-ahead electricity market price. The unit is €/MWh. | |
| Forecasted average future electricity price (the average price for the next optimization period—next day). The unit is €/MWh. | |
| C | Artificial penalty cost associated with water spillage. The unit is €/MWh. |
| The time delay, i.e., time it takes for the water from the upstream reservoir to reach the first downstream reservoir. | |
| The amount of electric energy in every hour t (expressed as a constant power for one hour) for every HPP i that is contracted in advance by bilateral contracts. The unit is MW. | |
| PTDF which determines the change of active power flow of transmission line k due to active power change of HPP i. | |
| PTDF which determines the change of active power flow of transmission line k due to active power change of the WPP i. | |
| Forecasted production of WPP v in the hour t. The unit is MW. | |
| The available transmission capacity of the transmission line k in the hour t. The unit is MWh/h. | |
| Output active power of HPP i in the hour t obtained in the first optimization stage. The unit is MWh/h. | |
| Variables: | |
| Discharge of the linear segment j in the discharge characteristic of production unit a in HPP i during the hour t. The unit is HE. | |
| Total discharge through production unit a in HPP i during hour t. The unit is HE. | |
| Total discharge of HPP i during hour t. The unit is HE. | |
| Output electric power of the unit a in the HPP i during hour t. The unit is MW. | |
| Total output electric power of HPP i during hour t. The unit is MW. | |
| An integer variable that is used to model forbidden zones of the discharge characteristic of production unit a in HPP i. | |
| Volume of water in the reservoir of HPP i at the end of hour t. The unit is HE. | |
| The total spillage of water by HPP i during hour t. The unit is HE. | |
References
- Hossain, J.; Mahmud, A. (Eds.) Green Energy and Technology. In Renewable Energy Integration; Springer: Singapore, 2014; ISBN 978-981-4585-26-2. [Google Scholar]
- Chandler, W.G.; Dandeno, P.L.; Glimn, A.F.; Kirchmayer, L.K. Short-range economic operation of a combined thermal and hydroelectric power system [includes discussion]. Trans. Am. Inst. Electr. Eng. Part III Power Appar. Syst. 1953, 72, 1057–1065. [Google Scholar] [CrossRef]
- Hicks, R.; Gagnon, C.; Jacoby, S.; Kowalik, J. Large scale, nonlinear optimization of energy capability for the pacific northwest hydroelectric system. IEEE Trans. Power Appar. Syst. 1974, 93, 1604–1612. [Google Scholar] [CrossRef]
- Kerola, M. Calibration of an Optimisation Model for Short-term Hydropower Production Planning; Helsinki University of Technology: Helsinki, Finland, 2006. [Google Scholar]
- Fosso, O.B.; Belsnes, M.M. Short-term hydro scheduling in a liberalized power system. In Proceedings of the 2004 International Conference on Power System Technology, PowerCon 2004., IEEE, Singapore, 21–24 November 2004; Volume 2, pp. 1321–1326. [Google Scholar]
- Conejo, A.J.; Arroyo, J.M.; Contreras, J.; Villamor, F.A. Self-scheduling of a hydro producer in a pool-based electricity market. IEEE Trans. Power Syst. 2002, 17, 1265–1272. [Google Scholar] [CrossRef] [Green Version]
- Chang, G.W.; Aganagic, M.; Waight, J.G.; Medina, J.; Burton, T.; Reeves, S.; Christoforidis, M. Experiences with mixed integer linear programming based approaches on short-term hydro scheduling. IEEE Trans. Power Syst. 2001, 16, 743–749. [Google Scholar] [CrossRef] [Green Version]
- Yıldıran, U.; Kayahan, İ.; Tunç, M.; Şisbot, S. MILP based short-term centralized and decentralized scheduling of a hydro-chain on Kelkit River. Int. J. Electr. Power Energy Syst. 2015, 69, 1–8. [Google Scholar] [CrossRef]
- Rajšl, I.; Ilak, P.; Delimar, M.; Krajcar, S.; Rajšl, I.; Ilak, P.; Delimar, M.; Krajcar, S. Dispatch method for independently owned hydropower plants in the same river flow. Energies 2012, 5, 3674–3690. [Google Scholar] [CrossRef]
- Catalão, J.P.S.; Pousinho, H.M.I.; Mendes, V.M.F. Scheduling of head-dependent cascaded hydro systems: Mixed-integer quadratic programming approach. Energy Convers. Manag. 2010, 51, 524–530. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Díaz, J.I.; Wilhelmi, J.R.; Arévalo, L.A. Optimal short-term operation schedule of a hydropower plant in a competitive electricity market. Energy Convers. Manag. 2010, 51, 2955–2966. [Google Scholar] [CrossRef]
- Hoseynpour, O.; Mohammadiivatloo, B.; Nazari-Heris, M.; Asadi, S. Application of dynamic non-linear programming technique to non-convex short-term hydrothermal scheduling problem. Energies 2017, 10, 1440. [Google Scholar] [CrossRef]
- Fleten, S.-E.; Kristoffersen, T.K. Short-term hydropower production planning by stochastic programming. Comput. Oper. Res. 2008, 35, 2656–2671. [Google Scholar] [CrossRef]
- Séguin, S.; Fleten, S.-E.; Côté, P.; Pichler, A.; Audet, C. Stochastic short-term hydropower planning with inflow scenario trees. Eur. J. Oper. Res. 2017, 259, 1156–1168. [Google Scholar] [CrossRef]
- Hjelmeland, M.N.; Helseth, A.; Korpås, M. Medium-term hydropower scheduling with variable head under inflow, energy and reserve capacity price uncertainty. Energies 2019, 12, 189. [Google Scholar] [CrossRef]
- Lu, P.; Zhou, J.; Wang, C.; Qiao, Q.; Mo, L. Short-term hydro generation scheduling of Xiluodu and Xiangjiaba cascade hydropower stations using improved binary-real coded bee colony optimization algorithm. Energy Convers. Manag. 2015, 91, 19–31. [Google Scholar] [CrossRef]
- Mo, L.; Lu, P.; Wang, C.; Zhou, J. Short-term hydro generation scheduling of Three Gorges–Gezhouba cascaded hydropower plants using hybrid MACS-ADE approach. Energy Convers. Manag. 2013, 76, 260–273. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Gharehpetian, G.B. Short-term scheduling of hydro-based power plants considering application of heuristic algorithms: A comprehensive review. Renew. Sustain. Energy Rev. 2017, 74, 116–129. [Google Scholar] [CrossRef]
- Bélanger, C.; Gagnon, L. Adding wind energy to hydropower. Energy Policy 2002, 30, 1279–1284. [Google Scholar] [CrossRef]
- Vardanyan, Y.; Amelin, M. The state-of-the-art of the short term hydro power planning with large amount of wind power in the system. In Proceedings of the 2011 8th International Conference on the European Energy Market (EEM), Zagreb, Croatia, 25–27 May 2011; pp. 448–454. [Google Scholar]
- Damodaran, S.K.; Sunil Kumar, T.K. Hydro-thermal-wind generation scheduling considering economic and environmental factors using heuristic algorithms. Energies 2018, 11, 353. [Google Scholar] [CrossRef]
- Ilak, P.; Rajšl, I.; Đaković, J.; Delimar, M. Duality based risk mitigation method for construction of joint hydro-wind coordination short-run marginal cost curves. Energies 2018, 11, 1254. [Google Scholar] [CrossRef]
- Knežević, G.; Topić, D.; Jurić, M.; Nikolovski, S. Joint market bid of a hydroelectric system and wind parks. Comput. Electr. Eng. 2019, 74, 138–148. [Google Scholar] [CrossRef]
- Matevosyan, J.; Olsson, M.; Söder, L. Hydropower planning coordinated with wind power in areas with congestion problems for trading on the spot and the regulating market. Electr. Power Syst. Res. 2009, 79, 39–48. [Google Scholar] [CrossRef]
- Matevosyan, J.; Soder, L. Optimal daily planning for hydro power system coordinated with wind power in areas with limited export capability. In Proceedings of the 2006 International Conference on Probabilistic Methods Applied to Power Systems, Stockholm, Sweden, 11–15 June 2006; pp. 1–8. [Google Scholar]
- Sauer, P. On the formulation of power distribution factors for linear load flow methods. IEEE Trans. Power Appar. Syst. 1981, 100, 764–770. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W. Chance-constrained programming. Manag. Sci. 1959, 6, 73–79. [Google Scholar] [CrossRef]
- Wang, Q.; Guan, Y.; Wang, J. A chance-constrained two-stage stochastic program for unit commitment with uncertain wind power output. IEEE Trans. Power Syst. 2012, 27, 206–215. [Google Scholar] [CrossRef]
- Yu, H.; Chung, C.Y.; Wong, K.P.; Zhang, J.H. A chance constrained transmission network expansion planning method with consideration of load and wind farm uncertainties. IEEE Trans. Power Syst. 2009, 24, 1568–1576. [Google Scholar] [CrossRef]
- Wu, J.; Li, G.; Sun, Y. Calculation of maximum injection power of wind farms based on chance-constrained programming. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition, Chicago, IL, USA, 21–24 April 2008; pp. 1–6. [Google Scholar]
- Wang, Q.; Wang, J.; Guan, Y. Wind power bidding based on chance-constrained optimization. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 24–29 July 2011; pp. 1–2. [Google Scholar]
- Söder, L.; Amelin, M. Efficient Operation and Planning of Power Systems, 11th ed.; Royal Institute of Technology: Stockholm, Sweeden, 2011. [Google Scholar]
- Olsson, M.; Soder, L. Hydropower planning including trade-off between energy and reserve markets. In Proceedings of the 2003 IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June; pp. 92–99.
- Giorsetto, P.; Utsurogi, K. Development of a new procedure for reliability modeling of wind turbine generators. IEEE Trans. Power Appar. Syst. 1983, PAS-102, 134–143. [Google Scholar] [CrossRef]
- Graeber, D.; Chatillon, O. Efficient integration of wind energy at EnBW TSO. In Proceedings of the 8th International Workshop on Large-Scale Integration of Wind Power into Power System as well as Transmission Networks for Offshore Wind Farms, Bremen, Germany, 1 July 2009. [Google Scholar]
- Willmott, C.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef] [Green Version]
- Hodge, B.M.; Lew, D.; Milligan, M.; Holttinen, H.; Sillanpää, S.; Gómez-Lázaro, E.; Scharff, R.; Söder, L.; Larsén, X.G.; Giebel, G.; et al. Wind power forecasting error distributions: An international comparison. In Proceedings of the 11th Annual International Workshop on Large-Scale Integration of Wind Power into Power Systems as well as on Transmission Networks for Offshore Wind Power Plants Conference, Lisbon, Portugal, 13–15 November 2012. [Google Scholar]
- Tinney, W.; Hart, C. Power Flow Solution by Newton’s Method. IEEE Trans. Power Appar. Syst. 1967, 86, 1449–1460. [Google Scholar] [CrossRef]
- Stott, B. Review of load-flow calculation methods. Proc. IEEE 1974, 62, 916–929. [Google Scholar] [CrossRef]
- Advanced Interactive Multidimensional Modeling System|AIMMS. Available online: https://aimms.com/ (accessed on 12 March 2019).
- Croatian Transmission System Operator HOPS. Available online: https://www.hops.hr/wps/portal/en/web (accessed on 19 March 2019).
- Croatian Transmission System Operator System Scheme. Available online: https://www.hops.hr/wps/portal/en/web/hees/data/present (accessed on 19 March 2019).
- European Power Exchange (EPEX SPOT). Available online: http://www.epexspot.com/en/ (accessed on 18 March 2019).
- Croatian Generating Company HEP Generation Ltd.—Hydro South. Available online: http://proizvodnja.hep.hr/proizvodnja/en/basicdata/hydro/south/default.aspx (accessed on 19 March 2019).
- PowerWorld Official Web Page. Available online: https://www.powerworld.com/ (accessed on 20 March 2019).









| HPP 1 | HPP 2 | HPP 3 | HPP 4 | |||||
|---|---|---|---|---|---|---|---|---|
| Rated power of production unit (MW) | 2 × 30 | 3 × 79 | 2 × 20.4 | 2 × 135 2 × 108 | ||||
| Rated turbine discharge (m3/s) | 2 × 60 | 3 × 23.3 | 2 × 110 | 2 × 60 2 × 50 | ||||
| Linearized discharge characteristic | Qas,max (HE) | µas (MWh/HEh) | Qas,max (HE) | µas (MWh/HEh) | Qas,max (HE) | µas (MWh/HEh) | Qas,max (HE) | µas (MWh/HEh) |
| 60 | 0.5 | 23.3 | 3.39 | 110 | 0.185 | 60 50 | 2.25 2.16 | |
| Maximal volume of water in the reservoir | 565 200 000 m3 157 000 HE | 799 200 000 m3 222 000 HE | 2 599 200 m3 722 HE | 4 399 200 m3 1 222 HE | ||||
| The minimal volume of water in the reservoir | 288 000 000 m3 80 000 HE | 648 000 000 m3 180 000 HE | 1 080 000 m3 300 HE | 2 520 000 m3 700 HE | ||||
| The volume of water in at the beginning of the optimization period | 360 000 000 m3 100 000 HE | 720 000 000 m3 200 000 HE | 1 800 000 m3 500 HE | 2 520 000 m3 700 HE | ||||
| Local inflow | 36 000 m3 10 HE | 36 000 m3 10 HE | 18 000 m3 5 HE | - | ||||
| The time delay of water from the upstream reservoir (h) | - | - | 7 (HE1) and 2 (HE2) | - | ||||
| Long-term bilateral contracts (MWh/h) | - | - | 10 | 100 | ||||
| Allowable daily discharge of water from the reservoir | 9 000 000 m3 2500 HE | 3 600 000 m3 1000 HE | No limit | No limit | ||||
| Hour | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Forecasted wind speed (m/s) | 11.2 | 12.7 | 12.7 | 13.6 | 14.3 | 14.4 | 13.7 | 14.3 | 12.9 | 12.5 | 11.9 | 13.2 |
| Forecasting error (%) | 0.1 | 0.6 | 1 | 1.4 | 1.9 | 2.2 | 2.6 | 3.1 | 3.2 | 3.3 | 3.35 | 3.4 |
| WPP power (MW) | 165.7 | 236.3 | 242.7 | 253 | 253 | 253 | 253 | 253 | 248.3 | 225 | 200.3 | 253 |
| Hour | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Forecasted wind speed (m/s) | 12.9 | 12.6 | 13.8 | 13.5 | 13.6 | 13.5 | 12.3 | 10.4 | 10.6 | 11.1 | 12.8 | 11.8 |
| Forecasting error (%) | 3.45 | 3.5 | 3.55 | 3.6 | 3.65 | 3.7 | 3.75 | 3.8 | 3.85 | 3.9 | 3.95 | 4 |
| WPP power (MW) | 253 | 253 | 253 | 253 | 253 | 253 | 253 | 165.5 | 179.4 | 216.9 | 253 | 253 |
| Hour | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Calculated ATC (MW) | 87.6 | 85.7 | 83.1 | 86.3 | 85.7 | 86.6 | 80.3 | 81.4 | 80.4 | 65.3 | 63.0 | 63.9 |
| Hour | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Calculated ATC (MW) | 63.2 | 62.6 | 74.4 | 67.3 | 59.8 | 62.0 | 63.7 | 64.0 | 63.4 | 78.7 | 66.0 | 82.3 |
| HPPs | HPP1 | HPP2 | HPP3 | HPP4 | WPP | |
|---|---|---|---|---|---|---|
| PTDFcr | 0.1238 | 0.0236 | 0.14 | 220 kV | 0.0211 | 0.2934 |
| 110 kV | 0.1076 | |||||
| Hour | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pv,cr (MW) | 165.7 | 238.8 | 242.7 | 253 | 253 | 253 | 253 | 253 | 253 | 253 | 253 | 253 |
| Hour | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Pv,cr (MW) | 253 | 253 | 253 | 253 | 253 | 253 | 253 | 165.5 | 179.4 | 216.9 | 253 | 253 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fekete, K.; Nikolovski, S.; Klaić, Z.; Androjić, A. Optimal Re-Dispatching of Cascaded Hydropower Plants Using Quadratic Programming and Chance-Constrained Programming. Energies 2019, 12, 1604. https://doi.org/10.3390/en12091604
Fekete K, Nikolovski S, Klaić Z, Androjić A. Optimal Re-Dispatching of Cascaded Hydropower Plants Using Quadratic Programming and Chance-Constrained Programming. Energies. 2019; 12(9):1604. https://doi.org/10.3390/en12091604
Chicago/Turabian StyleFekete, Krešimir, Srete Nikolovski, Zvonimir Klaić, and Ana Androjić. 2019. "Optimal Re-Dispatching of Cascaded Hydropower Plants Using Quadratic Programming and Chance-Constrained Programming" Energies 12, no. 9: 1604. https://doi.org/10.3390/en12091604
APA StyleFekete, K., Nikolovski, S., Klaić, Z., & Androjić, A. (2019). Optimal Re-Dispatching of Cascaded Hydropower Plants Using Quadratic Programming and Chance-Constrained Programming. Energies, 12(9), 1604. https://doi.org/10.3390/en12091604








