A Study on Deep Neural Network-Based DC Offset Removal for Phase Estimation in Power Systems
Abstract
:1. Introduction
Background
2. Data Acquisition
2.1. Data Generation
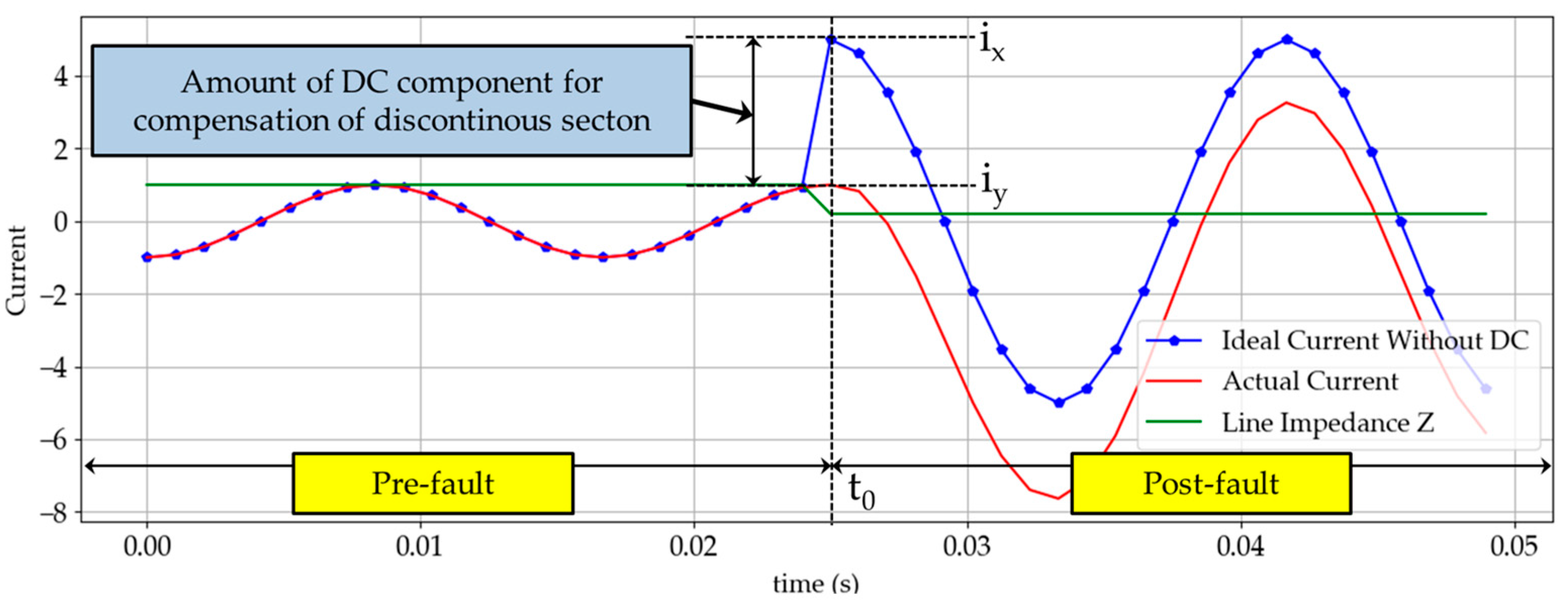
2.1.1. Exponentially Decaying DC Offset
2.1.2. Harmonics
2.1.3. Additive Noise
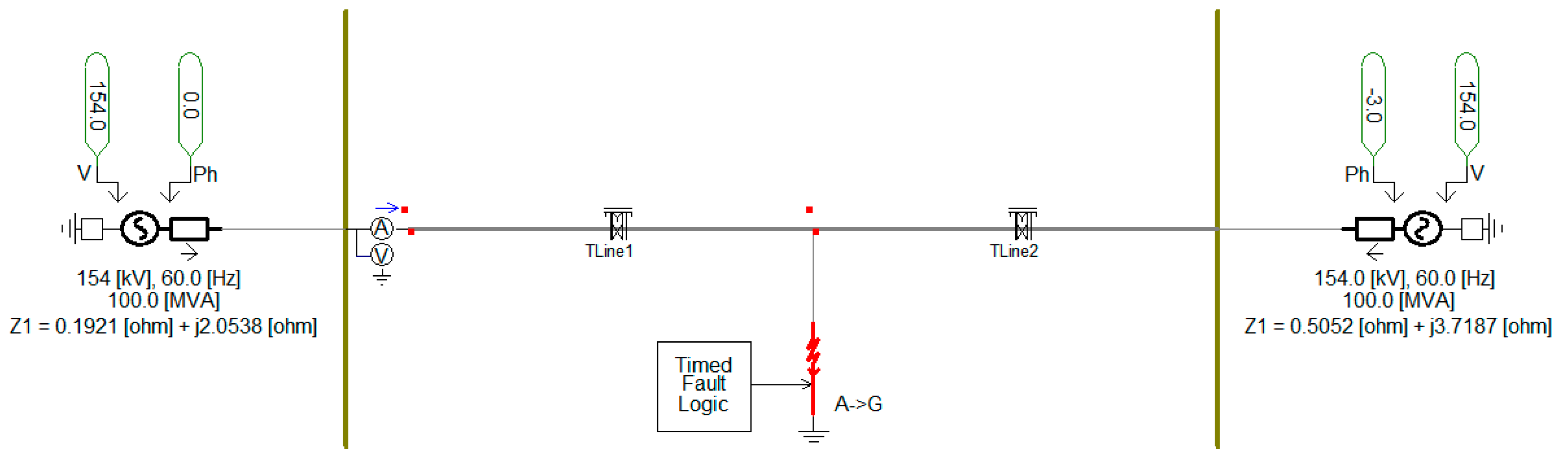
2.1.4. Simulation
2.2. Pre-Processing
3. Design of a DNN and Its Training
3.1. Autoencoder
3.2. Training Scenario of a DNN
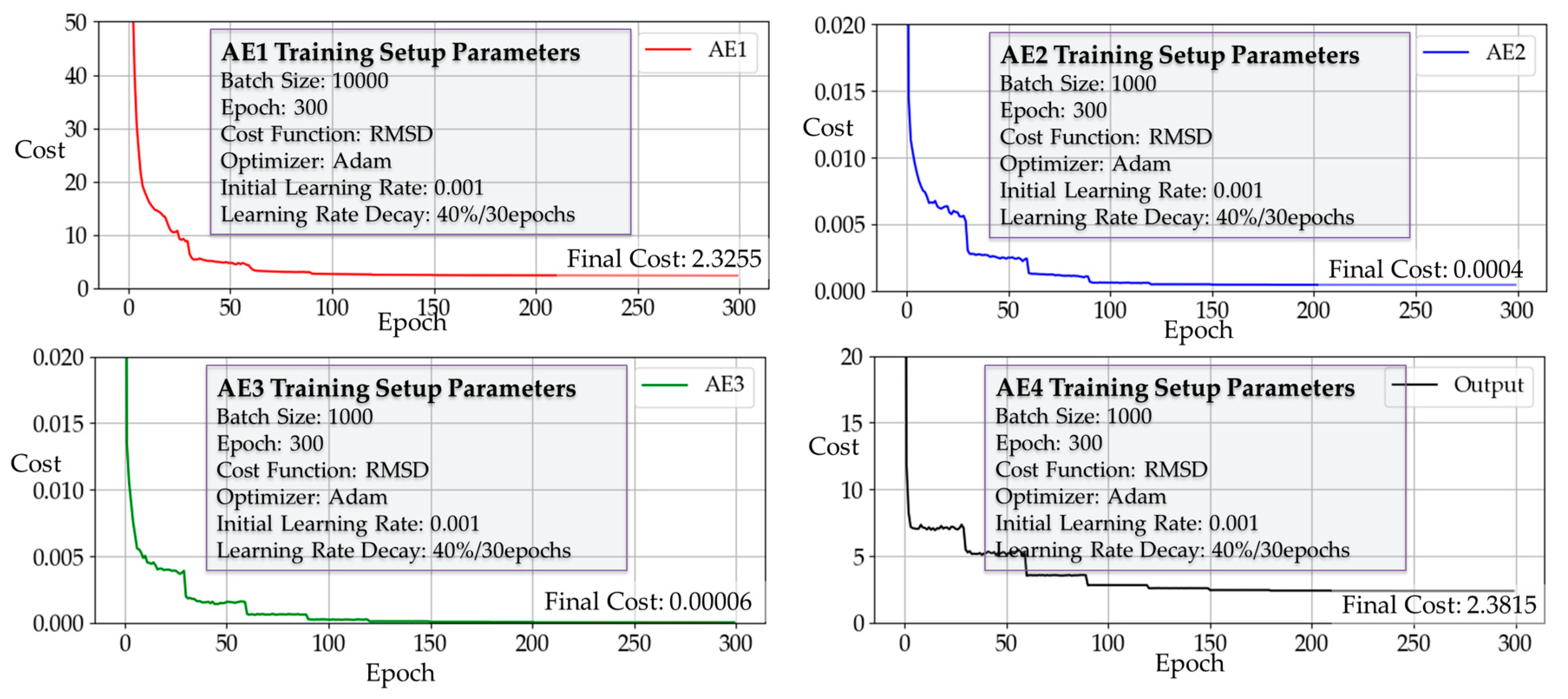
3.2.1. Pre-Training Hidden Layers
3.2.2. Pre-Training Output Layer
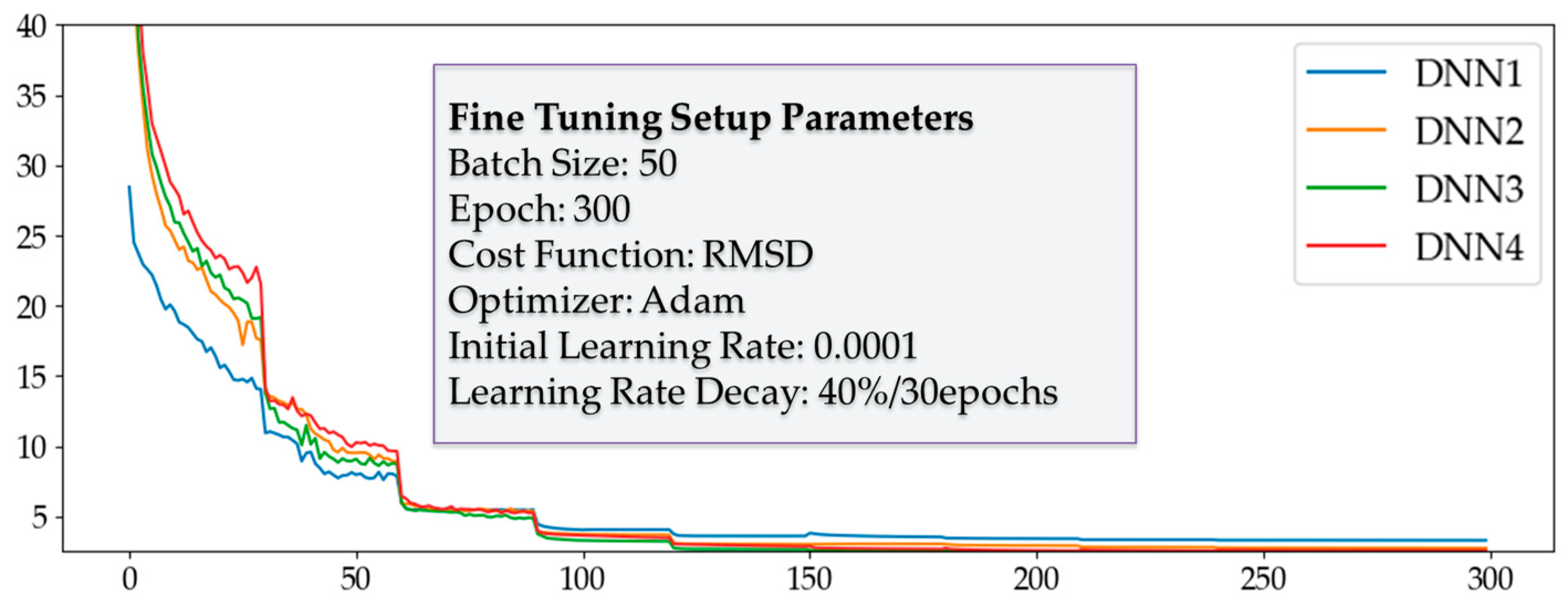
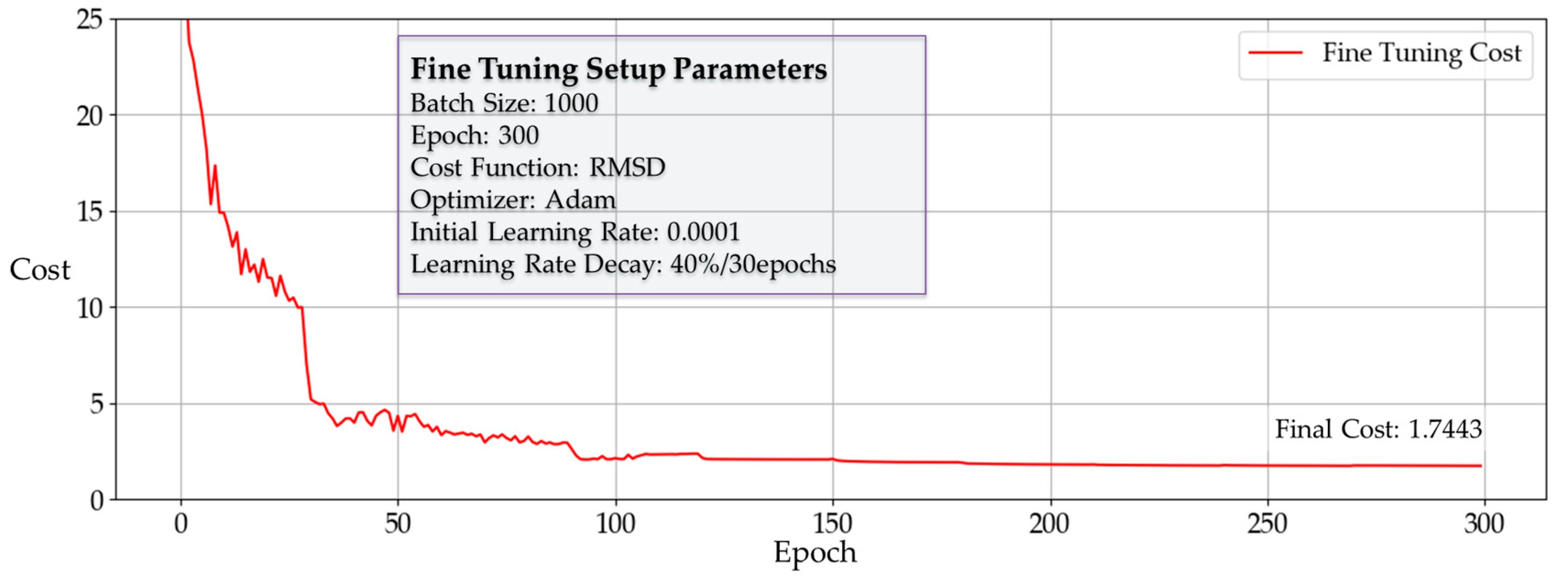
3.2.3. Supervised Fine Tuning
3.3. Determination of the DNN Size
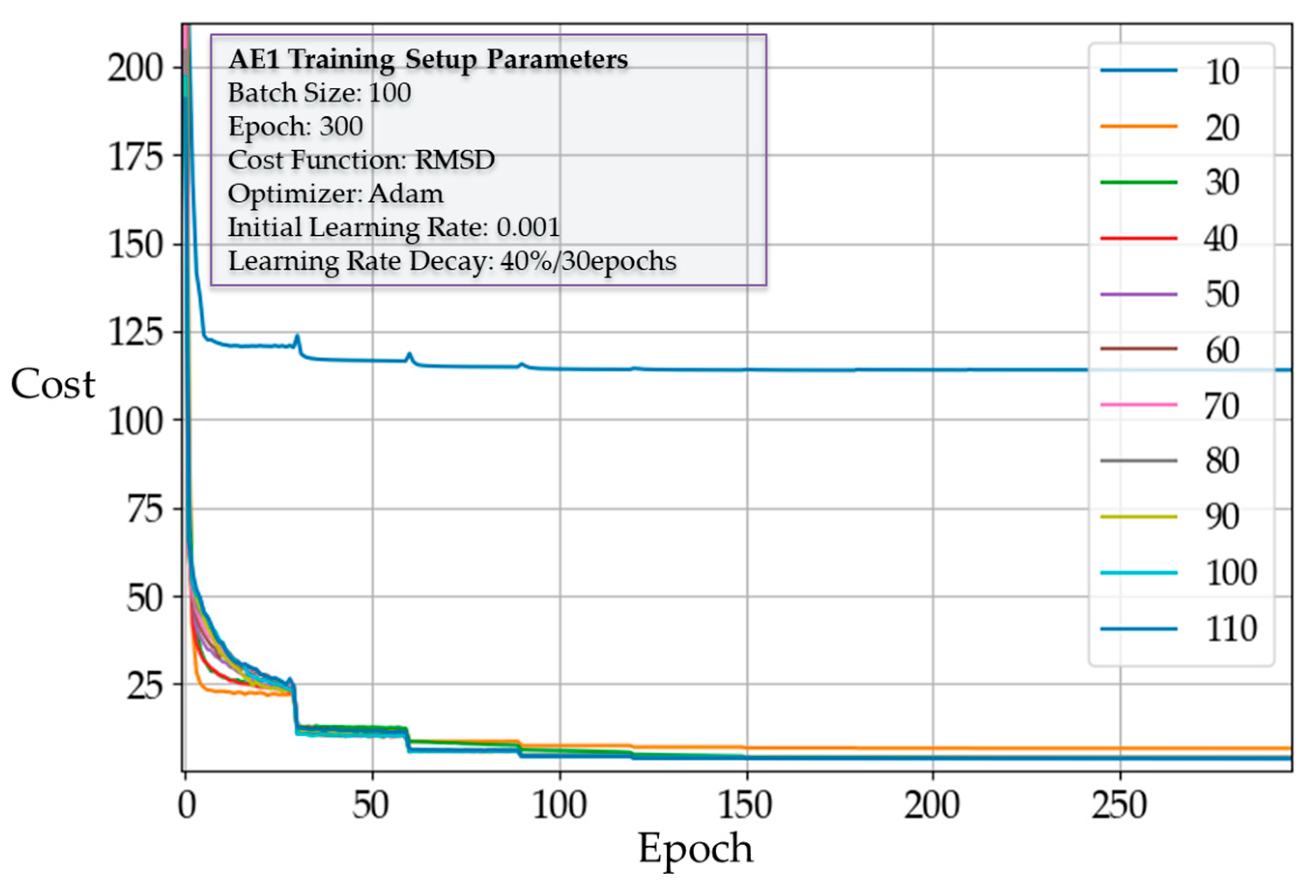
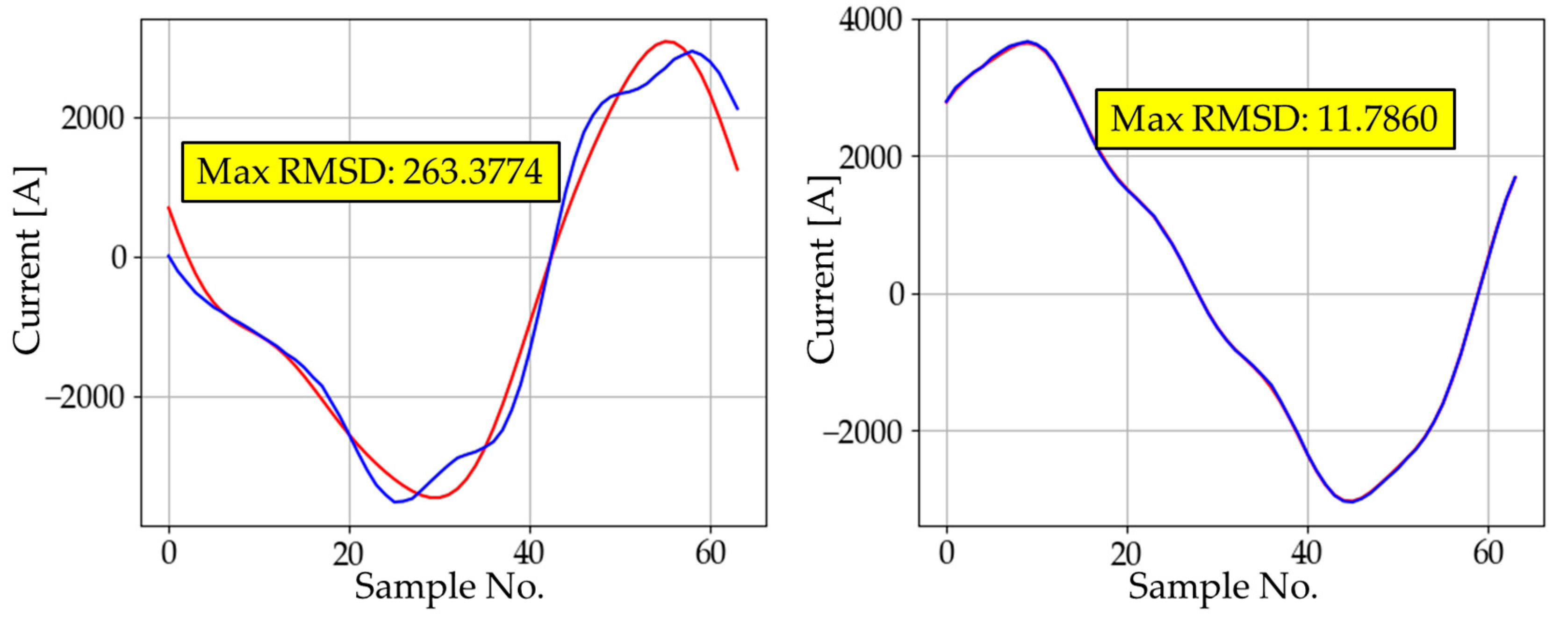
3.3.1. Number of Neurons in Each Layer
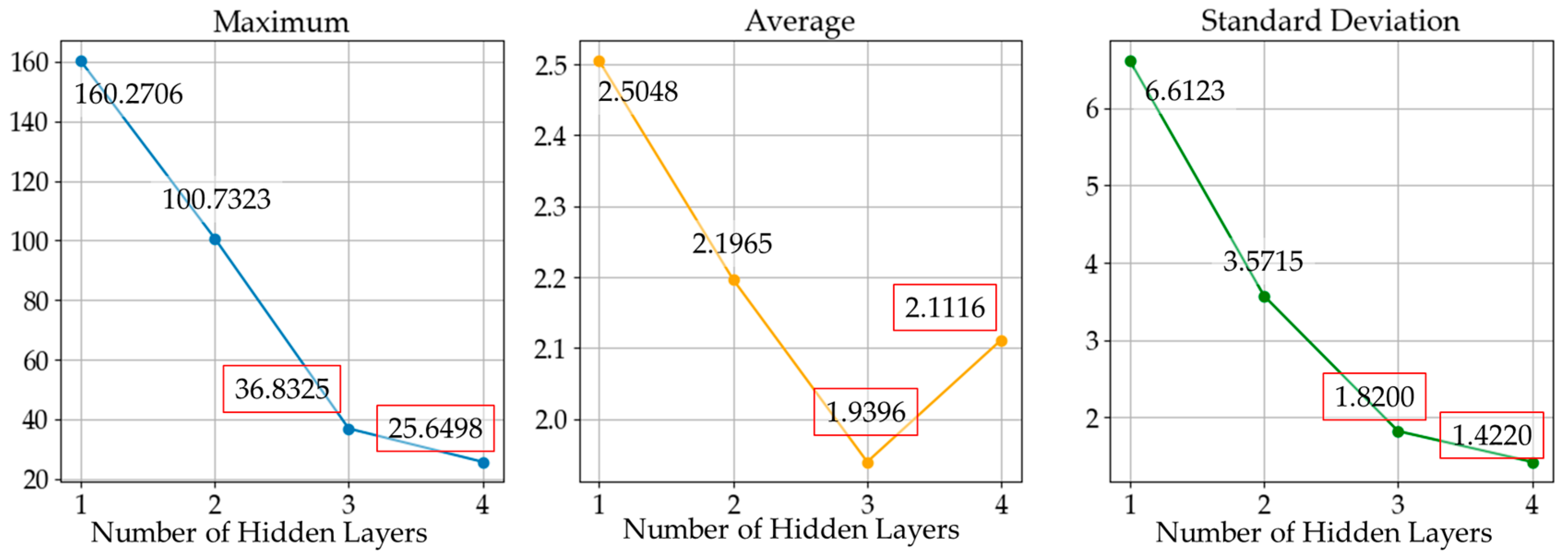
3.3.2. Number of Hidden Layers
3.4. DNN3 Training Result
4. Performance Tests and Discussions
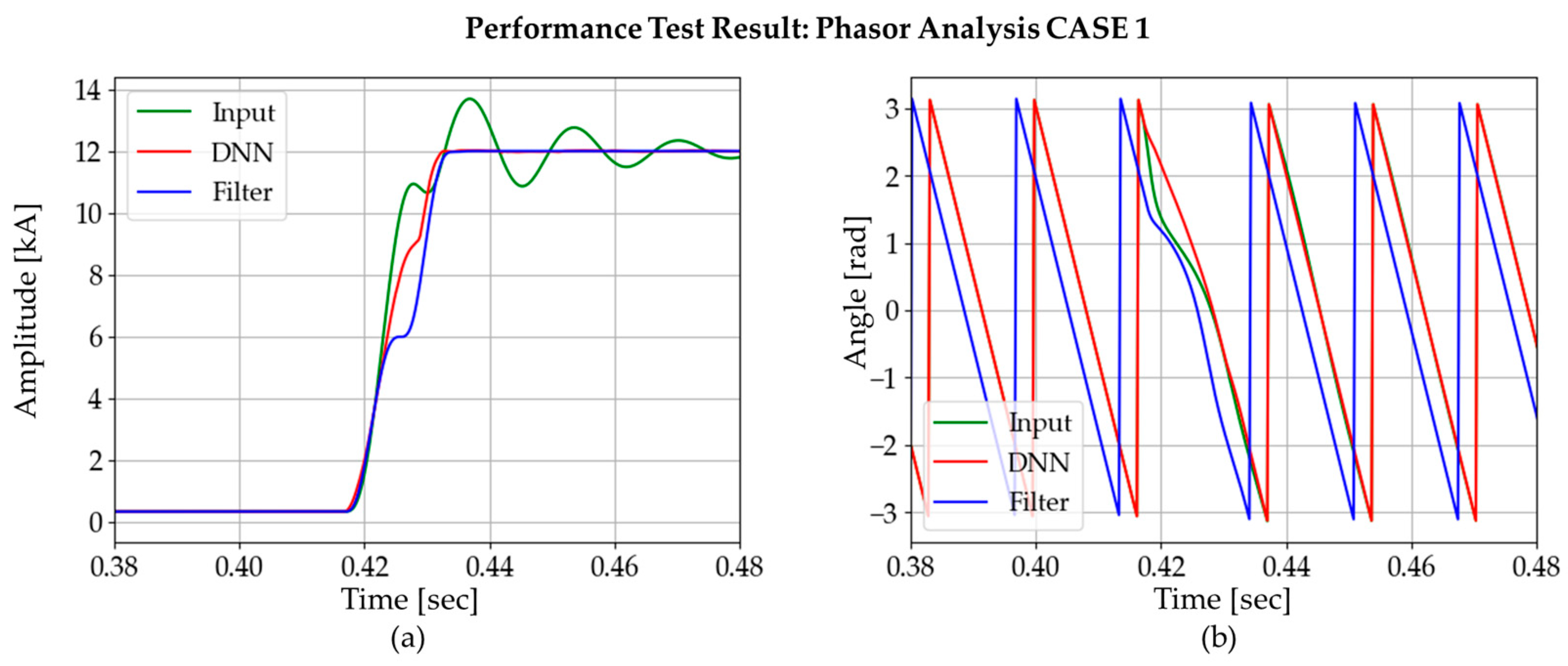
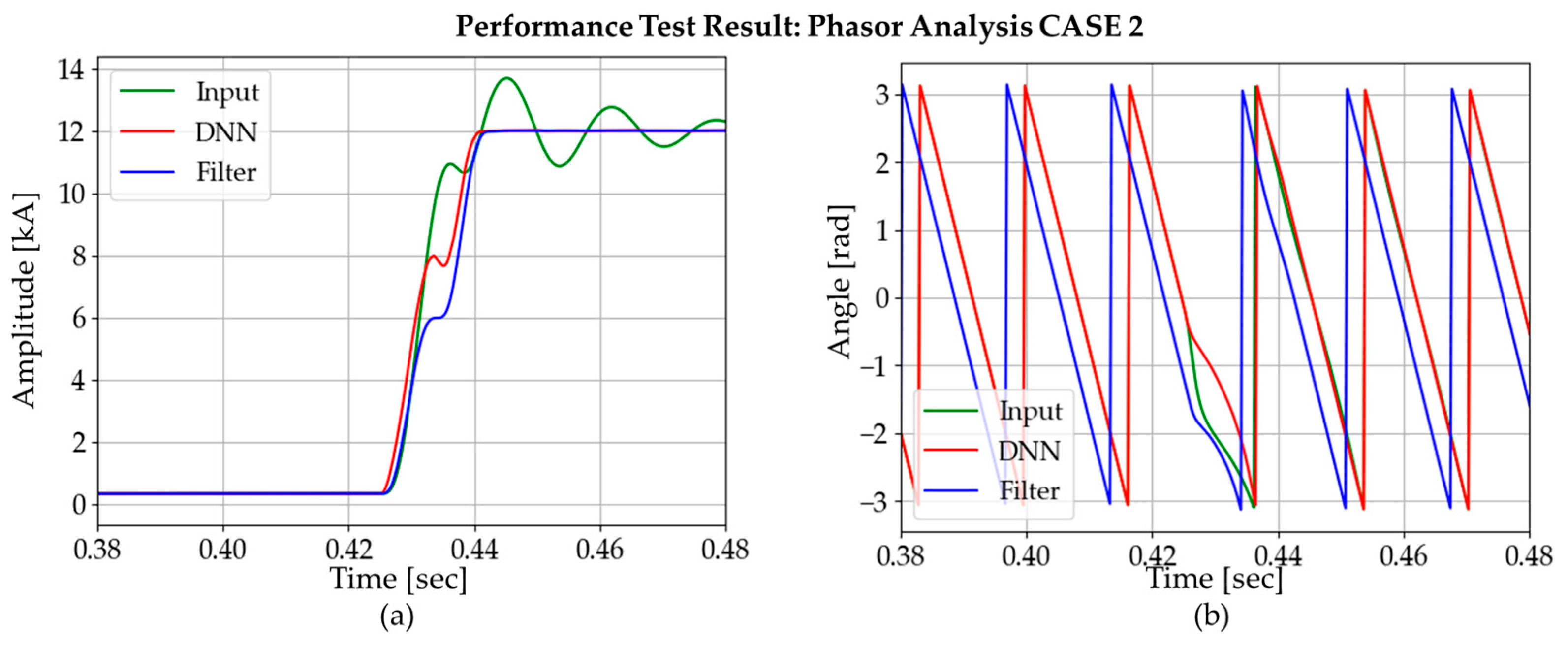
4.1. Response to Curents without Harmonics and Noise
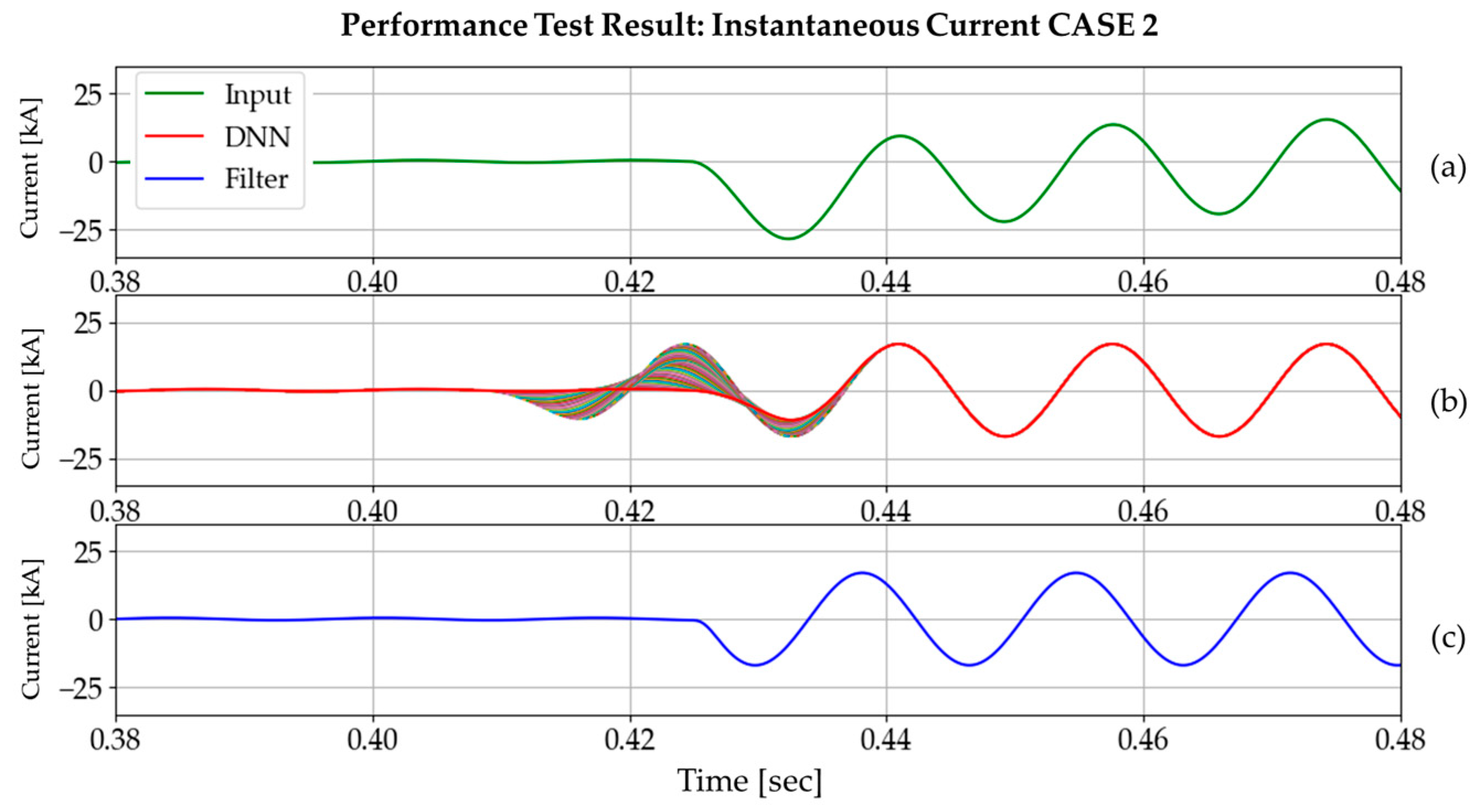
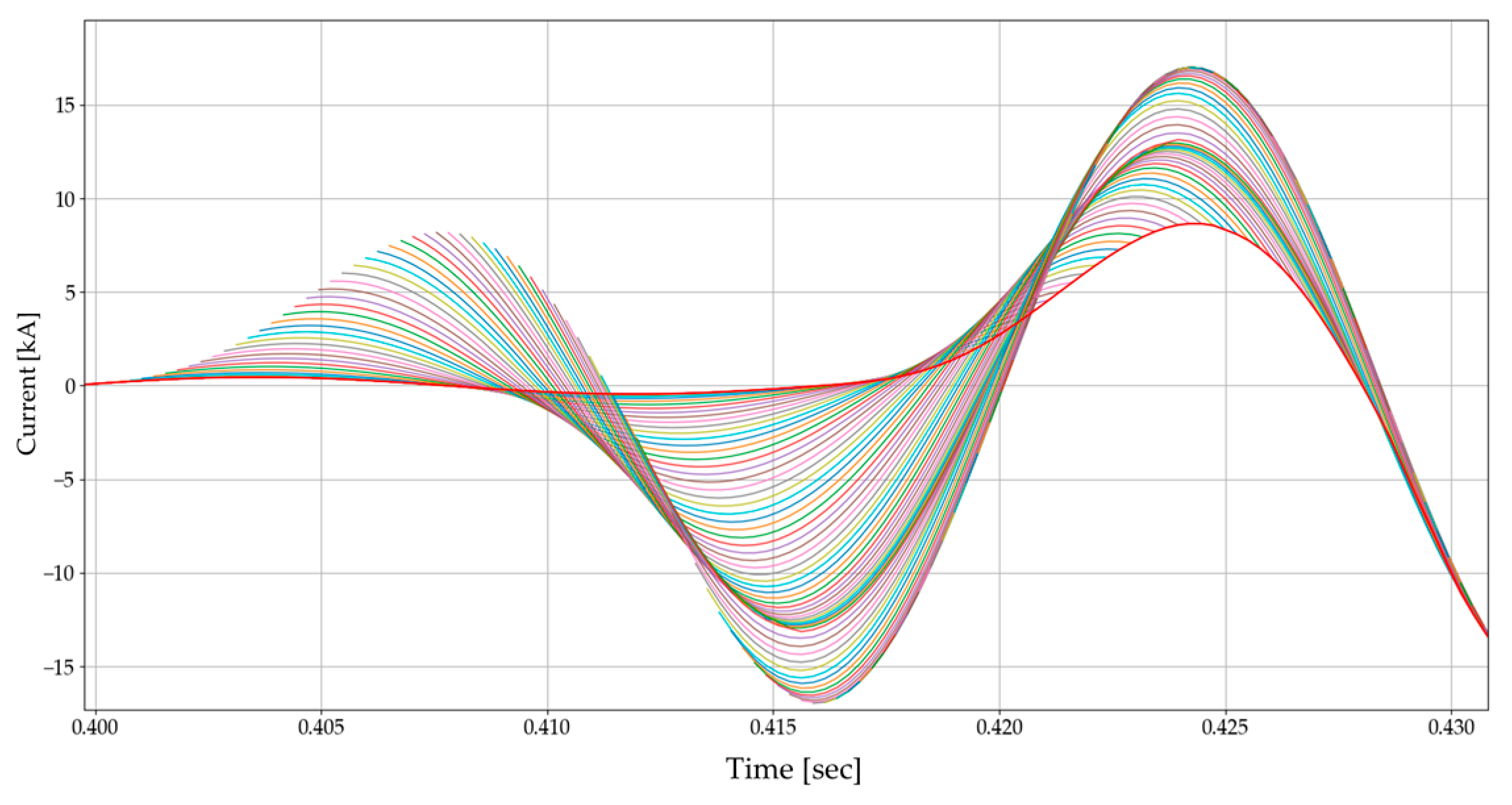
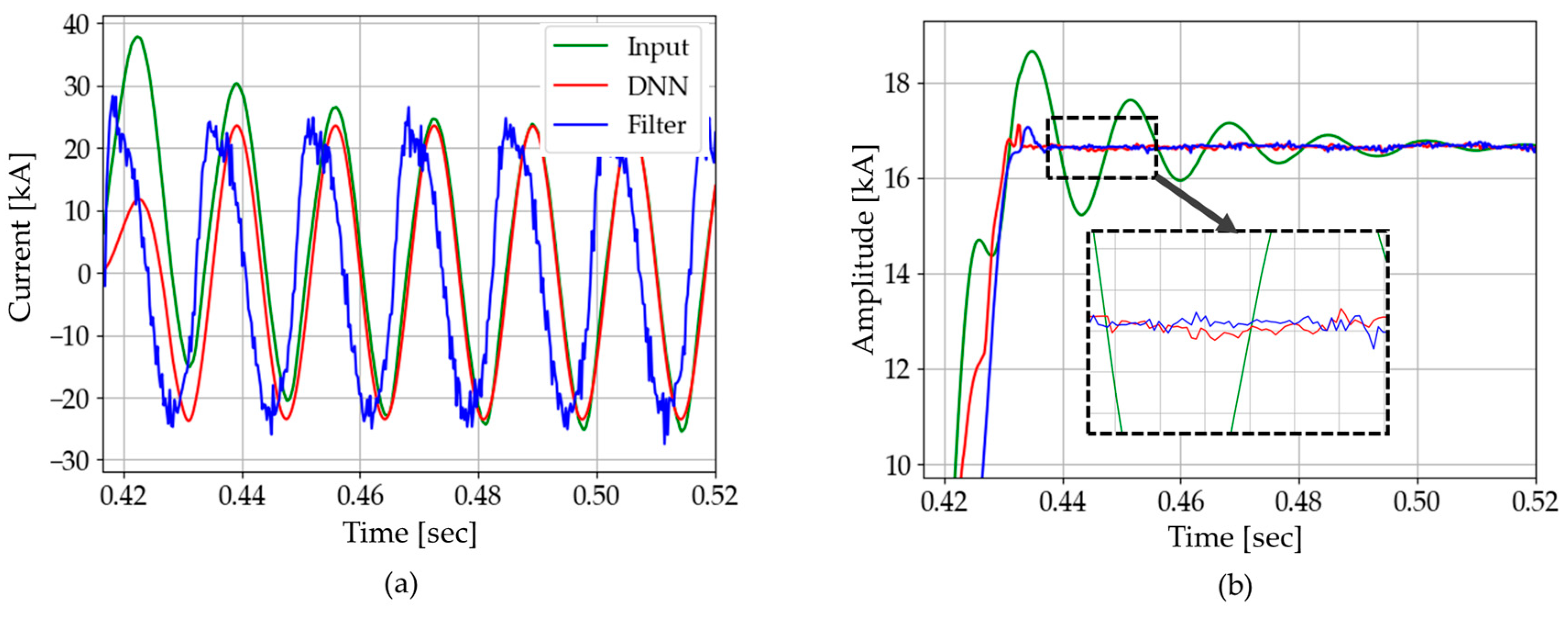
4.1.1. Instantaneous Current
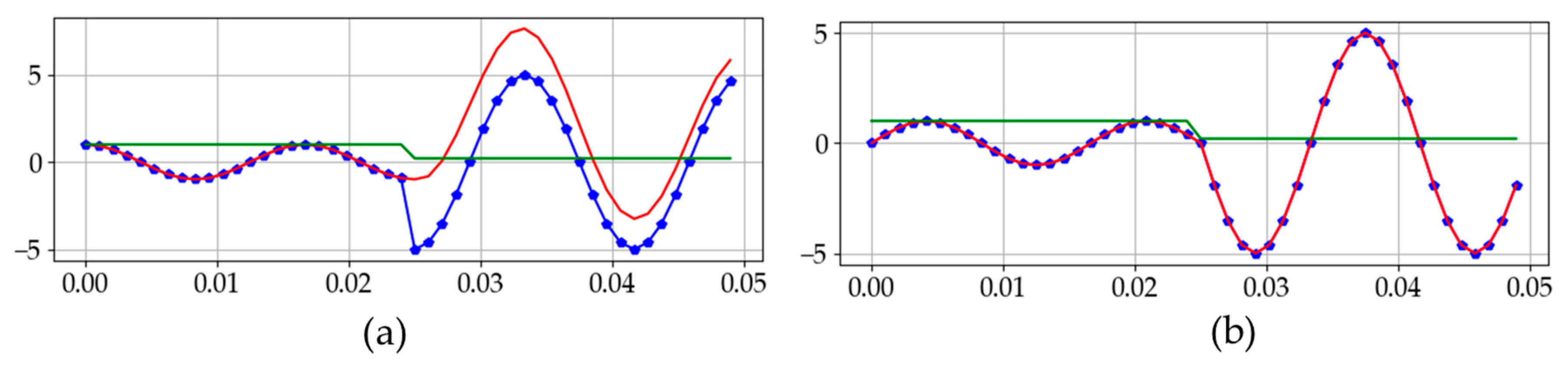
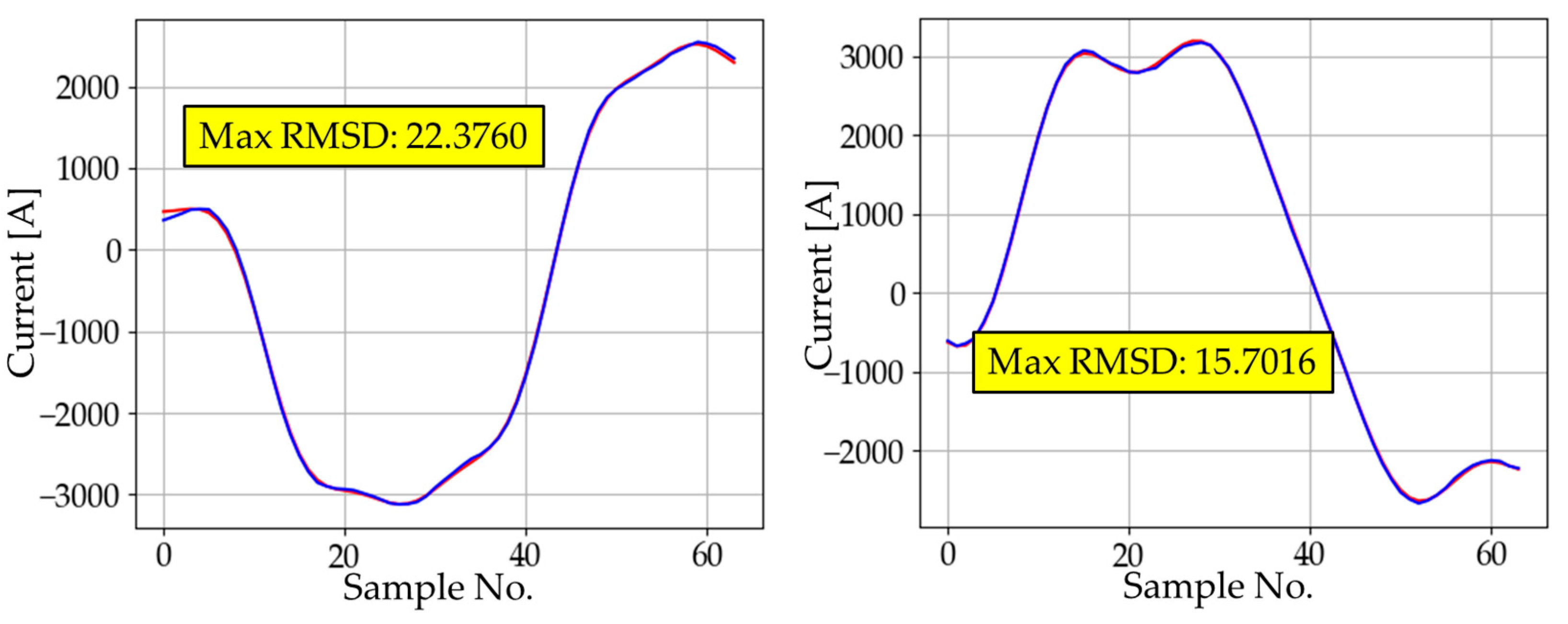
4.1.2. Results and Comparisons of Instantaneous Current
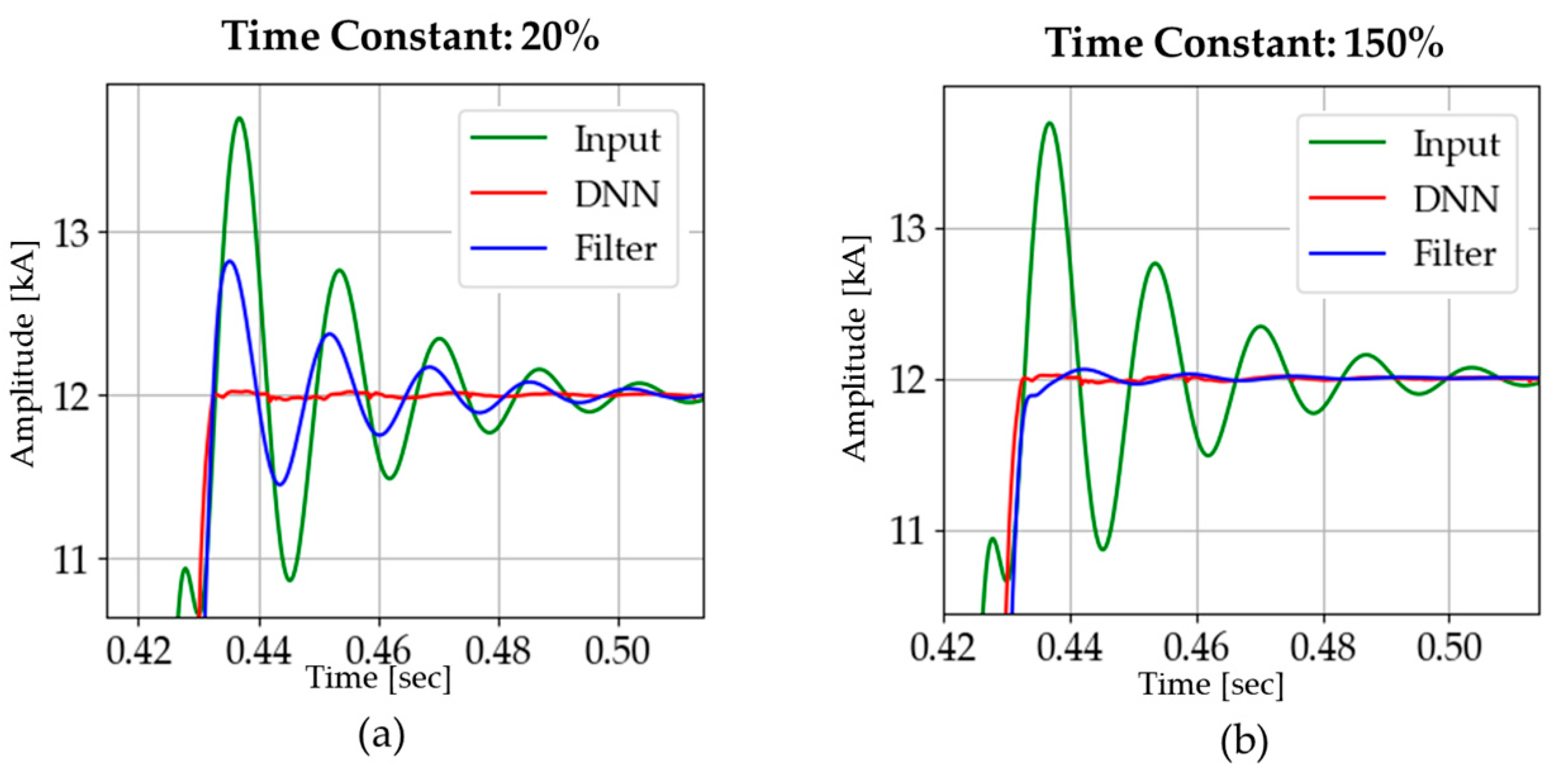
4.1.3. Comparison Using Inaccurate Time Constants
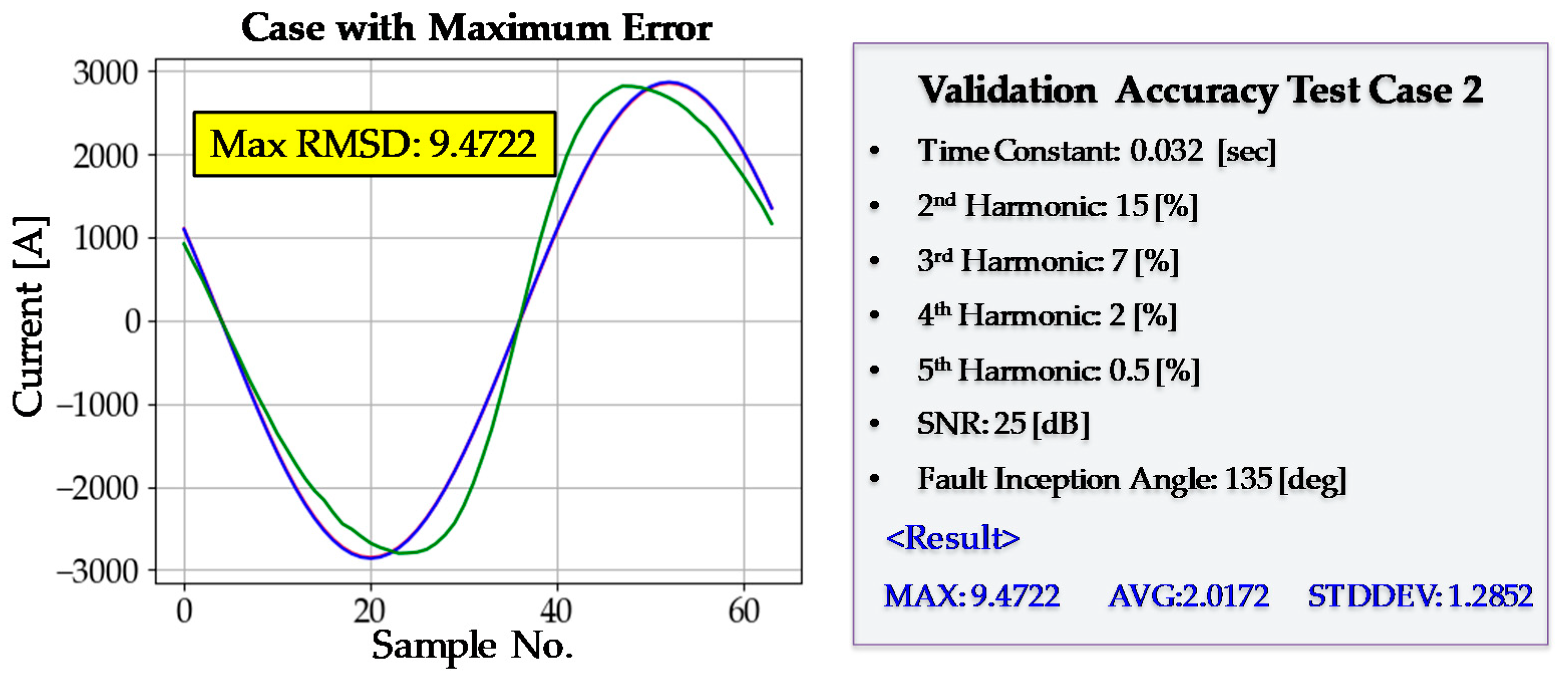
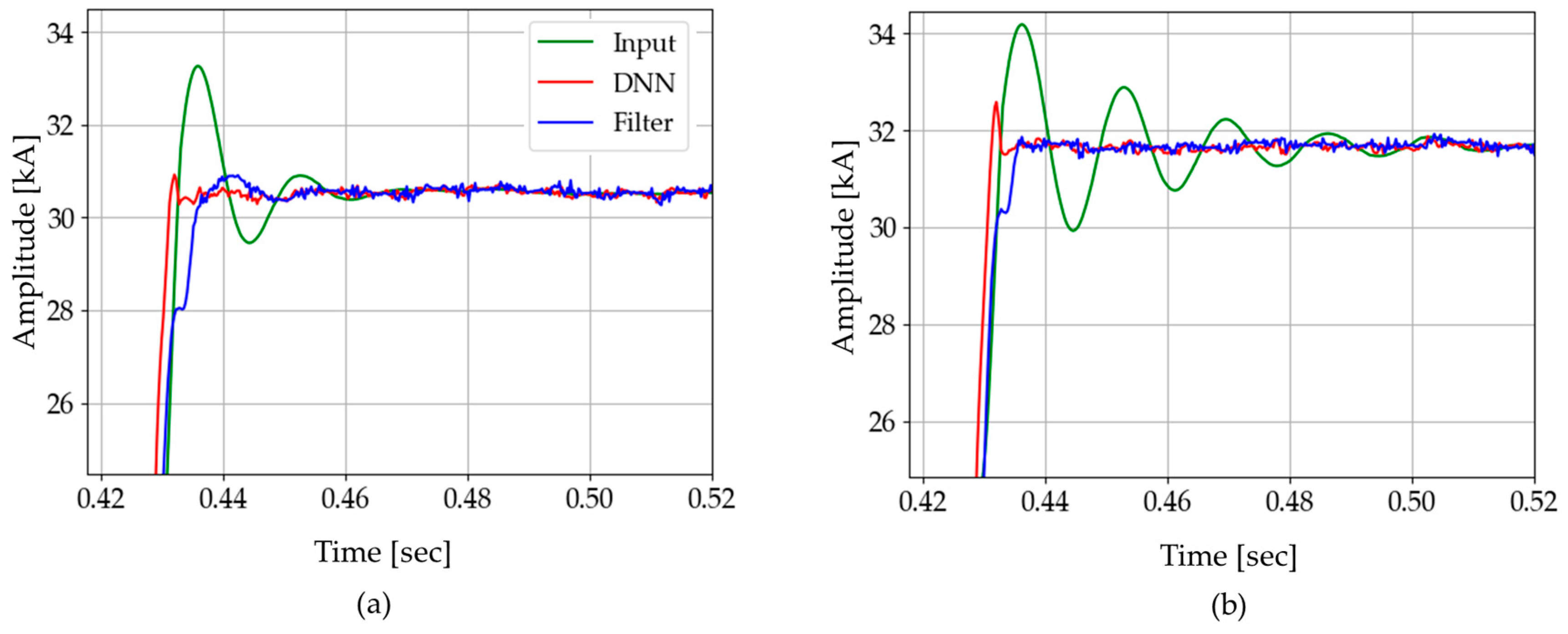
4.2. Case Study
4.2.1. Case A (Line to Line Fault)
- Voltage level: 154 kV
- Time constant: 0.0210 s
- Harmonics: 2nd = 11%, 3rd = 7%, 4th = 3%, 5th = 0.5%
- Noise: 25 dB
- Fault type: line to line fault (phase A and phase B short circuit)
- Fault inception angle: 30°
4.2.2. Case B (Different Power System Situation)
- Voltage level: 22.9 kV
- Time constant: 0.0402 s
- Harmonics: 2nd = 18%, 3rd = 12%, 4th = 8%, 5th = 4%
- Noise: 25 dB
- Fault type: single line to ground fault
- Fault inception angle: 0°
4.2.3. Case C (Different Power System Situation)
- Voltage level: 345 kV
- Time constant: 0.034 s
- Harmonics: 2nd = 12%, 3rd = 4%, 4th = 2%, 5th = 0.2%
- Noise: 25 dB
- Fault type: single line to ground fault (fault resistance 1 ohm)
- Fault inception angle: 0°
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, J.S.; Hwang, S.-H. DC Offset Error Compensation Algorithm for PR Current Control of a Single-Phase Grid-Tied Inverter. Energies 2018, 11, 2308. [Google Scholar] [CrossRef]
- Jyh-Cherng, G.; Sun-Li, Y. Removal of DC offset in current and voltage signals using a novel Fourier filter algorithm. IEEE Trans. Power Deliv. 2000, 15, 73–79. [Google Scholar] [CrossRef]
- Sun-Li, Y.; Jyh-Cherng, G. Removal of decaying DC in current and voltage signals using a modified Fourier filter algorithm. IEEE Trans. Power Deliv. 2001, 16, 372–379. [Google Scholar] [CrossRef]
- Soon-Ryul, N.; Sang-Hee, K.; Jong-Keun, P. An analytic method for measuring accurate fundamental frequency components. IEEE Trans. Power Deliv. 2002, 17, 405–411. [Google Scholar] [CrossRef]
- Yong, G.; Kezunovic, M.; Deshu, C. Simplified algorithms for removal of the effect of exponentially decaying DC-offset on the Fourier algorithm. IEEE Trans. Power Deliv. 2003, 18, 711–717. [Google Scholar] [CrossRef]
- Kang, S.; Lee, D.; Nam, S.; Crossley, P.A.; Kang, Y. Fourier transform-based modified phasor estimation method immune to the effect of the DC offsets. IEEE Trans. Power Deliv. 2009, 24, 1104–1111. [Google Scholar] [CrossRef]
- Nam, S.; Park, J.; Kang, S.; Kezunovic, M. Phasor Estimation in the Presence of DC Offset and CT Saturation. IEEE Trans. Power Deliv. 2009, 24, 1842–1849. [Google Scholar] [CrossRef]
- Silva, K.M.; Kusel, B.F. DFT based phasor estimation algorithm for numerical digital relaying. Electron. Lett. 2013, 49, 412–414. [Google Scholar] [CrossRef]
- Zadeh, M.R.D.; Zhang, Z. A New DFT-Based Current Phasor Estimation for Numerical Protective Relaying. IEEE Trans. Power Deliv. 2013, 28, 2172–2179. [Google Scholar] [CrossRef]
- Rahmati, A.; Adhami, R. An Accurate Filtering Technique to Mitigate Transient Decaying DC Offset. IEEE Trans. Power Deliv. 2014, 29, 966–968. [Google Scholar] [CrossRef]
- Silva, K.M.; Nascimento, F.A.O. Modified DFT-Based Phasor Estimation Algorithms for Numerical Relaying Applications. IEEE Trans. Power Deliv. 2018, 33, 1165–1173. [Google Scholar] [CrossRef]
- Nam, S.-R.; Kang, S.-H.; Sohn, J.-M.; Park, J.-K. Modified Notch Filter-based Instantaneous Phasor Estimation for High-speed Distance Protection. Electr. Eng. 2007, 89, 311–317. [Google Scholar] [CrossRef]
- Mahari, A.; Sanaye-Pasand, M.; Hashemi, S.M. Adaptive phasor estimation algorithm to enhance numerical distance protection. IET Gener. Transm. Distrib. 2017, 11, 1170–1178. [Google Scholar] [CrossRef]
- Gopalan, S.A.; Mishra, Y.; Sreeram, V.; Iu, H.H. An Improved Algorithm to Remove DC Offsets From Fault Current Signals. IEEE Trans. Power Deliv. 2017, 32, 749–756. [Google Scholar] [CrossRef]
- Benmouyal, G. Removal of DC-offset in current waveforms using digital mimic filtering. IEEE Trans. Power Deliv. 1995, 10, 621–630. [Google Scholar] [CrossRef]
- Cho, Y.; Lee, C.; Jang, G.; Lee, H.J. An Innovative Decaying DC Component Estimation Algorithm for Digital Relaying. IEEE Trans. Power Deliv. 2009, 24, 73–78. [Google Scholar] [CrossRef]
- Pazoki, M. A New DC-Offset Removal Method for Distance-Relaying Application Using Intrinsic Time-Scale Decomposition. IEEE Trans. Power Deliv. 2018, 33, 971–980. [Google Scholar] [CrossRef]
- Gosselin, P.; Koukab, A.; Kayal, M. Computing the Impact of White and Flicker Noise in Continuous-Time Integrator-Based ADCs. In Proceedings of the 2016 MIXDES—23rd International Conference Mixed Design of Integrated Circuits and Systems, Lodz, Poland, 23–25 June 2016; pp. 316–320. [Google Scholar]
- Nagamine, T.; Seltzer, M.; Mesgarani, N. On the Role of Nonlinear Transformations in Deep Neural Network Acoustic Models. In Proceedings of the INTERSPEECH 2016, San Francisco, CA, USA, 8–12 September 2016; pp. 803–807. [Google Scholar]
- Hu, W.; Liang, J.; Jin, Y.; Wu, F.; Wang, X.; Chen, E. Online Evaluation Method for Low Frequency Oscillation Stability in a Power System Based on Improved XGboost. Energies 2018, 11, 3238. [Google Scholar] [CrossRef]
- Sun-Bin, K.; Sun-Woo, L.; Dae-Hee, S.; Soon-Ryul, N. DC Offset Removal in Power Systems Using Deep Neural Network. In Proceedings of the Innovative Smart Grid Technologies Conference, Washington, DC, USA, 17–20 February 2019; pp. 1–5. [Google Scholar]
- Huang, X.; Hu, T.; Ye, C.; Xu, G.; Wang, X.; Chen, L. Electric Load Data Compression and Classification Based on Deep Stacked Auto-Encoders. Energies 2019, 12, 653. [Google Scholar] [CrossRef]
- Kim, M.; Choi, W.; Jeon, Y.; Liu, L. A Hybrid Neural Network Model for Power Demand Forecasting. Energies 2019, 12, 931. [Google Scholar] [CrossRef]
- Cegielski, M. Estimating of computation time of parallel algorithm of computations of dynamic processes in GPU systems. In Proceedings of the 2015 16th International Conference on Computational Problems of Electrical Engineering (CPEE), Lviv, Ukraine, 2–5 September 2015; pp. 14–16. [Google Scholar]
- IEEE Power and Energy Society. IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems; IEEE Std 519-2014 (Revision of IEEE Std 519-1992); IEEE: Piscataway, NJ, USA, 2014; pp. 1–29. [Google Scholar] [CrossRef]
- Chiorboli, G.; Franco, G.; Morandi, C. Uncertainties in quantization-noise estimates for analog-to-digital converters. IEEE Trans. Instrum. Meas. 1997, 46, 56–60. [Google Scholar] [CrossRef]
- Xie, Y.; Jin, H.; Tsang, E.C.C. Improving the lenet with batch normalization and online hard example mining for digits recognition. In Proceedings of the 2017 International Conference on Wavelet Analysis and Pattern Recognition (ICWAPR), Ningbo, China, 9–12 July 2017; pp. 149–153. [Google Scholar]
- Bilbao, I.; Bilbao, J. Overfitting problem and the over-training in the era of data: Particularly for Artificial Neural Networks. In Proceedings of the 2017 Eighth International Conference on Intelligent Computing and Information Systems (ICICIS), Cairo, Egypt, 5–7 December 2017; pp. 173–177. [Google Scholar]
- Shibata, K.; Yusuke, I. Effect of number of hidden neurons on learning in large-scale layered neural networks. In Proceedings of the 2009 ICCAS-SICE, Fukuoka, Japan, 18–21 August 2009; pp. 5008–5013. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504. [Google Scholar] [CrossRef]
- TensorFlow. API r1.13. Available online: https://www.tensorflow.org/api_docs/python (accessed on 23 October 2018).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2015, arXiv:1412.69802015. [Google Scholar]
- Almotiri, J.; Elleithy, K.; Elleithy, A. Comparison of autoencoder and Principal Component Analysis followed by neural network for e-learning using handwritten recognition. In Proceedings of the 2017 IEEE Long Island Systems, Applications and Technology Conference (LISAT), Farmingdale, NY, USA, 5 May 2017; pp. 1–5. [Google Scholar]
- GE Multili. Manual P/N: 1601-0089-F5 (GEK-106440D); GE Multili: Toronto, ON, Canadan, 2009. [Google Scholar]








| Parameter | Values | ||||
|---|---|---|---|---|---|
| Time constant [ms] | 10 60 | 20 70 | 30 80 | 40 90 | 50 100 |
| Fault inception angle [°] | 0 | 90 | 180 | −90 | |
| 2nd Harmonics ratio [%] | 0 | 10 | 20 | ||
| 3rd Harmonics ratio [%] | 0 | 7 | 14 | ||
| 4th Harmonics ratio [%] | 0 | 5 | 10 | ||
| 5th Harmonics ratio [%] | 0 | 3 | 6 | ||
| SNR [dB] | 25 | 40 | |||
| Parameter | Values | ||
|---|---|---|---|
| Time constant [ms] | 25 | 32 | 47 |
| Fault inception angle [°] | 45 | 92 | 135 |
| 2nd Harmonics ratio [%] | 15 | 18 | |
| 3rd Harmonics ratio [%] | 7 | 9 | |
| 4th Harmonics ratio [%] | 2 | 4 | |
| 5th Harmonics ratio [%] | 0.5 | 1 | |
| SNR [dB] | 25 | ||
| Number of Neurons | Maximum | Average | Standard Deviation |
|---|---|---|---|
| 10 | 263.3774 | 95.0713 | 54.2323 |
| 20 | 125.2946 | 7.5627 | 5.3217 |
| 30 | 34.1716 | 6.5513 | 0.7282 |
| 40 | 17.7876 | 6.5220 | 0.6824 |
| 50 | 11.7860 | 6.5247 | 0.6814 |
| 60 | 14.9845 | 6.5217 | 0.6825 |
| 70 | 22.3760 | 6.5260 | 0.6838 |
| 80 | 17.8318 | 6.5221 | 0.6849 |
| 90 | 26.2250 | 6.5210 | 0.6844 |
| 100 | 13.7827 | 6.5215 | 0.6821 |
| 110 | 15.7016 | 6.5884 | 0.6788 |
| Method | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| Input | 140.956 | 138.495 | 69.277 |
| DNN3 | 15.934 | 16.158 | 17.727 |
| Filter | 17.339 | 17.285 | 20.533 |
| Method | Convergence [ms] | Average [A] | Standard Deviation |
|---|---|---|---|
| Input | 123.362 | 16,659.86 | 289.72 |
| DNN3 | 33.085 | 16,645.36 | 29.28 |
| Filter | 36.253 | 16,648.87 | 43.47 |
| Method | Convergence [ms] | Average [A] | Standard Deviation |
|---|---|---|---|
| Input | 115.907 | 2843.29 | 53.81 |
| DNN3 | 33.127 | 2839.76 | 9.68 |
| Filter | 35.811 | 2840.58 | 13.80 |
| Method | Convergence [ms] | Average [A] | Standard Deviation | |||
|---|---|---|---|---|---|---|
| Resistance | 1 ohm | 0 ohm | 1 ohm | 0 ohm | 1 ohm | 0 ohm |
| Input | 65.631 | 117.102 | 30,588.60 | 31,683.76 | 309.66 | 371.09 |
| DNN3 | 33.121 | 33.091 | 30,588.03 | 31,659.30 | 64.81 | 62.09 |
| Filter | 49.332 | 35.301 | 30,557.72 | 31,675.29 | 176.84 | 108.77 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-B.; Sok, V.; Kang, S.-H.; Lee, N.-H.; Nam, S.-R. A Study on Deep Neural Network-Based DC Offset Removal for Phase Estimation in Power Systems. Energies 2019, 12, 1619. https://doi.org/10.3390/en12091619
Kim S-B, Sok V, Kang S-H, Lee N-H, Nam S-R. A Study on Deep Neural Network-Based DC Offset Removal for Phase Estimation in Power Systems. Energies. 2019; 12(9):1619. https://doi.org/10.3390/en12091619
Chicago/Turabian StyleKim, Sun-Bin, Vattanak Sok, Sang-Hee Kang, Nam-Ho Lee, and Soon-Ryul Nam. 2019. "A Study on Deep Neural Network-Based DC Offset Removal for Phase Estimation in Power Systems" Energies 12, no. 9: 1619. https://doi.org/10.3390/en12091619
APA StyleKim, S.-B., Sok, V., Kang, S.-H., Lee, N.-H., & Nam, S.-R. (2019). A Study on Deep Neural Network-Based DC Offset Removal for Phase Estimation in Power Systems. Energies, 12(9), 1619. https://doi.org/10.3390/en12091619






