Prediction of the Optimal Vortex in Synthetic Jets
Abstract
:1. Introduction
2. Model Description
3. The DMD-Based ROM: A Reduced Order Model Based on HODMD
Algorithm
- Step 1: SVD. With the aim at removing spatial redundancies or noise, SVD is applied to the snapshot matrix (5), aswhere the unit matrix, the diagonal of matrix contains the singular values , and is the reduced snapshot matrix, of dimension . Based on a tolerance (set by the user), it is possible to determine the number of N singular values retained in the previous equation, asAt this step, the spatial complexity of the data J is reduced to a set of N linearly independent vectors, determining the spatial dimension of the system, generally .In the analysis of complex data, SVD is replaced by a high-order singular value decomposition (HOSVD) [38], leading to the called multi-resolution HODMD algorithm. This decomposition organizes the original snapshot matrix in tensor form as , with being the number of velocity components ( and ), for ; and . HOSVD algorithm applies an SVD to the three matrices whose columns are formed by each one of the 3 data variables (similar to the fibers of a tensor). Thus, this method provides the following decomposition for each velocity component l (for simplicity the solution is particularized for a single velocity component)where is a third-order tensor (called the core tensor) and the columns of the matrices , and are known as the modes of the decomposition (two spatial and one temporal modes, respectively). The rank reduction in Equation (7) is then applied to each one of these modes. The temporal modes are used to construct the reduced snapshot matrix. Due to the complexity of the data analyzed in this article, this multi-resolution algorithm is used to construct the DMD-based ROM (see more details about the algorithm in [14]).
- Step 2: the DMD-d algorithm. DMD algorithm [23] is combined with the Takens’ delay embedding theorem [39], providing the following high order Koopman assumption that is applied to the reduced snapshot matrix asThe dynamics of the system is contained in the reduced Koopman operators , , ⋯, . These operators are encompassed into a single matrix. The eigenvalues of such matrix provide the frequencies and growth rates of the DMD expansion (4), and the eigenvectors are used to construct the DMD modes . It is remarkable that for values of , this algorithm is similar to standard DMD [23], providing similar solutions. Nevertheless, in the analysis of complex dynamical system, composed by large number of frequencies, transient modes, or even noisy data, values of will provide accurate approximations of the expansion (4), required to construct a ROM and to predict the attractor (note that the errors grow exponentially with time).
- Step 3: Amplitude calculations and RRMS error. The amplitude weighting the DMD modes are calculated in this step. For proper reconstruction of the original data (interpolation), a good way to calculate the amplitudes is by least squares fitting of the expansion (4). This amplitude will determine the number of M DMD modes retained in the expansion as function of a second tolerance , asOnce the DMD expansion (4) is approximated, the relative root mean square error (RRMSE) is used to quantify the difference between the original data and the approximated solution (4), aswhere represents the Frobenius norm.To minimize this error, the method is applied iteratively. In other words, the algorithm is applied over the solution reconstructed in (4), obtaining new reconstructions, until the number of singular values N is maintained similar in two consecutive iterations. It is possible to download a MATLAB [40] version of the HODMD algorithms in Ref. [41].
4. The DMDlr-ROM: A Low-Rank Spatial Approximation for the Data-Driven ROM
- Stage 1: rank reduction and generation of the new snapshot matrix. SVD is applied to reduce the spatial dimension of the original snapshots. In contrast to Step 1 from HODMD algorithm, SVD is applied separately to each one of the snapshots composing the snapshot matrix (5). Thus, the information contained in each snapshot is organized in tensor form as for and . For each snapshot k the SVD leads aswhere the dimension of is , the dimension of is and the dimension of is . This decomposition has been carried out using the function svd in MATLAB [40]. The spatial matrices and contain information related to the streamwise and radial spatial components, respectively, and is the matrix containing the singular values . The spatial matrices are weighted with the square root of the singular values asandbeing the matrix composed by the square root of the singular values .The same process is repeated for each one of the K snapshots of the initial snapshot matrix (5) for each velocity component and . Two new snapshot matrices are constructed with the results previously obtained, the called X-snapshots defined asand the called Y-snapshots, defined asIt is remarkable that matrices (15) and (16) are composed by sub-matrices of dimension and , respectively, thus the most efficient way to organize this information is in tensor form as and , being the variable defining the number of singular values, for . For each velocity component l the previous expressions lead as and .The reduction of memory size in the previous snapshot matrices is dependent on the number of singular values N retained in each one of such matrices. To ensure the proper performance of the model proposed, N can be determined according to a certain tolerance, as in Equation (7), or simply by identifying changes in the tendency of the singular values obtained in the SVD analysis carried out for each snapshot.
- Stage 2: modal decomposition using HODMD. The multi-resolution HODMD algorithm is applied to each one of the tensors obtained in the previous step, and . The following DMD expansion is obtained for the X-snapshots (for simplicity particularized of one velocity component)and for the Y-snapshots (for one velocity component)where and are the DMD modes retained for each expansion, and are the amplitudes and and are the DMD modes. Please note that the number of modes composing each expansion can be different, meaning that the amplitude of each mode describing the dynamics of the system varies in each analysis.
- Stage 3: temporal predictions and data reconstruction. The attractor is predicted by simply adjusting the time as in (17) and (18). Then, the new data predicted by the previous models are reconstructed as (for each velocity component)in matrix form defined aswhere the dimension of is and the dimension of is .As previously mentioned, the number of DMD modes defining each spatial matrix can be different, since the amplitude of the most relevant flow dynamics varies in the spatial domain. Thus, for some groups of tolerances , it is possible obtaining DMD modes defining expansion (17) and modes in expansion (18). Similarly, for some tolerances it is possible that and . Depending on the complexity of the data analyzed, and the influence of the global dynamics related to each spatial direction, a good alternative to reconstruct the solution predicted in time is using the following expansionwhere is the tensor obtained in Stage 1 of this algorithm. Similarly, the predicted solution could be reconstructed aswhere is the tensor obtained in Stage 1.
5. Generating Artificially the Optimal Vortex: A Way to Predict the Perfect Set-Up in Synthetic Jets
6. A ROM to Predict Spatio-Temporal Flow Structures in Synthetic Jets
6.1. Predictions Using the DMD-Based ROM
6.2. Efficient Computations Using the DMDlr-ROM
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Bandyopadhyay, P.R. Trends in Biorobotics Autonomous Undersea Vehicles. IEEE J. Ocean. Eng. 2005, 30, 109–139. [Google Scholar] [CrossRef]
- Nawroth, J.C.; Lee, H.; Feinberg, A.W.; Ripplinger, C.M.; McCain, M.L.; Grosberg, A.; Dabiri, J.O.; Parker, K.K. A tissue-engineered jellyfish with biomimetic propulsion. Nat. Biotechnol. 2012, 30, 792–797. [Google Scholar] [CrossRef]
- Ajith, A.M.; Sachin, K.S.; Sudheer, A.P. Design, fabrication and analysis of a bio-inspired tuna Fish Robot. ACM Int. Conf. Proc. Ser. 2015. [Google Scholar] [CrossRef]
- Aminur, R.B.A.M.; Hemakumar, B.; Prasad, M.P.R. Robotic Fish Locomotion Propulsion in Marine Environment: A Survey. In Proceedings of the 2nd International Conference on Energy, Power and Environment: Towards Smart Technology, Shillong, India, 1–2 June 2018. [Google Scholar]
- Buren, T.V.; Floryan, D.; Smits, A.J. Bio-inspired underwater propulsors. arXiv 2018, arXiv:1801.09714v2. [Google Scholar]
- Gharib, M.; Rambod, E.; Shariff, K. A universal time scale for vortex ring formation. J. Fluid Mech. 1998, 360, 121–140. [Google Scholar] [CrossRef]
- Glezer, A.; Amitay, M. Synthetic jets. Annu. Rev. Fluid Mech. 2002, 34, 503–529. [Google Scholar] [CrossRef]
- DeMont, E.; Gosline, J. Mechanics of jet propulsion in the hydromedusan jellyfish, polyorchis penicillatus. J. Exp. Biol. 1998, 134, 347–361. [Google Scholar]
- Wang, H.; Menon, S. Fuel-air mixing enhancement by synthetic microjets. AIAA J. 2001, 39, 2308–2319. [Google Scholar] [CrossRef]
- Pavlova, A.; Amitay, M. Electronic cooling using synthetic jet impingement. J. Heat Transf. 2006, 128, 897–907. [Google Scholar] [CrossRef]
- Cattafesta, L.M.; Sheplak, M. Actuators for active flow control. Annu. Rev. Fluid Mech. 2010, 43, 247–272. [Google Scholar] [CrossRef]
- Lin, C.-Y.; Lin, J.L. Flow characteristics of two-dimensional synthetic jets under diaphragm resonance excitation. Aircraft Eng. Aerosp. Technol. 2019. [Google Scholar] [CrossRef]
- Zong, H.; Kotsonis, M. Formation, evolution and scaling of plasma synthetic jets. J. Fluid Mech. 2018, 837, 147–181. [Google Scholar] [CrossRef]
- Le Clainche, S.; Vega, J.M.; Soria, J. Higher Order Dynamic Mode Decomposition for noisy experimental data: Flow structures on a Zero-Net-Mass-Flux jet. Exp. Therm. Fluid Sci. 2017, 88, 336–353. [Google Scholar] [CrossRef]
- Carter, J.E.; Soria, J. The evolution of round zero-net-mass-flux jets. J. Fluid Mech. 2002, 472, 167–200. [Google Scholar]
- Dabiri, J.O.; Collin, S.P.; Karija, K.; Costello, J.H. A wake-based correlate of swimming performance and foraging behaviour in seven co-occurring jellyfish species. J. Exp. Biol. 2010, 213, 1217–1225. [Google Scholar] [CrossRef]
- Mu, H.; Yan, Q.; Wei, W.; Sullivan, P.E. Unsteady simulation of a synthetic jet actuator with cylindrical cavity using a 3-D lattice Boltzmann method. J. Aerosp. Eng. 2018, 2018, 9358132. [Google Scholar] [CrossRef]
- Ziadé, P.; Feero, M.A.; Sullivan, P.E. A numerical study on the influence of cavity shape on synthetic jet performance. Int. J. Heat Fluid Flow 2018, 74, 187–197. [Google Scholar] [CrossRef]
- Holman, R.; Utturkar, Y.; Mittal, R.; Smith, B.L.; Cattafesta, L. Formation Criterion for Synthetic Jets. AIAA J. 2005, 43, 2110–2116. [Google Scholar] [CrossRef]
- Dabiri, J.O. Optimal Vortex Formation as a Unifying Principle in Biological Propulsion. Annu. Rev. Fluid Mech. 2009, 41, 17–33. [Google Scholar] [CrossRef]
- Krueger, P.S. The Significance of Vortex Ring Formation and Nozzle Exit Overpressure to Pulsatile Jet Propulsion. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2001. [Google Scholar]
- Bandyopadhyay, P.R.; Beal, D.N. Exception to Triantafyllou’s Strouhal number rule of flapping. In Proceedings of the American Physical Society, 60th Annual Meeting of the Divison of Fluid Dynamics, Salt Lake, UT, USA, 18–20 November 2007. [Google Scholar]
- Schmid, P. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Le Clainche, S.; Vega, J.M. Higher Order Dynamic Mode Decomposition. SIAM J. Appl. Dyn. Syst. 2017, 16, 882–925. [Google Scholar] [CrossRef]
- Le Clainche, S.; Vega, J.M. Higher order dynamic mode decomposition to identify and extrapolate flow patterns. Phys. Fluids 2017, 29, 084102. [Google Scholar] [CrossRef]
- Le Clainche, S.; Ferrer, E. A Reduced Order Model to Predict Transient Flows around Straight Bladed Vertical Axis Wind Turbines. Energies 2018, 11, 566. [Google Scholar] [CrossRef]
- Kou, J.; Le Clainche, S.; Zhang, W. A reduced-order model for compressible flows with buffeting condition using higher order dynamic mode decomposition with a mode selection criterion. Phys. Fluids 2018, 30, 016103. [Google Scholar] [CrossRef]
- Vinuesa, R.; Schlatter, P.; Malm, J.; Mavriplis, C.; Henningson, D.S. Some mathematical notes on three-mode factor analysis. Psikometrica 1966, 31, 279–311. [Google Scholar]
- Soria, J. Experimental Studies of the Near-Field Spatio-Temporal Evolution of Zero-Net-Mass-Flux (ZNMF) Jets. Fluid Mech. Its Appl. 2015, 111, 61–92. [Google Scholar]
- Le Clainche, S.; Viturro, M.; Vega, J.M.; Soria, J. Near and far field laminar flow structures in a zero-net-mass-flux jet. J. Fluid Mech. 2019. submitted. [Google Scholar]
- Viturro, M.; Le Clainche, S.; Vega, J.M.; Soria, J. The influence of the cavity in the flow structures of a zero-net-mass-flux jet. In Proceedings of the AIAA Fluid Dynamics Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Fischer, P.F.; Lottes, J.W.; Kerkemeier, S.G. Nek5000. Available online: https://nek5000.mcs.anl.gov (accessed on 12 December 2018).
- Ohlsson, J.; Schlatter, P.; Fischer, P.F.; Henningson, D.S. Direct numerical simulation of separated flow in a three-dimensional diffuser. J. Fluid Mech. 2010, 650, 307–381. [Google Scholar] [CrossRef]
- Kotapati, R.B.; Mittal, R.; Cattafesta, L.N., III. Numerical study of a transitional synthetic jet in quiescent external flow. J. Fluid Mech. 2007, 581, 287–321. [Google Scholar] [CrossRef]
- Le Clainche, S.; Moreno-Ramos, R.; Taylor, P.; Vega, J.M. New robust method to study flight flutter testing. J. Aircraft 2019, 56, 336–343. [Google Scholar] [CrossRef]
- Le Clainche, S.; Lorente, L.; Vega, J.M. Wind Predictions Upstream Wind Turbines from a LiDAR Database. Energies 2018, 11, 543. [Google Scholar] [CrossRef]
- Le Clainche, S.; Pérez, J.M.; Vega, J.M. Spatio-temporal flow structures in the three-dimensional wake of a circular cylinder. Fluid Dyn. Res. 2018, 50, 051406. [Google Scholar] [CrossRef]
- Tucker, L.R. Direct numerical simulation of the flow around a wall-mounted square cylinder under various inflow conditions. J. Turbulence 2015, 16, 555–587. [Google Scholar]
- Takens, F. Detecting Strange Attractors in Turbulence; Lecture Notes in Mathematics; Rand, D.A., Young, L.-S., Eds.; Springer: Berlin, Germany, 1981; pp. 366–381. [Google Scholar]
- MATLAB. Available online: www.mathworks.com (accessed on 12 December 2018).
- Code in Matlab: Higher Order Dynamic Mode Decomposition (HODMD). Available online: https://github.com/LeClaincheVega/ (accessed on 12 December 2018).


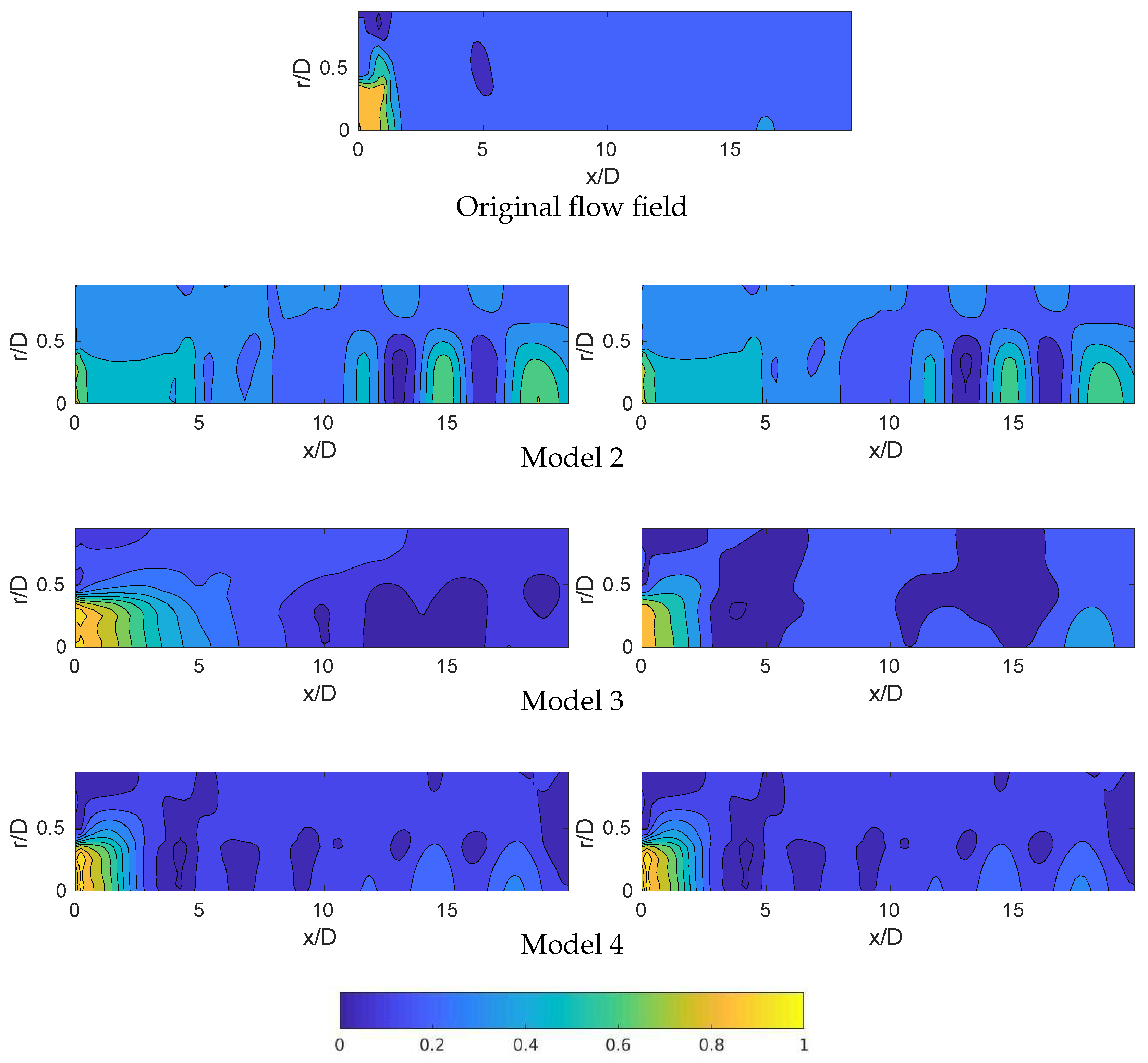


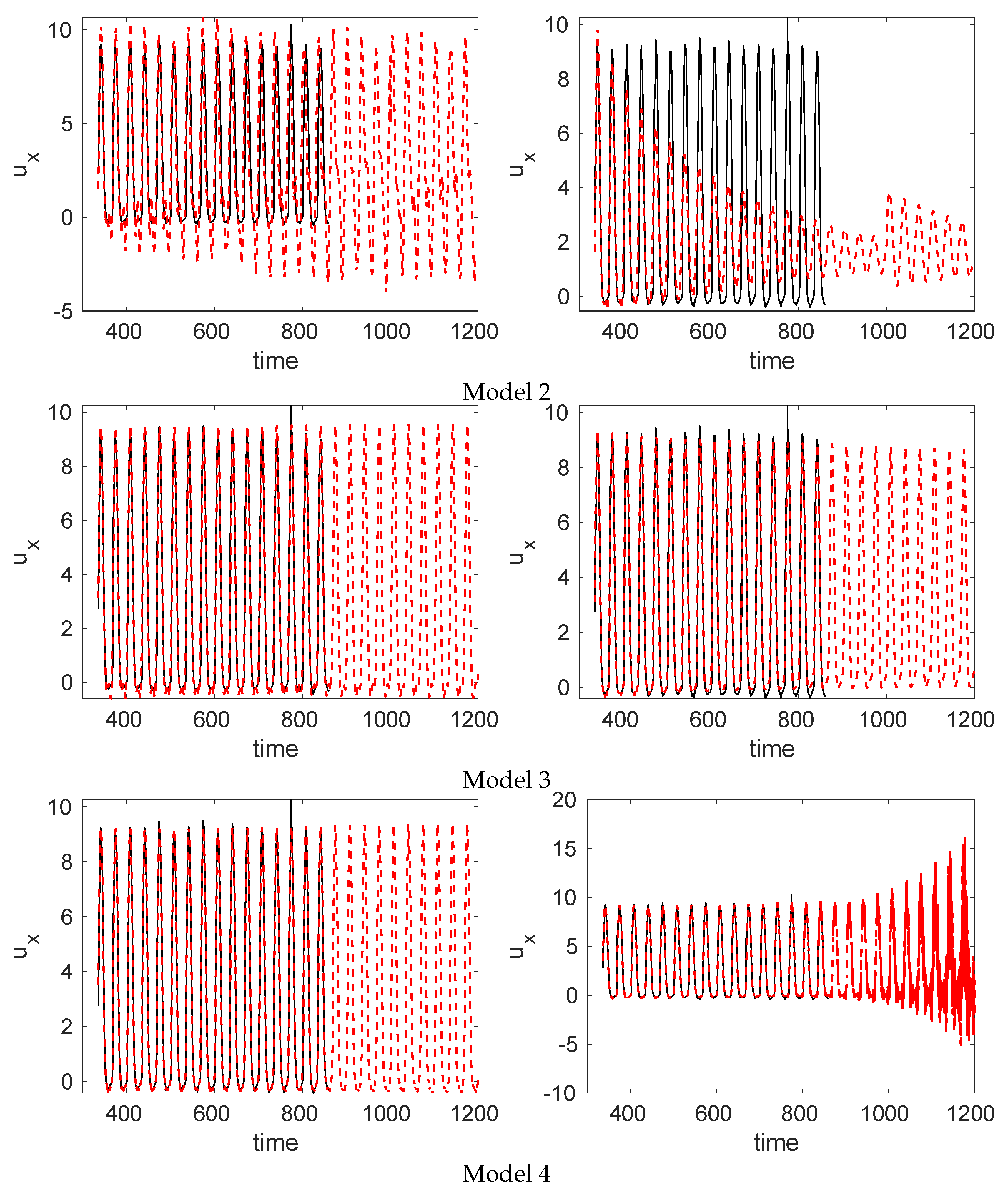
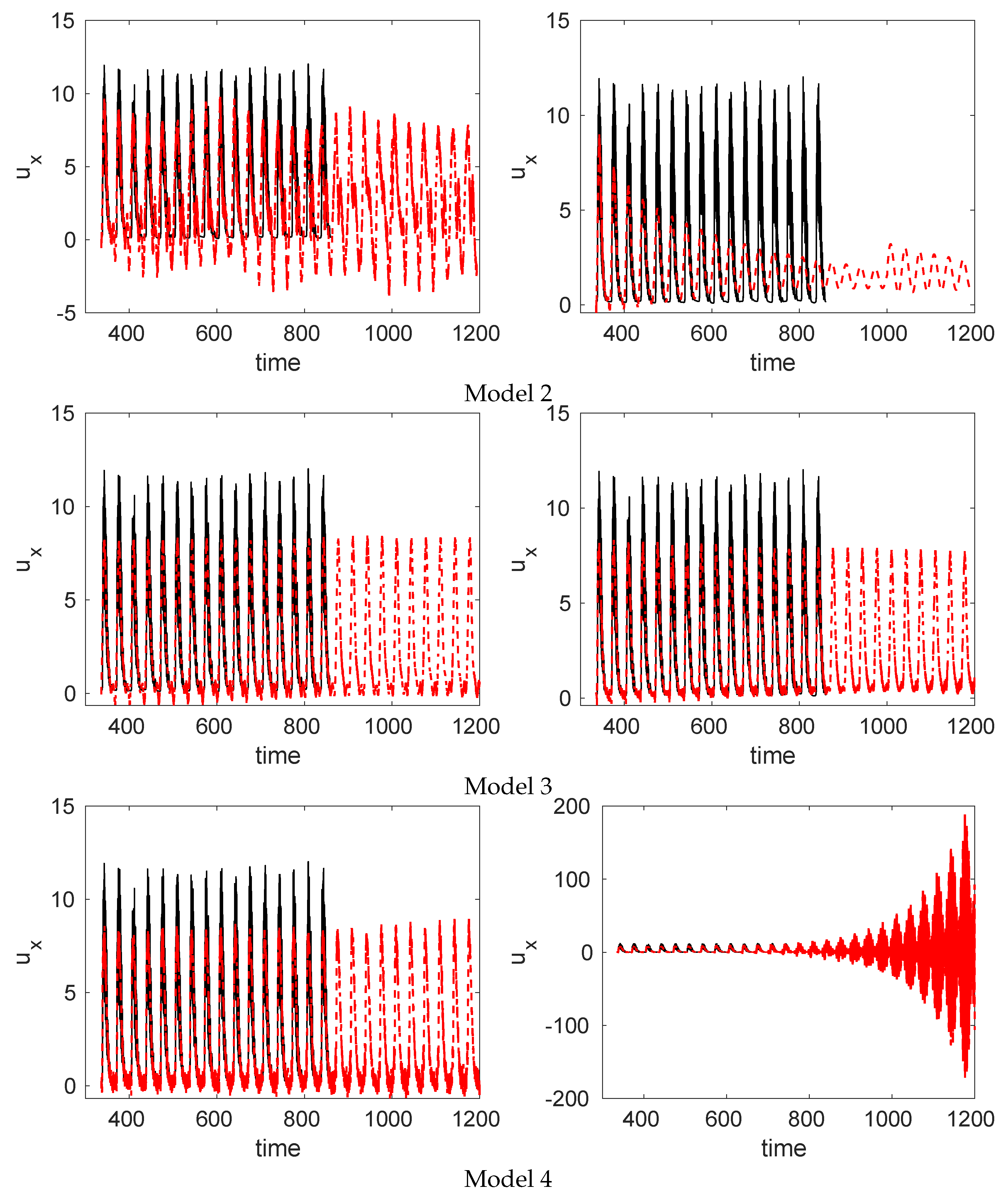





| Model | K | d | M | = 0 | RRMSE-N | RRMSE-F | RRMSE | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 625 | 1 | 344 | 13 | 0 (0) | Yes | ||||||
| No | 1 | 1 | 1 | |||||||||
| 2 | 1249 | 2 | 688 | 21 | 7 (0) | Yes | ||||||
| No | ||||||||||||
| 3 | 1873 | 3 | 1032 | 31 | 31 (13) | Yes | ||||||
| 31 | No | |||||||||||
| 13 | No | |||||||||||
| 4 | 3121 | 5 | 5 | 1720 | 57 | 57 (29) | Yes | |||||
| 57 | No | |||||||||||
| 29 | No |
| Model 3 | Eq. | RRMSE-N | RRMSE-F | RRMSE | |
|---|---|---|---|---|---|
| A | (21) | Yes | |||
| No | |||||
| B | (22) | Yes | |||
| No | |||||
| C | (19) | Yes | |||
| No |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le Clainche, S. Prediction of the Optimal Vortex in Synthetic Jets. Energies 2019, 12, 1635. https://doi.org/10.3390/en12091635
Le Clainche S. Prediction of the Optimal Vortex in Synthetic Jets. Energies. 2019; 12(9):1635. https://doi.org/10.3390/en12091635
Chicago/Turabian StyleLe Clainche, Soledad. 2019. "Prediction of the Optimal Vortex in Synthetic Jets" Energies 12, no. 9: 1635. https://doi.org/10.3390/en12091635
APA StyleLe Clainche, S. (2019). Prediction of the Optimal Vortex in Synthetic Jets. Energies, 12(9), 1635. https://doi.org/10.3390/en12091635









